0 引言
在现代工业中，过程监测是一种被广泛采用的提高过程安全性和产品质量的技术。由于分布式控制系统(distributed control system, DCS)的广泛应用,大量的数据被采集，多元统计过程控制(multivariate statistical process control, MSPC)方法发展迅速[1]。
PCA作为最基本的MSPC方法，已有很多研究成果。然而，如何选择主成分并利用主成分信息进行监测仍然是一个开放的问题。主成分选择中使用最广泛的方法是累计方差贡献率法(cumulative percentage variance, CPV)，选择具有较大方差的成分来构造主成分空间，剩余具有较小方差的成分构成残差空间[2]。不过这种方法不是以过程监测为目的设计出来的，故障发生时表现出的变异性不一定体现在方差信息较大的主成分，在主成分空间和残差空间都有可能体现，这会引起变异特征信息分散，而且每个子空间内的大量正常信息可能淹没变异特征信息。
已经有许多研究人员专门为过程监测提出了选择主成分的方法。Jiang等[3]提出了一种敏感PCA(sensitive principal component analysis, SPCA)方法，该方法直接检测每个主成分上T2统计量的变化率，并在线选择T2统计量变化率较大的主成分作为敏感主成分进行过程监测。Jiang等[4]提出了一种实时重组的PCA模型，通过核密度估计在线评估主成分的变异性，将具有故障检测的主成分集中到一个子空间进行监测。这两种方法客观地将大部分变异特征信息集中到一个子空间，不过只集中了变异性较大的主成分，忽略了变异性小的主成分，而部分变异性小的主成分也是有利于故障监测的。Jiang等[5]提出了一种数据驱动的多块PCA方法,该方法利用互信息(mutual information, MI)自动划分块，每个变量块通过支持向量数据描述(support vector data description, SVDD)监测，并将全部块中的结果集成在一起。Tong等[6]根据变量与主成分子空间和残差子空间的相关性或不相关性，将变量分成4个子空间，提出了一种4子空间贝叶斯(four-subspace construction and Bayesian inference, FSCB)监测方法。江伟等[7]提出了一种基于混合分块DMICA-PCA的过程监控方法。该方法先利用已知的部分过程知识对变量初步分块, 再利用各分块变量之间改进的广义Dice′s系数(modified general dice′s coefficient, MGDC)进行进一步的分块。然后采用DMICA-PCA方法对每个子块进行建模，通过加权方法求得总的联合指标进行监测。这些多块方法通常分解过程变量空间或成分空间，以简化监测过程变量间的复杂度。
PCA模型中载荷矩阵的向量体现了变量对主成分的影响，将其定义为对应主成分的特征向量。如果对主成分有重要影响的过程变量发生变异，相应的主成分也会具有变异特征，因此，具有相似特征向量的主成分具有相似的变异特征，将它们集中在同一子空间中监测有利于减少变异特征的分散。而在离线状态下选择的主成分不能保证具有变异特征，因此，根据在线信息选择具有变异特征的主成分作为特征成分并将与其具有相似变异特征的主成分集中监测可以提高监测效果[8]。笔者提出一种在线自适应挑选主成分的方法即自适应主成分分析方法(APCA)。首先利用载荷矩阵计算各成分与其余成分间特征向量的欧氏距离，为每个成分选择出与其欧氏距离较小的成分构成该成分的成分子空间；其次通过核密度估计计算出在线成分的变异概率，挑选变异概率最高的主成分作为CC；最后利用CC对应的子空间进行监测。
1 基于PCA的过程监测
PCA是应用最广泛的多变量过程监测算法。过程的数据矩阵表示为.∈.n×m(n为样本个数，m为测量变量个数)，先对该数据矩阵进行归一化处理，然后利用PCA方法建立模型，可以表示为[9]：
(1)
式中：
为主成分得分和其载荷矩阵；
为残差得分和其载荷矩阵；.为PCA残差矩阵；
中包含k个主成分个数，选取主成分可采用累积方差贡献率法。通过对.的协方差矩阵进行特征值或者奇异值分解可以得到主成分得分、残差得分和相应的载荷矩阵，即
∑=.T./(n-1);
(2)
(3)
(4)
(5)
.=diagλi，
(6)
式中：λi(i=1,2,…,m)为协方差矩阵的m个特征值，也就是主成分得分矩阵
和残差得分矩阵
每列的方差。经过PCA分解之后，原来的m维变量空间就被k维主成分空间和残差空间所代替。对于数据样本.，主成分空间的T2统计量可以构造为：
(7)
残差空间的SPE统计量被构造为:
(8)
SPE=.T.,
(9)
式中：.是残差向量。
T2和SPE统计量的控制限为:
(10)
(11)
(12)
(13)
式中：α表示显著水平；a和v分别表示样本SPE的均值和方差[10]。
2 基于APCA的过程监测
具有相似特征向量的主成分有相似的变异特征，应将其集中到一个子空间。基于APCA的过程监测以此建立多个成分子空间模型，根据在线信息挑选变异概率最高的主成分作为CC，以CC对应的成分子空间作为ACS(adaptive component space, ACS)构造T2统计量进行监测。本节对所提方法进行了详细描述。
2.1 APCA方法
2.1.1 子空间模型
假设有历史正常数据.∈.n×m,其中n是每个变量的样本数量，m是过程变量的数量。对过程数据.进行归一化处理后，利用奇异值分解得到主成分：
.=[t1,t2,…,tm]。
(14)
.∈.n×n为载荷矩阵，载荷矩阵.每一列都是载荷向量，可以表示为:
.=[.1,.2,…,.i,…,.m]。
(15)
采用主成分载荷向量之间的欧氏距离d来度量相似程度；
dij=(.i-.j)T(.i-.j);
(16)
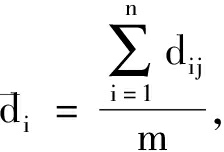
(17)
式中:i=1,2,…,m；j=1,2,…,m；dij表示第i和第j个主成分的欧氏距离；
为第i个主成分与其余主成分的欧氏距离的平均值。子空间设计结果为：
如果
那么
(18)
式中：.j为第j个成分；.i为第i个子空间；
为第i个子空间的载荷矩阵。
2.1.2 特征成分的选择
为选出具有变异特征的主成分，利用核密度估计每个主成分的变异概率，挑选变异概率最高的成分作为特征成分。具体如下：
对于在线数据样本.∈.m×1，进行归一化处理后，映射到主成分空间得到在线主成分得分
利用主成分.通过核密度估计可求出在线样本各个主成分概率密度
(19)
根据当前样本每一主成分对应的概率密度，计算第i个成分对应的变异概率fi和主成分的变异概率f：
(20)
f=[f1,f2,…,fm]。
(21)
选取变异概率最大的主成分作为特征成分CC：
如果 fα=max(f1,f2,…,fm)，
那么 CC=tα。
(22)
2.1.3 构造T2统计量
在线信息的变异特征主要集中在ACS中，构造T2统计量用于监测工业过程。特征成分对应的自适应子空间为.α，.α为自适应子空间.α的载荷矩阵。T2统计量构造如下：
T2=.αT.α(Λ)-1.αT.α。
(23)
2.2 方法实现
离线建模：
(1)得到正常运行观测数据.∈.n×m，通过各变量的均值和方差对其进行归一化。
(2)对归一化后的数据进行PCA分解。
(3)利用载荷矩阵计算各成分间载荷向量的欧氏距离来表示各主成分间的相似程度。
(4)为每个主成分挑选相似特征向量的主成分，并建立子空间模型。
在线监测：
(1)使用训练数据的平均值和方差来归一化当前时间点数据，并将归一化后的当前数据映射到主成分空间。
(2)通过核密度估计法计算每个主成分对应的概率密度，选概率密度小的成分为CC。
(3)挑选特征成分对应的子空间作为ACS。
(4)计算ACS的T2统计量和T2控制限。如果T2统计量超出控制限，则表明当前数据发生故障，发出警报；否则当前数据正常，继续运行。
基于APCA的化工过程监测方法流程图如图1所示。
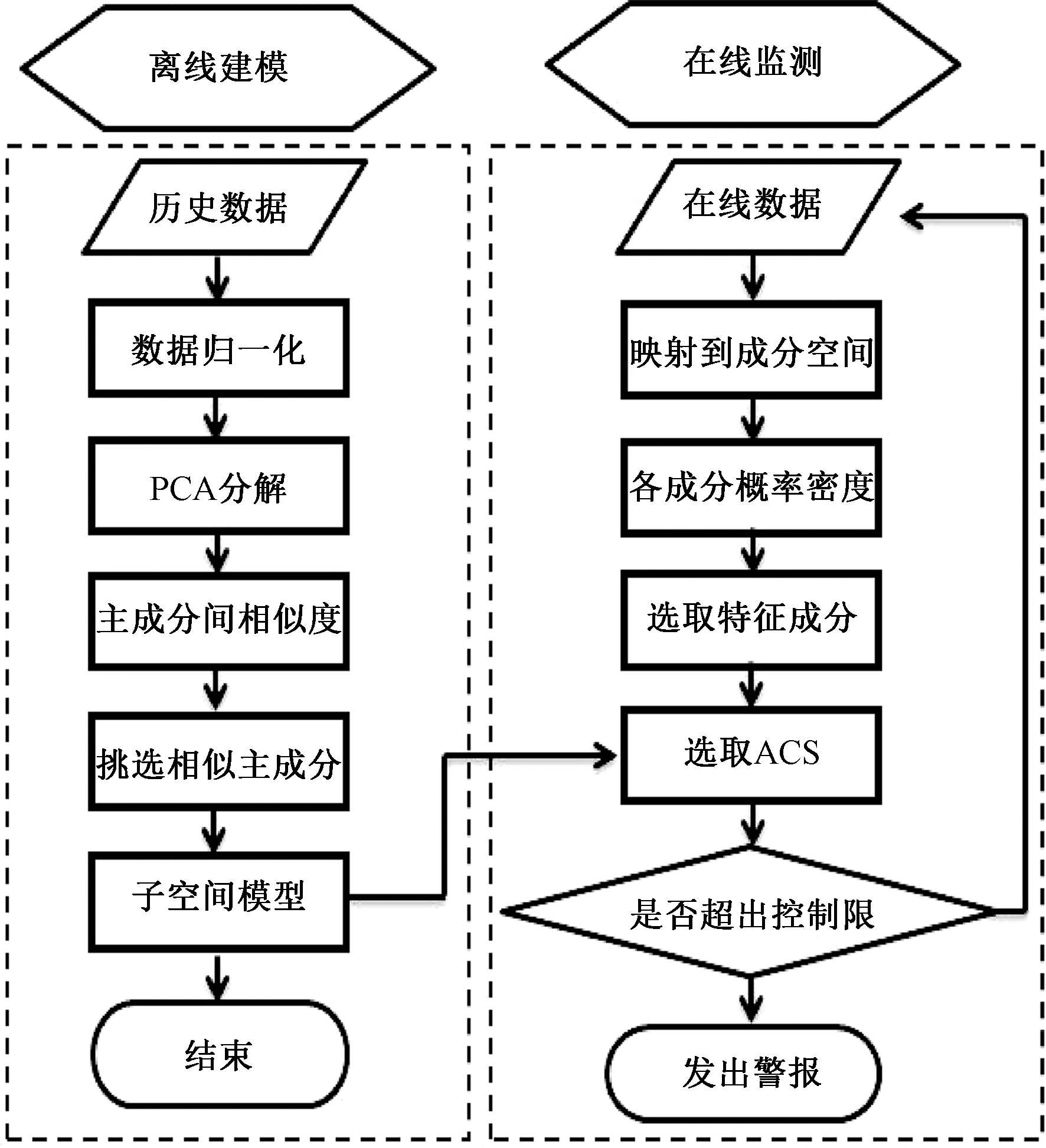
图1 APCA过程监测流程图
Figue 1 APCA process monitoring flow chart
3 TE仿真实验研究
TE过程有22个过程变量和12个操作变量，还可以仿真模拟21种不同的故障类型[11-12]。笔者选择其中的33个变量作为监测变量。为了性能评估，生成21个故障场景。每个故障场景有960个样本组成，故障场景中所有故障在161样本点引入[13]。
分别利用PCA和APCA方法对TE过程的21种故障进行监测，计算漏报率，并与SPCA和FSCB进行比较，结果如表1所示，其中最小的漏报率已用黑体标出。其中，故障1、2、4、6、7、8、12、13、14中每种监控方法的检测率几乎相同，因为故障幅度非常大，以至于所有这些方法都可以检测到几乎100%的故障。而故障3、9和15监测难度太大，因此，这些故障在本研究中没有被考虑。对于故障5、10、16、19、20，基于APCA的方法监测效果相对于其他方法有显著的提升。具体地，故障5、16、19的详细监测效果分别在图2、3、4中给出。从图中可以看出，APCA对这些故障有更高的灵敏度。
表1 TE过程APCA、PCA、SPCA和 FSCB漏报率比较
Table 1 Comparison of missing alarm rates of APCA, PCA, SPCA and FSCB in TE process
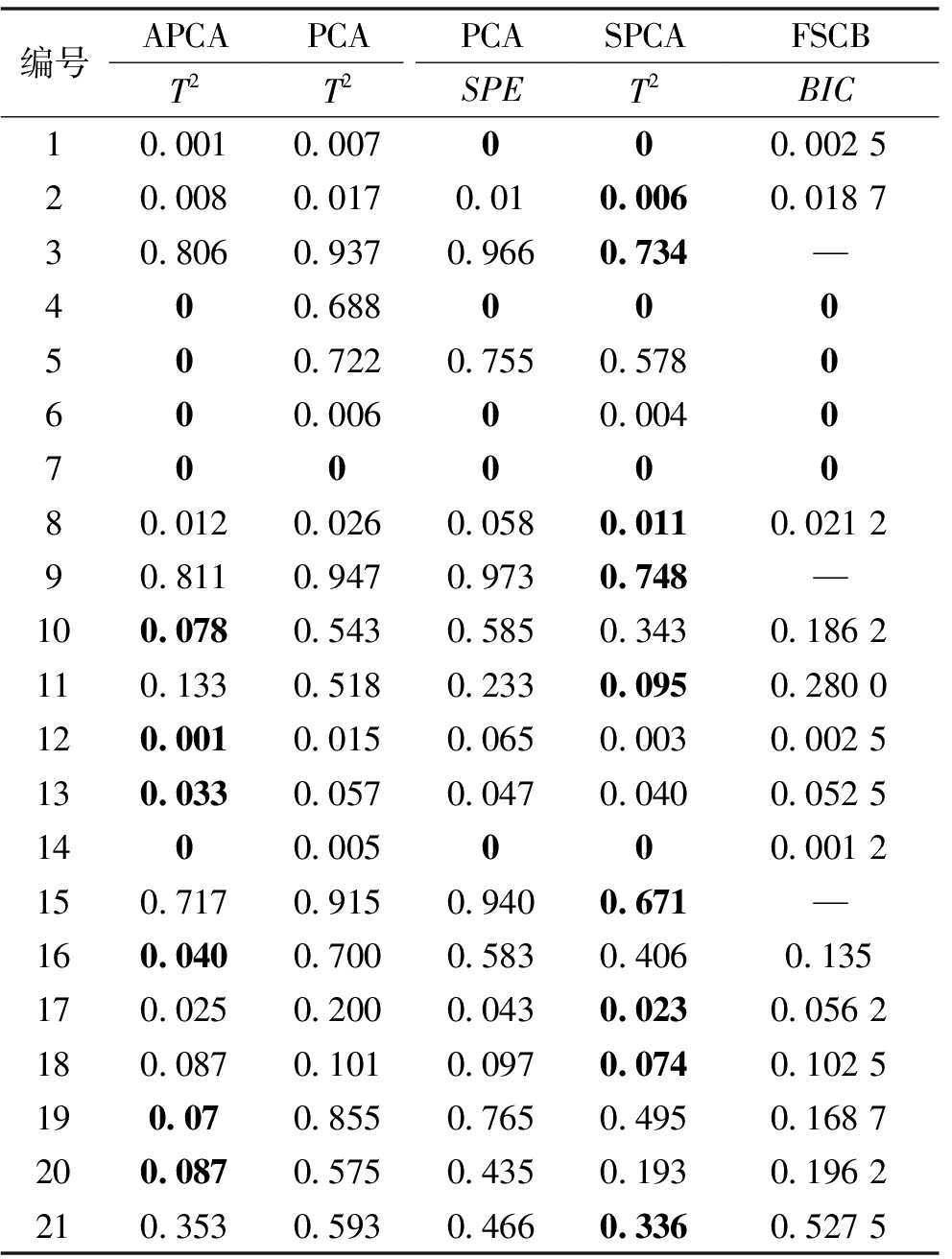
编号APCAPCAPCASPCAFSCBT2T2SPET2BIC10.0010.007000.002520.0080.0170.010.0060.018730.8060.9370.9660.734—400.688000500.7220.7550.5780600.00600.004070000080.0120.0260.0580.0110.021290.8110.9470.9730.748—100.0780.5430.5850.3430.1862110.1330.5180.2330.0950.2800120.0010.0150.0650.0030.0025130.0330.0570.0470.0400.05251400.005000.0012150.7170.9150.9400.671—160.0400.7000.5830.4060.135170.0250.2000.0430.0230.0562180.0870.1010.0970.0740.1025190.070.8550.7650.4950.1687200.0870.5750.4350.1930.1962210.3530.5930.4660.3360.5275
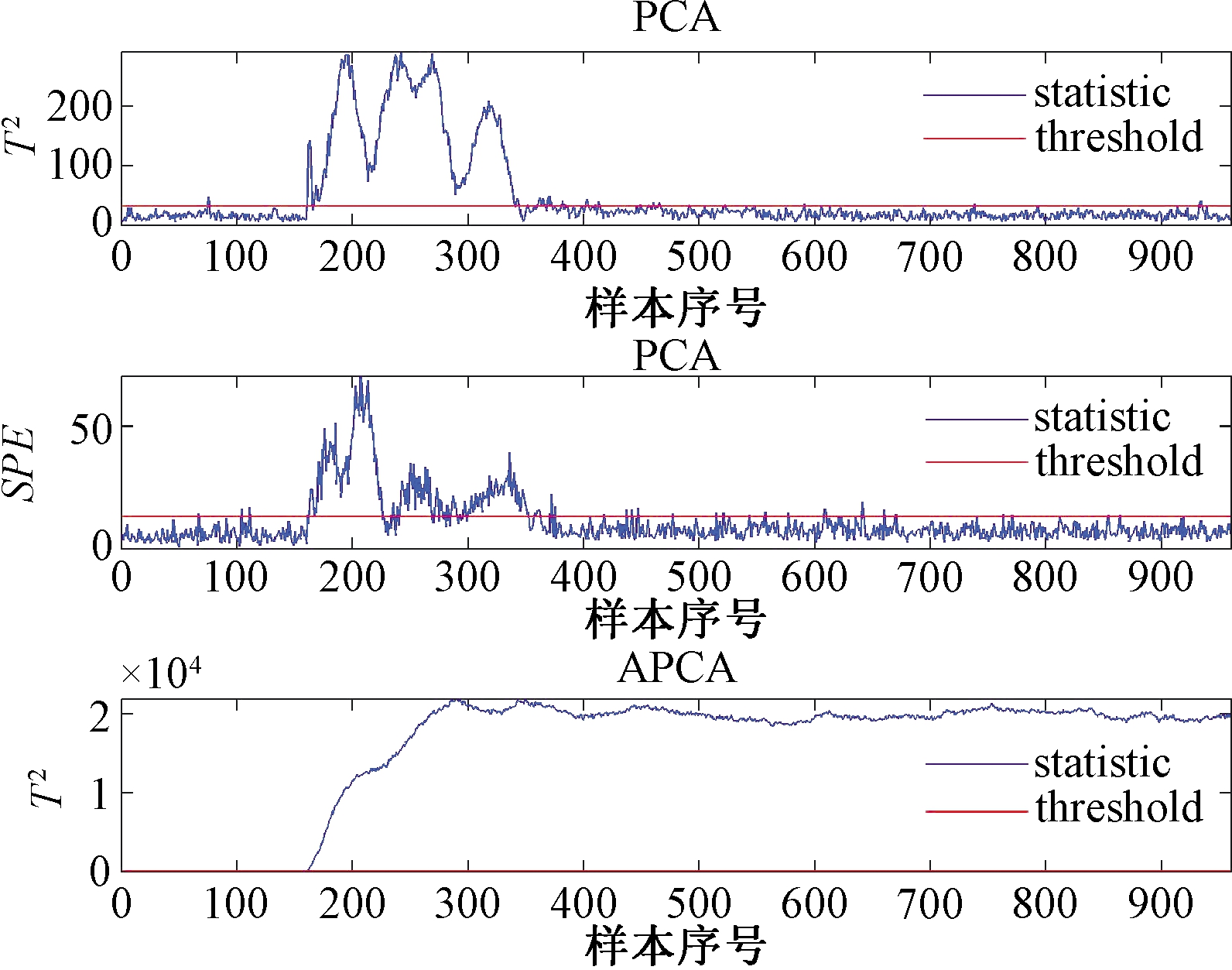
图2 TE过程中PCA和APCA对故障5的监测效果
Figue 2 Monitoring results of PCA and APCA for case 5 in TE process
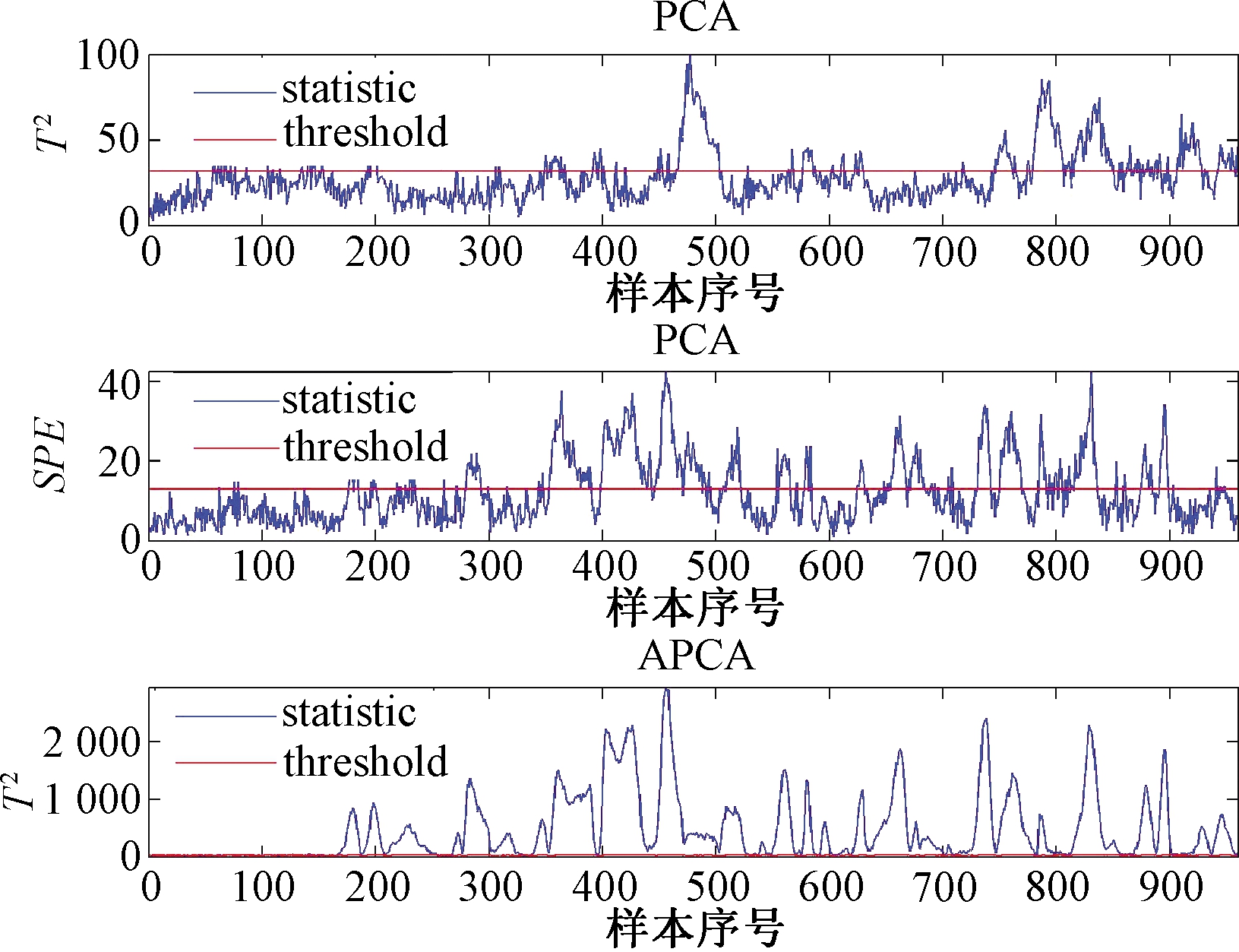
图3 TE过程PCA和APCA对故障16的监测效果
Figue 3 Monitoring results of PCA and APCA for case 16 in TE process
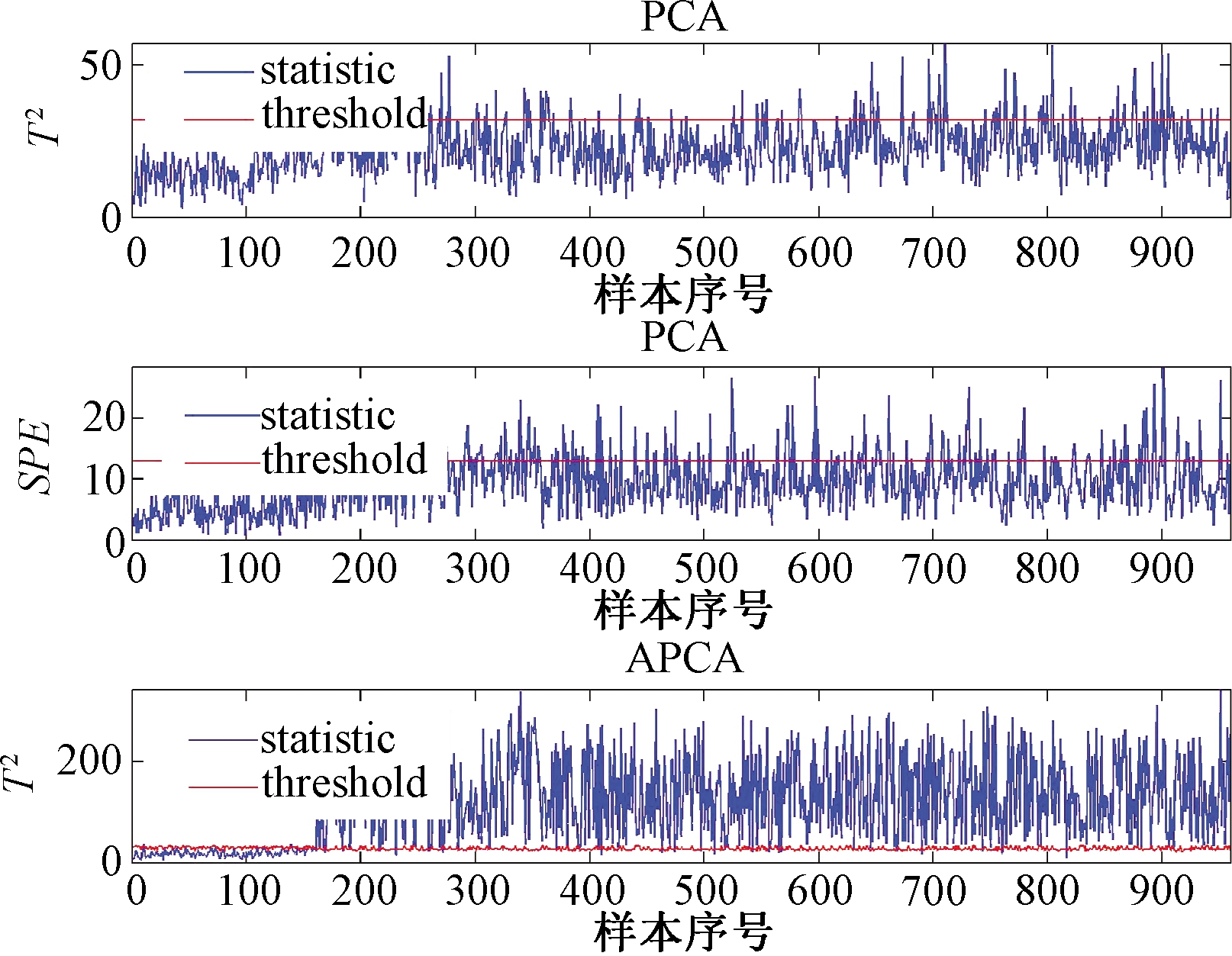
图4 TE过程PCA和APCA对故障19的监测效果
Figue 4 Monitoring effect of PCA and APCA on fault 19 in TE process
4 结论
笔者提出一种在线自适应挑选主成分的过程监测方法——APCA。该方法离线建模时为每个成分选出与其相似性较高的成分构成多个成分子空间，在线监测时实时选出变异概率最高的成分作为特征成分，以特征成分对应的子空间进行监测。所提方法实时进行成分的自适应挑选，降低了变异特征被分散和淹没的风险，同时可以有效地集中有利于故障检测的变异特征。通过数值仿真案例和TE过程案例证明了APCA的漏报率较低，具有较好的监测性能。未来的工作可以专注于开发一种确定主成分数量的策略，并使所提出的方法适用于非线性和非高斯过程。
[1] GE Z Q, SONG ZH, GAO F R.Review of recent research on data-based process monitoring[J].Industrial & engineering chemistry research, 2013, 52(10): 3543-3562.
[2] JACKSON J E.A user′s guide to principal components[M].New York: John Wiley & Sons, 2005.
[3] JIANG Q C, YAN X F, ZHAO W X.Fault detection and diagnosis in chemical processes using sensitive principal component analysis[J].Industrial & engineering chemistry research, 2013, 52(4): 1635-1644.
[4] JIANG Q C, YAN X F.Just-in-time reorganized PCA integrated with SVDD for chemical process monitoring[J].AIChE journal, 2014, 60(3): 949-965.
[5] JIANG Q C, YAN X F.Plant-wide process monitoring based on mutual information-multiblock principal component analysis[J].ISA transactions, 2014, 53(5): 1516-1527.
[6] TONG C D, SONG Y, Yan YAN X F.Distributed statistical process monitoring based on four-subspace construction and bayesian inference[J].Industrial & engineering chemistry research, 2013, 52(29): 9897-9907.
[7] 江伟, 王振雷, 王昕.基于混合分块DMICA-PCA的全流程过程监控方法[J].化工学报, 2017, 68(2):759-766.
[8] 吕照民.基于数据驱动子空间设计的间歇过程监测[D].上海：华东理工大学，2017.
[9] 葛志强.复杂工况过程统计监测方法研究[D].杭州：浙江大学，2009.
[10] 葛志强，宋热环.基于PICA的过程监控方法[J].化工学报，2008，59(7)：1665-1670.
[11] 童楚东, 蓝艇, 史旭华.基于互信息的分散式动态PCA故障检测方法[J].化工学报, 2016, 67(10): 4317-4323
[12] 王振雷, 江伟, 王昕.基于多块MICA-PCA的全流程过程监控方法[J].控制与决策, 2018, 33(2): 269-274.
[13] JIANG Q C, YAN X F.Plant-wide process monitoring based on mutual information-multiblock principal component analysis[J].ISA transactions, 2014, 53(5): 1516-1527.