0 引言
机器人技术是近年来兴起的一种现代科学技术,它的发展结合了许多高新技术学科,主要有机械电子、信息学、控制论、软件开发、人工智能等。移动机器人路径的研究是机器人学科中一个重要的研究领域,研究的问题是从工作空间中寻找一个从开始位置到目标位置的一个最优路径。本质上属于路径规划问题。智能算法是近年来提出用来解决机器人路径规划问题的算法,主要使用的方法有遗传算法、蚁群算法、粒子群算法、神经网络等等。
国内外学者对机器人路径规划也作了许多研究。Willms等[1]提出了一种高效的动态实时机器人路径规划系统,进行实时机器人路径规划。Fujimura等[2]提出了一种基于人工势场的机器人路径规划。Saska等[3]提出了一种采用Ferguson 样条的粒子群优化算法,该方法得到的路径比传统方法得到的路径光滑,而且易于执行。刘广瑞等[4]利用蚁群算法来进行最优路径的搜索,并对算法进行收敛性分析,从而提高了算法的收敛效果。赵开新等[5]通过梯度计算、节点探测、路径评估3种方式对机器人路径规划进行研究。陈志军等[6]将机器人路径规划是建立在三维空间里,建立了三维路径规划的评价指标和优化函数,提出了一种基于模糊神经网络和遗传算法的机器人路径规划。强宁等[7]采用了三次样条插值和粒子群算法来进行多机器人全局路径规划。
粒子群算法在解决机器人路径规划问题时主要存在两个缺陷:①算法迭代到后期,粒子群多样性下降,当路径陷入局部较差路径时,很难自动跳出,出现“早熟”现象。②算法的收敛性差,算法迭代后期,许多粒子适应度相差不大,导致粒子搜索进入停滞状态,路径寻优也会停滞,造成了路径的精度低。因此对算法进行改进十分必要。粒子群优化算法(PSO)和模拟退火算法(SA)是两种不同的智能优化算法,粒子群优化算法通过追随当前搜索到的最优解来寻找全局最优,模拟退火算法的机制便是以一定的概率来接受一个比当前解要差的解,从而可能跳出这个局部的最优解,达到全局的最优解。针对以上问题,笔者提出一种基于模拟退火的改进粒子群算法(APSO-SA),通过充分发挥粒子群算法和模拟退火算法的优势从而实现机器人全局最优路径规划。
1 标准粒子群算法
粒子群算法(PSO)是一种启发式随机算法。鸟群中每一个鸟相当于粒子群算法中的一个粒子。每个粒子好比寻找食物的鸟都有速度和位置,通过自身和社会两种学习方式,粒子在搜索空间中运动,从而得到全局最优解。假设种群有N个粒子在D维空间搜索,标准粒子群算法更新公式为:
(1)
(2)
式中:t为迭代次数;vij表示第i个粒子j维的速度大小;xij表示第i个粒子j维的位置大小;w表示惯性权重;c1、c2 表示学习因子;r1、r2表示随机数。粒子群算法虽然简单,但是算法迭代后期,由于粒子多样性差导致粒子容易陷入局部最优解,所以要对粒子群算法进行改进。
2 粒子群算法的改进
2.1 带压缩因子的粒子群算法
为了有效地控制粒子飞行速度使算法全局搜索和局部搜索平衡,Clerc等[8]提出了带压缩因子的PSO算法,其速度更新公式如下:
(3)
其中搜索因子:
带压缩因子的PSO算法相当于线性递减权重的PSO算法,该算法的优势在于去掉了惯性权重w,减少了算法参数,只有两个学习因子参数,所以只需对两个学习因子进行自适应调节。其调节公式如下:
当f(xi)≤favg,粒子xi需要进行局部搜索,学习因子取:
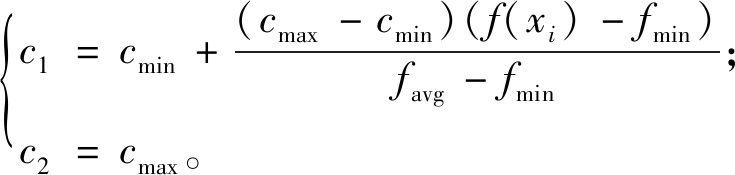
(4)
当f(xi)>favg,粒子xi要进行全局搜索,所以学习因子取:

(5)
式中:cmin=1.5;cmax=2.5;f(xi)表示粒子xi的适应度大小;favg表示所有粒子的平均适应度。
2.2 模拟退火算子
模拟退火算法是由Metropolis等于1953年提出的,该算法在搜索过程中具有概率突跳的能力,能够在一定程度上避免搜索过程中陷入局部最优解,由于粒子群算法对pg全局最优粒子依赖性很强,所以为了避免粒子搜索过程陷入pg,所以对pg引入模拟退火操作,其中Metropolis准则如下:
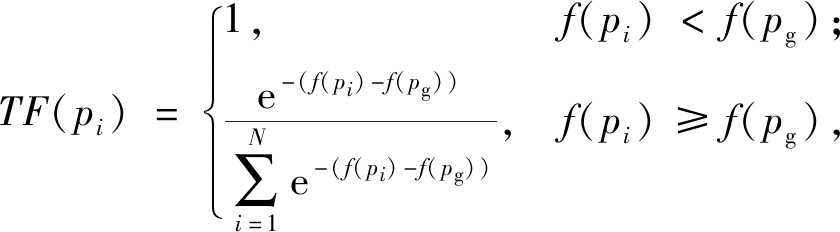
(6)
式中:f(pi)表示pi粒子的适应度;f(pg)表示当前粒子群算法迭代的全局最优适应度。采用轮盘赌策略从pi中确定全局最优的某个个体代替pg,初温和退温公式为:
(7)
以上为APSO-SA算法的基本思想,标准粒子群算法的时间复杂度为O(M,D,N),其中M为最大迭代次数,D为粒子维数,N为粒子个数。由于该算法是建立在压缩因子的粒子群算法的基础上,压缩因子的粒子群算法时间复杂度为O(M,D,N),学习因子的自适应调节策略和模拟退火操作的时间复杂度均为O(N),所以APSO-SA算法的时间复杂度为O(M,D,N)。
3 机器人路径规划模型建立
3.1 三次样条插值编码设计
两点法对机器人路径进行规划[9]会造成路径平滑性差,机器人运动不平稳,频繁转向会造成能源的极大浪费,本文机器人路径规划是建立在二维平面上,提出的APSO-SA算法在二维平面进行三次样条插值编码,根据文献[3]提出的Ferguson三次样条插值对路径进行编码优化,其原理如下。
假设有以下节点(xi,yi),其中xi<xj,∀i<j,三次样条插值曲线S(x)满足以下条件:
(1)每个分段区间[xi,xi+1],S(x)=Si(x)为三次多项式。
(2)每一个端点满足S(xi)=yi,i∈N∩i≤n。
(3)S(x)的1、2阶导数为S′(x)、S″(x),而且在[a,b]区间内连续,即Si(x)可以写成:
Si(x)=ai+bi(x-xi)+ci(x-xi)2+di(x-xi)3;
式中:i∈N∩i<n。
机器人在搜索空间搜索最优路径可以看作在三次样条空间中搜索最优样条,APSO-SA算法中的每一组粒子表示为一组路径的节点,每一组路径节点个数便为三次样条曲线的个数,由于三次样条插值的性质,每一组路径节点的个数体现了路径可以转向的最大次数。粒子编码的路径节点个数会随着工作环境的复杂而增加,实际生活中机器人转向3~5次便可以绕过所有的障碍物,本文的障碍物模型设置转向节点为3。
3.2 路径初始化
路径初始化决定着算法的好坏,PSO算法机器人路径规划均是在机器人工作空间随机取粒子,但是导致算法收敛性差,于是对粒子的初始化进行改进,提出基于高斯分布的随机初始化,初始化公式如下:
x=(xs+xt)/2+r3;
(8)
y=U(ymin,ymax,1,n),
(9)
式中:xs、xt分别为开始位置和目标位置的横坐标;r3为高斯分布产生的随机数;n表示产生粒子的个数;ymax、ymin分别为粒子初始化纵坐标的上下界;U表示在给定上下界中均匀产生n个粒子纵坐标的值。
3.3 障碍物处理
障碍物对机器人路径规划有很大的影响,若没有障碍物,机器人在二维空间中从开始位置到目标位置运动,直线运动最短,无须进行路径规划,然而现实机器人工作时,障碍物是客观存在的,笔者研究的是静态工作环境下的机器人路径规划,由于实际工作环境中障碍物形状千差万别,导致建模十分困难,为了方便统一研究,笔者对障碍物进行预处理,在二维空间中,障碍物均进行膨胀处理,即用原障碍物图形的外接圆表示该障碍物,具体见图1。
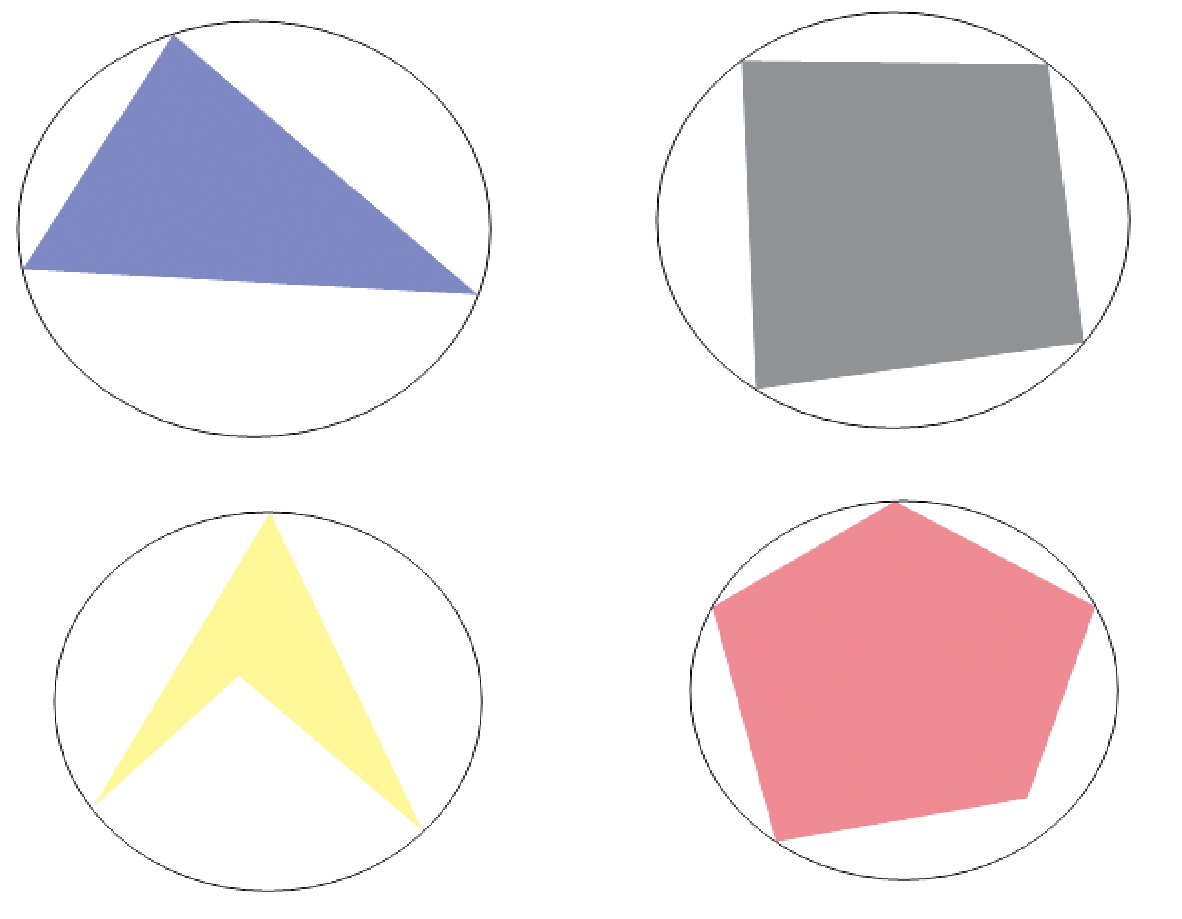
图1 不同形状障碍物膨胀处理
Figure 1 Different obstacle with different shapes expansion
3.4 适应度函数
适应度函数的值可以看作路径的长度,粒子通过三次样条编码,不断寻找最优适应度,而有些路径与障碍物相交会成为非法路径,如果直接去掉这些路径,那么存在的可行路径就会变得非常少,路径的多样性就会减弱,所以构造带有罚函数的适应度函数,通过附加较大的惩罚值,使路径在优化过程中自动淘汰非法路径。文献[8]中使用了一种带有罚函数的适应度函数,笔者对其做了一些简单的修改,得出适应度函数如下:
z=L(1+beta·V),
(10)
式中:L为机器人工作运行路径的长度;beta为惩罚值,一般设置为100;V为路径的非法度,当V=0时,z=L,此时适应度的大小就为路径的大小。
4 算法流程
APSO-SA算法机器人路径规划与粒子群算法机器人路径规划流程相似,具体算法流程如下:
步骤1 创建障碍物模型,初始化机器人开始位置以及机器人目标位置,初始化机器人工作空间。
步骤2 初始化APSO-SA算法的参数,包括粒子个数、学习因子、最大迭代次数、退火系数、路径节点个数。
步骤3 按照式(8)、(9)初始化每组粒子的位置,以及对粒子进行三次样条编码。
步骤4 按照式(4)、(5)自适应处理学习因子,同时按照式(3)更新粒子速度,按照式(2)更新粒子的位置。
步骤5 按照式(10)计算每组粒子当前的适应度,并根据式(6)和式(7)对当前适应度最好的粒子进行退火处理。
步骤6 判断算法是否达到最大函数评价次数,若满足,则停止搜索,输出结果,否则返回步骤4继续迭代。
5 仿真模拟
为了验证APSO-SA算法在机器人路径寻优中的优越性,笔者设计了以下实验,在3种障碍物模型中对APSO-SA算法与PSO算法进行比较测试。其中3种障碍物模型的最短路径长度通过几何计算得到,保留小数点后2位。见表1。算法比较采用固定粒子个数和最大函数迭代次数,试验在windows 7系统MATLAB 2012a中完成。电脑配置为Intel(R) Core(TM) i5-3317U CPU@1.70 GHz。
5.1 参数设置
笔者建立的3个障碍物模型参数如表1~3所示。
表1 3个模型基本参数
Table 1 Basic parameters of three models
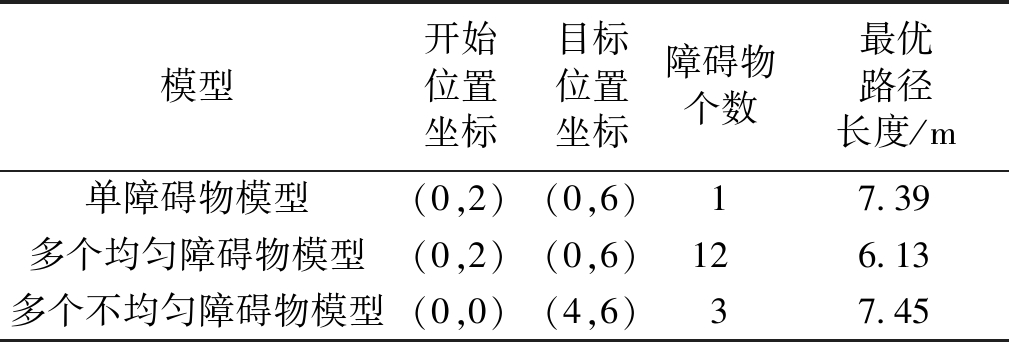
模型开始位置坐标目标位置坐标障碍物个数最优路径长度/m单障碍物模型(0,2)(0,6)17.39多个均匀障碍物模型(0,2)(0,6)126.13多个不均匀障碍物模型(0,0)(4,6)37.45
表2 3个模型圆心及其半径
Table 2 Center and rabius of three models

模型圆心及其半径模型1(2,3);r=2模型2(0,2),(0,4),(1,1),(1,3),(1,5),(2,2),(2,4),(3,1),(3,3),(3,5),(4,2),(4,4);r=0.5模型3(1.5,4.5);r1=1.5,(4,3);r2=1,(1.2,1.5);r3=0.8
表3 PSO和APSO-SA算法参数
Table 3 Algorithm parameters of PSO and APSO-SA

算法粒子数学习因子函数评价次数PSO100c1=2.05,c2=2.0510100APSO-SA100cmin=1.5,cmax=2.510100
5.2 数值实验
5.2.1 单障碍物模型
两种算法独立运行30次,数值结果用SPSS进行统计分析,结果如表4、5所示。
表4 单障碍物模型数值结果比较
Table 4 Comparison of numerical results of single obstacle model

算法最小路径长度/m平均路径长度/m标准差运行时间/sPSO7.437.460.2011.46APSO-SA7.427.410.0311.50
表5 单障碍物模型单因素方差分析结果比较
Table 5 One-way ANOVA results of single obstacle model
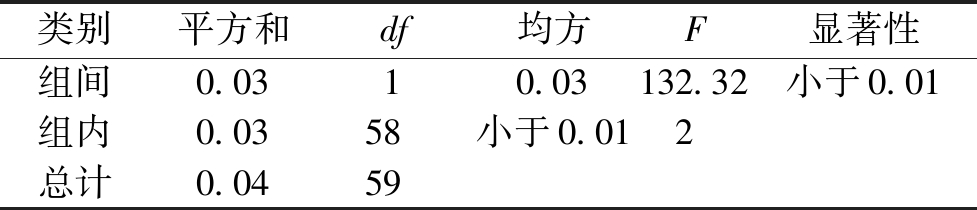
类别平方和df均方F显著性组间0.0310.03132.32小于0.01组内0.0358小于0.012总计0.0459
图2为单障碍物模型两种算法比较结果图,从图2可以看出,PSO算法和APSO-SA算法都能够在该模型中规划出一条无碰路径。PSO算法搜索出的最优路径长度为7.47 m,而APSO-SA算法得出的最优路径长度为7.41 m,同时APSO-SA路径搜索范围广,路径搜索前期变化比较大,10代以后趋于平稳,表4、5也表明APSO-SA算法的路径寻优能力优于PSO算法,通过方差同质性检验后进行单因素方差分析,结果表明,两种算法具有显著性差异。
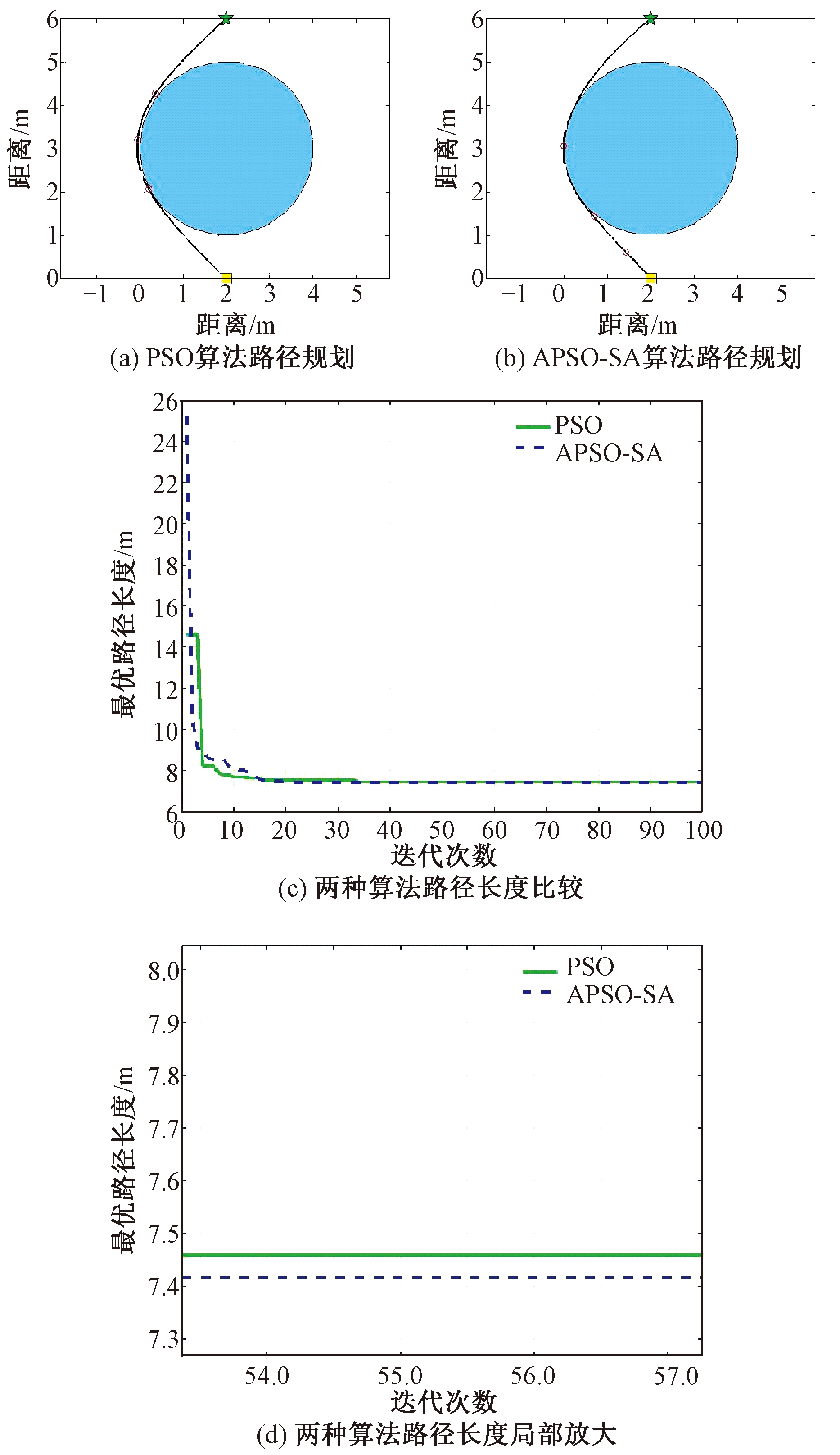
图2 单障碍物模型两种算法比较结果
Figure 2 The results of the two algorithms of single obstacle model
5.2.2 多个均匀障碍物模型
图3分别给出了多个均匀障碍物模型两种算法得出的最优路径和最优路径长度比较。从实验结果可以看出,APSO-SA算法的路径平滑度明显优于PSO算法。下面两种算法各自独立运行30次,运行结果及统计分析记录如表6、7所示。

图3 多个均匀障碍物模型两种算法比较结果
Figure 3 The results of the two algorithms of multiple uniform obstacle models
由于该模型存在许多局部最优路径,所以获得的路径为局部最优路径不可避免。从表6可以看出,APSO-SA有很好地跳出局部最优路径的性能,得到的路径为局部最优路径的概率仅为20%.从时间上来看两种算法相差不大,仅比传统的PSO算法高了0.04 s,总体路径平均长度却减少了0.27 m。这充分体现了APSO-SA算法多样化策略的优势。单因素方差分析也可以得到两种算法具有显著性差异。
表6 多个均匀障碍物模型数值结果比较
Table 6 Comparison of numerical results of multiple uniform obstacle models
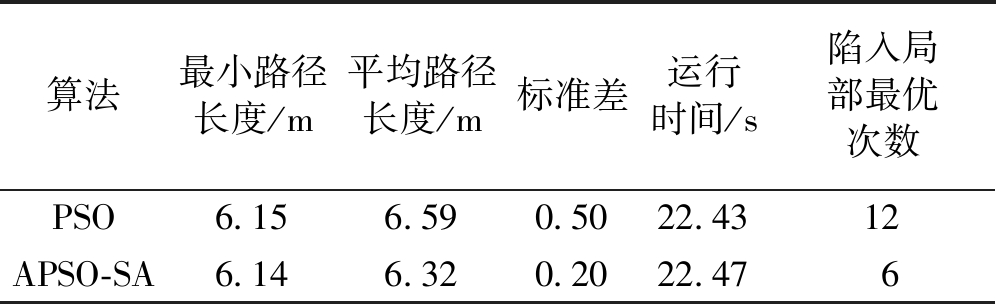
算法最小路径长度/m平均路径长度/m标准差运行时间/s陷入局部最优次数PSO6.156.590.5022.4312APSO-SA6.146.320.2022.476
表7 多个均匀障碍物模型单因素方差分析结果比较
Table 7 One-way ANOVA results of multiple uniform obstacle models
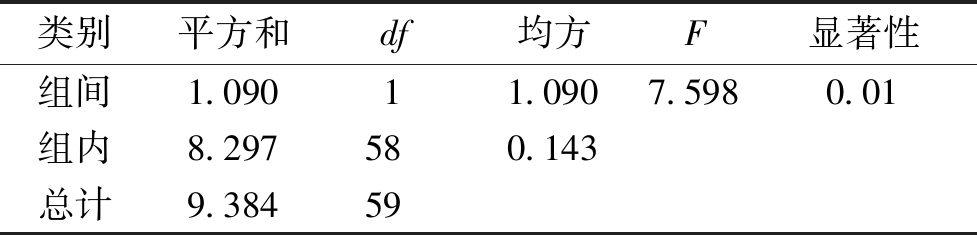
类别平方和df均方F显著性组间1.09011.0907.5980.01组内8.297580.143总计9.38459
5.2.3 多个不均匀障碍物模型
从图4和表8可以看出,在多个不均匀障碍物模型中,APSO-SA算法的路径寻优能力也优于PSO,这充分说明了在复杂的工作环境中PSO算法中的粒子在搜索过程中极易从可行域飞到不可行域,导致种群中大量的粒子进行约束处理后不能按最优方向去搜索最优值,最终影响搜索效果。
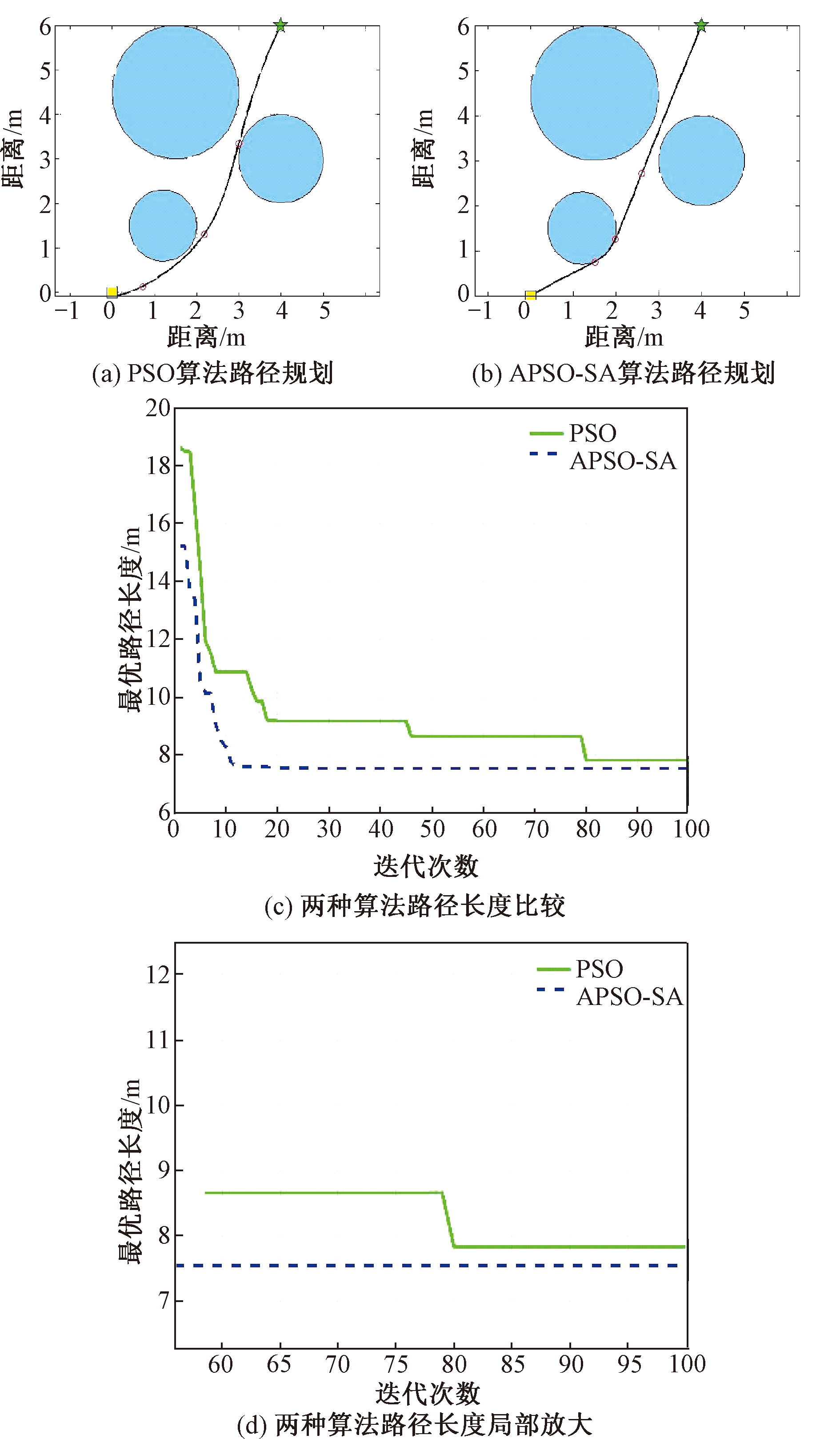
图4 多个不均匀障碍物模型两种算法比较结果
Figure 4 The results of the two algorithms of multiple inbomogeneous obstacle models
表8 多个不均匀障碍物模型数值结果比较
Table 8 Comparison of numerical results of multiple inbomogeneous obstacle models
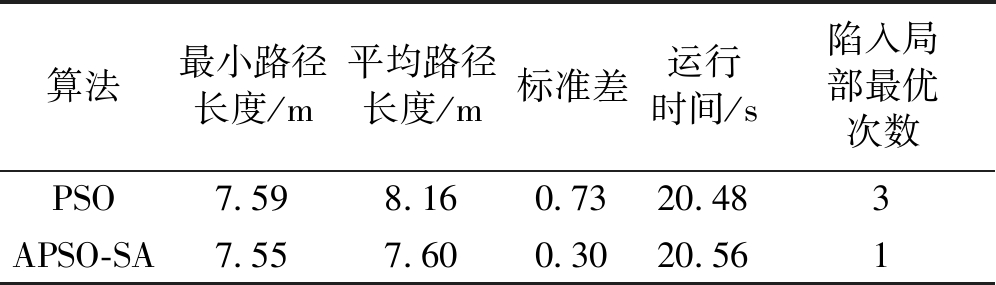
算法最小路径长度/m平均路径长度/m标准差运行时间/s陷入局部最优次数PSO7.598.160.7320.483APSO-SA7.557.600.3020.561
表9 多个不均匀障碍物模型单因素方差分析结果比较
Table 9 One-way ANOVA results of multiple inbomogeneous obstacle models

类别平方和df均方F显著性组之间4.7214.71515.25小于0.01组内17.93580.309总计22.6559
6 结论
笔者提出了一种基于模拟退火与自适应粒子群混合的算法,用来解决机器人路径规划问题。其中采用高斯分布和三次样条插值法来初始化并编码粒子,采用退火策略和罚函数策略进一步提高了算法的运行效率,使机器人路径更加合理化。通过对适应度函数的调整,APSO-SA算法也可以解决不同的应用问题。将来有可能应用于动态实时路径规划问题中。
[1] WILLMS A R,YANG S X.An efficient dynamic system for real-time robot-path planning[J].IEEE transactions on systems man and cybernetics,2006,36(4):755-766.
[2] FUJIMURA K,SAMET H.A hierarchical strategy for path planning among moving obstacles (mobile robot) [J].IEEE transactions on robotics and automation,1989,5(1):61-69.
[3] SASKA M,MACAS M,PREUCIL L,et al.Robot path planning using particle swarm optimization of ferguson splines[C] //IEEE Conference on Emerging Technologies and Factory Automation.Prague:IEEE,2006:833-839.
[4] 刘广瑞,刘军,孔令云.移动机器人路径规划蚁群算法及其收敛性分析[J].郑州大学学报(工学版),2012,33(2):24-27.
[5] 赵开新,王东署.未知环境中自主机器人的路径规划研究[J].郑州大学学报(工学版),2013,34(5):74-79.
[6] 陈志军,曾蒸.基于模糊神经网络和遗传算法的机器人三维路径规划[J].重庆师范大学学报(自然科学版),2018,35(1):93-99.
[7] 强宁,高洁,康凤举.基于PSO和三次样条插值的多机器人全局路径规划[J].系统仿真学报,2017,29(7):1397-1404.
[8] CLERC M,KENNEDY J.The particle swarm-explosion,stability and convergence in a multi-dimensional complex space[J].IEEE transactions on evolutionary computation,2002,6(1):58-73.
[9] 宋莉,李彩虹,朱宝艳,等.基于两点法的移动机器人局部路径规划算法[J].山东理工大学学报(自然科学版),2018,32(1):10-14.