0 引言
波纹钢腹板预应力混凝土桥(简称“波纹钢腹板PC桥”)源于法国[1],它是由混凝土顶底板、体外预应力筋和波纹钢腹板三者构成的组合结构,是对传统的混凝土桥梁的一种改进[2],它有效地发挥了混凝土和波纹钢板的特性,提高了它们的使用效率[3-4]。在波纹钢腹板PC桥中,有一种重要的结构,即抗剪连接件,它用于抵抗混凝土板与钢腹板间的纵向剪力,使二者之间不能相对滑移[5-8]。
波纹钢腹板PC桥可用的连接件形式很多,例如栓钉连接件、型钢连接件、PBL(perfobond-leiste)连接件以及嵌入式连接件[9-10]。嵌入式连接件没有翼缘板,在施工中支模浇筑极为麻烦,不利于现场施工进度。为解决这一问题,以嵌入式连接件为基础,在其两侧焊接两块钢板形成翼缘板(图1),笔者称为带翼缘板嵌入式连接件。这种连接件抵抗水平剪力由嵌入段斜板处混凝土块、接合钢筋、横桥向的贯穿钢筋以及混凝土销轴共同承担[11]。钢筋混凝土销轴还起到了抵抗拉拔力的作用[12]。
以往并未有学者研究该种新型连接件,笔者提出这种连接件形式仅把翼缘板作为混凝土浇筑模板来设计,而翼缘板对于连接件性能的影响需要试验研究确定。可以参考在形式上较为类似的连接件的研究成果包括:
(1)万水教授提出的开孔波折板连接件[13],这种连接件嵌入段为波纹钢板,但腹板为平板且与嵌入段不连续。承载力可用式(1)得出[14]:
(1)
式中:fcu为混凝土立方体抗压强度;fy为贯穿钢筋屈服强度;φ为开孔波折板开孔直径;φs为贯穿钢筋直径;hw为开孔波折板高度;dw为开孔波折板的波高;α=1.327;β为波折板对混凝土榫增强系数,β=-0.145,当开孔板为直钢板时β取0;γ为贯穿钢筋抗剪系数,γ=1.245;λ为波折板所围成混凝土齿板抗剪系数,λ=1.219,当开孔板为直钢板时λ取0。
(2)CJJT 272—2017《波形钢腹板组合梁桥技术标准》[15]指出,嵌入式连接件应分别满足混凝土齿键和混凝土剪力销的受剪承载力要求。
混凝土齿键的受剪承载力可通过式(2)得出:
Vu=fcdA1+μfsdAs,
(2)
式中:fcd为混凝土抗压强度设计值;A1为波纹钢腹板斜幅段在横桥向的投影面积;μ为系数,取1.0;fsd为接合钢筋抗拉强度设计值;As为接合钢筋截面积。
混凝土剪力销受剪承载力可通过式(3)得出:
(3)
式中:dp为开孔钢板孔径;ds为贯穿钢筋直径;fcd为混凝土抗压强度设计值;fsd为贯穿钢筋抗拉强度设计值;n为系数,当开孔钢板间距大于其高度的1.5倍时取2。
以CJJT 272—2017《波形钢腹板组合梁桥技术标准》[15]中嵌入式连接件的承载力计算公式为基础,以实际工程为背景,通过试验研究该公式的适用性,以及该种连接件的性能。
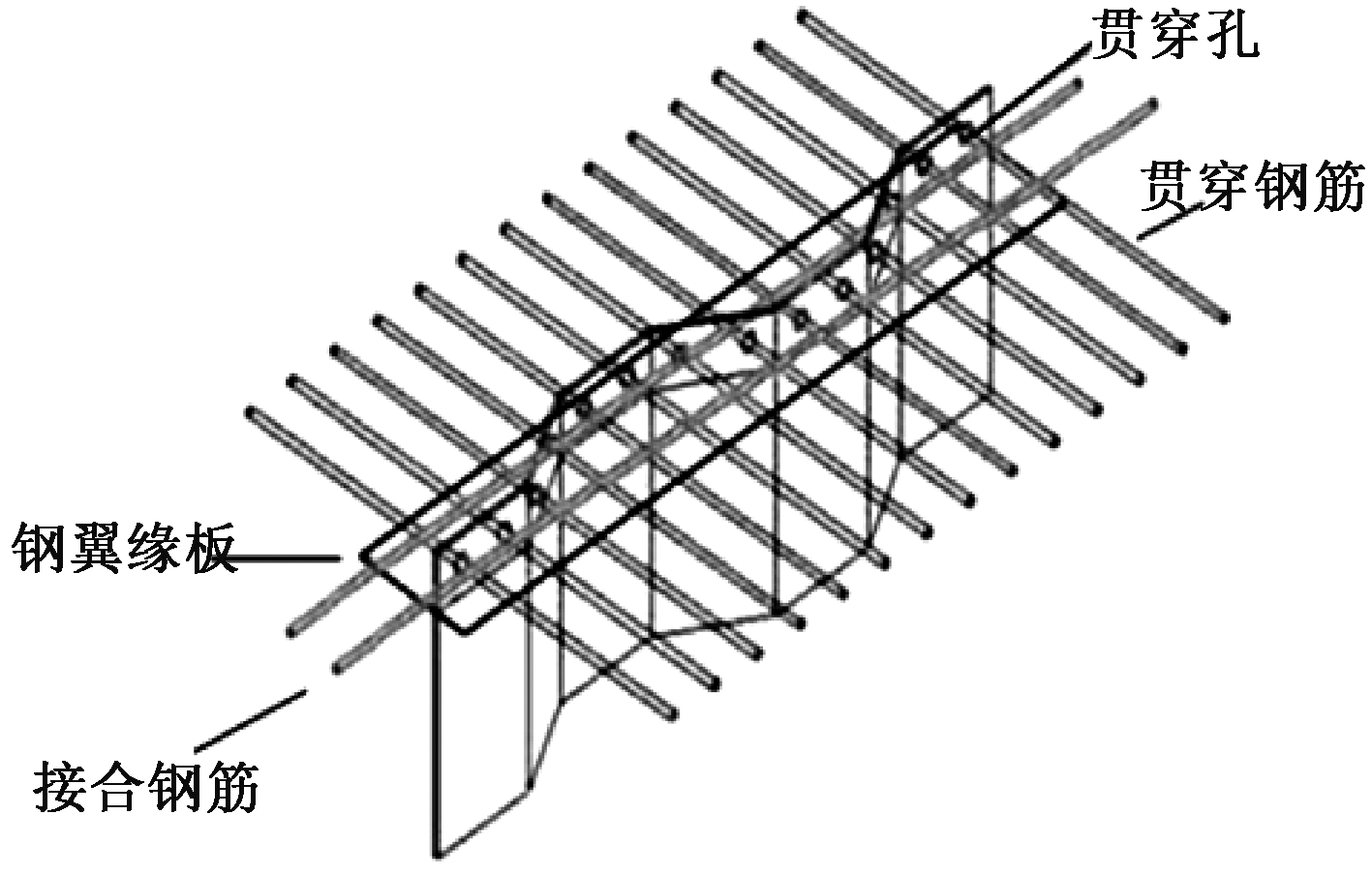
图1 带翼缘板嵌入式连接件
Figure 1 Embedded connector with flange plate
1 试验方案
1.1 试件设计
依托机西高速二期贾鲁河大桥工程,试件根据实际图纸选用1∶1尺寸制作。试验所用构件参数图如图2所示。为了确保试件的加载端不会局部损坏,加强设计试件的加载端。试件使用Q345D型钢材,波纹钢板的波形为1600型(图3)。横向贯穿钢筋型号为HRB335,直径为16 mm和22 mm,接合钢筋型号为HRB335,直径为22 mm(图2),试件参数为混凝土强度,贯穿钢筋直径以及翼缘板厚度。钢筋与钢板的力学性能如表1所示。试件采用C40和C55混凝土制作,混凝土的力学性能如表2所示。试件设计参数见表3。
1.2 量测方案
本次试验主要量测数据为:压力传感器读数,位移传感器读数。
试验共布置6个位移计,布置位置如图4所示,用于测量钢材与混凝土间的相对滑移。
1.3 加载方案
本次试验采用500 t万能压力机,试验装置布
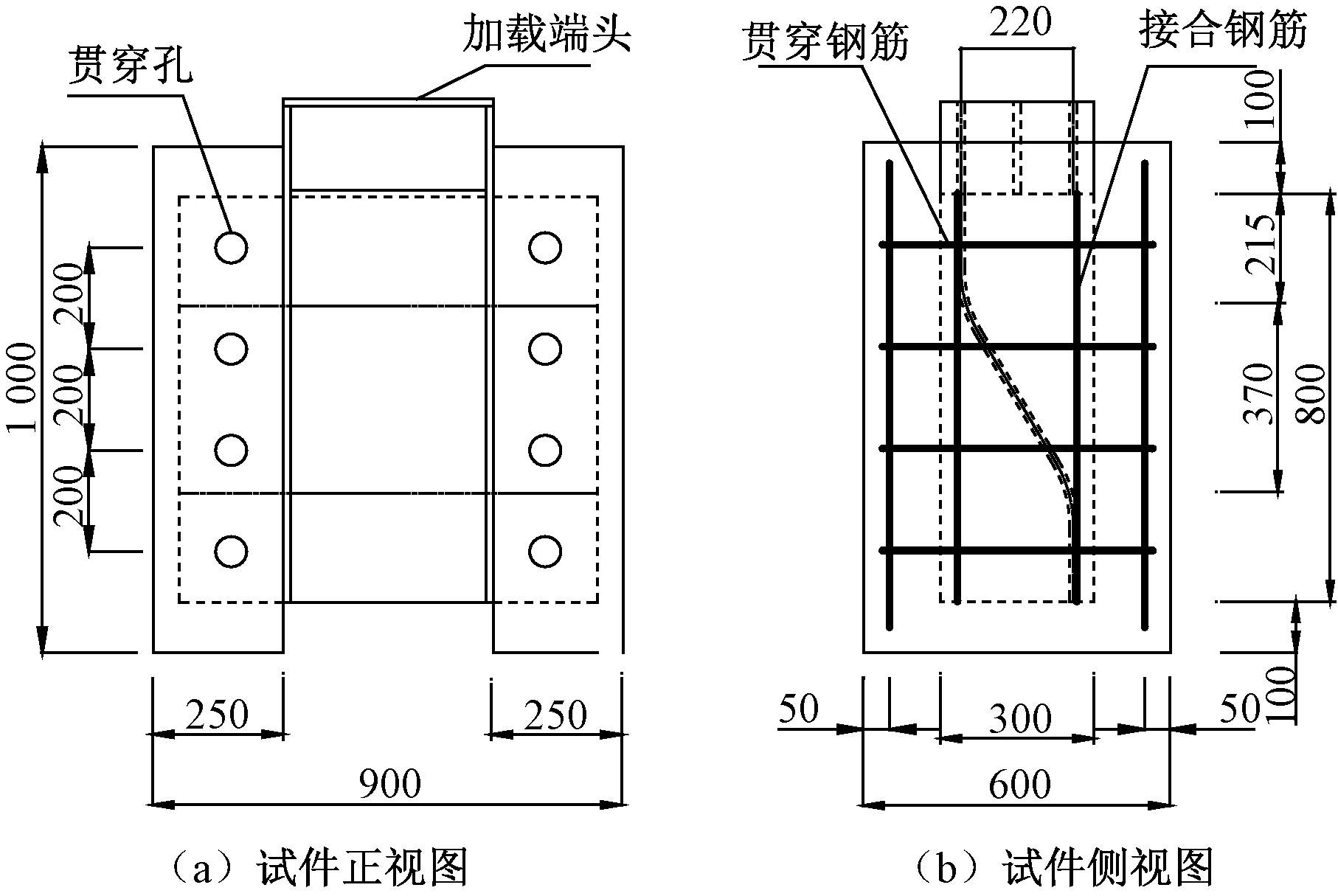
图2 试件几何尺寸
Figure 2 Geometrical dimension of test specimen
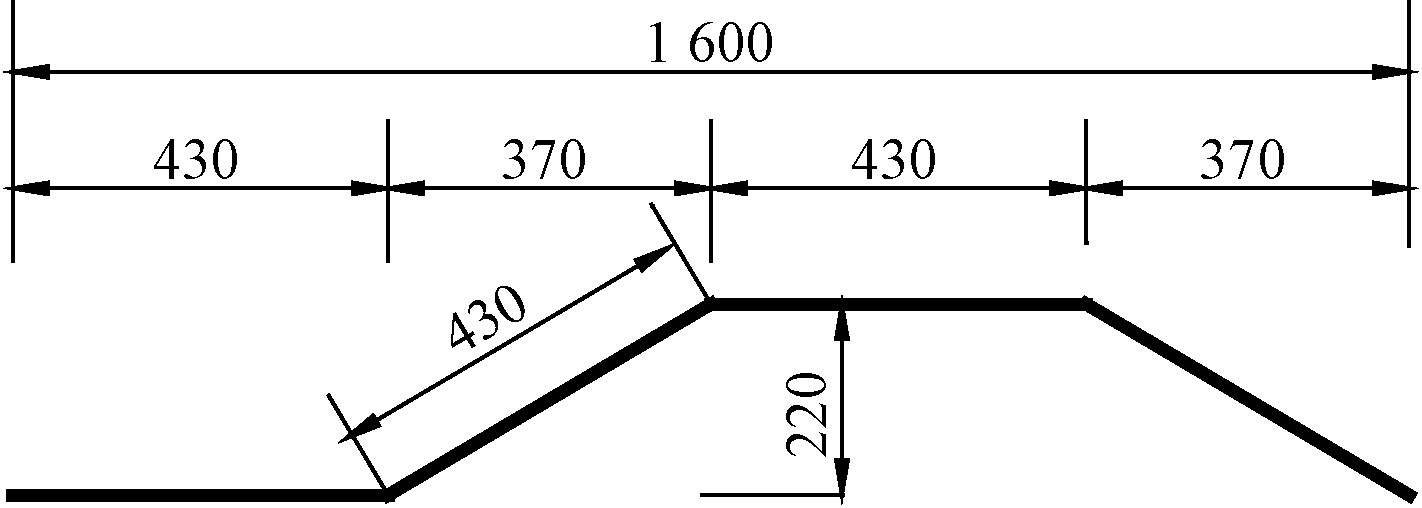
图3 1600型波形图
Figure 3 Geometrical properties of the 1600-type corrugated steel plate
表1 钢筋与钢板力学性能
Table 1 Mechanical properties of steel bar and steel
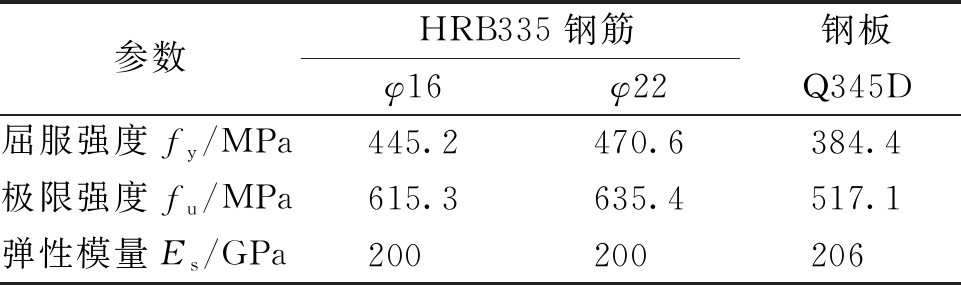
参数HRB335钢筋钢板φ16φ22Q345D屈服强度fy/MPa445.2470.6384.4极限强度fu/MPa615.3635.4517.1弹性模量Es/GPa200200206
表2 混凝土力学性能
Table 2 Mechanical properties of concrete

强度等级C40C55立方体抗压强度fcu/MPa46.457.5弹性模量Ec/MPa3.25×1043.55×104
表3 试件参数表
Table 3 Parameter list of test specimen
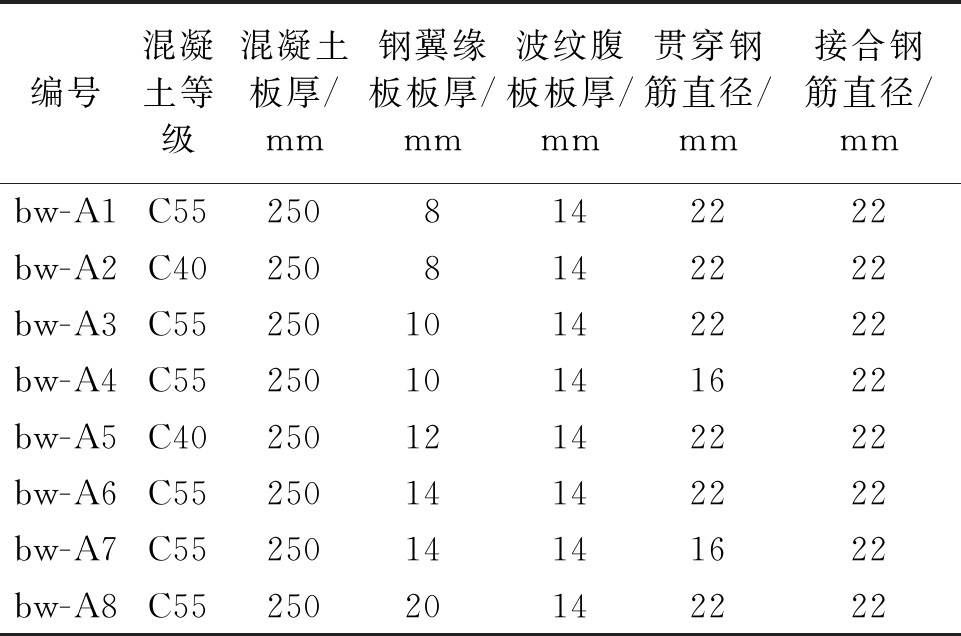
编号混凝土等级混凝土板厚/mm钢翼缘板板厚/mm波纹腹板板厚/mm贯穿钢筋直径/mm接合钢筋直径/mmbw-A1C552508142222bw-A2C402508142222bw-A3C5525010142222bw-A4C5525010141622bw-A5C4025012142222bw-A6C5525014142222bw-A7C5525014141622bw-A8C5525020142222
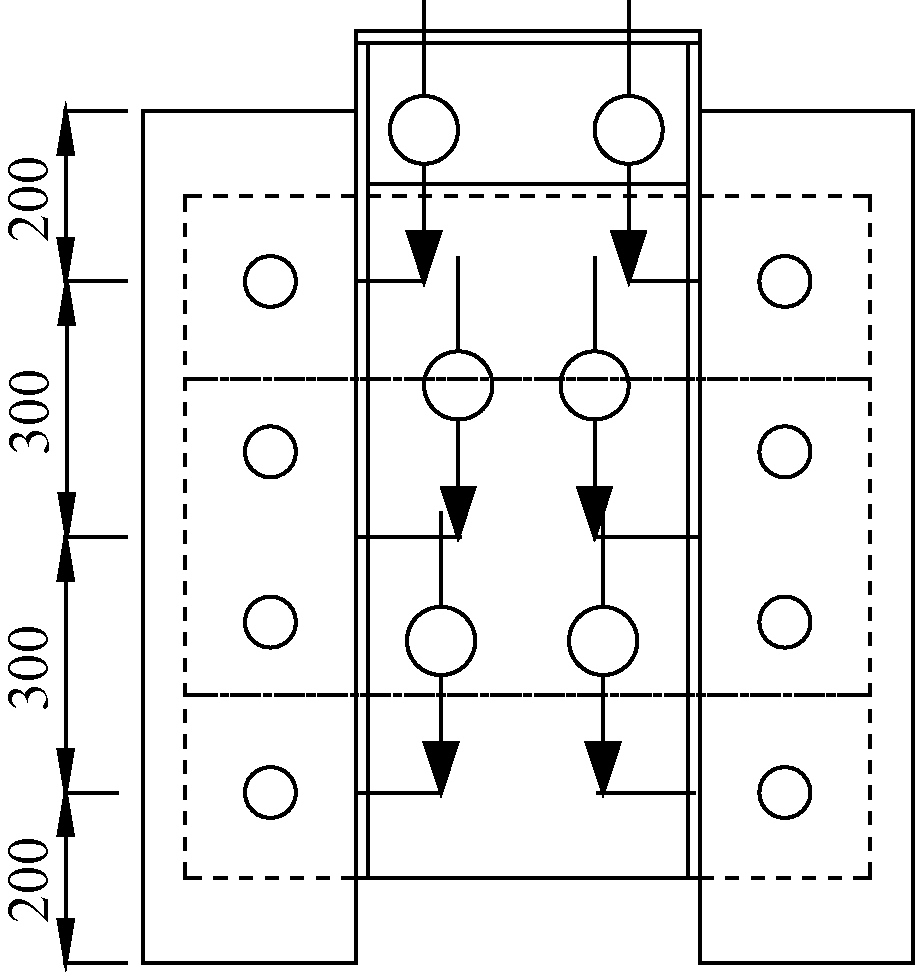
图4 位移传感器
Figure 4 Displacement sensors
置简图如图5所示。
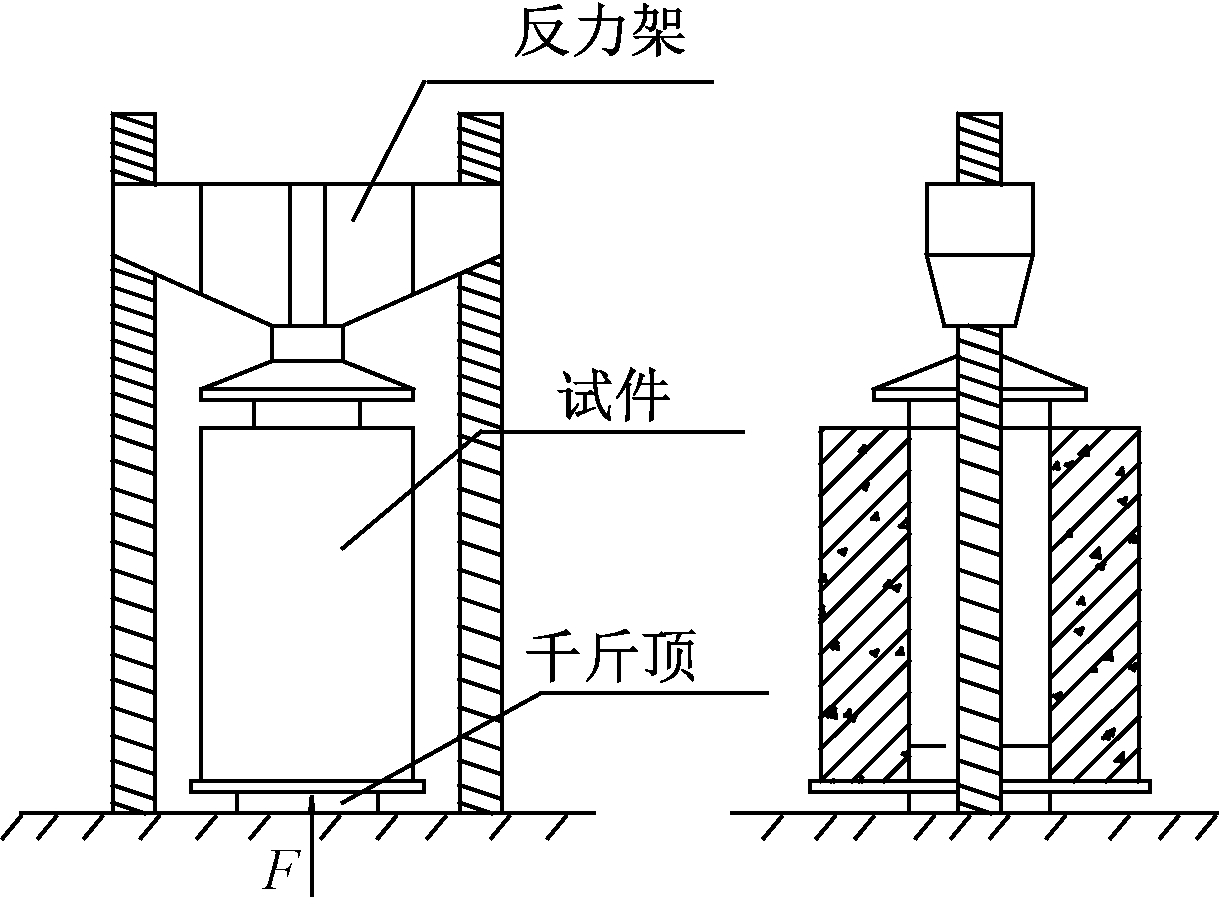
图5 加载装置
Figure 5 Loading device
在正式加载前进行预加载,参考欧洲规范4[16]预加载400 kN,持续2 min,待测量仪器读数稳定后,卸载到预估极限荷载的5%,循环5次。正式加载采用分级加载制度,每级加载200 kN,持荷5 min,待测量仪器读数稳定后记录数据。当加载至0.8倍的预估极限荷载后,选择每级加载100 kN直至试验结束。试验前在试件与压力机的接触面铺少量细沙,以保证试件均匀受力。
2 试验结果及分析
2.1 破坏模式
最终的试验现象显示,所有试件呈现两种破坏形态,它们之间存在着两种明显的区别:①混凝土破坏程度;②钢翼缘板是否发生失稳。
(1)试件bw-A1~bw-A5的破坏形态为混凝土仅局部破坏,钢翼缘板发生失稳。表现为:混凝土裂缝未充分发展,翼缘板在宽厚比较大处发生局部失稳。以试件bw-A4为例,试验现象如图6所示。

图6 翼缘失稳试件典型破坏现象(试件bw-A4)
Figure 6 Typical failure phenomenon of local buckling test specimens(specimen bw-A4)
(2)试件bw-A6~bw-A8的破坏形态为混凝土完全破坏,钢翼缘板未发生失稳。表现为:混凝土裂缝在厚度与宽度位置呈现直线与波纹线的形状。以试件bw-A8为例,试验现象如图7所示。

图7 翼缘未失稳试件典型破坏现象(试件bw-A8)
Figure 7 Typical failure phenomena of unstable flange plate test specimens(specimen bw-A8)
2.2 荷载滑移关系
图8为翼缘失稳试件的荷载-滑移曲线,图9为翼缘未失稳试件的荷载-滑移曲线,图10为两种破坏模式曲线对比。(其中荷载值为试验加载值的一半,即分析单侧连接件性能,滑移量取6个位移计读数平均值)。并将各试件试验结果对比绘制成表4。

图8 翼缘失稳试件荷载-滑移曲线
Figure 8 Load-slip curve of local bucking test specimens
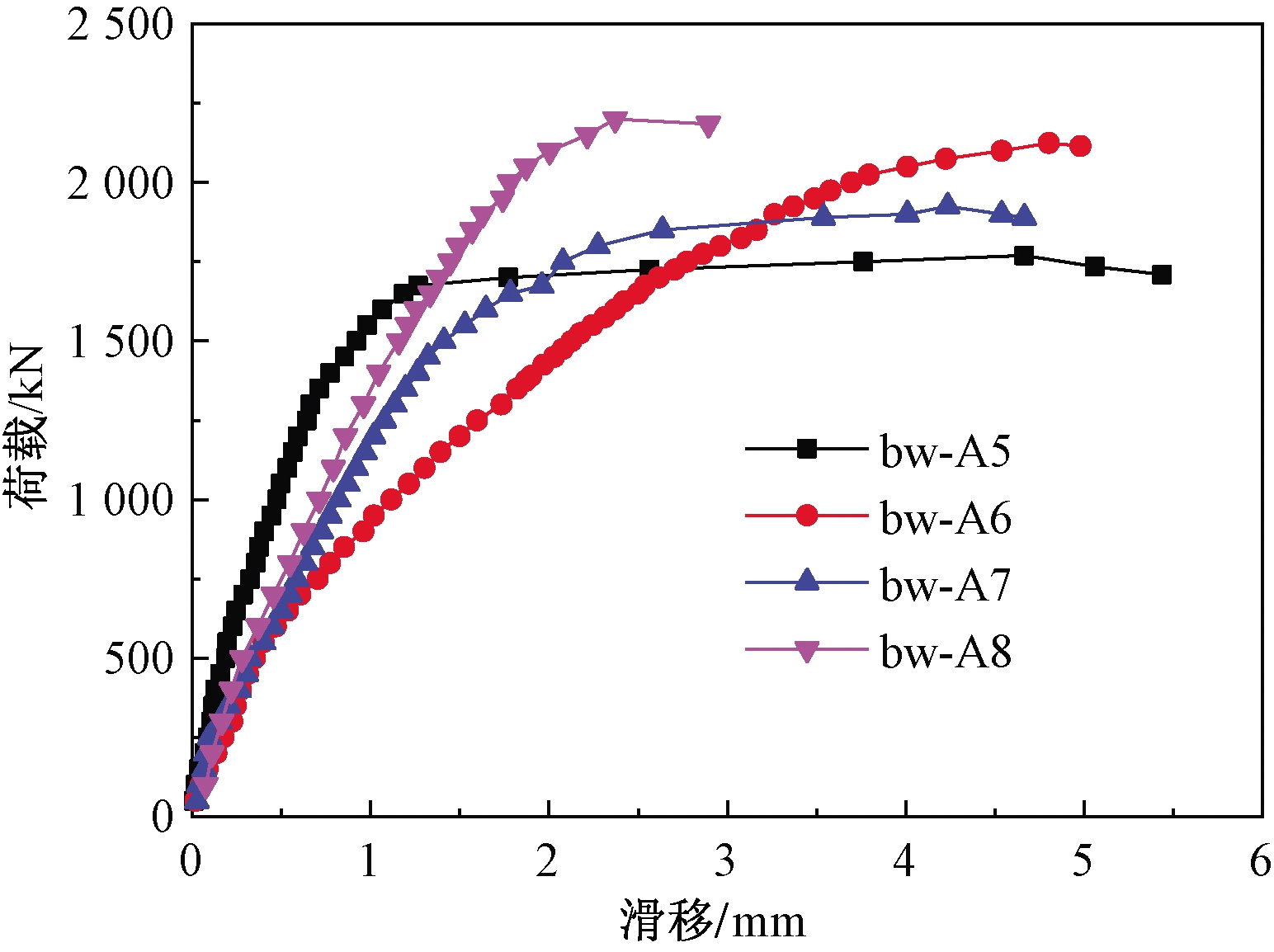
图9 混凝土破坏试件荷载-滑移曲线
Figure 9 Load-slip curve of concrete failure test specimens
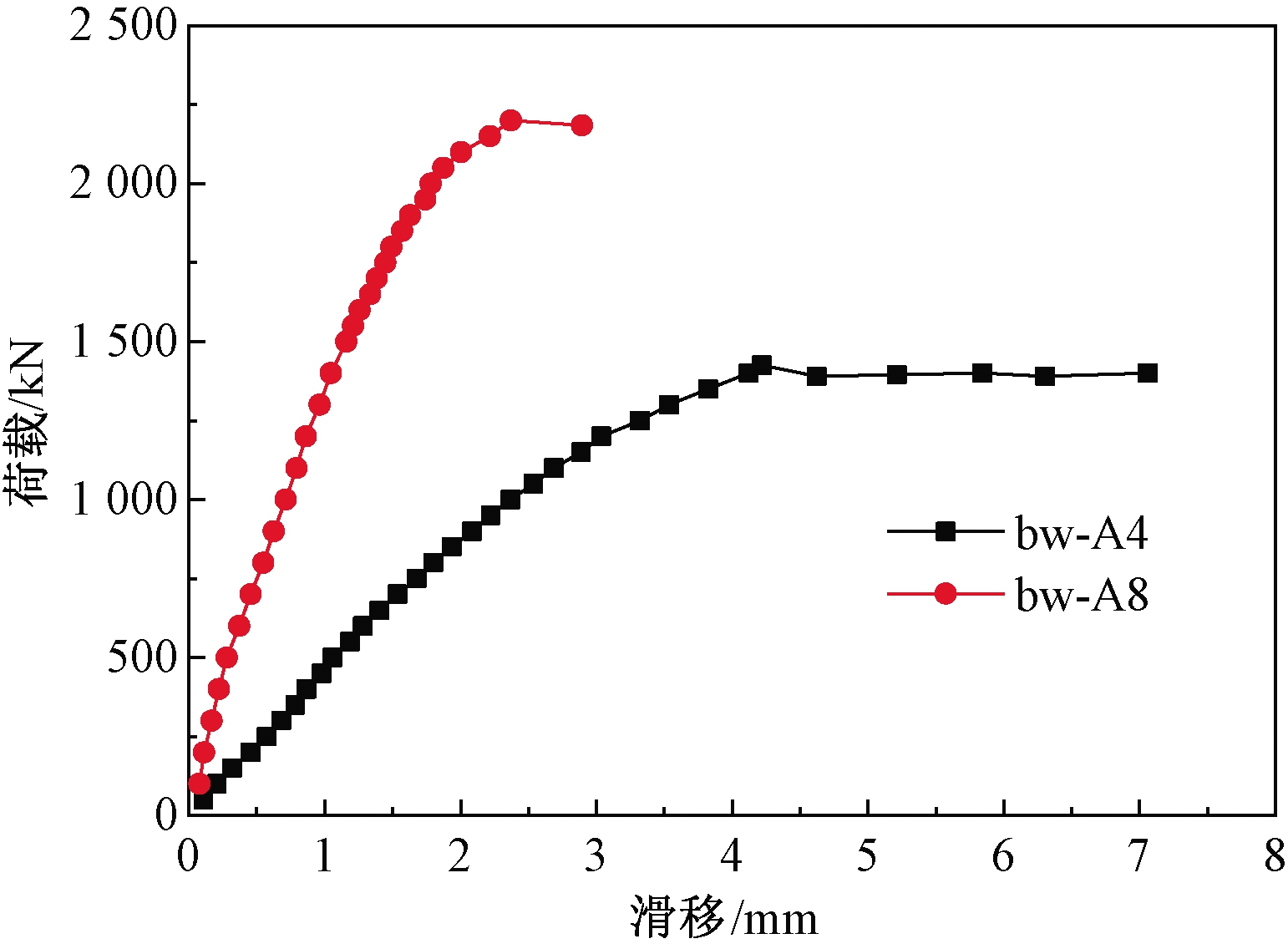
图10 两种破坏模式荷载-滑移曲线对比
Figure 10 Comparison of load-slip curves between two failure modes
从图8可看出,在加载初期,连接件与混凝土间滑移量较小,均不大于1 mm。随着荷载不断增大,滑移量逐渐增大。当翼缘板向内鼓起接近失稳时,位移计读数明显增加,滑移量迅速增大。
从图9可看出,在加载初期,连接件与混凝土间滑移量较小,均不大于0.7 mm,随着加载的进行,荷载-滑移曲线斜率逐渐变小,不再线形增长,此时裂缝开始出现。随着加载的继续,滑移迅速增长,直到破坏,最终各试件的最大滑移量均不超过5 mm。
从图8和图9可看出,试件bw-A5的曲线的发展规律与其余4个试件的曲线发展规律不尽相同,却与翼缘板未失稳试件的发展规律类似,但bw-A5的破坏形态为翼缘板发生失稳,因此可认为该试件处于两种破坏模式的临界状态。
从图10可看出,所有试件在加载开始时都保持了良好的弹性变形,荷载-滑移曲线的斜率随着试验加载值的不断增加而减小。两种破坏模式试件曲线差异表现在:(1)上部位移计因翼缘板失稳读数较大,导致曲线斜率较小;(2)翼缘板失稳无法继续传递荷载导致这些试件提前破坏,因此其极限承载力均低于翼缘板未发生失稳试件的极限承载力。
3 抗剪承载力分析
通过表4可发现,试件bw-A7极限承载力较试件bw-A6极限承载力提高了10.4%,这说明在其他参数一样的条件下,当贯穿钢筋直径由16 mm增加至22 mm时,连接件的极限承载力也随之提高。
通过分析试验结果并按照参考文献中算式计算承载力可以发现:
表4 试件试验结果
Table 4 Test results of test specimens
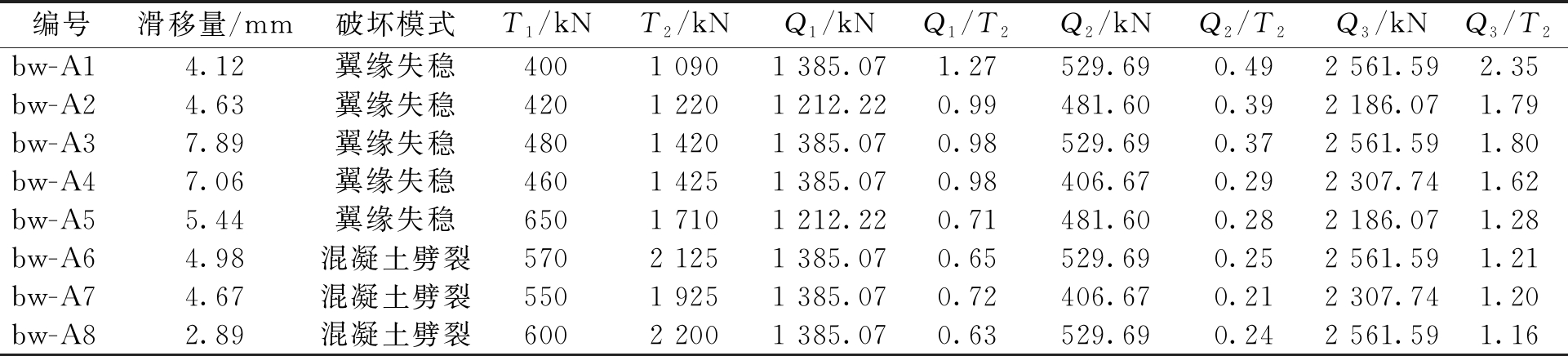
编号滑移量/mm破坏模式T1/kN T2/kNQ1/kNQ1/T2Q2/kNQ2/T2Q3/kNQ3/T2bw-A14.12翼缘失稳4001 0901 385.071.27529.690.492 561.592.35bw-A24.63翼缘失稳4201 2201 212.220.99481.600.392 186.071.79bw-A37.89翼缘失稳4801 4201 385.070.98529.690.372 561.591.80bw-A47.06翼缘失稳4601 4251 385.070.98406.670.292 307.741.62bw-A55.44翼缘失稳6501 7101 212.220.71481.600.282 186.071.28bw-A64.98混凝土劈裂5702 1251 385.070.65529.690.252 561.591.21bw-A74.67混凝土劈裂5501 9251 385.070.72406.670.212 307.741.20bw-A82.89混凝土劈裂6002 2001 385.070.63529.690.242 561.591.16
注:T1为试件单侧弹性承载力;T2为试件单侧极限承载力;Q1为式(2)所得理论值;Q2为式(3)所得理论值;Q3为式(1)所得理论值。
(1)对比T2和Q1,除试件bw-A5外,其余4个翼缘板失稳试件试验值比Q1小,原因是位移计因上部翼缘板失稳而无法继续记录数据,试验提前结束,此时混凝土仅局部破坏;对于翼缘板未失稳试件,试验值则大约为计算值的1.5倍,可知翼缘板存在,使得连接件的纵向刚度明显提高,改变了波纹板嵌入段的边界条件,进而斜板段混凝土抗剪齿键充分受压,提高了连接件的承载力。
(2)对比T2和Q2可发现,所有试件试验值均大于混凝土销的受剪承载力理论值,因此该连接件的混凝土销受剪承载力满足规范[13]要求,试验中也未发现混凝土销破坏的现象。
(3)对比T2和Q3可发现,翼缘板未发生失稳的试件T2与Q3较为接近,但均比Q3约小20%,原因是两种连接件的结构形式不同,受力机制也有所不同,因此对于笔者所提出的连接件仅具有一定的理论参考意义。
因此,对于笔者研究的连接件,如果翼缘板未发生失稳现象,式(2)的计算结果偏于保守。可借鉴嵌入式连接件承载力计算公式,加强混凝土影响系数,并参考开孔波折板计算公式进行修正。
4 结论
笔者针对带翼缘板嵌入式连接件,通过推出试验对其抗剪承载力、滑移、破坏模式等几个方面进行了研究和分析,得出以下结论:
(1)此种连接件的翼缘板起到提高波纹板纵向刚度的作用。试件破坏模式分为两类,翼缘板失稳破坏与混凝土劈裂破坏。
(2)翼缘板失稳试件的翼缘板宽厚比较大并失稳,试验提前结束,最终混凝土仅发生局部破坏。
(3)翼缘板未发生失稳试件的混凝土板裂缝发展完全,裂缝处混凝土存在压碎的情况。最终混凝土板板厚处裂缝形状为从下到上直线贯穿,板宽处的裂缝形状为波纹形。
(4)未失稳试件试验值比现有嵌入式连接件理论值大,除现有算式偏于保守这个原因外,还因为翼缘板的存在,提高了波纹板的纵向刚度,使得斜板处的混凝土充分受压,进而提高了连接件的承载力。
(5)建议设计中采取构造要求如控制翼缘宽厚比,防止翼缘板发生局部失稳现象。
[1] 李现辉, 李国强. 腹板嵌入式组合梁中抗剪连接件推出试验[J]. 建筑结构学报, 2009, 30(4): 78-84.
[2] 刘保东, 任红伟, 李鹏飞. 考虑波纹钢腹板箱梁特点的挠度分析[J]. 中国铁道科学, 2011, 32(3): 21-26.
[3] 武海鹏,李杰,陈淮.变截面波形钢腹板组合箱梁剪应力及剪力传递效率分析[J]. 郑州大学学报(工学版),2017,38(2): 83-87.
[4] 王东炜, 张奇伟, 王用中. 基于模态分析的鄄城黄河公路大桥优化设计[J]. 郑州大学学报(工学版), 2010, 31(6): 1-5.
[5] 陈宜言. 波形钢腹板预应力混凝土桥设计与施工[M]. 北京: 人民交通出版社, 2009.
[6] 陈宝春, 黄卿维. 波形钢腹板PC箱梁桥应用综述[J]. 公路, 2005, 50(7): 45-53.
[7] 陈建斌,万水,尤元宝. 开孔波折板连接件破坏机理及承载力试验研究[J]. 建筑结构, 2013,43(12): 74-80.
[8] MUTASHAR R, SARGAND S, AL RIKABI F T, et al. Response of a composite-adjacent box beam bridge with skewed beams under static and quasi-static loads[J]. Journal of performance of constructed facilities, 2019, 33(3): 04019022.
[9] 聂建国. 钢-混凝土组合梁结构: 试验、理论与应用[M]. 北京: 科学出版社, 2005.
[10] 吴继峰,汤意,吴萍. 卫河大桥波形钢腹板箱梁的设计[J].公路, 2010,(1): 57-61.
[11] 胡建华, 叶梅新, 黄琼. PBL剪力连接件承载力试验[J]. 中国公路学报, 2006, 19(6): 65-72.
[12] 程 宸,江越胜,蔡建中,等. 嵌入式双排孔抗剪连接件极限承载力[J]. 东南大学学报(自然科学版), 2016,46(2):341-346.
[13] 万水. 一种翼缘型抗剪连接件:中国CN201053146 [P].2008-04-30.
[14] 李淑琴, 万水. 钢-混组合结构开孔波折板剪力件静载推出试验[J]. 长安大学学报(自然科学版), 2015, 35(2): 75-82.
[15] 深圳市市政设计研究院有限公司.波形钢腹板组合梁桥技术标准:CJJT 272—2017[S]. 北京:中国建筑工业出版社,2017.
[16] European committee for standardization.Eurocode 4:Design of composite steel and concrete structures:BS EN 1994-1-1:2004.[S]. London:British standards institution,2005.