0 引言
由于能源危机、环境污染和气候变化,替代可再生能源的需求显著增加[1]。太阳能作为一种安全和清洁的可再生能源,近来得到了广泛关注[2]。太阳能主要应用于光伏发电,由于光伏发电系统能够直接将太阳能转换为电能,因此已在全球范围内应用。然而,由于对天气和环境因素的依赖性,特别是受温度和光辐射的影响,使得采用太阳能光伏系统发电成为了一项重要的挑战[3-4]。为了提高光伏发电的效率,需要根据测量的电压-电流数据来提取出准确的光伏模型参数。因此,高效提取PV模型参数的方法就变得尤为重要。目前,解决PV模型参数提取的方法主要是一些分析方法和确定性方法。分析方法实现起来很简单并且能够快速得到问题的解决方案,但需要做出某些假设,这可能会导致提取的参数不一定准确。对于确定性方法,如Newton-Raphson方法[5]等,它们对初始值非常敏感。更重要的是,确定性方法对目标函数有着严格的要求:连续、可微和凸函数。
近些年来,智能优化算法引起了越来越多的关注。许多研究者尝试用智能优化算法去提取PV模型的参数,如模式搜索(PS)[6]、模拟退火(SA)[7]、差分进化(DE)[8]、粒子群优化(PSO)[9]、基于教学优化(TLBO)[10]等。PS简单易实现,但对于不可导问题求解时比较困难;SA局部搜索能力强,而全局搜索能力差,容易受参数的影响;DE简单有效但受控制参数影响较大;PSO有着很强的局部搜索能力,却容易陷入局部最优[11];TLBO简单高效却收敛较慢。另外,这些智能优化算法在提取PV模型参数时,通常需要消耗大量的计算资源。因此,提出了一种基于自适应的差分演化算法,对不同的PV模型进行了参数提取,并且与已有智能优化算法的结果进行了比较。实验结果表明,提出的算法在PV模型参数提取中有着很大的优越性。
1 PV模型及目标函数
在实际应用中主要有两种广泛使用的模型来描述PV系统的V-I特性:单二极管模型和双二极管模型。
1.1 单二极管模型
根据单二极管模型的等效电路[8],其输出电流I满足式(1):
(1)
式中:Iph为可用于实际供电的光照产生的电流,A;Isd为二极管反向饱和电流,μA;Rs和Rsh分别为光伏电池板的等效串联和并联电阻,Ω;n为二极管理想因子;Vt=kT/q;k为玻尔兹曼常量(1.38×10-23 J/K);q为电子电量(1.6×10-18 C);T为环境温度,K。
1.2 双二极管模型
根据双二极管模型的等效电路[8],其输出电流I满足式(2):
(2)
式中:Isd1和Isd2分别为两个二极管反向饱和电流,μA;n1和n2分别为两个二极管理想因子。
1.3 目标函数
从上述两种模型可以看出,单二极管模型有5个参数待提取:Iph、Isd、Rs、Rsh 和 n;而双二极管模型则有Iph、Isd1、Isd2、Rs、Rsh、n1 和n2 7个参数待提取。直接求解PV模型各个参数十分困难,文献[8]中将参数提取问题转化为非线性最优化问题,可建立优化目标函数如式(3)所示:
(3)
式中:X包含各个模型待提取的参数;N为V-I数据集的个数;f(Vk,Ik,X)=Isim-Ik,即为仿真电流Isim与实验电流Ik的差值;采用均方根误差RMSE作为评价目标,即RMSE表示所有的仿真电流和实验电流的误差的平方和,这意味着RMSE越小,所提取到的参数越准确。
2 差分演化算法
差分演化算法(differential evolution, DE)[12]最初由Storn和Price在1997年提出,主要用于求解数值优化问题。在差分演化算法中,主要包含4种操作:初始化、变异、交叉和选择。
初始化:一般种群中有NP个个体(每个个体Xi表示一组解向量),初始化则是将每个个体在边界范围内随机产生一组值,如式(4)所示:
Xi,j=LBj+rand(UBj-LBj),
(4)
式中:LBj和UBj分别表示第j维的上下边界;j为1到D(维数)之间的整数;rand为0到1之间的随机数。
变异:变异操作是差分演化的核心部分,主要用于产生新的个体,常用的变异策略为DE/rand/1、DE/best/1、DE/current-to-best/1等,其中DE/rand/1策略如式(5)所示:
Vi=Xr1+F·(Xr2-Xr3),
(5)
式中:Vi为第i个个体的变异向量;r1、r2、r3为3个不同的1到NP之间的随机整数,且不等于i。
交叉:为了保持种群的多样性,DE算法在突变之后,采用交叉操作。通过将目标向量与突变向量进行交叉,得到试验向量。常用的有二项交叉和指数交叉,其中二项交叉如式(6)所示:
(6)
式中:CR为交叉率;jrand为1到D之间的随机整数。
选择:采用贪婪的思想,在试验向量和目标向量之间,选择更好的作为下一代的个体,如式(7)所示:
(7)
式中:f(Xi)为Xi对应的目标函数值。
3 自适应差分演化算法
传统的DE算法有3个参数:缩放因子F、交叉因子CR和种群大小NP。其中F和CR的取值对算法有非常大的影响,所以自适应差分演化算法有着广阔的前景。为了准确快速地提取PV模型参数,提出了一种新型变异策略自适应DE算法(SADE)。
3.1 新型变异策略
DE/rand/1策略,这种策略从随机群体中选择3个向量进行突变,然后在3个向量中随机选择基本向量,再将其他两个矢量的差矢量添加到基矢量上。 虽然这种策略能够保持种群多样性和全局搜索能力,但是没有任何确定的搜索方向,导致收敛速度慢。DE/best/1策略,这种策略虽然收敛快,但是总是朝着最优个体的方向搜索,容易陷入到局部最优。之后,为了更充分地利用贪婪思想,JADE[13]引入了一种新的变异策略:DE/current-to-pbest/1,这种策略在解决各种问题上被证明是一种非常成功的策略。DE/current-to-best/1策略,它在全局搜索和局部搜索中有着一定的平衡能力,是一种成功的策略。笔者提出的新突变策略可以显著提高DE算法的搜索能力,并增加在复杂和大规模优化问题中实现有希望和成功结果的可能性,这是差分演化算法研究中的一个重要的开放挑战。因此,笔者采用新的变异策略,引导个体朝着有希望的且远离希望较小的区域搜索,以提高算法的收敛速度。提出的变异策略如式(8)所示:
Vi=Xi+Fi(Xpbest-Xi)-ωi(Xi-Xpworst),
(8)
式中:Xpbest和Xpworst分别为种群中个体适应值由小到大排序后的前p%和后p%个体;Fi为第i个个体朝着有希望方向的缩放因子;ωi为第i个个体远离希望较小的区域搜索的缩放因子。
笔者提出的新型变异策略采用p%的贪婪原则,能够使得种群中的个体朝着希望较大的区域但又不总是同一个有希望的区域搜索;能够远离一些没有希望的搜索区域,但又不总是同一个没有希望的区域,这对提高DE算法的收敛速度是非常有效的。
3.2 参数自适应
综合上述,提出的DE算法主要有F、CR、ω、NP和p 5个参数,其中NP保持20固定不变,而p根据JADE中给出的比较好的取值范围,保持0.2不变。
对于F和ω,采用JADE中自适应方式如下:
Fi=randc(μF,0.1),
(9)
ωi=randc(μω,0.1),
(10)
μF=(1-c)μF+c·meanL(SF),
(11)
μω=(1-c)μω+c·meanL(Sω),
(12)
式中:randc为柯西分布;μF和μω的初值均为0.5;c为0.1;SF和Sω为成功缩放因子的集合;meanL为赖默均值,详细描述见JADE[13]。
对于CR自适应,每个个体的交叉率CRi的产生方式如下:
CRi=randn(μCR,0.1),
(13)
式中:randn为正态分布;μCR初始值为0.5,一代结束后,μCR采用式(14)更新:
μCR=(1-c)·μCR+c·meanA(SCR),
(14)
式中:meanA为算术平均值;SCR为成功交叉率的集合。
3.3 SADE算法及其应用
新型变异策略的自适应DE算法(SADE)用来提取PV模型的参数的计算流程如图1所示。初始化时,使待提取的PV参数在规定的范围内均匀产生,经过新型的变异策略进行变异,得到变异向量,再经过交叉和选择操作得到下一代个体。如果给定的最大函数评价次数没用完则采用自适应的方式去更新控制参数μF、μω和μCR,直至最大函数评价次数耗尽,输出提取的参数。
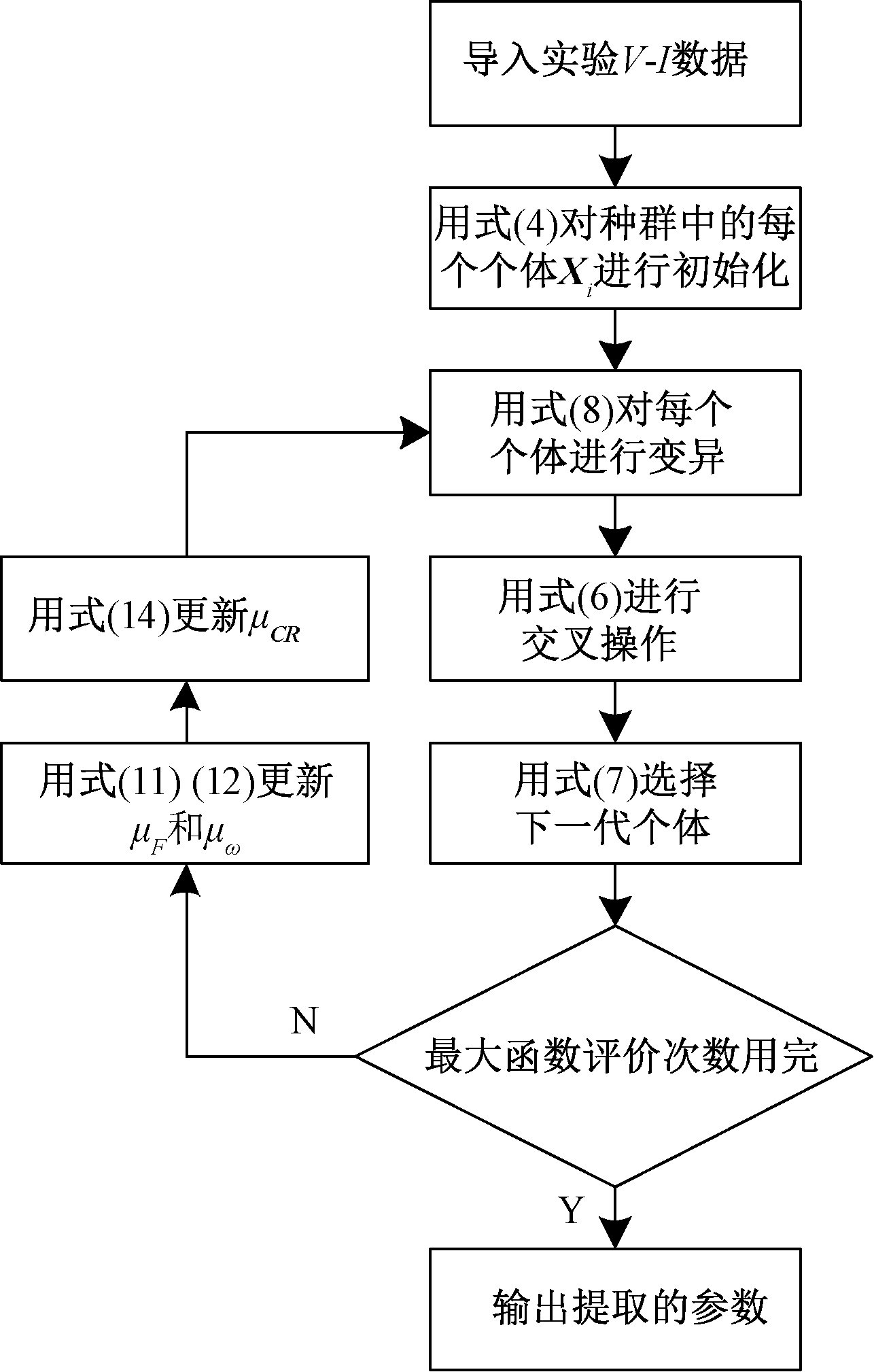
图1 SADE算法流程图
Figure 1 Flowchart of SADE algorithm
4 实验结果
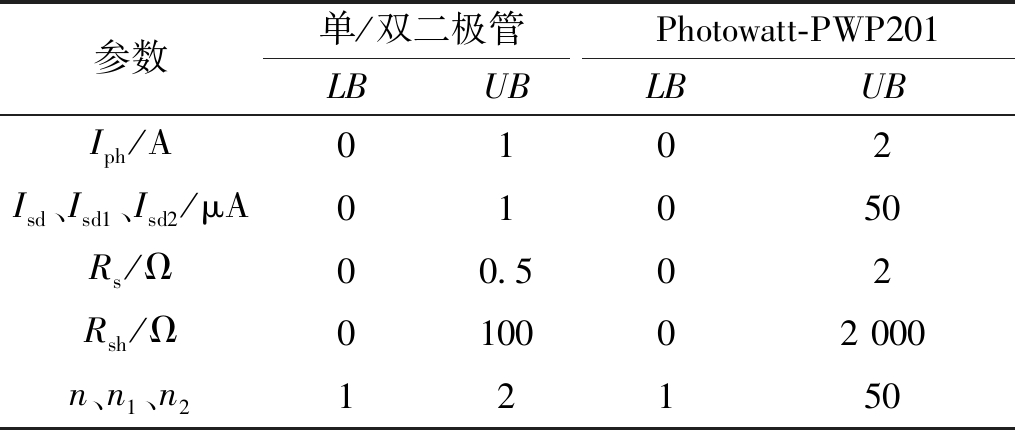
为了验证SADE的性能,它被用于提取单二极管模型,双二极管模型和PV组件模型的参数。其中,单、双二极管的数据均来自于33 ℃,57 mm直径的商业硅R.T.C.法国太阳能电池[5],PV组件模型的数据来自于45 ℃的多晶Photowatt-PWP201电池[5],所有待提取的参数范围如表1所示。所有模型的SADE的实验结果都是在Win7操作系统MATLAB2016b下独立运行30次获得的结果。
表1 待提取的参数范围
Table 1 Range of parameters to be extracted
参数单/双二极管Photowatt-PWP201LBUBLBUBIph/A0102Isd、Isd1、Isd2/μA01050Rs/Ω00.502Rsh/Ω010002 000n、n1、n212150
将SADE算法的实验结果与一些效果比较好的算法进行了比较,比较结果如表2、3和4所示。
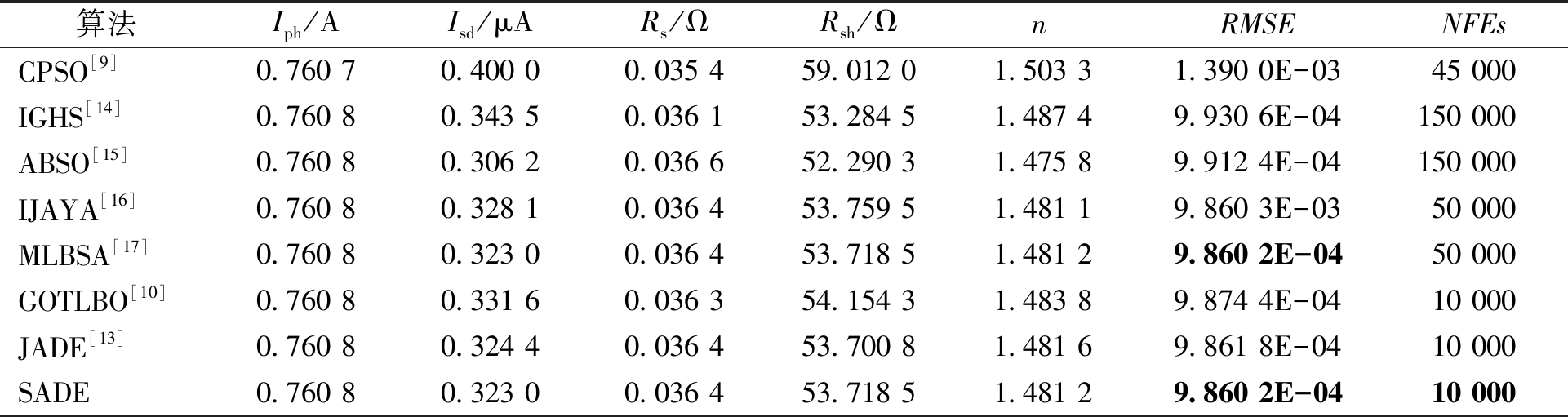
对于单二极管模型,从表2中可以看出,虽然SADE和MLBSA算法取得了最小的RMSE值,但是笔者提出的SADE只消耗了10 000次函数评价次数(NFEs),MLBSA却消耗了50 000次。其次是IJAYA、JADE、GOTLBO、ABSO、IGHS和CPSO。
表2 单二极管模型不同参数提取方法的比较
Table 2 Comparison of different parameter extraction methods for single diode model
算法Iph/AIsd/μARs/ΩRsh/ΩnRMSENFEsCPSO[9]0.760 70.400 00.035 459.012 01.503 31.390 0E-0345 000IGHS[14]0.760 80.343 50.036 153.284 51.487 49.930 6E-04150 000ABSO[15]0.760 80.306 20.036 652.290 31.475 89.912 4E-04150 000IJAYA[16]0.760 80.328 10.036 453.759 51.481 19.860 3E-0350 000MLBSA[17]0.760 80.323 00.036 453.718 51.481 29.860 2E-0450 000GOTLBO[10]0.760 80.331 60.036 354.154 31.483 89.874 4E-0410 000JADE[13]0.760 80.324 40.036 453.700 81.481 69.861 8E-0410 000SADE0.760 80.323 00.036 453.718 51.481 29.860 2E-0410 000
另外,利用提取到的参数进行仿真电流的计算,将得到的仿真电流与测量电流曲线进行对比,如图2所示,可以看出,测量电流与仿真电流有着非常好的拟合性。
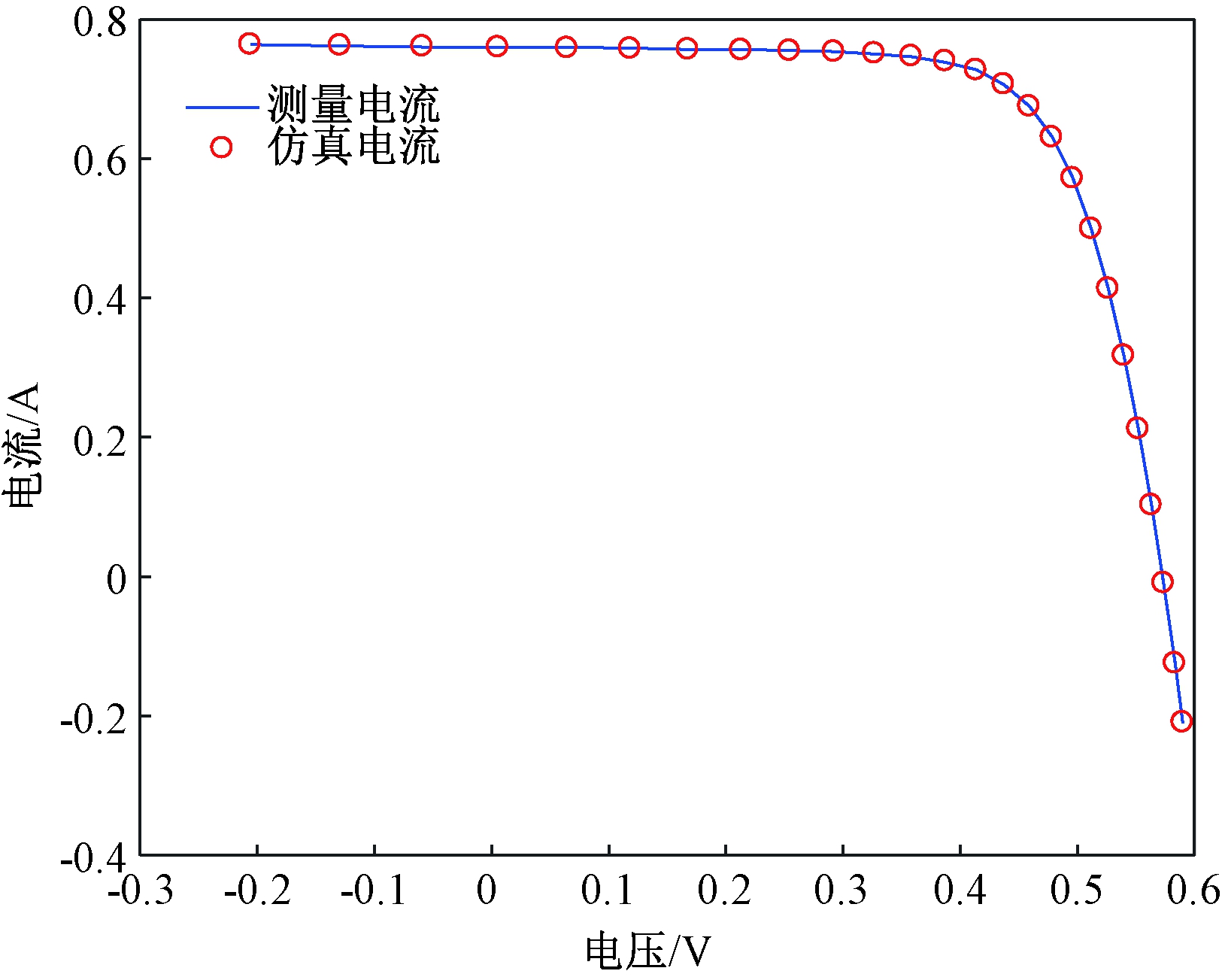
图2 单二极管模型测量数据与仿真数据比较
Figure 2 Comparison of single diode model measured data and simulated data
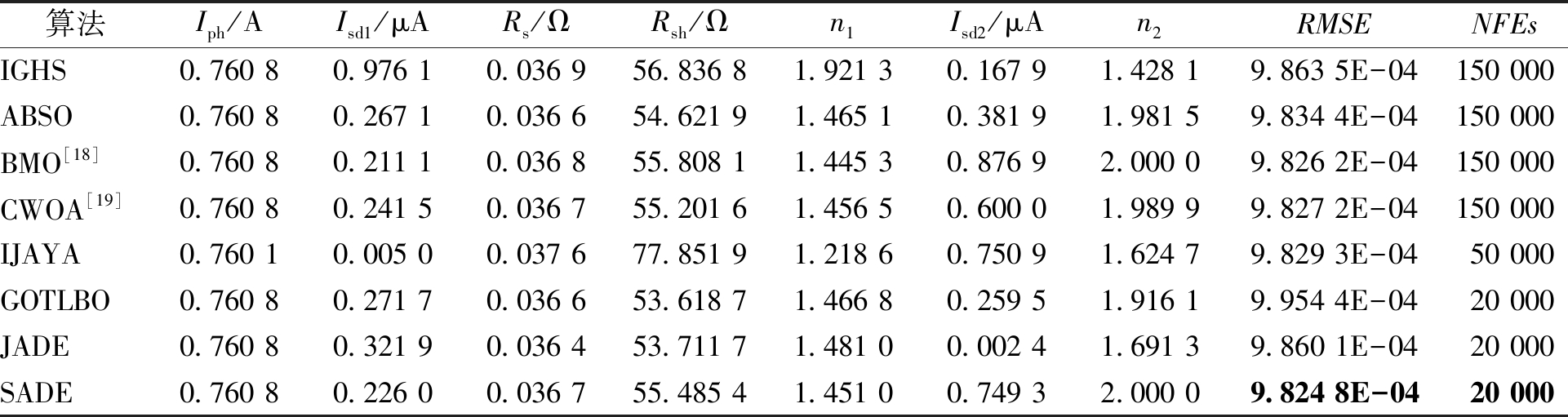
对于双二极管,有7个参数待提取。由表3的比较结果可知,SADE取得了最好的RMSE值(9.824 8E-04),并且使用的函数评价次数最少。BMO、CWOA和IJAYA的结果虽然很接近最优值的结果,但是消耗了大量的函数评价次数,也就是消耗了大量的计算资源。其余的几种参数提取方法也消耗了大量的计算资源,且提取的参数不够准确。图3的测量数据与仿真数据高度拟合也证明了笔者提出的SADE方法能够提供更准确的参数值。
表3 双二极管模型不同参数提取方法的比较
Table 3 Comparison of different parameter extraction methods for double diode model
算法Iph/AIsd1/μARs/ΩRsh/Ωn1Isd2/μAn2RMSENFEsIGHS0.760 80.976 10.036 956.836 81.921 30.167 91.428 19.863 5E-04150 000ABSO0.760 80.267 10.036 654.621 91.465 10.381 91.981 59.834 4E-04150 000BMO[18]0.760 80.211 10.036 855.808 11.445 30.876 92.000 09.826 2E-04150 000CWOA[19]0.760 80.241 50.036 755.201 61.456 50.600 01.989 99.827 2E-04150 000IJAYA0.760 10.005 00.037 677.851 91.218 60.750 91.624 79.829 3E-0450 000GOTLBO0.760 80.271 70.036 653.618 71.466 80.259 51.916 19.954 4E-0420 000JADE0.760 80.321 90.036 453.711 71.481 00.002 41.691 39.860 1E-0420 000SADE0.760 80.226 00.036 755.485 41.451 00.749 32.000 09.824 8E-0420 000
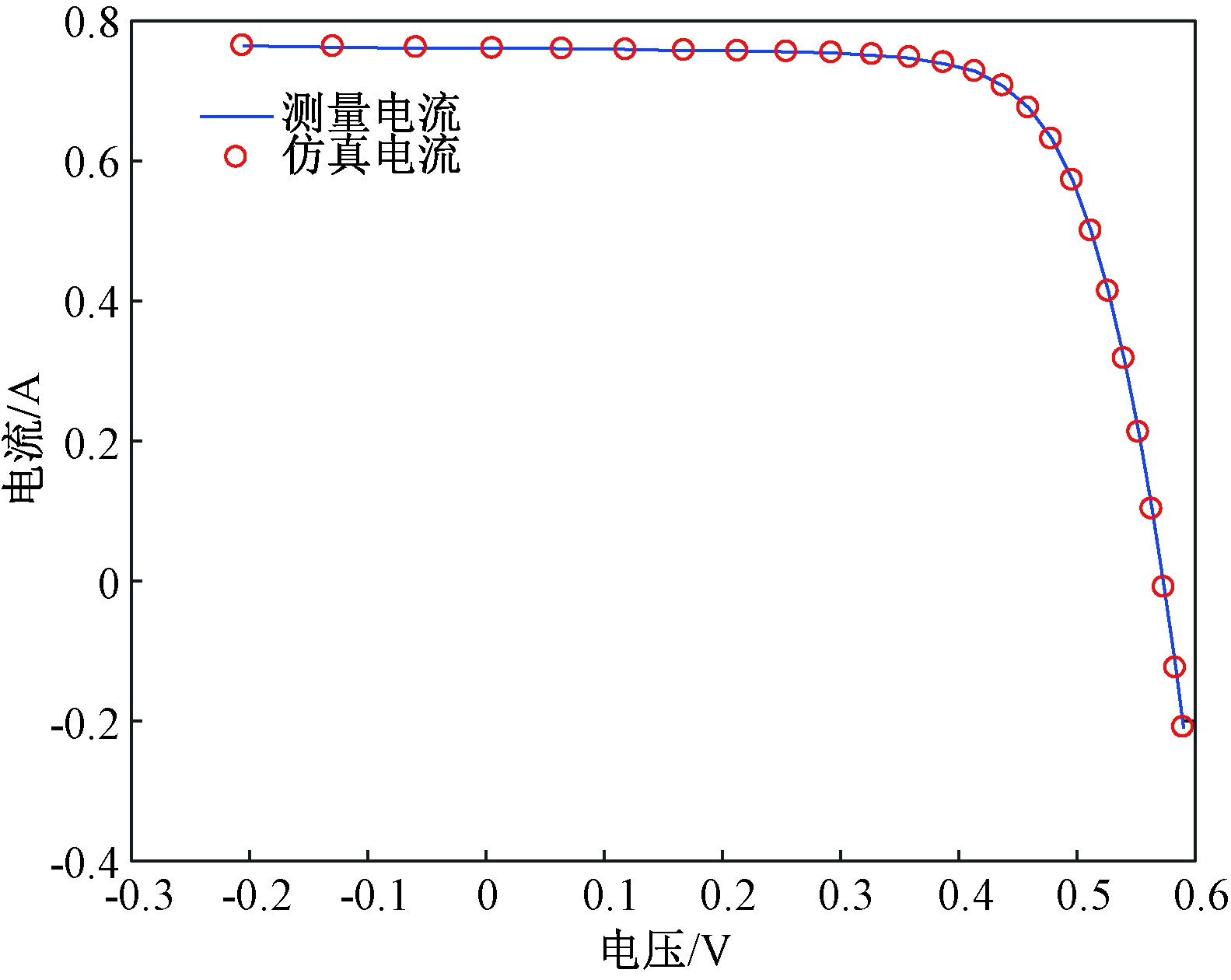
图3 双二极管模型测量数据与仿真数据比较
Figure 3 Comparison of double diode model measured data and simulated data
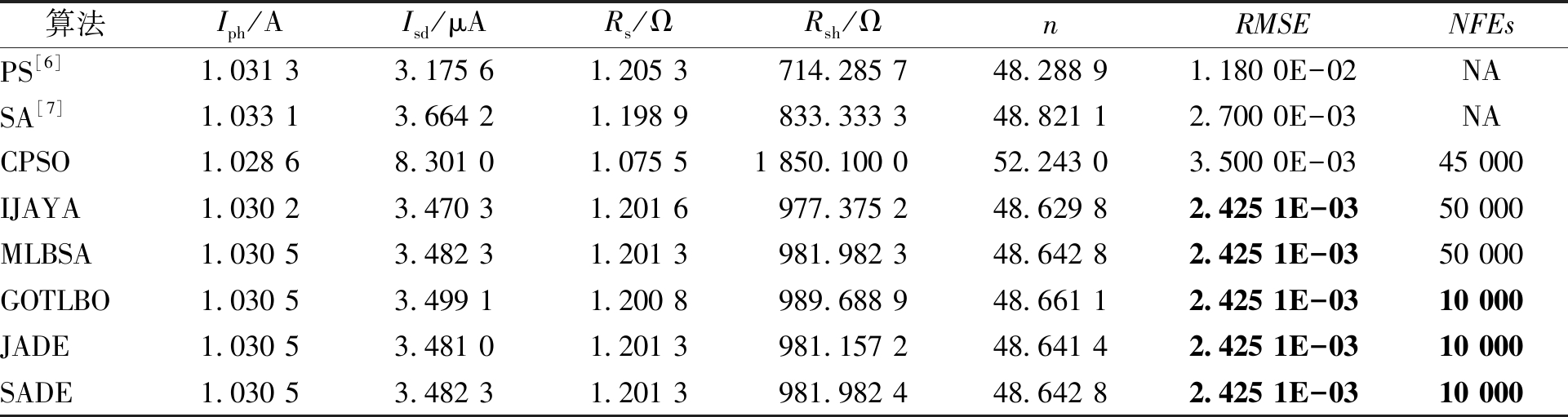
对于Photowatt-PWP201模型,从表4中可知,SADE、JADE和GOTLBO取得了最好的RMSE值(2.425 1E-03)以及消耗最少的函数评价次数(10 000);IJAYA和MLBSA虽然取得了同样的RMSE值,却消耗了50 000次函数评价次数;其次是CPSO、SA和PS,其中SA和PS所用的函数评价次数在原文中无法获取(NA)。像前面两种模型一样,将SADE利用提取到的参数得到的仿真数据与测量数据进行了拟合对比,如图4所示。可以看出,仿真数据与测量数据仍然有着良好的拟合性。
表4 Photowatt-PWP201模型不同参数提取方法的比较
Table 4 Comparison of different parameter extraction methods for Photowatt-PWP201
算法Iph/AIsd/μARs/ΩRsh/ΩnRMSENFEsPS[6]1.031 33.175 61.205 3714.285 748.288 91.180 0E-02NASA[7]1.033 13.664 21.198 9833.333 348.821 12.700 0E-03NACPSO1.028 68.301 01.075 51 850.100 052.243 03.500 0E-0345 000IJAYA1.030 23.470 31.201 6977.375 248.629 82.425 1E-0350 000MLBSA1.030 53.482 31.201 3981.982 348.642 82.425 1E-0350 000GOTLBO1.030 53.499 11.200 8989.688 948.661 12.425 1E-0310 000JADE1.030 53.481 01.201 3981.157 248.641 42.425 1E-0310 000SADE1.030 53.482 31.201 3981.982 448.642 82.425 1E-0310 000
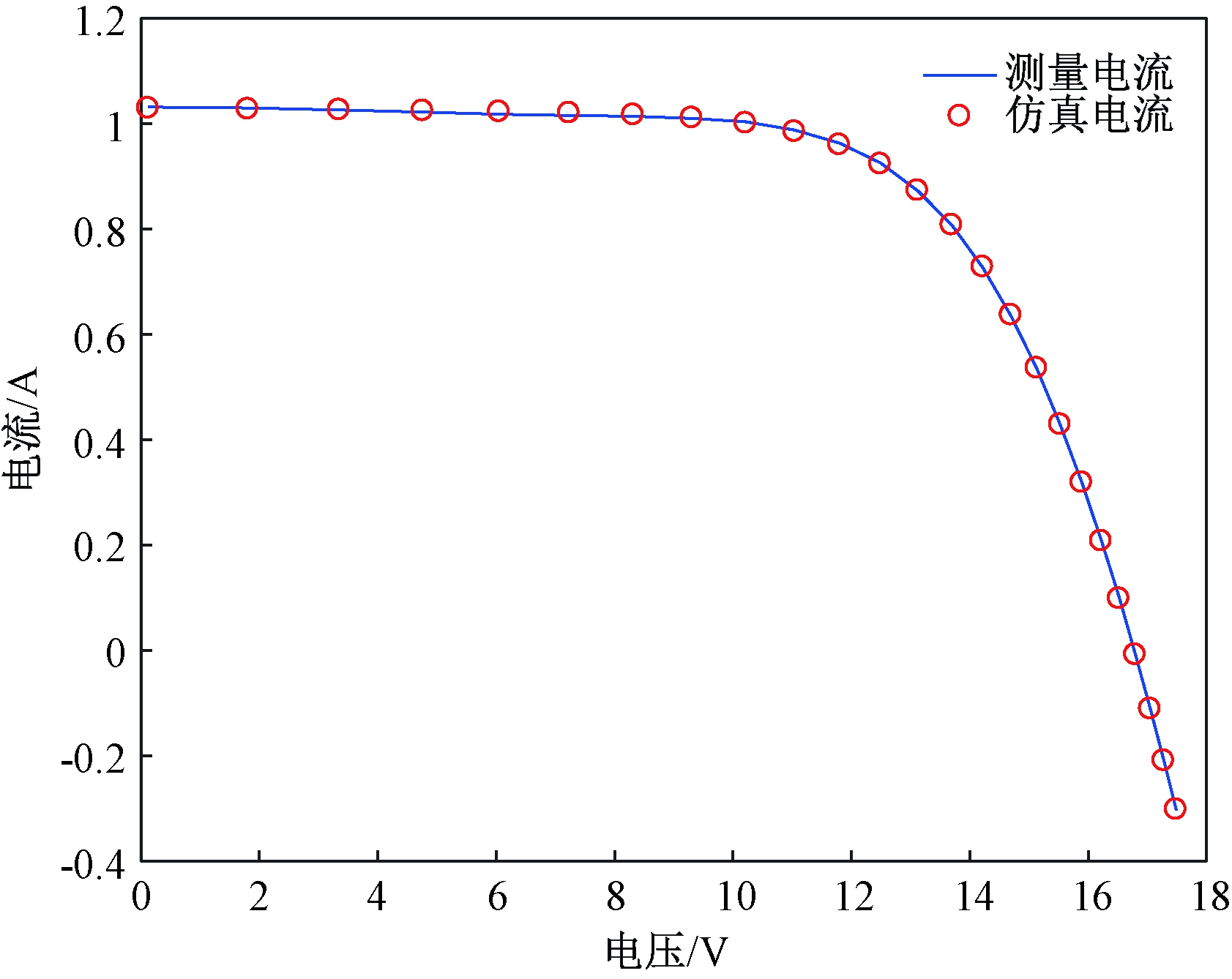
图4 Photowatt-PWP201模型测量数据与仿真数据比较
Figure 4 Comparison of Photowatt-PWP201 measured data and simulated data
5 结论
提出了一种新型的自适应差分演化算法,可以准确快速地提取不同光伏模型的未知参数。在SADE算法中,笔者提出了一种新型的变异策略,能够有效地促使种群中的个体朝着有希望的区域搜索,以提高算法的收敛速度。SADE算法的有效性可以通过单二极管模型、双二极管模型以及PV组件模型的参数提取问题来评估,并且将SADE的结果与一些最近提出的成熟算法进行了比较。结果表明,笔者提出的SADE算法能够提供更准确、更可靠的参数值。因此,SADE算法可以作为一种有效的PV模型参数提取的选择方法。
[1] MUHSEN D H, GHAZALI A B, KHATIB T, et al. Parameters extraction of double diode photovoltaic module’s model based on hybrid evolutionary algorithm[J]. Energy conversion and management, 2015, 105:552-561.
[2] 梁亮,詹智民,邓小磊,等. 基于电导增量法的太阳能光伏阵列MPPT仿真[J]. 郑州大学学报(工学版),2018,39(6):88-92.
[3] 孙园园,肖华锋,谢少军,等. 太阳能电池工程简化模型的参数求取和验证[J]. 电力电子技术,2009,43(6):44-46.
[4] 许天,陈晓强.并联式支路光伏发电系统的研究与仿真[J].郑州大学学报(工学版),2016,37(2): 25-28.
[5] EASWARAKHANTHAN T, BOTTIN J, BOUHOUCH I, et al. Nonlinear minimization algorithm for determining the solar cell parameters with microcomputers[J]. International journal of solar energy, 1986, 4 (1): 1-12.
[6] ALHAJRI M F, El-NAGGAR K M, ALRASHIDI M R, et al. Optimal extraction of solar cell parameters using pattern search[J]. Renewable energy, 2012, 44: 238-245.
[7] EL-NAGGAR K M, ALRASHIDI M R, ALHAJRI M F, et al. Simulated annealing algorithm for photovoltaic parameters identification[J]. Solar energy, 2012, 86 (1): 266-274.
[8] JIANG L L, MASKELL D L, PATRA J C. Parameter estimation of solar cells and modules using an improved adaptive differential evolution algorithm[J]. Applied energy, 2013, 112: 185-193.
[9] JIANG C, XUE L Y, SONG D Y, et al. Solar cells performance testing and modeling based on particle swarm algorithm[C]//International Conference on Computer Science and Information Processing. Xi’an:IEEE, 2012: 562-566.
[10] CHEN X, YU K J, DU W L, et al. Parameters identification of solar cell models using generalized oppositional teaching learning based optimization[J]. Energy, 2016, 99:170-180.
[11] 徐霜,万强,余琍. 基于学习理论的改进粒子群优化算法[J]. 郑州大学学报(工学版),2019,40(2):29-34.
[12] STORN R, PRICE K. Differential evolution-a simple and efficient heuristic for global optimization over continuous spaces[J]. Journal of global optimization, 1997, 11 (4): 341-359.
[13] ZHANG J Q, SANDERSON A C. JADE: adaptive differential evolution with optional external archive[J]. IEEE transactions on evolution computation, 2009, 13 (5):945-958.
[14] ASKARZADEH A, REZAZADEH A. Parameter identification for solar cell models using harmony search-based algorithms[J]. Solar energy, 2012, 86(11):3241-3249.
[15] ASKARZADEH A, REZAZADEH A. Artificial bee swarm optimization algorithm for parameters identification of solar cell models[J]. Applied energy, 2013, 102: 943-949.
[16] YU K J, LIANG J J, QU B Y, et al. Parameters identification of photovoltaic models using an improved jaya optimization algorithm[J]. Energy conversion and management, 2017, 150: 742-753.
[17] YU K J, LIANG J J, QU B Y, et al. Multiple learning backtracking search algorithm for estimating parameters of photovoltaic models[J]. Applied energy, 2018,226: 408-422.
[18] ASKARZADEH A, REZAZADEH A. Extraction of maximum power point in solar cells using bird mating optimizer-based parameters identification approach[J]. Solar energy, 2013, 90: 123-133.
[19] OLIVA D, AZIZ M A E, HASSANIEN A E. Parameter estimation of photovoltaic cells using an improved chaotic whale optimization algorithm[J]. Applied energy, 2017, 200:141-154.