0 引言
随着水泥固化土在道路、高速铁路、港口、填海等工程中的广泛应用，人们已不再局限于从工程应用角度研究增强固化的效果，而是更关注在车辆、风浪等循环或反复荷载作用下水泥固化土的力学性状及其重要影响因素[1-2]，进一步从本构理论的角度出发，深入研究复杂荷载作用下水泥固化土的应力-应变关系[3-4]。
水泥与原状土发生一系列的水化、火山灰和碳化等反应后，水泥固化土的强度与多种因素有关，其中最主要的是其胶结作用[2-4]。由于该胶结作用，水泥固化土呈现明显的结构性，亦称人造结构性土[3-4]。这种胶结作用随剪应力的增加而逐渐退化，其结构性逐渐丧失[1-4]。Kasama等[5]考虑其胶结作用，建立了水泥固化土的临界状态模型。虽然忽略了胶结退化现象，但其通过修正平均有效应力的方法来处理水泥固化土的胶结作用被其后的多个文献[4-8]所采用。如Suebsuk等[4]利用孔隙比的增量关系、Nguyen等[6]假设胶结退化是先期固结压力的函数等所建立的本构关系，由于不排水剪切试验过程水泥土的孔隙比几乎不变，或先期固结压力变化不大，均难以描述不排水条件下的胶结退化现象。常采用的屈服面多为剑桥[7]或修正剑桥模型[4-6,8]的椭圆面，少数采用扩展的Mohr-Coulomb模型[9]，仅考虑单调荷载作用，不便应用于循环等复杂荷载条件。
对于水泥土边界面模型，除对胶结及胶结退化处理的差异外，最大差别在于边界面和加载面的形状及其相互关系的处理和假定[10-12],其研究尚处于初期阶段[12]。具有代表性的是Rahimi等[10]把砂土液化的边界面模型[11]直接应用于水泥固化砂，根据其张拉强度，在平均有效应力p′和剪应力q平面上把边界面左移，但其加载面仍通过坐标原点，使得剪切过程中边界面与加载面的形状无法保持一致，其方法值得商榷。Xiao等[12]基于塑性功硬化定律，其屈服面随剪切过程黏聚力的减小由非椭圆形状逐步接近于椭圆。多个文献所提出的水泥固化土边界面模型，一些仅讨论了单调荷载条件[10,12]，大多数没有给出模型参数的拟合方法[12-14]。由于对胶结及胶结退化的描述，其模型参数一般有13～15个[10,12-13]，甚至更多[14]，参数拟合方法及方便性显得十分重要[8,12]。
本文基于Nguyen等[8]对剪切过程胶结退化的描述，通过修正平均屈服有效应力的方法建立水泥固化土的边界面双面模型，详细讨论了模型参数的拟合方法和步骤。通过对固结不排水试验数据和模拟结果对比分析及循环荷载作用的算例分析，验证了本文模型和数据拟合方法的可靠性和正确性，为水泥固化土及结构性黏土本构理论的研究提供一个有效方法。
1 胶结退化参数拟合
典型的水泥固化土等压固结试验结果如图1所示[1]。当平均有效应力p′较小时，孔隙比e和lg p′的关系近似于直线，称为弹性压缩线；当p′较大时，逐渐趋近于另一直线，该直线可认为是理论上重塑水泥固化土的等压固结线(ICL)[1,5-6]，本文称为参考ICL，即RICL。试验结果表明[1,3,5-6,8]，由于胶结作用，水泥固化土的等压固结曲线在其RICL的上方，并随压力的增加趋近于RICL，这与结构性黏土的固结特性类似[3]。
文献[1,3,8]认为，初始弹性段和RICL的斜率(分别用κ和λ表示)与土的结构性无关，可采用与修正剑桥模型参数类似的方法近似确定。文献[8]采用文献[1]的建议，κ由重塑土或添加少量固化剂后的等压固结曲线确定，而λ的确定需要引入水泥固化土RICL与重塑土ICL孔隙比的差值。本文在参数拟合过程中，κ和λ由水泥固化土等压固结试验结果的初始段和渐进段按Δe/Δln p′直接拟合计算，κ=0.044，λ=0.446。经对文献[1,4,8]中试验结果的拟合分析，其效果较好。图1显示了掺和量6%(质量分数，下同)水泥固化Ariake黏土压缩曲线拟合的参数和效果。图1中，M为平均有效应力p′和剪应力q平面上临界状态线的斜率(本例M=1.58)，pb为弹性压缩线与RICL交点所对应的应力，e0为参考状态(p′=1 kPa)的孔隙比(本例e0=4.37)。为了描述这种与结构性黏土类似的固结特性，采用修正平均有效应力的方法[6,8]，其修正后的应力比η为
η=q/(p′+pt)。
(1)
式中：pt为胶结作用对抗剪强度的贡献。
抗剪强度包线为
q=Mp′+c=M(p′+ξpt)。
(2)
式中：c为水泥固化土的黏聚力；ξ为胶结作用对抗剪强度贡献的影响因子。
为了描述水泥固化土的胶结作用和剪切过程中的胶结退化现象，pt采用如下表达式[8]：
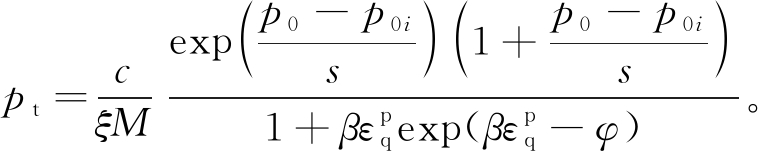
(3)
式中：p0为平均有效屈服应力；p0i为初始平均有效屈服应力(图1)；s为平均有效应力对胶结作用退化速率的影响参数；
为塑性偏应变；β和φ为胶结作用剪切退化速率参数。
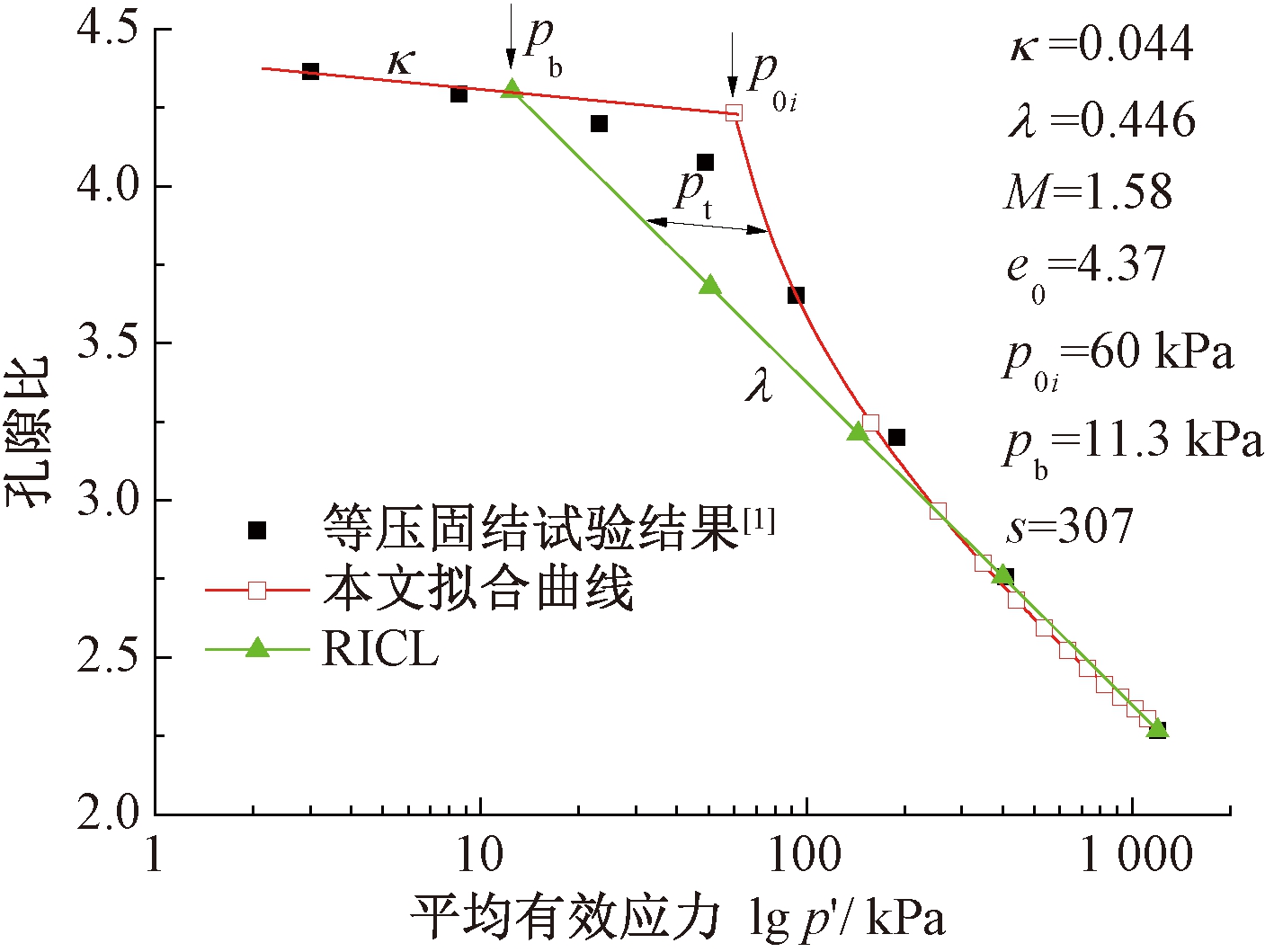
图1 6%水泥固化Ariake黏土压缩曲线[1]和拟合曲线
Figure 1 Fitting curves and compression tests[1] of 6% cement-treated Ariake clay
修正后的平均有效应力p*为
p*=p′+pt。
(4)
上式可理解为：水泥固化土等压固结线上的平均有效应力p*由重塑的水泥固化土即RICL上的应力p′和维持其结构性所需要的压力pt两部分组成。
以上对水泥固化土胶结作用和剪切过程胶结退化现象的描述，除不考虑结构性影响的临界状态参数κ、λ和M及孔隙比e0外，又引入了6个参数：p0i、s、c、ξ、β、φ。参数κ、λ和M及孔隙比e0可采用类似于临界状态参数的确定方法估算，或由上述所描述的方法近似确定。新引入的6个参数，可由等压固结线和三轴剪切试验结果拟合得到。其拟合方法和步骤如下。
(1)p0i和s。把水泥固化土等压固结线的初始弹性段适当延长并与曲线段相交，近似确定p0i，待确定s后可适当对其调整。这与先期固结压力的确定有些类似。得到p0i后，即得到pt的最大值pti=p0i-pb。
不考虑塑性应变偏量的影响，式(3)改写为
(5)
对等压固结试验离散点进行最小二乘拟合，令式(5)中的p0为p*，采用对数距离，有
(6)
式中：
为等压固结试验离散点
所对应的平均有效应力；p′取为过点
斜率为κ的直线与RICL交点的平均有效应力。公式省略了下标k，k=1,2,…,n，n为离散点数(扣除初始段接近于直线段的点)。p′和相应的孔隙比e′为
(7)
(8)
式中：eλ为RICL上p′=1 kPa所对应的e值。
式(6)仅包含一个变量s，可由最小二乘运算求得。本算例拟合后得到s=307，拟合曲线如图1所示。
(2) c和ξ。参数c可由水泥固化土不同围压下p′-q曲线峰值点的包线延长线与q轴的交点得到，或由p′-q曲线的峰值强度qpeak与相应的p′值由c=q-Mp′求得，可取不同围压下c值的平均值。参数ξ可根据已经求得的c和pti值，由式pti=c/(ξM)求得。在本算例中，求得c=54 kPa，ξ=0.702。
(3) β和φ。这两个参数可通过三轴剪切试验尤其是固结不排水剪切试验(CU)q-εq曲线拟合得到[8]。由于q-εq曲线在达到峰值强度之前上升很快，初始阶段的剪切变形主要以弹性变形为主，自峰值强度至残余强度的剪切过程中，主要以塑性剪切变形为主[3,8]，可从峰值强度点至残余强度段进行拟合计算，并忽略该阶段的弹性剪切变形。近似假定峰值点对应于q-Mp′=c，其塑性偏应变
残余强度对应于q-Mp′=0，之间对q进行插值。其表达式为
(9)
对文献[1]图8中围压为400 kPa的q-εq曲线进行拟合计算，得到的曲线和拟合参数值如图2所示。
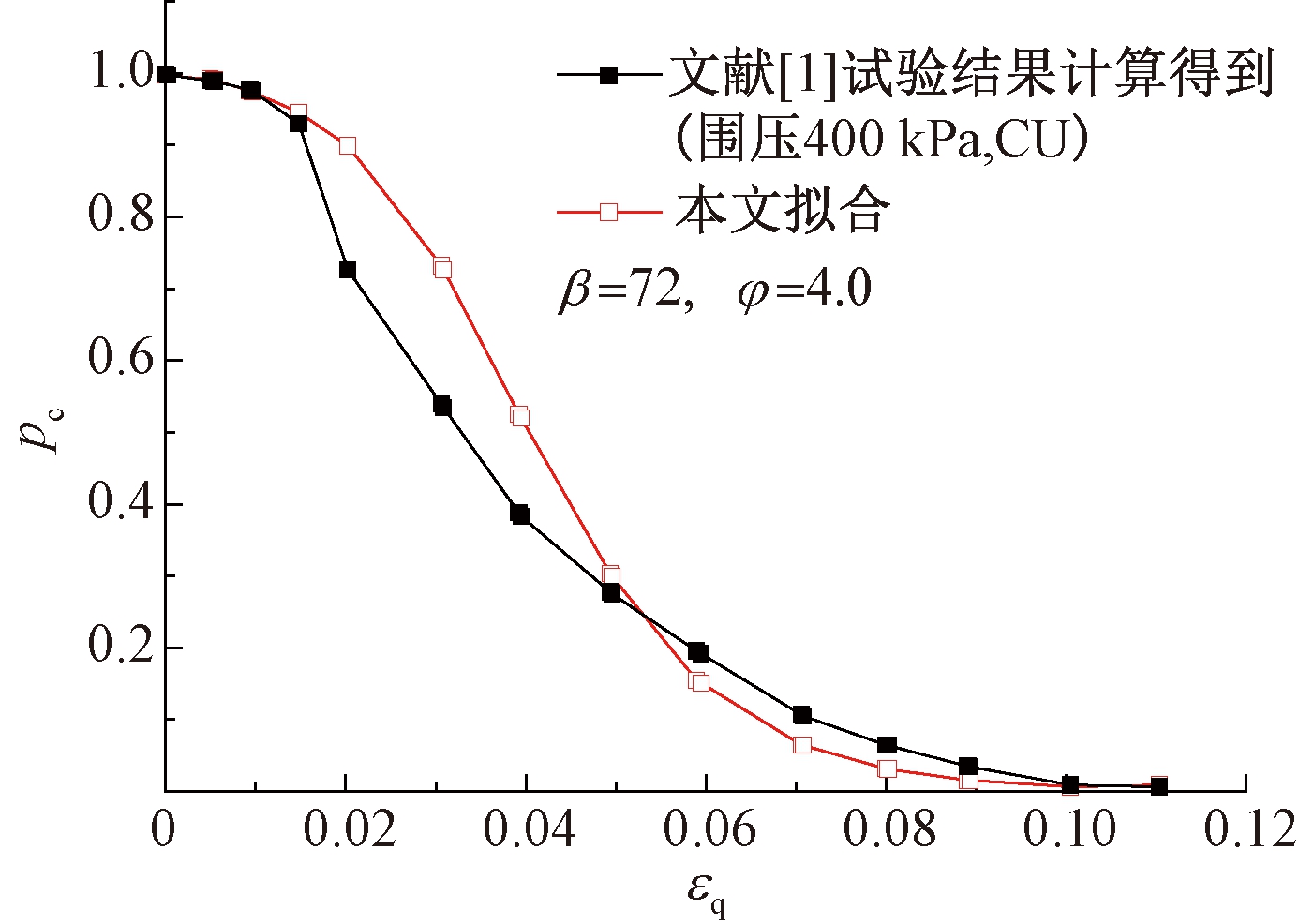
图2 6%水泥固化Ariake黏土参数β和φ拟合
Figure 2 Fitting parameters β and φ on 6% cement-treated Ariake clay
以上参数拟合，除式(3)需要借助于绘图工具外，其他可由所编制的C++程序计算完成。
2 边界面模型
对于描述复杂荷载条件下水泥固化土及结构性黏土的应力应变关系，边界面模型具有很大的优越性[10,14-15]。边界面的形状，需要借助于土的三轴剪切试验，尤其是不排水剪切试验来确定[15-16]。本文将UNSW边界面模型[15-17]进行修正，扩展应用于水泥固化土。
2.1 边界面与加载面
考虑水泥固化土的胶结作用，在p′-q应力空间，修正后的边界面定义为
(10)
式中：N和R为模型参数，其中N控制边界面的曲率；M为p′-q空间中临界状态线(CSL)的斜率；
控制边界面的尺寸，
为硬化参量，是边界面与p′轴右侧交点的横坐标(图3)；
和
为与当前应力p′和q相对应的像应力。
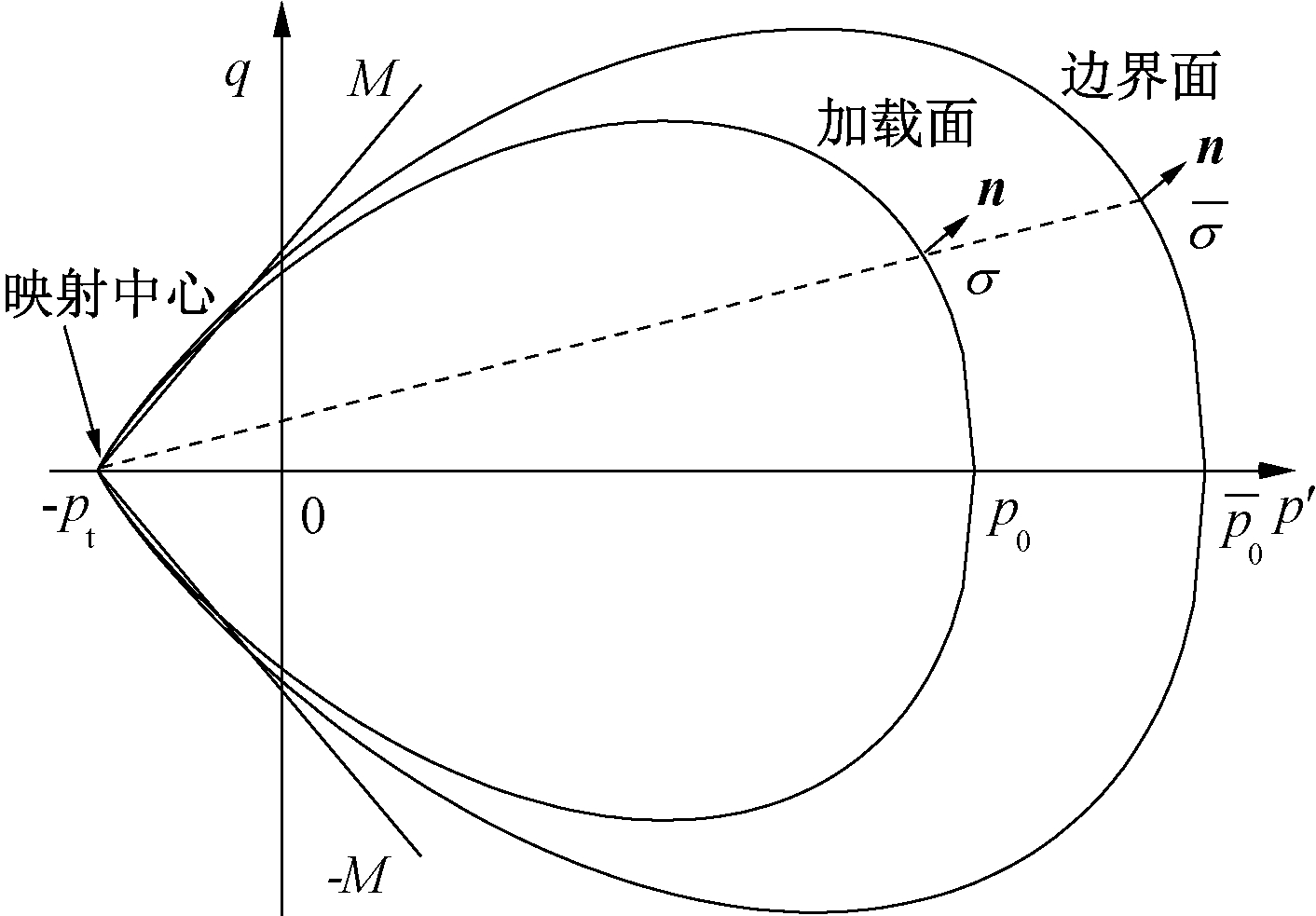
图3 边界面及首次加载映射准则
Figure 3 Bounding surface and the mapping rule during first loading
采用与边界面形状相似的加载面，其方程为
(11)
式中：p0为加载面与p′轴右侧交点的横坐标。
硬化参量
定义为塑性体积应变
的函数[15]，即
(12)
采用径向映射准则[16-17]，当前应力点σ和像应力点
的外法线单位矢量n相同(图3)。在p′-q空间，n的两个分量分别为
(13)
式中：
为像应力比。
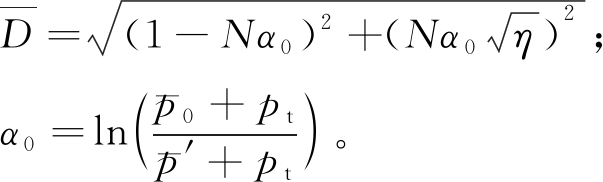
(14)
其中，把荷载划分为初始加载、卸载和再加载3种类型[15]。对于初始加载，在p′-q空间，点(pt,0)为映射中心，其应力映射关系如图3所示，其方程为
(15)
式中：b为应力映射因子。若b=1，表示边界面与加载面相同。
对于当前应力路径，若在应力点(p′,q)应力反向，表明开始卸载或再加载，该应力点即为新的应力映射中心，随后产生新的加载面，加载面与边界面相似。文献[15]提出的再加载和卸载映射准则，要求新的加载面与原加载面在新的应力映射点相切，采用中间边界面进行应力连续映射的方法，应用时很不方便。本文采用文献[17]提出的简化映射准则，即由新的加载面直接映射到边界面上，如图4所示。其应力映射关系同时满足式(16)和(17)：
(16)
(17)
式中：(αp,αq)为新的加载面的几何原点；(cp,cq)为新的应力映射中心，即当前的应力反向点。
图4 卸载或再加载的加载面及映射准则
Figure 4 Loading surface and mapping rule for unloading/reloading
2.2 本构关系
在边界面塑性理论中，体积应变增量dεv和应变偏量增量dεq为相应的弹性和塑性应变增量之和[15]，即
(18)
式中：上标e和p分别表示弹性和塑性部分；下标v和q分别表示体积和偏量部分。
体积模量和剪切模量分别为[15-16]
(19)
式中：v为泊松比。
采用非关联流动法则，以保证塑性体积应变在临界状态为零。基于塑性势函数g=0，剪涨参量d为[15]
(20)
式中：A为模型参数，反映了塑性势函数的形状；η为应力比，对于循环加载，η=(q-αq)/(p′-αp)，对于首次加载，η=q/(p′+pt)即式
与q同号。
在p′-q空间中，塑性势面外法线单位矢量m的分量分别为
(21)
塑性增量本构关系为
(22)
其中，加载因子Λ为
(23)
式中：
为边界面像应力点的塑性模量。
2.3 硬化模量
硬化模量Kp由和加载面上应力点的塑性模量Kf两部分组成[15,17]:
(24)
塑性模量可由一致性条件dF=0，并结合式(12)求得
(25)
Kf为与当前应力点和像应力点距离相关的函数，其具体表达式有些差异[15-17]。本文采用文献[15]的形式，修正后为
(26)
式中：比例系数km控制了Kf的幅度，对模拟三轴剪切试验所得的q-εq曲线的陡缓即斜率具有影响；ηp可取为p′-q曲线至峰值强度的斜率，或取为三轴排水剪切试验应力路径的斜率[15]。文献[15]将其表示为状态参数ζ和临界状态线斜率的函数：
ηp=(1-kζ)M。
(27)
式中：k为材料参数；ζ为状态参数，ζ=e-ec，e为当前应力状态的孔隙比，ec为临界状态孔隙比。
以上边界面模型，引入了5个参数：参数N、R和A为基本参数，可由水泥固化土不排水三轴试验的应力-应变曲线拟合得到；km和k为扩展参数，与应力路径及其变化有关。文献[15]针对砂土的剪切试验结果，引入新的参数后给出了km的经验公式，文献[16]给出了lg km形式的经验公式。目前，这两个扩展参数尚未有满意的确定方法，需根据具体情况按经验确定。对于正常固结土来说，仅考虑单调加载，仅用到3个基本参数。对于循环荷载计算，需要确定km和k。
3 模型验证
本文的水泥固化土边界面模型，共有15个参数。可分为3组：①与临界状态相关的参数κ、λ和M及孔隙比e0；②与胶结及胶结退化相关的6个参数，p0i，s，c，ξ，β和φ；③与本构模型相关的基本参数N、R和A，以及扩展参数km、k。
3.1 模型验证
对文献[8]水泥固化Ballina黏土的固结不排水剪试验结果，进行参数拟合。与临界状态和胶结退化相关的参数如表1所示[8]，取泊松比为0.25，模型参数拟合得到：N=2.2，R=2.35, A=0.5。
表1 水泥土模型参数[8]
Table 1 Model parameters for cement-treated clay[8]
模型类型Mλκξc/kPasp0i/kPaβφe010%水泥Ballina黏土1.210.3630.035 50.49681 250115.60645.32.9912%水泥Ballina黏土1.210.3630.035 50.54871 780133.26384.43.10
掺和量为10%(质量分数)的水泥固化Ballina黏土试验结果的q-εq曲线、应力路径和孔压曲线与模拟结果对比如图5所示。由图(5)可知，预测值与试验结果比较吻合，本文模型较好地反映了不同水泥含量的水泥固化土在固结不排水剪切过程中应力变化特征及应变软化现象。对于不同围压下的有效应力路径，尽管个别计算结果与试验数据具有一定差异，但从总体上较好地反映了应力路径的变化。表明本文边界面模型和参数拟合方法是合适的，可以很好地反映水泥固化土的应力-应变特征。
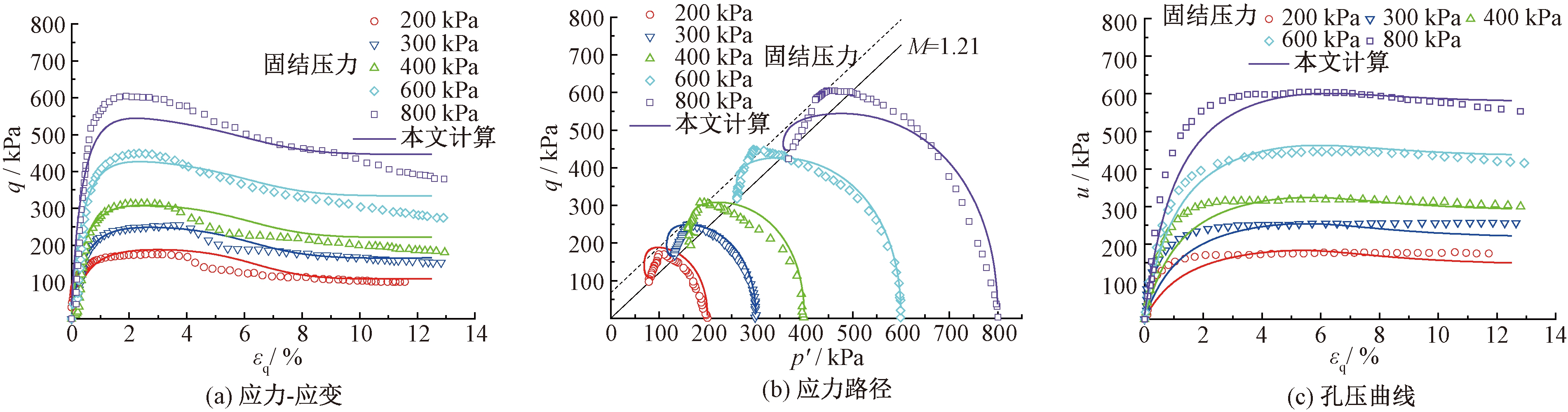
图5 10%水泥固化Ballina 黏土固结不排水剪切试验[8]与模拟结果比较
Figure 5 Simulation of undrained triaxial tests[8] of 10% cement-treated Ballina clay
3.2 循环荷载作用
为了进一步说明本文模型的特点，下面给出循环荷载作用下水泥固化土固结不排水剪切试验的模拟算例。采用显式“子步法”[17]并结合Pegasus搜索算法[18]进行应力更新。
对12%(质量分数)的水泥固化Ballina 黏土进行循环加载模拟，除前面的参数外，因缺少循环荷载作用下的试验数据，本构模型的扩展参数参考文献[15]选取。取k=2.0，首次加载km=3.5，卸载和再加载取km=40.5。固结压力p0=600 kPa，q的峰值取为120 kPa，最小值为0。其偏应力q随应变偏量εq的变化如图6所示。由图6可知，在初步加载的几个循环中，水泥固化土的塑性变形较大。经过多个加载循环后，逐步趋于稳定，这与文献[15]的结果类似，对于研究复杂荷载如地震荷载等作用下水泥固化土的承载与变形特性提供了一个有效方法。
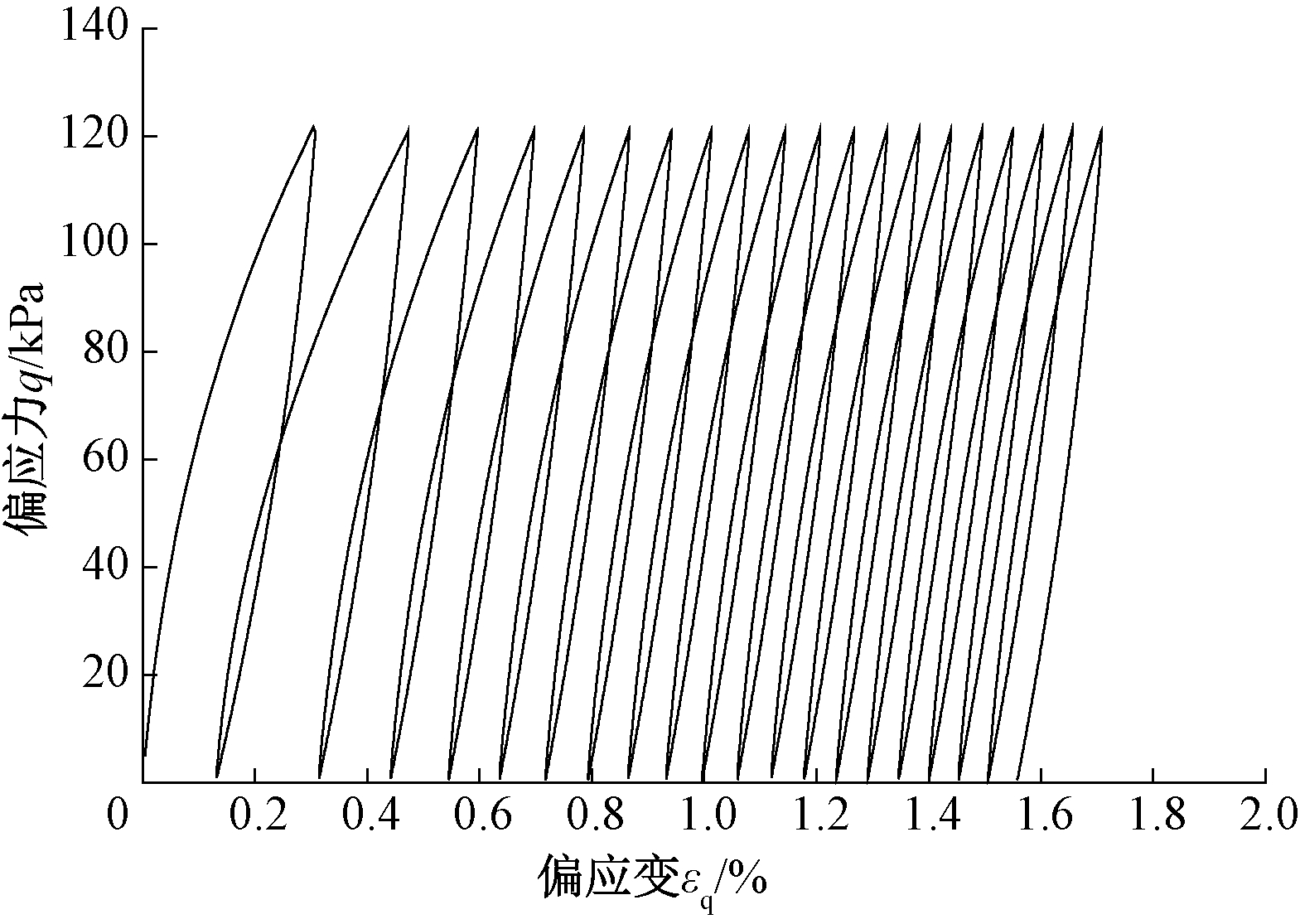
图6 12%水泥固化Ballina 黏土循环荷载不排水剪切试验模拟结果
Figure 6 Simulation of undrained cyclic triaxial tests of 12% cement-treated Ballina clay
4 结论
基于修正平均有效应力的概念，描述了水泥固化土胶结作用和剪切过程的胶结退化现象，结合算例，详细讨论了参数的数据拟合方法和步骤,建立并发展了水泥固化土双面边界面本构模型和模型参数的拟合方法。主要结论如下：
(1)通过修正平均有效应力的方法描述水泥固化土胶结作用和剪切过程的胶结退化现象，虽然引入的参数较多，但根据等压固结和固结不排水剪切试验结果，结合本文的参数拟合方法和步骤，除少部分参数需要借助于其他绘图软件外，多数均可通过程序计算自动完成，为研究水泥固化土以及结构性黏土提供了一种有效方法。
(2)所建立的考虑水泥固化土胶结作用和胶结退化现象的双面边界面模型，可以较好地描述水泥固化土在初始加载、卸载和再加载过程中应力的变化、孔隙水压力的累积及结构性逐步丧失的力学特性，拓展了水泥固化土的数值模拟空间，发展了水泥固化土的本构理论。
[1] HORPIBULSUK S, MIURA N, BERGADO D T. Undrained shear behavior of cement admixed clay at high water content[J]. Journal of geotechnical and geoenvironmental engineering, 2004,130(10): 1096-1105.
[2] ABU-FARSAKH M, DHAKAL S, CHEN Q M. Laboratory characterization of cementitiously treated/stabilized very weak subgrade soil under cyclic loading[J]. Soils and foundations, 2015, 55(3): 504-516.
[3] SASANIAN S, NEWSON T A. Basic parameters governing the behaviour of cement-treated clays[J]. Soils and foundations, 2014,54(2):209-224.
[4] SUEBSUK J, HORPIBULSUK S, LIU M D. Modified structured cam clay: a generalised critical state model for destructured, naturally structured and artificially structured clays[J]. Computers and geotechnics, 2010, 37(7/8): 956-968.
[5] KASAMA K, OCHIAI H, YASUFUKU N. On the stress-strain behaviour of lightly cemented clay based on an extended critical state concept[J]. Soils and foundations, 2000,40(5): 37-47.
[6] NGUYEN L D,FATAHI B,KHABBAZ H. A constitutive model for cemented clays capturing cementation degradation[J]. International journal of plasticity，2014, 56: 1-18.
[7] ARROYO M, CIANTIA M, CASTELLANZA R, et al. Simulation of cement-improved clay structures with a bonded elasto-plastic model: a practical approach[J]. Computers and geotechnics, 2012,45: 140-150.
[8] NGUYEN L, FATAHI B, KHABBAZ H. Development of a constitutive model to predict the behavior of cement-treated clay during cementation degradation: C3 model[J]. International journal of geomechanics, 2017,17(7): 04017010.
[9] YAPAGE N N S, LIYANAPATHIRANA D S, POULOS H G, et al. Numerical modeling of geotextile-reinforced embankments over deep cement mixed columns incorporating strain-softening behavior of columns[J]. International journal of geomechanics, 2015, 15 (2):04014047.
[10] RAHIMI M, CHAN D, NOURI A. Bounding surface constitutive model for cemented sand under monotonic loading[J]. International journal of geomechanics, 2016,16(2): 04015049.
[11] IMAM S M R, MORGENSTERN N R, ROBERTSON P K, et al. A critical-state constitutive model for liquefiable sand[J]. Canadian geotechnical journal, 2005, 42(3): 830-855.
[12] XIAO H W, LEE F H, LIU Y. Bounding surface cam-clay model with cohesion for cement-admixed clay[J]. International journal of geomechanics, 2017,17(1): 04016026.
[13] QUIROGA A J, THOMPSON Z M, MURALEETHARAN K K, et al. Stress-strain behavior of cement-improved clays: testing and modeling[J]. Acta geotechnica, 2017, 12(5): 1003-1020.
[14] RAHIMI M, CHAN D, NOURI A. Constitutive model for monotonic and cyclic responses of loosely cemented sand formations[J]. Journal of rock mechanics and geotechnical engineering, 2018, 10(4): 740-752.
[15] RUSSELL A R, KHALILI N. A bounding surface plasticity model for sands exhibiting particle crushing[J]. Canadian geotechnical journal, 2004, 41(6): 1179-1192.
[16] RUSSELL A R, KHALILI N. A unified bounding surface plasticity model for unsaturated soils[J]. International journal for numerical and analytical methods in geomechanics, 2006, 30(3): 181-212.
[17] KAN M E, TAIEBAT H A, KHALILI N. Simplified mapping rule for bounding surface simulation of complex loading paths in granular materials[J]. International journal of geomechanics, 2014, 14(2): 239-253.
[18] SLOAN S W, ABBO A J, SHENG D C. Refined explicit integration of elastoplastic models with automatic error control[J]. Engineering computations, 2001,18(1/2): 121-129.