0 引言
凸轮设计的基本内容是根据工作要求的凸轮机构形式、推杆的运动规律和有关的基本尺寸,以及从动件的运动规律设计出凸轮应有的轮廓曲线。凸轮轮廓曲线设计方法有作图法和解析法。作图法难以满足对凸轮精度的要求,解析法设计的凸轮精度高,但计算量较大,过程繁琐。虚拟样机分析软件的应用解决了解析法设计过程繁琐复杂的问题[1]。凸轮机构设计的常用方法为解析法。
目前,国内外关于凸轮轮廓曲线设计方面的研究主要为基于计算机仿真的凸轮机构运动规律设计,其中MATLAB、ADAMS、Solidworks、Pro/E等软件常作为分析、设计工具应用在凸轮机构的设计研究中[2-6]。利用仿真软件设计凸轮轮廓曲线相比传统设计方法,具有精确度高、设计周期短等优点。
ADAMS软件可以用于对虚拟机械系统进行静力学、运动学和动力学分析[7],输出位移、速度、加速度和反作用力曲线。文献[8-9]利用ADAMS软件进行了凸轮机构的解析法设计,并对从动件的运动规律(位移、速度及加速度)进行仿真分析,以实现凸轮轮廓曲线的较高精度设计。
利用ADAMS软件,可以很方便地设计出尖顶从动件凸轮,现有的文献大多数为设计尖顶从动件凸轮[10-15],关于设计平底从动件的研究内容较少。尖顶从动件凸轮的设计方法不能应用于平底从动件凸轮,因为平底从动件凸轮的推杆与凸轮的接触点不固定,仅靠单一固定的marker点生成凸轮轮廓曲线,误差较大且不合理。笔者利用ADAMS设计平底从动件凸轮,通过将平底从动件离散为多个marker点,生成多条曲线,取这些曲线的交集即可得到所需的凸轮轮廓曲线。为使用ADAMS设计平底从动件凸轮提供了一种新的方法。
1 从动件运动规律
在算例1中,凸轮类型为平底直动盘形凸轮,基本尺寸参数如下:凸轮基圆半径50 mm,从动件推程20 mm,推程运动角120°,远休止角30°,回程运动角150°,近休止角60°。
推程和回程采用简谐运动规律,在一个运动周期凸轮旋转360°,从动件运动方程为:
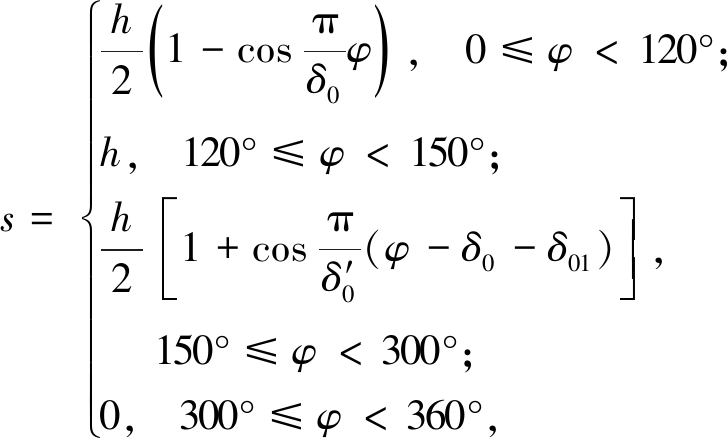
(1)
式中:s代表从动件的位移,mm;h代表推杆的行程,mm;δ0代表推程运动角,(°);φ代表转角,(°);δ01代表远休止角,![]() 代表回程运动角,(°)。 将以上物理量的数据代入式(1),得到式(2):
代表回程运动角,(°)。 将以上物理量的数据代入式(1),得到式(2):
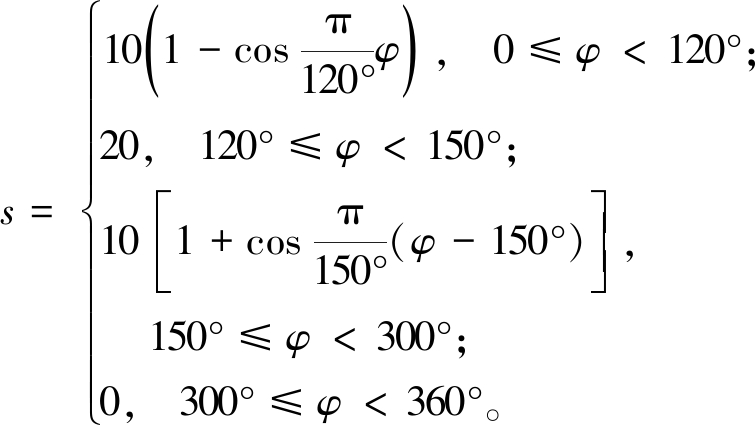
(2)
凸轮转速为30°/s,所以将上式中“φ”替换为“t·30”,得到式(3)。
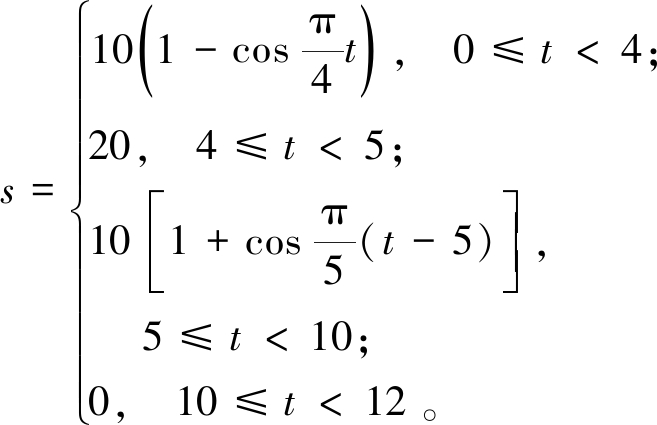
(3)
式中:t为时间。
在ADAMS软件中,时间t用TIME表示。因此式(3)在ADAMS软件中的函数表达为:“IF(TIME-4:10*(1-COS(TIME*PI/4)),10*(1-COS(TIME*PI/4)),IF(TIME-5:20,20,IF(TIME-10:10*(1+COS((TIME-5)*PI/5)),10*(1+COS((TIME-5)*PI/5)),0)))。”
为了更直观地表达凸轮机构从动件推杆的运动规律,在ADAMS软件中建立凸轮机构模型,按照式(3)的函数表达式,仿真模拟生成理想凸轮的推杆位移s与运动时间t的曲线图,如图1所示。
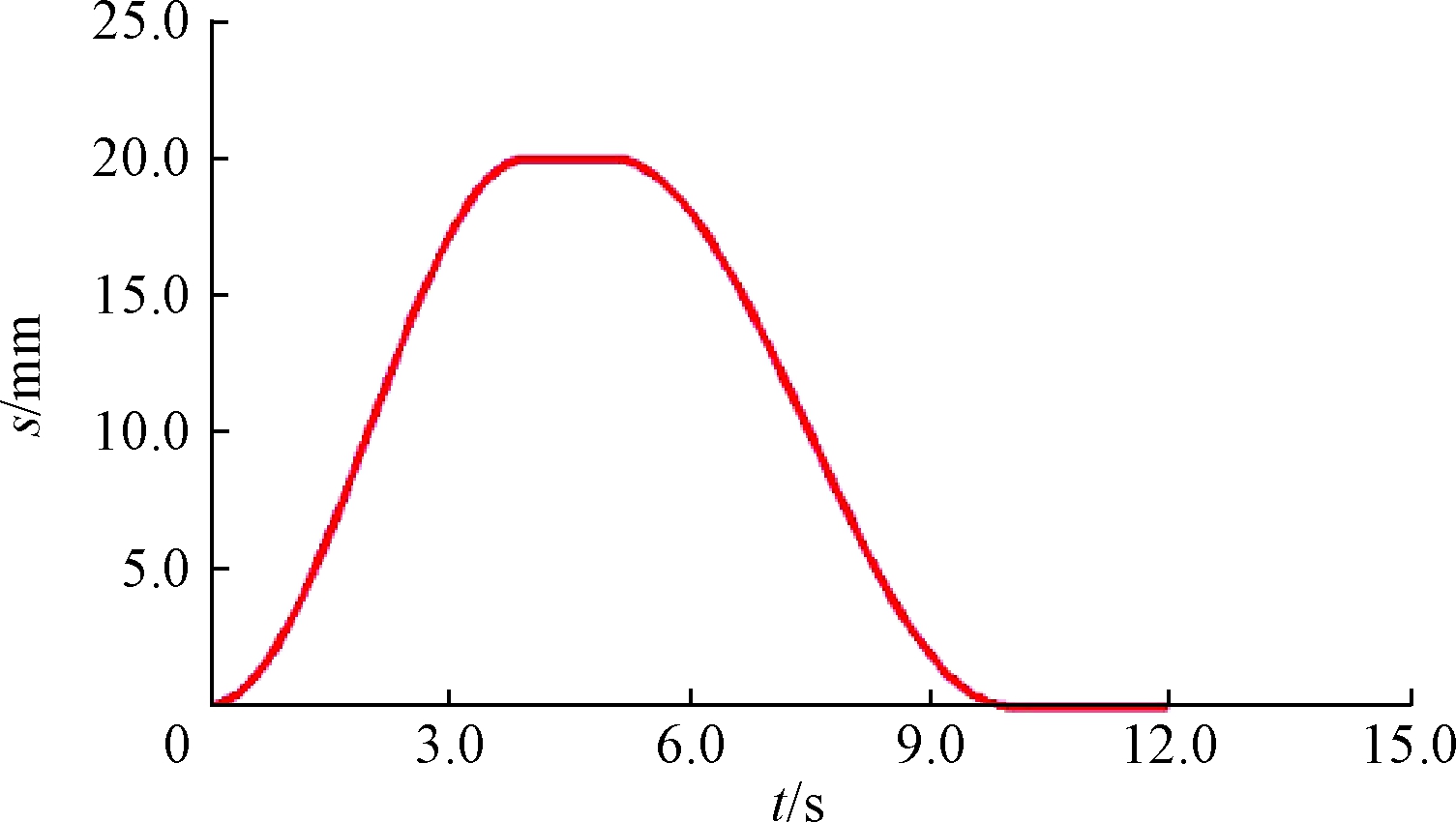
图1 理想凸轮从动件位移曲线图
Figure 1 The displacement curve of the ideal cam follower
2 反转法设计平底从动件凸轮
在ADAMS软件中设计平底推杆凸轮的主要步骤:一是建立从动件模型,画凸轮基体及建立相关约束;二是驱动凸轮和从动件按照预定规律运动;三是建立多个marker点生成多条curve,将不同curve生成的body求交,得到凸轮轮廓。
2.1 建立从动件模型
本次设计的凸轮参照第1部分的算例,为平底直动盘形凸轮,并已知凸轮机构的相关参数和从动件运动方程。在ADAMS软件中建立从动件模型,画出凸轮基体。建立圆心坐标为(0,0,0),半径为50 mm的Sphere,在(0,50,0)坐标处建立Frustum。Sphere与ground建立旋转副约束,Frustum与Sphere 建立移动副约束。选择旋转驱动,速度值设置为30 °/s,建立驱动装置MOTION_1。选择移动驱动,参数默认,在Function Builder栏中输入从动件运动方程式(3)的函数表达式,建立驱动装置MOTION_2,得到从动件模型,如图2所示。点击仿真按钮,时间选择12 s,步数选择50。
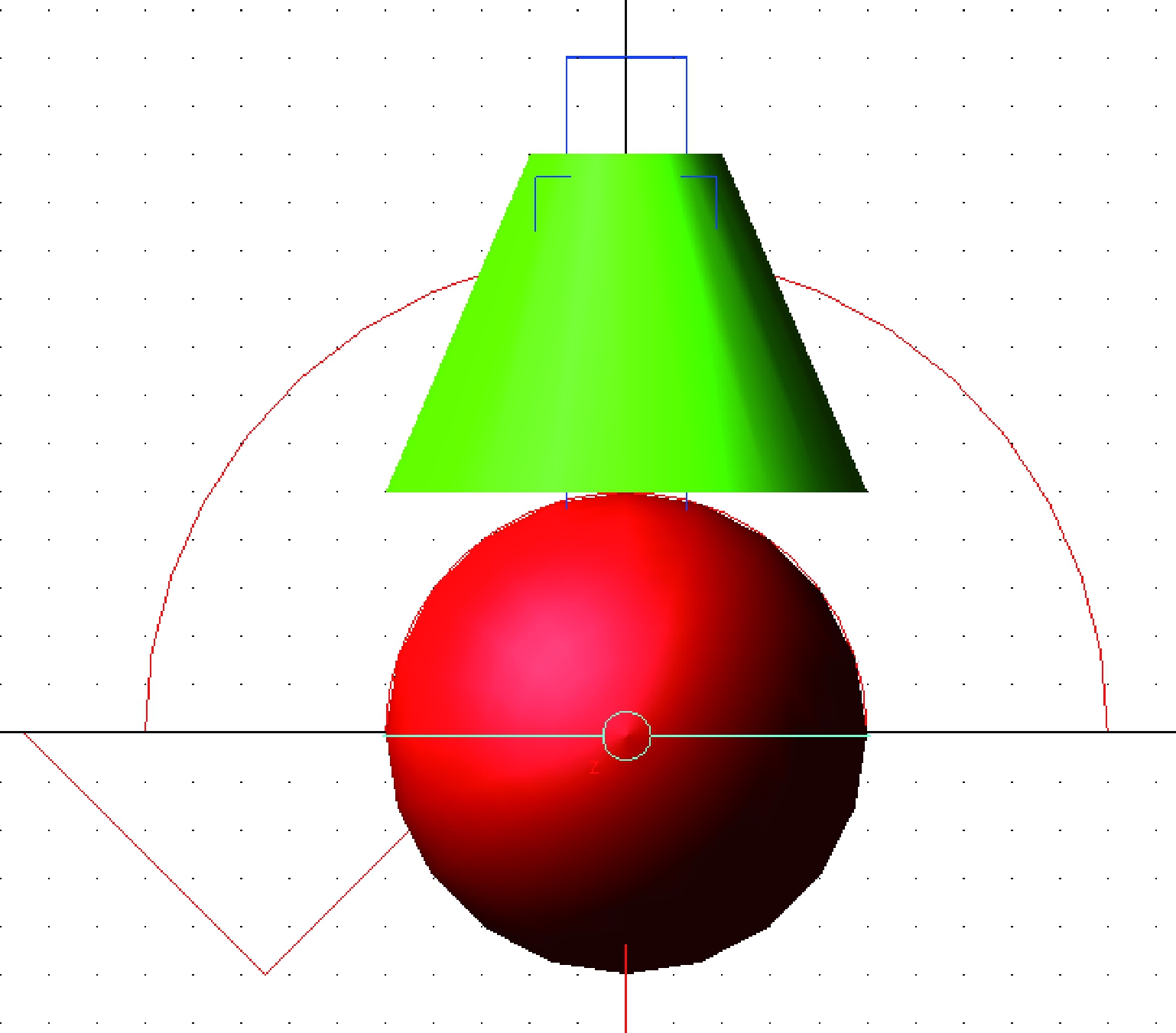
图2 ADAMS从动件模型
Figure 2 ADAMS follower model
2.2 生成curve
从动件模型运动仿真后,在从动件上建立marker点,点击Create Trace Spline,根据从动件的运动规律,生成curve。因为平底推杆凸轮在运动过程中推杆与凸轮的接触点不固定,首先确定平底推杆中心到推杆平底与凸轮廓线的接触距离l,其最大距离lmax为:
(4)
式中:s为从动件的位移,mm;δ为转角,(°);|ds/dδ|max应根据推程和回程推杆的运动规律分别进行计算,取其最大值。
代入数据计算,lmax为15 mm。接触点的取值范围在从动件底部中心位置左右15 mm,底部中心位置坐标为(0,50,0),坐标取值范围为点(-15,50,0)到点(15,50,0)。
为了提高轮廓曲线的精度,满足设计预期目标,在选取marker点时,在取值范围内点的个数尽可能多且分布在不同的区域。在选取点的个数时,考虑到实际操作和坐标取值范围为30 mm,选择13个点,中心位置点1个,左右两侧各6个;在选取点的位置时,采用均值法,等间距(2.5 mm)取点,所选取数据具有代表性与合理性。建立marker点,以中心坐标(0,50,0)为中间点,左右间隔2.5 mm取一个点,在点(-15,50,0)到点(15,50,0)区间内共取13个marker点,共生成13条curve。
2.3 取多条curve交集得到轮廓曲线
取curve交集在CAD软件中进行处理。将curve的坐标提取出来,导入CAD中,生成多条曲线,建立多条曲线的面域。利用INSECT命令,可以得到多个面域的交集,即凸轮轮廓曲线。将CAD中的凸轮轮廓曲线坐标导出,将坐标数据导入ADAMS软件中建立凸轮模型,如图3所示。
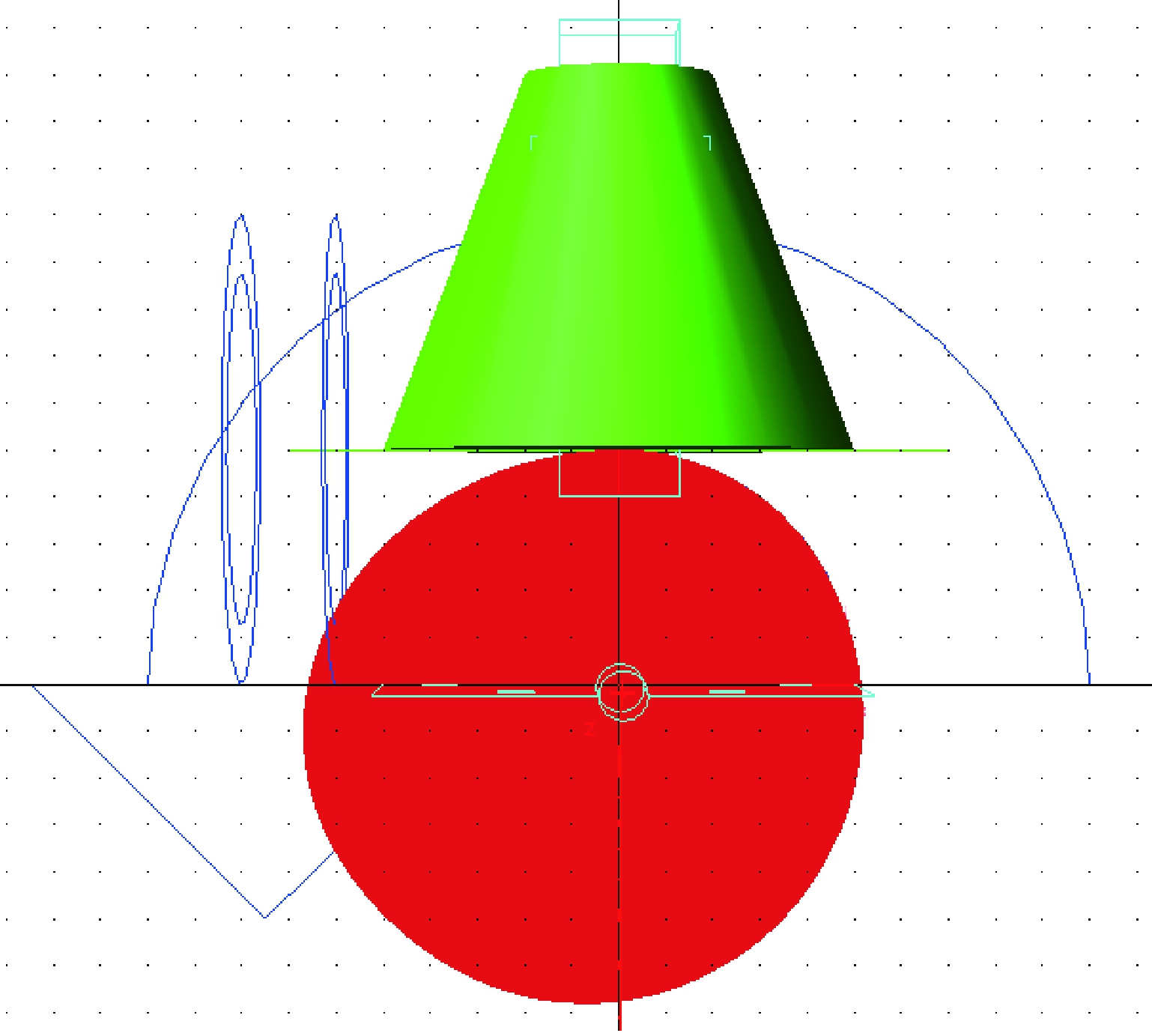
图3 平底直动盘型凸轮模型
Figure 3 Flat bottom straight disc type cam model
2.4 仿真及分析
在ADAMS软件中,对凸轮模型进行相关约束和设置。点击仿真按钮,时间选择12 s,步数选择50。在ground建立marker点,测量从动件在Y轴的移动距离,得到从动件位移曲线图,如图4所示。
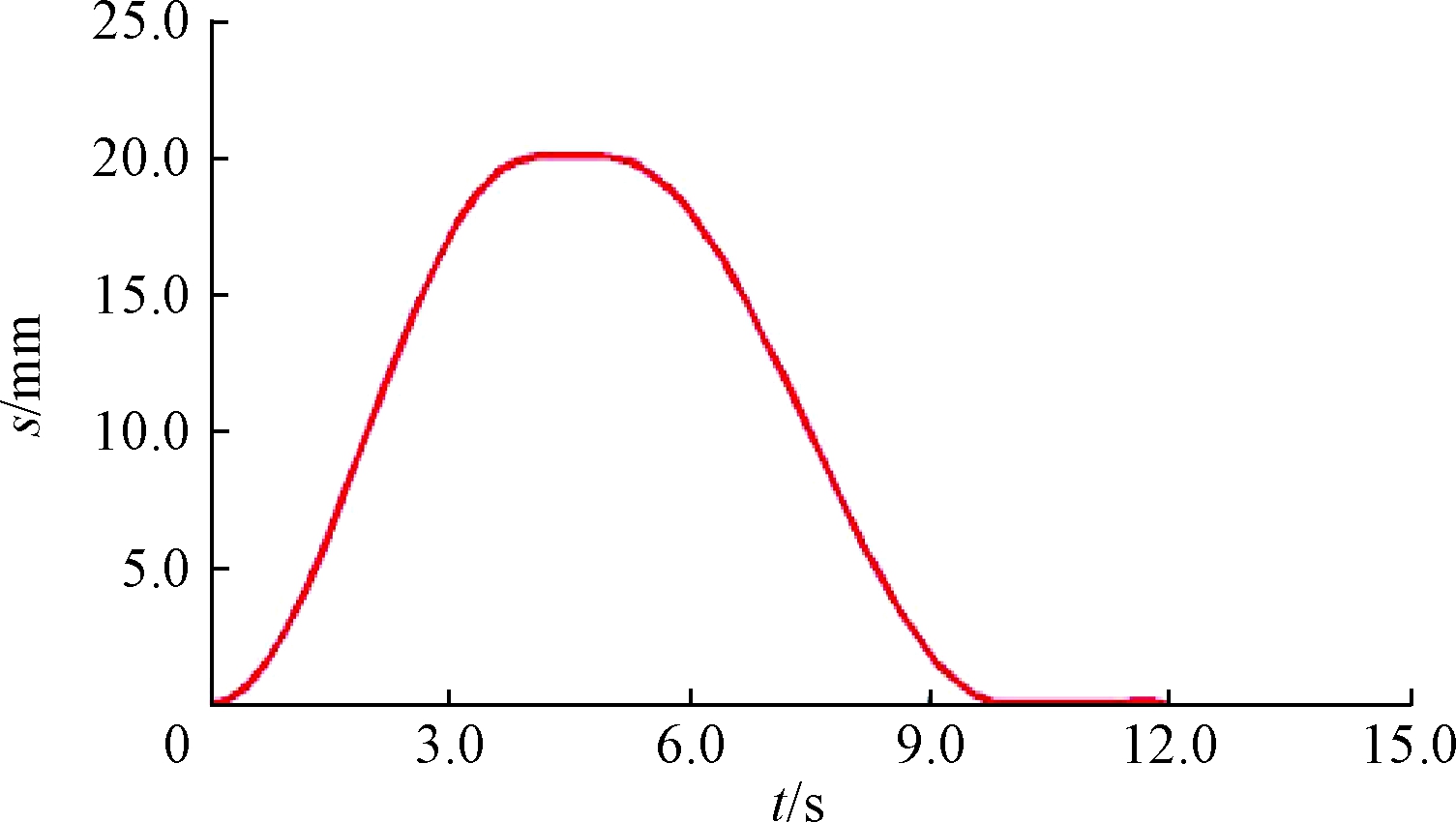
图4 实际凸轮从动件位移曲线
Figure 4 Actual cam follower displacement curve
为了更加直接地对比分析检测凸轮的设计是否达到预期运动规律,将两次位移数据和曲线导出进行对比,查看计算误差是否在理想范围内。实际从动件与理想从动件位移误差如图5所示。
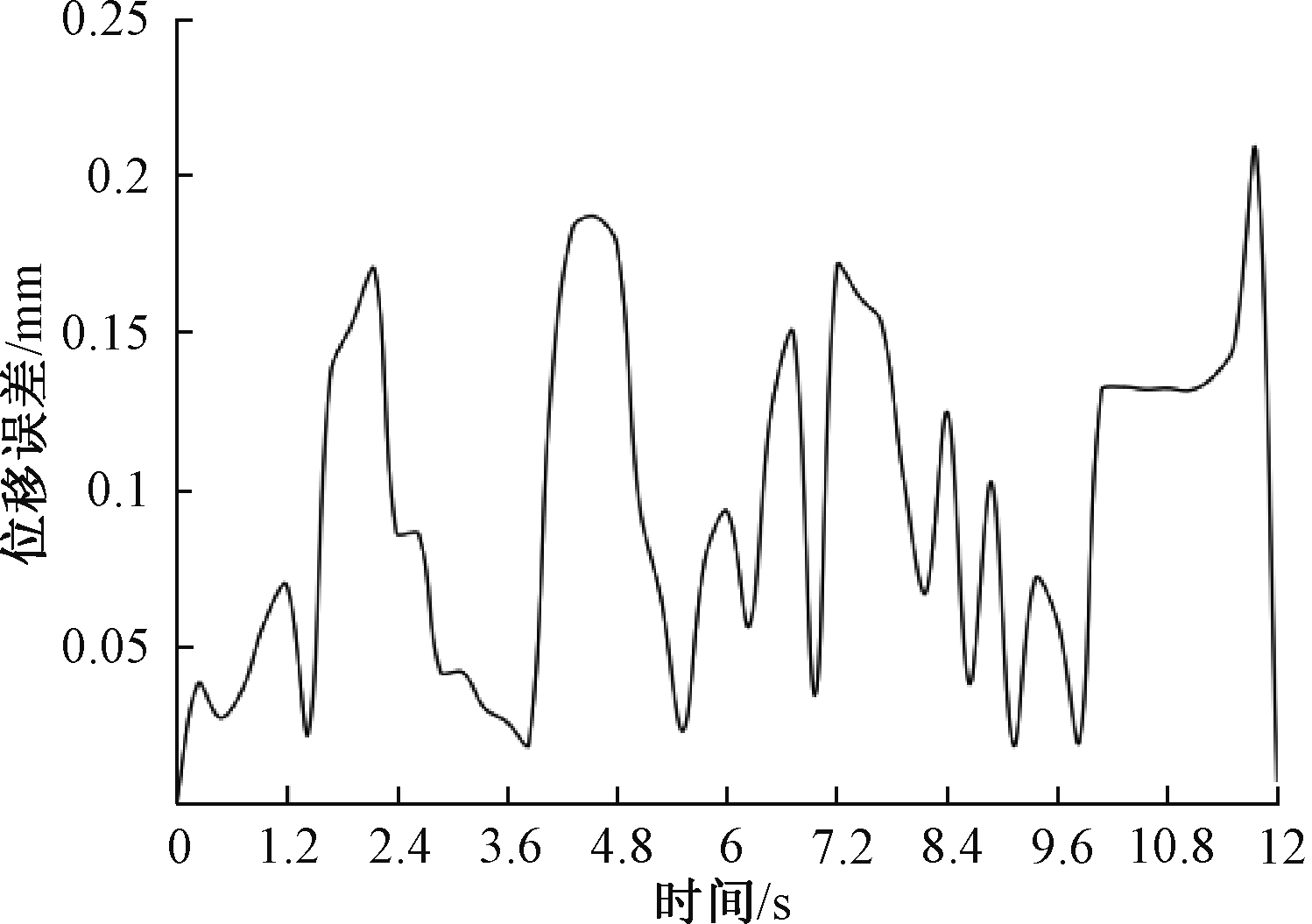
图5 位移误差分析
Figure 5 Displacement error analysis chart
根据位移误差分析图和导出数据可知,最大误差约为0.207 mm,从动件的推程为20 mm,最大误差比例为1%,误差大部分在0.1 mm范围内,整体误差比例为0.5%。在凸轮设计中其误差在理想范围以内,达到预期目标。
2.5 设计位移误差的分析
在ADAMS软件中,在平底推杆与凸轮接触点取值范围内,建立marker点个数分别取7个点、3个点。按照以上的操作步骤,得到从动件位移误差分析图,如图6所示。
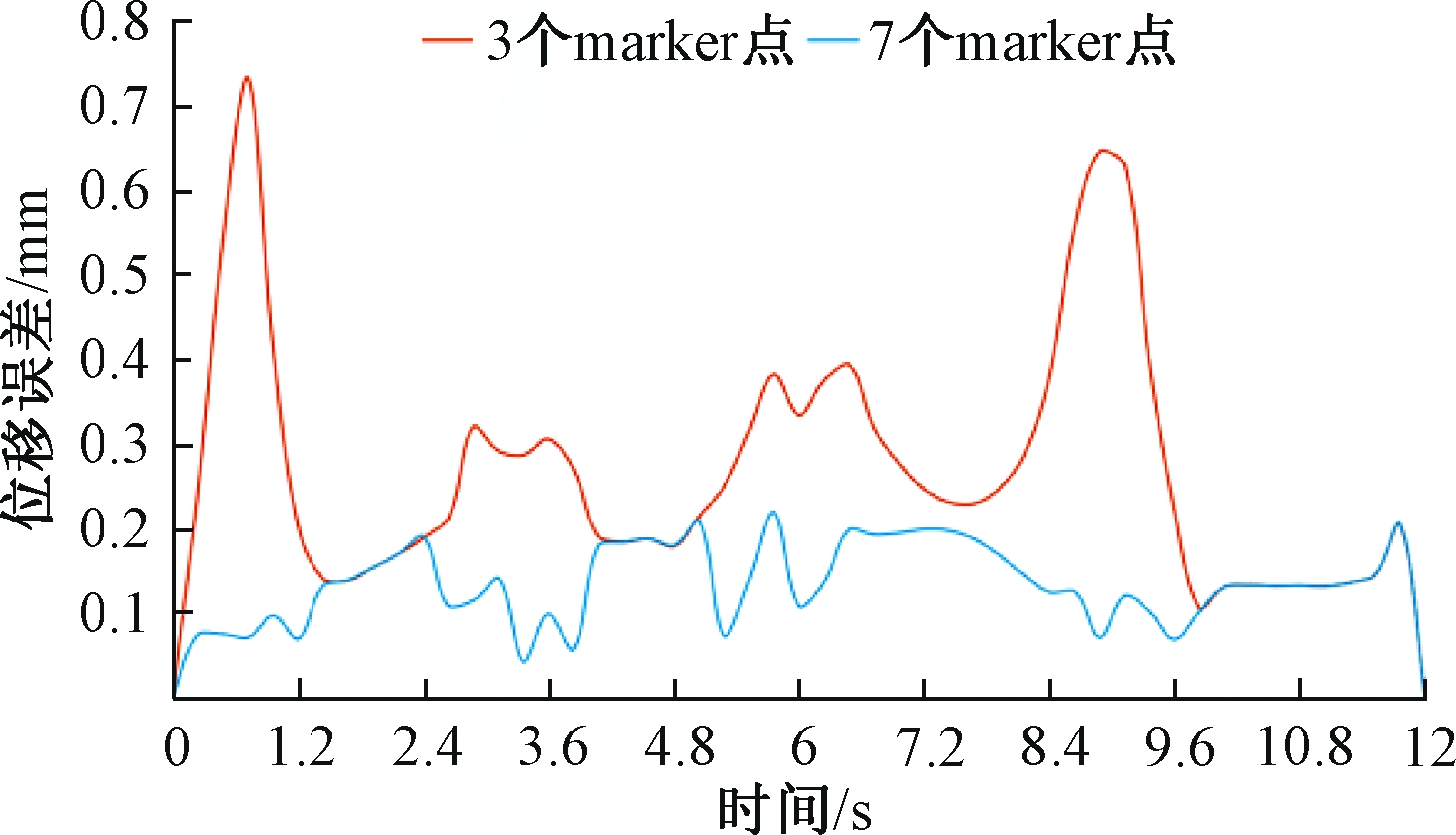
图6 不同marker点位移误差分析
Figure 6 Different marker point displacement error analysis chart
根据图5、图6对比分析可知,图5的marker点个数为13个,其位移最大误差为0.207 mm,误差大部分在0.1 mm范围内;图6中marker点个数为7个,其位移最大误差为0.218 mm,误差大部分在0.1~0.2 mm;图6中marker点个数为3个,其位移最大误差为0.73 mm,误差大部分在0.1~0.7 mm。通过3次对比分析,在接触点的取值范围内,增加marker点个数,从动件位移误差在不断减小,设计出的凸轮轮廓曲线精确度有所提高。在本次算例中,最终设计的凸轮轮廓曲线,其从动件位移最大误差比例为1%,误差大部分小于0.1 mm,整体误差比例为0.5%。
在ADAMS软件中设计平底从动件凸轮轮廓曲线,依据传统的反转法原理,生成的凸轮轮廓线实际是推杆轮廓的包络线,误差较大。在本算例中将推杆轮廓离散化,其轮廓被离散为多个点与凸轮接触,不同于尖顶从动件的单点接触,从而在模拟中增加了凸轮与推杆真正接触的概率,仿真的结果更加接近凸轮真实工作的状况。这些离散的marker点通过仿真在凸轮基体上生成多条曲线,将这些曲线进行交集运算可以得到较理想的轮廓曲线。
通过分析不同marker点的设计位移误差可知,在接触点的取值范围内,通过增加marker点个数可以得到更加理想的凸轮轮廓曲线,提高设计精度。
3 结论
针对ADAMS软件反转法设计平底从动件凸轮轮廓曲线误差较大的问题,提出了一种新的凸轮机构设计方法。对凸轮机构进行仿真分析,主要结论如下:
(1)利用ADAMS软件反转法设计平底从动件凸轮时,使用离散化方法将从动件轮廓离散为多个点,多个marker点通过仿真在凸轮基体上生成多条曲线,将这些曲线进行交集运算可以得到更接近理想的轮廓曲线,提高了设计精度,为设计平底从动件凸轮机构提供了新的方法。
(2)使用离散化方法所设计的凸轮,从动件位移最大误差约为0.207 mm,从动件的推程为20 mm,最大误差比例为1%;误差大部分在0.1 mm范围内,整体误差比例为0.5%,符合设计目标。
(3)将推杆轮廓离散化,在接触点的取值范围内,增加离散点个数可以提高凸轮轮廓设计的精度。
(4)利用ADAMS软件设计滚子从动件凸轮采用的离散化方法也可推广应用于从动件与凸轮始终保持相切的凸轮机构设计中。
[1] 刘建波.一种基于ADAMS的凸轮设计方法[J].船电技术,2014,34(12):78-80.
[2] 范志锋,徐敬青,崔平.基于ADAMS和MATLAB的凸轮机构仿真设计[J].煤矿机械,2018,39(1):141-143.
[3] 肖思伟,张晋西,陈江洪,等.基于SolidWorks和Excel的凸轮设计与运动仿真[J].重庆理工大学学报(自然科学),2017,31(8):73-75,92.
[4] 肖帮东,黄浩,徐中.基于Matlab和Pro/E的凸轮轮廓曲线设计及从动件运动学仿真[J].制造技术与机床,2016(2):48-53.
[5] CHANG Y, LIN R F. Design and analysis of cam mechanisms with a flat-faced follower by the application of support function[C]//Proceedings of 2013 2nd International Conference on Manufacture Engineering, Quality and Production System(ICMEQP 2013). Hong Kong: Information Engineering Research Institute, 2013:514-520.
[6] TSUHA N A H, NONATO F, CAVALCA K L. Formulation of a reduced order model for the stiffness on elastohydrodynamic line contacts applied to cam-follower mechanism[J]. Mechanism and machine theory,2017, 113:22-39.
[7] 唐琼.基于ADAMS的凸轮机构分析与动态仿真[J].安徽理工大学学报(自然科学版),2010,30(4):22-24,30.
[8] 田涛,邓双城,杨朝岚,等.基于ADAMS软件的偏置直动尖顶推杆盘形凸轮机构设计[J].新技术新工艺,2015(11):31-33.
[9] 张志峰,周力,杨建辉.排气门强制开启机构的动态性能研究[J].郑州大学学报(工学版),2013,34(2):108-111,124.
[10] 蒋新萍.基于ADAMS凸轮机构的动态分析[J].科技通报,2014,30(7):100-103.
[11] 范云霄,尤振环.基于ADAMS的凸轮设计[J].煤矿械,2011,32(2):35-37.
[12] 廖炜隽,王新海.基于ADAMS的凸轮机构设计及运动学分析[J].轻工科技,2017,33(11):42-43,47.
[13] 罗卫平,王珺.基于ADAMS/VIEW凸轮机构的设计及仿真[J].机械工程师,2012(1):28-29.
[14] 宫鹏涵.ADAMS2014虚拟样机从入门到精通[M].5版.北京:高等教育出版社, 2015.
[15] CHEN X M, PENG B Y, LI Q G,et al. Research on the sliding mode control in cam grinding[C]//Proceedings of 2017 2nd International Conference on Computer, Mechatronics and Electronic Engineering(CMEE 2017). Xiamen:Advanced Science and Industry Research Center,2017:458-463.