0 引言
近年来,为综合考虑电力系统运行的经济效益和污染排放问题,并同时兼顾不同调度周期之间的相互影响,动态环境经济调度(dynamic economic emission dispatch,DEED)得到了众多研究者的青睐[1-4]. DEED兼顾了总调度周期内污染排放和发电成本这两个相互竞争的目标,在满足包括机组平衡约束、爬坡速率约束等多个等式和不等式约束的前提下,通过分时段调配各个机组的出力大小,实现这两个目标的同时最小化. 显然,DEED是一种更实用、更符合实际短期调度需求的模型,但这也使得DEED问题更加难以求解. 在综合考虑上述因素的前提下,DEED问题成为一个典型的高维度、强耦合、非线性和非凸的多目标优化问题(multi-objective optimization problem,MOP).
目前,依据所用优化算法的不同,对于多目标DEED问题的求解,大致可分为两类:基于单目标优化算法的求解方法和基于多目标优化算法的求解方法. 基于单目标优化算法的求解利用约束条件法[5]或权重系数法[6-7]等将多目标DEED问题转化为单目标问题,以降低求解难度. 但该方法无法在单次运行中为决策者提供多而优的选择方案. 基于多目标优化算法的求解将DEED问题当作一个真正的MOP,应用启发式算法对两个目标进行同时优化. 目前已经有文献报道的该类算法包括NSGA-Ⅱ[3]、改进的NSGA-Ⅱ[8]、改进的自适应多目标差分算法 (MAMODE)[4]、改进的基于差分进化的混合化学反应算法(HCRO)[9]、改进的细菌觅食算法[10]以及群搜索优化算法[11]等. 然而,针对复杂的DEED问题,设计出更优的优化算法进一步改进其调度性能,将会是DEED领域一个持续的研究重点.
鸽群优化(pigeon-inspired optimization,PIO)[12]算法是Duan等提出的一种新型仿生群体智能优化算法,通过模拟鸽群归巢过程的特殊导航行为,设计出地图和指南针算子以及地标算子来分阶段指导鸽群个体的飞行. 目前,PIO已成功应用于无人机紧密编队协同控制[13]、舰载机控制器设计[14]、直流无刷电机参数设计[15]等单目标优化问题的求解. 然而,对于MOP的求解,PIO还很少涉及. 2015年,Qiu等[16]提出了基于帕累托排序机制和合并算子的多目标鸽群优化算法(multi-objective pigeon-inspired optimization,MPIO). 但是,MPIO在解决较为复杂的MOP时,容易出现早熟收敛,陷入局部最优区域而无法获得全局最优解集.
笔者提出了一种基于多学习策略的多目标鸽群优化算法(multiple learning multi-objective pigeon-inspired optimization,MLMPIO)对DEED问题进行求解. 在多学习策略中,鸽群个体向多个全局最优位置进行学习,加强种群的社会学习能力,从而增强种群的全局探索能力;多学习策略还引入个体对历史最优位置的认知学习,以增强种群的局部搜索能力. 此外,MLMPIO采用容量自适应调整的外部存档集来存储当前帕累托最优解集,以提升算法的运行效率,并引入小概率变异扰动机制,进一步增强种群的多样性. 为验证所提算法求解DEED问题的有效性,笔者采用10机组电力系统进行算例研究.
1 DEED数学模型
本节首先对DEED的目标和约束进行描述,从而建立起多目标DEED的数学模型.
1.1 目标函数
(1)燃料费用.在考虑发电机组阀点效应的前提下,每台机组的燃料成本函数可由一个正弦函数和一个二次函数之和构成. 因此,在所有调度周期内,N台机组的总燃料费用可表达为:
|disin[ei(Pimin-Pit)]|}.
(1)
式中:T代表调度周期的个数;ai、bi、ci、di 和ei分别为第i台发电机的燃料费用系数;Pit是第i台机组在调度周期t的有功出力;![]() 是机组i的最小出力.
是机组i的最小出力.
(2)污染排放.系统污染排放量的目标函数可表达为:
(2)
式中:αi、 βi、 γi、 ηi、 δi是机组i的污染气体排放系数.
1.2 约束
(1)功率平衡约束.功率平衡约束为等式约束:
(3)
式中:PDt 和 PLt分别代表第t个调度周期内的负荷和网损大小. 网损PLt可通过B系数法求得:
(4)
式中:Bij、Bi0、B00是网损计算的B系数.
(2)机组出力约束.
(5)
式中:![]() 和
和![]() 分别代表机组i的最小出力和最大出力.
分别代表机组i的最小出力和最大出力.
(3)机组出力爬坡约束.
(6)
式中:URi 和DRi分别代表机组i出力的上升及下降爬坡速率.
1.3 数学模型
基于以上分析,DEED问题可转换为带有约束的多目标优化问题,其数学模型为:
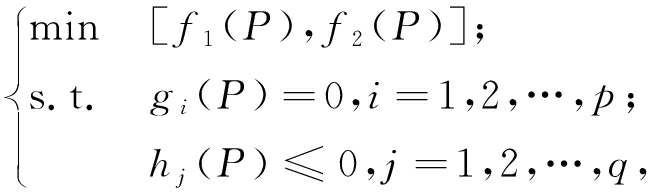
(7)
式中:p和q分别为等式和不等式约束的数量.
对于多目标DEED问题而言,在满足所有等式和不等式约束的条件下,使得燃料费用f1和污染排放f2这两个相互矛盾的目标同时实现最小化,进而得到全部发电机组在所有调度周期内的最优调度方案.
2 MLMPIO算法
2.1 MPIO算法
PIO[12]是一种模拟自然界中鸽群归巢行为的新型群体智能优化算法.在初始进化阶段,鸽群依赖于地图和指南针算子进行导航;在旅程中期,导航工具切换为地标算子,重新评估飞行路线并进行修正. 该算法具有理论简单、收敛速度快等特点,但标准PIO主要适用于单目标问题. 因此,为解决多目标优化问题,Qiu等[16]提出了基于Pareto排序机制和合并算子的多目标鸽群优化算法(MPIO).
(1)Pareto排序机制.Pareto排序机制由非支配排序算子和拥挤距离算子两部分构成. 首先,依据个体间的支配关系,利用快速非支配排序[17]将鸽群个体划分为不等的非支配等级,其中位于第一等级的个体构成了当前种群的非支配解集. 然后,利用拥挤距离算子计算不同非支配等级中个体间的拥挤距离,并依据拥挤距离的大小对个体再次进行排序. 在两个算子的操作完成后,鸽群个体依据其非支配等级的不同被划入不同的集合,同时集合中的个体依据拥挤距离的大小按降序排列. Pareto排序机制的流程如图1所示.
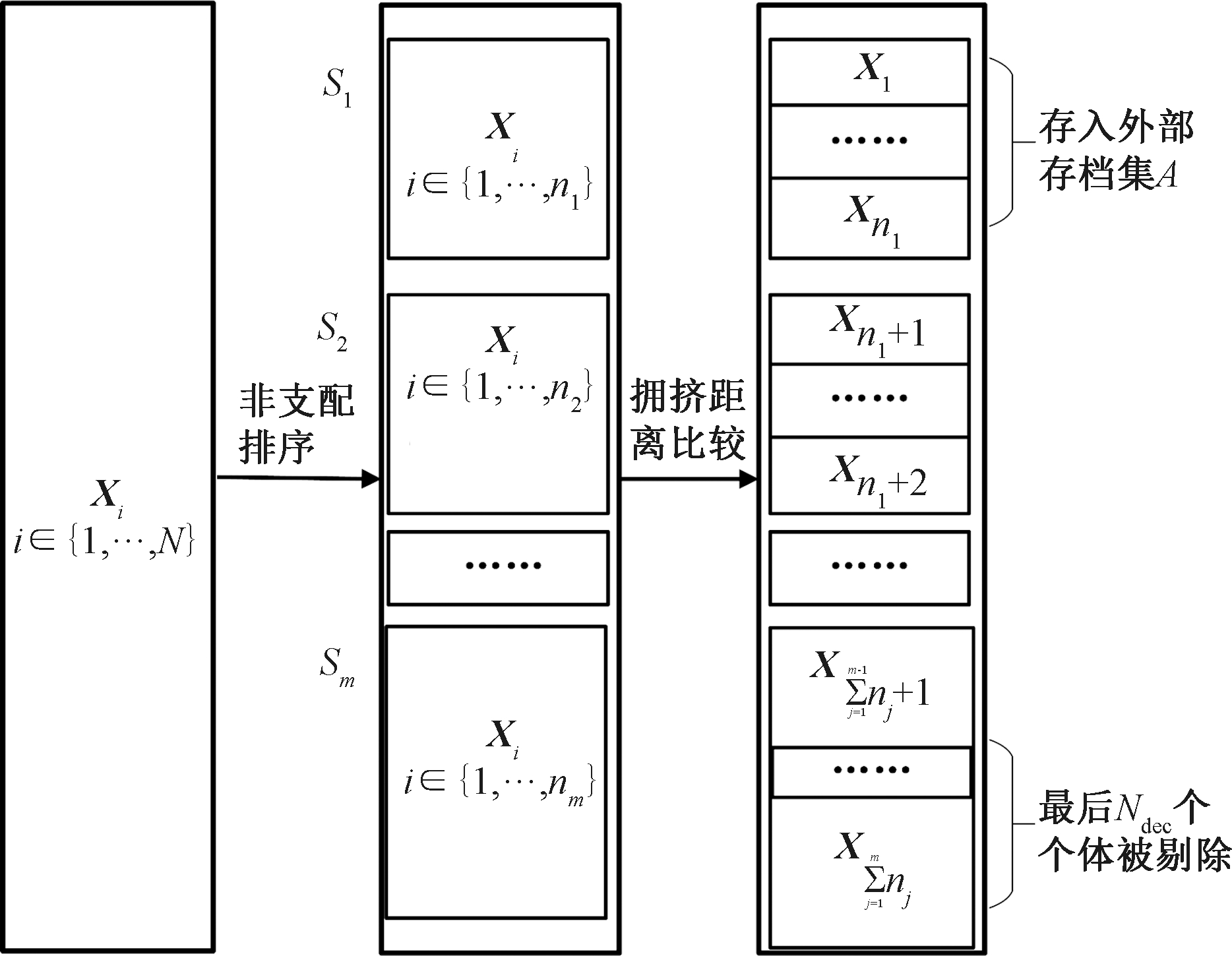
图1 Pareto排序过程
Fig.1 Process of Pareto sorting
如图1所示,Pareto排序完成后,当前种群的非支配解集被存入外部存档集;同时,具有最大非支配等级且拥挤距离最小的后Ndec个个体被当作劣等鸽剔除.
(2)合并算子.MPIO将地图和指南针算子以及地标算子进行融合,得到一个新的合并算子,进而利用该算子对鸽群个体进行速度和位置更新. 合并算子的具体形式如下:
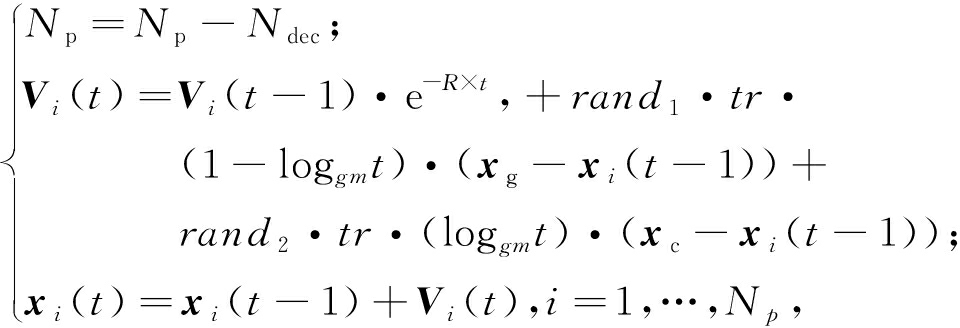
(8)
式中:Np和Ndec分别代表t次迭代后的种群数量和每代需剔除的个体数量;gm代表最大迭代次数;Vi代表xi的速度;R是地图和指南针因子;tr表示过渡因子; xg表示当前种群的全局最优位置;xc代表上一代非支配解集的中心位置,其计算公式如下:
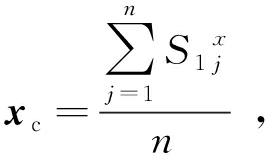
(9)
式中,![]() 代表上一代非支配解集中第j个个体的位置;n代表该非支配解集的大小.
代表上一代非支配解集中第j个个体的位置;n代表该非支配解集的大小.
2.2 基于多学习策略的多目标鸽群优化算法(MLMPIO)
(1)多学习策略.如式(8)所示,在MPIO的种群搜索过程中,鸽群个体同时向全局最优个体xg和非支配解集的中心位置xc学习. 在社会学习方面,MPIO通过随机选择的方式从外部存档集中选择一个个体作为全局最优个体xg,进而利用该个体引导所有个体的移动搜索. 该方法虽然能够增强MPIO的收敛速度,但是,若所选择的全局最优个体处于局部最优区域或远离全局最优区域,就可能导致种群陷入局部最优,停止向全局最优解进化. 此外,MPIO的引导个体xg和xc均是从全局角度考虑而设计的引导个体,种群个体缺乏对自身的认知学习以及对局部区域的搜索和开发.
为解决上述问题,笔者在MPIO中引入多学习策略,对个体的速度与位置更新公式进行改进. 改进后的更新公式为:
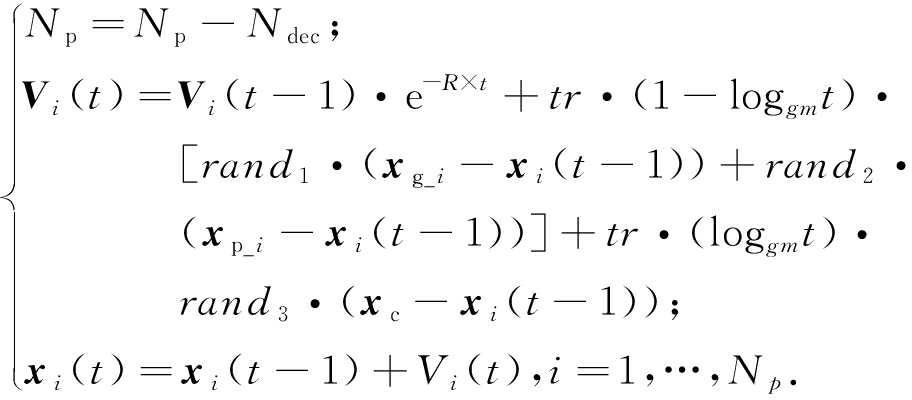
(10)
式中:xg_i是个体xi对应的全局最优个体. 在对个体xi进行位置更新前,首先从外部存档集中随机选择两个非支配个体作为该个体所对应的全局最优个体的备选集,然后选择其中拥挤距离较大的个体作为xi的全局最优个体xg_i. 在该策略作用下,整个种群的进化由多个全局最优个体进行引导,种群中的个体可以向不同的全局最优位置进行学习. 该策略能够保持种群的多样性和全局探索能力,避免早熟收敛. 式(10)中,xp_i表示个体xi的历史最优位置. xp_i的引入能够增强鸽群个体对自身历史信息的认知学习,从而改善种群的局部搜索能力,帮助算法跳出局部最优. 因此,个体认知学习的引入能够增强算法的局部开发能力,改进PIO求解复杂优化问题的性能. 对于xp_i的更新,笔者采用如下方法:
步骤1 使用xi的初始值来初始化xp_i;
步骤2 根据式(10)更新xi;
步骤3 如果xi<xp_i,则xp_i=xi;反之,xp_i保持不变;如果xi和xp_i互不支配,则xp_i=xi的概率为0.5.
(2)小概率变异扰动.为进一步增强种群的多样性,种群个体位置更新完成后对个体进行小概率变异扰动. 该机制使得个体xi以一定概率Pm在以xi为中心,半径为r的区域内进行随机变异.变异形式如下所示:
(11)
(3)容量自适应变化的外部存档集.在MPIO算法中,采用外部存档集的方式来存储已经找到的Pareto最优解,并随机从该外部存档集中选取全局最优位置. 但随着迭代次数的增加,外部存档集中最优解的数量也会越来越多,这会降低算法的运行速度,影响算法的运行效率. 因此,笔者采用自适应变化机制来动态调整每次迭代中外部存档集的容量,该动态调整机制为:
EA(t)=EAmin+[EAmax-EAmin·(t/gm)],
(12)
式中:EA(t)表示第t代的外部存档集大小;EAmin和EAmax分别表示外部存档集的最小容量和最大容量.
3 MLMPIO在DEED中的应用
3.1 种群初始化
对于多目标DEED问题,每个机组在每个调度周期内的功率输出都应该作为种群个体的决策变量,因此,在MLMPIO中,种群大小为Np,其中每个个体包含NT维决策变量,表达形式如下:
X={x1 x2 … xNp}.
(13)

(14)
式中:N是发电机组的数量;T是调度周期的个数;Pij根据式(5)在其出力上下限之间随机产生.
3.2 算法流程
MLMPIO求解多目标DEED问题的流程如下所示:
步骤1 初始化种群,包括种群大小Np,位置xi,速度Vi,个体历史最优xp_i,迭代次数t.
步骤2 初始化一个外部存档集A=∅,利用Pareto排序机制找到初始种群的非支配解集,并存入A.
步骤3 从A中分别为每个个体选择合适的全局最优xg_i,并根据式(10)更新其速度Vi和位置xi.
步骤4 依据式(11)对更新后的个体进行小概率变异扰动.
步骤5 更新xp_i.
步骤6 找到当前种群的非支配解集,并将其合并存入外部存档集A;利用帕累托排序机制对外部档案集A进行排序,保留前EA(t)[大小由式(12)求解]个个体作为当前代的Pareto最优解集.
步骤7 令t=t+1,如果t<T,返回步骤3;否则,停止运行,输出Pareto最优解集.
需要注意的是,笔者对于DEED中等式和不等式约束的处理采用动态启发式约束处理方法;此外,对于最优折中解的计算采用基于模糊集理论的折中解求解方法,具体可见文献[18].
4 实验结果与分析
4.1 系统描述与参数设置
笔者采用10机组电力系统验证MLMPIO算法的有效性,调度周期为24 h,以1 h为间隔分为24个调度时段. 机组参数、分时段负荷以及网损系数见文献[3].所有仿真实验均采用Matlab R2014b 编程实现,测试环境为i7-6 700 K处理器(4.00 GHz),16 GB内存,Windows 64位Windows 7操作系统.
MLMPIO算法的参数设置如表1所示. 需要说明的是,由于算法在每次迭代更新后均会剔除Ndec个劣等个体,所以MLMPIO的种群大小和最大迭代次数设置为298和100,其他参数均可依据算法性能进行调整,表1中所列参数为多次试验后得到的最优选择. 此外,MPIO算法所选参数与MLMPIO一致.
表1 本文算法参数
Tab.1 Optimal parameters for MLMPIO
NdecRtrpmrNpgm20.0530.40.3298100
4.2 结果分析
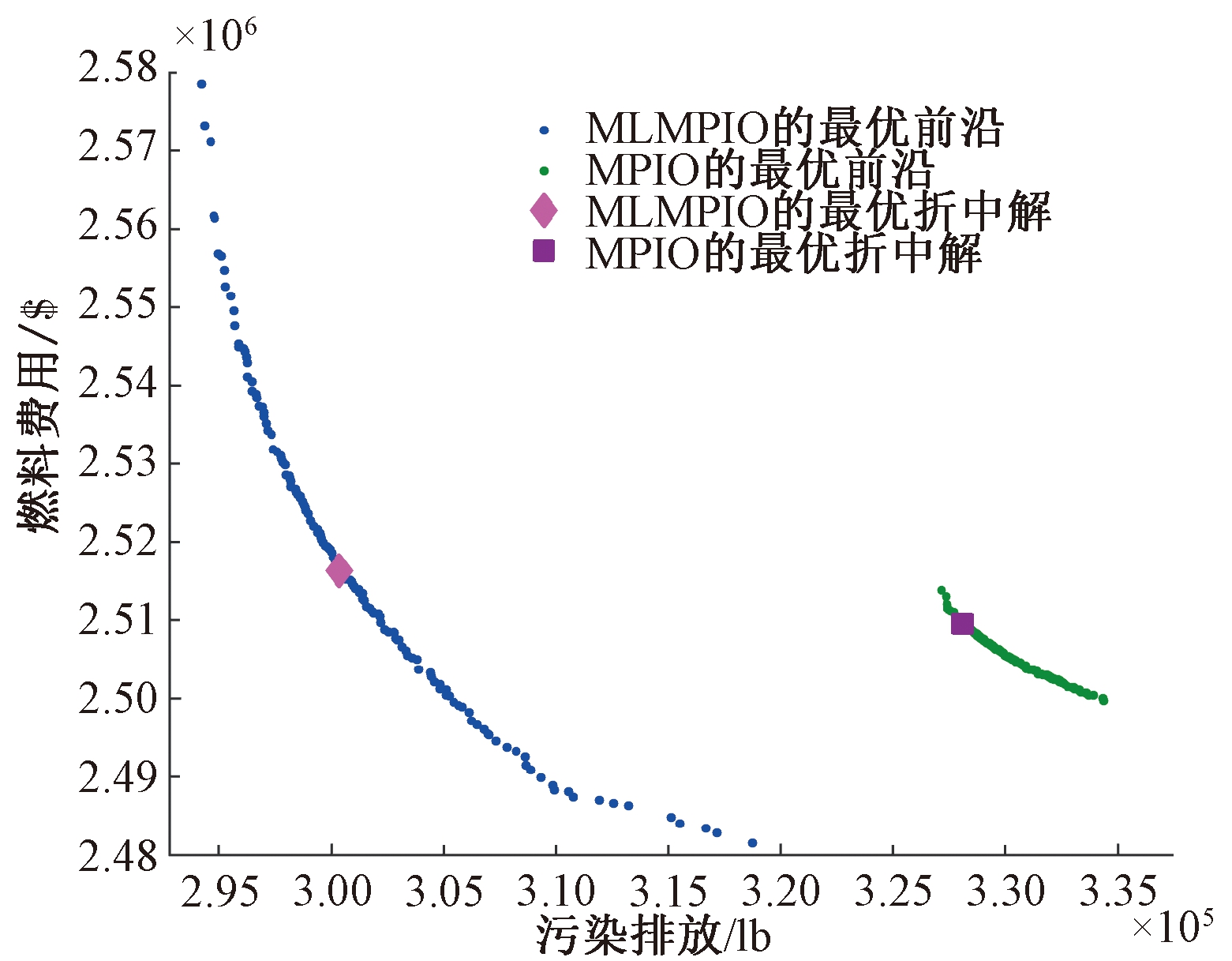
图2 MLMPIO与MPIO所获得的帕累托前沿
Fig.2 The Pareto optimal fronts obtained by MLMPIO and MPIO
图2是MLMPIO与MPIO所获得的Pareto前沿对比图,从图2中可以看出,MPIO所求得的帕累托前沿分布密集且局限于较窄的区域,这表明MPIO算法在求解时可能陷入局部最优区域. 而MLMPIO所求得的帕累托前沿分布更加广泛也更加均匀,且各目标的极端解也更好,可为决策者提供更优的调度方案. 此外,图2的结果对比也验证了MLMPIO算法中多学习策略及小概率变异扰动的有效性.
表2列出了MLMPIO与MPIO所获得的最优目标值和最优折中解. 从表2中可以看出,MLMPIO所求得的经济目标最优值和环境目标最优值均优于MPIO. 在最优折中解方面,MPIO的燃料费用目标值(2.509 541×106 $)仅比MLMPIO(2.516 345×106 $)低0.27%,而在污染排放方面,MPIO(3.280 98×105 lb)却比MLMPIO(3.003 67×105 lb)要多8.45%. 综上可知,笔者提出的MLMPIO算法相比于基本MPIO来说,表现出更优的全局搜索能力和计算精度,同时也展现出更好的调度性能.
表2 MLMPIO与MPIO实验结果对比
Tab.2 Comparison of experiment results between MLMPIO and MPIO
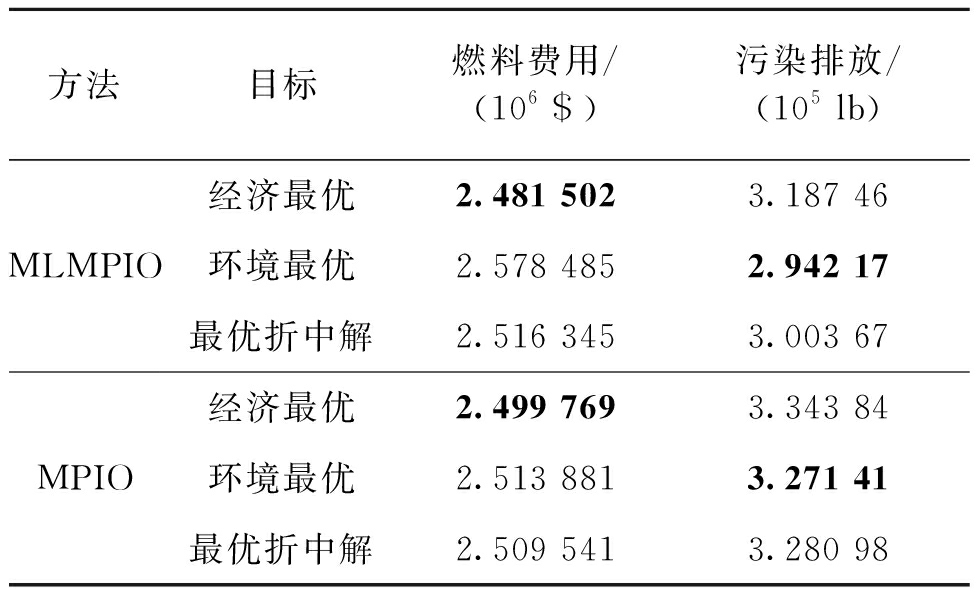
方法目标燃料费用/(106 $)污染排放/(105 lb)MLMPIOMPIO经济最优2.481 5023.187 46环境最优2.578 4852.942 17最优折中解2.516 3453.003 67经济最优2.499 7693.343 84环境最优2.513 8813.271 41最优折中解2.509 5413.280 98
表3将MLMPIO的调度结果与近年来文献中采用相同机组模型的其他5种算法的结果进行对比.分析表3中的结果可知,在经济目标和环境目标的最优解(极端解)方面,相比于IBFA、RCGA/NSGA-Ⅱ、MAMODE以及CRO 4种算法,MLMPIO的结果(2.481 502×106 $和2.942 17×105 lb)都是最优的;与HCRO算法相比,其经济目标最优值(2.479 931×106 $)仅比MLMPIO(2.481 502×106 $)低0.06%,但在环境目标方面,HCRO(2.984 56×105 lb)却比MLMPIO(2.942 17×105 lb)要高1.42%. 综合两个目标的最优解情况可知,MLMPIO的性能要优于HCRO. 在最优折中解方面,MLMPIO要优于RCGA/NSGA-Ⅱ和CRO;IBFA的污染排放目标值最小,但其燃料费用(2.517 117×106 $)要高于MLMPIO(2.516 345×106 $);MAMODE得到的燃料费用目标值最小,但其污染排放目标值比MLMPIO高2.375×103 lb. 综上,与其他5种算法相比,MLMPIO无论在极端解还是折中解方面均表现出较好的优化性能.
表3 不同算法的结果对比
Tab.3 Results comparison of different methods
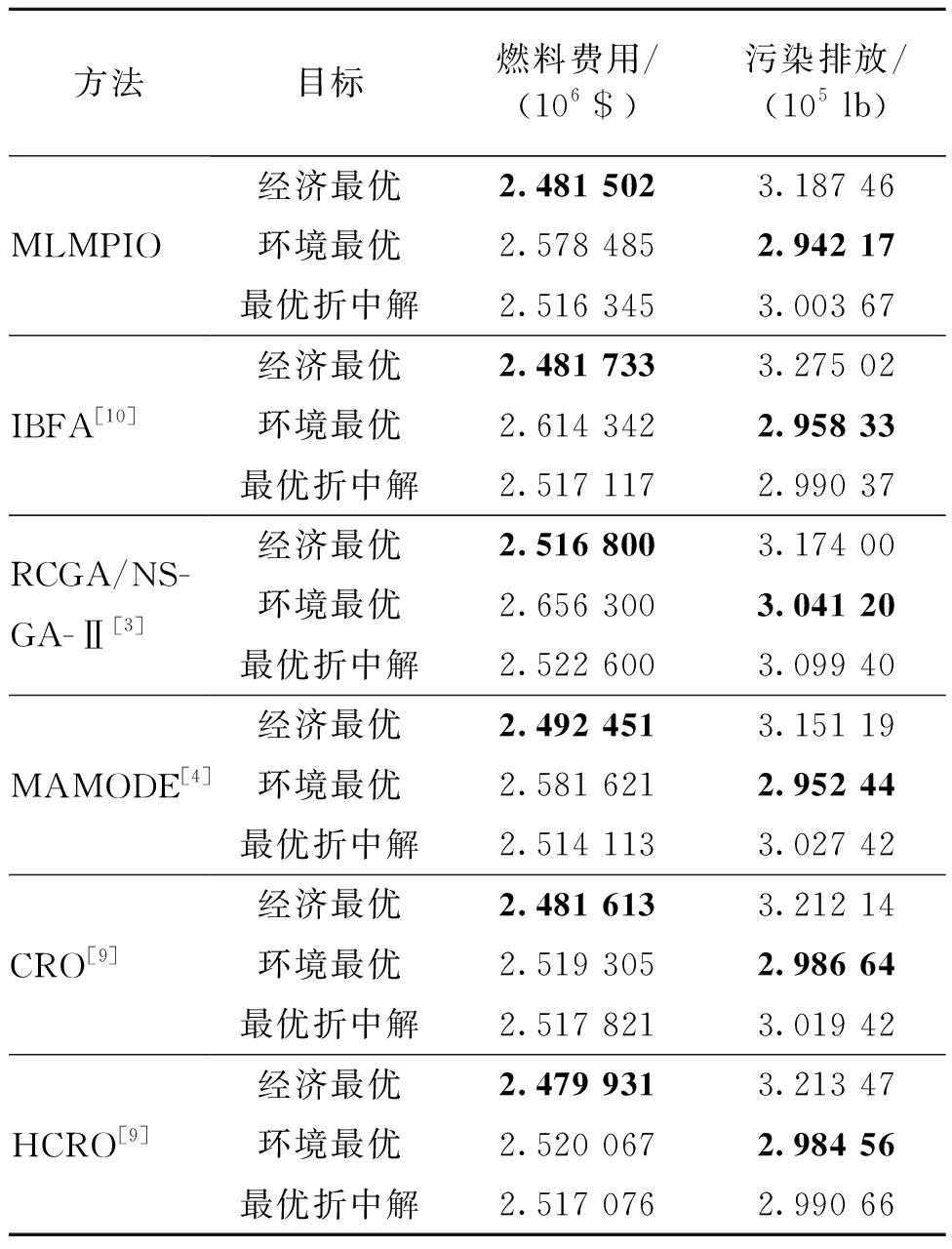
方法目标燃料费用/(106 $)污染排放/(105 lb)MLMPIOIBFA[10]RCGA/NS-GA-Ⅱ[3]MAMODE[4]CRO[9]HCRO[9]经济最优2.481 5023.187 46环境最优2.578 4852.942 17最优折中解2.516 345 3.003 67经济最优2.481 7333.275 02环境最优2.614 3422.958 33最优折中解2.517 1172.990 37经济最优2.516 8003.174 00环境最优2.656 3003.041 20最优折中解2.522 6003.099 40经济最优2.492 4513.151 19环境最优2.581 6212.952 44最优折中解2.514 1133.027 42经济最优2.481 6133.212 14环境最优2.519 3052.986 64最优折中解2.517 8213.019 42经济最优2.479 9313.213 47环境最优2.520 0672.984 56最优折中解2.517 0762.990 66
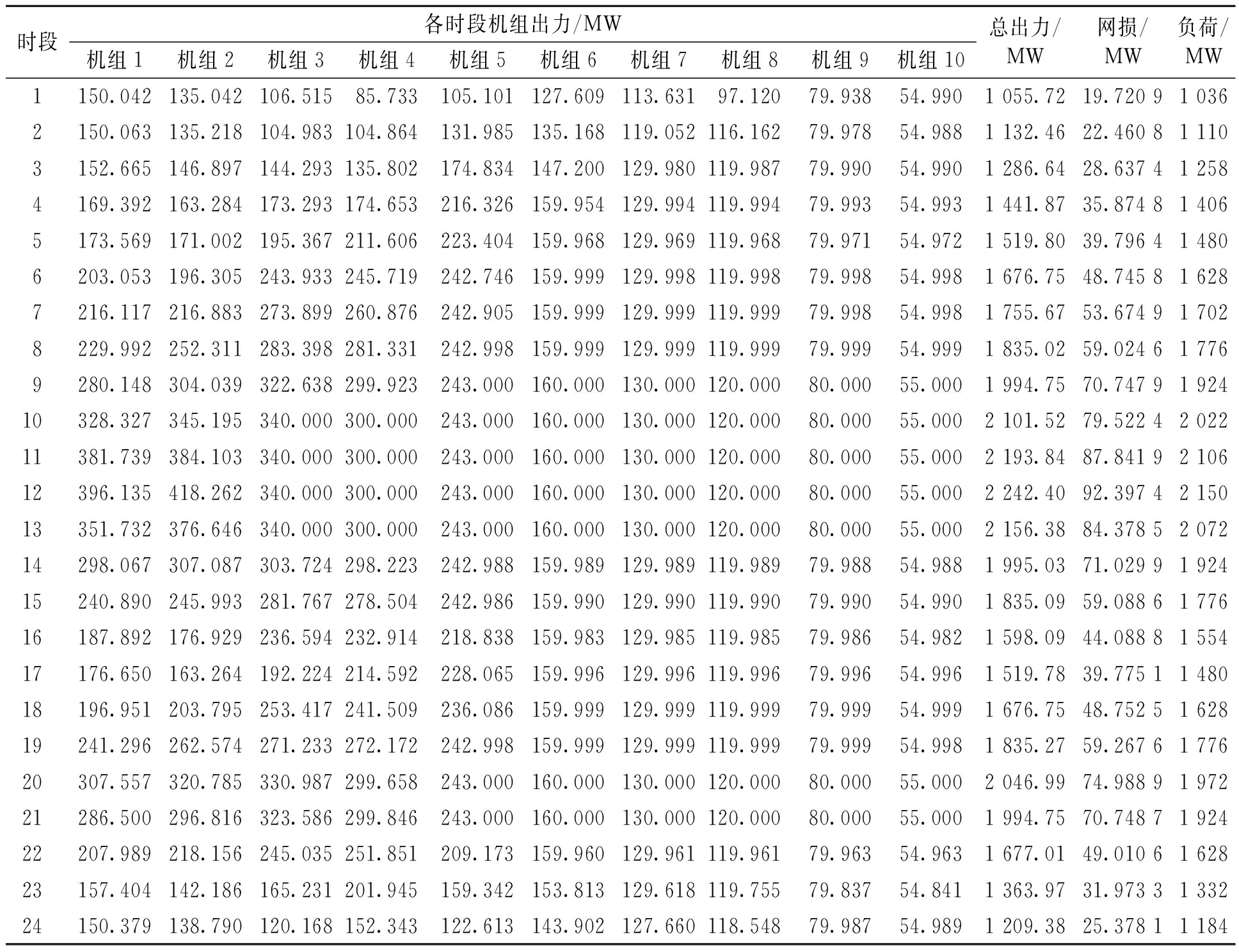
表4给出了MLMPIO所求得的最优折中解,涵盖了每个机组在全部调度时段的出力大小,同时给出了不同时段内系统的网损和负荷大小. 通过计算可得,机组在各调度时段的总出力均等于该时段系统的网损与负荷之和,这表明MLMPIO求得的最优折中解满足式(3)所示的功率平衡约束,同时,各机组调度出力大小也满足机组出力约束和爬坡约束. 这进一步验证了笔者所提出MLMPIO算法在求解DEED问题时的可行性和有效性.
表4 MLMPIO的最优折中解
Tab.4 Best compromise solution obtained by MLMPIO
时段各时段机组出力/MW机组1机组2机组3机组4机组5机组6机组7机组8机组9机组10总出力/MW网损/MW负荷/MW1150.042135.042106.51585.733105.101127.609113.63197.12079.93854.9901 055.7219.720 91 0362150.063135.218104.983104.864131.985135.168119.052116.16279.97854.9881 132.4622.460 81 1103152.665146.897144.293135.802174.834147.200129.980119.98779.99054.9901 286.6428.637 41 2584169.392163.284173.293174.653216.326159.954129.994119.99479.99354.9931 441.8735.874 81 4065173.569171.002195.367211.606223.404159.968129.969119.96879.97154.9721 519.8039.796 41 4806203.053196.305243.933245.719242.746159.999129.998119.99879.99854.9981 676.7548.745 81 6287216.117216.883273.899260.876242.905159.999129.999119.99979.99854.9981 755.6753.674 91 7028229.992252.311283.398281.331242.998159.999129.999119.99979.99954.9991 835.0259.024 61 7769280.148304.039322.638299.923243.000160.000130.000120.00080.00055.0001 994.7570.747 91 92410328.327345.195340.000300.000243.000160.000130.000120.00080.00055.0002 101.5279.522 42 02211381.739384.103340.000300.000243.000160.000130.000120.00080.00055.0002 193.8487.841 92 10612396.135418.262340.000300.000243.000160.000130.000120.00080.00055.0002 242.4092.397 42 15013351.732376.646340.000300.000243.000160.000130.000120.00080.00055.0002 156.3884.378 52 07214298.067307.087303.724298.223242.988159.989129.989119.98979.98854.9881 995.0371.029 91 92415240.890245.993281.767278.504242.986159.990129.990119.99079.99054.9901 835.0959.088 61 77616187.892176.929236.594232.914218.838159.983129.985119.98579.98654.9821 598.0944.088 81 55417176.650163.264192.224214.592228.065159.996129.996119.99679.99654.9961 519.7839.775 11 48018196.951203.795253.417241.509236.086159.999129.999119.99979.99954.9991 676.7548.752 51 62819241.296262.574271.233272.172242.998159.999129.999119.99979.99954.9981 835.2759.267 61 77620307.557320.785330.987299.658243.000160.000130.000120.00080.00055.0002 046.9974.988 91 97221286.500296.816323.586299.846243.000160.000130.000120.00080.00055.0001 994.7570.748 71 92422207.989218.156245.035251.851209.173159.960129.961119.96179.96354.9631 677.0149.010 61 62823157.404142.186165.231201.945159.342153.813129.618119.75579.83754.8411 363.9731.973 31 33224150.379138.790120.168152.343122.613143.902127.660118.54879.98754.9891 209.3825.378 11 184
5 结论
笔者以电力系统在一定调度周期内的总燃料费用和污染排放为目标,建立了电力系统多目标DEED模型,并在模型中计及了火电机组的阈点效应、机组爬坡速率约束、网络损耗以及负荷变化.为求解复杂的多目标DEED问题,提出了一种基于多学习策略的多目标鸽群优化算法,该算法通过一种新的多学习策略来增强种群的多样性和全局搜索能力,避免陷入局部最优;同时,引入小概率变异扰动机制来进一步增强种群的多样性;采用容量自适应变化的外部存档集来存储当前Pareto最优解集,提升算法的运行效率. 为验证所提算法的有效性,以10机组电力系统的DEED问题为算例进行求解,并与MPIO及其他调度方案进行对比分析.实验结果表明,MLMPIO是一种可行且有效的多目标DEED问题求解算法,同其他算法相比,表现出更优的全局搜索能力及寻优能力,能够为决策者提供更多更优的选择.
[1] QU B Y, ZHU Y S, JIAO Y C, et al. A survey on multi-objective evolutionary algorithms for the solution of the environmental/economic dispatch problems[J]. Swarm and evolutionary computation, 2018, 38: 1-11.
[2] 肖俊明, 周谦, 瞿博阳,等. 多目标进化算法及其在电力环境经济调度中的应用综述[J]. 郑州大学学报(工学版), 2016, 37(2): 1-9.
[3] BASU M. Dynamic economic emission dispatch using nondominated sorting genetic algorithm-Ⅱ[J]. International journal of electrical power & energy systems, 2008, 30(2): 140-149.
[4] JIANG X W, ZHOU J Z, WANG H, et al. Dynamic environmental economic dispatch using multiobjective differential evolution algorithm with expanded double selection and adaptive random restart[J]. International journal of electrical power & energy systems, 2013, 49:399-407.
[5] SONG Y H, YU I K. Dynamic load dispatch with voltage security and environmental constraints[J]. Electric power systems research, 1997, 43(1): 53-60.
[6] BASU M. Particle swarm optimization based goal-attainment method for dynamic economic emission dispatch[J]. Electric power components and systems, 2006, 34(9): 1015-1025.
[7] BASU M. Dynamic economic emission dispatch using evolutionary programming and fuzzy satisfying method[J]. International journal of emerging electric power systems, 2007, 8(4): 1-15.
[8] ZHU Z J, WANG J, BALOCH M H. Dynamic economic emission dispatch using modified NSGA-Ⅱ[J]. International transactions on electrical energy systems, 2016, 26(12): 2684-2698.
[9] ROY P K, BHUI S. A multi-objective hybrid evolutionary algorithm for dynamic economic emission load dispatch[J]. International transactions on electrical energy systems, 2016, 26(1): 49-78.
[10] PANDIT N,TRIPATHI A,TAPASWI S,et al.An improved bacterial foraging algorithm for combined static/dynamic environmental economic dispatch[J].Applied soft computing,2012,12(11):3500-3513.
[11] GUO C X, ZHAN J P, WU Q H. Dynamic economic emission dispatch based on group search optimizer with multiple producers[J]. Electric power systems research, 2012, 86: 8-16.
[12] DUAN H B, QIAO P X. Pigeon-inspired optimization: a new swarm intelligence optimizer for air robot path planning[J]. International journal of intelligent computing and cybernetics, 2014, 7(1): 24-37.
[13] 段海滨, 邱华鑫, 范彦铭. 基于捕食逃逸鸽群优化的无人机紧密编队协同控制[J]. 中国科学(技术科学), 2015, 45(6): 559-572.
[14] DOU R, DUAN H B. Pigeon-inspired optimization approach to model prediction control for unmanned air vehicles[J]. Aircraft engineering and aerospace technology, 2016, 88(1):108-116.
[15] XU X B, DENG Y M. UAV power component-DC brushless motor design with merging adjacent-disturbances and integrated-dispatching pigeon-inspired optimization[J]. IEEE transactions on magnetics, 2018,54(8):1-7.
[16] QIU H X, DUAN H B. Multi-objective pigeon-inspired optimization for brushless direct current motor parameter design[J]. Science china technological sciences, 2015, 58(11): 1915-1923.
[17] DEB K, PRATAP A, AGARWAL S, et al. A fast and elitist multiobjective genetic algorithm: NSGA-Ⅱ[J]. IEEE transactions on evolutionary computation, 2002, 6(2): 182-197.
[18] ZHU Y S, WANG J, QU B Y. Multi-objective economic emission dispatch considering wind power using evolutionary algorithm based on decomposition[J]. Electrical power & energy systems, 2014, 63: 434-445.