0 引言
作为共享经济的一种新形态,共享单车不仅解决了市民“最后一公里”出行的问题[1],更以无桩、便捷等优势,在一定程度上改变了人们的出行方式,缓解了城市交通拥堵.但是,由于在高峰时段,公司、居民区等客流量高发区域的潮汐现象[2],容易出现共享单车的积聚或者短缺问题,因此需要快速构建出一种最佳的共享单车的调度方案,对共享单车进行调度.共享单车调度[2]是根据整个区域的单车分布情况以及各区域的需求信息,依靠调度算法来使得整个区域的单车数目趋向于合理,即将共享单车从积聚区域及时运送到短缺区域.既不会因为单车的过多聚集而影响其他交通方式,也不会因为缺少单车而导致人们的出行困难,是一个将整个区域的共享单车数量和布局进行调整的过程.良好的调度算法不仅能够使共享单车调度体系正常运转,同时也能有效提升整个共享单车系统的服务水平.
1 离散差分进化算法原理及步骤
1.1 离散差分进化算法原理
离散差分进化算法[3-4](discrete differential evolution, DDE)框架与传统的进化算法[5](differential evolution, DE)相同,首先在问题的定义域内随机产生第0代种群作为初始种群[6];然后通过将每一个个体进行变异,变异的方式为在每一个个体上加上或者减去随机两个个体的差分量的缩放值,并将此个体作为变异个体,如有非法解则需要进行修补;然后对此变异个体与当前个体进行杂交操作,生成实验个体;最后将实验个体与当前个体进行竞争,较优者保留下来[7].通过迭代,逐渐将种群引导到最优解位置.主要步骤如图1所示[8].
图1 DDE算法主要步骤
Fig.1 Main steps of DDE algorithms
不同之处在于,将其个体编码、变异算子和修补算子重新设计,使其适合求解共享单车调度问题.每个区域的编号作为每个个体的元素,将传统变异算子改造成可以进行离散变异的变异算子,同时,一旦产生非法解,则进行修补操作.
1.2 个体编码设计
考虑到所使用的区域编号为整数,笔者拟采用整数进行个体编码[9].
每条可行线路编码成长度为l的个体{x1,1(G),x1,2(G),…,x1,l(G)},其中,xi,k(G)表示第G代种群中的第i个个体的第k个分量.其中,分量表示的是区域的编号.如个体为5→2→3→4→2→5→3表示从配送中心1出发,最后又返回配送中心1的一条调度路线.个体编码长度l由式(1)表示.
(1)
式中:T表示整个高峰期的时间;shortest(u,v)表示任两区域之间通行时间最小值.
1.3 变异操作设计
与传统的差分进化算法的变异操作不同,本文设计的简单的变异算子如下[8].
vi(G)=xr1+F(xr2(G)-xr3(G)),
(2)
式中:F为缩放因子且F∈{1,2,…,n}.在本实例中,选取F=1,示意图如图2所示[10].
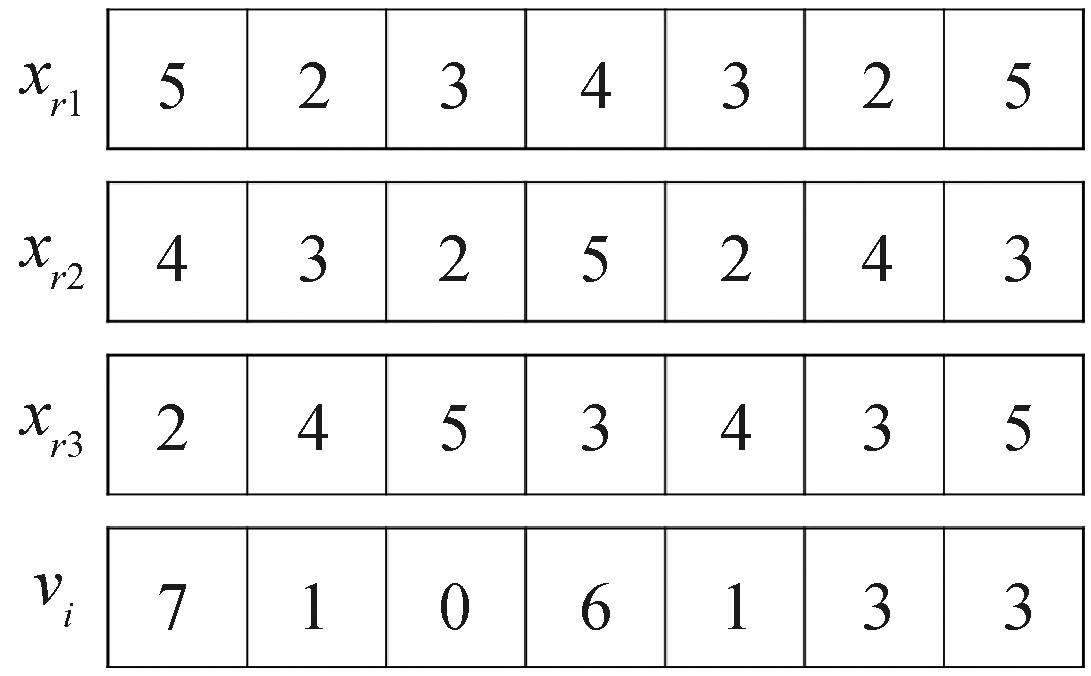
图2 变异操作示例图
Fig.2 Variation operation diagram
1.4 修补算子设计
相比其他优化问题,共享单车调度问题对解的限制有所不同[2]:①相邻两个变量不能相同;②个体中的每一维取值都必须在区域列表中.因此,修补操作设计步骤如下.
输入:item为个体,n为染色体个数,Rlower为定义域下界,Rupper为定义域上界
1:function REPAIR(item,n,Rlower,Rupper)
2: for i=1→n do
3: item[i]←(item[i]-Rlower) mod (Rupper-Rlower+1)+Rlower
4: end for
5: for i=2→n-1 do
6: while item[i]=item[i-1] or item[i]=item[i+1] do
7: item[i]=Random(Rlower,Rupper)
8: end while
9: end for
10: return item
11:end function
1.5 DDE算法流程
通过以上对DDE算法各个操作的描述,DDE算法的流程如下.
步骤1 初始化:确定编码方式后,选择合适的种群大小,种群规模、CR、F值,种群代数G=0,初始化第0代随机种群,并计算每个个体的适应度值.
步骤2 变异操作:种群代数G=G+1,根据新设计的变异操作对X(G)中的每个个体进行变异操作,操作方式如上述变异操作所示.
步骤3 修补操作:根据新设计的修补算子对变异后的每个个体进行修补操作,使得每个个体能够满足之前问题的两个限制条件.
步骤4 杂交操作:使用“bin”杂交方式对原本个体与变异个体进行操作,生成实验个体.
步骤5 选择操作:通过新设计的适应度函数,选择适应度值更大的个体,从而得到下一代种群.
步骤6 中止判断:如果条件满足,则中止当前算法执行,并输出最优路径,否则,转步骤2.
2 共享单车调度模型
2.1 问题描述
通常,在早高峰期,居住区域对共享单车需求量较大,工作区域则单车到达量较多;在晚高峰期则相反.这种出行量和到达量的差异决定了各区域存在调度需求,具体来看,这种需求分为两种[2]:调入需求和调出需求.因此共享单车的调度问题可描述为:在早晚高峰期,存在一定数量具有调度需求的区域,从调度中心出发的一辆调度车在已知各区域位置、区域单车分布、调度车容量、各区域租还速率等信息,要求在一定的约束条件下,完成调度区域间的单车调度,计算出调度路线和各区域的调度车辆数量.
2.2 调度过程
调度区域分为3种类型:调度中心、出行区域以及到达区域.调度中心无法存放单车,也无单车调度需求,t=0时刻调度车从调度中心空车出发,前往各个区域进行调度;出行区域的单车数量会随时间均匀减少,当调度车抵达出行区域时,按照一定的调度规则卸下一定数量的单车;到达区域的单车数量会随时间均匀增多,当调度车抵达到达区域时,按照一定的规则装走一定数量的单车.
如果抵达某一区域时尚未超出调度时间段的范围,则按照一定的调度规则完成对该区域的单车调度,然后调度车前往下一区域;如果超出调度时间段的范围,则终止整个调度过程并返回调度中心.
鉴于主目标是满足用户需求,所以优化目标确定为实现最大限度的调度量,因为在系统规模一定的情况下,经过最大量的调度可实现较高的利用率,因此调度目标是使在调度时间段内调度车的总装卸量Q尽可能大.
为了表达更简洁,本文引入一些符号,其含义如表1所示.
表1 符号说明
Tab.1 Symbol declaration

变量含义i区域编号,i∈{1,2,…,n},i=1表示调度中心j调度次数编号,j∈{1,2,…,m},m表示最大调度次数C调度车的容量,即调度车能够容纳的最大单车数量td调度车装上或卸下一辆单车所需的时间T调度终止时刻tj第j次调度的开始时刻qit=0时刻i区域的单车数量Qi[0,T]时间段内i区域单车数量的净变化量Fi到达区域i在调度终止时刻希望保持的单车数目Cj第j次调度开始时调度车上的单车数量ni,j第j次调度开始时i区域单车的数量Bi,j第j次调度开始时i区域的调度需求bj第j次调度实际装卸的单车数目Q调度车在整个调度过程中的总装卸量,Q=∑mj=1bj
2.3 调度规则
当第j次调度调度车抵达i区域时,首先计算i区域的当前单车数目ni,j,计算方法为:
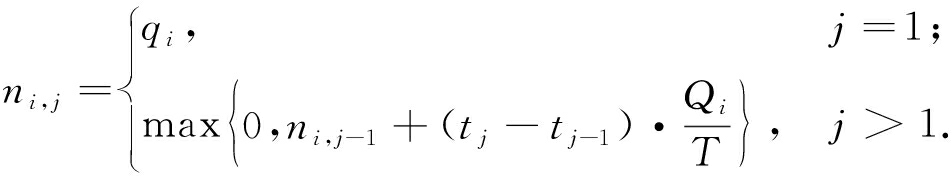
(4)
然后计算i区域对单车的需求,计算方法为:
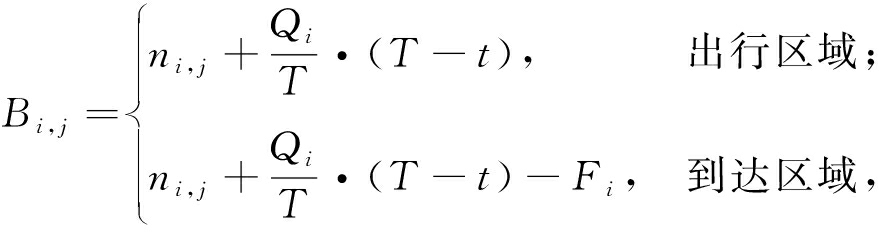
(5)
当Bi,j<0时,表示该区域车辆短缺,需要补充单车.若调度车上的单车数量不足以满足该区域的需求,则将调度车上所有车卸下;若调度车上的车辆足以满足该区域的需求,则从调度车上卸下-Bi,j辆单车,如式(6)所示.
bj=max{-Cj,Bi,j}.
(6)
当Bi,j>0时,表示该区域车辆过剩,需要装走多余单车.若调度车上的剩余空间不足,则将调度车装满;若调度车的剩余空间足够,则将Bi,j辆单车装上调度车,如式(7)所示.
bj=min{C-Cj,Bi,j}.
(7)
3 实验及结果
3.1 参数设置
总调度时间T=60 min,调度车容量C=20,装卸一辆单车的时间td=0.2 min.一共有5个区域,区域1为调度中心,区域2、3为出行区域,区域4、5为到达区域.各个区域间的最短通行时间如表2所示.各区域的初始车辆变化如表3所示.
表2 各区域最短通行时间
Tab.2 Shortest passage time between different zones
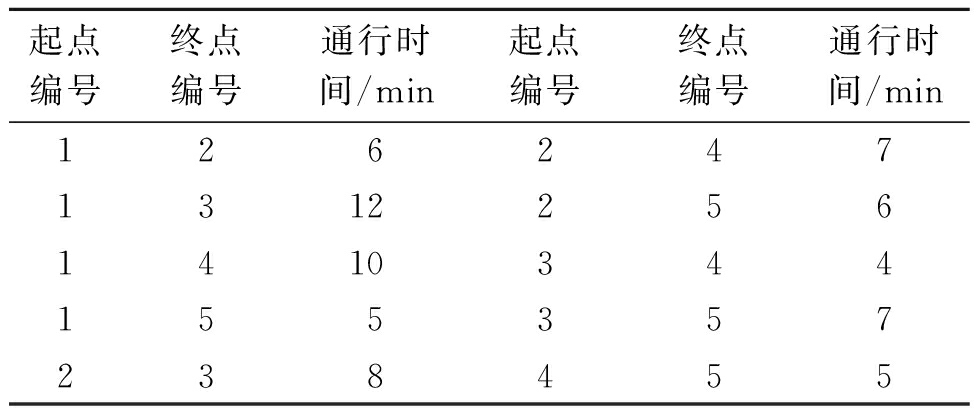
起点编号终点编号通行时间/min起点编号终点编号通行时间/min12624713122561410344155357238455
*注:本文的双向距离相同
表3 各区域初始车辆数和车辆变化
Tab.3 The initial number of vehicles and vehicle changes in each zone

区域编号初始单车数量qi调度时间段内单车数量的净变化量Qi调度结束时期望维持的车辆数目Fi100 (无)—210-40 (净出行40辆)—315-25 (净出行25辆)—41040 (净到达40辆)2051030 (净到达30辆)15
设置种群规模NP为30,每个个体表示一条调度路径,维度D设置为15,缩放因子F为1,杂交概率CR为0.6,迭代次数为100次.执行过程中会判断每个个体的有效长度,保证调度路径可以在规定时间内完成.
3.2 实验结果及分析
DDE算法收敛曲线如图3所示.图3表明,种群在第2代左右得到最优解,在50代左右所有个体收敛到最优值,最终平均调度量为85.9,收敛速度较快.
最优的调度路线、调度车辆数量和调度时间节点如表4所示,其中,调度顺序为调度次数,
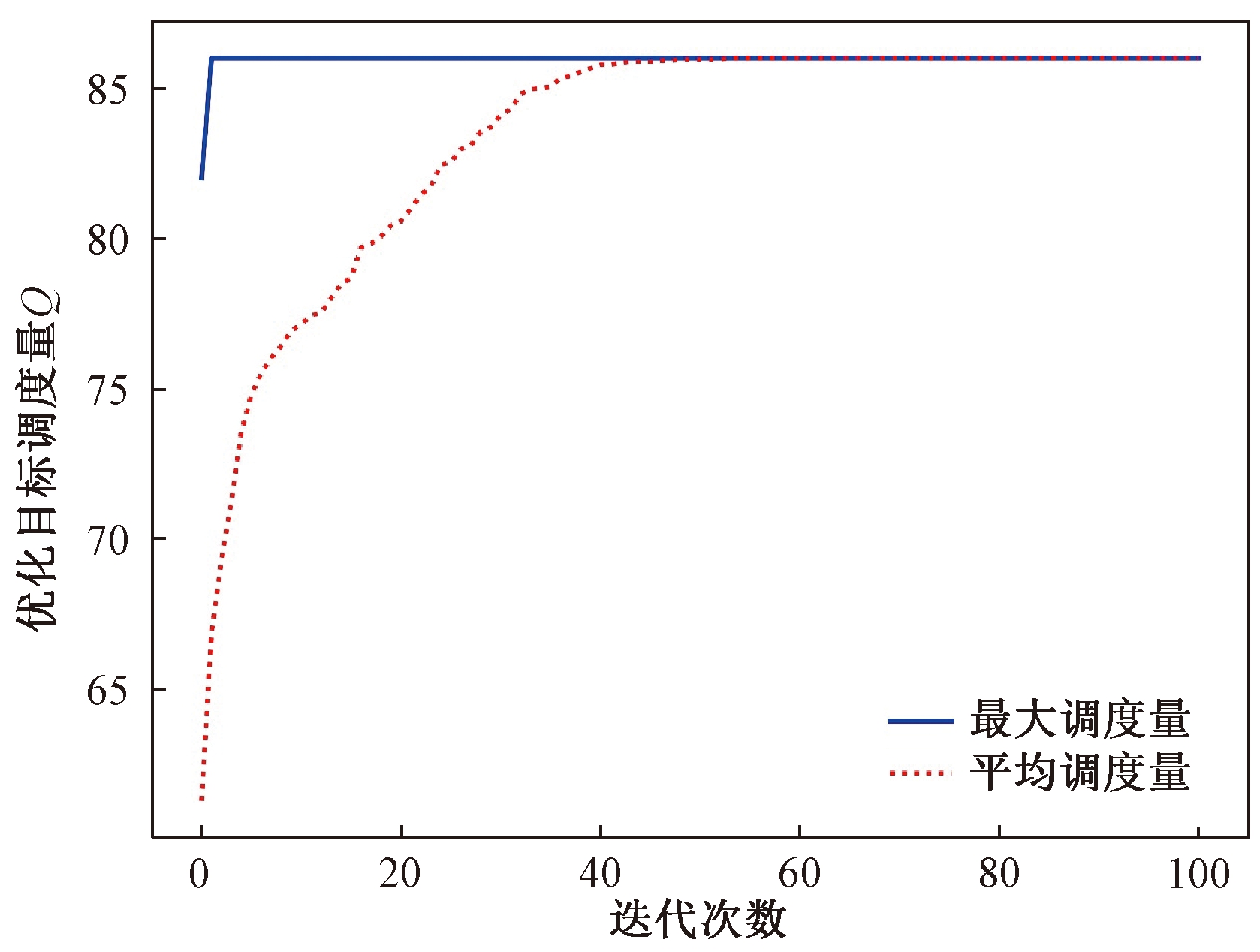
图3 DDE算法收敛曲线图
Fig.3 The convergence curve of DDE algorithm
0表示初始状态,区域编号为当前调度次数下调度车辆所在的区域,调度量为此次调度下调度车辆的装卸量,正数表示装车,负数表示卸车,总调度量表示截至当前次数下已经调度的车辆总和,包括装车和卸车,最终得到的路径为1→5→2→4→3→2→4→5→1,总调度量Q=86.
DDE算法得到的解所模拟的调度过程如图4所示.其中,红色方框表示每一时刻小车所在的区域,方框内的数表示当前时刻调度车辆的装载量.红色线段表示调度车辆的路径变化,即行驶路径.其中左上角图例中的ni,j和Bi,j的含义与表1中的变量说明一致.每个子图下方标示了该子图所处的时间点t和总调度量Q.该图的每一张子图都为一个时间点,如第一张子图表示初始状态,当前时刻t=0,总调度量Q=0,调度车辆当前所处的区域为调度中心1,每个区域的当前单车数目ni,j和需求量Bi,j在其下方显示.
表4 DDE算法调度过程
Tab.4 The scheduling process of DDE algorithm
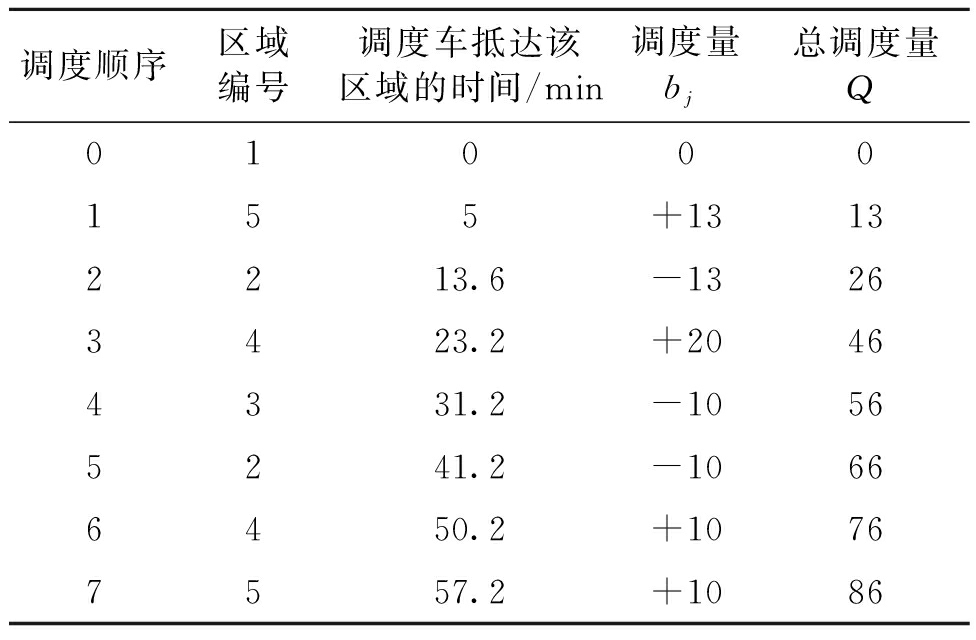
调度顺序区域编号调度车抵达该区域的时间/min调度量bj总调度量Q01000155+13132213.6-13263423.2+20464331.2-10565241.2-10666450.2+10767557.2+1086
3.3 与其他算法对比
(1) 应用贪心算法,贪心策略为每次选择使单位时间调度数量最大的区域作为前往的下一个区域,所得结果如表5所示,最终的调度量Q=84.
表5 贪心算法调度过程
Tab.5 The scheduling process of greedy algorithm
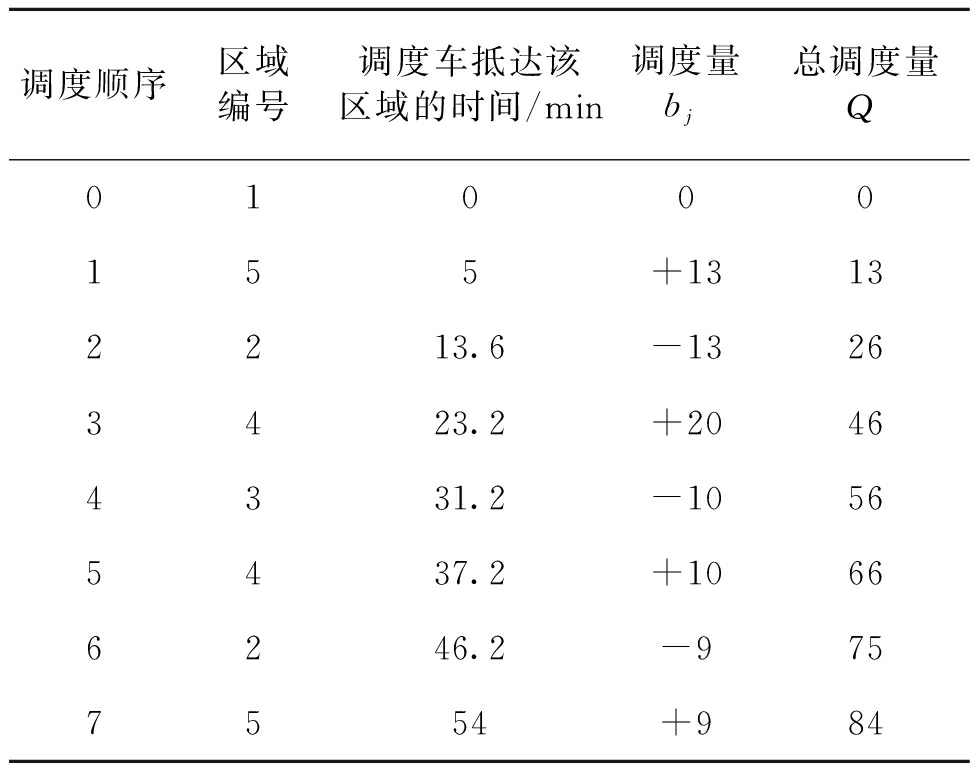
调度顺序区域编号调度车抵达该区域的时间/min调度量bj总调度量Q01000155+13132213.6-13263423.2+20464331.2-10565437.2+10666246.2-9757554+984
(2) 应用蚁群算法[11],重复运行50次,所得解的平均质量同DDE算法的对比如表6所示;其中两种算法一次运行的情况对比如图5所示.图5的横纵坐标以及图的各项说明与图4相同.
表6 蚁群算法与DDE算法得到的平均调度量对比
Tab.6 Comparison of average scheduling volume of ant colony optimization and DDE algorithm
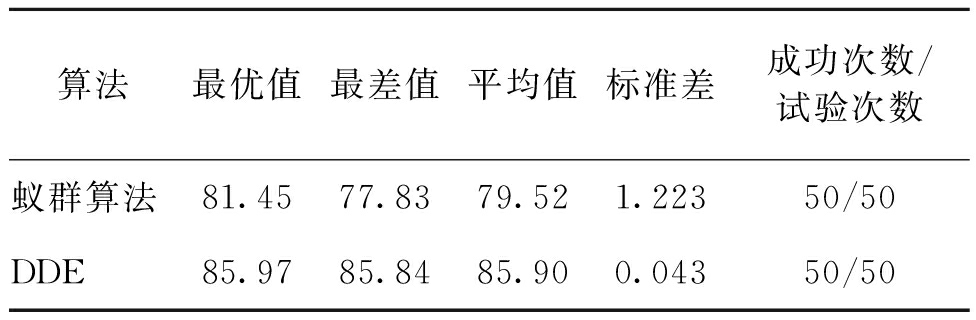
算法最优值最差值平均值标准差成功次数/试验次数蚁群算法81.4577.8379.521.22350/50DDE85.9785.8485.900.04350/50
图6表明,在相同的较小规模问题下,蚁群算法得到的最优解与DDE算法相同,但相比蚁群算法,DDE算法得到的解的平均质量更高,且收敛速度更快.表6表明,蚁群算法和DDE算法均能稳定求解共享单车调度问题,图6的情况具有一般性和代表性.
综合比较之下,DDE算法在这个问题中具有收敛快、解的质量高的优点.
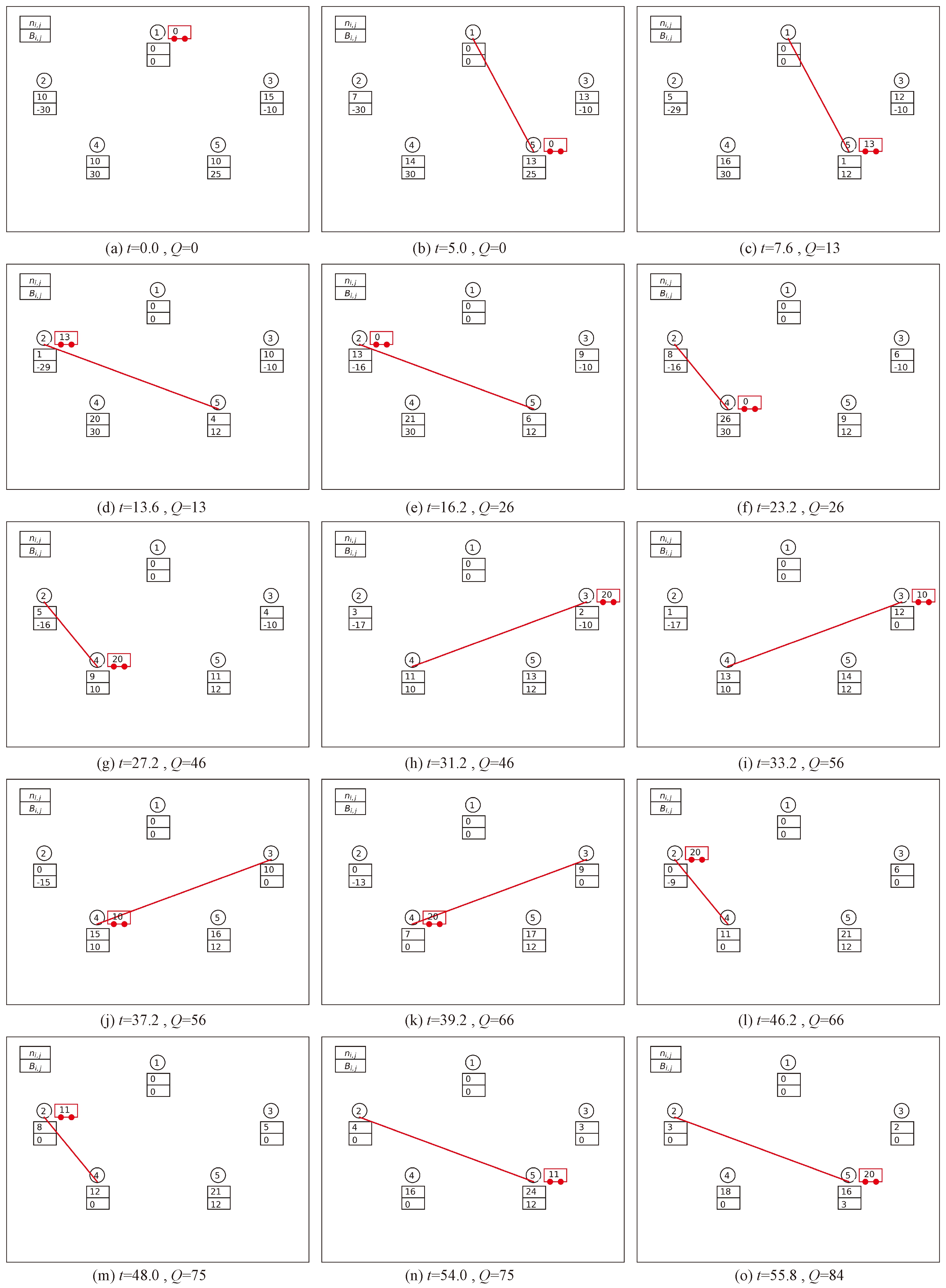
图4 DDE算法模拟调度过程
Fig.4 The specific route finding process of DDE algorithm
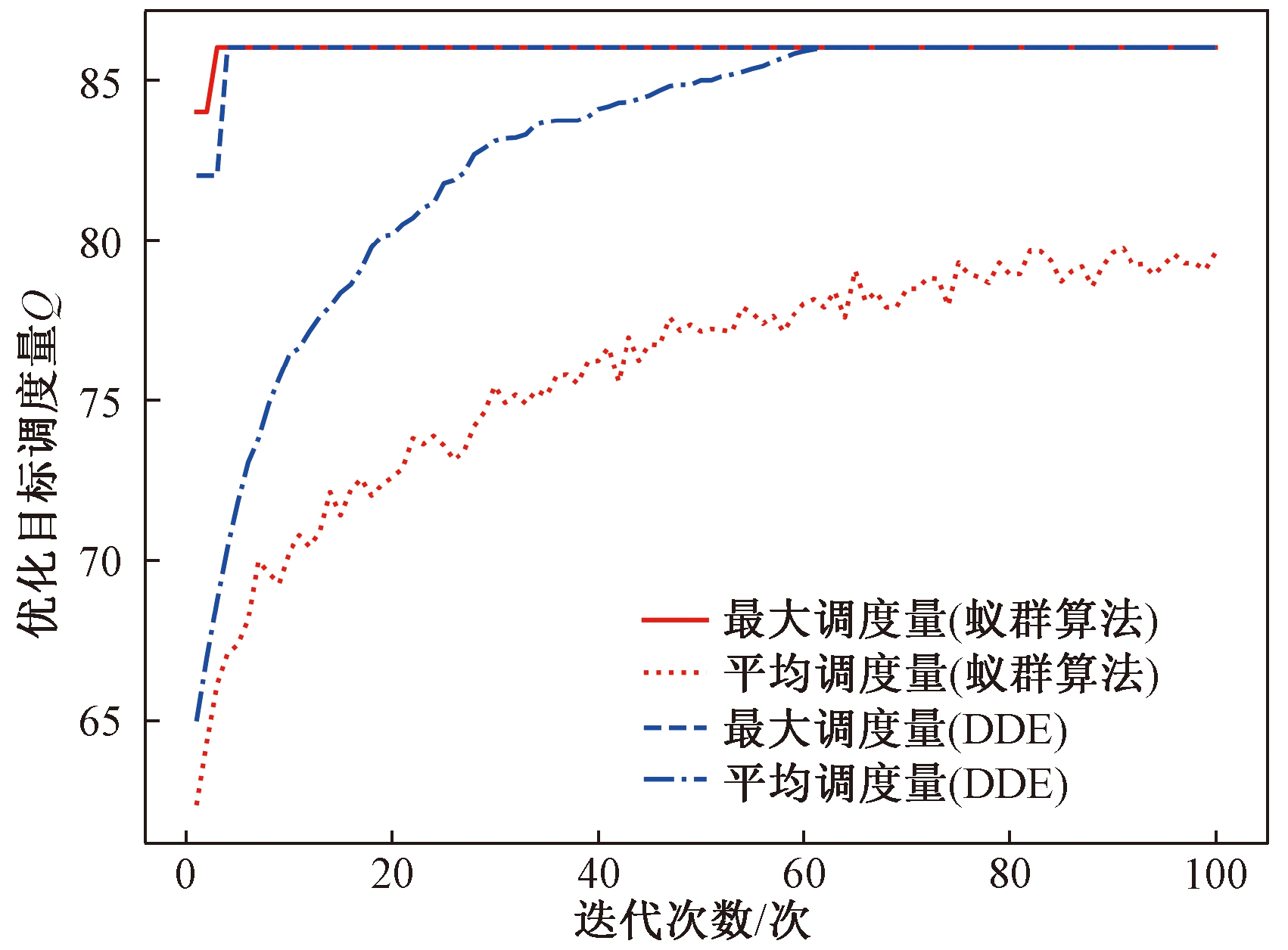
图5 蚁群算法与DDE算法收敛曲线对比图
Fig.5 Comparison of convergence curves of ant colony optimization and DDE algorithm
4 结论
笔者针对共享单车调度问题,设计了相应的DDE算法进行求解.实验结果表明,DDE算法可以稳定求解共享单车调度问题,相比贪心算法和蚁群算法,DDE算法在较小规模下求解共享单车调度问题时解的质量更优、收敛速度更快.下一步的工作将优化本身的调度模型,并逐步将问题的规模扩大,使得模型更符合现实生活.
[1] 高楹,宋辞,舒华,等.北京市摩拜共享单车源汇时空特征分析及空间调度[J].地球信息科学学报,2018,20(8):1123-1138.
[2] 周传钰. 共享单车投放量测算和调度方法研究[D]. 北京:北京交通大学交通运输学院,2018.
[3] 薛羽,庄毅,顾晶晶,等. 自适应离散差分进化算法策略的选择[J]. 软件学报,2014,25(5):984-996.
[4] AKGÜNGÖR A P, KORKMAZ E. Estimating traffic accidents in turkey ssing differential evolution algorithm[J]. Selected scientific papers-journal of civil engineering,2017,12(1):75-84.
[5] 梁静,周钦亚,瞿博阳,等. 基于混合策略的差分进化算法[J].郑州大学学报(工学版),2013,34(5):59-62.
[6] 程适,王锐,伍国华,等. 群体智能优化算法[J]. 郑州大学学报(工学版),2018,39(6):1-2.
[7] 曾冰,王梦雨,高亮,等.改进鲸鱼群算法及其在炼钢连铸调度中的应用[J].郑州大学学报(工学版),2018,39(6):14-22.
[8] 汪慎文,丁立新,张文生,等.差分进化算法研究进展[J].武汉大学学报(理学版),2014,60(4):283-292.
[9] 侯玲娟,周泓,梁春华. 不确定需求和旅行时间下的车辆路径问题[J]. 计算机集成制造系统,2011,17(1):101-108.
[10] SAKR W S, EL-SEHIEMY R A, AZMY A M. Adaptive differential evolution algorithm for efficient reactive power management[J]. Applied soft computing,2017,53:336-351.
[11] DORIGO M,GAMBARDELLA L M. Ant colony system: a cooperative learning approach to the traveling salesman problem[J]. IEEE Transactions on Evolutionary Computation,1997,1(1):53-66.