0 引言
一般来说,某一指尖的位置,就是该指尖区域中心的坐标. 人们利用指尖区域的特征,能够从手部区域中得到所有指尖的位置,这一图像处理的过程就是指尖定位. 目前,解决指尖定位问题的方法有:基于人手骨架的方法、基于手部边缘曲率的方法等.
在手部区域中,指尖区域位于手指区域的最外部. 与人手的其他区域相比,指尖区域具有两个特点: 一是指尖区域的人手边界形状最接近半圆弧,二是指尖区域与手掌中心的距离最远. 根据这两个特点,文献[1]提出了用于选择指尖区域像素点的多目标优化模型. 通过求解这一优化模型,能够得到某一手部区域中的所有指尖区域像素点. 根据指尖伸出的数量,对得到的指尖区域像素点进行聚类,能够得到任一指尖区域的像素点. 然后,对于某一指尖区域的所有像素点计算它们的坐标的平均值,这一平均值就是指尖区域中心的坐标. 对于上述指尖定位的优化模型,为了得到比较准确的指尖位置,需要保证选择出的指尖区域像素点是准确的. 由此可见,在求解指尖定位的优化模型时,采用适合的求解方法,才能保证选择出准确的指尖区域像素点.
笔者对求解指尖定位优化模型的分布估计算法进行研究,提出决策变量的维数、种群规模、最大采样方差、最小采样方差等分布估计算法的主要参数. 当这些主要参数均取最佳值时,得到的指尖中心位置最接近其真实的位置.
本研究有3个方面的贡献: ①对于求解指尖定位优化模型的分布估计算法,提出了它的主要参数; ②提出这些主要参数均存在最佳值; ③通过实际手部图像中的指尖定位实验,证明了所提参数及其最佳值的有效性.
1 相关工作
1.1 指尖定位
文献[2]计算了手部边缘曲线上所有像素点的曲率,进而给出某一阈值;如果某一像素点的曲率大于这一阈值,就认为该像素点的位置是指尖的位置. 文献[3]把指尖定位的过程分为两个阶段,第一个阶段进行粗定位,第二个阶段进行精确定位, 这样可以在不同的尺度上对定位的精度进行调节.
近年来,很多新的方法和技术在指尖定位领域出现. 文献[4]通过计算手部边界曲线包含的凸多边形,得到多个候选的指尖位置,进而选择出指尖的准确位置. 文献[5]在手部边界曲线上均匀地选择出一系列的像素点,计算其中的任一像素点与手掌中心的距离,然后通过比较这些像素点的距离值,得到指尖位置的像素点.
1.2 分布估计算法
生产生活中的很多实际问题都能够归结为优化问题.有些优化问题中存在多个目标函数,它们可称为多目标优化问题[6-7]. 进化算法模拟生物种群的进化过程,能够有效地求解多目标优化问题[8].
对于某些多目标优化问题,其中的任一问题的最优解集具有一定的分布规律,并且,在求解前,这一分布规律是已知的. 如果在这一问题的求解过程中,进化算法利用最优解集的分布规律,得到临时种群,那么,这一进化算法可称为分布估计算法. 分布估计算法利用了最优解集的分布规律,因此,它与一般的进化算法相比,具有理论上的优势.
文献[9]提出了基于规则模型的多目标分布估计算法. 文献[10]根据手部像素点的坐标分布在某一区间以内,并且手部像素点分布在某些直线段的两侧,建立了用于选择手部像素点的多目标分布估计算法.
2 指尖定位的求解方法
2.1 算法流程
与手部其他区域的像素点相比,指尖区域的像素点也具有两个特点: 一是指尖像素点对应的人手边界形状最接近半圆弧,二是指尖像素点与手掌中心的距离最远.如果手部像素点具有上述两个特点,我们就可以认为这些手部像素点是指尖像素点.
文献[6]根据指尖像素点的两个特点,提出了选择指尖像素点的多目标优化模型. 该模型用于从手部像素点中选择出一系列指尖像素点. 该模型的表达式如下:
(1)
式中:X是模型的决策空间,它是某一含有人手的图像中,手部区域包含的所有像素点的集合; 2X是X的幂集;x是决策变量,它是位置互不重合的像素点的集合,它的表达式是x=(x1,x2,…,xn),xi=(xi,yi),i=1,2,…,n,n是决策变量中包含的像素点个数.
目标函数f1(x)使选取的像素点对应的人手边界形状最接近半圆弧;目标函数f2(x)使选取的像素点与手掌中心的距离最远.
目标函数f1(x)的数学表示:
(2)
式中:Z1(xi)是xi对应的人手边界形状与半圆弧的相似程度,Z1(xi)的数值越小,表明这一人手边界形状越接近半圆弧.
目标函数f2(x)的数学表示:
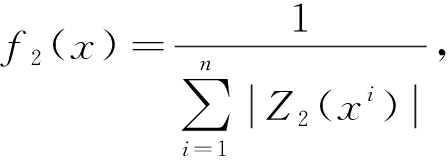
(3)
式中:Z2(xi)为xi与手掌中心的距离.
通过求解模型(1),能够得到一系列位于指尖区域的像素点. 模型(1)的最优解集,包含一系列的指尖像素点. 另外,这些指尖像素点分布在多个指尖区域中心的周围,或者说,这些指尖像素点分布在多个点的周围. 因此,模型(1)的最优解集具有一定的分布规律. 这一分布规律是模型(1)的最优解分量xi分布在多个点的周围.
文献[6]根据模型(1)最优解集的上述分布规律,提出了用于求解该模型的多目标分布估计算法. 这一算法的流程如下.
步骤1 令迭代次数t=0,在决策空间中随机采样,产生初始种群P(0);
步骤2 如果迭代次数t增加到最大值,停止迭代,输出种群P(t)的最优解集;
步骤3 根据P(t)的最优解集,建立多个点作为候选解分量xi的概率分布模型;
步骤4 在上述多个点附近采样,得到临时种群Q(t);
步骤5 采用快速非支配排序的方法,在P(t)和Q(t)的合并种群中,选择出子代种群P(t+1);
步骤6 令t=t+1,转至步骤2.
上述算法流程中,P(0)、P(t)、Q(t)、P(t+1)中个体的数量均是N.
2.2 概率分布模型
对于一个人的手,如果其伸出的指尖数量是K,其指尖区域的像素点分布在K个指尖区域中心附近. 对于模型(1)的最优解集,其包含的指尖像素点也分布在这K个中心点的附近.
在上述分布估计算法的流程中,对于每一代的种群P(t),其最优解集包含的像素点可以认为分布在K个中心点附近. 算法经过多次迭代之后,这K个中心点的位置会逐渐接近K个指尖区域中心的位置. 同时,随着种群P(t)的进化,其最优解集也会逐渐接近模型(1)的最优解集. 由此可见,在每一次迭代过程中,可以把种群P(t)的K个中心点作为候选解分量xi的概率分布模型.
对于种群P(t)的最优解集包含的所有像素点,计算任意两个像素点之间的距离进而根据它们之间的距离,采用K-means聚类算法,把它们分成K类. 对于每一类中的所有像素点,其中心位置就是上述P(t)的某一个中心点的位置. 这样,就得到种群P(t)的K个中心点的位置,它们也是本次迭代的过程中候选解分量xi的概率分布模型.
由模型(1)可知,如果决策变量x的维数比较大,x中包含的像素点个数也比较大,那么种群P(t)的最优解集包含的像素点,其数量也比较大. 如果种群P(t)中个体的数量,即种群的规模比较大,那么一般情况下,P(t)中最优解的数量比较大,因此P(t)的最优解集包含的像素点其数量也比较大.
当P(t)的最优解集包含的像素点比较多时,这些像素点中存在指尖像素点的可能性就会比较大,那么通过对这些像素点进行K-means聚类得到的K个中心点的位置就会更加接近K个指尖区域中心的位置.
由此可见,如果决策变量的维数比较大,或者种群的规模比较大,根据其建立的K个中心点的位置,即候选解分量xi的概率分布模型就会更加准确.
另外,如果P(t)的最优解集包含的像素点比较多,对这些像素点进行K-means聚类,就需要迭代更多的次数,那么该聚类方法的计算时间就会增加. 因此,如果决策变量的维数比较大,或者种群的规模比较大,聚类的计算时间会比较长.
如果对决策变量的维数和种群规模均合理取值,这样能够使指尖定位的求解方法在比较短的计算时间内,得到比较准确的最优解集,那么决策变量的维数和种群规模的数值都是最佳值.
2.3 采样
对于模型(1)的最优解集,其包含的指尖像素点分布在K个指尖区域中心的附近. 因此,对于上述候选解分量的概率分布模型,在其K个中心点的附近采样,就可能得到指尖像素点. 通过这一采样的方法,在决策空间中进行一次采样,得到一个候选解的分量xi,进而通过n次采样,得到一个候选解x.
令候选解x=φ. 对于概率分布模型中的K个中心点,基于任一点产生候选解分量的概率,均是同一数值.
采用如下的流程,产生一个候选解x.
步骤1 按照同一概率,从K个中心点中选择出一个中心点;
步骤2 在选择出的中心点坐标附近,通过高斯采样得到一个新的坐标![]() 或
或![]() 采样的方差均是λ.当迭代次数逐渐增加时,λ的数值逐渐线性减少;λ的最大值可称为最大采样方差,其最小值可称为最小采样方差;
采样的方差均是λ.当迭代次数逐渐增加时,λ的数值逐渐线性减少;λ的最大值可称为最大采样方差,其最小值可称为最小采样方差;
步骤3 如果![]() 是手部像素点,并且
是手部像素点,并且![]() 令
令![]()
步骤4 如果x中存在n个像素点,结束算法;否则,执行步骤1.
在上述的采样方法中,采样方差λ决定了得到的候选解分量xi的分布范围. 如果λ的数值与指尖区域的尺寸相似,采样点的分布就比较符合指尖像素点的分布,那么,通过上述的采样方法,就比较容易得到指尖区域的像素点. 另外,根据上述的采样方法,λ的数值由最大采样方差和最小采样方差决定. 因此,如果最大采样方差和最小采样方差的取值均比较合适,才能通过采样得到指尖像素点.
在模型(1)的求解过程中,最大采样方差和最小采样方差的取值过大,不利于种群的进化和最优解集的获得;它们过小,也不利于种群的进化和最优解集的获得.
如果最大采样方差和最小采样方差均合理取值,这样能够使指尖定位的求解方法得到比较准确的最优解集,那么最大采样方差和最小采样方差的数值都是最佳值.
3 实验部分
根据以上分析可知,决策变量的维数、种群规模、最大采样方差、最小采样方差是用于指尖定位的分布估计算法的主要参数,并且这些参数均存在最佳值.
采用NSGA-Ⅱ和MOCell作为对比方法,与所提的求解方法进行比较. NSGA-Ⅱ通过交叉和变异操作,得到临时种群.该算法的其他部分与所提的求解方法一致. MOCell在每次迭代过程中,均保存前几代的一定数量的最优个体,在这些最优个体中,选择一部分个体代替种群中相同数量的个体,进而通过对种群进行交叉和变异操作得到临时种群. MOCell的其他部分与NSGA-Ⅱ一致.
采用文献[6]中的标准美国手语图像库进行指尖定位的实验. 所用的手部区域图像共630幅. 对于其中任一幅手部区域图像,首先,根据选择指尖像素点的多目标优化模型,计算每一个手部像素点的f1(x)和f2(x);然后,采用所提方法求解模型(1),得到一系列像素点,进而对得到的像素点进行聚类,并计算每一类像素点的中心位置;最后,把得到的指尖位置与真实的指尖区域中心位置比较,计算其误差值. 实验中,采用文献[6]中的方法,人工确定真实的指尖区域中心位置. 在求解模型(1)之前,对于任一个手部区域,指尖伸出的数量K是已知的.
在求解过程中,首先,决策变量的维数取60,种群规模取30,最大采样方差取15,最小采样方差取4; 然后,决策变量的维数分别取40、50、70、80,其他3个参数的取值不变. 种群规模分别取20、25、35、40,最大采样方差分别取13、14、16、17,最小采样方差分别取2、3、5、6. 当一个参数的取值变化时,其他3个参数的取值不变. 除了这4个主要参数以外,其他参数的取值与文献[6]一致.
实验使用的计算机配置:Intel Core i5-4590, 3.30 GHz CPU, 4.00 GB 内存.
对于上述第121、301、491、506、551幅手部区域图像,通过一次模型(1)的求解,得到一系列像素点,如图1中的(a)~(e)所示. 图1(a)~(e)中,伸出的指尖数量依次是5、4、3、3、2. 在这一求解过程中,决策变量的维数取60,种群规模取30,最大采样方差取15,最小采样方差取4.
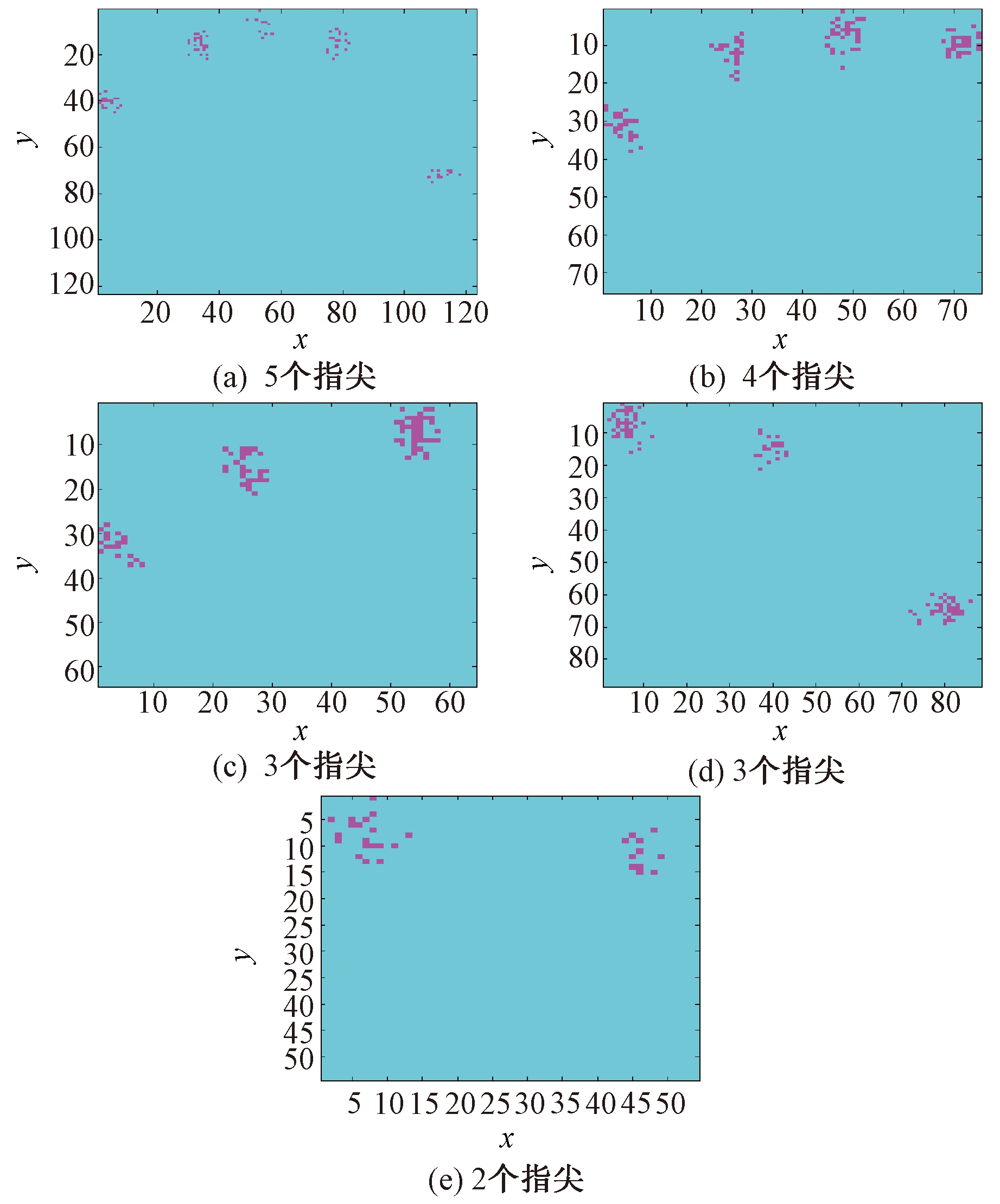
图1 所提方法得到的像素点集
Fig.1 The pixel sets obtained by the proposed method
从图1可以看出,采用所提算法,能够得到指尖区域的一系列像素点. 根据伸出的指尖数量,对得到的指尖像素点进行聚类操作,能够得到每一个指尖区域的一系列像素点,进而得到该指尖区域中心的位置.
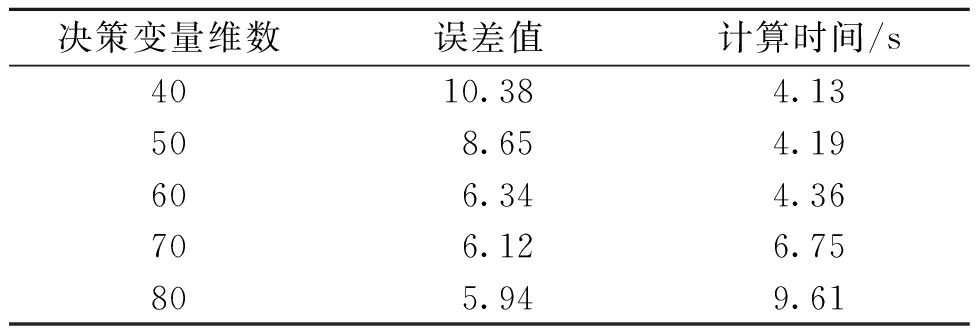
决策变量的维数分别取40、50、60、70、80,种群规模取30,最大采样方差取15,最小采样方差取4,所有手部图像的平均误差值和计算时间如表1所示. 种群规模分别取20、25、30、35、40,决策变量的维数取60,最大采样方差取15,最小采样方差取4时,所有手部图像的平均误差值和计算时间如表2所示. 最大采样方差分别取13、14、15、16、17,决策变量的维数取60,种群规模取30,最小采样方差取4,所有手部图像的平均误差值如表3所示. 最小采样方差分别取2、3、4、5、6,决策变量的维数取60,种群规模取30,最大采样方差取15,所有手部图像的平均误差值如表4所示.
表1 决策变量维数的实验结果
Tab.1 Experiment results of decision variable dimension
决策变量维数误差值计算时间/s4010.384.13508.654.19606.344.36706.126.75805.949.61
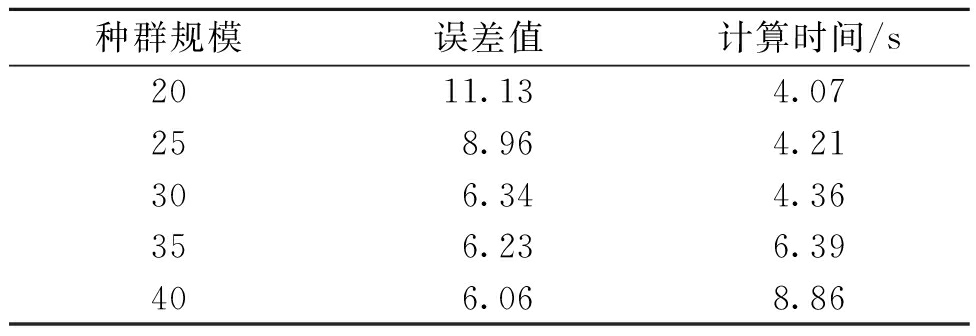
表2 种群规模的实验结果
Tab.2 Experiment results of population size
种群规模误差值计算时间/s2011.134.07258.964.21306.344.36356.236.39406.068.86
表3 最大采样方差的实验结果
Tab.3 Experiment results of maximum sampling variance
最大采样方差1314151617误差值9.247.866.347.938.64
表4 最小采样方差的实验结果
Tab.4 Experiment results of minimum sampling variance
最小采样方差23456误差值10.238.756.348.6411.36
从表1可以看出,当决策变量的维数从40增加到60时,误差值快速的减小,计算时间缓慢增加. 当决策变量的维数从60增加到80时,误差值缓慢减小,计算时间快速增加. 因此,决策变量维数的最佳值是60.
从表2可以看出,当种群规模从20增加到30时,误差值快速减小,计算时间缓慢增加. 当种群规模从30增加到40时,误差值缓慢减小,计算时间快速增加. 因此,种群规模的最佳值是30.
从表3可以看出,当最大采样方差的取值是15时,误差值最小. 因此,最大采样方差的最佳值是15. 从表4可以看出,当最小采样方差的取值是4时,误差值最小. 因此,最小采样方差的取值是4.
由此可见,决策变量维数的最佳值是60,种群规模的最佳值是30,最大采样方差的最佳值是15,最小采样方差的最佳值是4.
采用对比方法计算同样的手部区域图像时,NSGA-Ⅱ中的交叉概率和分布指数分别是0.9和2,变异概率和分布指数分别是0.1和2.在MOCell中,保存的最优个体数量是50,选择的最优个体数量是10. 两种对比方法的进化代数和种群规模与所提方法一致. 对于所提方法与两种对比方法,其所有手部图像的平均误差值如表5所示. 其中,所提方法的上述4个主要参数均取最佳值.
表5是依次采用所提算法、NSGA-Ⅱ、MOCell,计算同样的手部区域图像得到的大量指尖位置误差值的平均值. 从表5可以看出,所提算法的平均误差值与NSGA-Ⅱ、MOCell的平均误差值相比较最小. 因此,所提方法优于两种对比方法.
表5 不同求解方法的实验结果
Tab.5 Experiment results of different solution methods
求解方法NSGA-ⅡMOCell所提算法误差值36.8224.566.34
从表1和2可以看出,当所提算法的4个主要参数均取最佳值时,平均计算时间是4.36 s. 这主要是由多目标进化算法普遍具有的计算复杂度决定的. 对于静止指尖的识别系统,比如用指尖点击特定的位置,这一计算时间是可以接受的. 但是,对于运动指尖的识别系统,比如用指尖移动鼠标,这一计算时间是无法接受的. 因此,需要对所提算法及其主要参数进行深入研究,进而减少计算时间.
4 结论
指尖区域的像素点分布在指尖中心的附近,是指尖像素点的分布规律. 对于选择指尖像素点的优化模型,采用符合上述分布规律的求解方法,能够得到比较准确的结果. 笔者提出决策变量的维数、种群规模、最大采样方差、最小采样方差是这一分布估计算法的主要参数. 当这些主要参数均取最佳值时,所提的求解方法能够快速得到准确的指尖位置,并且优于已有方法. 实验结果证明了上述理论分析的结果.
[1] GONG D W, LIU K. A multi-objective optimization model and its evolution-based solutions for the fingertip localization problem[J]. Pattern recognition, 2018, 74: 385-405.
[2] HO C, WU C, CHIANG Y, et al. Fingertip detection technique for a wearable projection device[J]. Journal of computational information systems, 2014, 10(24): 10839-10848.
[3] WANG Y M, CHEN J S, SU G D. Efficient hand segmentation and fingertip detection using color features of skin and fingernail[J]. IEICE transactions on information and systems, 2013, 96(8): 1894-1897.
[4] ZHENG B J, ZHAO L Y, WANG Y X. Fingertip detection and gesture recognition based on kinectdepth data[J]. Transactions on computer science and technology, 2014, 3(1): 9-14.
[5] JIN L, RUI X, YIN J. Fingertip detection using mathematical morphology and template matching[J]. Asian journal of information technology, 2014, 3(4): 265-269.
[6] 梁静, 刘睿, 瞿博阳, 等. 进化算法在大规模优化问题中的应用综述[J]. 郑州大学学报(工学版), 2018, 39 (3): 15-21.
[7] 梁静,宋慧,瞿博阳, 等.基于改进粒子群算法的路径优化问题研究[J].郑州大学学报(工学版), 2014, 35 (1): 34-38.
[8] 孙晓燕, 朱利霞, 陈杨. 基于可能性条件偏好网络的交互式遗传算法及其应用[J]. 郑州大学学报(工学版), 2017, 38 (6): 1-5.
[9] ZHANG Q F, ZHOU A M, JIN Y C.RM-MEDA: a regularity model-based multiobjective estimation of distribution algorithm[J]. IEEE transactions on evolutionary computation, 2008, 12(1): 41-63.
[10] LIU K, GONG D W, MENG F L, et al. Gesture segmentation based on a two-phase estimation of distribution algorithm[J]. Information sciences, 2017, 394/395: 88-105.