0 引言
钢筋混凝土剪力墙在高层建筑结构体系中是主要的抗侧力构件，因其具有较大的抗侧移刚度，能够有效地限制结构的水平位移，往往在高层建筑设计中作为主要的抗震构件。在实际结构中，钢筋混凝土剪力墙主要承受水平和竖向荷载的作用，即承受墙体平面内的作用力，但是，垂直平面方向的刚度较小可能会引起墙体产生垂直于墙面的平面外变形，在长期竖向荷载作用下，该变形会逐渐增大[1]，剪力墙便可能发生失稳破坏。
目前，对于剪力墙在结构中的稳定性问题，国内外在这方面的研究还没有形成比较完善的理论，文献[2]给出了在不同楼板约束形式下高层剪力墙的临界荷载并分析了相应的失稳破坏形态；文献[3]采用特征值屈曲分析法通过ABAQUS软件给出了当墙体为四边支撑时的屈曲模态；文献[4]通过有限元软件分析了在横肋和竖肋互相作用时钢板剪力墙的屈曲临界系数的求解方法；文献[5]给出了不同截面形式的空心剪力墙临界应力的求解公式，并分析了空心截面孔径设计对稳定性的影响；文献[6]采用有限元方法研究了钢板剪力墙在侧边具有不同形式配筋时的屈曲失稳问题。由此可见，关于剪力墙稳定性问题的研究大多基于有限元理论，没有进行完整的推导与计算，从而得到墙体发生失稳时的承载力求解公式，并且所得结论存在一定的差别。
鉴于目前对于剪力墙稳定性研究中存在的各种不同问题，防止剪力墙因稳定性不足而破坏，根据工程结构中剪力墙的内力分布，将墙体视为正交各向异性薄板，对竖向荷载作用下墙体出现失稳破坏时的临界应力进行理论解析。胡拜尔[7]提出了基于正交各向异性材料的构件主刚度的计算公式，以此为依据，进一步推导得到适用于剪力墙的失稳临界应力求解公式。进而对钢筋混凝土剪力墙进行分析和计算，建议了提高竖向荷载下墙体稳定性的措施。
1 剪力墙的理论分析模型
在实际工程结构中，通常剪力墙厚度t与墙中面最小尺寸b(墙宽)之比小于 1/5，因而能够把墙体等效为薄板。对于钢筋混凝土剪力墙，虽然混凝土可以视为均匀分布，但是墙内配置的竖向和水平钢筋不同，造成墙体的各向异性性质，因而可以按照均质正交各向异性板建立计算模型[8]，横向箍筋和竖向纵筋的对称分布在墙体内产生3个相互垂直的弹性对称面，将x、y、z轴置于弹性主向上。同时，考虑到剪力墙自身重力和其受到的顶部竖向荷载所产生的面力都与墙面平行，沿墙体厚度方向没有外力作用，并且面力大小沿厚度方向保持不变，可以作为正交各向异性薄板在平面内的稳定性问题求解。
以图1所示钢筋混凝土框架—剪力墙结构为例[9]，每层剪力墙高2.8 m，墙宽1.2 m，墙厚0.2 m，墙底部与钢筋混凝土基础固定连接。因而，建立的剪力墙模型如图2所示。
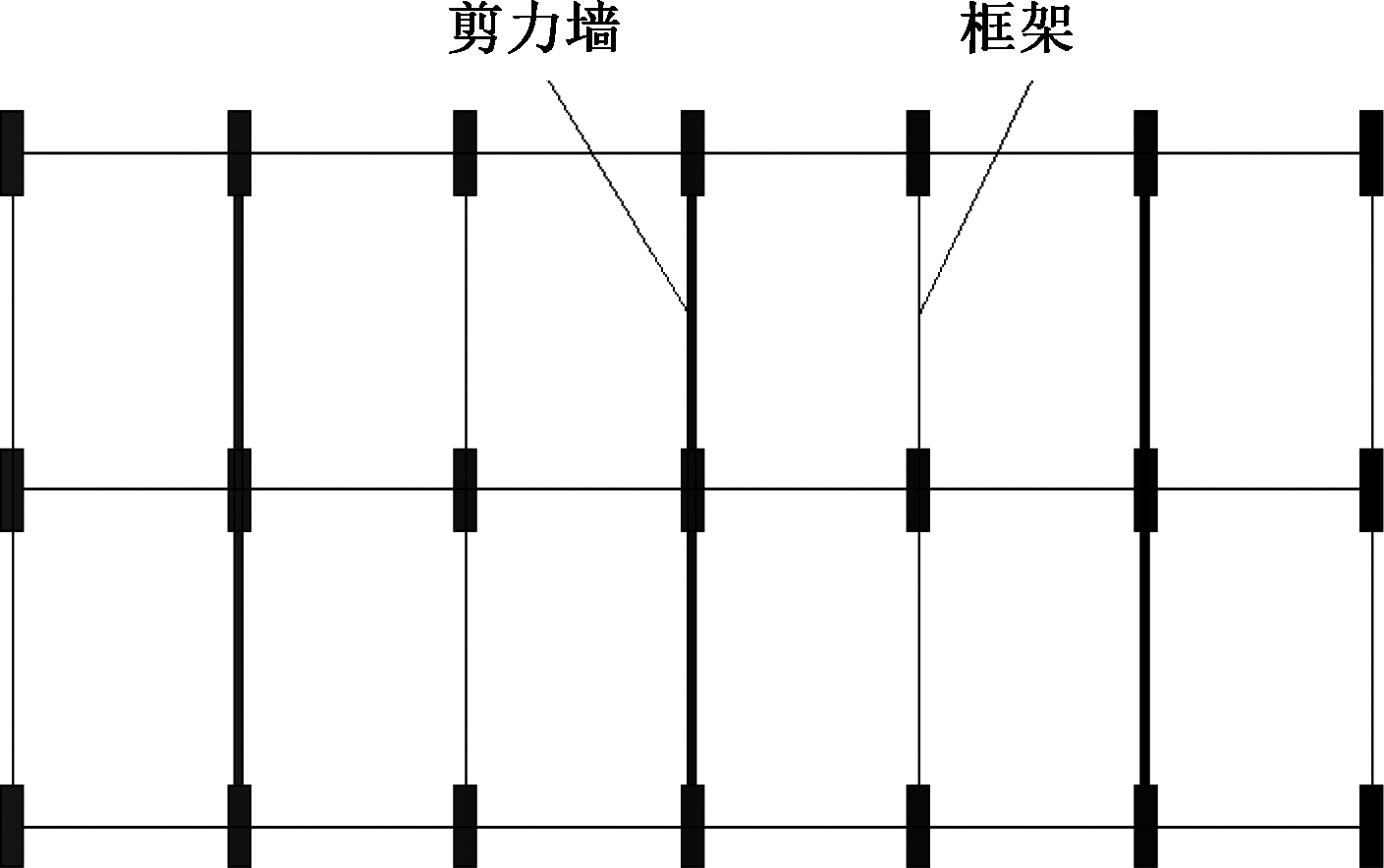
图1 某框架剪力墙结构平面图
Figure 1 Plane plan of a frame shear wall structure
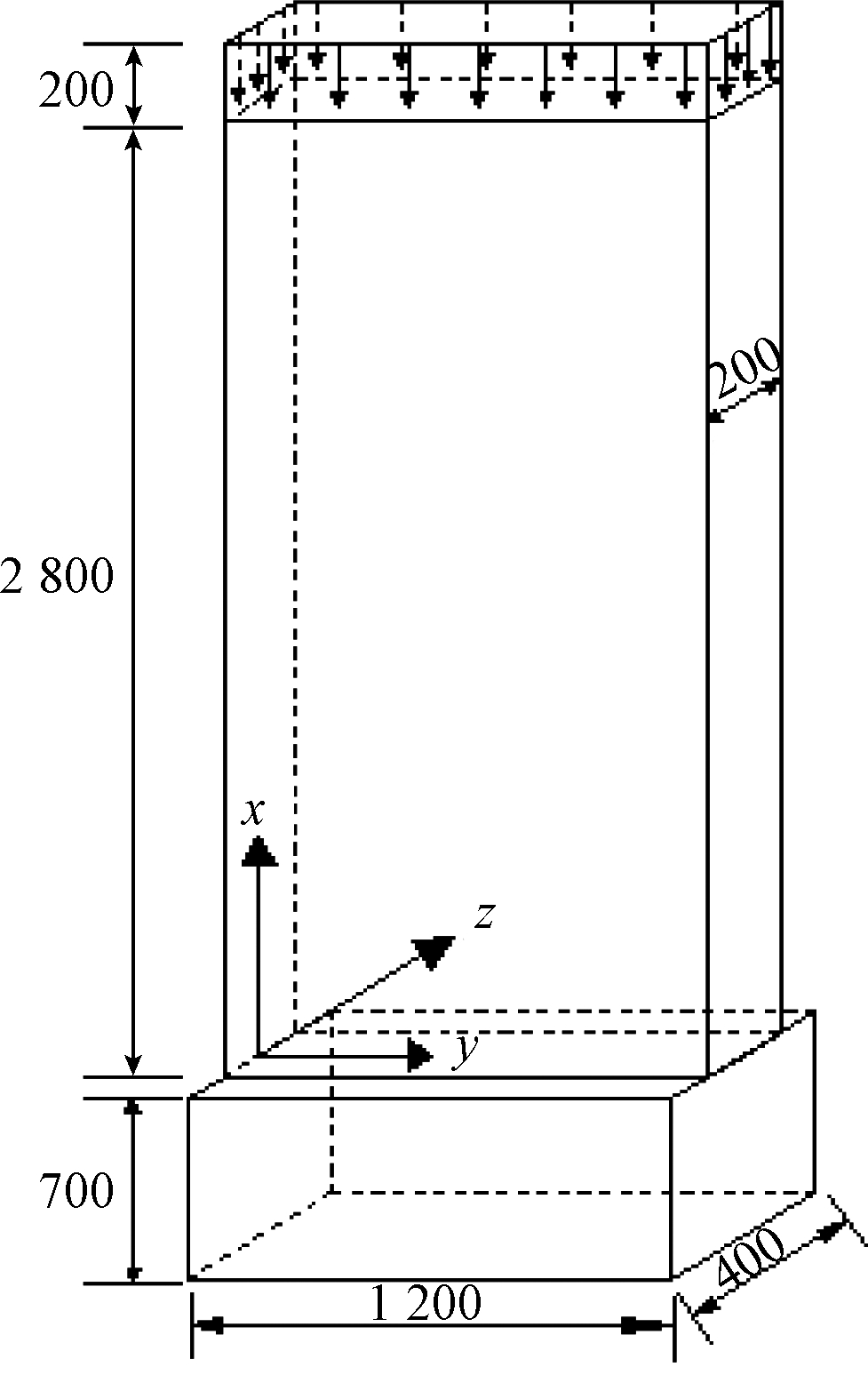
图2 剪力墙计算模型
Figure 2 Calculation model of the shear wall
接下来，对剪力墙的边界进行简化，以便得到墙体上、下端处合理的边界条件。剪力墙上端梁的横截面为边长c=0.2 m的正方形，计算其抗弯刚度为
其中E表示混凝土弹性模量。在剪力墙丧失稳定之前，顶端梁的抗扭刚度[10]可以按照弹性阶段计算为GIn=Gβc4=0.9×10-4E，其中取混凝土剪切弹性模量
矩形截面扭转梁的抗扭系数由表[12]给出，正方形截面梁取β为0.141。上述计算结果表明，顶端梁能够较大程度地限制墙体上边界的弯曲和扭转，但考虑到实际结构中剪力墙受到水平荷载的作用，其上部边界会产生沿水平方向的运动，所以顶端梁并不完全约束墙体上部边界的水平位移，所以其对墙体边界属于定向约束[13]。而且，墙体下边界一般固定于基础中，应将墙体下边界作为固定端约束。
在剪力墙结构设计中，剪力墙两侧大多设置轻质墙体，不考虑其承担的作用力，在结构设计中不参与内力计算，因而可以忽略剪力墙两侧的约束，将墙体两侧视为自由边，在两侧边界上不存在支反力和分布弯矩。剪力墙在竖向荷载的作用下，位于底部的梁会对墙体下边界产生平行于墙面、竖直向上的均布荷载作用。因此，剪力墙在顶部竖向荷载作用下的稳定性问题就可以近似为其在上述边界约束条件下两对边受均布荷载的稳定性问题。当墙体上下边界截面只承受竖向荷载作用时，这两个边界截面上都不出现弯矩，可以进一步认为是简支约束。
由此可见，在竖向荷载下对钢筋混凝土剪力墙进行稳定性计算时，可以建立边界条件为两对边自由、两对边简支的正交各向异性板计算模型。
2 临界应力的理论解
如前所述，建立对边简支、对边自由的正交各向异性矩形薄板的剪力墙理论计算模型见图3。墙高为a，墙宽为b，单位宽度上的竖向荷载应力集度用px表示，图中虚线表示墙体上、下边界简化后的简支约束。
图3 剪力墙理论计算模型
Figure 3 Theoretical calculation model of shear wall
在工程结构设计中，通常习惯用E1、E2和μ1、μ2表示正交各向异性材料沿x、y两个弹性主向的弹性模量和泊松比，用G表示τxy相对应的剪切模量。根据刚性薄板弯曲理论的基本假定，板的纵向截面在板变形前后始终垂直于板中面，只是绕板中面的中心轴线旋转了特定角度，因而可以忽略板厚度方向(即z轴方向)的位移，如图3所示，认为εz=0，并且有γzx=γyz=0，同时考虑到σz≪σy,σx，从而能够认为σz≈0。进一步地，可以将应变和应力分量按照弹性弯曲理论用薄板的平面外位移项w表示为式(1)和式(2)，其中
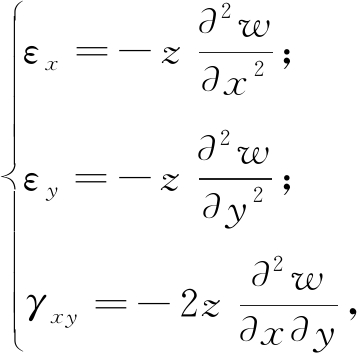
(1)
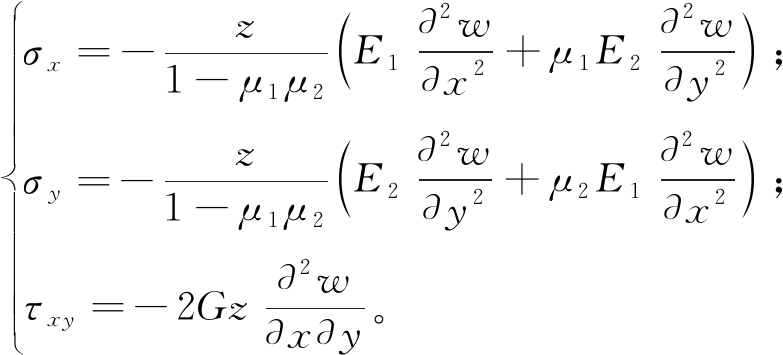
(2)
接下来采用位能驻值原理，通过推导板总位能的极值，得到图3中剪力墙简化计算模型的失稳临界应力。
将正交各向异性板整体视作三维弹性体Ω，式(3)给出其应变能V的计算式。将式(1)和式(2)代入式(3)，便能够将正交各向异性板的应变能V用位移表示。
(3)
图3所示的均布力对板做的功为[14]：
(4)
进而力函数U可以表示为
(5)
应变能V与力函数U作差，得到板的总位能Π：
Π=V-U。
(6)
根据位能驻值原理，总位能Π取极值时板处于稳定的平衡态，那么有：
δΠ=0。
(7)
通过将图3约束条件下正交各向异性板的边界条件用板的内力表示出来，便可以采用瑞利-李兹法[15]分析式(7)。
依据弹性理论，从板内取出一个体积为dx×dy×t的微元体，分别计算微元体各面上的应力，然后进行积分可得板的内力为：
(8)
(9)
(10)
(11)
(12)
根据前文墙体顶部和底部边界约束简化后的结果，图3中正交各向异性板在x=0和x=a两个边界上视为简支约束，这两条边上的边界条件为：
(13)
由于剪力墙存在自由边界y=0和y=b，而在自由边界上的内力弯矩My、剪力FSy和扭矩Mxy都将为0，此时利用文献[16]建议的广义剪力的计算方法，可将边界上3个内力为0的条件转化为2个自由边上的边界条件：
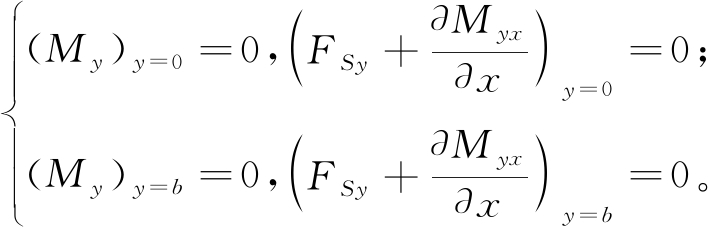
(14)
将式(8)代入式(13)中的Mx项，则x=0和x=a处的边界条件便能够由位移给出：
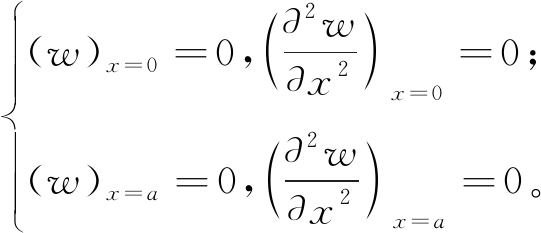
(15)
将式(9)、(10)、(11)、(12)代入式(14)中的对应项，则y=0和y=b处的边界条件亦可由位移给出，如式(16)。
图3中，正交各向异性板受力失稳时，在边界x=0和x=a上的位移为零，而在边界y=0和y=b上会产生垂直于板面的位移。考虑到板的对称性，两条自由边上的失稳位移必须完全同步，并且失稳波形应具有周期性正弦曲面的失稳形状。可见，与自由边平行的截面在失稳发生时垂直于板面的位移始终相同，即失稳位移与y的取值无关。
(16)
因而可以用式(17)所示的单三角级数来表达失稳挠曲面：
(17)
其中，Am是待定系数，当m取1时，板达到临界应力，此时的失稳挠曲面为：
(18)
式(18)完全满足式(15)所表示的简支约束条件。将式(18)代入式(16)可以看到，广义剪力为零的条件可以满足，但弯矩为零的条件却无法满足，也即式(18)能够使得所有位移边界条件得到满足，却不能使得自由边界上力的边界条件完全符合假设，但文献[14]和[17]举例说明了利用类似的基函数仍可以得到与真实结果较吻合的近似解。因为在实际结构中，剪力墙顶部梁和底部基座梁通常一体浇筑，当墙体出现墙面外的位移时，两侧边端点处会受到来自上、下边界的作用力，一定范围内会存在较小的分布弯矩，不属于完全意义上的自由边，所以可以将式(18)认为是剪力墙压曲失稳挠曲面的近似表达式。
最后，联立式(6)、式(7)和式(18)，并考虑到Π对A的一阶偏导数为零，求得系数A，从而得到图3中计算模型单位宽度上的临界应力为
(19)
式(19)为剪力墙发生失稳时对应的临界应力计算公式。
3 分析与讨论
3.1 弹性模量和泊松比的转换关系
正交各向异性材料沿x、y方向的弹性模量E1、E2、泊松比μ1、μ2与其主刚度之间存在一定的关系，将其与胡拜尔对正交各向异性板的主刚度的近似推导相比较[18]，可以得到剪力墙沿x、y方向的弹性模量E1、E2、剪切模量G和泊松比μ1、μ2与钢筋混凝土构件的混凝土弹性模量Ec、钢筋弹性模量Es和泊松比μ之间存在转换关系式(20)：
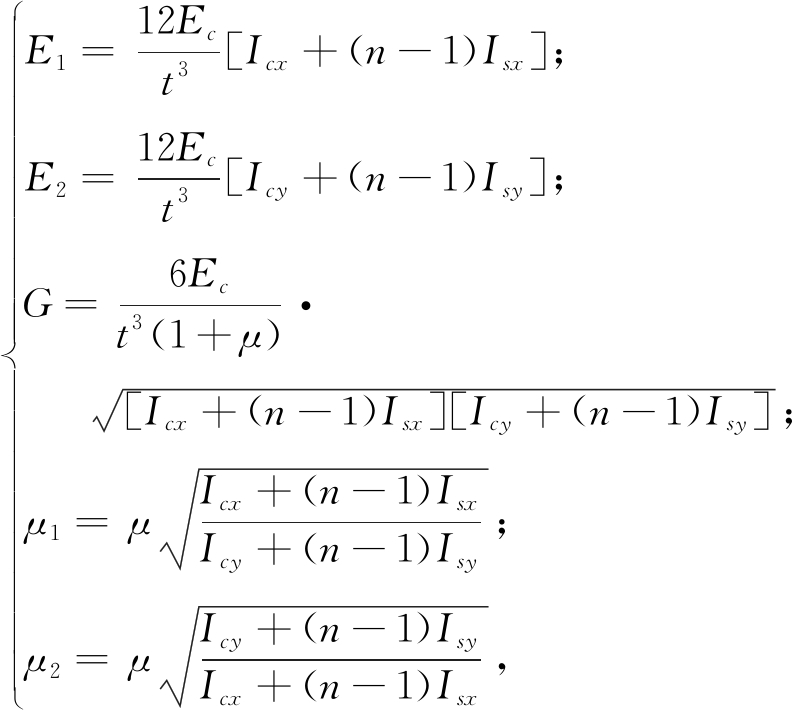
(20)
式中：
表示全薄板截面、钢筋截面对x为常量的中性轴的惯性矩；Icy、Isy表示全薄板截面、钢筋截面对y为常量的中性轴的惯性矩。然后可将式(20)代入式(19)得到临界应力计算公式(21)：
(21)
3.2 提高剪力墙稳定性的有效措施
采用式(21)可以计算出钢筋等间距分布的剪力墙截面的临界应力表达式(22)，该剪力墙截面配筋图如图4所示。
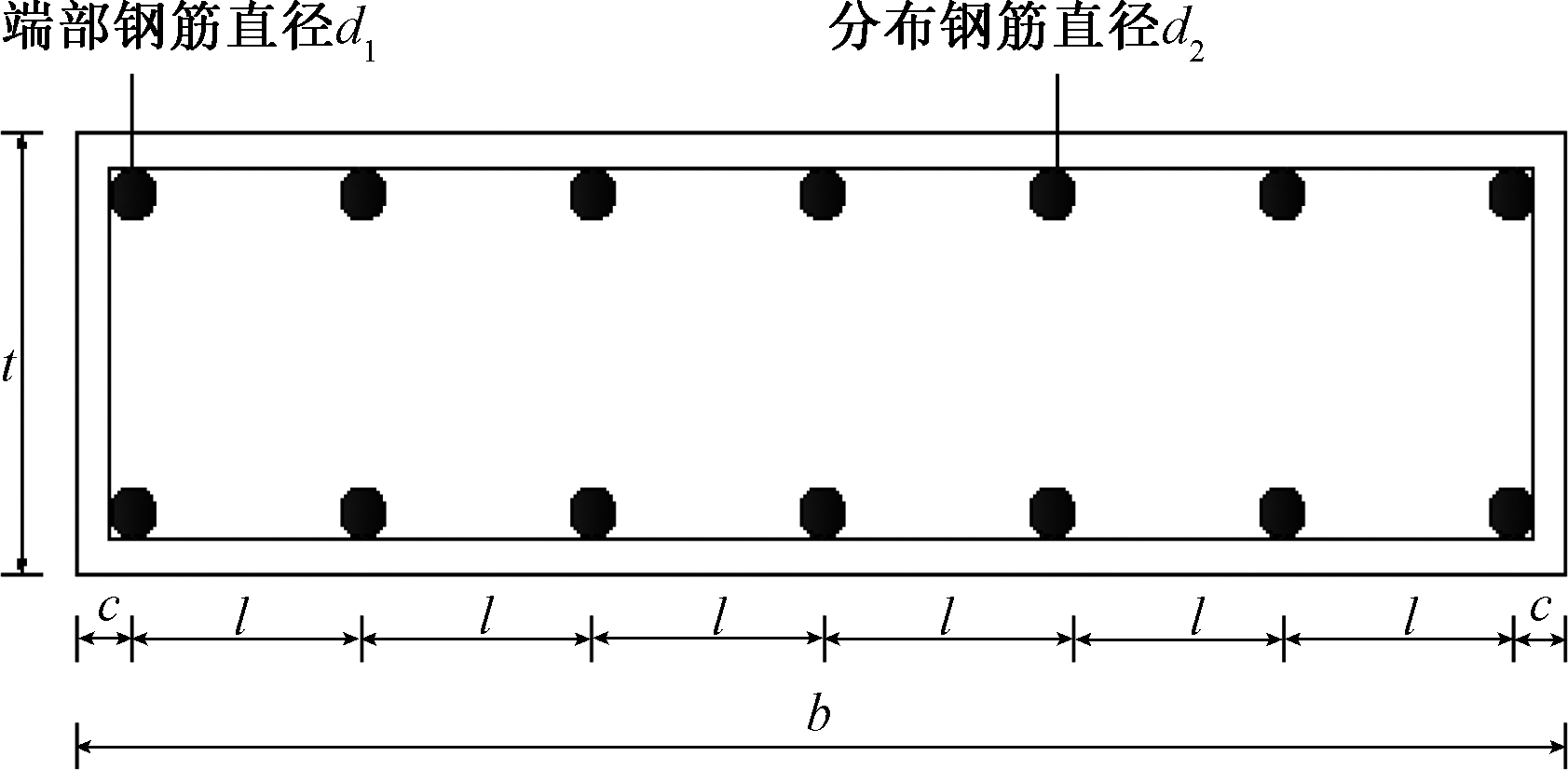
图4 钢筋等间距分布的剪力墙截面配筋图
Figure 4 Distribution reinforcement layout of shear wall
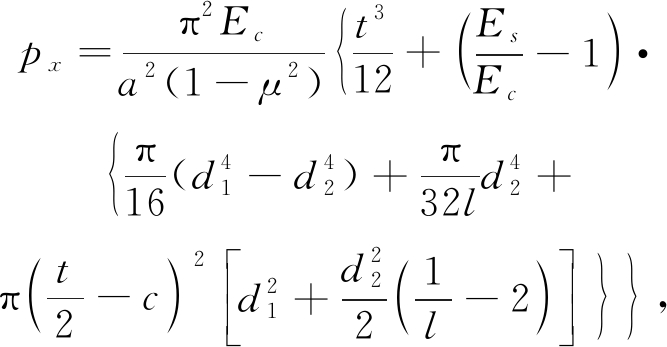
(22)
式中：d1表示端部钢筋直径；d2表示分布钢筋直径；l表示钢筋间距；c表示混凝土保护层厚度。记式(22)中后面一项为B：
(23)
可以发现，式(23)反映出钢筋对剪力墙稳定性的贡献。
对于剪力墙不同钢筋间距的配筋截面计算表明，当竖向钢筋间距为100～200 mm，钢筋直径从10 mm增大到20 mm时，竖向钢筋配筋率增加了4倍，而钢筋对临界应力的影响占临界应力的比值从2.9%提高到19.3%，钢筋对稳定性的影响增大了近7倍；当竖向钢筋直径为10～20 mm，竖向钢筋间距从100 mm提高到200 mm时，竖向钢筋配筋率降低了50%，钢筋对临界应力的影响所占的比例最大从19.3%减小为10.7%，钢筋对稳定性的影响降低了50%。由此可以认为，提高竖向钢筋配筋率可以明显提高墙体的稳定性[19]。
采用式(21)可以计算出设置边缘约束构件的剪力墙截面的临界应力表达式(24)，其配筋图如图5所示。
(24)
对设置边缘构件的不同配筋形式的截面计算表明，纵向钢筋间距不变，而钢筋直径在10～20 mm变化时，钢筋对剪力墙临界应力的影响占临界应力的比例从4.4%提高为11.6%；若只是在10～20 mm变化钢筋直径，发现钢筋对临界应力的影响比例为2%以内。所以，边缘构件中纵向钢筋配筋率对剪力墙的稳定性影响较大，而分布钢筋配筋率的影响较小。所以，对于设置边缘构件的剪力墙可以通过增加纵筋配筋率来改善其稳定性[19]。
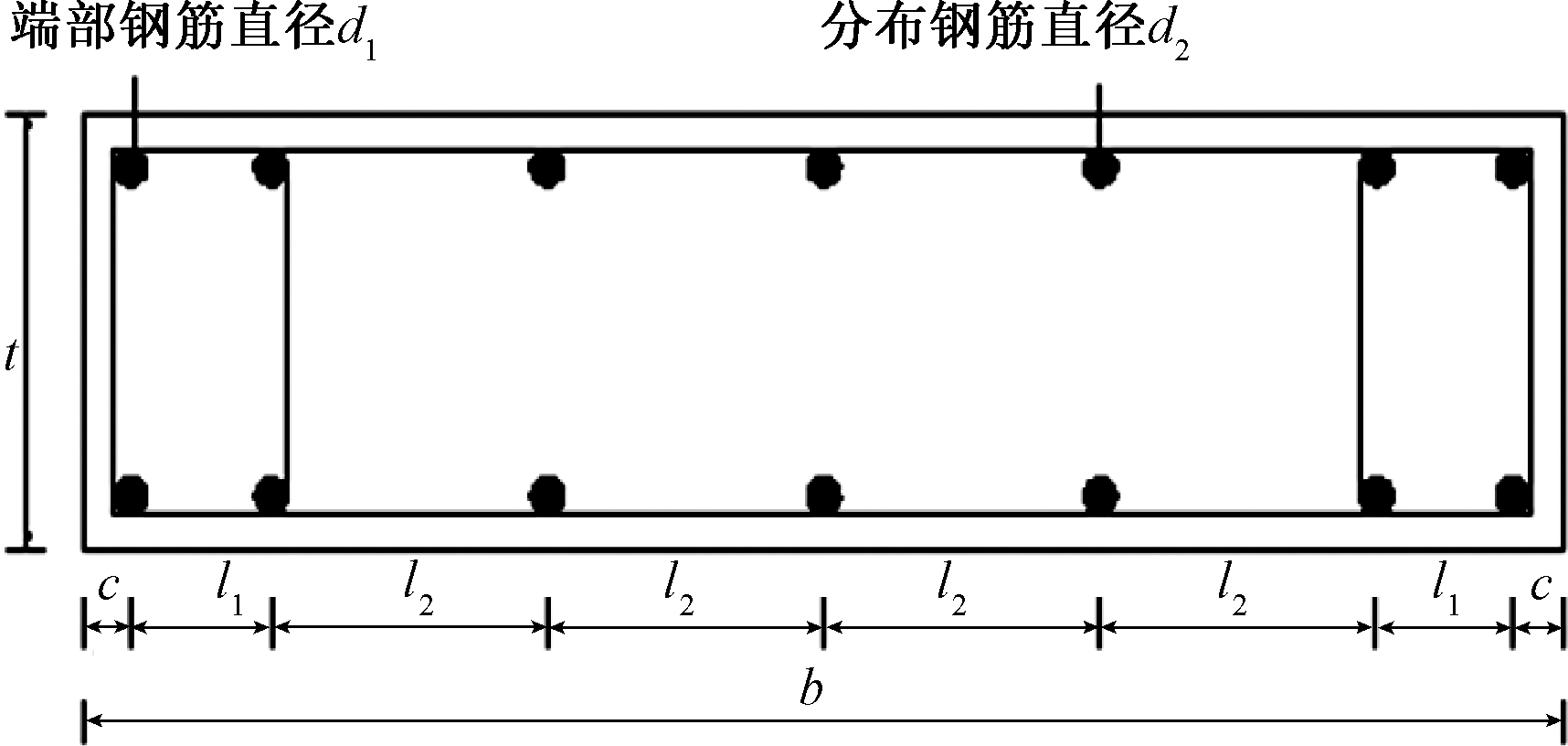
图5 设置边缘构件的剪力墙截面配筋图
Figure 5 Reinforcement layout of shear wall with boundary columns
由式(22)和式(24)进一步地计算表明，对于特定配筋形式的剪力墙横截面，当墙体厚度由120 mm变化至370 mm时，钢筋对稳定性的影响占整个临界应力的比例可由12.3%降至3.9%，可见，随着墙体厚度的增大，虽然剪力墙的临界应力显著增加，但钢筋对临界应力的贡献却减小。因此，对于厚度较薄的剪力墙增大钢筋配筋率能改善其稳定性，而对于墙体厚度较大的剪力墙，增大钢筋配筋率对其稳定性影响较小[19]。
4 结论
(1)在进行钢筋混凝土剪力墙的稳定性分析时，可以建立对边简支、对边自由的正交各向异性矩形薄板理论模型来分析计算。
(2)分析时采用位能驻值原理，能够得出钢筋混凝土剪力墙合理的临界应力计算公式。
(3)降低剪力墙的高厚比、增加纵向钢筋配筋率都能改善墙体的稳定性。当墙体较薄时，可采用提高纵向钢筋配筋率的方法保证剪力墙的稳定性。
[1] 贺芳. 剪力墙结构设计常见问题及注意事项[J]. 工程技术研究,2017(2):202，207.
[2] 万子华. 高层住宅混凝土剪力墙稳定性分析[D]. 南昌: 南昌大学, 2014.
[3] 陈柯,郏建磊,杨健兵,等.某工程无楼板支承的楼梯间剪力墙稳定性分析[J].结构工程师,2018,34(4):37-43.
[4] 高逸. 考虑横肋和竖肋相互作用的加劲钢板剪力墙的弹性稳定性[D]. 杭州: 浙江大学, 2018.
[5] 武敏刚, 冯瑞玉, 李守恒, 等. 轴向压力作用下空心剪力墙的稳定性分析[J]. 西安建筑科技大学学报(自然科学版), 2002, 34(4): 358-361.
[6] 马欣伯, 张素梅, 郭兰慧. 侧边加劲肋对两边连接钢板剪力墙弹性屈曲的影响[C]//庆祝刘锡良教授八十华诞暨第八届全国现代结构工程学术研讨会论文集. 北京：全国现代结构工程学术研讨会学术委员会, 2008: 1251-1256.
[7] 王耀先.复合材料结构设计[M]. 北京: 化学工业出版社，2001:10-25,71-94.
[8] HACIYEV V C, SOFIYEV A H, KURUOGLU N. Free bending vibration analysis of thin bidirectionally exponentially graded orthotropic rectangular plates resting on two-parameter elastic foundations[J]. Composite structures, 2018, 184: 372-377.
[9] 张香成, 陈娜, 罗芳, 等. 铅-磁流变阻尼器在减震结构中的位置优化[J]. 郑州大学学报(工学版), 2018, 39(2): 44-49.
[10] 王仲秋. 矩形截面钢筋混凝土构件的抗扭刚度[J]. 哈尔滨建筑工程学院学报, 1983(3): 27-37.
[11] 王娟, 王会娟, 许耀群, 等. 单轴荷载作用下混凝土强度代表体尺寸定量研究[J]. 郑州大学学报(工学版), 2018, 39(1): 12-17, 28.
[12] 杨在林. 工程力学[M].哈尔滨：哈尔滨工程大学出版社,2010：147-148.
[13] 龙驭球,包世华,袁驷. 结构力学Ι[M].北京：高等教育出版社,2012：2-10.
[14] GORMAN D J. Free vibration analysis of rectangular plates[M]. New York: McGraw-Hill,1982:2-29.
[15] RAHBAR-RANJI A，SHAHBAZTABAR A. Free vibration analysis of non-homogeneous orthotropic plates resting on Pasternak elastic foundation by Rayleigh-Ritz method[J]. Journal of central south university, 2016, 23(2): 413-420.
[16] 李璐. 正交各向异性矩形薄板的弯曲、振动和屈曲[D]. 西安: 西安建筑科技大学, 2007.
[17] 盖秉政.弹性力学(下册)[M].哈尔滨：哈尔滨工业大学出版社,2008:727-734.
[18] 徐芝纶. 弹性力学(下册)[M].北京：高等教育社,2016:135-156.
[19] 宋林涧. 钢筋混凝土剪力墙稳定性和弹塑性分析[D].郑州：郑州大学,2019.