0 引言
仿生智能计算作为一种研究复杂系统的新方法，被广泛用于优化计算、机器学习、自动控制等领域[1-3].受自然界中鸽子归巢行为启发，Duan等[4]首次提出鸽群优化算法(pigeon-inspired optimization, PIO).PIO针对鸽子寻找目标的两个阶段，提出地图和指南针算子(map and compass operator)和地标算子(landmark operator)两种计算模型.PIO因其在收敛速度和搜索效率方面具有优势，已得到广泛应用[5-8].然而，算子的独立计算限制了参数之间的相互协调与最优分配，导致算法易陷入局部最优.
在演化博弈理论(evolutionary game theory, EGT)[9]中，演化稳定策略(evolutionary stable strategy, ESS)和复制动态(replicator dynamics, RD)分别表征演化博弈的稳定状态和向这种稳定状态的动态收敛过程，将EGT与PIO相结合形成新的算法EGTPIO，将提升原始PIO算法的搜索效率，解决算法易陷入局部最优的问题.
作为一种新型非线性反馈控制方法，ADRC不依赖被控对象模型[10]，具有超调小、精度高以及抗干扰能力，被广泛用于控制工程领域[11-13].但是繁琐的参数整定工作不仅耗时，影响控制器的控制效果，还会限制被控对象的性能.
笔者将EGTPIO算法用于ADRC控制器参数的动态调节，将使控制器参数整定工作更加准确、高效.更进一步，将这种全新的控制器用于自主设计开发的可变形地面移动机器人(deformable ground mobile robot, DGMR)的姿态控制，通过对系统阶跃响应的超调量、上升时间、稳态误差进行分析，建立系统性能评价指标，对所提出的方法进行验证.仿真结果显示：笔者提出的方法能够提升ADRC控制器的性能，使DGMR的姿态控制更加高效.
1 演化博弈鸽群优化
1.1 鸽群优化
PIO中, 设D维搜索空间的N只鸽子的位置和速度分别为Xi=[xi1,xi2,…,xiD]和Vi=[vi1,vi2,…,viD]，其中i=1,2,…,N，地图和指南针算子如式(1)所示:
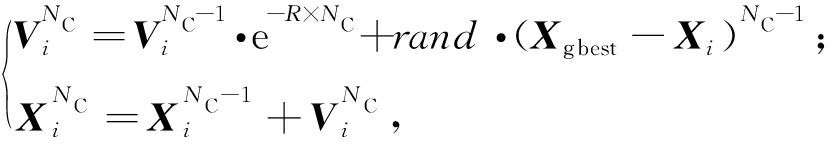
(1)
式中：R是地图和指南针因数；NC是目前迭代次数；rand是随机数；Xgbest是NC-1次迭代后比较所有鸽子得到的全局最优位置.当循环次数达到要求后，鸽群的位置和速度由地标算子计算.地标算子中，每次迭代后N会减半以舍弃适应度函数较差的鸽子地标算子,如式(2)所示.
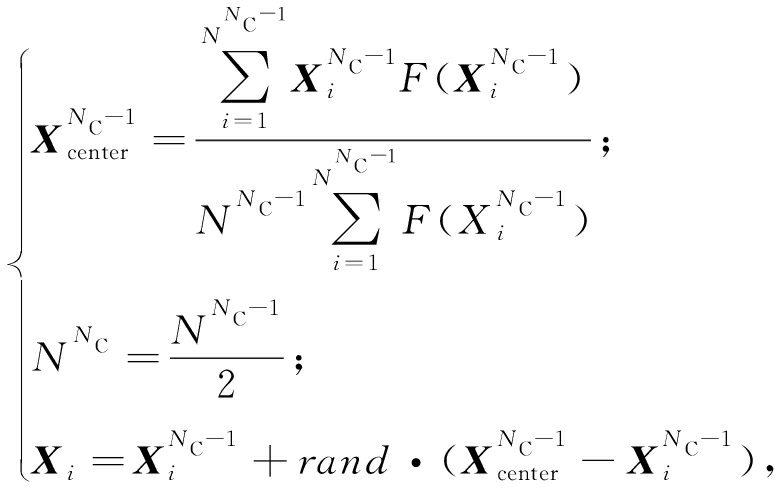
(2)
式中：Xcenter为鸽群的参考位置；rand是随机数.
1.2 演化博弈理论
演化博弈理论(evolutionary game theory, EGT)将博弈理论分析和生物进化过程分析相结合[14].演化稳定策略(evolutionary stable strategy, ESS)[15]基于策略在迭代过程中的适应性，用以表现策略的动态调整过程.假设多参与者博弈中存在n种纯策略，令pi为使用策略i的参与者比例，状态向量p=(p1,p2,…,pn)表示参与者的概率集合.当状态q≠p令(1-ε)p+εq满足F(q|p)<F(p|p)(ε为足够小的正数)时，状态p是一个ESS.F(i|p)表示每个参与者单位时间内使用策略i的收益是p的函数.
模仿者动态(replicator dynamics, RD)描述了p的变化，设线性博弈过程收益矩阵为A，则F(q|p)=qAp.动态方程用以表达某一策略的适应度与平均适应度的差异，可由式(3)表示.
(3)
式中：
为策略i的比例,N=∑ni为所有参与者数量,ni=rini，ri为策略变化率.
1.3 演化博弈鸽群优化
PIO由两个独立迭代循环部分组成，段海滨等[7]引入导航工具过渡因子将两个算子进行整合.然而，由于两种算子的配置权重问题导致算法中参数无法相互协调.鉴于ESS和RD的优势，可将PIO中的鸽子抽象为博弈参与者，地图和指南针算子与地标算子为参与者使用的两种纯策略，通过ESS和RD计算算子的最优配置，记为y1和y2.根据式(3)，可建立鸽群的RD方程：
(4)
其中，向量ai表示A的第i列，A包含鸽群的全部适应度信息，如式(5)所示.
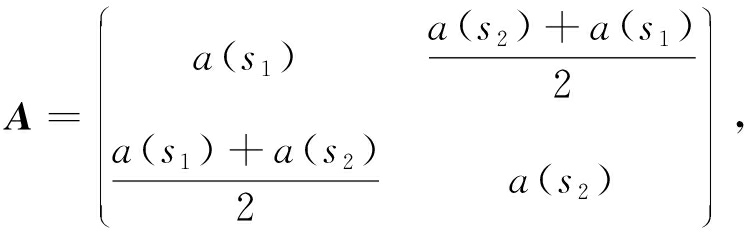
(5)
其中，a(si)中i=1,2，表示一只鸽子使用策略i的收益，其计算式：
(6)
式中：t为迭代次数；
为一组ESS值.此时，根据笔者的设计，EGPIO的迭代方程：
(Xgbest-Xi)NC-1+
(7)
式中：tr表示导航工具过渡因子，通常取常数2；y1和y2是式(5)的一组解，且规定y1+y2≈1.
结构上，演化博弈鸽群优化将鸽群优化中两个独立的循环迭代过程进行了整合，这使得算法无需通过人为设定迭代次数进行计算，大大提高了搜索效率；同时，演化博弈过程为两个算子的作用分配了权值，使得算法具备一定的适应性，降低算法陷入局部最优的概率，提升了搜索的准确度.但是，算法的局限性表现在它的搜索结果完全依赖于演化博弈中的模仿者动态方程的平衡解，如果方程无法输出平衡解，算法无效.
2 仿真实验与结果分析
2.1 DGMR的ADRC模型
ADRC由跟踪微分器(tracking differentiator, TD)、扩张状态观测器(extended state observer, ESO)和非线性状态误差反馈控制律(nonlinear state error feedback law, NSEFL)组成[16].其基本结构如图1所示.
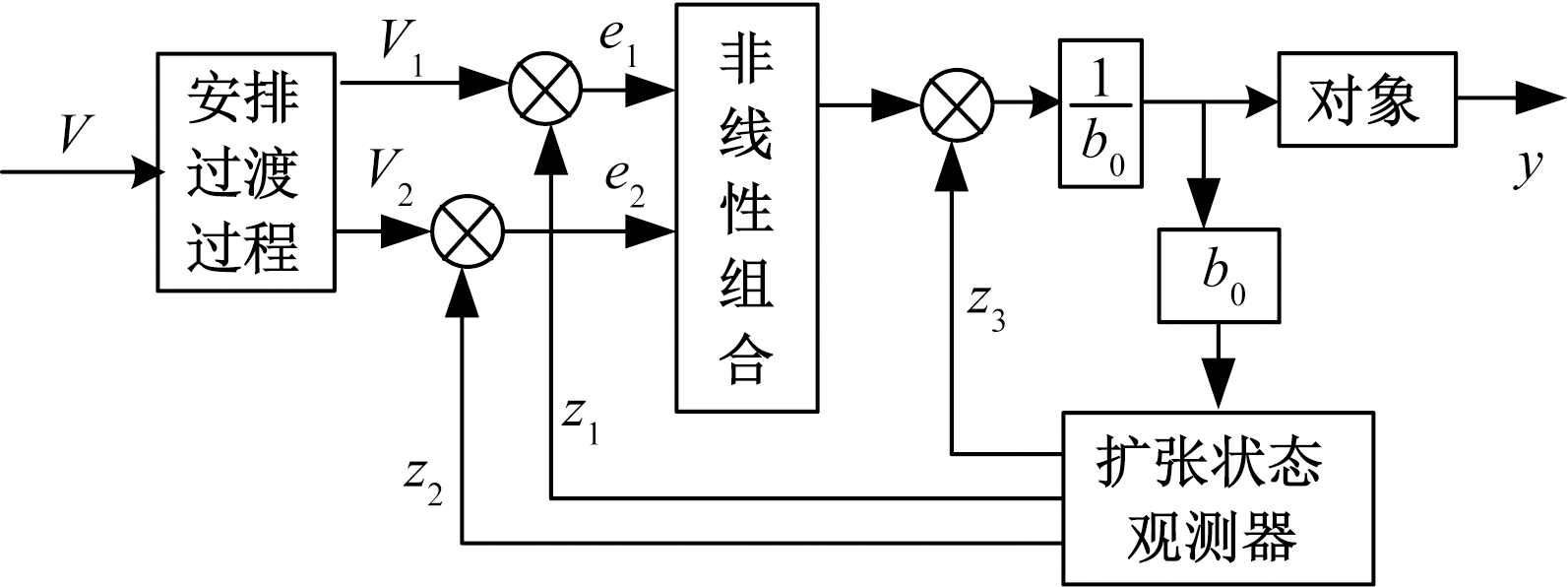
图1 自抗扰控制器结构
Fig.1 Structure of ADRC controller
笔者以自主设计开发的一款可变形地面移动机器人(DGMR)模型为研究对象，通过ADRC对其运动系统核心部分——推杆变形机构加以控制，其控制过程如图2所示.
由图2可知，传感器对DGMR姿态角信号进行监测并将其传递给控制器，控制器经过分析和计算给予驱动器信号以驱动电机，连接可动轮与固定点之间的连杆因此绕固定点转动，使可动轮的位置发生改变，进而改变DGMR姿态. 其中，DGMR推杆变形机构模型参数如表1所示.
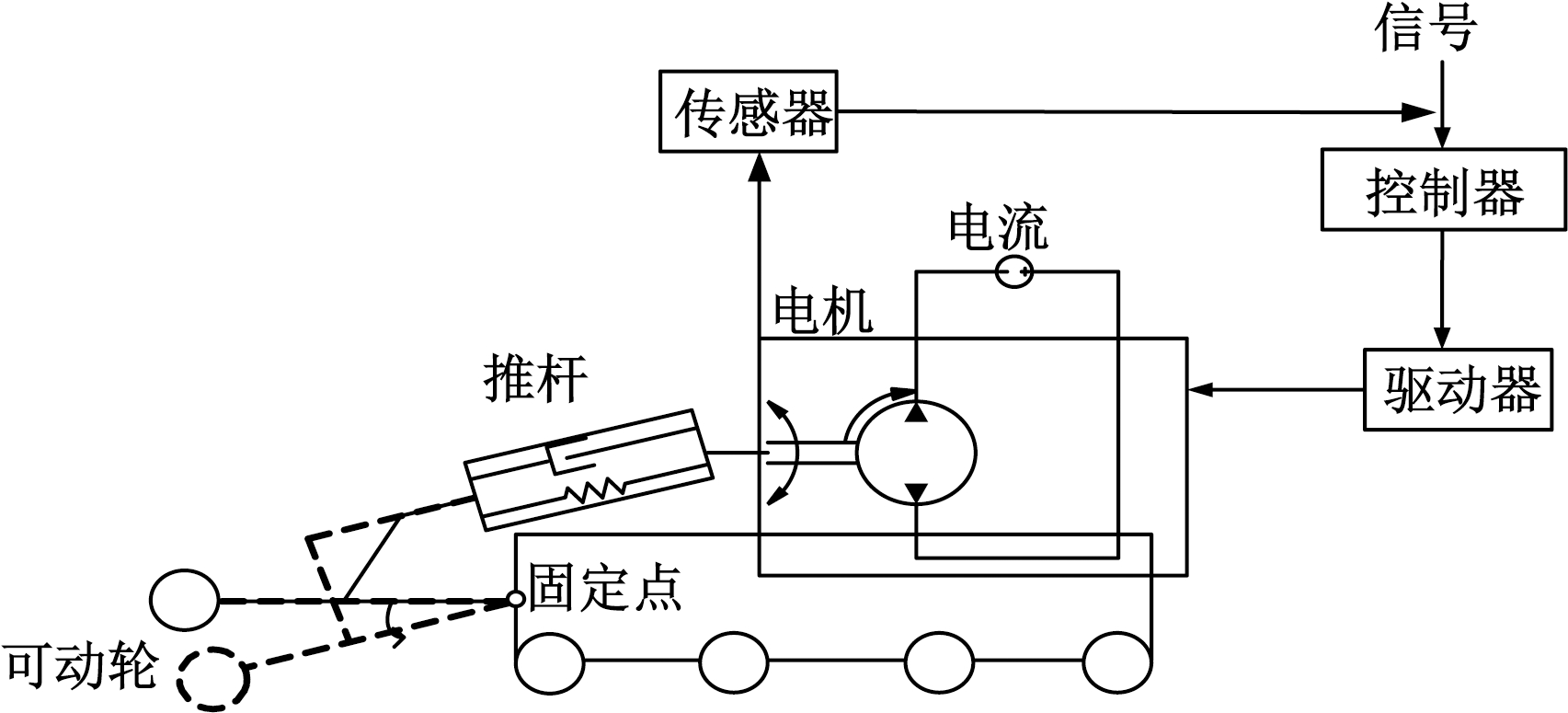
图2 DGMR运动系统推杆变形机构控制过程图
Fig.2 Control chart of pusher deformation mechanism in motion system of DGMR
通过对系统物理模型分析，可使用键合图[17]对系统结构进行描述，随后根据键合图规则[18]将模型转换成Simulink 方块图，最后在Simulink 中完成模型的搭建.笔者拟使用3个二阶ESO串联形成1个三阶ADRC控制器对DGMR进行控制，由此可得，安排过渡过程如式(8)所示.
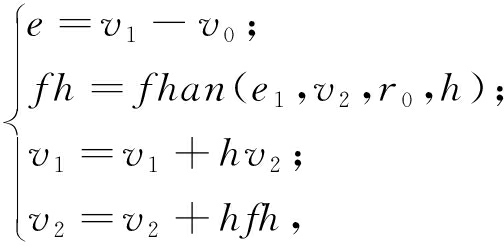
(8)
表1 可变形地面移动机器人推杆变形机构模型参数取值
Tab.1 Parameter values of pusher deformation mechanism for DGMR
描述取值描述取值电机推杆输入电压Va/V24质量M/kg2齿轮半径r1/m0.025连杆旋转半径r2/m0.100感抗R/Ω1弹性系数k2/(N·m-1)8阻尼b/(N·s·m-1)4驱动系数K1弹性系数k1/(N·m-1)8系统传感器系数a1
式中：v0为系统输入(角度)；v1为v0的跟踪信号；v2为v1的微分值；r0和h为控制器参数.非线性函数为：
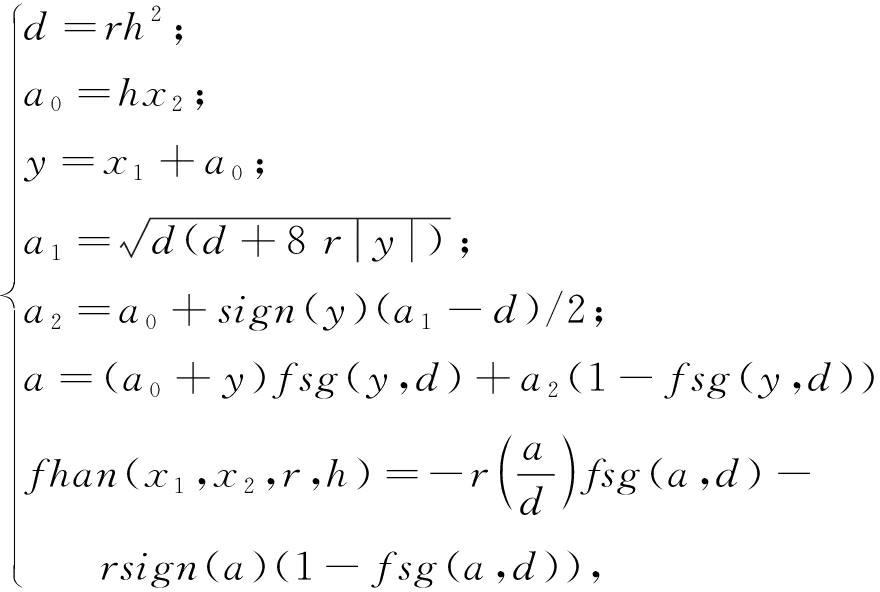
(9)
ESO如式(10)～(12)所示.
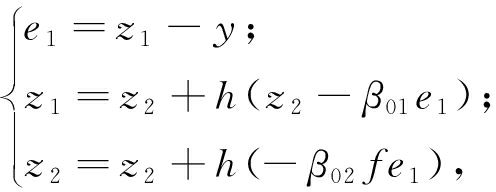
(10)
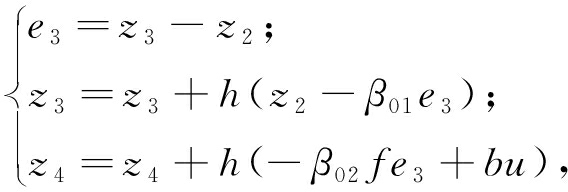
(11)
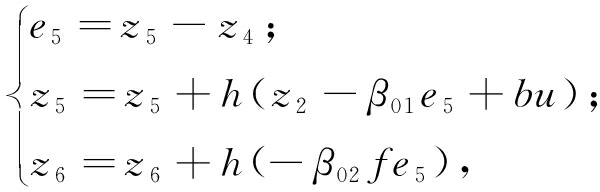
(12)
其中，
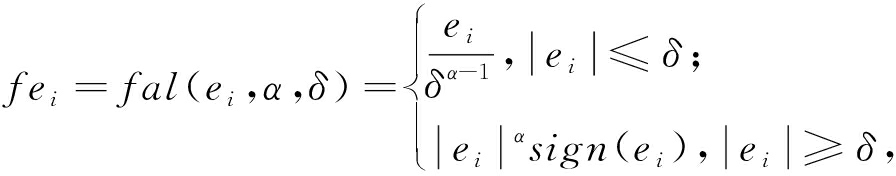为非线性函数；y为系统的输出反馈信号；z1、z3、z5 为状态e的估计值； z2、z4、z6为系统总扰动的估计值；β01 和β02分别影响状态变量e和系统总扰动的估计值；b为补偿因子.
NSEFL如式(13)所示：
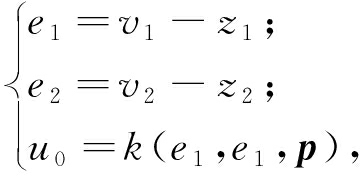
(13)
式中：e1和e2为状态误差；u0=-fhan(e1,ce2,r,h1)为误差反馈控制量；p为一组参数.
2.2 适应度函数评价
将DGMR模型中的两个ADRC控制器的控制参数取相同值，因此共有来自安排过渡过程、扩张状态观测器和误差状态反馈律的7个参数C(r0,r,h,α,β01,β02,c)需进行调节. 本工作利用系统阶跃响应的超调量fo、上升时间ftr和稳态误差fe作为阶跃响应的评价指标，设计适应度函数及相应评价指标计算方法为：
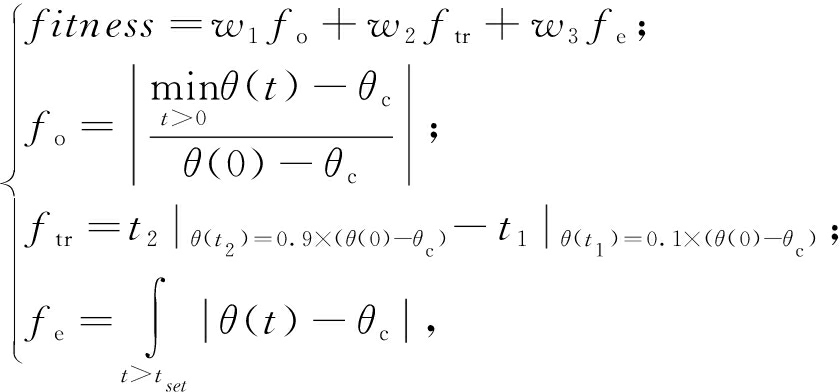
(14)
式中：w1、w2、w3分别为评价指标对应的权值，w1=200，w2=100，w3=30，笔者取较大值以保证响应的稳定性.以上3种性能指标越小，性能越好，因此以最小化适应度函数为优化目标.
2.3 基于EGTPIO的控制器参数优化
基于EGTPIO优化算法的参数优化流程如下.
步骤1 DGMR模型参数初始化，确定模型目标姿态角度θ=0 rad，仿真步长为0.01 s，仿真采样时间为30 s.
步骤2 初始化参数.包括EGTPIO算法参数、种群以及适应度函数的权值.
步骤3 计算每只鸽子适应度函数.利用鸽子的位置计算适应度函数值，更新鸽群中最优个体的位置.
步骤4 分别单独执行地图和指南针算子与地标算子，并利用式(4)～(6)计算收益，得到一组ESS.
步骤5 根据式(7)，利用上一步得到的ESS值执行EGTPIO.
步骤6 如果循环次数小于最大迭代次数，返回Step 3，否则输出优化结果.
2.4 仿真结果与分析
为验证EGTPIO算法的有效性，在相同初始条件下，分别利用粒子群 (particle swarm optimization, PSO)、PIO、含有导航工具过渡因子的鸽群优化[7](CPIO)和EGTPIO算法对DGMR系统ADRC控制器参数进行优化，不同算法的参数取值如表2所示，算法参数优化的进化曲线如图3所示.
表2 算法参数取值
Tab.2 Parameters values of different algorithms
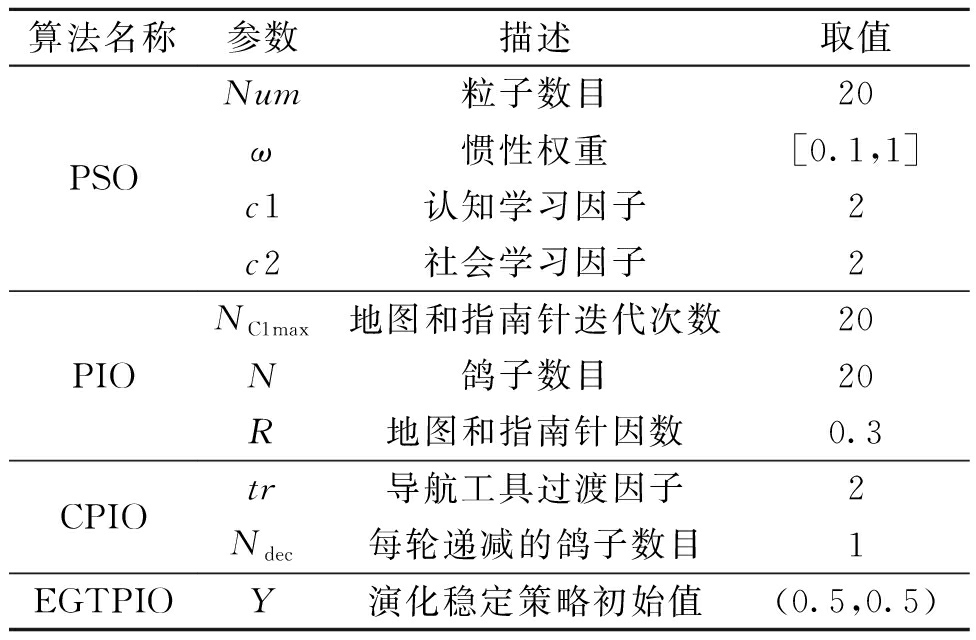
算法名称参数描述取值PSOPIOCPIOEGTPIONum粒子数目20ω惯性权重[0.1,1]c1认知学习因子2c2社会学习因子2NC1max地图和指南针迭代次数20N鸽子数目20R地图和指南针因数0.3tr导航工具过渡因子2Ndec每轮递减的鸽子数目1Y演化稳定策略初始值(0.5,0.5)
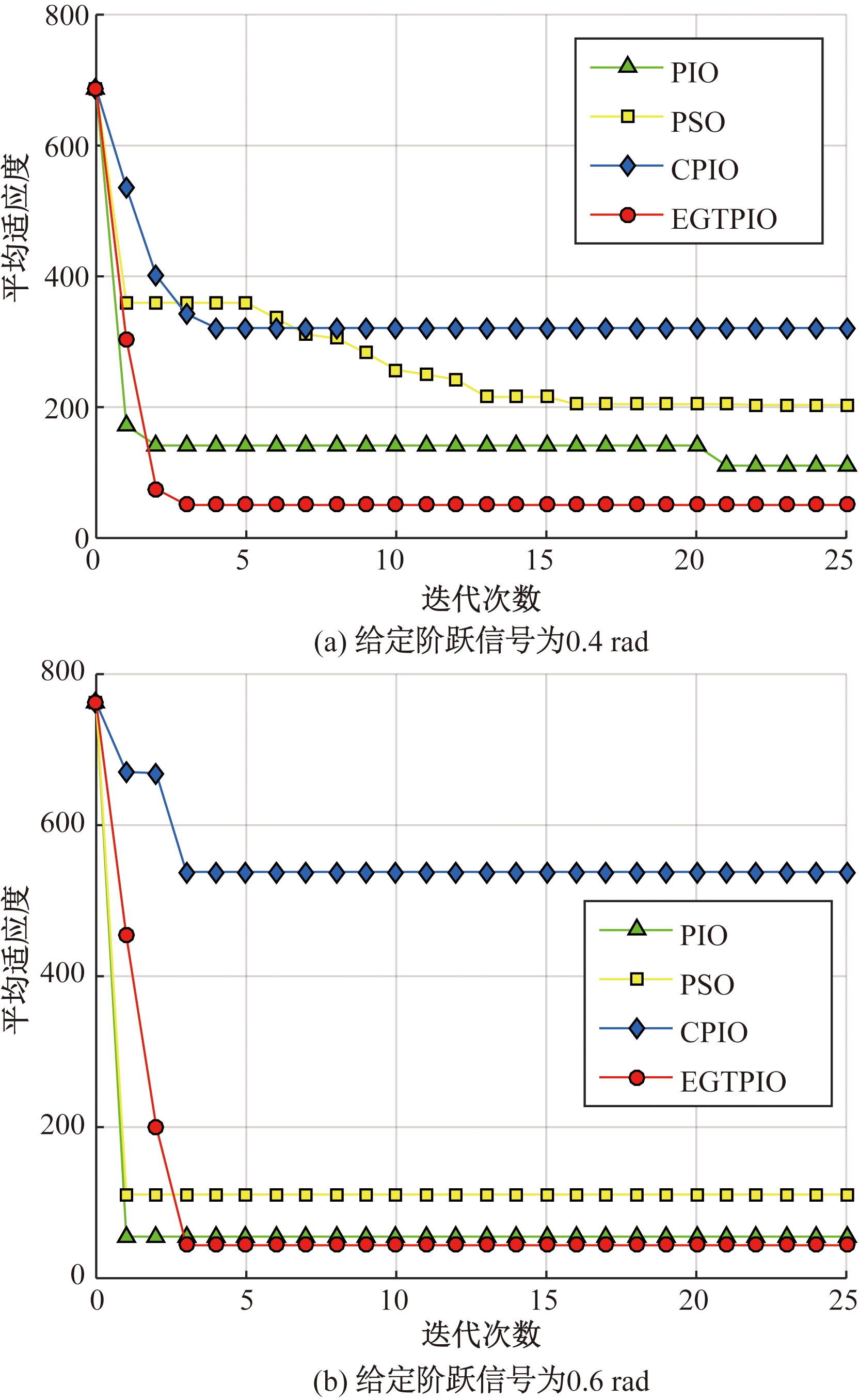
图3 自抗扰控制器参数优化收敛曲线
Fig.3 Convergence map of parameter optimization in ADRC
图3(a)为系统在阶跃信号为0.4 rad下的不同算法适应度曲线变化20次的平均值； 图3(b)为系统在阶跃信号为0.6 rad下的不同算法适应度曲线变化20次平均值. 从进化曲线可以看到，EGTPIO、PIO和PSO在参数优化中表现较好，都找到了较优的解，而CPIO则陷入局部最优，最终得到的解与其他3种算法相比，质量差距较明显.相比于PSO、PIO，EGTPIO在阶跃信号为0.4 rad时能够在较短时间内搜索到最优解，有着较为理想的收敛速度和搜索效率；在0.6 rad时虽然收敛较缓慢，但是能够找到最优解.
通过图4可直观看到，4种算法优化下的系统两种阶跃信号的响应曲线EGTPIO在超调量、上升时间方面较其他3种方法都有着较明显的优势；除此之外，EGTPIO作用下的稳态误差较其他集中算法也要小.
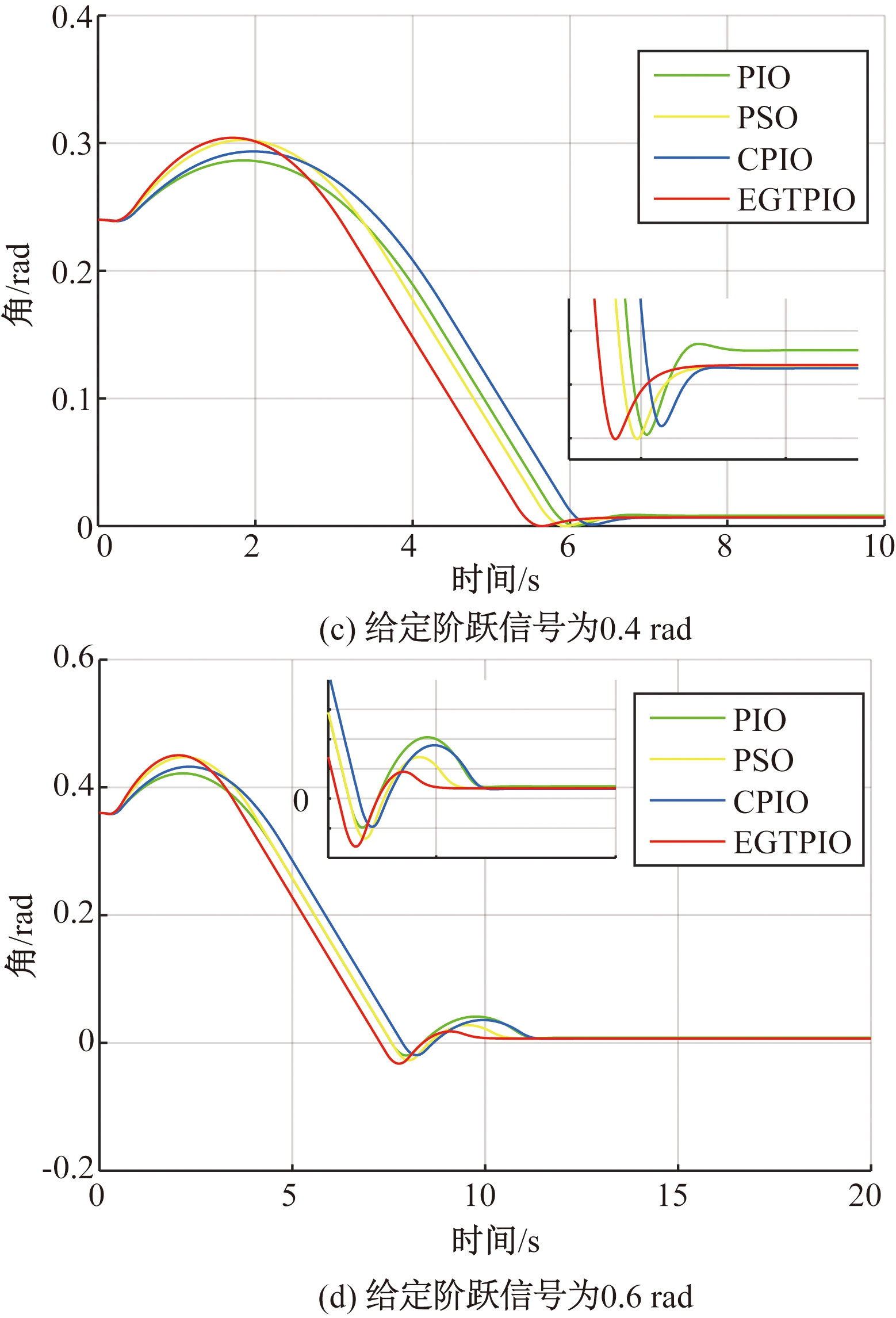
图4 算法优化结果的系统阶跃响应对比
Fig.4 Comparative result of step response of system for different algorithms
3 结论
(1)针对PIO中两个算子独立计算的问题，提出一种基于演化博弈理论的鸽群优化算法.将传统PIO中两个独立循环进行合并，并利用鸽群演化博弈过程对参数相互协调与最优配置进行整体改进.
(2)将演化博弈鸽群优化应用于自主设计开发的可变形地面移动机器人自抗扰控制模型，针对ADRC参数过多且参数物理意义不明确、难以整定的缺陷，使用对控制器参数进行优化. 相同初始条件下对比4种算法的效果，仿真结果表明：相比于PSO、PIO、CPIO，EGTPIO的搜索质量、效率均明显.
(3)系统时域响应进一步验证了EGTPIO的优良性能，证明其可通过优化控制器参数提升可变形移动机器人的整体性能.
[1] 王守娜，刘弘，高开周. 一种应用于函数优化问题的多种群人工蜂群算法[J]. 郑州大学学报(工学版), 2018, 39(6):30-35.
[2] 孟祥萍,王圣镔,王欣欣. 基于蚁群算法和轮盘算法的多Agent Q学习[J].计算机工程与应用, 2009, 45(16):60-62.
[3] 梁静，宋慧，瞿博阳，等.基于改进粒子群算法的路径优化问题研究[J]. 郑州大学学报(工学版), 2014, 35 (1):34-38.
[4] DUAN H B, QIAO P X. Pigeon-inspired optimization: a new swarm intelligence optimizer for air robot path planning[J]. International journal of intelligent computing and cybernetics, 2014, 7(1):24-37.
[5] DENG Y M, DUAN H B. Control parameter design for automatic carrier landing system via pigeon-inspired optimization[J]. Nonlinear dynamics, 2016, 85(1): 97-106.
[6] ZHANG S J, DUAN H B. Gaussian pigeon-inspired optimization approach to orbital spacecraft formation reconfiguration[J]. Chinese journal of aeronautics, 2015, 28(1):200-205.
[7] 段海滨,邱华鑫,范彦铭. 基于捕食逃逸鸽群优化的无人机紧密编队协同控制[J]. 中国科学(技术科学), 2015, 45(6):559-572.
[8] 段海滨,杨之元. 基于柯西变异鸽群优化的大型民用飞机滚动时域控制[J]. 中国科学(技术科学), 2018,48(3):277-288.
[9] SMITH J M. Evolution and the theory of games[M]. Cambridge：Cambridge University Press, 1982.
[10] HAN J Q. From PID to active disturbance rejection control[J]. IEEE transactions on industrial electronics, 2009, 56(3):900-906.
[11] ZHANG H, ZHAO S, GAO Z Q. An active distur-bance rejection control solution for the two-mass-spring benchmark problem[C]//2016 American Control Conference. Boston.MA: IEEE, 2016：1566-1571.
[12] 马光远, 沈为群, 刘旺开,等. 自抗扰控制技术在高低温环境模拟系统中的应用[J]. 计算机测量与控制, 2015,23(11):3644-3647.
[13] 吴云洁,李琛,马征.基于自抗扰滑模的三轴挠性卫星姿态控制[J]. 系统仿真学报, 2015, 27(8):1831-1837.
[14] SMITH J M. The theory of games and the evolution of animal conflicts[J]. Journal of theoretical biology, 1974, 47(1):209-221.
[15] TAYLOR P D, JONKER L B. Evolutionary stable strategies and game dynamics[J]. Mathematical biosciences, 1978,40(1/2):145-156.
[16] 韩京清. 自抗扰控制技术[M]. 北京：国防工业出版社, 2008.
[17] KARNOPP D C, MARGOLIS D L, ROSENBERG R C. 系统动力学: 机电系统的建模与仿真[M]. 刘玉庆, 译.北京： 国防工业出版社, 2012.
[18] 黄洪钟，祖旭，张旭. 基于Matlab/Simulink的键合图仿真[J]. 大连理工大学学报，2003，43(5): 632-635.