0 引言
自20世纪60年代提出在轨服务技术概念以来，至今已经历几十年的发展历程.在这几十年间各国积极开展了一系列空间、地面实验和应用研究，展现了良好的应用前景.各国已进行过多次在轨服务项目的研究与实验[1].在轨服务变质量特性航天器是指在轨服务航天器中，由于燃料的消耗，某些大型天线的展开等航天器构型的变化，从宇宙飞船或航天飞机上释放卫星，空间机器人捕获目标，清除轨道垃圾等载荷的在轨捕获与释放和与其他航天器的对接等[2]，导致系统的质量特性发生变化的航天器.而这种系统在执行任务的过程中存在非线性、时滞等问题，传统的线性系统分析方法对这种系统不适用.许多学者利用鲁棒控制、神经网络等[3]理论进行研究并取得了大量成果，例如反馈线性化、PID控制、自适应控制等.但对于参数一直变化的系统而言，上述所提方法均有局限性，诸多问题需要进一步探索研究.
其中国内外学者将鲁棒控制应用到航天器系统中进行了许多的研究. Wu等[4]利用混合方法研究了小卫星的姿态稳定问题，以期解决控制器的输出过大问题.Chu等[5]考虑到模型参数的不确定性，制定了具有不确定参数的近似动态模型，提出了一种鲁棒的自适应控制策略来分别补偿或拒绝这些不确定性.Huang等[6]针对航天器太空执行任务过程中遇到的各种干扰以及参数变化的问题，将滑膜控制应用于PID控制中，两者结合以完成航天器姿态鲁棒控制. 秦靖[7]针对奇异摄动系统提出了控制器设计方法. 周燕茹等[8]针对存在外部干扰以及摄动干扰的航天器姿态机动问题,给出一种新的非线性鲁棒H∞控制方法. 袁国平等[9]提出了一种基于鲁棒自适应方法的解耦控制算法，以解决带有干扰及转动惯量不确定的航天器姿态控制问题.仝西岳等[10]使用多目标综合技术给出了静态输出反馈控制器，研究了控制输入有饱和约束的参数变化航天器的鲁棒稳定性及抑制干扰问题.但是该方法并未考虑附件频率以及刚柔耦合矩阵的不确定性.Yang等[11]研究了低地球轨道航天器在交会时轨道转移过程中参数变化情况下的轨道鲁棒控制问题.
随着控制理论的发展，逐渐将自适应控制、变结构控制等先进控制理论应用到航天器控制领域中，以提高参数变化航天器控制系统不确定情况下的鲁棒性能.笔者针对变质量特性航天器，采用飞轮和控制力矩陀螺联合使用的混合执行机构.飞轮具有高精度、高稳定度，但是控制力矩较小，动态响应慢；而控制力矩陀螺可以提供较大力矩且动态响应快，两者可以发挥各自优势，共同实现航天器的高性能姿态控制.考虑到卫星姿态控制系统是一个复杂的非线性系统，以及实际卫星大角度姿态机动过程中会出现力矩饱和、角速度限制等问题，笔者设计了基于遗传算法的变质量特性航天器姿态机动控制方法，将其与具有模型依赖的递阶饱和PD姿态控制方法的控制性能进行比较.仿真结果表明,基于遗传算法的模型独立姿态控制更适合非线性系统环境，航天器的姿态控制在参数变化的情况下具有更高的精度与稳定性.
1 建立卫星模型
1.1 卫星姿态运动学和动力学模型
由四元数描述的姿态运动学方程为[12]：
,
(1)
式中:
为姿态四元数；ω为姿态角速度.假设卫星为刚体模型，则姿态动力学方程为：
(2)
式中：J为转动惯量；ω为姿态角速度； Tc为控制力矩；Td为干扰力矩.
1.2 干扰力矩建模
在轨服务卫星在执行任务期间，会受到很多干扰力矩的影响，笔者考虑了其中几种主要的干扰力矩：气动力矩、地磁力矩、重力梯度力矩，并分别对其建模[13].
(1)气动力矩.气动干扰力矩表示为：
(3)
式中：Cd为阻力系数；ρ为空气密度；VR表示卫星与大气之间的相对速度；Ap为迎风面积；Rp为卫星质心气动压力作为的中心的矢量；v为入射空气流的速度单位矢量.
(2)地磁力矩.卫星地磁干扰力矩为:
(4)
式中:
为星上总剩磁磁矩;
为地球磁场强度.为了方便仿真，对干扰力矩模型进行简化，如下式所示：
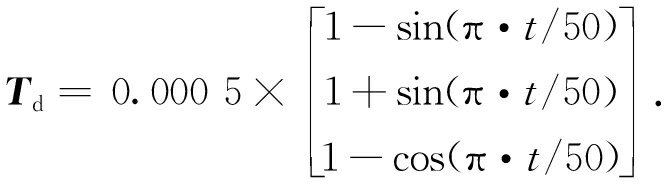
(5)
(3)重力梯度力矩.若地球质量均匀分布，则相对于轨道坐标系，重力梯度力矩向量可以表示为：
(6)
式中：μ为万有引力常数；r为卫星质心到地球中心的距离；E为卫星质心指向地球的单位矢量；J为卫星的转动惯量矩阵.
2 变质量特性航天器模型独立姿态控制律设计
具有模型独立的姿态控制系统不依赖于模型参数的变化，控制律设计如下[14]：
引理2-1 设姿态四元数为q，单位矢量为u，则可以定义qu、qR：
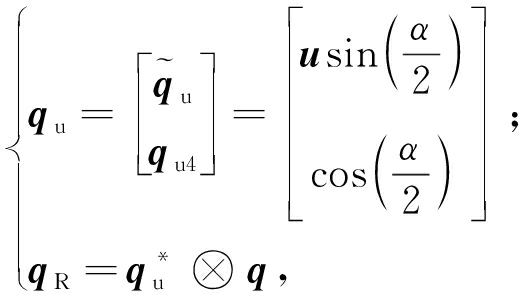
(7)
式中：
为qu的共轭四元数.定义
那么有
其中ωu是绕qu的角速度.
引理2-2 设ωu为星体绕qu欧拉轴的角速度，ωR为星体绕qR欧拉轴的角速度，即满足
可得星体角速度为：
(8)
在基于欧拉轴转动时， ‖qR-1‖=0，其中qu=q.
定理2-1 对于∀ε>0，当k1、k2、k3、d>0且k1≠k2时，∃δ>0满足控制律
且有如下结论成立： q渐近稳定，即q(∞)=1； ∀t>0时，有‖qR(t)-1‖≤ε.
可将ω(t)分解：ω=uuTω+(I3-uuT)ω,
式中：I3是3×3单位阵;u为单位矢量，将定理
所以整理得：
(9)
设计控制律时，应保证d2>d1.
定理2-2 ∀ε>0，当k1、k2、k3、d1、d2>0且k1≠k2时，∃δ>0， 0≤‖qR(0)-1‖≤δ,故有q渐近稳定，即q(∞)=1，∀t>0时，有‖qR(t)-1‖≤ε.
设当前四元数q=(q1,q2,q3,q4)，目标四元数qf=(q1f，q2f,q3f,q4f)，则误差四元数
记
则有：
[d1uuT+d2(I3-uuT)]ω}/k3.
(10)
上式中
和d2(I3-uuT)ω/k3较小，可忽略不计.记ω′=uuTω，则控制律为：
(11)
设计刚性航天器控制律为：
(12)
式中：Pi、Qi是控制律增益.
是关于x的规范化的饱和函数,σ(x)是以x为变量的正标量函数，取
或
(13)
根据式(13)，定义
为：
(14)
式中:qemax为
中最大值，此时，模型独立控制律为：
(15)
式中:u为单位矢量；ω为星体角速度；qe为误差四元数；I3为3×3单位阵；u为单位矢量；k1、k2、k3、d1、d2为控制参数.由上述控制律可知，该控制律复杂且参数较多，控制系统参数需要人为调整确定，无法保证控制参数的最优性.笔者在模型独立的基础上，提出基于遗传算法(genetic algorithms, GA)的模型独立姿态控制算法，以期完成参数的在线整定，得到最优控制参数，更加快速高效地完成姿态机动.
遗传算法是一种人工智能仿生算法，其根据适者生存、优胜劣汰等规则搜索计算候选解以求得最优解.对于许多传统数学无法解决的复杂问题，尤其是优化问题，遗传算法都能很好地解决.由此，笔者将遗传算法这种仿生智能算法应用于模型独立的姿态控制系统中，解决传统方法无法实现的参数优化问题.
遗传算法是通过遗传和变异而形成的一种概率搜索方法[15]．遗传算法涉及3个运算，分别是选择、交换和变异.选择主要是对候选参数去劣存优，笔者采用的是适应度比例法.为了创造出新的候选参数，保证候选参数的数量，对候选参数进行交换操作，产生新的优秀参数进入下一次迭代.为了保证候选参数在经过选择交换后不会破坏控制参数的多样性，会对某些候选控制参数进行变异操作.
由于变质量特性航天器姿态控制器的参数和所预定的优化指标之间不存在明显的映射，所以选择合适的目标参数是优化变质量特性航天器控制器参数的重要步骤.笔者提出了一种变质量特性航天器系统优化策略,其优化模型如图1所示.
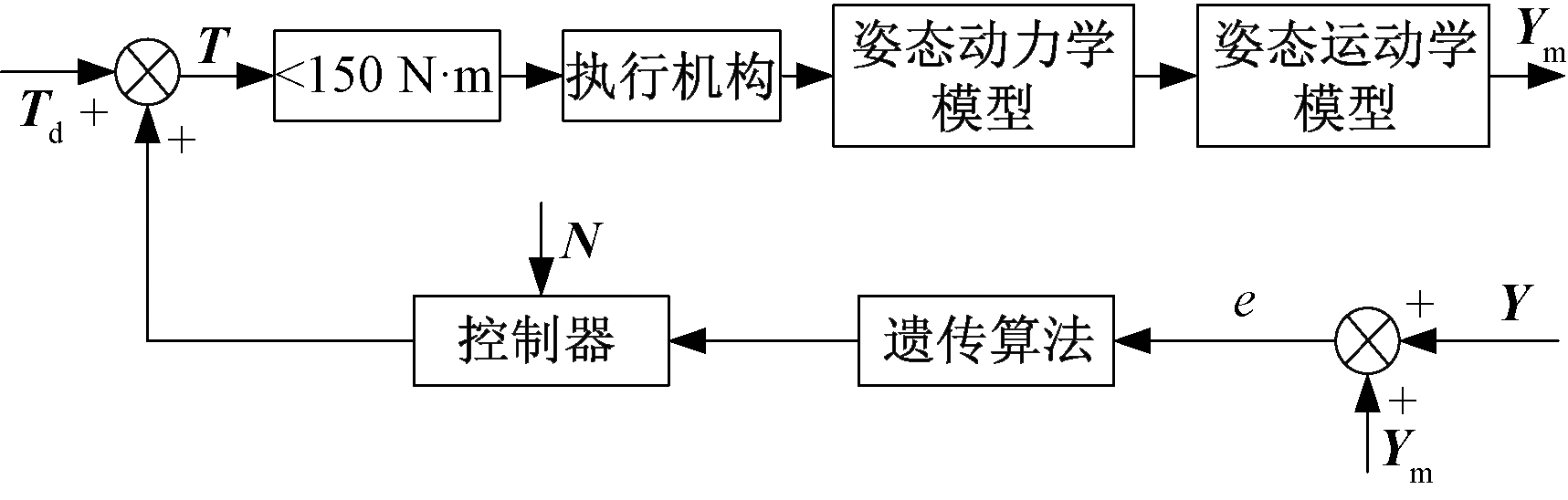
图1 姿态控制系统优化模型图
Fig.1 Attitude control system optimization model diagram
图1中，Y为期望的姿态角速度；Ym为卫星实际输出姿态角速度；T为控制力矩；e为实际输出与期望输出的误差绝对值; Td为干扰力矩；N为系统控制器输入.将误差绝对值作为目标函数，遗传算法程序通过判断目标函数的值以调整控制器参数，直到输出的误差达到一定的范围值，从而得到参数近似最优解.
算法开始时会先随机地产生大量一系列候选参数，根据这些候选参数计算它们的适应度.然后根据所要求的适应度标准，筛出适应度低的参数，留下性能好的候选参数进入下一次迭代，这样不断迭代直到找到满足预定优化指标的近似最优解.变质量特性航天器的姿态控制系统优化流程图如图2所示.
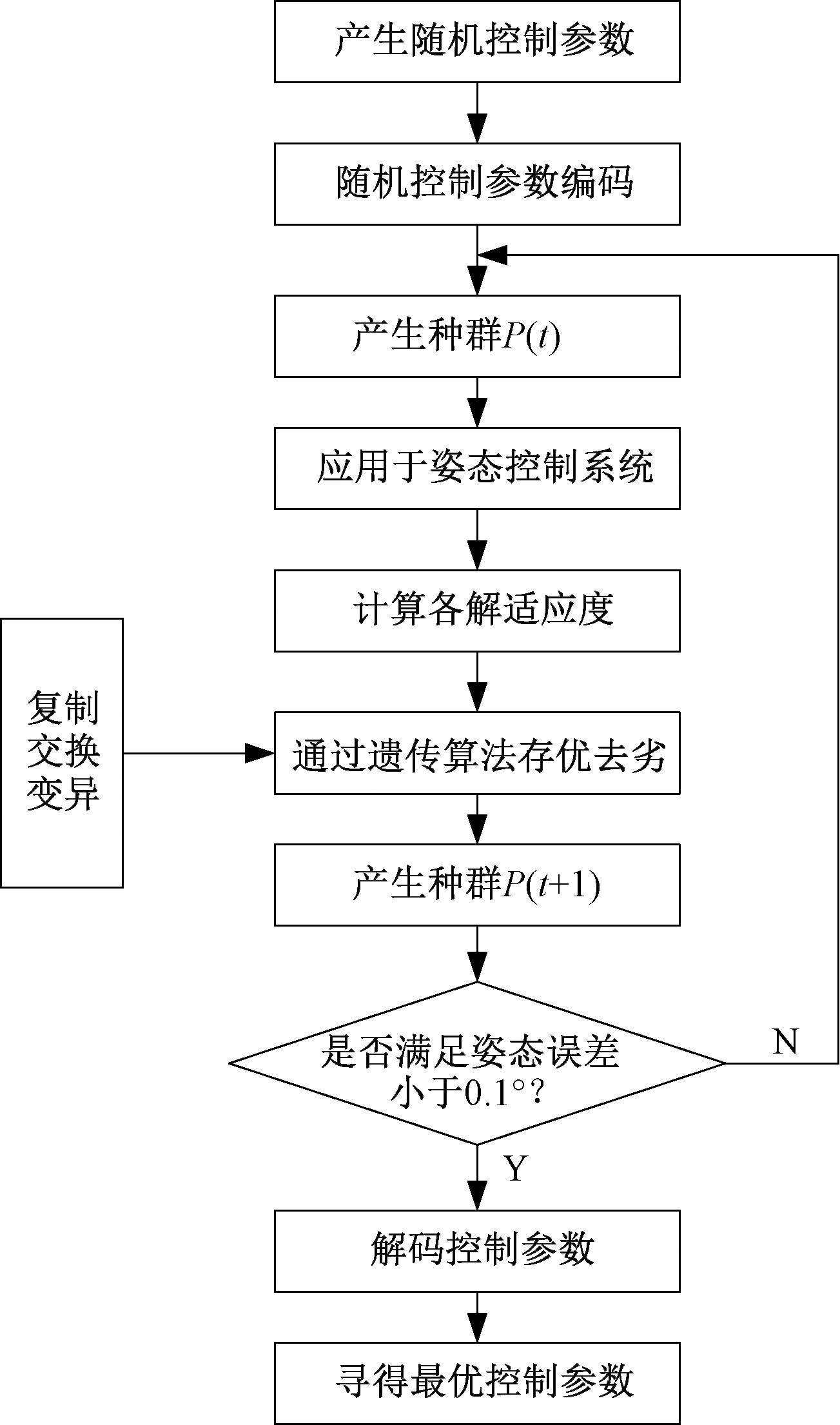
图2 姿态控制系统优化流程图
Fig.2 Attitude control system optimization flow chart
3 仿真结果
为了更好地分析基于遗传算法的模型独立姿态控制方法的控制性能及精度，本节给出了两种算法的仿真结果.分别对模型依赖的递阶饱和PD控制方法以及基于遗传算法的模型独立控制方法进行仿真.
3.1 模型依赖的递阶饱和PD控制仿真结果及分析
模型依赖的递阶饱和PD控制方法是在基于欧拉轴转动的PD控制的基础上，针对卫星在大角度机动过程中会出现初始误差很大从而导致姿态控制过程中存在初始控制力矩过大的问题，给出的一种当输入受限时的鲁棒控制方法[16].在本文姿态动力学和运动学的条件下，限制了参与反馈的四元素的大小和执行机构的输出控制力矩，避免了执行机构饱和，强迫星体加速度提前穿越零点，由此得到的控制律形式如下:
(16)
式中:
为转动惯量；ω为星体角速度；k、d为控制参数；qv为星体四元数.该种方法在控制力矩受限的情况下，保证了航天器姿态角速度在限定范围内也可以得到良好的控制精度，但是机动执行时间超过100 s，且机动初始阶段力矩超过了所要求的范围.且该种方法会依赖于模型参数的变化，对于变质量特性航天器的控制系统来说，其控制性能以及控制精度都会受到影响.
设置卫星的转动惯量：
J=
变质量特性航天器初始四元数：q(0)=[-0.234 2,-0.211 0,0.211 0,0.925 2]T，初始角速度[0,0,0] rad/s.参数变化航天器目标四元数q(∞)=1，目标角速度[0,0,0] rad/s，本仿真考虑了重力梯度力矩和随机干扰力矩.姿态测量误差视为白噪声.陀螺测量精度为0.001 (°)/s，执行机构最大力矩限制为±150 (N·m).
控制器其他参数分别选取为：
k=0.06，d=0.43.
该控制律作用下的仿真结果如图3～7所示.
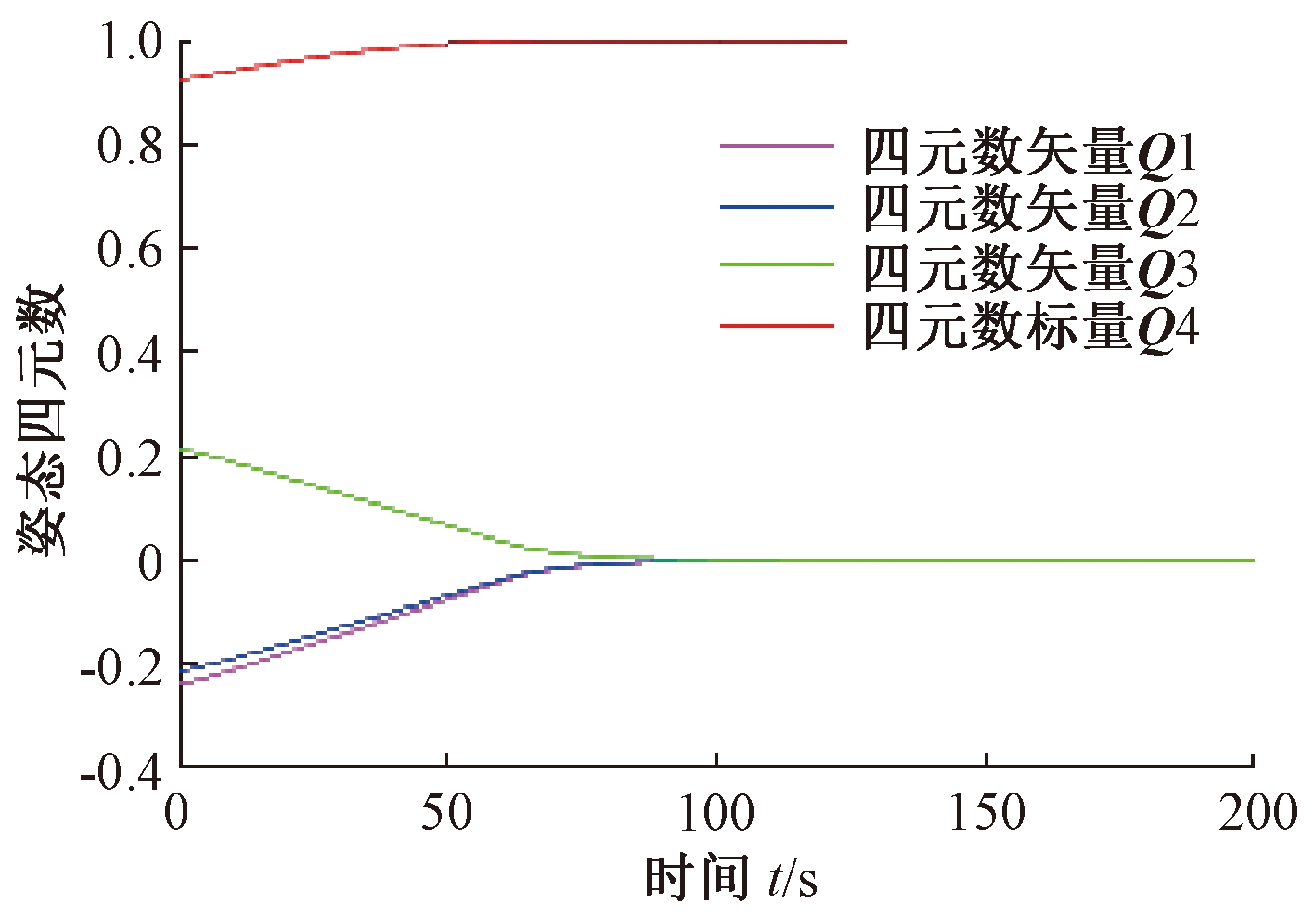
图3 姿态四元数
Fig.3 Attitude quaternion
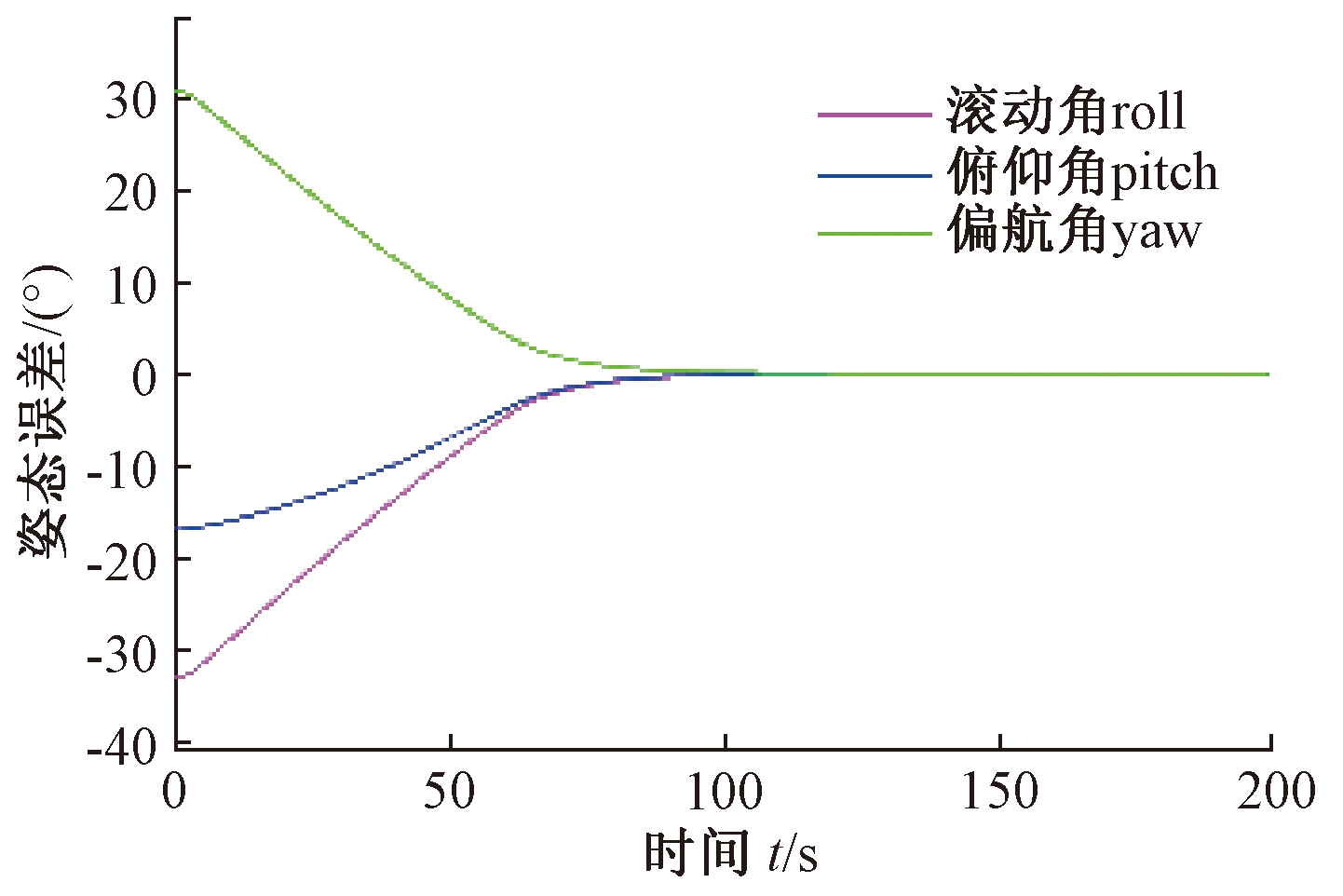
图4 姿态误差
Fig.4 Attitude error
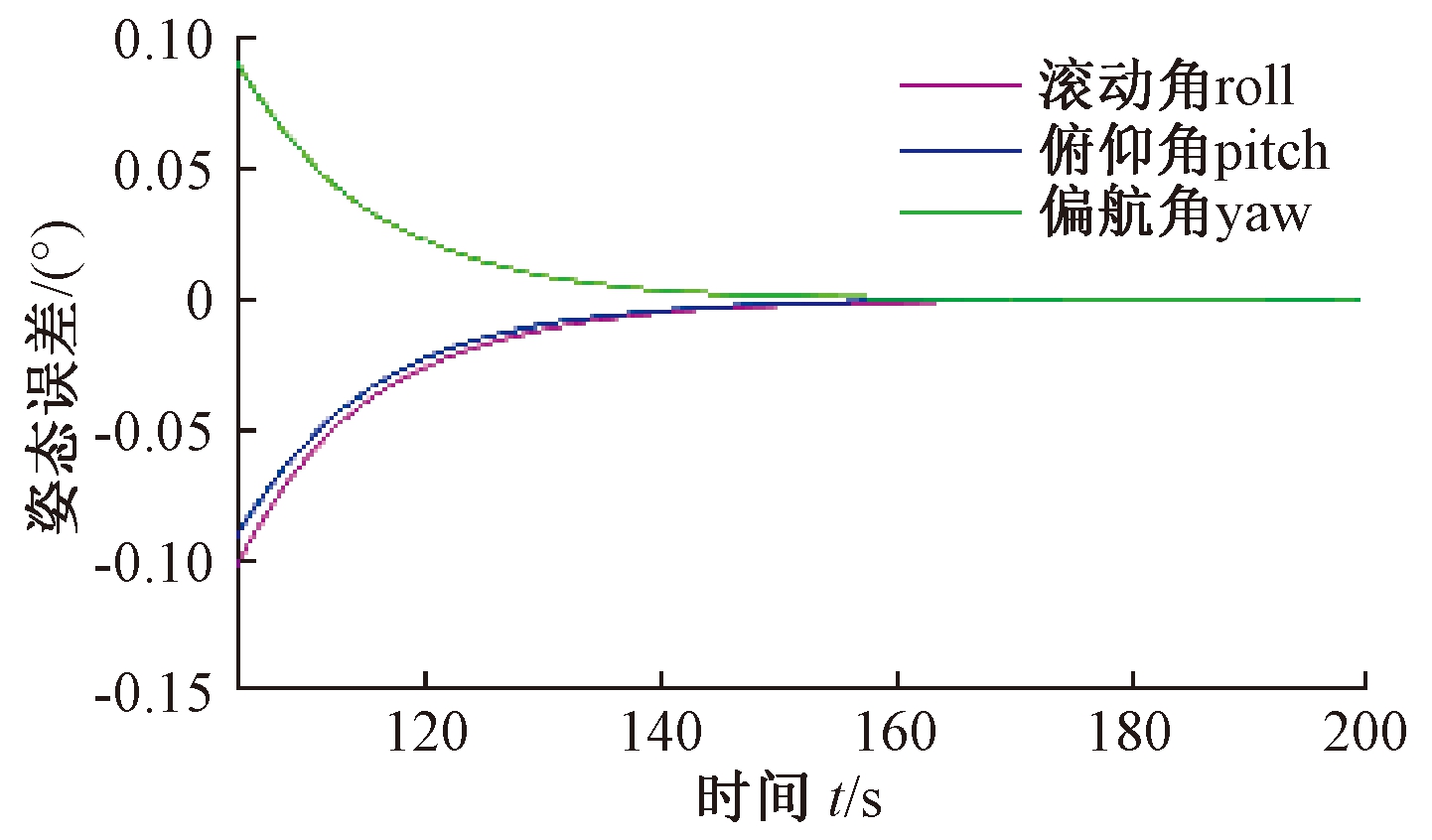
图5 姿态误差局部放大
Fig.5 Attitude error partial amplification
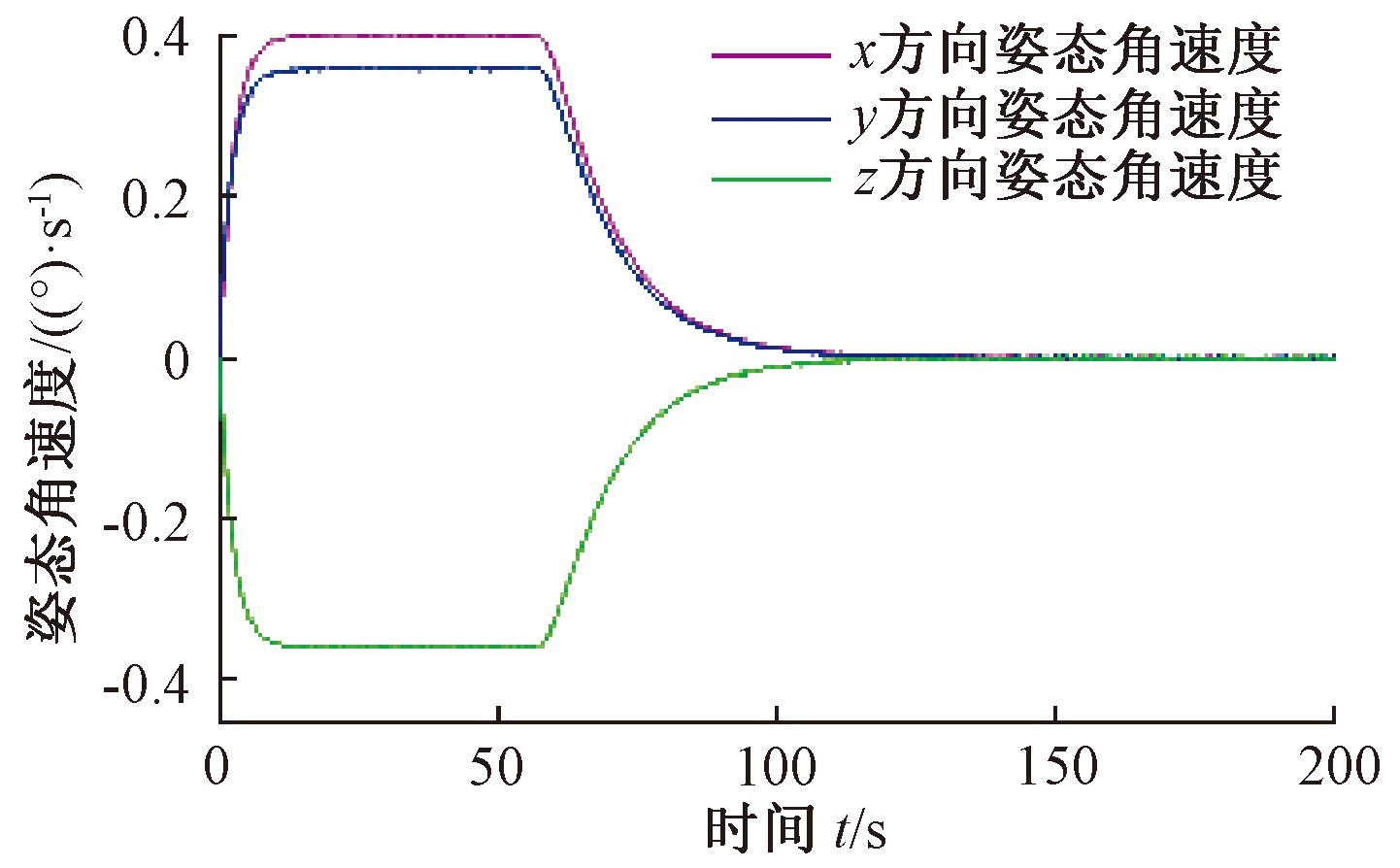
图6 姿态角速度
Fig.6 Attitude angular velocity
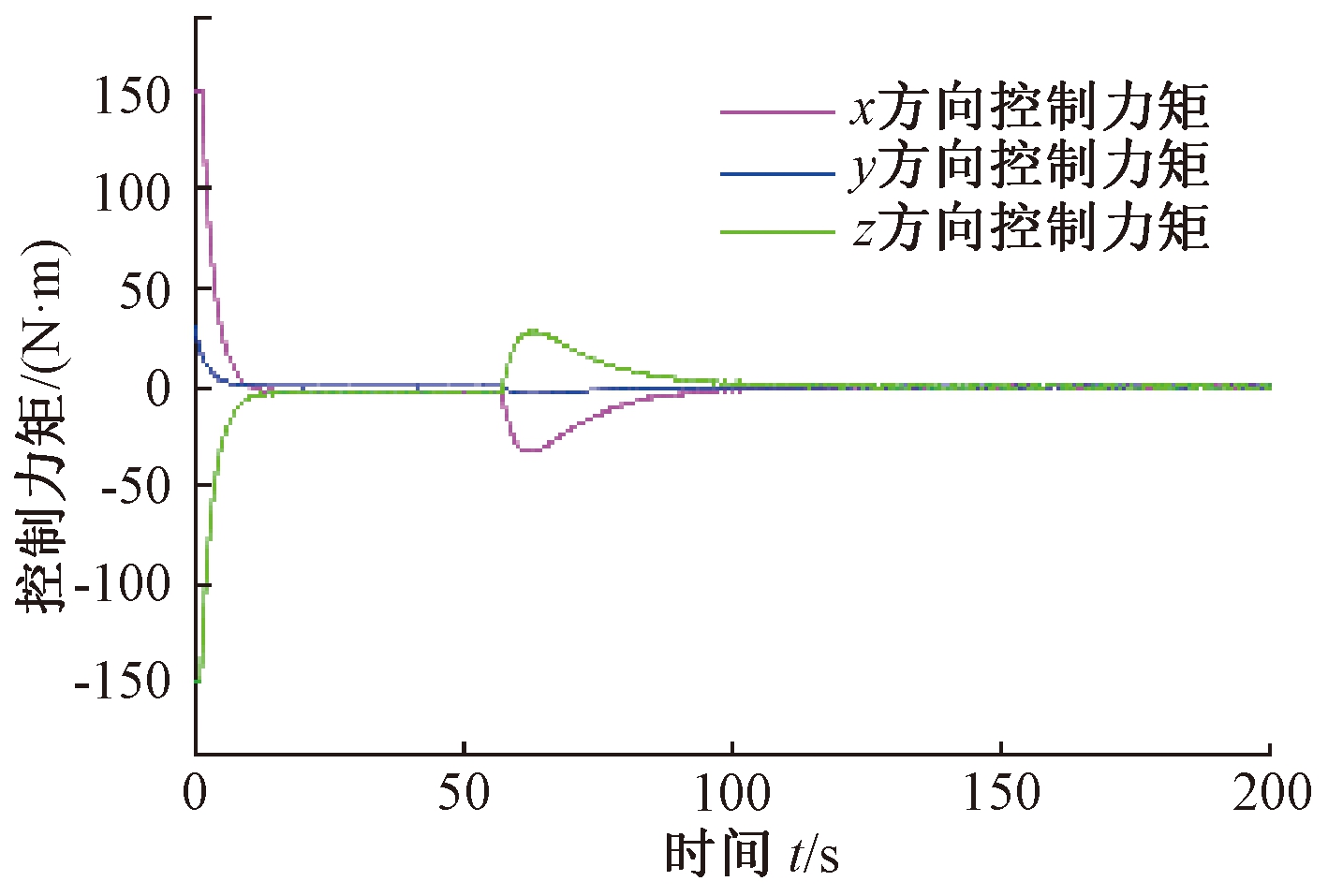
图7 三轴控制力矩
Fig.7 Three-axis control torque
从仿真结果可以看出，具有模型依赖的递阶饱和PD控制约在104 s完成姿态机动，控制精度≤0.1°.在该方法控制下卫星本体角速度均在0.5 (°)/s以内，没有超过允许的最大转动角速度的限制.若控制输入不受限，则仅在初始阶段超出150 N·m.
3.2 基于遗传算法的模型独立姿态控制仿真结果及分析
控制律为：
U=-sat{[k1sat(qe)+k2qR+
(d1uuT+d2(I3-uuT))ω]/k3}.
(17)
该仿真中卫星的转动惯量、参数变化航天器的初始四元数、初始角速度、目标四元数、目标角速度均与上节相同.为使条件0≤‖qR(0)-1‖≤δ满足，u与
夹角应尽量小，实际可取u=[-0.617 4 -0.556 2 0.556 2 ]T，ωemax=0.5 (°)/s.本仿真考虑了重力梯度力矩和随机干扰力矩，并将姿态测量误差视为白噪声.遗传算法中，种群数量取50个，交换概率取0.4，变异概率取0.01，进行100代GA运算后近似得到d1=90.
控制器其他参数分别选取：k1=15,k2=150,d2=300,k3=160.
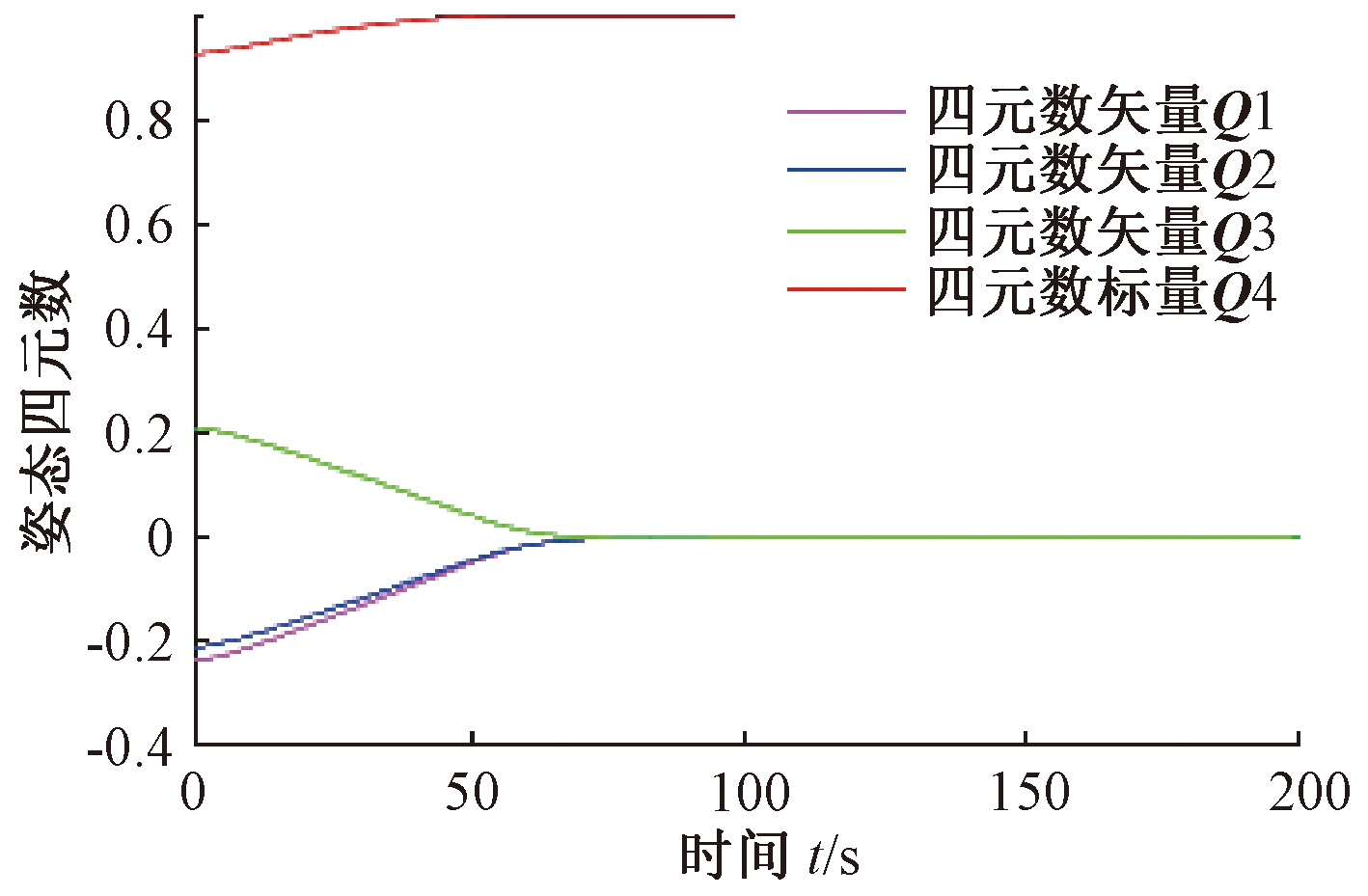
图8 姿态四元数
Fig.8 Attitude quaternion
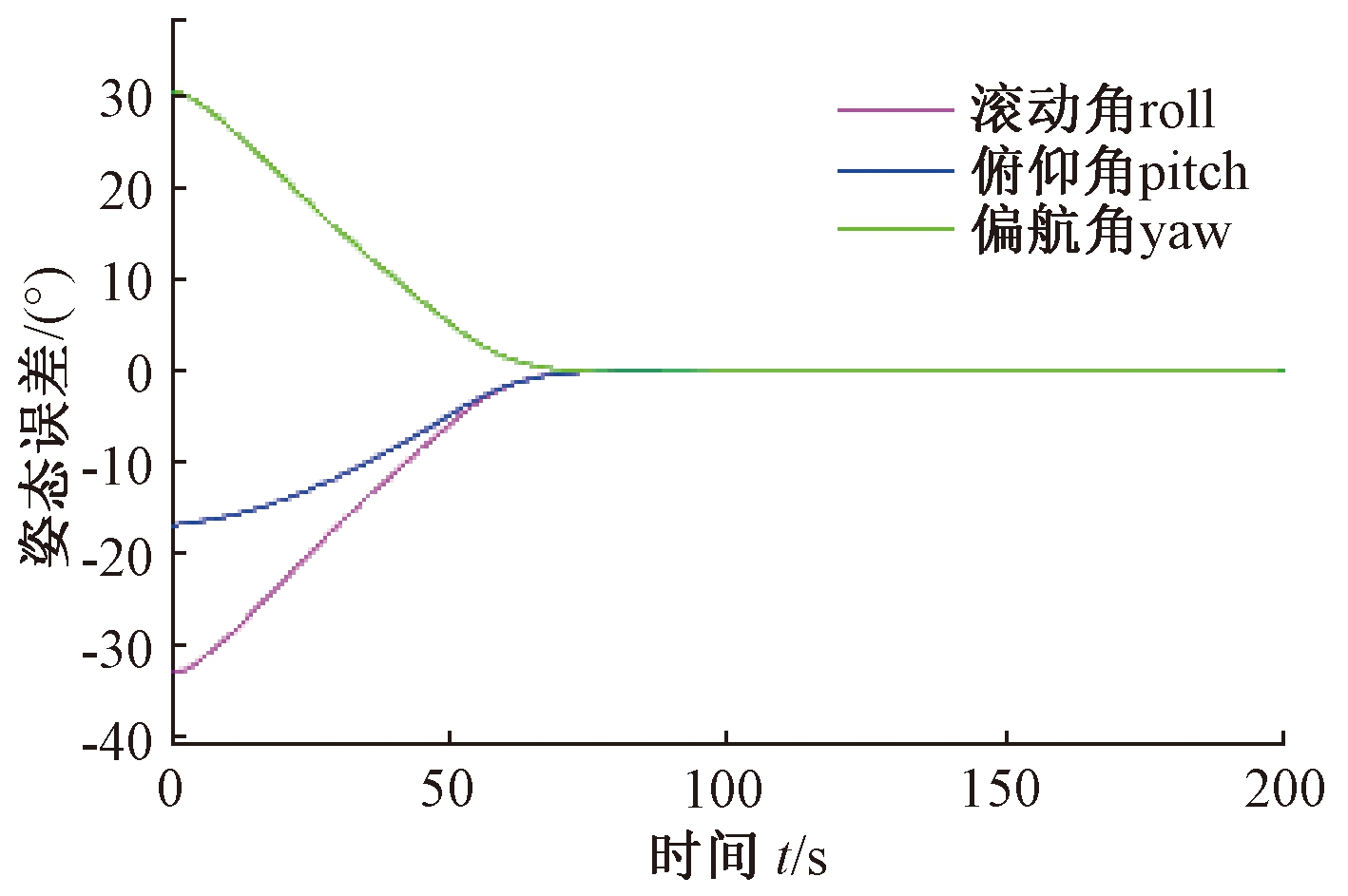
图9 姿态误差
Fig.9 Attitude error
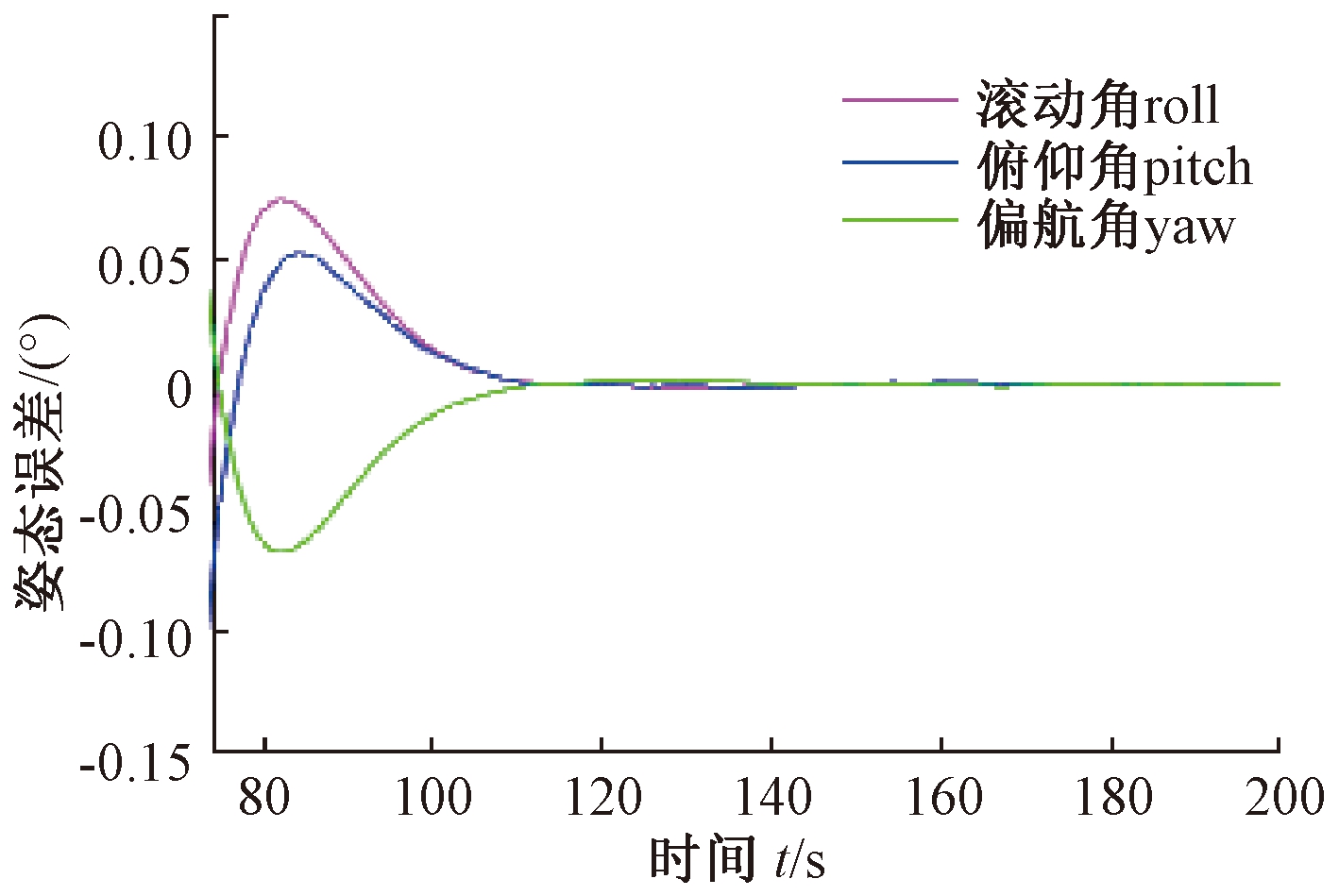
图10 姿态误差局部放大
Fig.10 Attitude error partial amplification
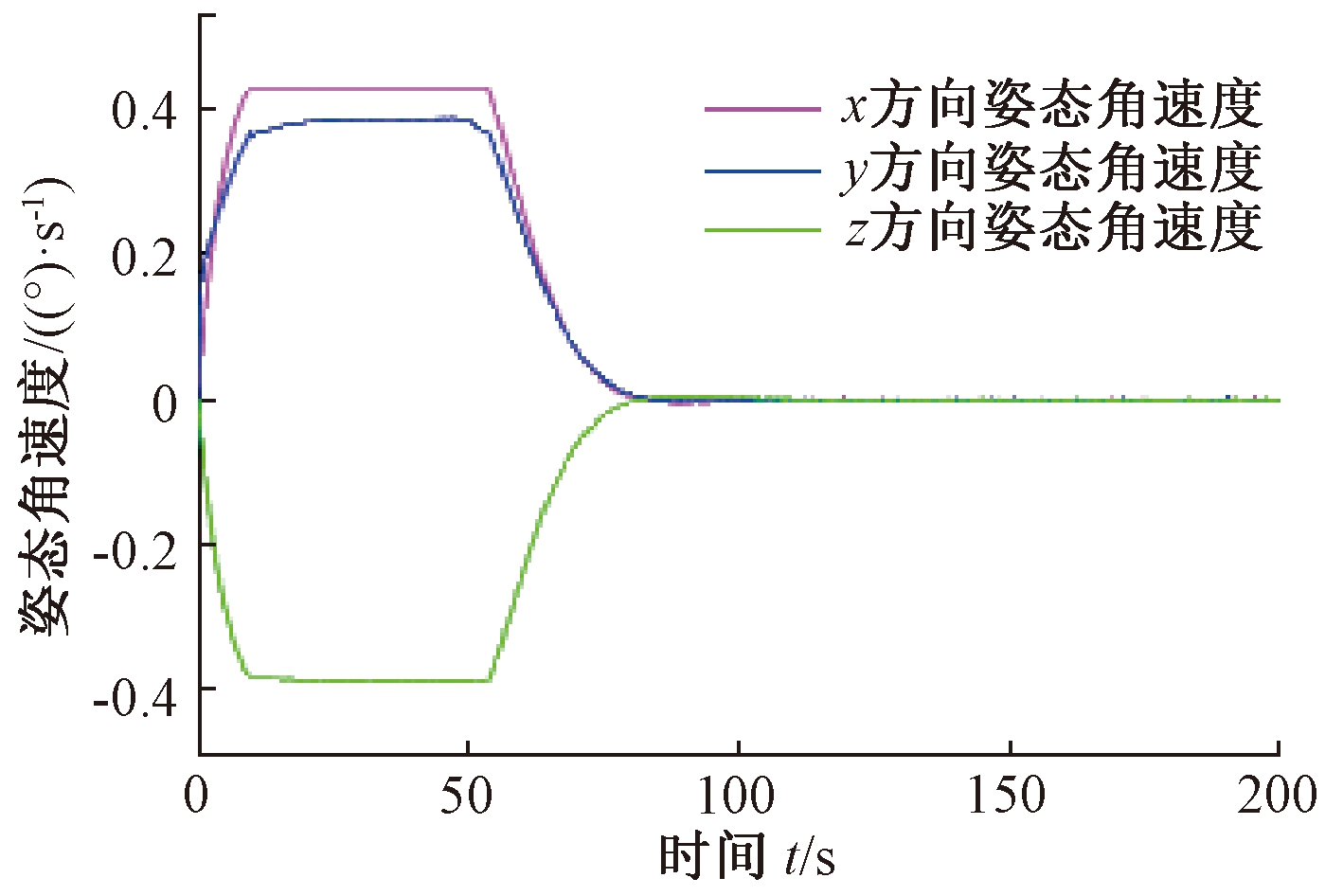
图11 姿态角速度
Fig.11 Attitude angular velocity
控制律作用下的仿真结果如图8～12所示.从仿真结果可以看出，基于遗传算法的模型独立姿态控制约在74 s完成姿态机动，控制精度≤0.1°.在该方法控制下卫星本体角速度均在0.5 (°)/s以内，没有超过允许的最大转动角速度的限制.且三轴控制力矩均未超过150 N·m.
对笔者提到的两种控制方法进行进一步详细比较，具体比较结果如表1所示.
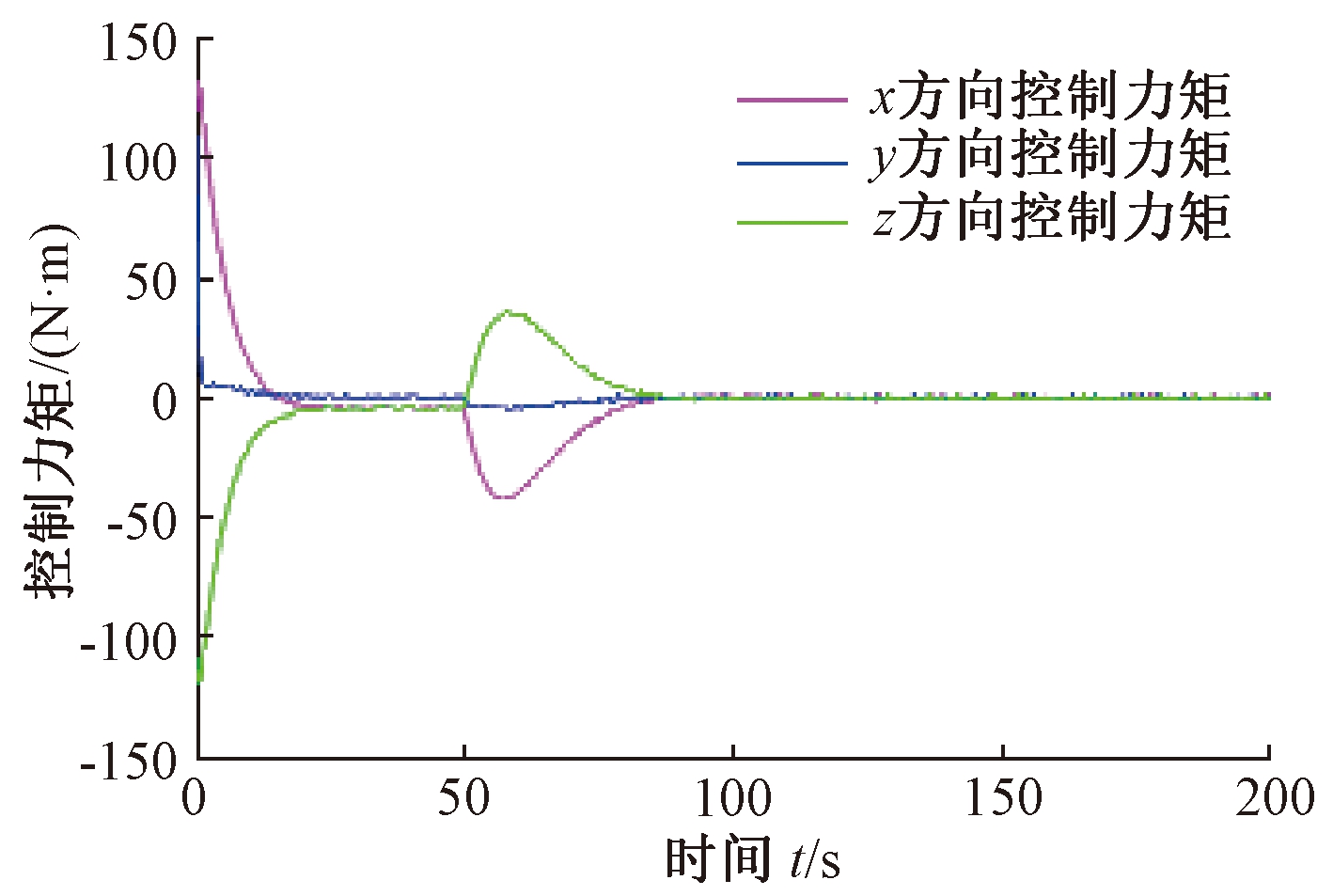
图12 三轴控制力矩
Fig.12 Three-axis control torque
表1 姿态控制算法对比
Tab.1 Attitude control algorithm comparison
方法结果模型依赖的递阶饱和PD控制控制律简单,控制参数少;执行机动时间和控制精度依赖模型转动惯量估计精度;若转动惯量估计精确,执行机动时间约为104 s;机动过程中,控制器最大输出在执行机构限值外;机动过程中,最大姿态角速度在限值内;控制精度≤0.1°基于遗传算法的模型独立姿态控制控制律稍复杂,控制参数较多;执行机动时间和控制精度不依赖模型转动惯量估计精度;执行机动时间约为74 s;机动过程中,控制器最大输出在执行机构限值内;机动过程中,最大姿态角速度在限值内;控制精度≤0.1°
3.3 遗传算法稳定性分析
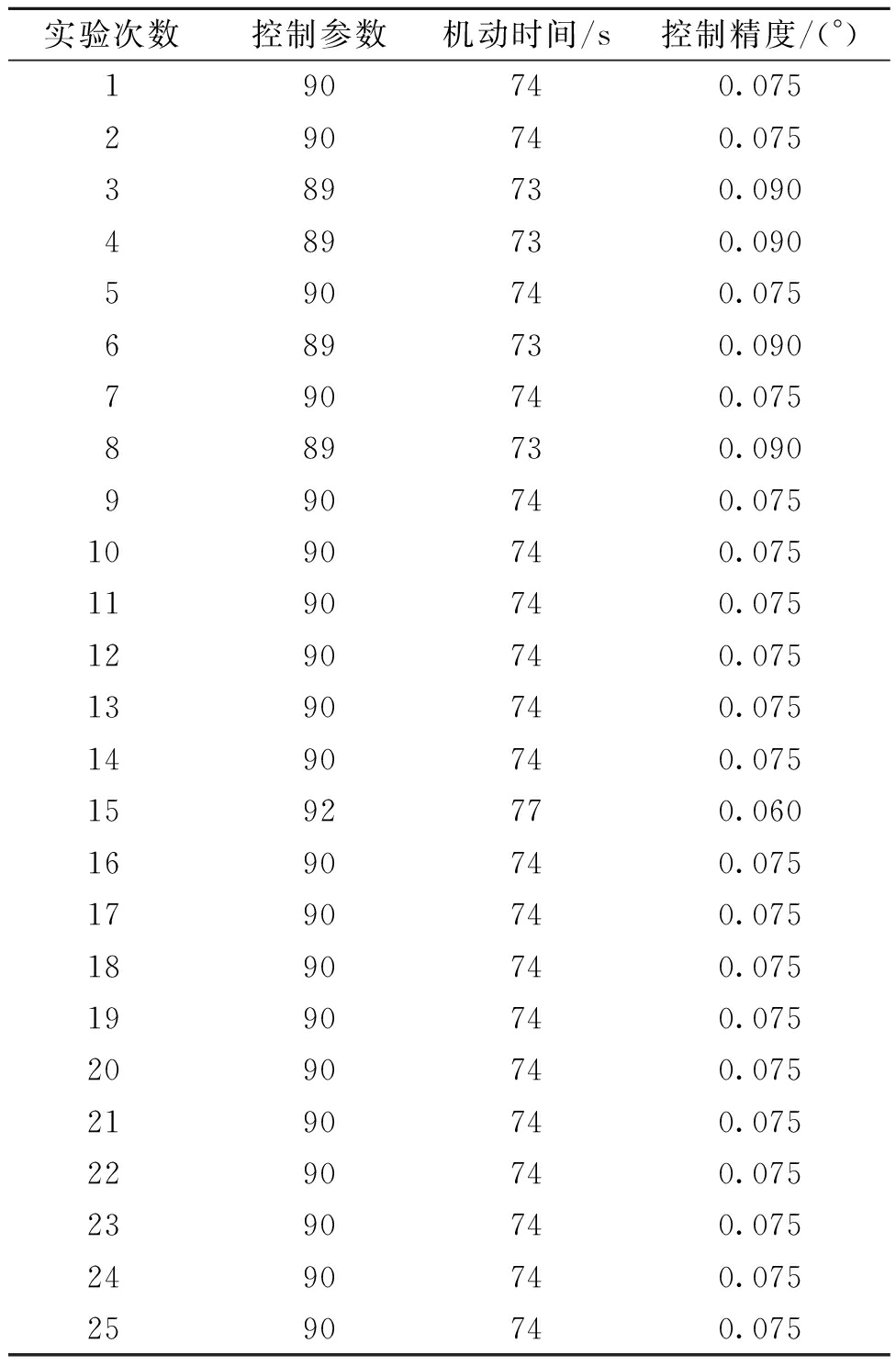
由于遗传算法中交叉和变异的过程是靠选择机制实现结果的趋优，故遗传算法存在随机性.为分析本实验仿真的稳定性，进行了25次仿真实验，实验结果统计如表2所示.由表2可知，经过遗传算法优化迭代得到的控制参数十分近似，机动时间也都在74 s左右，并且控制精度均≤0.1°，具有一定的稳定性.
4 结论
笔者设计了基于遗传算法的变质量特性航天器模型独立姿态控制算法.由仿真结果可知，笔者提出的基于遗传算法的模型独立姿态控制方法相比于模型依赖的递阶饱和控制算法，具有更高的控制精度，机动执行时间缩短，且控制力矩以及姿态角速度均可控制在要求范围内. 综合比较，基于遗传算法的模型独立姿态控制方法更适用于变质量特性航天器，对于在轨服务航天器的姿态控制具有重要意义.
表2 实验结果统计表
Tab.2 Experimental result statistics
实验次数控制参数机动时间/s控制精度/(°)190740.075290740.075389730.090489730.090590740.075689730.090790740.075889730.090990740.0751090740.0751190740.0751290740.0751390740.0751490740.0751592770.0601690740.0751790740.0751890740.0751990740.0752090740.0752190740.0752290740.0752390740.0752490740.0752590740.075
[1] 王晓海.空间在轨服务技术及发展现状与趋势[J].卫星与网络,2016(3):70-76.
[2] 徐文福,何勇,王学谦,等.航天器质量特性参数的在轨辨识方法[J].宇航学报,2010,31(8):1906-1914.
[3] 陈海涛,宋申民.考虑执行器性能约束的刚体航天器鲁棒姿态跟踪控制[J].控制与决策， 2018,34(4):735-742.
[4] WU B L, CAO X B, LI Z X. Multi-objective output-feedback control for microsatellite attitude control: an LMI approach[J]. Acta astronautica, 2009, 64 (11/12):1021-1031.
[5] CHU Z Y, LEI Y A, LI D. Dynamics and robust adaptive control of a deployable boom for a space probe[J]. Acta astronautica,2014,97:138-150.
[6] HUANG G S, UANG H J. Robust adaptive pid tracking control design for uncertain spacecraft systems: a fuzzy approach[J]. IEEE transactions on aerospace and electronic systems, 2006, 42(4): 1506-1514.
[7] 秦靖. 不确定线性奇异摄动系统鲁棒控制研究[D].杭州:浙江大学信息学院,2007.
[8] 周燕茹,曾建平.航天器姿态机动的非线性鲁棒H∞控制方法[J].控制与决策,2017,32(4):625-631.
[9] 袁国平,史小平,李隆.航天器的自适应鲁棒姿态控制器设计[J].系统工程与电子技术,2012,34(12):2524-2528.
[10] 仝西岳,李东旭.基于迭代LMI的航天器的姿态静态输出反馈[J].宇航学报,2007, 28(3):539-544.
[11] YANG X B, GAO H J, SHI P. Robust orbital transfer for low earth orbit spacecraft with small-thrust[J]. Journal of the franklin institute, 2010, 347(10):1863-1887.
[12] 吴云华. 编队飞行卫星相对姿态确定与控制方法研究[D].哈尔滨:哈尔滨工业大学航天学院卫星技术研究所,2006.
[13] 叶东.敏捷卫星姿态快速机动与稳定控制方法研究[D].哈尔滨:哈尔滨工业大学航天学院卫星技术研究所, 2013.
[14] 王峰. 在轨服务航天器对目标逼近过程动力学与控制研究[D]. 哈尔滨:哈尔滨工业大学航天学院卫星技术研究所,2009.
[15] 穆瑞杰.基于遗传算法的地铁车站引导标识布点探析[J].郑州大学学报(工学版),2018,39(1):73-77.
[16] 胡雅博.姿态角速度受限的微小卫星姿态敏捷机动控制方法研究[D].南京:南京航空航天大学航天学院, 2016.