0 引言
遥感影像分类是提取地物信息的重要手段,被广泛应用在专题制图、专题信息提取、动态变化监测和地理空间数据库建设中[1-3]。其中,分类算法是遥感影像研究的重点内容,选择合适的分类算法能够有效地提高分类精度。模糊聚类算法是聚类分析研究的主要算法之一,其中模糊C均值聚类(fuzzy C-means, FCM)算法的应用最为广泛[4-5]。传统的FCM算法存在很多不足,为此研究学者对其进行改进使其适用于遥感影像分类。郝玉等[6]利用直方图选取聚类中心和聚类数并使用叉熵距离代替欧式距离,克服了传统FCM算法选样时的随机性和依赖球状分布的缺点,从而提高了遥感影像分类的精度。谢福鼎等[7]通过改进FCM算法的目标函数和迭代过程,充分发挥了有标签样本点在迭代过程中的作用,实验结果表明,样本点越多,分类精度也越高。但这些改进的FCM算法在对遥感影像进行分类时并没有体现像元间具有相关性、相邻像元间具有相似特征值的依赖关系,只是简单地依据像元特征向量的维数构成特征空间进而对影像进行分类[8]。在这样的特征空间中,像元间的空间特性使得表示不同地物的像元通常是线性不可分的,从而降低了遥感影像的分类精度。为了弥补FCM算法在这方面的不足,史云松等[9]将单个核函数引入到FCM算法对遥感影像进行分类。该算法通过非线性变化关系将像元的特征向量映射到高维空间中,提高了异物像元在特征空间中的线性可分性,从而改善了影像的分类精度。但当遥感数据特征含有异构信息并且在高维特征空间中分布不平坦时,使用单个核函数进行映射处理就不合理了[10-12]。
综上所述,多光谱遥感影像中的像元记录了不同波段的波谱响应强度,在分类时这些波段值组成了像元的特征向量。由于相邻像元间具有相关性,使得相邻异物像元的特征向量在特征空间中常常是线性不可分的。FCM算法进行分类时仅考虑了像元的特征向量,忽略了相邻像元间具有空间关系的特性。引入单个核函数时增加了数据的线性可分性,但单个核函数并不能很好地对具有多个特征的数据进行映射。为了使FCM算法更加适合遥感影像的分类,笔者将多个核函数与FCM算法融合,构建多核模糊C均值算法(multiple kernel fuzzy C-mean, MKFCM)。为了检验MKFCM算法对不同分辨率影像的分类结果,选取郑州市区中高分辨率Landsat8 OLI影像和郑州大学新校区的高分辨率的Pleiades卫星影像对地物进行分类,并与FCM算法、KFCM算法的分类结果进行了对比分析。
1 MKFCM算法原理
FCM算法被研究人员广泛地应用在遥感影像分类中[13-14],它把n个向量xi(i=1,2, 3,…,n)分为c个模糊组,分别计算出每个模糊组的聚类中心,然后利用迭代法使得非相似性指标的价值函数达到最小。代价函数的表达式为:
(1)
式中:uij为隶属度矩阵;指数m为平滑因子,间接影响着聚类的效果; dij=‖xj-vi‖为向量xj与聚类中心vi的距离[15]。
利用拉格朗日乘子法对方程(1)进行求解,得到更新公式为:
(2)
(3)
目前大多数改进的FCM算法在对遥感影像进行分类时并没有考虑到异物相邻像元间具有特殊的空间相关性关系。因此,笔者在FCM算法基础上引入多个核函数建立MKFCM算法,其优点是多核函数通过非线性映射关系将原始数据映射到新的特征空间中。这样不仅可以增强数据的线性可分性,而且也可以将数据的多种特征用不同的核函数进行描述,并能根据数据的分布特点,自动选取最佳权重进行核函数间的组合。本文MKFCM的目标函数为:
(φ(xi)-Vj);
(4)
φ(x)=ω1φ1(x)+ω2φ2(x)+…+ωMφM(x),
(5)
式中:φM为第M个特征映射;M为特征映射的个数及核函数的个数;ωM为第M个核函数的权重值;U为隶属度矩阵;V为聚类中心矩阵。使用拉格朗日乘子法对方程进行求解,得到更新公式为:
(6)
(7)
其中,
![]()
![]()
(8)
αijk=![]()
(9)
式中:f为核函数个数;K为核函数;![]() 为标准化隶属度;ω 为核函数之间的权重值。
为标准化隶属度;ω 为核函数之间的权重值。
在核函数的选择方面,笔者使用高斯函数进行实验,该函数属于鲁棒径向基核。该径向基核对数据有很好的抗噪作用,并且高斯核函数的取值是0~1,有效地简化了计算过程[16]。
2 MKFCM算法应用
2.1 研究区概况
以郑州市区和郑州大学新校区作为研究区域,郑州包括郑州市区和登封、巩义、新密、荥阳、新郑5市和中牟县,总面积达7 446 km2,其中郑州市区面积占1 010.3 km2。郑州大学新校区位于郑州市,校区南北长约2.1 km,东西宽约1.1 km,占地面积约2.31 km2。选取郑州市区2017年12月8日的Landsat8 OLI影像作为地物分类的数据源,如图1(a)所示。为对比不同影像的分类结果,又选取郑州大学新校区2014年5月15日的Pleiades影像融合产品作为地物分类的数据源,如图1(b)所示。

图1 研究区影像图
Figure 1 Image of study area
2.2 研究数据概况
对于Landsat8 OLI影像数据源,选择影像的前6个波段进行实验,分别为蓝波段(0.450~0.515 μm)、绿波段(0.525~0.600 μm)、红波段(0.630~0.680 μm)、近红外波段(0.845~0.885 μm)、短波红外1波段(1.560~1.660 μm)和短波红外2波段(2.100~2.300 μm),空间分辨率30 m×30 m。为了提高影像的质量,需要对研究区的影像进行预处理,主要操作包括辐射定标和大气校正。辐射定标使用ENVI中的Radiometric Calibration工具,大气校正使用Flash工具。由于Landsat8数据在发布前做过基于地形数据的几何校正,因此本研究中不再对研究区域的Landsat8数据进行几何校正操作。Pleiades影像数据源属于SPOT卫星家族的后续卫星,由两颗完全相同的卫星Pleiades 1和Pleiades 2组成,具有0.5 m的超高分辨率,幅宽可达20 km×20 km[17]。选择Pleiades融合影像的3个波段进行实验,分别为蓝波段(0.430~0.550 μm)、绿波段(0.500~0.620 μm)、红波段(0.590~0.710 μm)。
2.3 MKFCM分类结果
采用MATLAB对MKFCM算法进行模型构建。首先,提取待分类遥感影像中的像元特征值,构建特征值矩阵,对于Landsat8影像使用的是band2~band7 6个波段作为特征值,Pleiades影像使用的是红绿蓝3个波段作为特征值。其次,根据实际地物分布状况确定分类类别,郑州市区划分为建筑、植被、水体、裸地、道路5类地物,郑州大学新校区划分为建筑、植被、水体、道路4类地物。再次,对MKCM模型中核函数进行最优化组合,采用梯度下降法进行参数迭代,判断![]() 是否小于停止阈值ε或者迭代次数是否大于最大限制,若符合两条件之一,则停止迭代,最终权值即为核函数之间的最优组合权重。最后,使用组合的最优MKFCM算法对影像进行分类。
是否小于停止阈值ε或者迭代次数是否大于最大限制,若符合两条件之一,则停止迭代,最终权值即为核函数之间的最优组合权重。最后,使用组合的最优MKFCM算法对影像进行分类。
使用FCM、KFCM与MKFCM 3种算法分别对Landsat8影像和Pleiades影像进行分类,分类结果如图2、3所示。

图2 Landsat8影像分类结果
Figure 2 Landsat8 image classification results

图3 Pleiades影像分类结果
Figure 3 Pleiades image classification results
3 精度分析
通过对精度的分析可以有效地评价分类结果的好坏,所以精度评价是遥感分类过程中必不可少的一部分。在验证Landsat8影像的分类结果时,利用高分辨率影像验证低分辨遥感数据的方法[18],选用谷歌高分辨率遥感数据作为验证影像。谷歌影像是目前全球最大的免费影像数据库,可以方便快捷地获取不同时期各个地区的影像数据,在一定程度上给遥感、地信工作者带来许多便利[19]。本研究选取2018年2月22日第18级的影像作为验证影像,该级影像分辨率为0.5 m×0.5 m。该影像包括0~19级,共20级,共选取1 629个验证像元,其中道路323个像元,建筑用地352个像元,水体620个像元,植被127个像元,裸地207个像元。对Pleiades影像分类结果的验证则通过实地勘察测量的方式,在郑州大学新校区中选取2 515个验证像元进行精度检验,其中建筑用地628个像元,水体770个像元,植被644个像元,道路473个像元。
混淆矩阵能够直观展示出每类地物的分类正确率以及该类地物错分为其他地物的情况。对采用不同算法处理不同影像数据得到的分类结果建立混淆矩阵,如表1和表2所示。由于遥感影像上水体与建筑阴影和植被阴影有着相似的光谱特征,道路与建筑用地也有着相似的光谱特征,因此相互之间错分的可能性较高。通过表1的混淆矩阵可知,FCM和KFCM算法对建筑、植被、水体、裸地和道路错分比较严重,特别是与水体光谱特征相似的建筑物的阴影存在大量的错分;MKFCM算法能清晰地将道路、建筑和水体提取出来,并能够正确地区分建筑物的阴影区域,分类效果明显优于FCM算法。而对于表2的混淆矩阵可知,3种算法都能将建筑用地比较明显地提取出来,但FCM与KFCM算法对与水体光谱特征相似的阴面植被存在严重错分的现象,MFKCM算法能将二者正确地区分开来。
表1 郑州市区Landsat8 OLI影像分类的混淆矩阵
Table 1 Confusion matrix of Landsat8 OLI image classification in Zhengzhou urban area
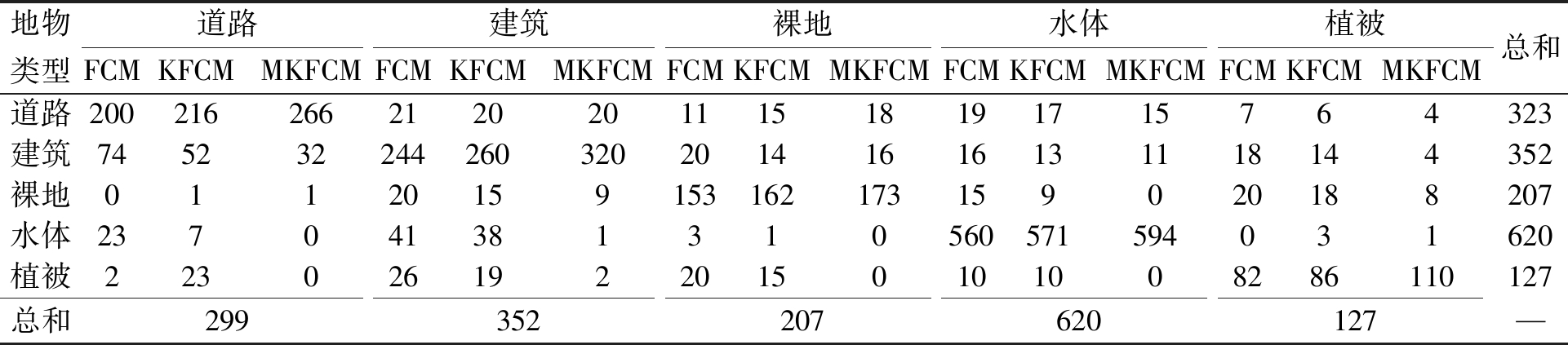
地物类型道路建筑裸地水体植被FCMKFCMMKFCMFCMKFCMMKFCMFCMKFCMMKFCMFCMKFCMMKFCMFCMKFCMMKFCM总和道路200216266212020111518191715764323建筑74523224426032020141616131118144352裸地01120159153162173159020188207水体237041381310560571594031620植被22302619220150101008286110127总和299352207620127—
表2 郑州大学新校区Pleiades影像分类的混淆矩阵
Table 2 Confusion matrix of Pleiades image classification in new campus of Zhengzhou university

地物类型道路建筑水体植被FCMKFCMMKFCMFCMKFCMMKFCMFCMKFCMMKFCMFCMKFCMMKFCM总和道路32035039263483221171111122473建筑96622353255359800018157628水体12151553482360162364015611392770植被222320313026452716498543582644总和450679667683—
为了对分类结果进行精度评价,采用用户精度、生产者精度、总体分类精度和Kappa系数4个评价指标[20]。用户精度和生产者精度评价特定类别的分类精度如图4和图5所示,其中同比增长是指与FCM相比,KFCM、MKFCM分类精度的增长值。采用总体分类精度和Kappa系数评价整体分类结果的精度,如图6所示。
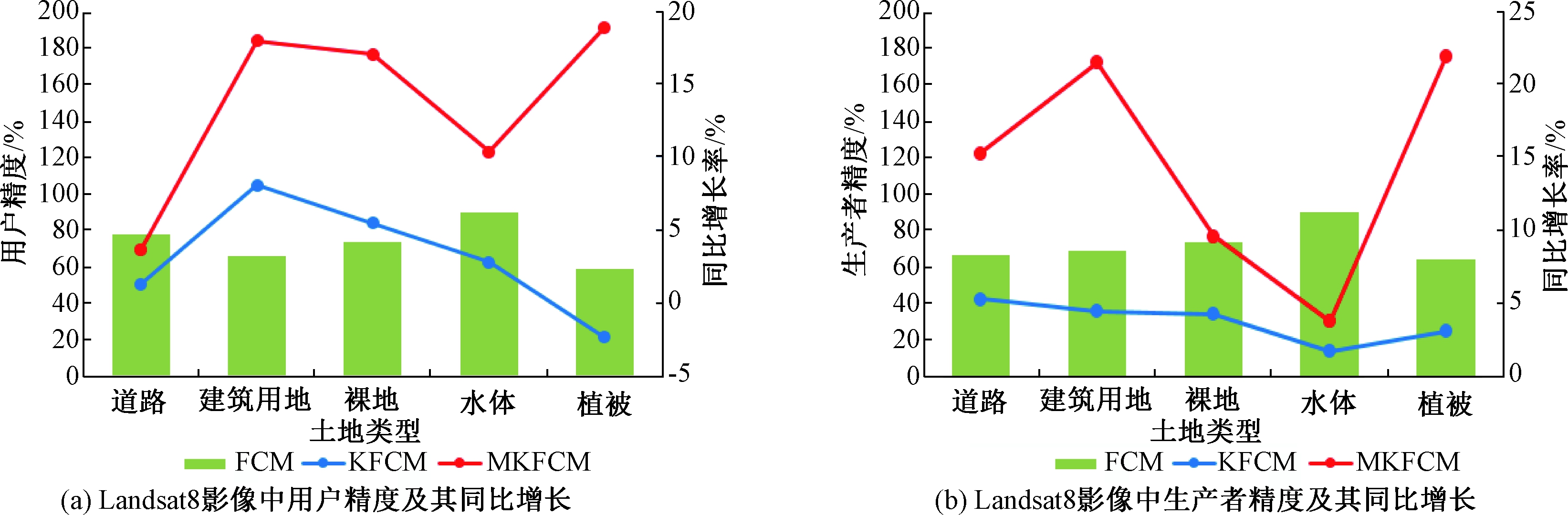
图4 Landsat8影像中MKFCM的用户精度、生产者精度及其同比增长
Figure 4 User accuracy,producer accuracy and growth rate of MKFCM in Landsat8 images
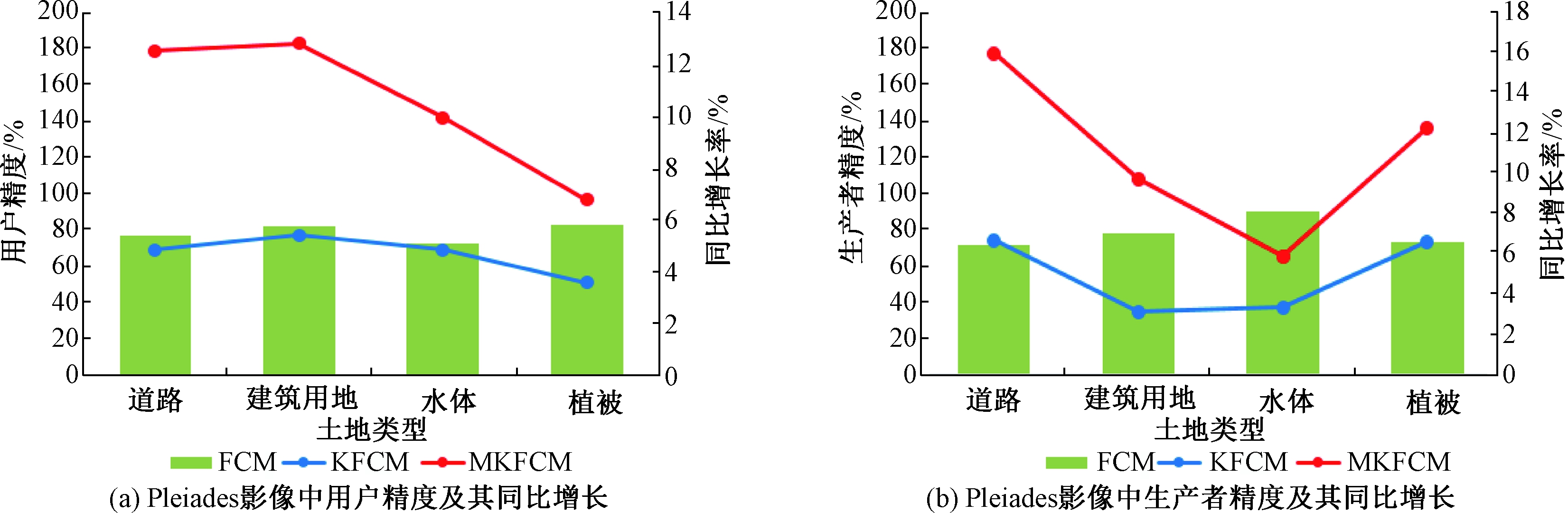
图5 Pleiades影像中MKFCM的用户精度、生产者精度及其同比增长
Figure 5 User accuracy, producer accuracy and growth rate of MKFCM in Pleiades images
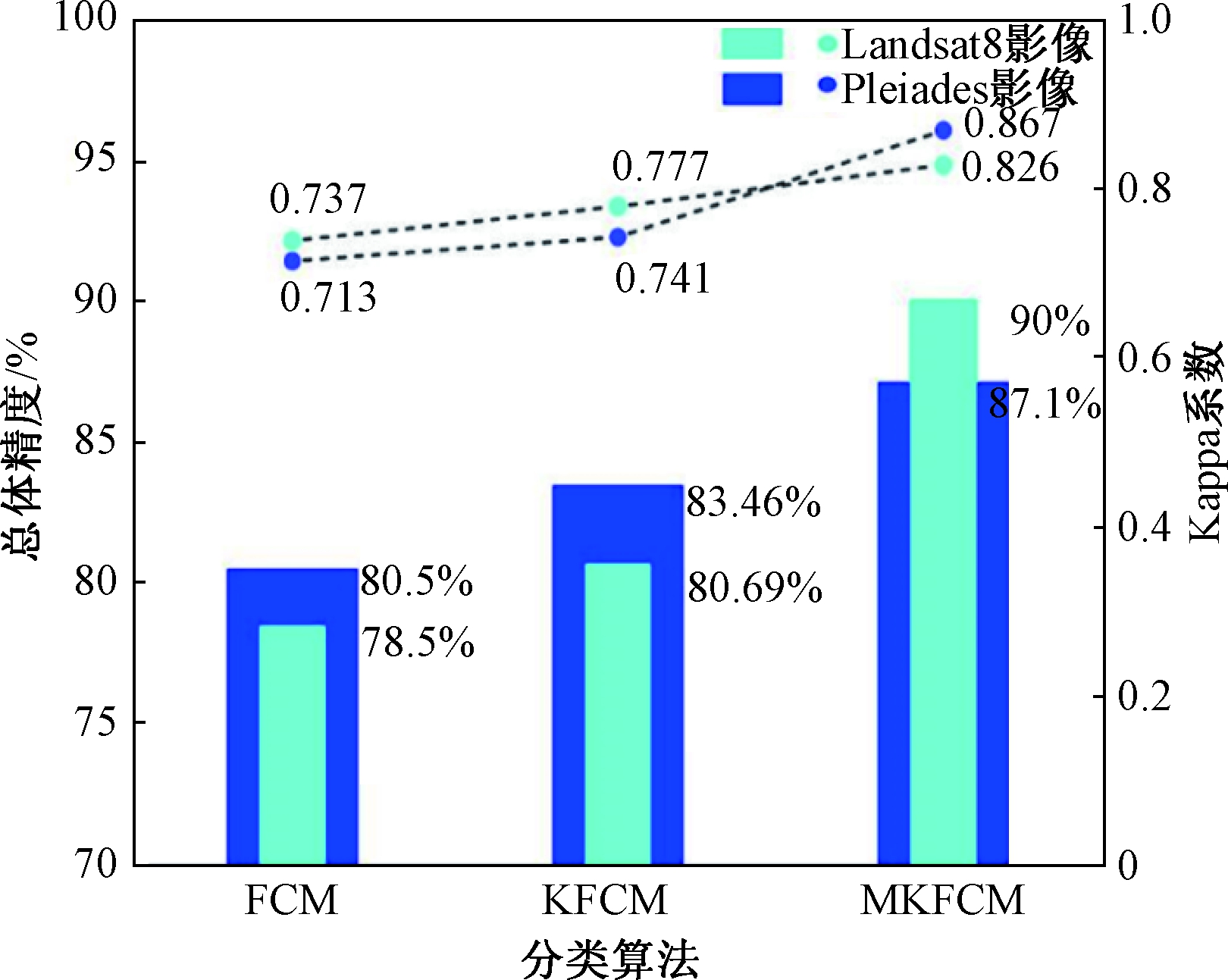
图6 总体分类精度及Kappa系数对比图
Figure 6 Comparison chart of overall classification accuracy and Kappa coefficient
由图4和图5可知,MKFCM算法对两种影像单个地物的分类,无论用户精度还是生产者精度其百分比都很高,且与FCM与KFCM算法的分类结果相比有明显提升。在Landsat8影像中,与其他两种算法相比,MKFCM算法对建筑的分类精度同比增长最多; Pleiades影像中对建筑和道路的分类精度同比增长的最多。这是因为建筑中存在的建筑阴影与水体有着相似的像元特征值,而建筑又与道路有着类似的像元特征值。FCM算法并不能很好地区分具有相似特征值的异物像元,KFCM中只有单个核函数不能对具有多个特征值的像元进行区分,而MKFCM算法不仅能将像元的特征向量通过核函数映射到高维空间中,还能依据多个核函数对不同的特征值进行映射,从而提高了异物像元间的可分性。
由图6可知,在对Landsat8影像分类时,MKFCM比FCM算法总体分类精度提高了11.5%,Kappa系数提高了0.089;与KFCM算法相比,MKFCM算法在总体精度上提高了9.31%,Kappa系数提高了0.049。在对Pleiades影像进行分类时,MKFCM比FCM算法总体精度提高了6.6%,Kappa系数提高了0.15;与KFCM算法相比,MKFCM算法在总体精度上提高了3.64%,Kappa系数提高了0.13。相比之下,MKFCM算法在两种影像的分类上无论是总体分类精度还是Kappa系数都是最佳的。
综上所述,MKFCM算法能通过核函数将原始特征向量映射到高维特征空间中,并根据特征向量在空间中的分布特点自动对核函数进行最优化组合,提高不同类型数据间的线性可分性,从而能区分相似光谱特征的异类地物,尤其是对道路、建筑和植被的分类精度明显提高。
4 结论
将多个核函数与FCM算法融合构建MKFCM算法,不仅能提高遥感影像在特征空间中的线性可分性,而且还能将像元具有的不同特征分量分别输入到对应的核函数进行映射,使像元在组合的特征空间中得到更好地表达,进而提高遥感影像的分类精度。笔者采用FCM、KFCM和MKFCM算法分别对中高分辨率(Landsat8)和高分辨率(Pleiades)遥感影像进行分类,并使用混淆矩阵和4个评价指标对分类精度进行评价。结果表明,MKFCM算法对两种影像的分类结果,无论是单个类别的精度还是整体的分类精度都高于FCM与KFCM算法,尤其对具有相似光谱的像元具有很好的区分效果,提高了土地覆盖信息提取的准确度。
[1] LUNETTA R S, JOHNSON D M, LYON J G, et al. Impacts of imagery temporal frequency on land-cover change detection monitoring[J]. Remote sensing of environment, 2004, 89(4):444-454.
[2] 李爱民,刘杉,吕安民.基于卫星遥感影像的郑州市建成区扩展变化研究[J].郑州大学学报(工学版),2011,32(2):125-128.
[3] 张琪曼. 遥感图像分类方法的研究[J]. 环球人文地理, 2017(2):271.
[4] SPRAGINS J. Learning without a teacher[J]. IEEE transactions on information theory, 1966, 12(2):223-230.
[5] 毛晓波,张勇杰,陈铁军.基于蚁群及空间邻域信息的FCM图像分割方法[J].郑州大学学报(工学版),2014,35(1):1-4.
[6] 郝玉, 徐建华, 周坚华. 一种模糊C均值聚类的影像分类方法[J]. 遥感信息, 2017, 32(3):86-92.
[7] 谢福鼎, 李壮. 基于改进的半监督FCM算法的高光谱遥感影像分类[J]. 测绘通报, 2016(9):60-62.
[8] DHANALAKSHMI L, RANJITHA S, SURESH H N. Image processing using modified multiple kernel fuzzy C-means clustering (MMKFCM) technique[C]// International Conference on Applied and Theoretical Computing and Communication Technology. Bangalore, India: IEEE, 2016:641-646.
[9] 史云松, 史玉峰. 基于核模糊聚类的遥感影像分类[J]. 南京林业大学学报(自然科学版), 2010, 34(6):164-166.
[10] 汪洪桥, 孙富春, 蔡艳宁,等. 多核学习方法[J]. 自动化学报, 2010,36(8):1037-1050.
[11] 何妮蔓. 多核学习算法研究及其在图像分类中的应用[D]. 无锡:江南大学, 2017.
[12] 胡湘萍. 基于多核学习的多特征融合图像分类研究[J]. 计算机工程与应用, 2016, 52(5):194-198.
[13] KIVINEN J, SMOLA A J,WILLIAMSON R C. Online learning with kernels[J]. IEEE transactions on signal processing, 2004, 52(8):2165-2176.
[14] 张子石, 潘聪, 陈红顺. 基于有监督模糊C-均值算法的混合像元分解[J]. 遥感技术与应用, 2009, 24(6):813-817.
[15] WU Z D, XIE W X, YU J P. Fuzzy C-means clustering algorithm based on kernel method[C]// International Conference on Computational Intelligence and Multimedia Applications, 2003.Xi’an, China: IEEE, 2003:49-54.
[16] 焦亚召. 基于多核函数FCM算法在数据挖掘聚类中的应用研究[D]. 昆明:昆明理工大学, 2015.
[17] PINFIELD D J, HODGKIN S T, JAMESON R F, et al. A six-square-degree survey for Pleiades low-mass stars and brown dwarfs[J]. Monthly notices of the royal astronomical society, 2000, 313(2):347-363.
[18] 黄婷, 师庆三, 师庆东,等. 利用高分辨率影像验证低分辨率遥感数据的分类精度研究[J]. 新疆大学学报(自然科学版), 2013, 30(2):238-242.
[19] 李朝奎, 张多才, 陶建军,等. 基于Google影像的城市道路网提取及其应用[J]. 遥感技术与应用, 2012, 27(1):100-105.
[20] 裴欢, 孙天娇, 王晓妍. 基于Landsat 8 OLI影像纹理特征的面向对象土地利用/覆盖分类[J]. 农业工程学报, 2018, 34(2):248-255.