0 引言
生物的感知与认知普遍依赖不同脑区间的相互作用，深入了解多个脑区间的作用关系有助于阐明正常或病理状态下特定脑功能的神经机制[1]。目前对大脑不同脑区间交互性连接关系研究主要有3类分析视角：结构连接、功能性连接和效应性连接。结构连接一般指解剖连接的网络，研究不同的大脑结构之间如何通过直接或间接的神经纤维通路产生相互影响，常采用体内侵入性同位素标记示踪技术或无创的磁共振扩散加权成像方法；功能性连接是指大脑信息处理过程中各区域间的神经活动存在时间上的相关性，通过相关性度量来探究脑区间的功能联系，常用的方法有时域相关、谱相干、锁相值等[2]；效应性连接被定义为一个神经系统对另一个神经系统施加的直接或间接影响，侧重描述大脑各区域间的动态定向相互作用与因果关系[3]。考虑到不同脑区间的交互作用是定向的，效应性连接分析越来越受到研究者的关注，出现了多种典型算法，在使用时应对其原理与特点有所了解，才能合理选择和有效使用。
效应性连接可直接基于指定因果关系的模型估计，也可从数据驱动的角度直接从信号本身估计，其中基于格兰杰因果关系(Granger causality，GC)派生出的一类效应性连接分析的方法得到了广泛应用。代表性算法包括：定向传递函数(directed transfer function，DTF)、直接定向传递函数(direct DTF，dDTF)、偏定向相干(partial directed coherence，PDC)、广义偏定向相干(generalized PDC，GPDC)。在对包括脑电图(electroencephalogram，EEG)、脑磁图(magnetoencephalography，MEG)、局部场电位(local field potential，LFP)、锋电位(spike)、功能磁共振成像(functional magnetic resonance imaging，fMRI)等不同模态与尺度的神经数据分析中取得了良好效果[4-8]。首先对此类常用算法的基本原理及其特点进行了系统介绍，接着对实际应用中的模型拟合、非平稳数据处理、阈值估计等注意事项进行总结，最后以较具代表性的广义正交化的偏定向相干(generalized orthogonalized PDC，GOPDC)算法为例，展示了此类方法的应用效果。
1 方法原理及功能特性
1.1 二元因果连接分析
格兰杰因果的基本思想可追溯到维纳提出的概念[9]：若对时间序列x(t)的预测可以通过纳入时间序列y(t)的信息而得到改进，则表明y(t)会对x(t)产生因果影响。然而维纳的概念缺乏能够实际执行的机制，格兰杰后来在线性回归模型的背景下将该预测思想进行了形式化表示：
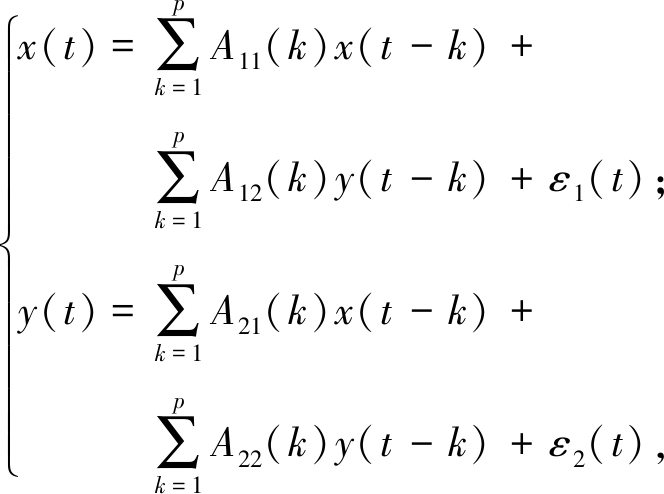
(1)
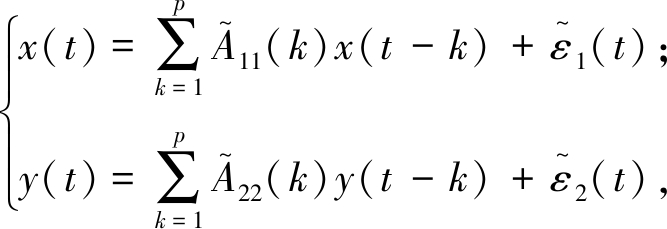
(2)
式中：p为模型阶数；A11、A12、A21、A22和
分别为回归模型式(1)与自回归模型式(2)两种情形下模型中的系数；ε1、ε2和
为这两种情形下模型中各个时间序列对应的预测误差。
与自回归模型(2)中x(t)的误差项相比，若回归模型(1)中x(t)的预测误差项ε1的方差显著减小，则认为时间序列y(t)对x(t)有因果影响。结合式(1)和(2)中误差项的方差可对因果影响进行量化，量化后的值称为格兰杰因果指数GCI(Granger causality index)，可表示为[10]：
(3)
同理也可判断是否存在反方向因果影响的问题。
GCI直接在时域度量因果关系，Geweke首次提出二元情况下的频域格兰杰因果关系。对式(1)两端进行傅里叶变换(Fourier transform，FT)：
(4)
依据式(4)可将两通道间的谱矩阵分解为：
S(w)=H(w)ΣH*(w)，
(5)
式中：Σ为式(1)中二者残差项的协方差矩阵；*表示该矩阵的复共轭转置。
结合式(4)与式(5)将不同频率w下序列y(t)对x(t)产生的因果影响度量定义为[11]：
GCy→x(w)=
(6)
式中：Sxx为序列x(t)自身的功率谱；Σxx=var(ε1(t))，Σyy=var(ε2(t))，二者之间的协方差为Σxy= cov(ε1(t),ε2(t))。
在特定频率w下，若序列y(t)对x(t)无因果影响，则对应序列x(t)自谱成分分解中不包含序列y(t)的影响，GCy→x(w)为0。反之，GCy→x(w)值越大，表明在此频率成分序列y(t)对x(t)的影响越大。同理，可定义序列x(t)对y(t)在不同频率w下产生的因果影响[12]。
1.2 多元因果连接分析
格兰杰因果关系最初只涉及二元概念，格兰杰本人在后续研究中也指出[13]：只有在没有其他变量影响这一二元判定过程的情况下，因果关系原则才成立。然而多通道神经信号之间通常存在复杂的相互作用，对信号进行两两分析无法有效区分直接和间接效应而可能导致错误的结论[14]。为分析多通道神经信号中的整体多元结构，主要采用多变量自回归模型(multivariate autore-gressive，MVAR)解决这一问题。
用p阶MVAR模型表示一组n通道同步记录的信号X(t)=[x1(t),…,xn(t)]T：
(7)
式中：C(r)为滞后r时的系数矩阵,大小为n×n；E(t)∈Rn为一个均值为零的多变量高斯白噪声序列。
系数矩阵C包含的因果耦合信息可以采用时域或频域分析提取，鉴于大脑中普遍存在的节律与振荡活动，以下重点介绍所涉及的频域分析方法。对MVAR模型两端同时进行FT可得到对应关系：
(8)
E(w)=C(w)X(w)，
(9)
X(w)=C-1(w)E(w)=H(w)E(w)，
(10)
式中：I为单位矩阵；H(w)为系统转移矩阵。
基于C(w)或H(w)，国外学者提出了多种具有不同功能特点的多元因果连接分析方法。
1.2.1 DTF
基于MVAR模型中转移矩阵H(w)的性质，Kaminski等[15]在1991年提出了DTF的分析方法：
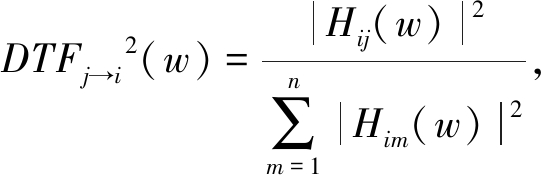
(11)
式(11)为广泛应用的归一化形式的DTF(w)，取值范围为[0,1]。它描述了在频率为w时通道j对通道i产生的影响，从信息传递角度可理解为通道j流入通道i的信息量占所有通道流入通道i信息量的比例。DTF无法区分两通道信号间所有直接与间接因果连接的关系。
1.2.2 dDTF
为区分直接和间接的交互影响，Korzeniewska等[16]在2003年将重新定义的全频定向传递函数(full-frequency DTF，ffDTF)与偏相干(partial coherence，pCOH)相结合提出了dDTF，用于刻画多通道情形下通道间的直接因果连接关系：
dDTFj→i(w)=ffDTFj→i(w)pCOHij(w)。
(12)
ffDTF侧重在全频段分析确定通道j对i在不同频带上施加的因果作用，而pCOH在多通道情况下分析两通道间的无向耦合，排除了其他通道的影响。
1.2.3 PDC
对以上基于DTF及其改进方法的计算过程都需对矩阵求逆，带来的计算精度问题会对结果造成一定影响。2001年Baccala等基于系数矩阵C(w)的角度对pCOH进行因式分解，将pCOH的思想进行扩展提出了PDC分析方法[17]：
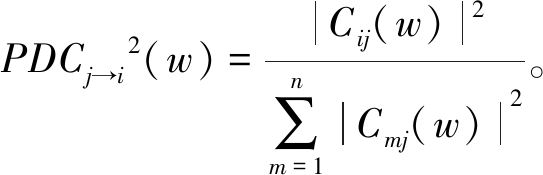
(13)
PDC度量了通道情形下两两通道之间的直接因果连接关系，从信息传递角度可理解为从通道j流出到通道i的信息量占通道j所有流出信息量的比例。
1.2.4 GPDC
考虑到不同通道间数据幅度量级不同，或由信噪比不同造成模型拟合后各通道误差项处于幅度量级不同时，PDC值会受到较大影响。
等[18]为改善该问题在2007年提出了GPDC分析方法：
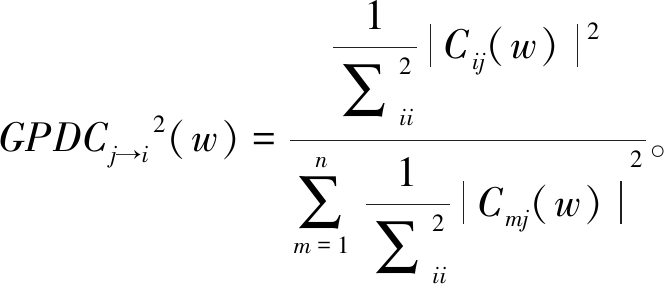
(14)
GPDC通过引入目标通道对应的误差方差项进行量级的规范，大大改善了PDC的性能，成为多元因果连接分析方法中的代表。
1.2.5 GOPDC
当采用以上方法对神经信号分析时，不可避免会受到容积传导效应的影响，多个潜在的信号源因距离或传导介质差异会导致各通道不同程度的混叠，MVAR模型参数对这种潜在的涂抹效应较敏感，可能导致电极间出现虚假连接[19]。研究表明:这种虚假连接能通过正交化信号功率进行消除，而且谱相干方法中虚部不受容积传导伪迹的影响[20]。Omidvarnia等[21]结合这两种处理方式在2014年对PDC作出了进一步改进，提出正交化的偏定向相干(orthogonalized PDC，OPDC)，并借鉴GPDC推导，进一步提出了GOPDC。
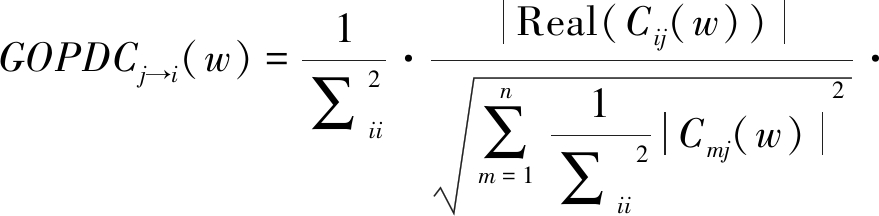
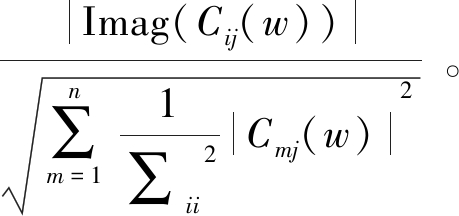
(15)
该方法是在MVAR模型参数水平上进行正交化，Omidvarnia通过模型仿真进行方法对比，结果表明，GOPDC在减轻容积传导效应伪迹影响的同时，仍能抑制由通道误差项幅度量级不同而产生的影响。
2 实际应用需考虑的问题
实际应用中，模型拟合、非平稳数据的分析和非零值对应阈值的估计是需要注意的问题。
2.1 模型拟合
2.1.1 数据平稳性判断
以上因果连接分析方法均要求数据为“弱平稳”或协方差平稳[22]，对数据平稳性一般采取单位根检验。但由于最终目的是用数据拟合对应的模型，因此数据拟合的角度更适用，首先要求MVAR模型中系数矩阵C平方可和[23]：
(16)
若MVAR模型系数矩阵C进一步满足[24]：
(17)
将此条件进一步简化可表示为：
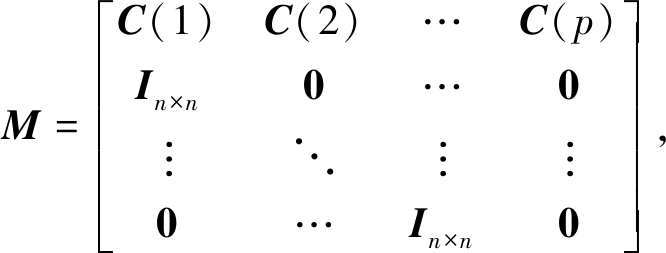
(18)
式(18)中矩阵M为系数矩阵C的增广矩阵。
若矩阵M所有特征值的模均小于1，则认为模型系数表征了协方差平稳的过程。在M的构造过程中涉及模型系数矩阵C的求取，目前对MVAR模型系数矩阵C及误差协方差Σ的估计算法较多，其中，Nuttall-Strand方法在不同数据集上均表现更好[25]。
2.1.2 模型阶数选择
MVAR模型阶数p的选取非常重要，若p过小，模型不足以包含原数据的信息，反之会增加计算量，同时也易造成过拟合。最优阶数的选取常常依据一些常用的准则，包括Akaike信息准则(Akaike information criterion，AIC)与贝叶斯信息准则(Bayesian information criterion，BIC)。已有研究表明，BIC准则比AIC准则更适合时间序列分析[22]。此外，估计理论要求已知样本数量大于待估计未知参数数量[26]，因此p也存在上限，假设所分析数据的长度为L，则要求nL≥n2p；否则MVAR模型参数估计误差将增大，导致模型合理性检验不能通过。
2.1.3 模型合理性检验
模型合理性检验是为确定选定阶数后的模型是否对原数据进行充分地拟合，一般从一致性、稳定性和残差白噪声性三方面进行检验。
模型一致性检验描述了原数据中所存在的相关结构能被模型表征的程度[27]，对原始数据和模型产生的数据的所有通道分别做自相关与互相关处理，用Rr和Rs分别表示真实数据和模型产生数据得出的相关性向量，则一致性百分比可表示为：
(19)
当PC值大于80%时，表示模型充分体现了原始数据的相关结构[23]。
模型稳定性与数据平稳性判断中所要求的条件相同，若系数矩阵C构成的增广矩阵M所有特征值的绝对值均小于1，则认为拟合模型稳定。
模型残差白噪声检验的目的是为了判断模型残差中是否仍存在一些未被描述的相关结构，若模型充分拟合了原始数据，则残差项间近似于白噪声。一般采用Durbin-Watson统计检验[28]对模型的残差E(t)进行相关性判断。
以上三方面的检验均满足的情况下，由数据所拟合的MVAR模型才可用于下一步的因果分析。
2.2 非平稳数据处理
实际应用中EEG、LFP等神经数据多是高度非平稳的，且与脑区间因果连接关系的变化有关[22]，而对数据进行“平稳化”操作的方式往往会破坏其中所蕴含的结构，得出的结果往往与所采取的处理方式有关，具有一定的虚假性。为研究非平稳数据中所蕴含的时变因果连接变化，目前时变MVAR模型已成为主流，其中应用较广泛的两种方式包括[29]：数据截段滑窗法和状态空间法。
数据截段滑窗法最早由Ding等[27]在2000年提出，主要策略是认为原数据在足够小的时间窗口内近似平稳，从而对原数据进行高度重叠的窗口截段，可从这些高度重叠的数据段内得到随时间变化的系数矩阵C等其他参数，进而得到随时间变化的因果连接关系的度量。该方法需要考虑数据窗口大小的选择，一般依据以下4个原则进行折中[30]：
(1)数据截段的同时保证窗口内数据局部平稳；
(2)数据截段重叠滑窗本质上为时域平滑操作，窗口大小选择应在考虑平滑性的同时保留原数据中动态变化的特征；
(3)保证已知数据的数量大于模型中所需估计未知参数的数量；
(4)数据段对应的时间间隔需大于生理意义下该过程动态变化所预期的最大时间间隔。
状态空间法从参数自适应估计角度出发，对数据是否平稳并无要求，其实质是将时变MVAR模型参数用状态空间形式进行表示，然后结合数据采用卡尔曼滤波算法进行参数自适应估计。Wan等[31]在2003年提出的对偶扩展卡尔曼滤波(dual extended Kalman filter，DEKF)算法实现了上述过程，该方法采用了两个相互交错的状态空间方程，分别用于系统状态估计和参数估计，详细推导过程可见Omidvarnia等[32]2011年发表的论文。采用状态空间方法可估计出时变MVAR模型中不同时刻的系数矩阵C等参数，由此推导出的多种时变因果连接关系度量更能体现连接关系的瞬时变化。
2.3 阈值估计问题
实际应用中的干扰因素会导致不存在真正相互作用的通道间的因果连接度量在某些频率上出现非零情况，因此估计不同频率下因果连接关系度量阈值具有十分重要的现实意义。
阈值估计一般通过统计检验方法来解决，首先，基于无相互因果作用的零假设，计算通道间不同频率下的因果连接关系值的经验分布，然后根据得出的置信区间上限确定出所需阈值，其中基于原数据生成替代数据来确定阈值是国内外学者广泛采用的方式。由于不同通道间因果连接关系的存在与其相位有关，生成替代数据的基本思想是将原数据对应的相位随机化，即破坏原数据间相位的依赖关系[33]。替代数据的生成步骤主要包括：①将原数据FT转换到频域；②对各频率对应的相频部分施加随机扰动；③通过傅里叶逆变换得到替代数据。替代数据产生方式因牵涉到傅里叶变换也被称为FT surrogate，其产生的替代数据仅打乱了原数据间的相位信息，但同时保留了时域和幅频特征，十分适合因果连接阈值估计。
考虑到非任务态与任务态脑活动中存在因果连接模式的区别，利用两种状态下通道间因果连接关系在统计意义上的差异性程度也可达到去阈值的效果[21]。该方式比FT surrogate所需的计算量少，且可以消除因大脑自发活动产生的因果连接关系的影响，并突出差异部分，去阈值效果更好，但该方式的应用受限于实验范式中对照组的设置，其通用性不如FT surrogate方法。
3 实际数据集应用
算法示例选择来自于Delorme等[34] 2002年研究视觉处理过程中脑电动力学变化的EEG数据，随机抽选5位受试者看到图像中包含动物并作出正确反应时的脑电数据，依据文中确定的偶极子空间位置及生理视觉通路相关信息，选取F3、C3、T5、O1、F4、C4、T6、O2共8个通道来研究图片刺激后脑区间的信息交互关系。对数据进行去基线漂移、去工频干扰等操作并剔除眼动干扰试次，选择受试者各自反应时间相对集中的试次(反应时间为0.3～0.4 s，每位受试者平均约85个试次)，分别截取刺激前后各0.3 s的数据进行分析，其中前0.3 s数据作为对照组用于阈值的估计。采用GOPDC方法进行数据分析，其中时变MVAR模型中参数的估计采用DEKF算法，模型阶数依据BIC准则进行确定，5位受试者所有试次的平均结果如图1所示。
图1 基于GOPDC的5位受试者的平均结果
Figure 1 Average results for 5 subjects based on GOPDC
从图1的结果中可看出，基于DEKF方式的时变GOPDC能够捕获非平稳脑电信号间的动态交互变化，并具有良好的时频分辨率。可以看到，在图像呈现后，主要是额叶与顶叶对颞叶和枕区产生因果影响，这与生理上视觉通路信息的传递机制相符。此外容积传导所产生的影响一般在3 Hz以下[26]，从图中可以看到3 Hz以下部分均未产生容积传导中伪迹的影响。结果表明：采用GOPDC方法能够有效地削弱这种影响，且所确定的交互频段集中在θ频段，与Delorme等采用信号独立成分建立的等价偶极子模型确定的频段相符。
4 结束语
对格兰杰因果关系引申出的常用效应性连接分析方法进行了概述，分别阐明了这些常用方法的优缺点及其在因果连接关系度量中的意义。
对于实际应用中MVAR模型拟合的相关问题，分别从数据平稳性的判断、模型阶数的选择、拟合后模型合理性验证3个互相联系的方面对需注意的要点进行概述，并建议从模型拟合的角度进行数据平稳性的判断。一般选用BIC准则进行模型阶数的选择，分别从模型一致性、平稳性和残差白噪声性等3个方面进行模型合理性验证。针对非平稳数据的处理，建议采用时变MVAR模型分析非平稳数据中所蕴含的因果连接关系。针对数据截段滑窗法和状态空间法这两种常用的时变MVAR模型参数估计方式，给出数据截段滑窗法中窗长的选择原则，并指出状态空间法在数据处理和时域解析度上的优势。最后，关于因果连接分析中必须解决的阈值估计问题，对于无对照组的实验建议采用国内外学者广泛使用的FT surrogate方式，而在有对照组的实验中建议根据任务态与非任务态的差异进行阈值估计。
在实际EEG数据的应用示例中，采用基于DEKF方式的时变GOPDC方法进行分析，结果证实了该方法能减轻容积传导效应中伪迹的影响。
[1] HÖLLER Y, BUTZ K, THOMSCHEWSKI A, et al. Reliability of EEG interactions differs between measures and is specific for neurological diseases[J]. Frontiers in human neuroscience, 2017, 11: 350.
[2] DUFF E P, MAKIN T, COTTAAR M, et al. Disambiguating brain functional connectivity[J]. Neuroimage, 2018, 173: 540-550.
[3] NAKAGAWA T, DECO G. Multiscale brain connec-tivity[M]. New York: Springer, 2015.
[4] 张立伟,周前祥,柳忠起,等.基于因果关系的步枪射击pre-shot阶段脑电网络分析[J].生物医学工程学杂志,2018,35(4): 518-523.
[5] GRA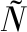
A M, OZAETA L, CHYZHYK D. Resting state effective connectivity allows auditory hallucination discrimination[J]. International journal of neural systems, 2017, 27(5): 1750019.
[6] XU X, ZHANG Q, TIAN X, et al. Sevoflurane anesthesia induces neither contextual fear memory impairment nor alterations in local population connectivity of medial prefrontal cortex local field potentials networks in aged rats[J]. Fundamental & clinical phar-macology, 2016, 30(4): 338-346.
[7] HU M, LI W, LIANG H. A copula-based Granger causality measure for the analysis of neural spike train data[J]. IEEE/ACM transactions on computational biology & bioinformatics, 2018, 15(2)：562-569.
[8] SOHRABPOUR A, YE S, WORRELL G A, et al. Noninvasive electromagnetic source imaging and Granger causality analysis: an electrophysiological connectome (eConnectome) approach[J]. IEEE transactions on biomedical engineering, 2016, 63(12): 2474-2487.
[9] WU X Q, WANG W H, ZHENG W X. Inferring topologies of complex networks with hidden variables[J]. Physical review E: statistical nonlinear & soft matter physics, 2012, 86(4): 046106.
[10] HESSE W, MOLLER E, ARNOLD M, et al. The use of time-variant EEG Granger causality for inspecting directed interdependencies of neural assemblies[J]. Journal of neuroscience methods, 2003, 124(1): 27-44.
[11] BASTOS A M, SCHOFFELEN J M. A tutorial review of functional connectivity analysis methods and their interpretational pitfalls[J]. Frontiers in systems neuroscience, 2016, 9: 175.
[12] DING M, CHEN Y, BRESSLER S L. Granger causality: basic theory and application to neuroscience[EB/OL]. (2006-08-23)[2019-05-20].https://arxiv.org/abs/q-bio/0608035.
[13] BLINOWSKA K J. Review of the methods of determination of directed connectivity from multichannel data[J]. Medical & biological engineering & computing, 2011, 49(5): 521-529.
[14] KUS R, KAMINSKI M, BLINOWSKA K J. Determination of EEG activity propagation: pair-wise versus multichannel estimate[J]. IEEE transactions on biomedical engineering, 2004, 51(9): 1501-1510.
[15] KAMINSKI M J, BLINOWSKA K J. A new method of the description of the information flow in the brain structures[J]. Biological cybernetics, 1991, 65(3): 203-210.
[16] KORZENIEWSKA A, 
M, et al. Determination of information flow direction among brain structures by a modified directed transfer function (dDTF) method[J]. Journal of neuroscience methods, 2003, 125(1/2): 195-207.
[17] BACCAL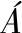
L A, SAMESHIMA K. Partial directed coherence: a new concept in neural structure determination[J]. Biological cybernetics, 2001, 84(6): 463-474.
[18] BACCAL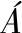 L A, SAMESHIMA K, TAKAHASHI D Y. Generalized partial directed coherence[C]//Proceedings of the 2007 15th International Conference on Digital Signal Processing. Cardiff，Wales, UK: IEEE, 2007: 163-166.
[19] ANZOLIN A, PRESTI P, VAN DE STEEN F, et al. Effect of head volume conduction on directed connectivity estimated between reconstructed EEG sources[EB/OL]. (2018-01-22)[2019-05-20].https://www.biorxiv.org/content/biorxiv/early/2018/01/22/251223.1.full.pdf.
[20] HIPP J F, HAWELLEK D J, CORBETTA M, et al. Large-scale cortical correlation structure of spontaneous oscillatory activity[J]. Nature neuroscience, 2012, 15(6): 884.
[21] OMIDVARNIA A, AZEMI G, BOASHASH B, et al. Measuring time-varying information flow in scalp EEG signals: orthogonalized partial directed coherence[J]. IEEE transactions on biomedical engineering, 2014, 61(3): 680-693.
[22] SETH A K. A MATLAB toolbox for Granger causal connectivity analysis[J]. Journal of neuroscience methods, 2010, 186(2): 262-273.
[23] BARNETT L, SETH A K. The MVGC multivariate Granger causality toolbox: a new approach to Granger-causal inference[J]. Journal of neuroscience methods, 2014, 223: 50-68.
[24] SCHELTER B, TIMMER J, EICHLER M. Assessing the strength of directed influences among neural signals using renormalized partial directed coherence[J]. Journal of neuroscience methods, 2009, 179(1): 121-130.
[25] SCHLÖGL A. A comparison of multivariate autoregressive estimators[J]. Signal processing, 2006, 86(9): 2426-2429.
[26] SHAW L, MISHRA S, ROUTRAY A. Generalised orthogonal partial directed coherence as a measure of neural information flow during meditation[C]// GUPTA S，BAG S, GANGULY K, et al.Advance-ments of Medical Electronics: Proceedings of the First International Conference, ICAME, Berlin: Springer, 2015: 137-148.
[27] DING M Z, BRESSLER S L, YANG W M, et al. Short-window spectral analysis of cortical event-related potentials by adaptive multivariate autoregressive modeling: data preprocessing, model validation, and variability assessment[J]. Biological cybernetics, 2000, 83(1): 35-45.
[28] SETH A K, CHORLEY P, BARNETT L C. Granger causality analysis of fMRI BOLD signals is invariant to hemodynamic convolution but not downsampling[J]. Neuroimage, 2013, 65: 540-555.
[29] CEKIC S, GRANDJEAN D, RENAUD O. Time, frequency, and time-varying granger-causality measures in neuroscience[J]. Statistics in medicine, 2018, 37(11): 1910-1931.
[30] DARVISHI M J, NASRABADI A M, CURRAN T. Effective connectivity measuring of ERP signals in recognition memory process by generalized partial directed coherence[C]//Proceedings of the 2016 23rd Iranian Conference on Biomedical Engineering and 2016 1st International Iranian Conference on Biomedical Engineering (ICBME). Tehran, Iran : IEEE, 2017: 64-68.
[31] WAN E A, NELSON A T. Dual extended Kalman filter methods[M]//HAYKIN S. Kalman Filtering and Neural Networks. New York: John Wiley & Sons, 2003.
[32] OMIDVARNIA A H, MESBAH M, KHLIF M S, et al. Kalman filter-based time-varying cortical connectivity analysis of newborn EEG[C]//Proceedings of the 2011 Annual International Conference of the IEEE Engineering in Medicine and Biology Society. Boston, MA: IEEE, 2011: 1423-1426.
[33] FAES L, PORTA A, NOLLO G. Testing frequency-domain causality in multivariate time series[J]. IEEE transactions on biomedical engineering, 2010, 57(8): 1897-1906.
[34] DELORME A, MAKEIG S, FABRE-THORPE M, et al. From single-trial EEG to brain area dynamics[J]. Neurocomputing, 2002, 44/45/46: 1057-1064.