0 引言
铁路信号系统是整个铁路安全运营的大脑，承担着保障列车安全运行的重任。国外在铁路信号安全领域已自成体系，并制定相关标准。我国铁路信号相关安全标准是在借鉴欧标的基础上形成的，与国际上安全风险评价技术还存在差距。其原因是维修资料少、数据利用率低。常用的风险分析方法无法满足铁路信号设备风险分析的需求。如王艺霏[1]通过对轨道电路载频分析，进行故障判断，但其故障影响因素众多，无法全面反映轨道电路的故障特性；杨杰[2]利用故障树分析法对轨道电路安全性与可靠性进行研究，与实际检修联系不够紧密；陈星[3]基于FCM方法对轨道电路故障进行研究,但其数据来源仅来自微机监测，数据单一；豆晓东[4]基于RBM的方法来分析轨道电路的预防性维修，存在着数据匮乏、划分不够精细、缺乏对各故障事件之间的关系识别。
而灰色系统理论可以很好地解决数据贫瘠、不确定性的问题[5]。灰色系统理论可以通过对“有限”信息的挖掘，提取重要的信息，实现对运行系统行为的正确描述，即灰理论着重研究“外延明确而内涵不明确的对象”。灰色系统理论的优点很好地克服了铁路信号系统少数据、贫信息以及基本故障数据较难获得等缺陷。
笔者在FMECA的基础上，结合模糊数理论的特点，提出了基于灰理论的风险优先级综合评价法，并应用于ZPW-2000A轨道电路设备单元风险分析中。
1 基于模糊灰理论的风险优先级(RPN)综合评价
风险优先级指数(risk priority number,RPN)是严重度(severity)、发生度(occurrence)、检测度(detection)的乘积，而这3个指标由专家根据严重度、发生度、检测度等级表给出，这就带有很大的主观不确定性，很可能因为专家经验的不同导致得出的风险水平与实际不符。因此，本文提出了基于模糊灰理论的风险优先级综合评价法。
1.1 传统的风险优先级指数分析法
传统的风险优先级指数分析法流程如下:
(1)对设备作故障模式影响分析(FMEA)；
(2)确定故障模式的严重度(S)、发生度(O)、检测度(D)；
(3)将严重度(S)、发生度(O)、检测度(D)3者相乘计算求得故障模式的风险优先级指数；
(4)将风险优先级指数进行排序,风险优先级指数越大风险就越大。
然而这种方法存在几个问题，首先，S、O、D的确定主观成分太大，不同的专家可能会给出不同的值；其次，S、O、D的简单相乘可能会得到相同的风险优先级指数，这与实际风险水平不符。S、O、D的等级范围为1～10，它们的排列组合共有1 000种，但它们的积只有120个不同的值，因此这样计算的风险优先级指数有着大量的重复，比如80=2×8×5=4×4×5，虽然风险优先级指数相同，但风险程度明显不同，如果在风险排序中把这两种情况同等对待，显然不合理。
1.2 基于模糊灰理论的风险优先级综合评价法
基于模糊灰理论的风险优先级综合评价法流程如下:
(1)系统各部件作FMEA分析；
(2)参照欧洲EN50126标准对严重度、发生度、检测度的描述进行模糊等级的划分；
(3)按步骤(2)划分的模糊等级确定系统各故障模式的严重度、发生度、检测度；
(4)对各模糊等级进行反模糊化处理，得到模糊脆性系数；
(5)通过灰理论求出S、O、D系数，依据变权综合原理求取各系数的权重，将各关联系数与对应的权重相乘，再将各乘积求和从而得到风险优先级指数；
(6)对风险优先级指数排序，并对较大的RPN采取一定的预防措施，降低设备的风险。基于灰理论的风险优先级综合评价流程图如图1所示。
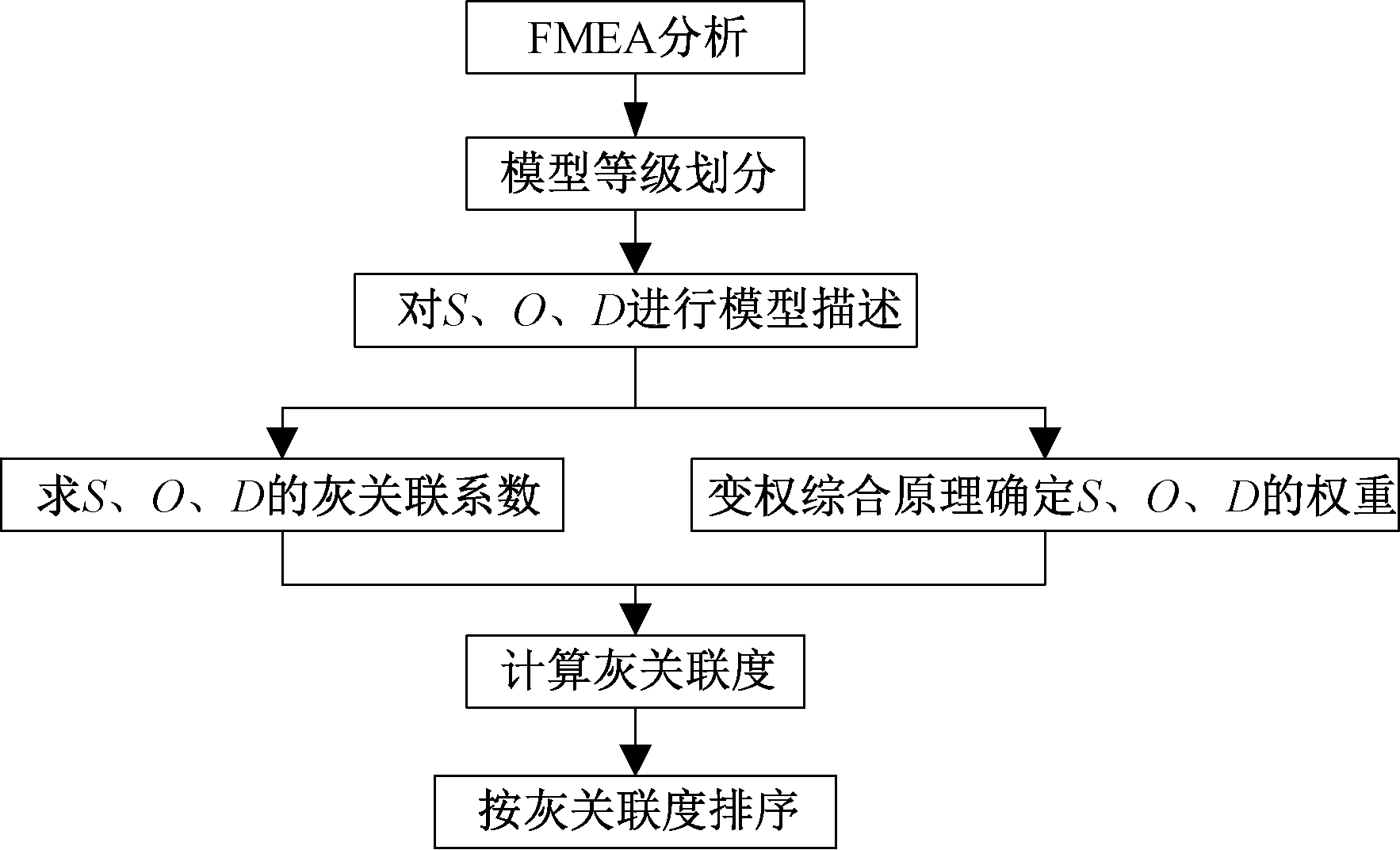
图1 灰RPN评价流程
Figure 1 Grey RPN evaluation process
1.3 模糊等级划分及模糊等级的反模糊化
依据文献[6]，常规风险优先级指数各指标等级如表1所示。
表1 严重度、发生度、检测度等级划分
Table 1 The classification of severity, occurrence and detection
等级严重度发生度检测度描述标准描述标准描述标准1很低不足以导致人员伤害较低不太可能发生很高大部分都能检测到2低故障引起人员轻度伤害低在寿命期某时可能发生高基本可以检测3高故障引起人员严重伤害高发生多次,危害经常出现低偶尔能检测到4很高故障造成人员死亡较高频繁的出现很低几乎不能检测到
采用文献[7]的三角模糊隶属度函数法，将模糊语义分别描述为很低、较低、低、中等、高、较高、很高。其模糊隶属度函数如图2所示。
通过对图2中的7个模糊语义反模糊化运算，求得反模糊脆性系数K(X)[8]。
(1)
式中：c=0为隶属度函数的起点；d=13为隶属度函数的最大值；a0为每个模糊语义所对应的下边界；b0为每个模糊语义所对应的上边界；而ai=bi对应模糊语义的中间值。
以模糊语义“较低”为例，由上图可知，a0=2，
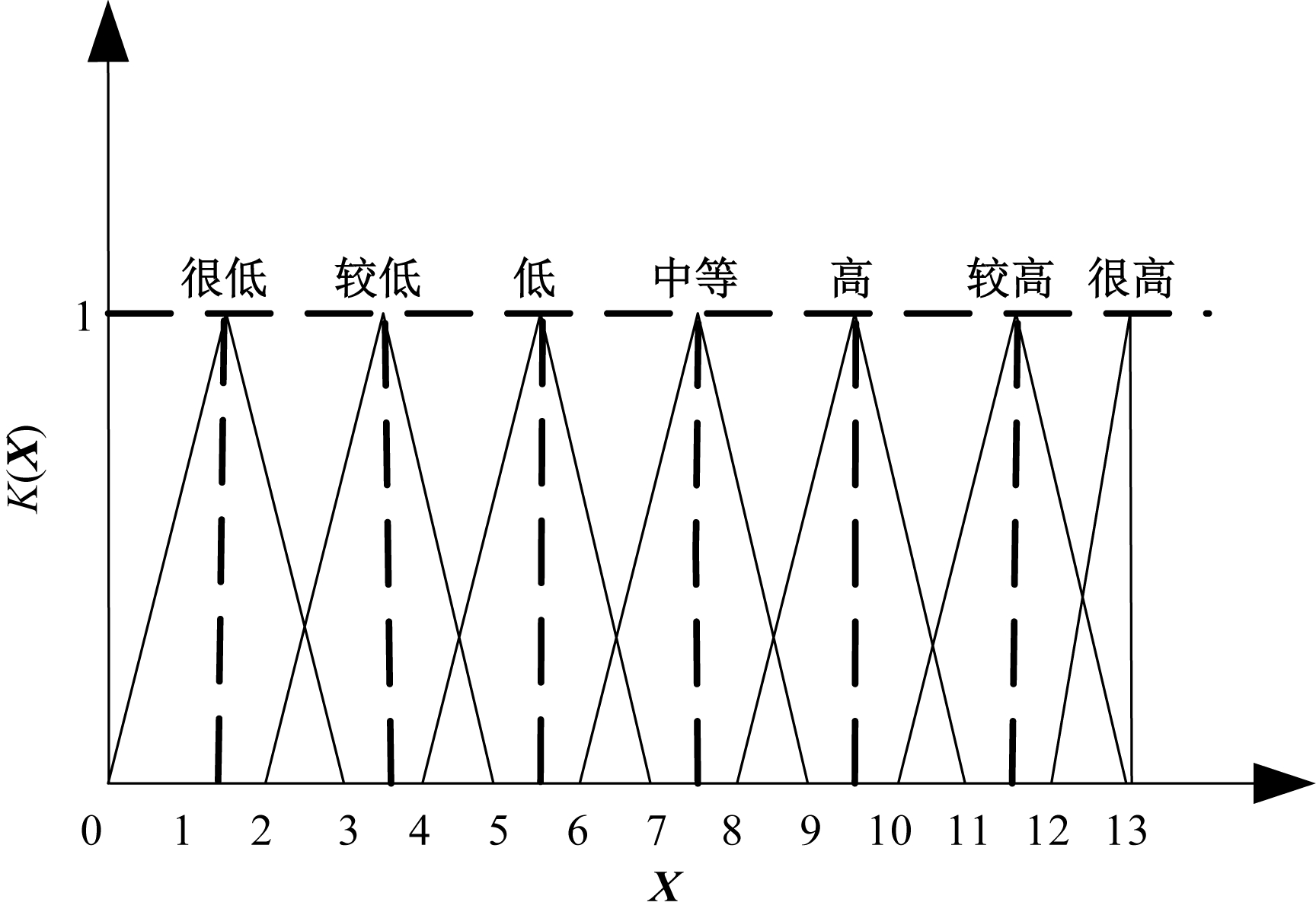
图2 模糊隶属度函数
Figure 2 Membership function
b0=5，a1=b1=3.5，c=0，d=13, 代入式(1)有K(X)=0.293；同样的方法，可以计算出其他反模糊脆性系数，具体数据如表2所示。
表2 反模糊脆性系数
Table 2 Anti fuzzy brittleness coefficient
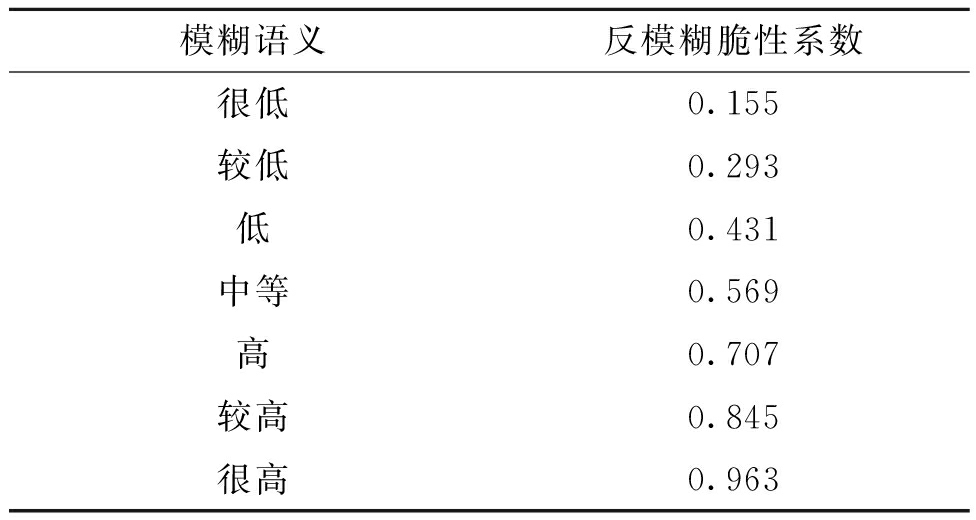
模糊语义反模糊脆性系数很低0.155较低0.293低0.431中等0.569高0.707较高0.845很高0.963
1.4 变权综合原理
变权综合原理的方法既考虑到各基本要素的重要程度,又考虑了要素的目标值。这两方面的优势同时体现在可变的权重中[9-10]。
定义1 作映射
S:[0,1]m→[0,1]m,X→S(X)=
(S1(X),…,Sm(X)),
其中，X是变权的要素，S(X)是m维惩罚型变权向量(即变权权重)，若满足如下公理：
(1)xi≥xj→Si(X)≤Sj(X);
(2)Sj(X)(j=1,2…,m)对每个变元连续;
(3)对任何常权向量W=(w1,…,wm),则称式(2)为变权公式：
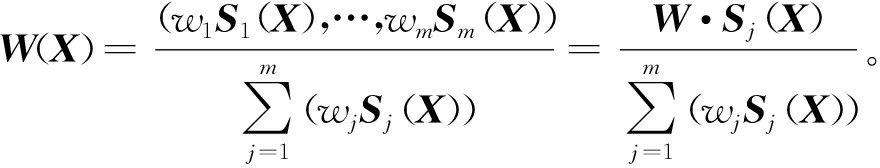
(2)
如果xi≥xj→Si(X)≥Sj(X)，则S为激励型变权。由于状态变权向量构造形式的多样化,可以得到不同的变权公式：
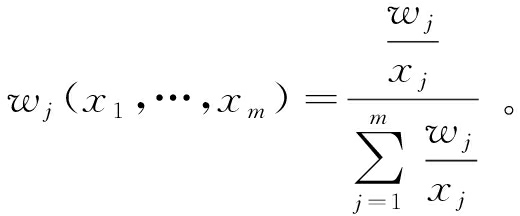
(3)
状态变权向量
在此基础上，将均衡函数
0)引入到变权综合中，此时
因此，可得到意义更明确的变权公式：
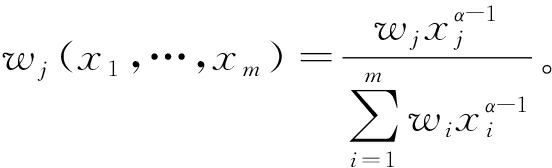
(4)
本文中，(x1,…，xm)常权wj=1/3,当0≤α<1时，wj(x1,…，xm)为负指数函数，每个变元xj满足惩罚性；当α>1时，wj(x1,…，xm)为正指数函数，关于每个变元xj满足激励性。我们需要根据实际数据对S、O、D 3个变量进行权重的增加或者惩罚。
1.5 灰关联系数法
灰关联法是灰理论重要方法之一，它依据系统内各因素间相同或相异程度来衡量各因素间相关联的程度。它既不需要数据满足常见的分布规律，对样本数据的多少也没有苛刻的要求。但灰关联度法需要满足一定的条件，即关联系数的规范性，序列之间的接近性等[11]，实际问题一般满足这个条件。下面给出灰关联法的实施步骤及相关公式。
(1)建立比较矩阵。假设系统有m种故障模式，分别记为X1,X2,…，Xm，其中，Xi表示第i种故障模式，由于每种故障模式有S、O、D 3个变量，所以第i种故障模式的序列可表示为：Xi=(xi=(1),xi=(2),xi=(3))，其中xi=k(k=1,2,3)表示对S、O、D 3个变量的模糊评价，可由式(1)计算得到。从而获得m种故障模式的比较矩阵。
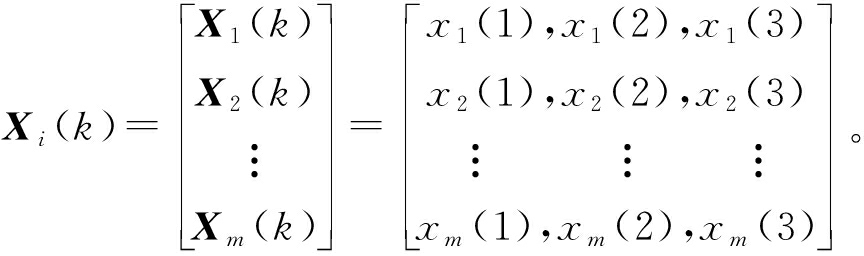
(5)
(2)建立参考矩阵。故障模式的风险大小是相对一定的参考标准而言的，从系统可靠度角度考虑，参考矩阵的选择应以故障模式的各变量最优或最差值作为标准[12]。为方便计算，本文选取最优值作为参考标准，即参考矩阵X0为零矩阵。这样计算的灰关联度在排序时，数值越小风险越高。
(3)灰关联系数的计算。由文献[13]可得出各故障模式变量与参考基准的灰关联系数为：
γ(x0(k),xi(k))=
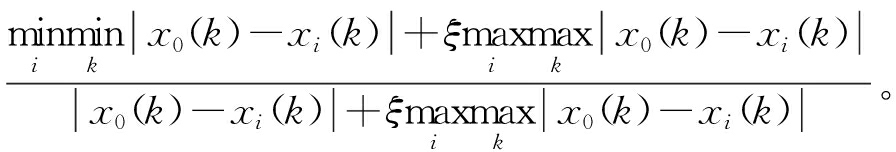
(6)
式中：ξ∈(0,1)为分辨系数。
(4)计算灰关联度。基于S、O、D对评价各故障模式风险时的影响不同，对各变量引入变权系数，记为βi(i=1,2,3)，再结合变权原理得到改进的灰关联度公式为：
γ(X0,Xi)=β1γ(x0(1),xi(1))+β2γ(x0(2),
xi(2))+β3γ(x0(3),xi(3))。
(7)
其中βi(i=1,2,3)需要根据变权综合原理进行计算。
(5)风险排序。灰关联度越小，风险越高。对高风险的故障模式采取一定的预防性措施，降低风险发生率。
2 ZPW-2000A轨道电路风险分析
ZPW-2000A无绝缘移频轨道电路是在法国UM71轨道电路的基础上引进、消化、吸收、再创新的结果。与之相比，ZPW-2000A轨道电路解决了调谐区的断轨检查，减少了调谐区的死区长度，实现了对调谐单元断线故障的检查，通过系统参数优化，提高了轨道电路的传输长度。ZPW-2000A轨道电路采用1 700～2 600 Hz载频段、具有FSK制式轨道电路传输特性，其主要参数及计算机技术满足主体机车信号的自动闭塞及超速防护系统要求。其系统结构如图3所示。
3 基于灰理论的铁路信号系统风险评判
首先对ZPW-2000A轨道电路进行FMECA分析[14],利用模糊集表示各故障模式的严重度(S)、发生度(O)、检测度(D)；再根据灰关联系数法和变权综合原理求得各故障模式的风险优先级指数。由于篇幅关系，这里只分析发送器和接收器的部分故障模式，其FMECA如表3。
根据表3对各故障模式下的严重度(S)、发生度(O)、检测度(D)的模糊表述，以及表2中各模糊语义所对应的反模糊化脆性系数，可建立如下比较矩阵：
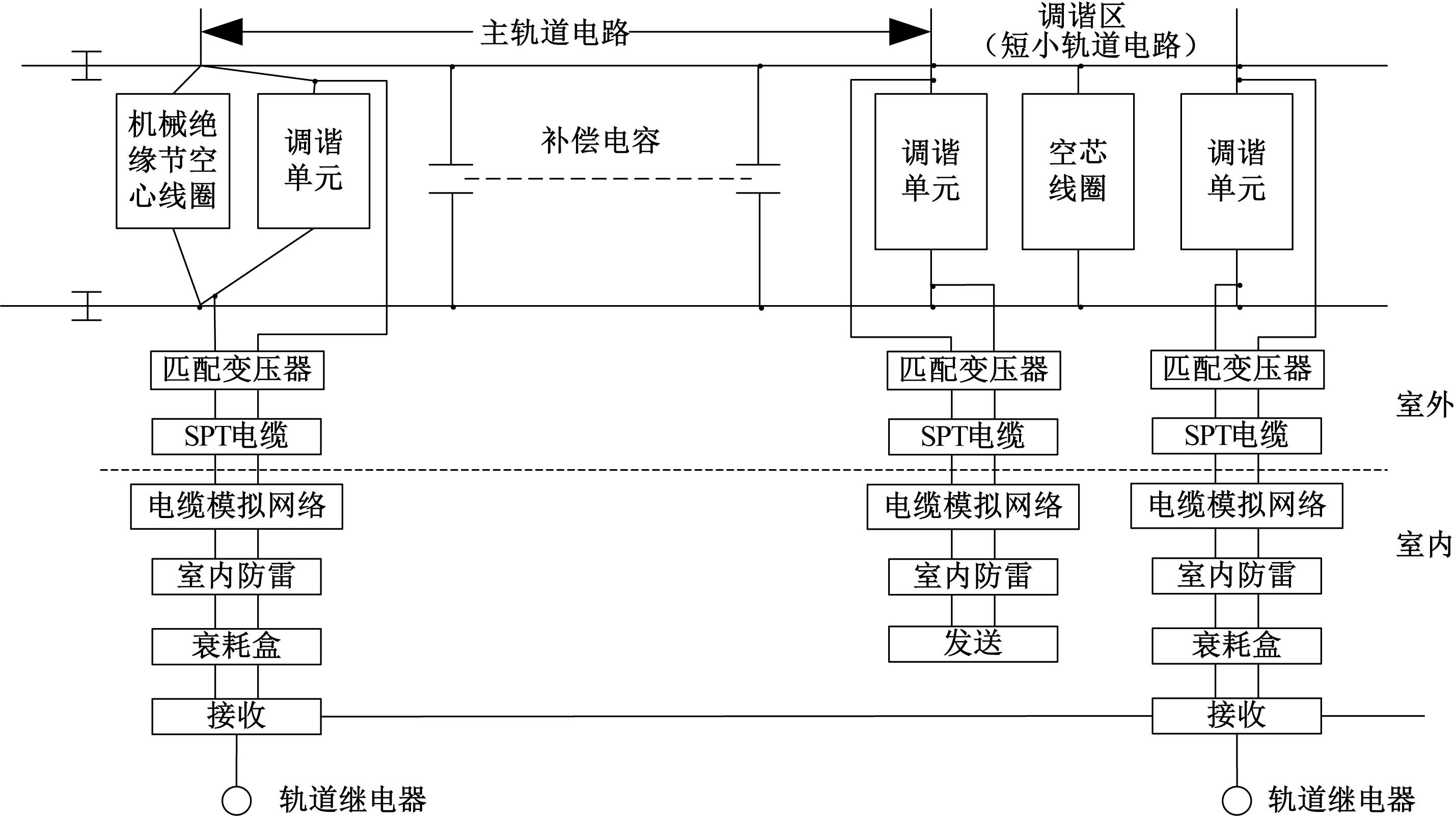
图3 ZPW-2000A轨道电路
Figure 3 ZPW-2000A track circuit
表 3 ZPW-2000A轨道电路FMECA分析表
Table 3 ZPW-2000A track circuit FMECA analysis
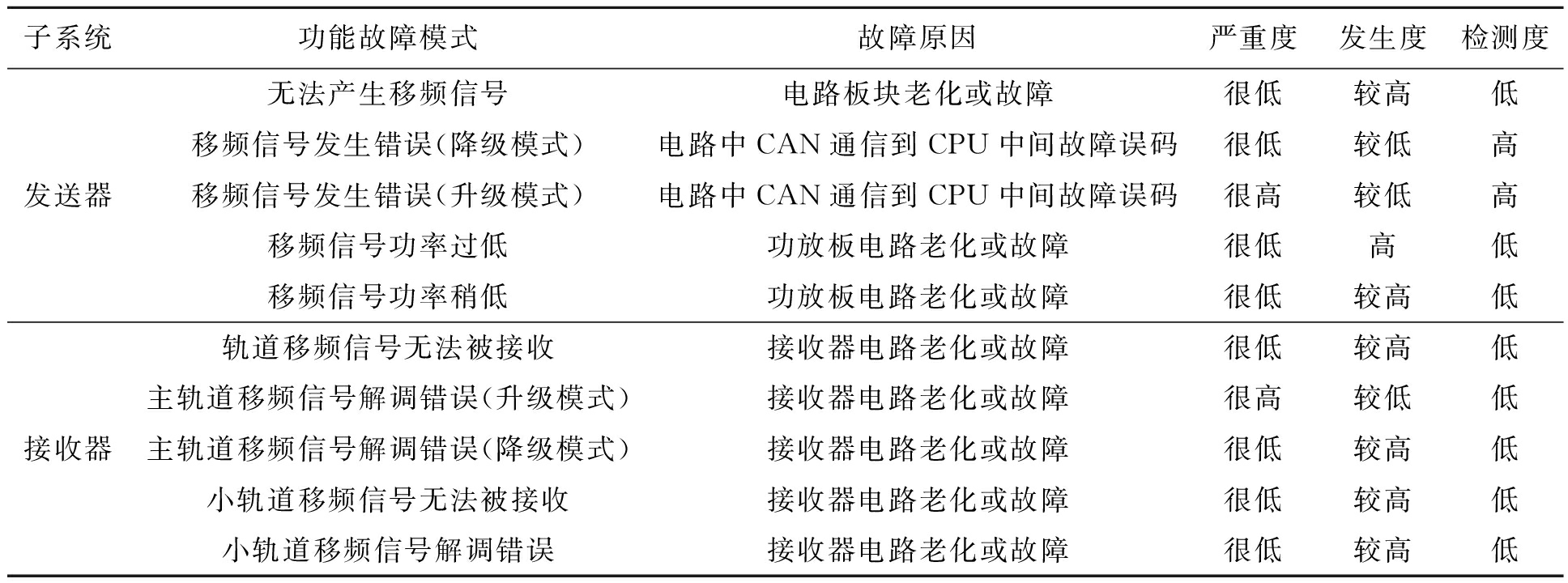
子系统功能故障模式故障原因严重度发生度检测度无法产生移频信号电路板块老化或故障很低较高低移频信号发生错误(降级模式)电路中CAN通信到CPU中间故障误码很低较低高发送器移频信号发生错误(升级模式)电路中CAN通信到CPU中间故障误码很高较低高移频信号功率过低功放板电路老化或故障很低高低移频信号功率稍低功放板电路老化或故障很低较高低轨道移频信号无法被接收接收器电路老化或故障很低较高低主轨道移频信号解调错误(升级模式)接收器电路老化或故障很高较低低接收器主轨道移频信号解调错误(降级模式)接收器电路老化或故障很低较高低小轨道移频信号无法被接收接收器电路老化或故障很低较高低小轨道移频信号解调错误接收器电路老化或故障很低较高低
为方便计算，这里标准序列取零矩阵，分辨系数ξ通常取0.5，则：
由式(6)可知，灰关联系数为：
(8)
从而可求得严重度、发生度、检测度的灰关联系数γs、γo、γd；以第1个故障模式不能产生移频信号为例，其严重度为很低，发生度为较高，检测度为低，因此其对应的脆性系数为x1(1)=0.155，x1(2)=0.845，x1(3)=0.431，则由式(8)可计算各因素的灰关联系数为：γs=1，γo=0.48，γd=0.698。由式(4)可求得各因素变权权重，因为3个因素中的任意一个过大,都会使得设备处于较高危险水平，即它们的权重应是激励型的,即α>1[15]，这里
同理，β2=0.174，β3=0.304，所以第1个故障模式对应的灰关联度为β1×γs+β2×γo+β3×γd=0.82。最后将所有故障模式的灰关联度数值按照升序排列，灰关联度数值越小风险越高。各故障模式的灰理论RPN排序与传统RPN排序如表4所示。
表 4 各故障模式的灰排序与常规风险优先级指数排序
Table 4 Grey ranking of each failure mode and conventional RPN sequencing
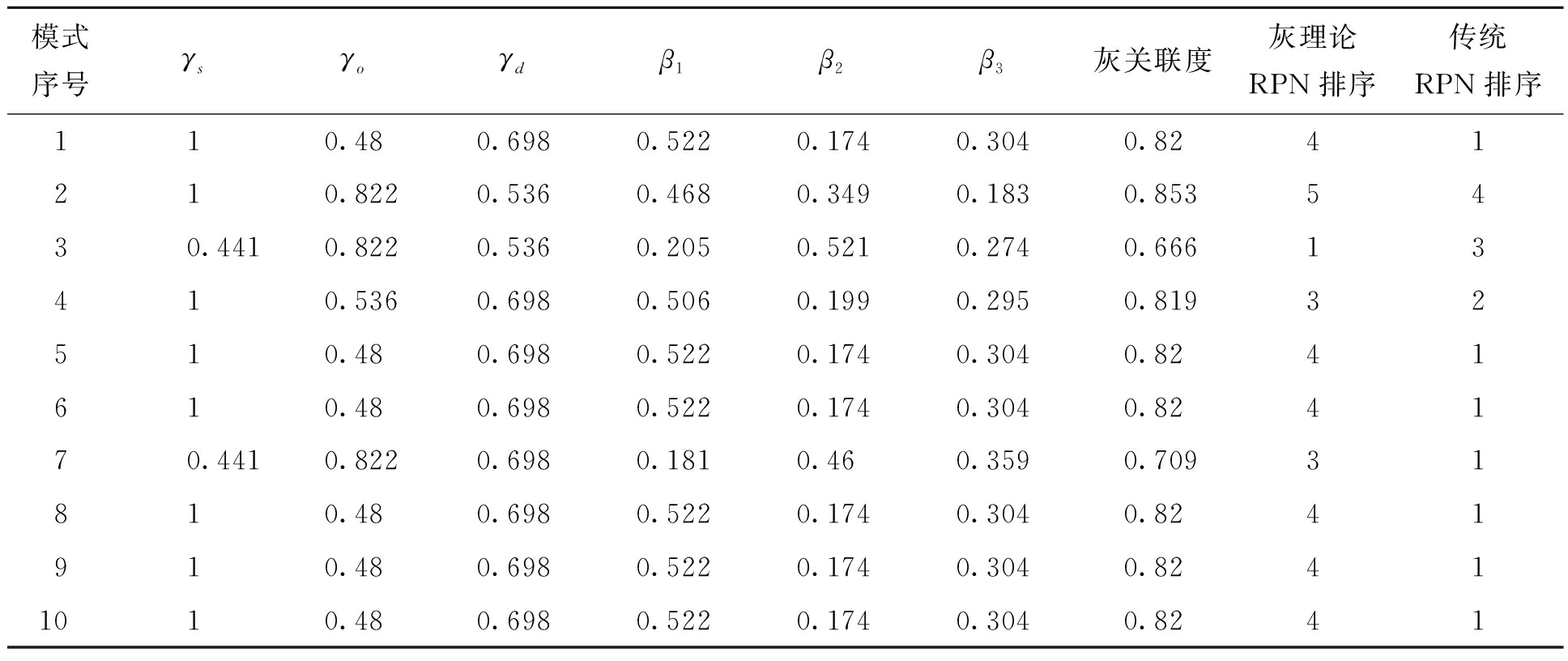
模式序号γsγoγdβ1β2β3灰关联度灰理论RPN排序传统RPN排序110.480.6980.5220.1740.3040.8241210.8220.5360.4680.3490.1830.8535430.4410.8220.5360.2050.5210.2740.66613410.5360.6980.5060.1990.2950.81932510.480.6980.5220.1740.3040.8241610.480.6980.5220.1740.3040.824170.4410.8220.6980.1810.460.3590.70931810.480.6980.5220.1740.3040.8241910.480.6980.5220.1740.3040.82411010.480.6980.5220.1740.3040.8241
通过表 4对各故障模式的灰理论RPN排序与传统RPN排序，不难发现，传统的RPN排序只有4个等级而本文的灰理论RPN排序有5个风险等级，从而表明灰关联法更加精细。在灰关联分析方法计算过程中，通过引入变权综合原理来确定各指标的权重，其作用可由故障模式1、7得出。用传统方法求得它们有相同的RPN值，其风险水平相同，但引入变权之后，可以发现它们的风险水平明显不同。故障模式7为主轨道移频信号解调错误(升级模式)，故障模式1为无法产生移频信号。升级模式对铁路信号是致命的，显然根据灰关联度法及变权原理得出的风险排序更加符合实际。同样由故障模式3可以发现，用灰关联法计算的风险等级为1级，而传统的RPN计算的风险等级为3级，故障模式3是产生错误的移频信号(升级模式)，显然，灰关联度法能够很好地识别高风险故障模式。
4 结论
基于铁路信号系统的安全运营特点，结合灰关联度法、变权综合法、模糊数理论，对信号系统的严重度、发生度、检测度进行风险等级划分，在此基础上提出了铁路信号系统风险优先级综合评价法。给出了其具体实施流程，并以ZPW-2000A轨道电路为例，进行了详细的风险分析，结果表明其比传统的RPN方法具有更高的精度，更符合现场实际情况。该方法可在铁路信号安全领域推广使用，使铁路信号系统风险分析更加科学，精度也更接近实际，为进一步制定有效的维修策略提供依据。
[1] 王艺霏. 基于LabVIEW的ZPW-2000A型轨道电路故障诊断系统设计[D].石家庄:石家庄铁道大学,2019.
[2] 杨杰. ZPW-2000A型轨道电路可靠性与安全性研究[D].北京:北京交通大学,2018.
[3] 陈星. 基于FCM的ZPW-2000A轨道电路故障分类研究[D].兰州:兰州交通大学,2017.
[4] 豆晓东. 基于RBM分析的ZPW-2000A轨道电路预防性维修方法研究[D].兰州:兰州交通大学,2017.
[5] 刘思峰,杨英杰,吴利丰,等. 灰色系统理论及其应用[M].7版.北京：科学出版社,2014.
[6] 单娜. 基于FMEA和RCM的客专ZPW2000A轨道电路设备维修研究[D].成都:西南交通大学,2010.
[7] GEORGES H M.车载自组网中车辆定位导航的混合协作定位和融合技术[D].长沙:湖南大学,2016.
[8] 秦娜,金炜东,黄进,等.高速列车转向架故障信号的聚合经验模态分解和模糊熵特征分析[J].控制理论与应用,2014,31(9):1245-1251.
[9] 汪培庄.因素空间理论：机制主义人工智能理论的数学基础[J].智能系统学报,2018,37(54):37-54.
[10] 王灵芝. 以可靠性为中心的高速列车设备维修决策支持系统研究[D].北京:北京交通大学,2011.
[11] 马庚华,杜牧青,张小丽.不确定因素下的综合运输网络容量可靠性分析[J].郑州大学学报(工学版),2018,39(1):1-6.
[12] ARNO R,DOWLING N,SCHUERGER R J.Equipment failure characteristics and RCM for optimizing maintenance cost[J].IEEE transactions on industry applications,2016,52(2):1257-1264.
[13] 张亚东，郭进,单娜.铁路信号系统风险严重度综合评判[J].西南交通大学学报，2010,45(5):758-762.
[14] 易高明，蒋艳.基于目标相对重要性的模糊多目标进化算法[J].计算机应用与软件，2018,35(6):272-278.
[15] 彭涛.基于灰色关联度分析法的电网评价体系建模仿真[J].电子设计工程,2018,26(20):114-118.