0 引言
几何误差占机床总误差的25%~30%,在温度可控的工况下,几何误差的影响还会升高[1]。当前对五轴机床误差进行测量的方法主要有两种:直接测量法和间接测量法。直接测量即对五轴机床单项误差进行测量[2],由于五轴机床单项误差太多,直接测量效率低。间接测量又称误差辨识[3],通过检测刀尖位置,应用机床运动模型对其单项误差进行分离,一次测量便可获得多项误差,测量效率有了很大的提高。
传统的间接测量方法主要有:球杆仪测试、激光测量、平面正交光栅法、R-Test方法[4-5]。这些方法主要存在以下问题:①测量设备价格昂贵、操作过程复杂费时,无法真实反映机床实际加工时的运动误差;②各种测量方法目标都是快速有效地测量,均未考虑实际加工状态,测量结果是静态的,在工程实际中,系统之间存在着耦合关系,静态误差已经不能解决实际中的问题[6]。
样件测试法[7-8]可以解决传统间接测量方法存在的主要问题,更好地模拟实际加工过程。如图1所示,该方法通过对不同的样件进行模拟切削或实际切削,从而对五轴机床误差进行间接测量。由于测量过程充分考虑了机床的切削加工状态,测量结果是动态的,测量精度更高。
笔者在充分考虑切削加工状态的前提下,对五轴机床的动态误差测量方法进行了研究。为了对实际切削加工状态下的机床误差进行测量,在样件设计的基础上,提出了一种基于样件加工的五轴机床动态误差间接测量方法。通过对样件进行实际切削加工,根据样件加工误差,对五轴机床的动态误差进行间接分离和识别。

图1 Ibaraki设计的测试法与Erkan设计的样板
Figure 1 Test method designed by Ibaraki and model designed by Erkan
1 阶梯轴样件的设计
样件测试法尚处于研究阶段,目前主要存在以下问题:①样件设计缺乏统一的标准,如Erkan等[9]和Liebrich等[10]设计的样板,通过对图1(右)所示的主球间距进行测量,可获得五轴机床的空间误差。Keaveney等[11]和Kato等[12]设计的圆台样件,通过进行模拟切削,可检测机床运动精度。杜丽等[13]设计了一种“S”形样件,可以检测五轴机床的联动精度。但是目前还没有最佳的样件结构能表征五轴机床精度。②现有测试主要还是模拟刀具运动轨迹,且仍然在机床冷态和空切的情况下进行。虽然Ibaraki等[14]和Hong等[15]对样件进行了实际加工,但却并未考虑切削加工状态对五轴机床动态误差的影响规律。③样件测试过程对机床误差源缺乏敏感性,难以对机床误差进行分离和识别。Ibaraki等[16]和Mchichi等[17]都对这一问题进行了探索,但却没有获得理想的辨识模型。
为对五轴机床进行样件加工测试,笔者在基于圆轨迹运动的机床误差测量方法的基础上,设计了图2所示的阶梯轴样件。

图2 本文设计的阶梯轴样件
Figure 2 Stepped shaft prototype designed in this paper
为对样件加工参数进行优化选择,笔者对其进行了正交实验设计。本实验属于四因素实验,根据影响加工误差的主要因素(主轴转速、进给量、径向切深和轴向切深),选择L9(34)表进行正交设计,材料以45钢为例。样件加工过程中,选择径向切深Ae为20 mm、40 mm和60 mm,轴向切深Ap设置为0.5 mm、1.0 mm和1.5 mm,切削速度和进给参考刀具说明设定,初步实验方案如表1、2所示。用45钢样件完成了一组实验后,按照相同方法以Inconel600合金和6066铝合金为材料进行实验,获得不同样件材料的最优加工参数。
综合误差模型为刀具成形点在工件坐标系内的实际位置和理想位置之差Pw-Pwideal。
式(1)所示为某五轴机床沿X轴方向的综合误差模型。式(1)中,Δx表示刀具成形点在工件坐标系内沿X轴方向的轨迹偏差;x、y、z分别表示X、Y、Z轴的位置偏移;α、γ分别表示A、C轴的方向偏移;其余和C、S、ε相关的参数如Cae、Sce、εx(y)等,均表示五轴机床的不同误差项。
表1 样件加工正交实验方案
Table 1 Sample processing experiment plan
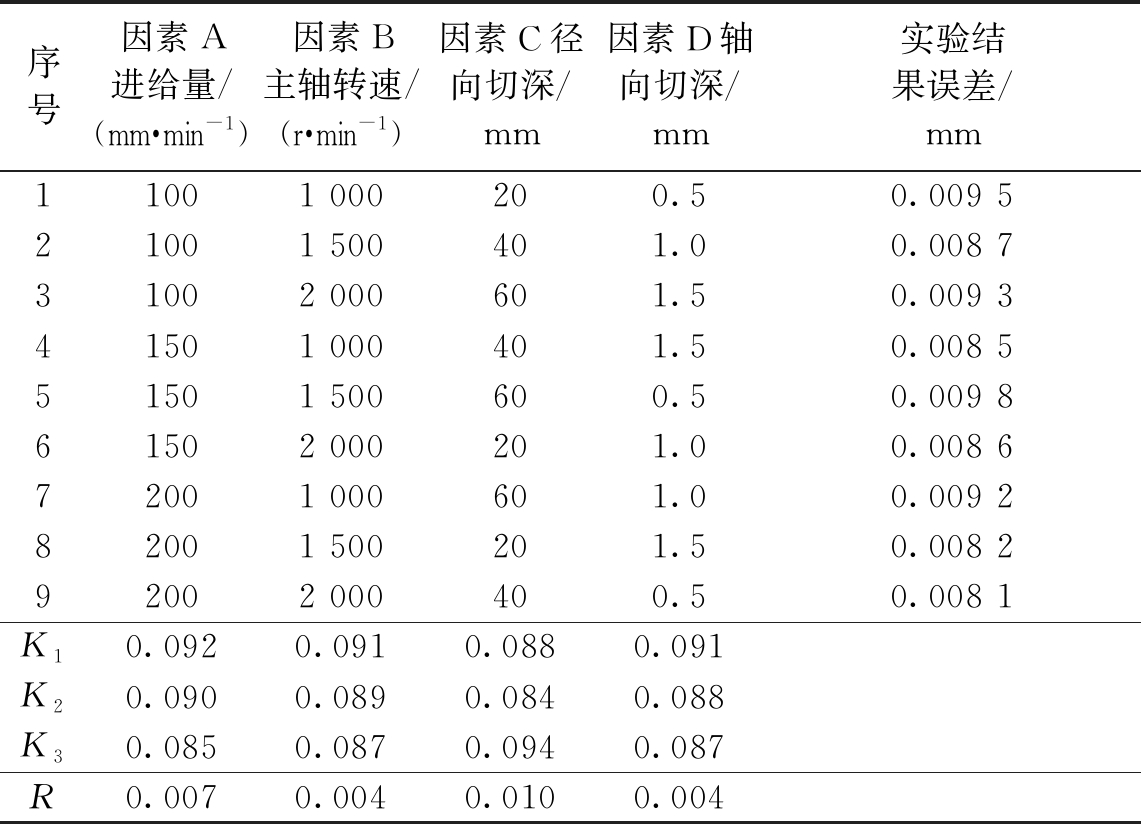
序号因素A进给量/(mm·min-1)因素B主轴转速/(r·min-1)因素C径向切深/mm因素D轴向切深/mm实验结果误差/mm11001 000200.50.009 521001 500401.00.008 731002 000601.50.009 341501 000401.50.008 551501 500600.50.009 861502 000201.00.008 672001 000601.00.009 282001 500201.50.008 292002 000400.50.008 1K10.0920.0910.0880.091K20.0900.0890.0840.088K30.0850.0870.0940.087R0.0070.0040.0100.004
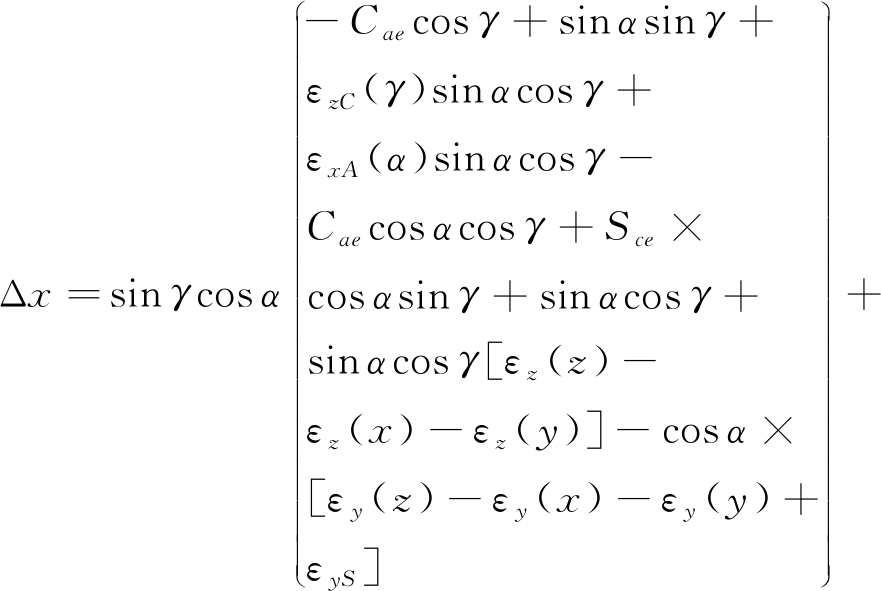
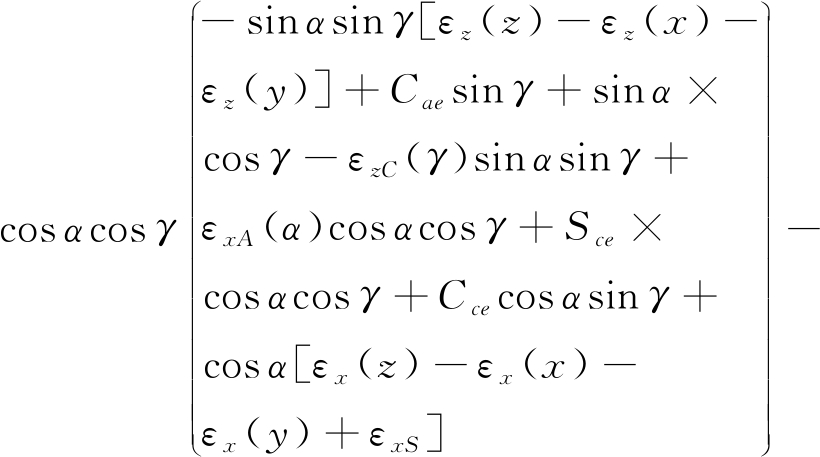
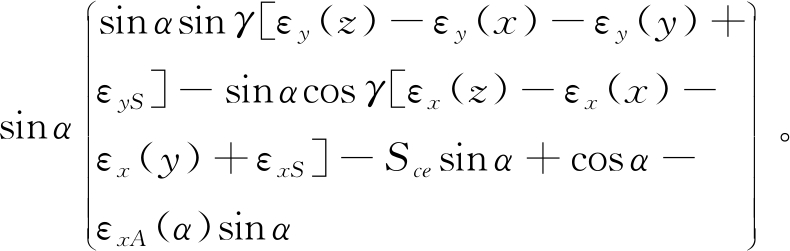
(1)
由式(1)可知,建立综合误差模型后,便确定了样件加工误差与机床各误差项之间的数学关系。将式(1)中的x、y、z和α、γ看作已知,Δx可通过样件加工误差获得,通过对式(1)进行反求,便可间接识别出五轴机床的相关误差项。
为获得求解式(1)所需的x、y、z和α、γ值,笔者对五轴机床的移动轴和转动轴偏置进行研究。加工过程中,X、Y、Z轴偏置根据成形点的空间位置确定,偏置对数目与测量点数相对应,根据方程未知量确定。与移动轴不同,A、C两个转动轴如何进行偏置,缺乏理论依据,为此重点对A、C两个转动轴的偏置进行了设计,具体方案如图3所示。
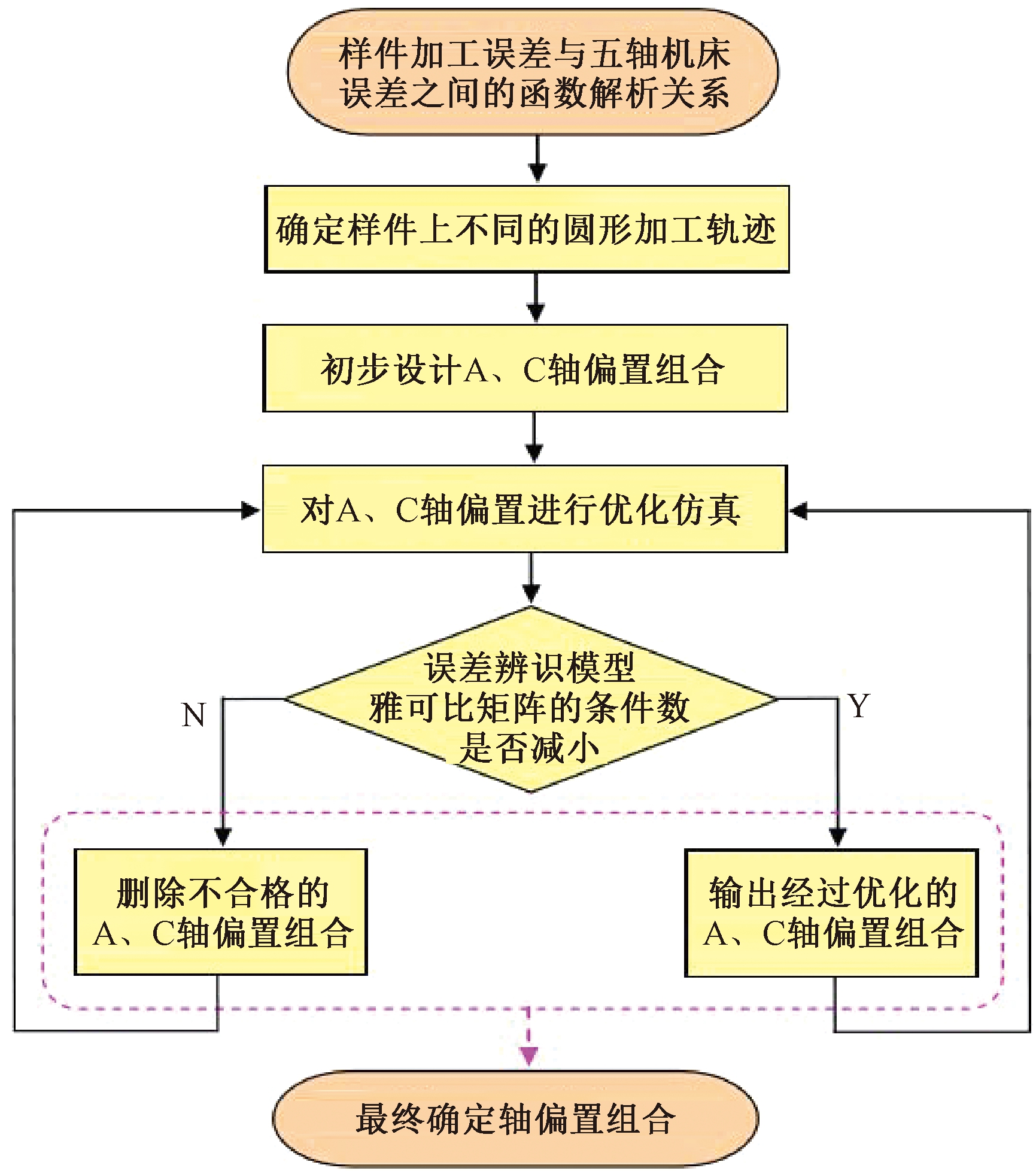
图3 A轴和C轴偏置方案
Figure 3 A axis and C axis offset scheme
首先,根据样件加工误差与五轴机床误差之间的函数解析关系,确定不同的样件加工轨迹,并根据不同加工轨迹初步设计出A、C轴的偏置组合。在此基础上,通过对A、C轴偏置进行优化设计和仿真加工,求解误差辨识模型的雅可比矩阵,并确定其条件数是否减小。若条件数减小,便说明该偏置组合有利于机床误差辨识,否则就应该删除该偏置组合,进行下一个偏置组合的优化仿真过程。循环进行上述过程,直至最终确定出最优A、C轴偏置组合。
由于实际坐标是由坐标测量机测得的,获得的坐标值是相对于测量机坐标系的,式(1)中的Δx并非实际的样件加工误差。为获得样件在工件坐标系中的实际坐标值,建立测量机坐标系和工件坐标系二者之间的空间位姿模型。获得样件在工件坐标系中的实际坐标值后,与其理论坐标值相比较,求得所需的Δx。
2 实验验证
五轴机床动态误差的间接测量验证了笔者提出的间接测量方法的可行性及先进性,对应用设计的样件进行了加工试验,并对样件加工误差进行了测量,根据测量结果间接分离出五轴机床的不同误差项。同时,对五轴机床的相关误差项进行直接测量,比较直接测量与间接测量结果的差异,验证间接测量方法的先进性,测量方案如图4所示。
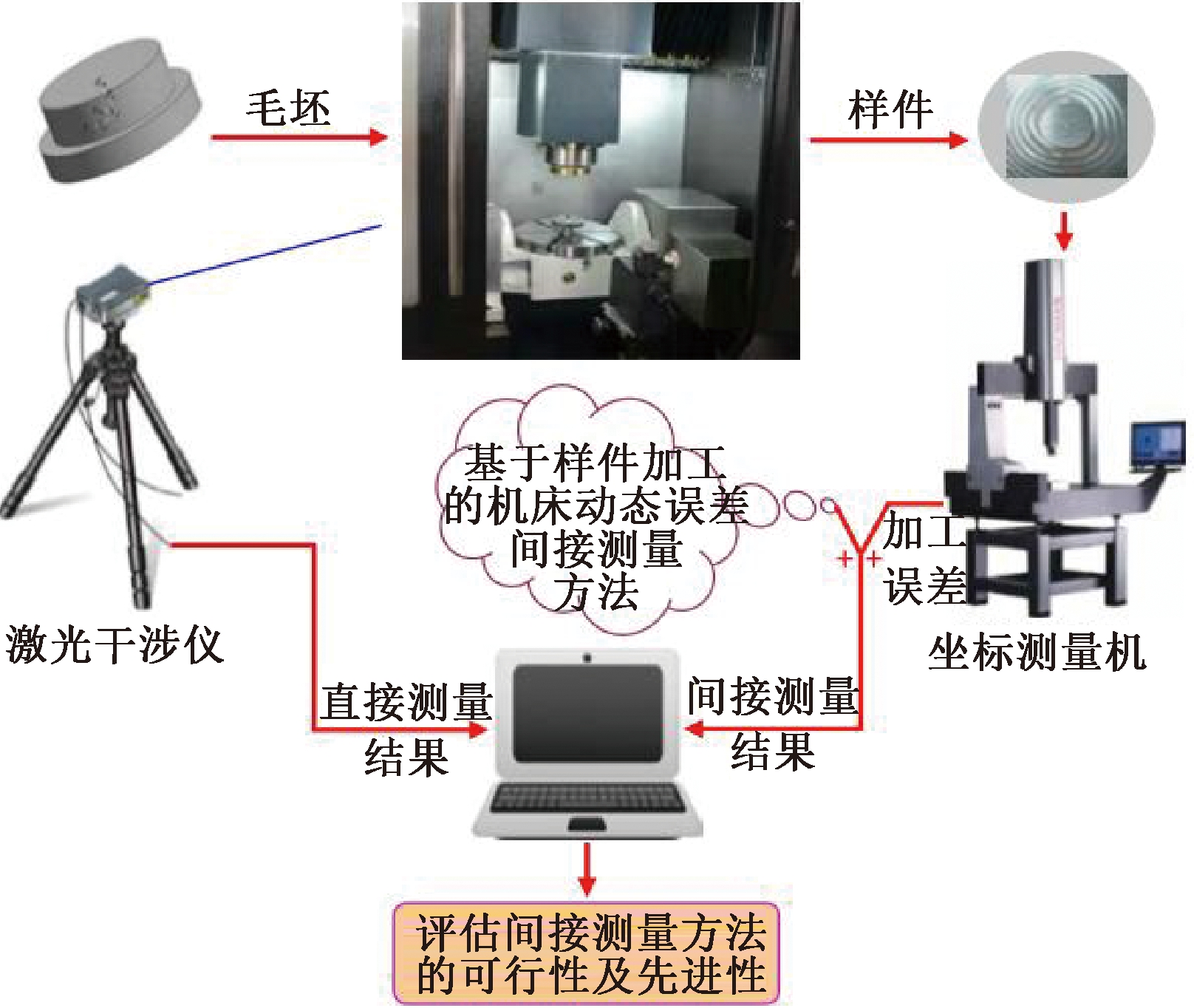
图4 五轴数控机床动态误差间接测量方案
Figure 4 Five-axis CNC machine tool dynamic error indirect measurement scheme
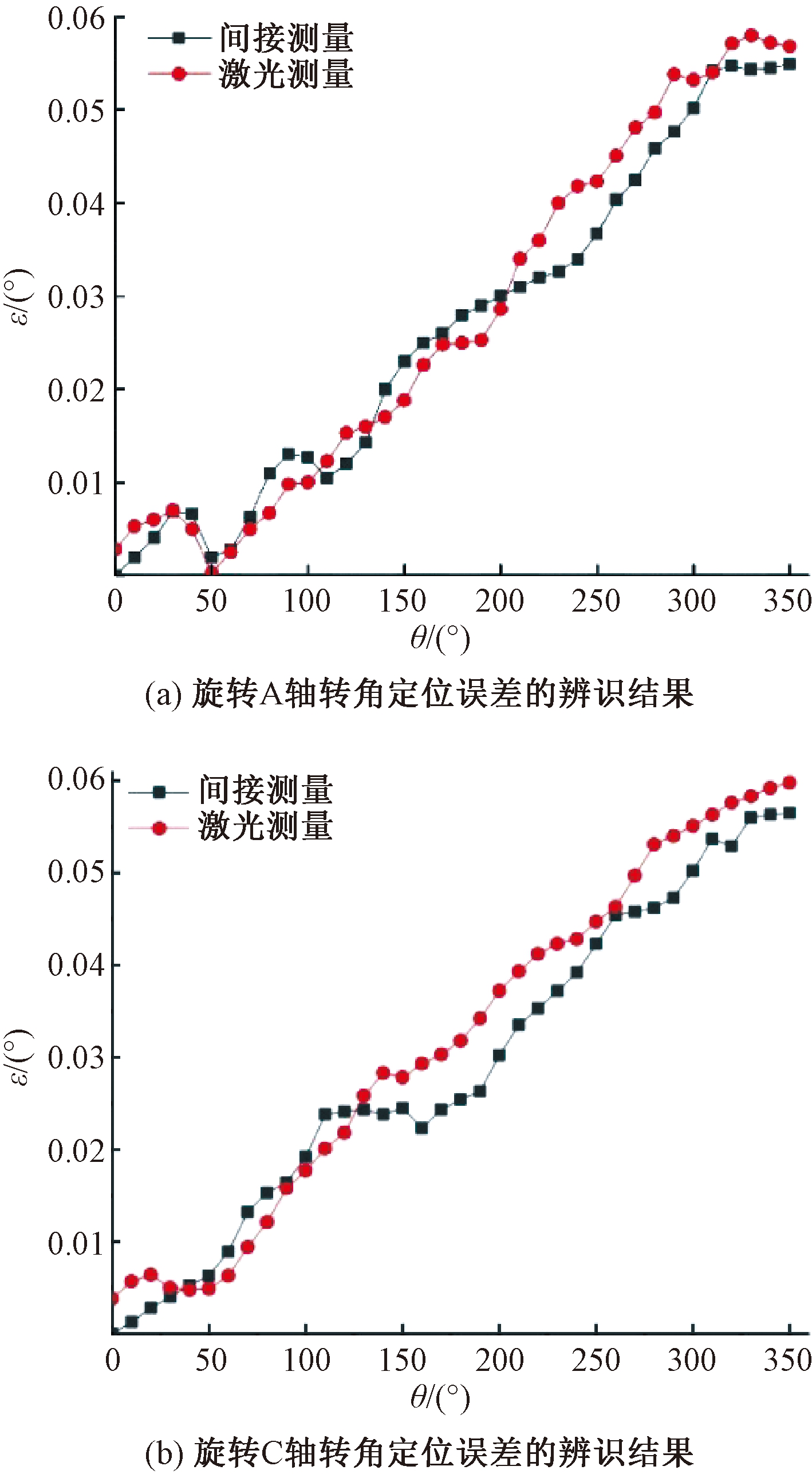
图5 旋转轴转角定位误差的辨识结果
Figure 5 The identification result of the rotation axis′s rotation angle positioning error
首先在五轴数控机床上进行样件加工试验,然后在坐标测量机上测量样件加工误差,并应用基于样件加工的机床动态误差间接测量方法,用激光干涉仪对机床相关误差项进行间接分离和识别。与此同时,对机床相关误差项进行直接测量。最后,对样品测量结果和直接测量结果进行比较得到结果如图5所示。由图5可以看出,两种方法对旋转轴A轴转角定位误差的测量结果差异ε≤0.007 5°,C轴测量结果差异ε≤0.008 2°,可以看出,两种方法的辨识结果差距不大。用激光干涉仪对机床X轴、Y轴和Z轴的定位误差进行直接测量,然后用间接测量的方法进行测量,两种方法测量的结果如图6所示,可以看出,两种测量方法的测量结果吻合较好,所以间接测量的方法在五轴机床误差测量方面是可行的。
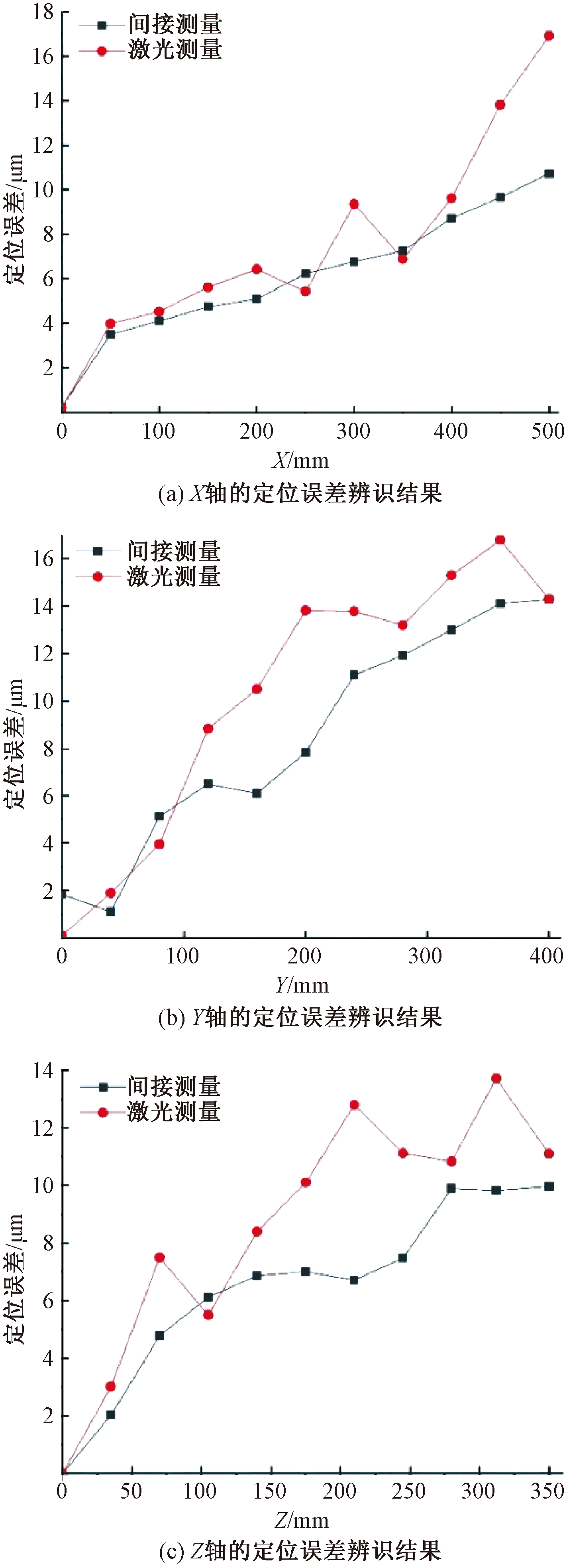
图6 定位误差辨识结果
Figure 6 Positioning error identification results
3 结论
提出了一种基于样件测试法的五轴机床误差间接测量方法,通过对机床空间误差模型进行反求,建立样件加工误差与机床不同误差项之间的函数解析关系,间接测量出五轴机床的动态误差。该方法具有以下特点:该方法设备便宜、操作简单;测量的机床误差的结果都是动态的,测量精度较高。该方法可以比较便捷地测得机床的动态误差,提高在实际制造过程中误差模型的预测能力。
[1] 郭世杰,姜歌东,梅雪松,等.转台-摆头式五轴机床几何误差测量及辨识[J].光学精密工程,2018,26(11):2684-2694.
[2] HE Z Y, FU J Z, ZHANG L C, et al. A new error measurement method to identify all six error parameters of a rotational axis of a machine tool[J]. International journal of machine tools and manufacture, 2015, 88:1-8.
[3] 张根保, 范秀君. 机床关键几何误差辨识方法研究[J]. 中国机械工程, 2014, 25(7):853-856.
[4] 陈江义,焦利明.基于多学科协同算法的机床主轴优化设计[J].郑州大学学报(工学版),2012,33(2):103-106.
[5] 皮世威,刘强,孙鹏鹏.基于激光干涉仪的旋转轴误差快速检定方法[J].仪器仪表学报,2017,38(10):2484-2491.
[6] 郭前建,赵国勇,程祥,等.双转台五轴机床空间误差补偿技术研究[J].机械工程学报,2016,52(13):189-194.
[7] ALESSANDRO V, GIANNI C, ANTONIO S. Axis geometrical errors analysis through a performance test to evaluate kinematic error in a five axis tilting-rotary table machine tool[J]. Precision engineering, 2015, 39(1):224-233.
[8] 仇健.数控机床切削性能测试典型试件综述[J].制造技术与机床, 2014(9):193-203.
[9] ERKAN T, MAYER J R R, DUPONT Y. Volumetric distortion assessment of a five-axis machine by probing a 3D reconfigurable uncalibrated master ball artefact[J]. Precision engineering, 2011, 35(1):116-125.
[10] LIEBRICH T, BRINGMANN B, KNAPP W. Calibration of a 3D-ball plate[J]. Precision engineering, 2009, 33(1):1-6.
[11] KEAVENEY S, CONNOLLY P, AHEARNE E, et al. Investigation of a multi-cone variant of the standard cone frustum test for 5-axis machine tools[J]. Procedia CIRP, 2014, 14:317-322.
[12] KATO N,TSUTSUMI M,SATO R. Analysis of circular trajectory equivalent to cone-frustum milling in five-axis machining centers using motion simulator[J]. International journal of machine tools and manufacture, 2013, 64:1-11.
[13] 杜丽, 张信, 王伟, 等. “S”形试件的五轴数控机床综合动态精度检测特性研究[J]. 电子科技大学学报, 2014, 43(4):629-635.
[14] IBARAKI S, OTA Y. A machining test to evaluate geometric errors of five-axis machine tools with its application to thermal deformation test[J]. Procedia CIRP, 2014, 14:323-328.
[15] HONG C F,IBARAKI S,MATSUBARA A. Influence of position-dependent geometric errors of rotary axes on a machining test of cone frustum by five-axis machine tools[J]. Precision engineering, 2011, 35(1):1-11.
[16] IBARAKI S, SAWADE M, MATSUBARA A, et al. Machining tests to identify kinematic errors on five-axis machine tools[J]. Precision engineering, 2010, 34(3):387-398.
[17] MCHICHI N A, MAYER J R R. Axis location errors and error motions calibration for a five-axis machine tool using the SAMBA method[J]. Procedia CIRP, 2014, 14:305-310.