0 引言
随着全球经济快速发展,能源问题日益突出。为了解决能源资源短缺问题,有效降低化石能源带来的环境污染,近年来人们一直在积极寻找可替代化石燃料的清洁能源。光伏资源具有较大的开发优势,分布广泛、能源效率较高、开发便捷、无污染等特点使其成为人类关注的焦点。然而光伏发电易受气象环境等因素影响,发电时间具有明显随机性。为了确保大规模太阳能电站的安全、稳定运行,提高太阳能发电功率预测精度最为关键。光伏发电功率主要受到气象环境影响,对历史发电数据以及环境数据进行分析,在此基础上,对光伏电站所建位置以及其他人为因素进行分析。然后针对短期内光伏发电功率大小建立相应的数学模型进行预测,重点围绕一种基于NARX神经网络-小波分解组合的光伏发电模型展开研究。
目前,这些预测方法已有十余种之多,并且不同方法适用于不同的微电网应用场景,由于其应用场景各不相同,很难给出一种更有效的判断方法。胡梦月等[1]提出一种组合预测方法,所提方法主要基于改进的AdaBoost.RT和KELM算法,该方法预测精度有所提高但算法稳定性较差。黄辰等[2]建立神经网络预测模型对可再生能源24 h出力状况进行预测,虽然单一的神经网络算法运行时间短,但误差较大。张岚等[3]通过建立3层BP神经网络模型预测微电网中光伏发电功率,但由于BP神经网络的静态特性,使得其预测准确度以及适用性都相对较低。朱永强等[4]主要通过配置储能容量来消除光伏预测误差,但文献中是以最大储能容量来进行配置从而减小预测误差,该方法不具备经济性。陈昌松等[5]提出利用神经网络来对相关天气预报值进行模糊处理,从而建立基于模糊控制的神经网络预测模型,较好地解决了太阳能发电随机性的问题,但其预测误差仍然较高。代倩等[6]通过分析空中云量信息天气类型进行聚类识别,采用自组织特征映射,对于不同的天气、气候类型采用不同预测方法,预测准确度有所提高,但仍无法满足当前精度要求。
针对以上光伏预测精度较差、系统预测模型较为复杂等问题,本文提出一种基于NARX神经网络-小波分解的光伏发电功率预测算法,相较于其他类型的神经网络-小波分解组合预测模型算法,所提算法预测精度更高、计算时间更短。该算法以神经网络为基础,采用小波分解法分析参数的时间序列数据的响应行为,建立基于NARX神经网络-小波分解的预测模型,通过仿真实验对未来一日内发电功率进行预测,证实了所建模型的合理性。仿真结果表明,相较于传统预测算法而言,所提方法既提高了预测精度又得到了更好的全局最优解,并且运行速度更快、时间更短,实验数据证实了该方法的可行性。
1 改进的基于NARX神经网络-小波分解算法
1.1 Mallat小波分解
本研究结合Mallat小波较好的频、时域局部化特征和对细节信号细致分析的特点,分析了两个重要参数的时间序列数据的响应行为,将原始数据分解得到了高低频信号的局部特征[7]。Mauat小波序列方法电路为:
(1)
式中:Cj,k为容许性函数;若函数φj,k(t)满足容许性条件![]() 则称φj,k(t)为母小波,φ(ω)是φ(t)的傅里叶变换;Wj,k为小波变换;φj,k(t)为径向基函数。
则称φj,k(t)为母小波,φ(ω)是φ(t)的傅里叶变换;Wj,k为小波变换;φj,k(t)为径向基函数。
利用小波分析方法对2个最具影响力的气象参数进行了预测分析[8]。由于比例因子a和位移因子b均不连续,故使用尺度离散化方法来降低小波变换系数的冗余度,设![]() 得到离散小波φj,s(x):
得到离散小波φj,s(x):
(2)
式中:j、s为整数;a0为大于1的常数;b0为大于0的常数。
信号f(x)的离散小波变换:
W(j,k)=![]() f(x)φj,k(t)dt,j,k∈Z。
f(x)φj,k(t)dt,j,k∈Z。
(3)
采用Mallat重构算法对神经网络输出数据进行处理,其方法可参考文献[9],以下仅给出相应重构公式。
Mallat给出的分解与重构公式如下:
(4)
(5)
(6)
式中:![]() 分别为小波分解系数;hj、gj分别为小波离散滤波器;
分别为小波分解系数;hj、gj分别为小波离散滤波器;![]() 分别表示对hj和gj进行共轭转置运算。
分别表示对hj和gj进行共轭转置运算。
若f为初始信号,c1,c2,c3,…,cn分别为信号每一层的低频部分;d1,d2,d3,…,dn分别为不同层的高频部分。由分解结构图可看出,先将初始信号f分解得到c1、d1,进而将低频信号逐层分解得到最终信号cn和d1,d2,d3,…,dn,以下为f与cn和d1,d2,d3,…,dn信号之间关系:
f=cn+d1+d2+d3+…+dn。
(7)
1.2 改进的基于NARX的神经网络-小波算法
NARX(nonlinear autogressive with exogenous inputs)是一种动态带有反馈的递归神经网络机器模型[10],其相当于在原有BP神经网络基础上增加有输入时延以及输出到输入的时延反馈,NARX神经网络输出的最终结果与对应输入以及历史的输出有关[11]。NARX神经网络模型定义如下:
y(t)=f[y(t-1),y(t-2),…,y(t-ny),
x(t-1),x(t-2),…,x(t-nx)]。
(8)
式中:f(·)是非线性过程函数;y(t)是输出量;x(t)是输入量。
原理图如图1所示,d为时延数;F1为隐含层的激活函数;b为偏置;m为神经元个数;W为权值;F2表示输出层的激活函数。

图1 改进的NARX神经网络-小波结构原理图
Figure 1 The improved NARX neural network-
wavelet structural schematic
通过采用RTRL(real-time recurrent learning)算法来调整NARX神经网络的权值,RTRL算法通过前向传播梯度来进行计算,使得NARX神经网络收敛速度更快,其具体推导文献[12]已给出,公式的最终推导结果如下:
(9)
其中,
(10)
(11)
式中:W是神经网络中需要进行自适应调节的所有连接权重;e是实际输出与期望输出之间的差值;η是学习速率。
1.3 神经网络模型评价标准
权值向量W通常在对网络进行训练之前以任意值给出,在不断的学习过程中对其按照模型需满足的误差进行调整[13]。选用均方误差来评判NARX网络训练、预测数据与实际数据之间的偏离大小,均方误差越小,表明所建模型预测准确度越高[14]。均方误差公式如下:
(12)
式中:N为总训练样本数据量;y(t)是第t组训练数据的期望输出;y′(t)为所选用第t组数据的实际输出值。
2 光伏预测模型
如今已有较多关于光伏、负荷功率预测的方法,即使预测方法各不相同,但预测精度不高,并未获得较为满意的预测结果[15]。另外,就太阳能电池板发电原理而言,影响其光生伏特效应的主要因素是太阳光的辐射强度[16]。太阳辐照度主要受到大气中云层数量、光伏电池安装倾斜角以及在日内各时段太阳所在位置等因素影响。本次主要选择光伏电场多组历史数据作为预测模型训练数据,将其外部环境因素作为所提出方法的输入信息,然后采用智能算法-小波分解模型对光伏出力进行预测。
将两个重要参数的时间序列数据即温度和太阳光辐射强度作为输入,将光伏出力作为输出,通过NARX神经网络分析这两个参数的相关性,然后进行小波变换重构后得到最终信号,所采用预测算法具体步骤如下。
步骤1 获得太阳能电站的历史发电功率数据,选择合适时段并对其进行多层小波分解,最终分解为一个低频、多个高频部分。
步骤2 进行模型训练,即将低频部分作为NARX网络输入、目标输出,训练完毕后预测得到未来时刻的低频部分。
步骤3 再将已获得数据的高频信号部分同样输入NARX神经网络中进行训练、预测,从而获得数据高频信号的数值。
步骤4 将步骤2、3中由预测得到的高、低频信号叠加,最后获得整个系统的光伏预测值。
3 预测算法在光伏发电系统中的应用
3.1 数据来源
主要对光伏功率进行短期预测,所用仿真实验数据采自真实光伏电站的运行数据,光伏电站的峰值功率为20 MW。本次共选取6 000组数据进行训练,分别选取夏、冬两季中某一典型日进行光伏发电功率预测,预测时间尺度为间隔15 min。每隔15 min采样记录一次光伏电站太阳光辐射强度(kW/m2)、温度(℃)以及光伏发电功率(kW)。图2为光伏电站多组历史输出功率数据。从图2中可以明显看出在一些时段,光伏出力表现出较大的波动性以及非平稳特性,这对于神经网络-小波分解组合预测模型的泛化、收敛性能以及预测精度都有较大的影响。
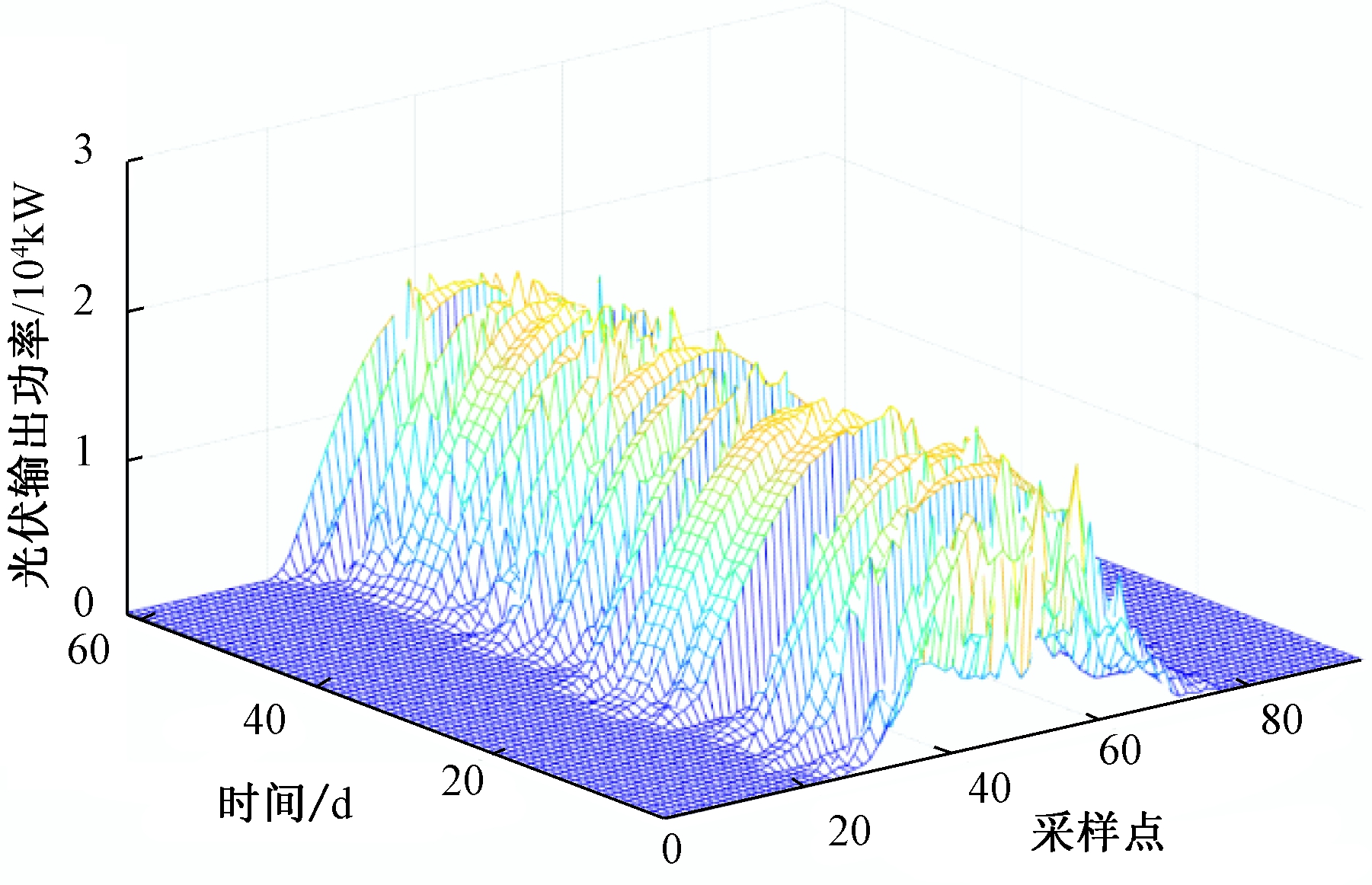
图2 多组历史光伏输出功率数据
Figure 2 Historical photovoltaic output power data
3.2 异常数据分析
异常值通常被分为属同一总体与不属同一总体两种。在对光伏发电数据进行预测研究以前,所用历史数据中异常值类型包含以上提到的两种情况。数据来源主要是光伏电场环境数据与光伏发电功率之和,由于所需采集数据较多,加之这些数据变化复杂、规律不明显,并且在进行仿真实验之前对于所用历史数据是否符合要求没有明确的定义,故需要对数据进行预处理,预处理通常需要进行有效的检测、修正。
3.3 光伏原始数据预处理
通常来讲,由于光伏发电受到环境因素影响而表现出较强的不确定性,需要对历史数据进行预处理。通常需要对原始数据进行归一化。归一化主要是指将数据分布范围处理至较小区间内,这样处理后的数据更易操作。在采用相应算法对光伏出力进行预测之前,需要对原始样本数据进行规范化处理。在对所用训练数据处理之后,才能使得不同维度的样本数据保持在同一数量级上,以进行综合的比较和评价。
对数据进行预处理时,将所需光伏预测输入数据处理至[0,1]内,采用min-max标准化方法对实验所需数据进行归一化处理,公式如下:
(13)
式中:xmax、xmin分别为所需采样数据中最大值与最小值。此方法优势在于数据操作较为简单,并且可以通过计算机程序进行处理。
3.4 预测结果
对光伏输出功率数据进行小波分解如图3所示。光伏输出功率的近似系数曲线反映了其输出功率变化趋势。经过Mallat小波分解得到特征分量a1、a2、a3、a4、a5、a6,第1~5层的细节系数曲线则反映了信号高频部分的构成以及变化规律。
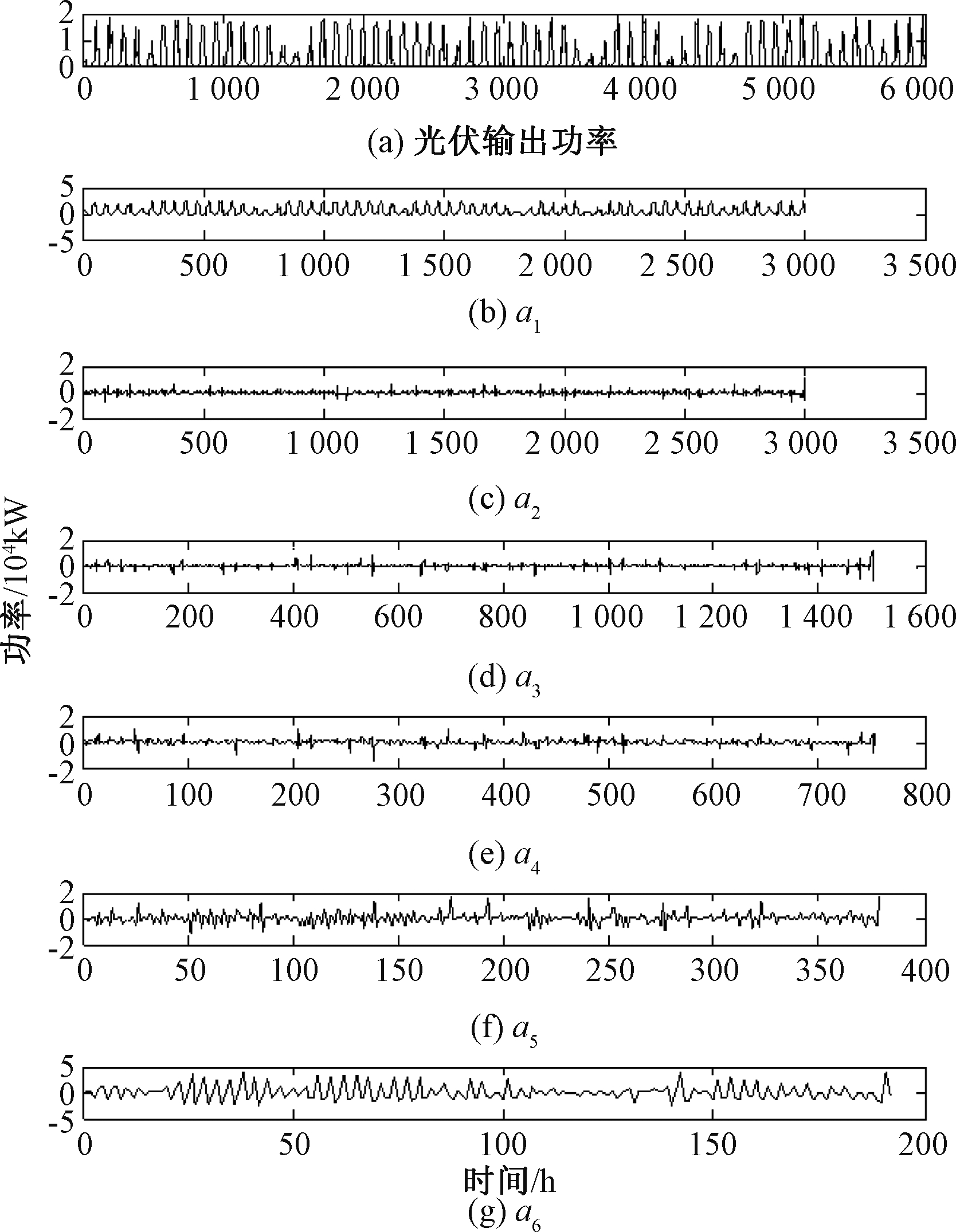
图3 光伏输出功率小波分解
Figure 3 Photovoltaic output power wavelet decomposition
将影响光伏发电输出功率的辐照强度和温度进行小波分解如图4和图5所示。其中,b1、b2、b3、b4、b5、b6为辐照强度的特征分量,c1、c2、c3、c4、c5、c6为温度的特征分量。将太阳光辐射强度、温度分解后的近似系数与细节系数作为NARX神经网络的输入向量,将光伏发电功率分解后的近似信号与细节信号作为其目标向量,神经网络训练完成后将光伏输出功率重构得到图6,其中d1、d2、d3、d4、d5为光伏功率训练后的5个特征分量。由图6可知,经过5层小波分解重构后的太阳能电池输出功率细节系数部分表现出良好的平稳性能,且经过NARX神经网络训练重构后的近似系数与细节系数叠加还原后较为接近实际输出功率。
根据上面所建立的光伏发电功率近似系数与各层细节系数预测模型,分别预测夏季、冬季某典型日光伏电站的输出功率。将不同季节典型日的光伏预测结果与实际输出功率进行对比,如图7所示。

图4 辐射强度小波分解
Figure 4 Solar radiation dose wavelet decomposition

图5 温度小波分解
Figure 5 Temperature wavelet decomposition
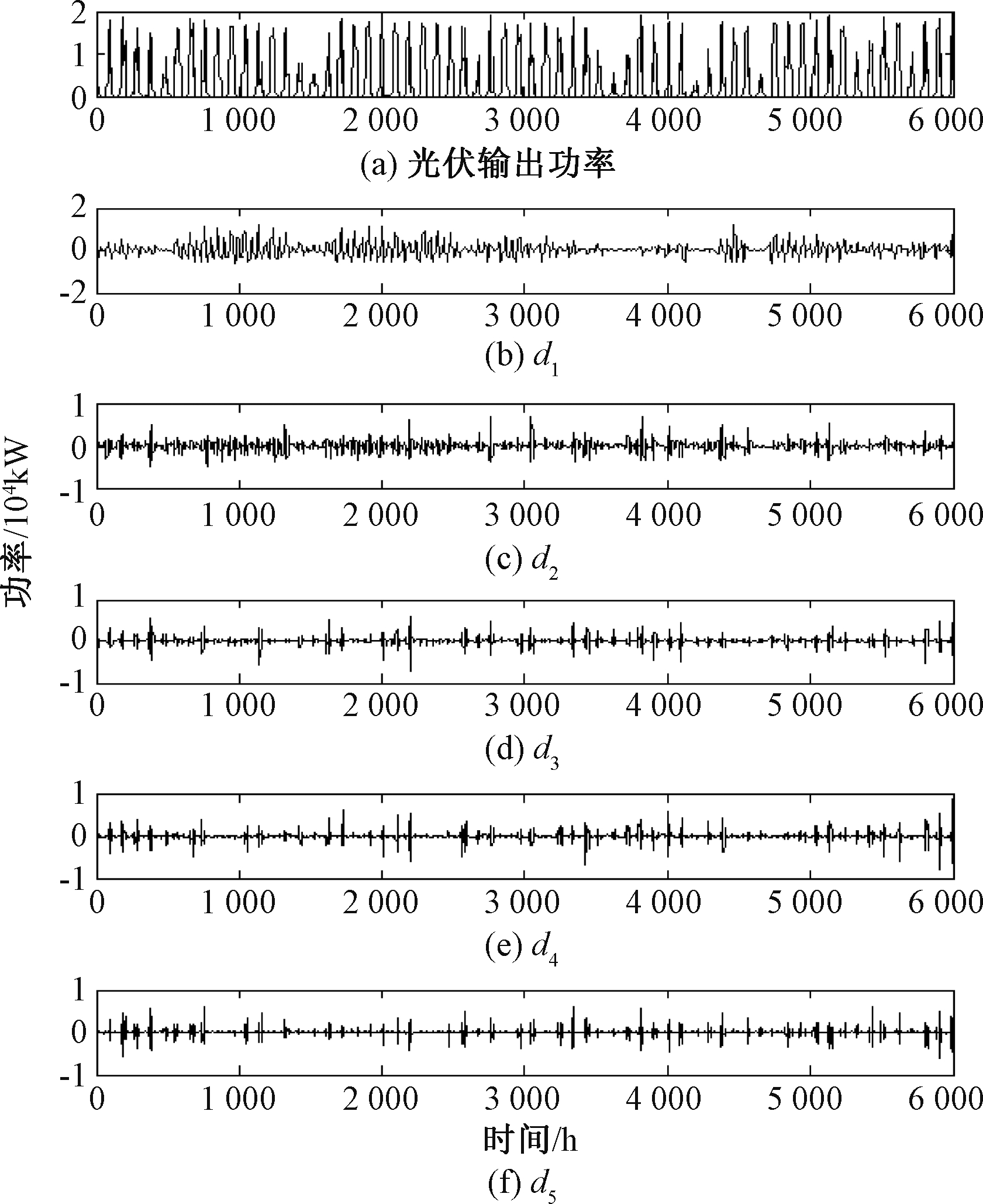
图6 光伏输出功率重构信号
Figure 6 Photovoltaic output power reconstruction signal

图7 改进算法的功率预测与实际输出曲线
Figure 7 Improved algorithm power prediction and
actual output curve
对典型日预测结果进行分析,夏季预测误差较冬季小,可能是由于冬季气温较低以及云层遮挡等因素造成光伏输出实际功率发生较大波动,进而造成预测结果出现较大偏差。改进的算法预测精度要优于BP神经网络预测精度。对所提算法冬夏典型日的标准误差、最大误差进行对比,夏季功率预测标准误差与最大误差分别为0.854、1.193 MW;冬季功率预测标准误差与最大误差分别为1.292、3.541 MW。预测误差大小均在可控范围之内。
对两者运行时间以及均方误差大小进行对比,所提算法运行时间约为8.45 s,BP神经网络算法运行时间为13.08 s,所提组合预测算法较之传统BP神经网络而言,运行时间更短、收敛速度更快。对比两种预测算法的均方误差,新的组合预测算法的均方误差仅为4.38%,而反向传播算法达到5.85%。所提算法预测误差与BP神经网络相比更小。
4 结论
本文提出的基于NARX神经网络-小波分解的光伏发电功率组合预测模型,主要考虑影响太阳能电池发电的两大因素:太阳光辐射强度、温度,并将其作为模型的输入信息,将对应光伏发电功率作为输出,通过训练将最终得到的预测数据进行小波重构。通过对所建模型进行大量数据测试,验证了其对于光伏发电功率的预测是较为准确、有效的。因此NARX神经网络相比于传统BP神经网络具有更好的非线性映射能力,具有较高的预测精度和调整能力。
[1] 胡梦月,胡志坚,仉梦林,等.基于改进AdaBoost.RT和KELM的风功率预测方法研究[J].电网技术,2017,41(2):536-542.
[2] 黄辰,吴峻青.基于人工神经网络的短期风电功率预测[J]. 华东电力, 2014, 42(7):1408-1410.
[3] 张岚,张艳霞,郭嫦敏,等.基于神经网络的光伏系统发电功率预测[J].中国电力,2010,43(9):75-78.
[4] 朱永强,田军.最小二乘支持向量机在光伏功率预测中的应用[J].电网技术,2011,35(7):54-59.
[5] 陈昌松,段善旭,蔡涛,等.基于模糊识别的光伏发电短期预测系统[J].电工技术学报,2011,26(7):83-89.
[6] 代倩,段善旭,蔡涛,等.基于天气类型聚类识别的光伏系统短期无辐照度发电预测模型研究[J].中国电机工程学报,2011,31(34):28-35.
[7] 刘卫亮,刘长良,林永君,等.计及雾霾影响因素的光伏发电超短期功率预测[J].中国电机工程学报,2018,38(14):4086-4095,4315.
[8] MELLIT A,PAVAN A M.Performance prediction of 20 kWP grid-connected photovoltaic plant at Trieste (Italy) using artificial neural network[J]. Energy conversion and management,2010,51(12):2431-2441.
[9] 王晓兰,王明伟.基于小波分解和最小二乘支持向量机的短期风速预测[J].电网技术,2010,34(1):179-184.
[10] 谢吉洋,闫冬,谢垚,等.基于NARX神经网络的热负荷预测中关键影响因素分析[J].计算机应用,2018,38(11):3180-3187.
[11] 米增强,刘兴杰,张艳青,等.基于混沌分析和神经网络的风速直接多步预测[J].太阳能学报,2011,32(6):901-906.
[12] PLETT G L.Adaptive inverse control of linear and nonlinear systems using dynamic neural networks[J]. IEEE transactions on neural networks, 2003, 14(2): 360-376.
[13] 周品.MATLAB神经网络设计与应用[M].北京:清华大学出版社,2013.
[14] 赵唯嘉,张宁,康重庆,等.光伏发电出力的条件预测误差概率分布估计方法[J].电力系统自动化,2015,39(16):8-15.
[15] GUO M, LAN J H, LI J J, et al.Traffic flow data recovery algorithm based on gray residual GM(1,N)model[J].Journal of transportation systems engineering and information technology,2012,12(1):42-47.
[16] CHEN J L, LI G S, WU S J.Assessing the potential of support vector machine for estimating daily solar radiation using sunshine duration[J].Energy conversion and management,2013,75:311-318.