0 引言
分布式发电与配电网发展的迫切需求催生了主动配电网(ADN)[1]的概念。主动性指的是ADN具备主动管理能力,能够对网络的各类资源进行协调控制和主动管理。与传统配电网相比,主动配电网在满足安全运行要求的前提下,可以尽量减少运行成本[2]。
在功率表达中考虑概率特性,已有不少的研究成果[3-10]。文献[3]基于Monte Carlo模拟技术提出了一种能够准确计及任意分布的光伏功率和负荷相关性的概率潮流计算方法。此方法避免了烦琐的公式推导,并且在样本合理、数量足够的前提下,蒙特卡洛法可达到较高的精度,但相应的计算量会随着样本数的增大而增大[4]。随机响应面法[5]的基本原理是在已知输入随机变量概率分布的基础上,将输出响应表达为关于已知参数的混沌多项式,通过少量采样确定多项式中的待定系数,进而得到所估计的输出响应的概率分布。以随机响应面为代表的多项式混沌展开方法[6]在概率分析中受到广泛关注。文献[7]介绍一种基于点估计和Gram-Charlier展开的概率潮流实用算法,无须知道输入随机变量的概率密度函数。点估计法是一种逼近技术,利用输入随机变量的统计信息来逼近输出随机变量的统计信息。在计算时,无须知道输入与输出之间具体的函数关系表达式。
现有ADN的优化研究中,建立了考虑经济性、风险性等优化模型,用概率潮流实现风险指标的计算,并在优化算式求解上采用了各种求解方法[8-10]。文献[9]建立了运行成本与越限风险最小的多目标日前优化调度模型,计及各种ADN调度手段,用“理想点”法处理多目标模型,以和声搜索算法为求解工具,并基于半不变量法随机潮流实现越限风险指标的计算。文献[9]考虑了时序性和随机性,对光伏发电和负荷建立分时段多状态模型,以高于置信水平的年费用最小为上层规划目标函数,光伏电源和电容器安装位置和容量为上层优化变量,以高于置信水平的运行年费用最小为下层规划目标函数,每个时段光伏发电无功出力和电容器投切状态为下层优化变量,建立嵌入机会约束规划的二层规划模型。文献[10]建立基于三相潮流的辐射状配电网多时段有功-无功协调动态优化模型,采用混合整数二阶锥规划算法进行求解。
笔者基于已得到的功率预测误差的分布特性,采用解析表达的方式求解。尽管考虑到预测误差与时序的随机扰动不一致,但在处理方法上类似。由于功率预测误差的分布特性会对随机变量的均值产生影响,因此在求解过程中,通过方差修正来提高均值计算的准确度。在优化模型求解中,依据量的实际特点,对离散变量和连续变量采用了不同的处理方式。
基于上述分析,笔者计及功率预测误差的分布特征,以综合运行费用的均值为目标函数,节点功率平衡方程、节点电压和支路功率等变量的运行范围构成约束条件,建立主动配电网运行方式的概率优化模型,并在随机变量的均值表达中计及方差的修正。对离散变量和连续变量进行分类处理。
1 算法的选择
虽然本文的均值表达计及了功率预测误差的分布特性,但是此处的均值表达与概率潮流中的均值表达在表达式上基本一致。因此,在处理方法上也可以选择蒙特卡洛法、随机响应面法等。但基于以下两个因素:
(1)如果对协方差采用计及高阶项表达,结果更为准确,但计算量急剧增加;阶数越高,贡献量也越小。结合本文均值表达的用途,对均值表达保留到二阶,对方差保留到一阶。
(2)如果蒙特卡洛法在本文中即用在概率潮流表达中,也用到优化计算中,则对每一种样本都有一个优化结果,这会使目标函数的优化复杂化。
因此,笔者采用了计及方差修正的均值表达。
2 计及方差修正的均值表达
2.1 随机变量均值运算
对于常数a和随机变量x、y,有均值运算[12]:
(1)
(2)
(3)
(4)
其中,协方差[6]Cxy为:
(5)
式(4)中,随机变量乘积的均值等于均值的乘积加协方差,形成计及二阶协方差修正的均值表达。
2.2 方差对均值的修正
配电网优化中,存在多种功率表达,例如节点注入功率表达、支路功率表达等。以潮流计算中的节点功率为例进行说明。
直角坐标下节点i的潮流方程式[12]为:
(6)
(7)
式中:Pi和Qi为节点i的注入有功和无功功率。
直角坐标下,节点功率是节点电压的二次函数。因此,可将潮流方程(6)、(7)写成通式:
.=.(.)=.(X1X1,…,XiXi,…,X2NX2N),
(8)
式中:列向量.由PQ点的有功和无功功率构成;列向量.由节点电压的实部和虚部构成。
将式(8)在均值![]() 处按照泰勒级数展开,并考虑到二阶项和零阶项有相同的形式,得到:
处按照泰勒级数展开,并考虑到二阶项和零阶项有相同的形式,得到:
(9)
式中:![]() 为雅克比矩阵。
为雅克比矩阵。
由于式(6)~(8)中的最高阶为二阶,所以式(9)为完整表达式。
参照式(4)、(6)~(8),.的均值可表示成:
![]()
![]()
(10)
式(10)中计及协方差的影响,也是完整表达。
由偏差表达式:
Δ.=.XΔ.,
(11)
得到电压的协方差为:
(12)
概率潮流计算的迭代算式为:
(13)
式(13)第1式中的均值计算采用式(10)的完整表达,第2式中的协方差.X为线性化表达。如果对协方差采用计及高阶项表达,结果更为准确,但计算量急剧增加,阶数越高,贡献量也越小。计算量和精确度之间的折中处理,笔者采用了均值完整表达,计算量增加不多,用来保证目标函数计算的相对准确;在协方差计算中仅采用线性化处理。
计算概率潮流时,采用均值、方差的交替迭代方式,几次均值迭代加一次方差迭代。配电网优化中,各种功率表达均采用类似处理方式。
3 约束条件的概率表达
在约束条件中考虑预测误差的分布特性,约束条件变为概率约束。
假设t时刻第i节点的电压概率分布如图1所示。h(Vi,t)为t时刻i节点的电压概率密度函数;1.05、0.95分别为节点电压标幺值允许范围的上下限;阴影区域代表电压越限概率。
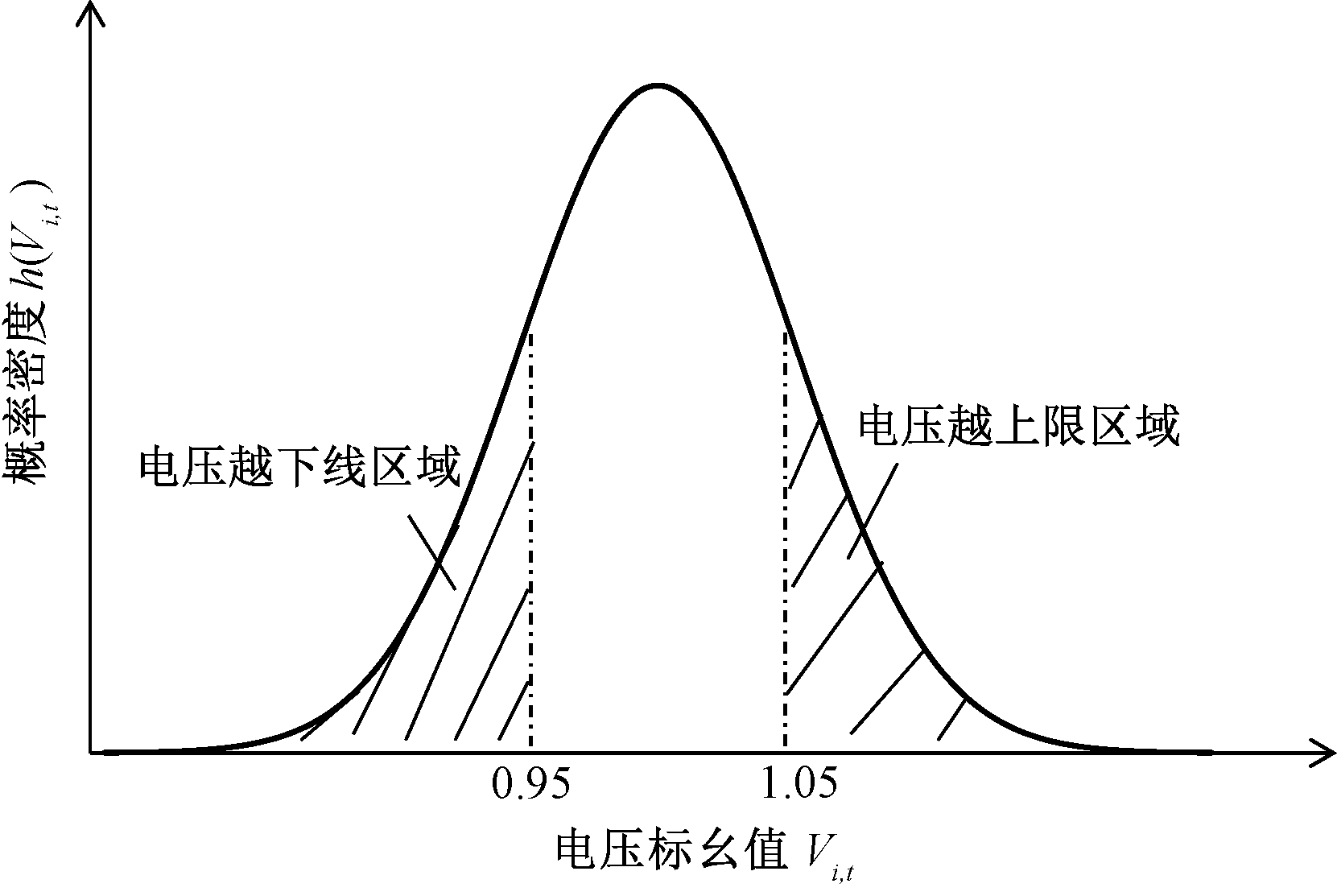
图1 节点电压越界区域
Figue 1 Node voltage across boundaries
在只考虑均值和方差的情况下,节点电压Vi,t的概率密度为:
(14)
则节点电压越界风险KVi,t为:
KVi,t=![]() h(Vi,t)dVi,t+
h(Vi,t)dVi,t+![]() h(Vi,t)dVi,t。
h(Vi,t)dVi,t。
(15)
实际计算中,将Vi,t分布转化为0-1分布,用插值法从累积概率分布表中快速查取式(15)等号右边的第一项和第二项,得到K(Vi,t)。
满足要求的电压分布范围为![]() 节点电压分布范围的上界应小于1.05,下界大于0.95。约束表达式为:
节点电压分布范围的上界应小于1.05,下界大于0.95。约束表达式为:
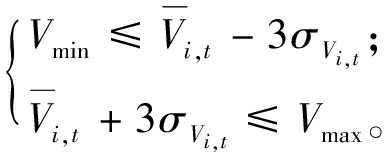
(16)
4 基于信赖域管理技术的优化模型
近年来,混合整数二阶锥优化[13-14](mixed integer second-order cone programming,MISCOP)求解技术愈见成熟。文献[10]构建了主动配电网的三相无功优化模型,并应用MISCOP技术进行求解,验证了该方法的可行性,上述文献中利用二阶锥优化技术处理连续变量,利用分支定界和割平面方法处理其他变量。因此,笔者尝试利用信赖域管理技术构建优化模型。算例验证了笔者所提模型的有效性。
信赖域管理技术[15]主要应用于求解非线性的全局优化问题。该管理技术将复杂非线性设计空间分割成一系列子空间(信赖域)。
4.1 目标函数
参照文献[8-9],笔者考虑了以下9种因素:向上级电网净购电成本、向DG购电成本、网损成本、削减DG有功出力的赔偿成本、对可中断负荷控制成本、ESS调节成本、变压器分接头调节成本、并联电容器调节成本和电压。
假定用t代表时刻,ΔT代表时段,Nt代表总时段数,P代表有功功率,M代表费用系数,ΔN代表变压器分接头档位和电容器投切状态变化次数。
Mcomp=1.5,Mloss,t=Mgrit,t,MCL,i=0.8元/(kW·h),MESS,i=0.05元/(kW·h)。
(17)
式(17)右侧累加项中各项依次为:向上级电网净购电成本、向DG购电平均成本、网损平均成本、削减DG有功出力的平均赔偿成本、对可中断负荷控制平均成本、ESS平均调节成本、变压器分接头调节成本、并联电容器调节成本,变量下标与此对应。
由于考虑了功率预测误差的统计特性,因此式(17)中的各量都是计及二阶项修正后的均值,从而保证了目标函数的准确性。
优化控制变量包括离散变量和连续变量。
离散变量:变压器档位、并联电容器投切状态。
连续变量:可控光伏发电(PV),风电(WT)的有功、无功出力,其他可控分布式电源(例如沼气发电厂BG、垃圾电厂RI)的有功、无功出力,储能设备(ESS)的有功、无功功率,可控负荷(CL)的调节功率,SVC的无功出力。连续变量可表达为节点电压向量.的显函数。
4.2 等式约束
(1)概率潮流约束。
(18)
式中:Pi,t+jQi,t为第i点的功率。
(2)储能设备容量约束。
(19)
式中:W表示电量;P为有功;η为充放电效率,本文取93.81%[16]。近似用功率的均值计算储能设备的储电量。
4.3 不等式约束
(1)储能设备的荷电状态上下限。
(20)
由于式(20)是均值约束,因此其上下限取额定容量的60%和40%[8]。
(2)节点电压、功率约束。
为简化计算过程,将节点电压、支路功率、储能设备充放电功率、风光分布式电源的有功无功、SVC的无功、可控负荷的调节功率的约束写成通用表达式:
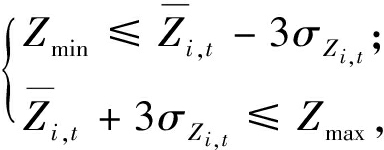
(21)
式中:Zi,t可以是节点电压、支路功率、储能设备充放电功率、风光分布式电源的有功无功、SVC的无功、可控负荷的调节功率的值;![]() 分别为第i节点第t时刻的均值和标准差。
分别为第i节点第t时刻的均值和标准差。
(3)并联电容器组数约束。
0≤Nc,i,t≤Nc,i,max,
(22)
式中:Nc,i,t为节点i处所安装的电容器组数;Nc,i,max为节点i安装的最大电容器组数。
(4)可调分接头档位数约束。
0≤Ntap,i,t≤Ntap,i,max,
(23)
式中:Ntap,i,t为第i个变压器的档位值;Ntap,i,max为第i个变压器的档位值的最大值。
4.4 信赖域管理技术基本思想
对于连续变量,均值计算中都计及协方差的修正,而协方差又可以表达成节点电压的函数。因此,直接利用节点电压的协方差进行二阶项修正。
对目标和约束构建信赖域模型。于是将优化问题转化为下面的形式:
Minimize .(.),
subjected to mi(.)≥0, i=1,2,…,p;
nj(.)=0, j=1,2,…,q,
max[.l,.l(k)]≤.≤min[.u(k),.u],
.∈[X1,X2,…,Xn],
其中,.(.)、m(.)、n(.)分别表示设计目标函数、不等式和等式约束函数模型;.l、.u分别表示设计变量的上下界;.l(k)、.u(k)分别表示设计变量在第k个信赖域上的上下界。
设当前点.k在约束条件内,则它的邻域可以定义为Ωk={.∈.n|‖.-.k‖≤r},其中,r称为信赖域半径。
目标函数在极值点附近近似一个二次函数,因此对于有约束条件问题,利用二次逼近,构造如下信赖域子问题:
(24)
式中:.=.-.k; .k为目标函数.(.)在当前迭代点.k处的梯度;.k是.(.)在.k处Hesse的近似矩阵。
.k为目标函数.(.)在当前迭代点.k处的梯度;.k是.(.)在.k处Hesse的近似矩阵。
设.k是信赖域子问题的解,目标函数.(.)在第k步的实际下降量:
Aredk=.(.k)-.(.k+.k)。
(25)
二次模型q(k)(.)的下降量:
Predk=q(k)(.)-q(k)(.k)。
(26)
定义比值:
ρ(k)=Aredk/Predk,
(27)
它衡量了二次模型与目标函数的逼近程度,ρ(k)越接近于1,表明接近程度越好。因此,我们也用这个量来确定下次迭代的信赖域半径,并把ρ(k)称为信赖度。
5 算例分析
5.1 算例系统
以IEEE 118节点系统为算例,在系统上增加主变和分布式电源、可调负荷。按所述算法,使用Fortran 6.5编写程序进行计算。
图2中分为工业负荷和生活负荷。

图2 10 kV配电网
Figue 2 10 kV distribution network
工业负荷为线路(150,66)所联的馈线2。该馈线上,节点85所接的光电功率为1.2 MW,出力可调;其余节点所接的光电功率均为0.2 MW,不可调;节点72所接的SVC容量为0.2 MVar;节点77所接的垃圾发电厂的额定功率为2 MW;节点75所接的电动汽车日平均负荷均为0.6 MW;节点85所接的储能设备额定容量均为1 MW·h,最大充放电功率0.45 MW,荷电下限19%,荷电上限89%,荷电初值40%。
生活负荷为线路(1,2)所联的馈线1和线路(150,105)所联的馈线3。两条馈线上节点27、54、121所接的出力可调的光电和风电功率与节点85处的一致;出力不可调的风电和光电功率为0.2 MW;节点121、54、27所接的储能设备额定容量与节点85处的一样;节点52所接的SVC容量与节点72处的一样;节点113所接的沼气发电厂的额定功率为2 MW;节点61、112的可调负荷功率分别为0.55+j0.35 MV·A、0.49+j0.42 MV·A;节点21、33、75、111的电动汽车日平均负荷均为0.5 MW。根据预测负荷曲线预测出标准差,表1为风电各时刻的初始标准差。图3为风电和光电标准化日运行曲线;图4为电动汽车标准化日运行曲线。
表1 风电初始标准差
Table 1 Wind power initial standard deviation
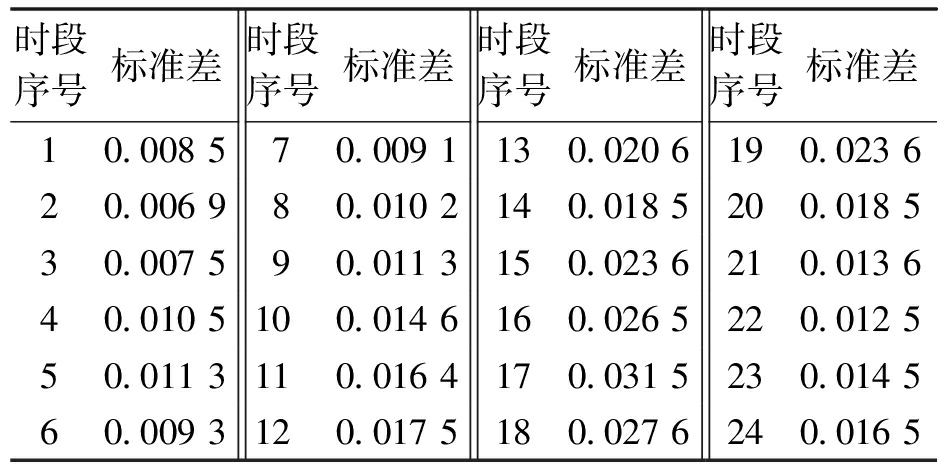
时段序号标准差时段序号标准差时段序号标准差时段序号标准差10.008570.0091130.0206190.023620.006980.0102140.0185200.018530.007590.0113150.0236210.013640.0105100.0146160.0265220.012550.0113110.0164170.0315230.014560.0093120.0175180.0276240.0165
以下价格的选取参考文献[11],风电上网电价取0.60元/(kW·h),光伏上网电价取1.00元/(kW·h),微型燃气轮机的发电成本为0.66元/(kW·h)。主动配电网与上级电网间的电能交易采用峰谷平电价制,1~7时段0.49元,8~17、23~24时段0.74元,18~22时段0.98元。离散变量调节成本系数取Ktap=20元/档,KC=2元/次[17-18]。
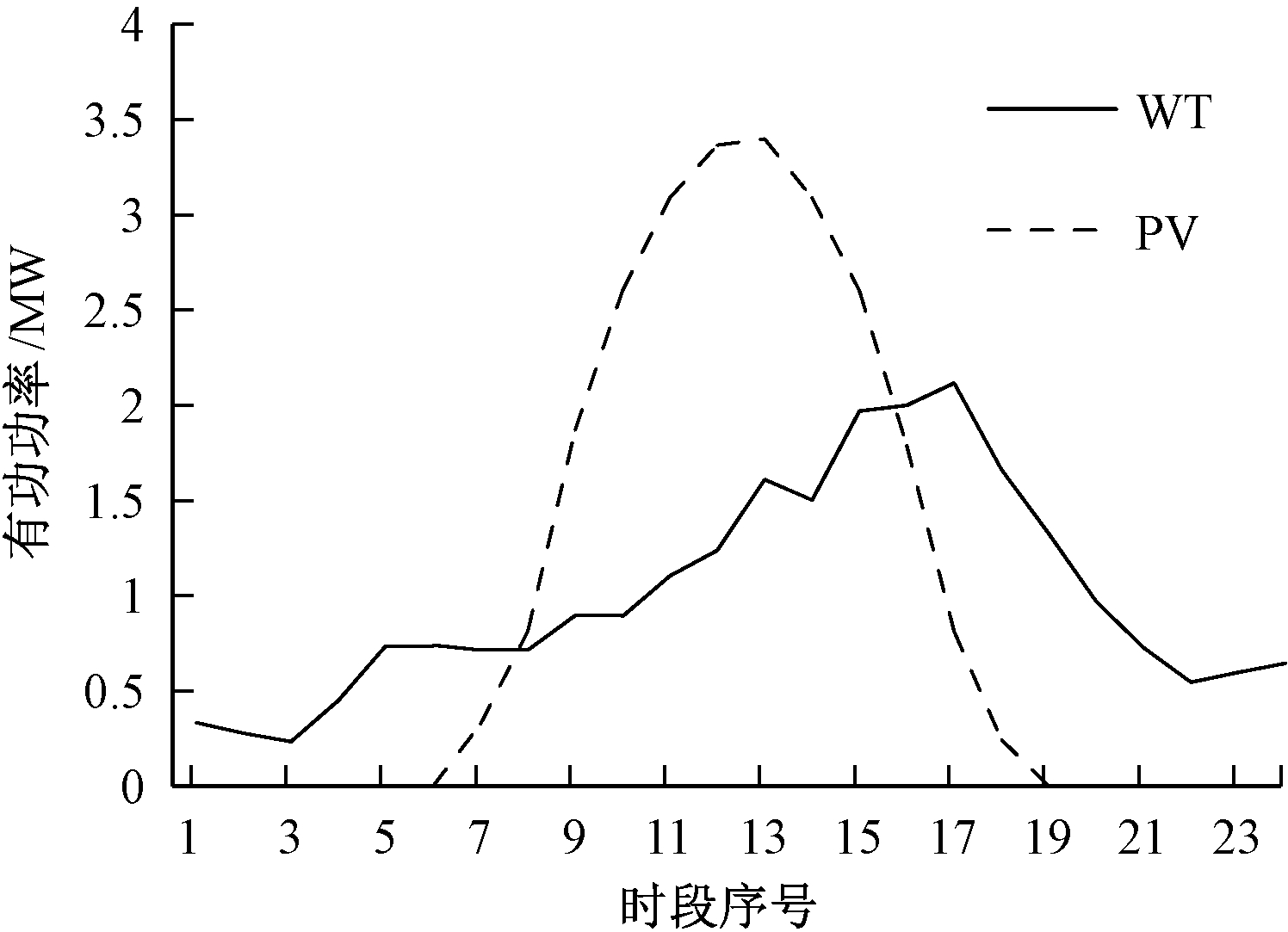
图3 风电和光电标准化日运行曲线
Figue 3 Wind power and photoelectric standardization daily operation curve
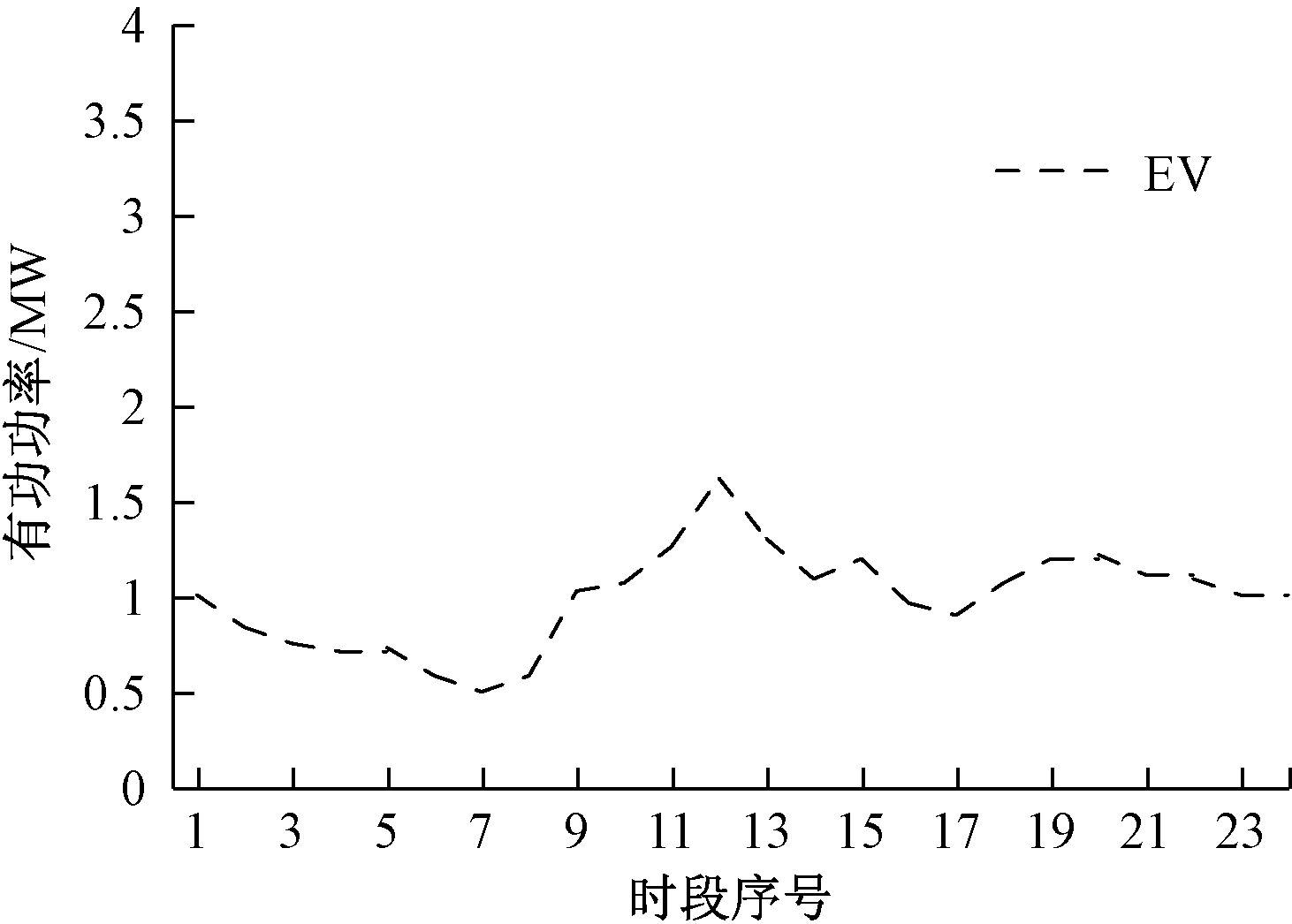
图4 电动汽车标准化日运行曲线
Figue 4 Standardized daily operation curve of electric vehicle
5.2 主动配电网运行方式优化
以日前24 h进行优化,时间间隔ΔT为1 h。
5.2.1 电容器投切状态和变压器分接头档位调整
由于算例中只有两个电容器组和两台变压器(参数为0.0345+j0.794 Ω,额定电压和分接头为110±8×0.012 5/11 kV,初始运行档位7),在变压器分接头初始运行档位的基础上取3~11档作为可选档位。电容器组投切状态及变压器分接头可调档位见表2和表3,因此优化过程中采用了更为实用的枚举法来确定电容器组的投切状态和变压器分接头的选取。
表2 电容器投切状态
Table 2 Capacitor switching state

电容器电容器投切状态C101C201
表3 变压器分接头可选档位
Table 3 Transformer tap optional gear

变压器变压器分接头档位T134567891011T234567891011
利用枚举法得到优化后电容器投切状态和变压器分接头档位,其中C1处于全切除状态。图5为电容器C2的投切状态,图6为T2变压器分接头档位变化状态。
从图5可以看出,C2在第9时段开始投切。这是由于C2连接的馈线处有生活负荷和工业负荷,该电容器在高负荷时投切,但为满足线路低压要求在低负荷时处于切除状态,选取电容器组投切状态和变压器分接头档位后再进行连续变量的优化。
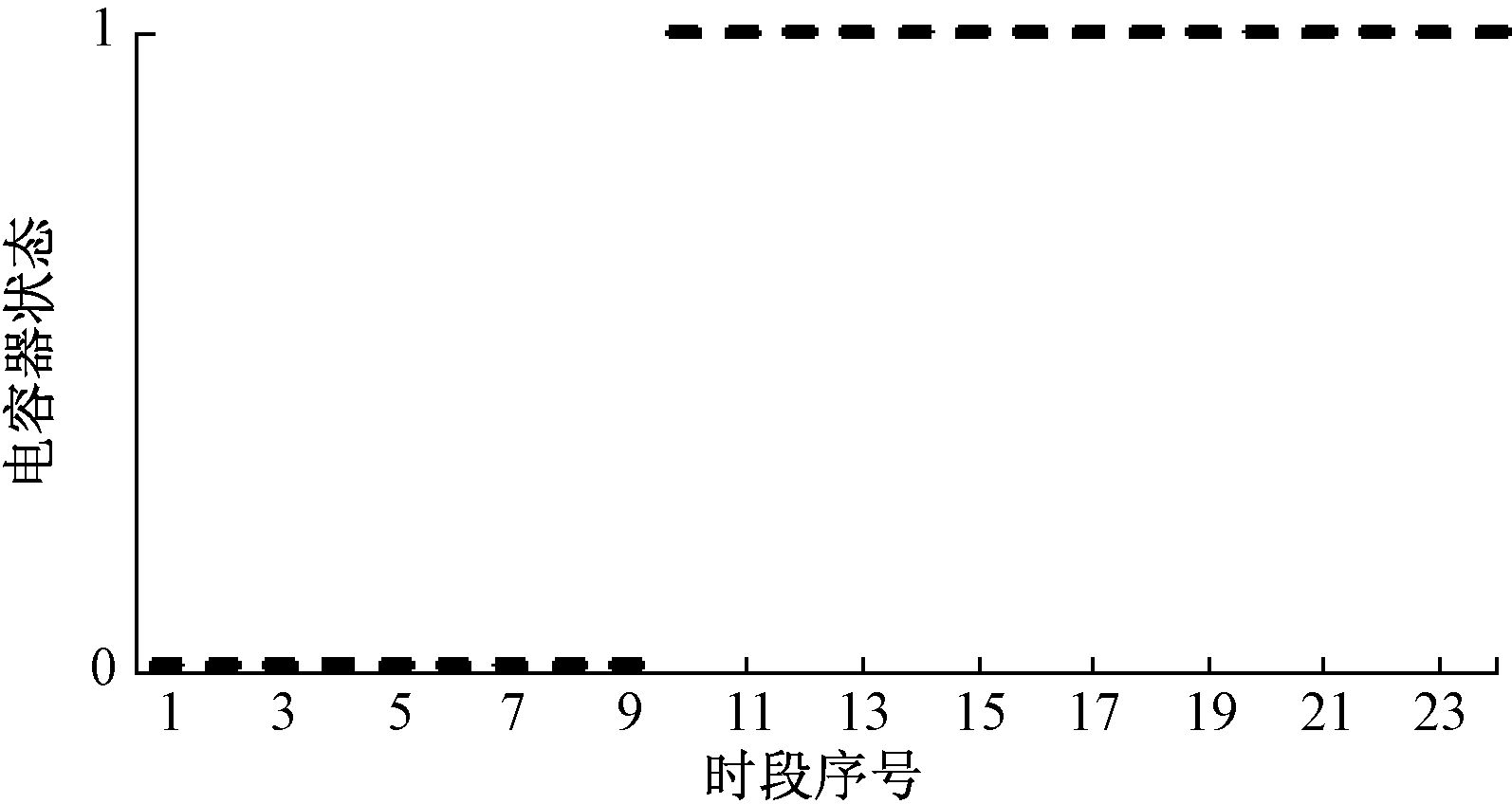
图5 电容器C2投切状态
Figue 5 Capacitor C2 dropping state
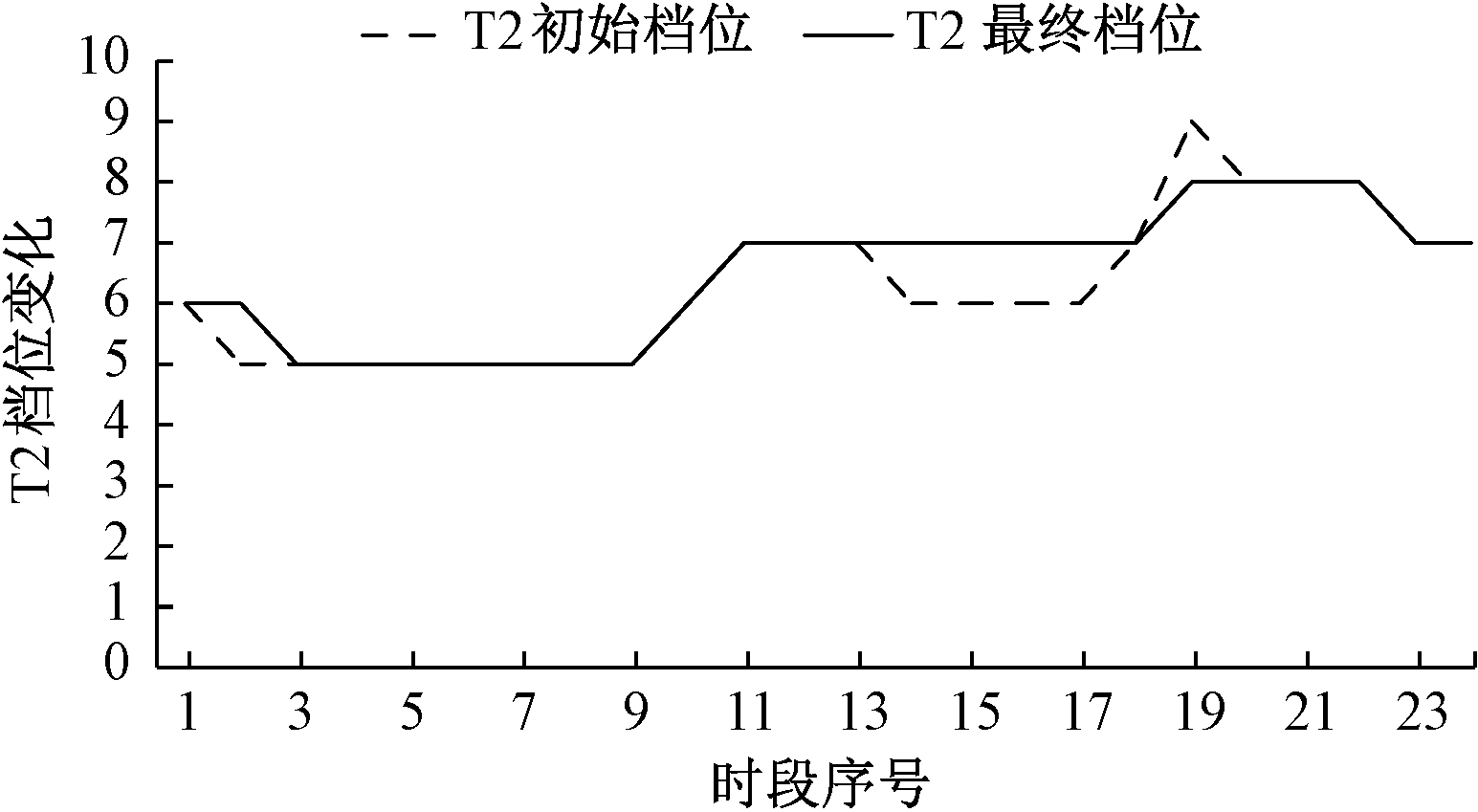
图6 T2档位变化
Figue 6 T2 change
5.2.2 约束条件概率分析
在约束条件中考虑预测误差的分布特性,使约束条件变为概率表达的形式,可以使约束边界值更加合理。在满足4.1节中约束条件下得到优化结果。优化结果表明,节点电压和支路功率都满足各自的约束条件。由于线路容量充裕,配电网中暂无功率越界风险。
以节点13为例,图7为节点13在第12时段合格的电压分布范围。图中阴影区域为该点在12时段合格的电压分布区域,其中上边界值大于0.95,下边界值小于1.05,满足约束条件。
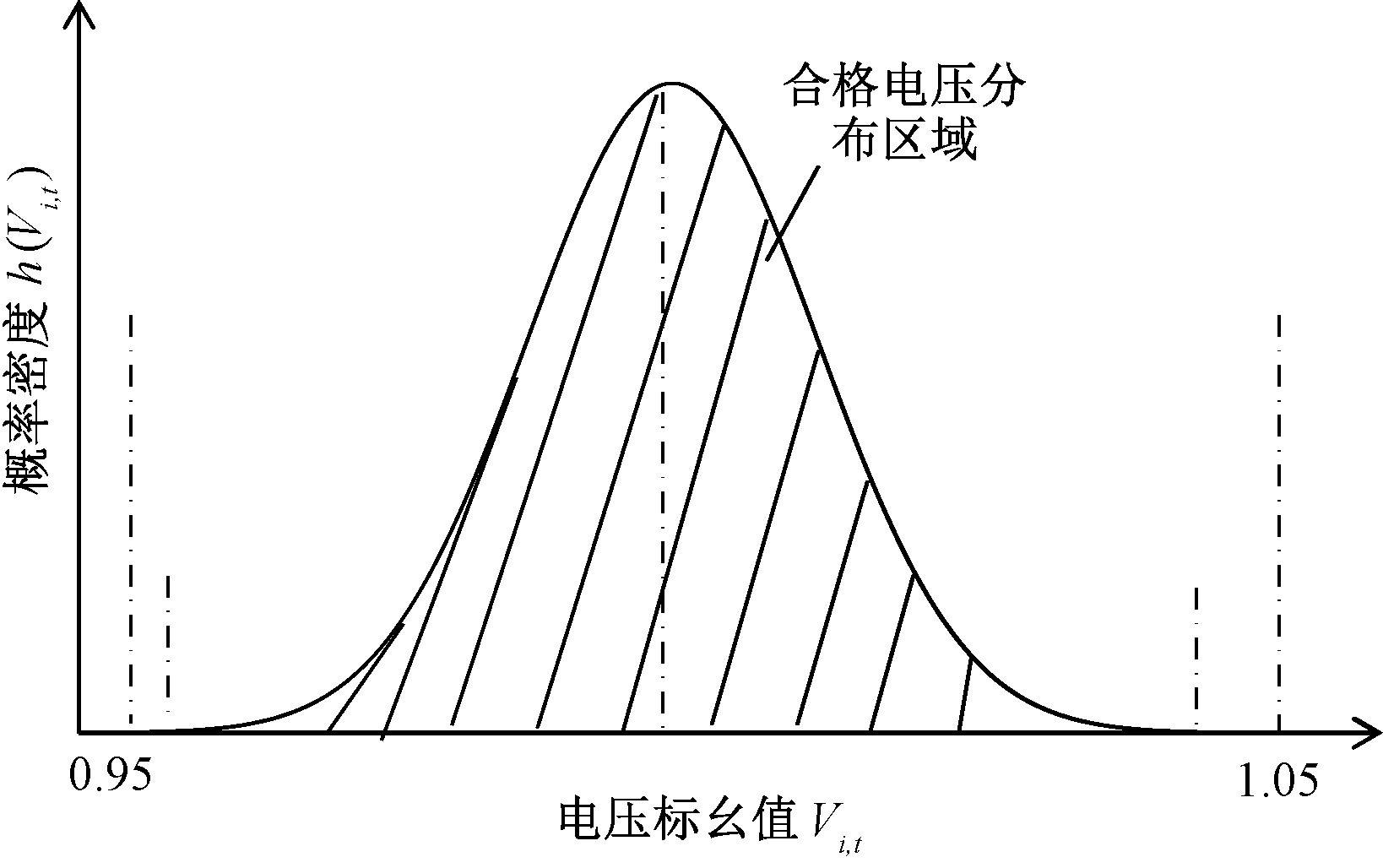
图7 合格的电压分布
Figue 7 Qualified voltage distribution
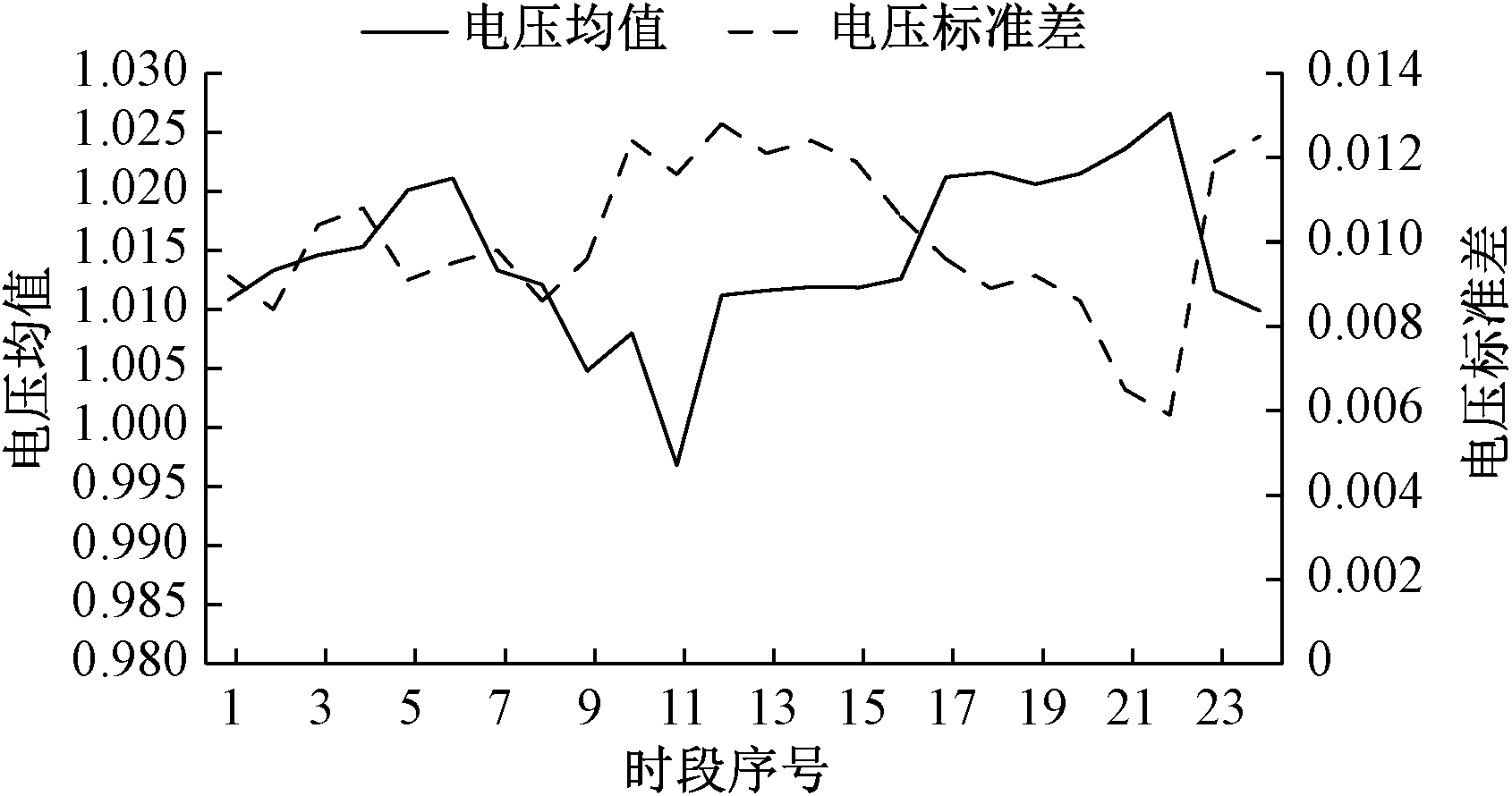
图8 节点13的电压均值和标准差
Figue 8 Voltage mean of 13 node and standard deviation
结合图2,节点13处接有光伏发电但未接储能设备。由于光伏发电的随机性,会引起电压越界风险。图8为节点13在24 h内的电压均值曲线和电压均值对应的标准差。由图8可以看出,节点13的电压值满足约束条件。
5.2.3 计及二阶修正的目标函数优化结果
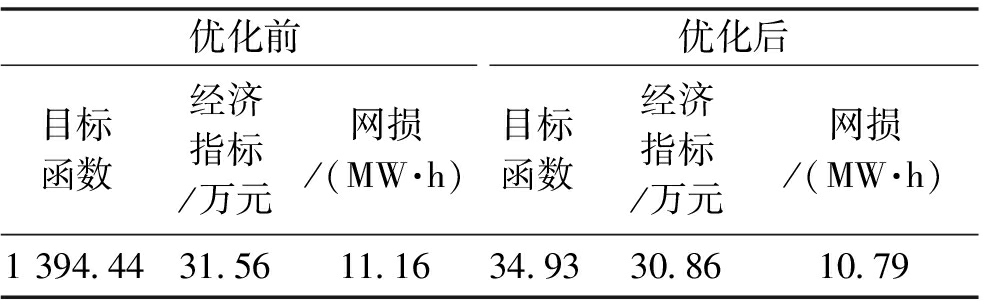
表4列出优化前后指标情况。其中第1列为式(18)中的目标函数,优化时采用。第2列为式(18)中的经济指标,即配电网的运行成本,供比较。优化前的目标函数大于经济指标,说明有电压越界。优化后二者接近,基本满足电压要求。通过优化,一天减少运行成本0.70万元,其中网损下降0.37 MW·h。
表4 优化前后指标
Table 4 Indices before and after optimization
优化前优化后目标函数经济指标/万元网损/(MW·h)目标函数经济指标/万元网损/(MW·h)1394.4431.5611.1634.9330.8610.79
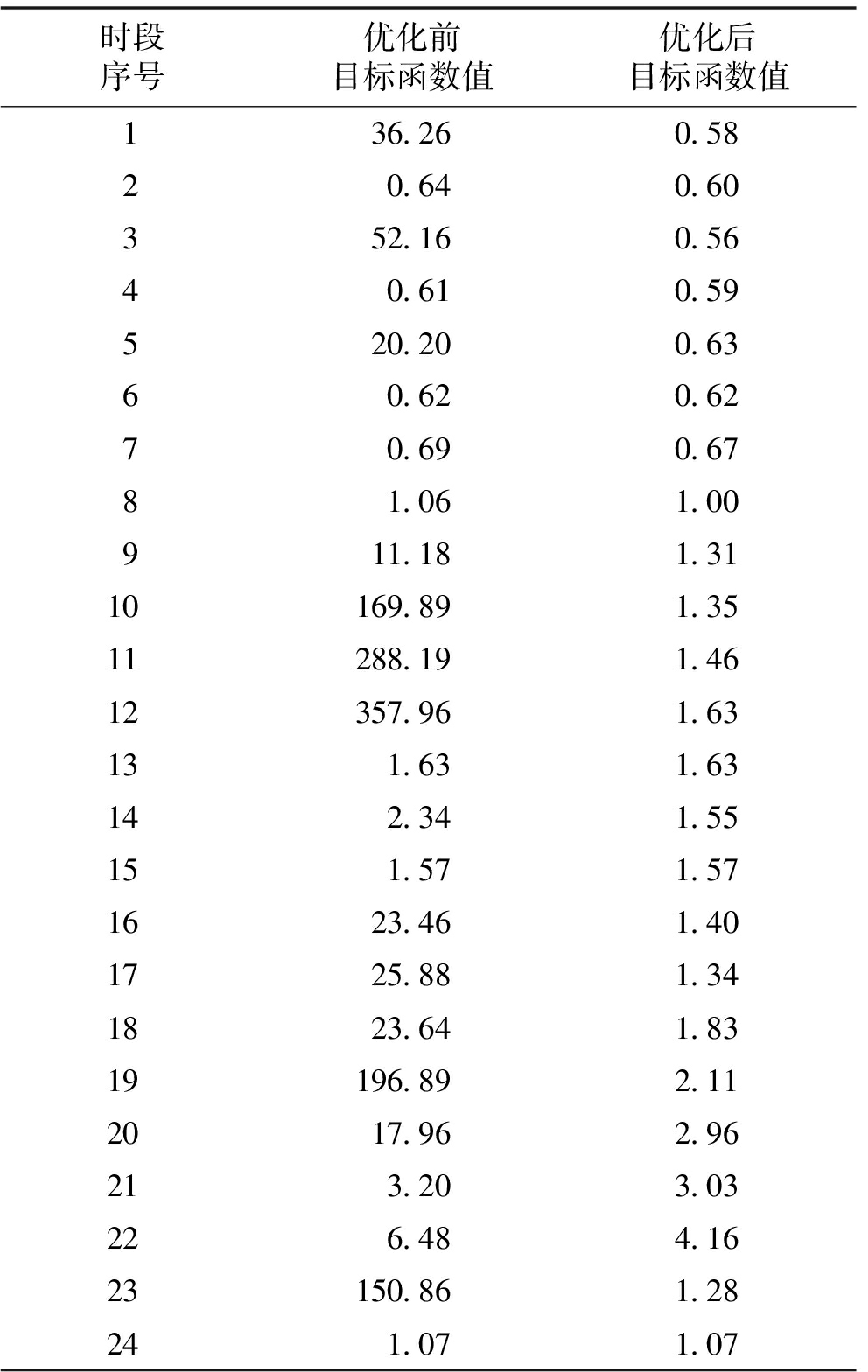
表5列出计及二阶修正的各时段指标优化前后指标情况。例如第9~12时段,优化前后,目标函数值存在偏差,优化后目标函数中的各个量均满足各自的约束条件,运行成本下降。
综上,笔者所提算法是在满足约束条件的基础上进行的优化,并且在进行连续变量优化前先对变压器分切头和电容器进行了合理的优化。因此,所提算法能较好地满足工程实用计算。
表5 各时段指标
Table 5 Indices of all time intervals
时段序号优化前目标函数值优化后目标函数值136.260.5820.640.60352.160.5640.610.59520.200.6360.620.6270.690.6781.061.00911.181.3110169.891.3511288.191.4612357.961.63131.631.63142.341.55151.571.571623.461.401725.881.341823.641.8319196.892.112017.962.96213.203.03226.484.1623150.861.28241.071.07
6 结论
笔者计及功率预测误差的分布特征,以综合运行费用的均值为目标函数,节点功率平衡方程、节点电压和支路功率等变量的运行范围构成约束条件,建立主动配电网运行方式的概率优化模型。通过分析优化算式的特点,采用二阶潮流表达的概率描述,在随机变量的均值计算中计及方差修正,提高均值计算的准确度。依据变量的实际特点,对离散变量和连续变量采用不同的处理方式,应用信赖域管理技术处理连续变量。
通过118节点配电系统进行仿真分析,不计及方差影响的功率均值比计及功率预测误差的分布特性的功率均值偏小,进而考虑分布特性的优化结果会更接近实际。与传统的分支定界、割平面等方法相比,笔者采用的迭代方式计算量小,利于实际应用,并且可与二阶锥优化方法达到相同的优化效果。
[1] 范明天,张祖平,苏傲雪,等.主动配电系统可行技术的研究[J].中国电机工程学报,2013,33(22):12-18.
[2] 杨卓,王利利,杨博,等.不同类型供电区域间典型供电模式过渡方案研究[J].郑州大学学报(工学版),2017,38(3):54-57.
[3] 任洲洋,颜伟,项波,等.考虑光伏和负荷相关性的概率潮流计算[J].电工技术学报,2015,30(24):181-187.
[4] 方斯顿,程浩忠,徐国栋,等.基于Nataf变换和准蒙特卡洛模拟的随机潮流方法[J].电力自动化设备,2015,35(8):38-44.
[5] 鲍海波,韦化.考虑风电的电压稳定概率评估的随机响应面法[J].中国电机工程学报,2012,32(13):77-85.
[6] 何琨,徐潇源,严正,等.基于稀疏多项式混沌展开的孤岛微电网概率潮流计算[J].电力系统自动化,2019,43(2):67-75.
[7] 艾小猛,文劲宇,吴桐,等.基于点估计和 Gram-Charlier 展开的含风电电力系统概率潮流实用算法[J].中国电机工程学报,2013,33(16):16-22.
[8] 符杨,廖剑波,李振坤,等.考虑越限风险的主动配电网日前优化调度及运行[J].中国电机工程学报,2017,37(21): 6328-6338.
[9] 张璐,唐巍,丛鹏伟,等.含光伏发电的配电网有功无功资源综合优化配置[J].中国电机工程学报,2014,34(31):5525-5533.
[10] 刘一兵,吴文传,张伯明,等.基于混合整数二阶锥规划的主动配电网有功-无功协调多时段优化运行[J].中国电机工程学报,2014,34(16): 2575-2583.
[11] 盛骤,谢式千,潘承毅.概率论与数理统计[M].北京:高等教育出版社,2008.
[12] 陈珩.电力系统稳态分析[M].北京:中国电力出版社,2007.
[13] ALIZADEH F, GOLDFARB D.Second-order cone programming[J].Mathematical programming, 2003,95(1):3-51.
[14] BEN-TAL A, NEMIROVSKI A.On polyhedral approximations of the second-order cone[J].Mathematics of operations research, 2001,26(2):193-205.
[15] 陈国栋.基于代理模型的多目标优化方法及其在车身设计中的应用[D].长沙:湖南大学,2012.
[16] 王成山,于波,肖峻,等.平滑可再生能源发电系统输出波动的储能系统容量优化方法[J].中国电机工程学报,2012,32(16):1-8.
[17] 周晓娟,王奎英,张将.基于辅助函数思想的城市高压电网无功优化[J].郑州大学学报(工学版),2014,35(4):79-82.
[18] 张红斌,王克文.采用模块化求解的主动配电网优化运行[J].郑州大学学报(工学版),2019,40(1):24-31.