0 引言
2004 年,英国曼彻斯特大学的Andre Geim和Konstantin Novoselov利用透明胶带成功地将石墨烯从石墨中剥离[1].石墨烯是理论单层厚度约为0.34 nm[2]的准二维材料,石墨烯的抗拉强度为125 GPa,杨氏模量为1 TPa[3],是目前已知强度最大的材料;同时,其优异的机械性能与电学性能[4-5],使其成为纳机电系统理想的应用材料.
2007年,美国康奈尔大学Bunch课题组首次将石墨烯膜应用于谐振器[6],并对石墨烯谐振频率进行测量和分析.2010年,Zande等[7]利用化学气相沉积法制作出单层石墨烯谐振器,发现谐振频率随静电栅极电压而变化,品质因数随温度冷却显著提高,在10 K情况下可以达到9 000.2016年,Habibi等[8]提出一种基于石墨烯的微型场致发射压力传感器,在5 V的偏置电压下实现约21.9 μA/Pa的最大灵敏度.综上所述,石墨烯作为谐振子有望使得谐振式压力传感器实现更高灵敏度的测量.但石墨烯谐振式传感技术的研究尚处于理论分析和数值仿真阶段,针对低压力下传感器结构的设计以及相关的实验研究还缺乏公开文献报道.
笔者提出一种用石墨烯材料作为谐振子的压力传感器的方案:通过ANSYS有限元分析软件,对谐振器的参数进行探究.研究梁的尺寸、硅膜片的结构参数对于传感器性能的影响,总结这些因素对压力传感器测量灵敏度的影响规律,从而建立起石墨烯谐振式压力传感器结构的有限元模型.最后对于此谐振子的制备提出初步方案.
1 敏感结构设计
石墨烯谐振式压力传感器敏感结构如图1所示.采用硅作为基底材料,用热氧化的方法形成二氧化硅绝缘层.硅基底下方刻蚀出的凹槽作为一次敏感元件,直接感受被测压力,将被测压力转化为二氧化硅膜片上的应力与应变;在二氧化硅绝缘层刻蚀出凹槽,将石墨烯梁转移到凹槽上作为二次敏感元件,感受二氧化硅膜片上的应力,即间接感受被测压力.压力变化导致石墨烯梁的等效刚度发生变化,从而使梁的固有频率随被测压力的变化而变化.通过测量石墨烯梁的谐振频率,即可解算出被测压力大小.
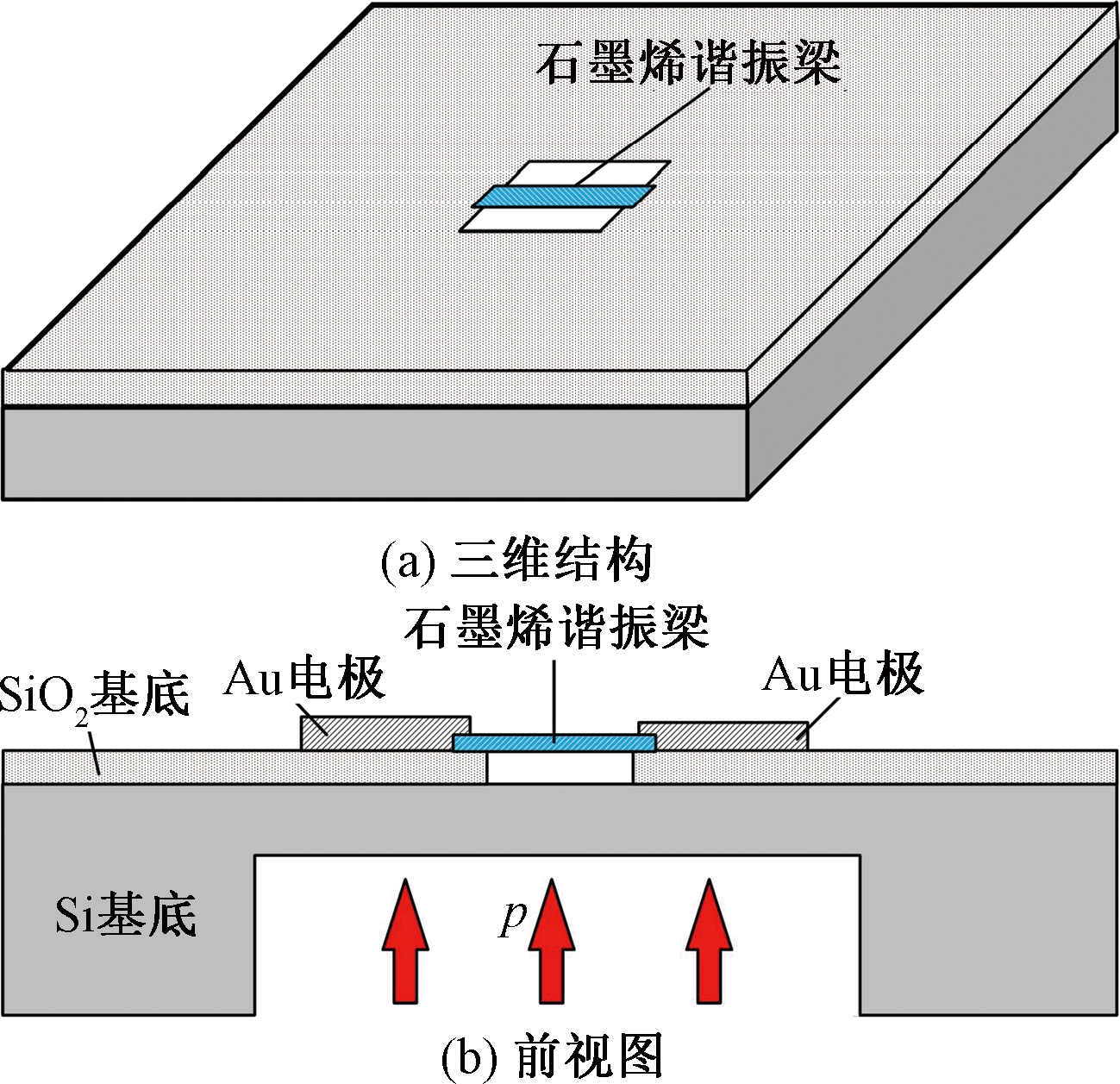
图1 石墨烯谐振式压力传感器结构示意图
Fig.1 Graphene resonant pressure sensor structure
2 压力膜片理论分析
首先对所建立的石墨烯谐振式压力传感器模型进行理论分析.在方形膜片中心建立直角坐标系,如图2所示.xOy平面与方形膜片中平面重合,z轴向上,在均布载荷p下,膜片法向位移为[9]
(1)
(2)
式中:w(x,y)为膜片法向位移,m;μ为梁材料的泊松比;p为膜上均布载荷(压力),![]() 为在均布载荷p的作用下方形膜片的最大法向位移和其厚度的比值,无量纲;A、H分别为膜片半边长和厚度,m;E为梁材料的杨氏模量,Pa.
为在均布载荷p的作用下方形膜片的最大法向位移和其厚度的比值,无量纲;A、H分别为膜片半边长和厚度,m;E为梁材料的杨氏模量,Pa.
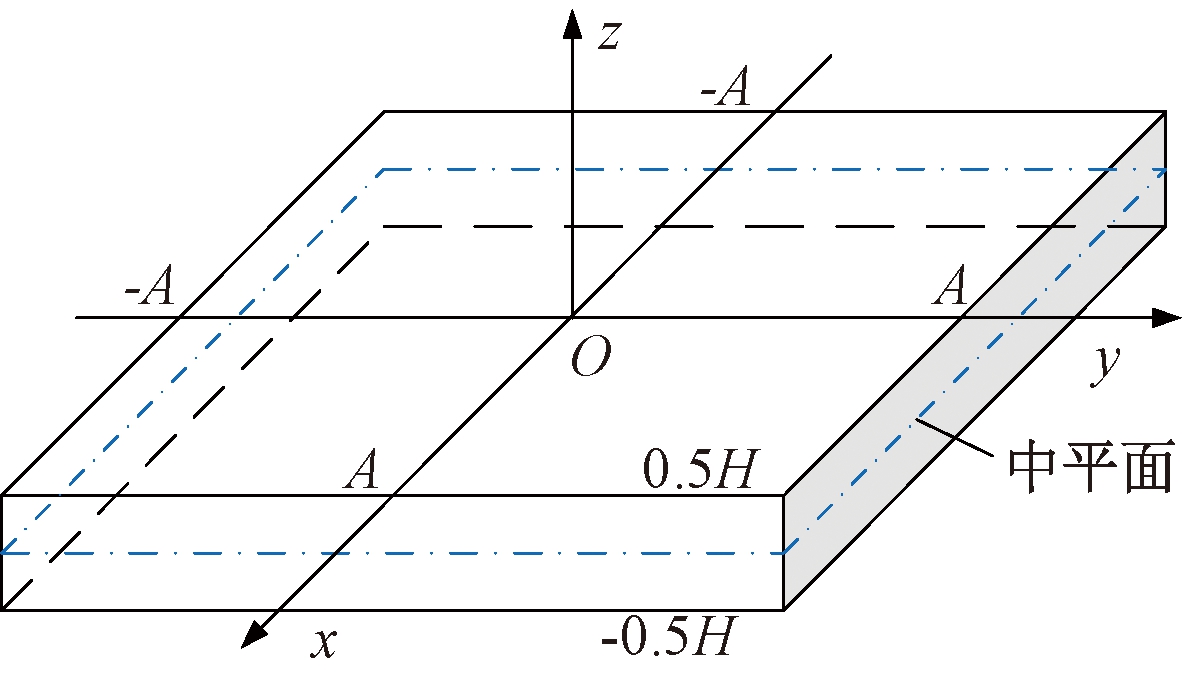
图2 方形膜片示意图
Fig.2 Diagram of square membrane
根据敏感结构的工作机理,当谐振子梁沿着横轴设置在x∈[X1,X2](X1<X2),由均布载荷p所引起的谐振子梁的初始应力[9]为:
(3)
(4)
(5)
式中:σ0为梁所受的轴向应力,Pa;X1、X2为梁在方形膜片直角坐标系中的坐标值,m;u1、u2为梁在两个端点X1、X2处的轴向位移,m;L、h分别为梁的长度和厚度,m.
在初始应力σ0(即均布载荷p)作用下,双端固支梁的一阶固有频率[9]为:
(6)
(7)
(8)
(9)
式中:ρ为梁材料密度,kg/m3;fB1、fB1(p)分别为双端固支梁在无均布载荷和有均布载荷的情况下的一阶固有频率,Hz.
3 敏感结构有限元仿真
笔者利用ANSYS Workbench18.0对石墨烯谐振子进行有限元仿真.有限元方法可以探究不同参数的石墨烯谐振子的振动性质,从而对基于石墨烯的谐振器进行准确建模,在实践中更好地指导实验设计.
在仿真中将石墨烯梁当作壳体单元进行处理,硅基底和二氧化硅绝缘层当作固体单元建模,通过多点约束方式实现壳体-固体单元的连接.
ANSYS仿真参数如图3所示,初始参数硅基底边长2A=100 μm,厚度H1=20 μm;二氧化硅绝缘层边长2A=100 μm,厚度H2=1 μm;凹槽边长l=60 μm,深度D=15 μm;石墨烯梁长度L=10 μm,宽度B=2 μm,厚度h=0.34 nm.
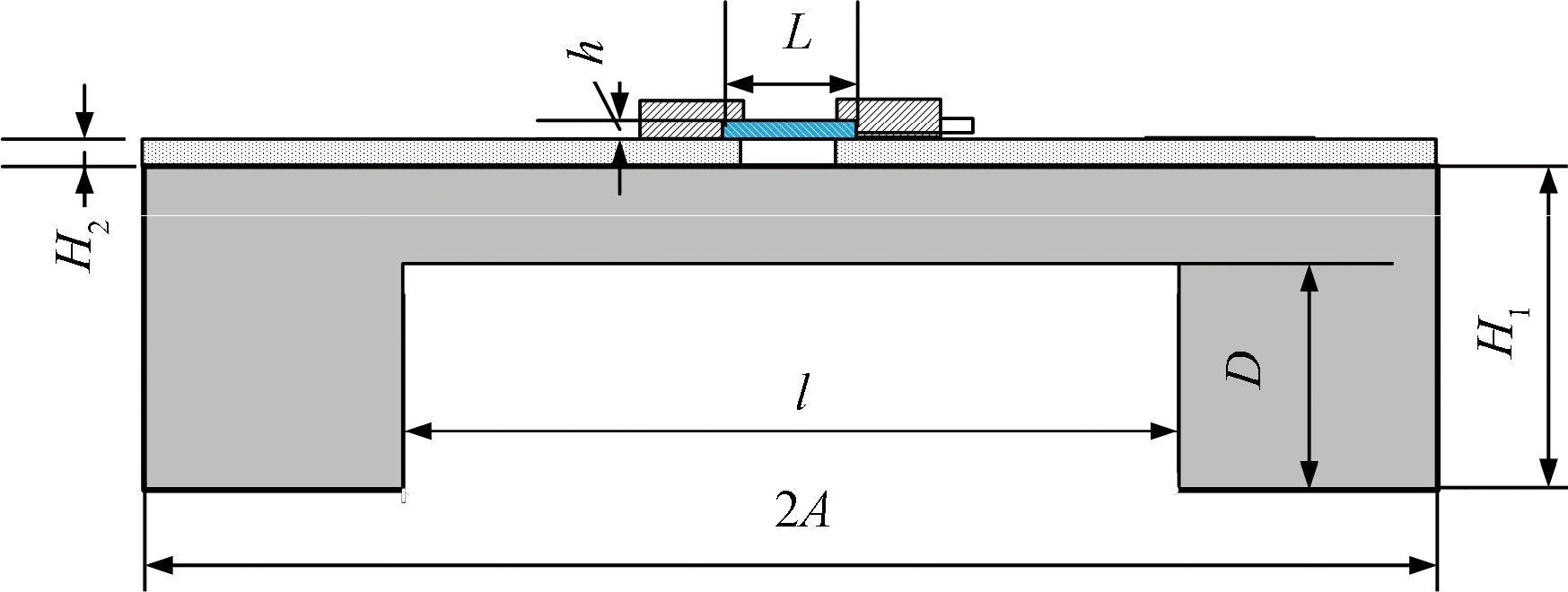
图3 谐振子仿真参数图
Fig.3 Resonator simulation parameter diagram
3.1 谐振子静力学分析
谐振子底端凹槽受静态均布载荷的作用,惯性和阻尼可以忽略,在静态载荷作用下,谐振子处于静力平衡状态.为仿照硅基座的固定作用,对硅基底底面施加固定约束,由于不考虑惯性,质量对于谐振子无影响.同时载荷周期远远大于谐振子自振周期,这种情况下可以简化为线性静力进行分析.谐振子在上述约束作用下,等效应力、应变仿真如图4、图5所示.由图可见,谐振子上应力、应变分布同理论分析一致.方形硅膜片直接感受被测压力,将被测压力转化为膜片的应力与应变;石墨烯梁作为二次敏感元件感受膜片上的应力,当发生较大的应变时,等效刚度发生变化.
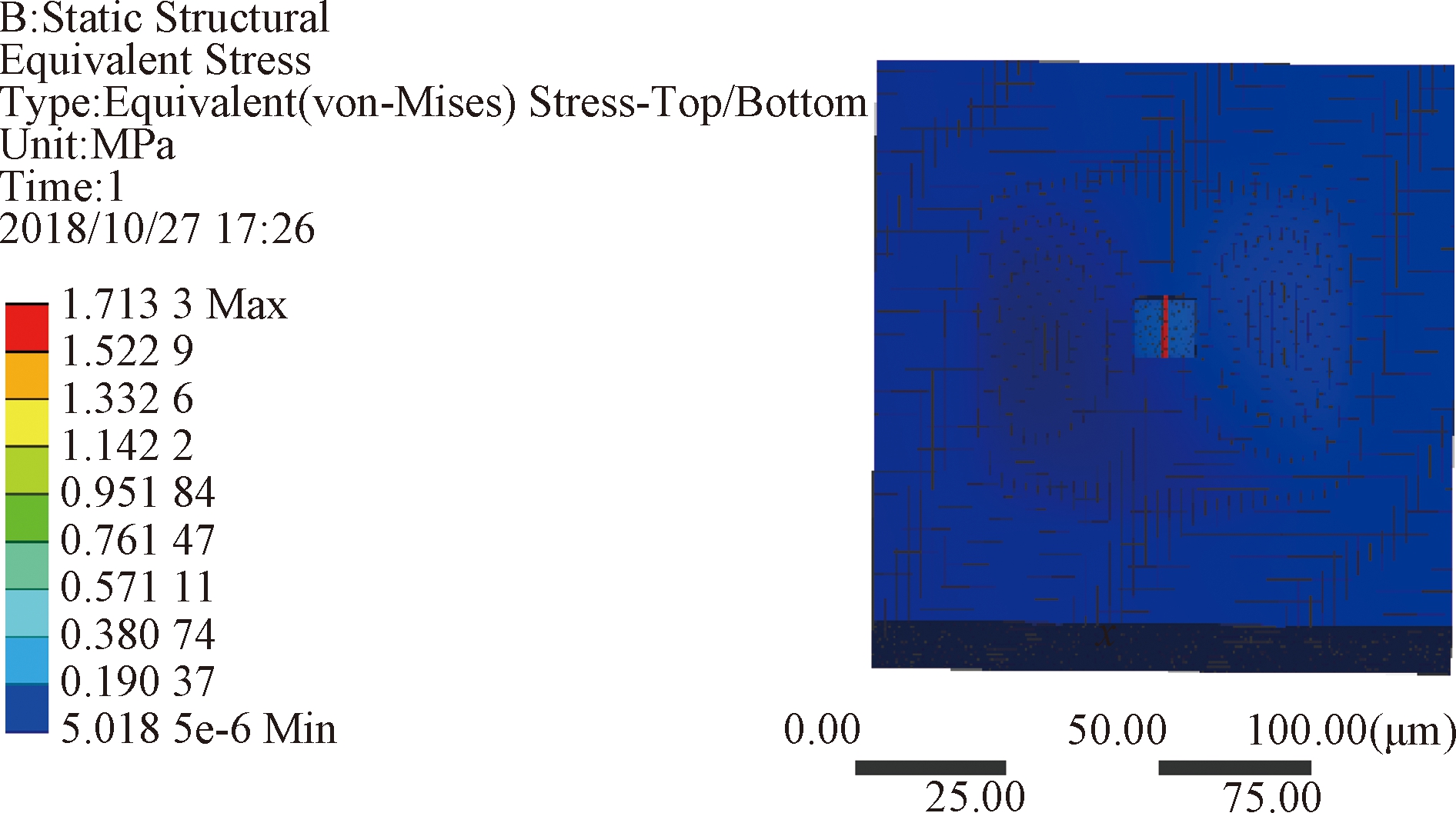
图4 谐振子等效应力分布
Fig.4 Resonator equivalent stress distribution
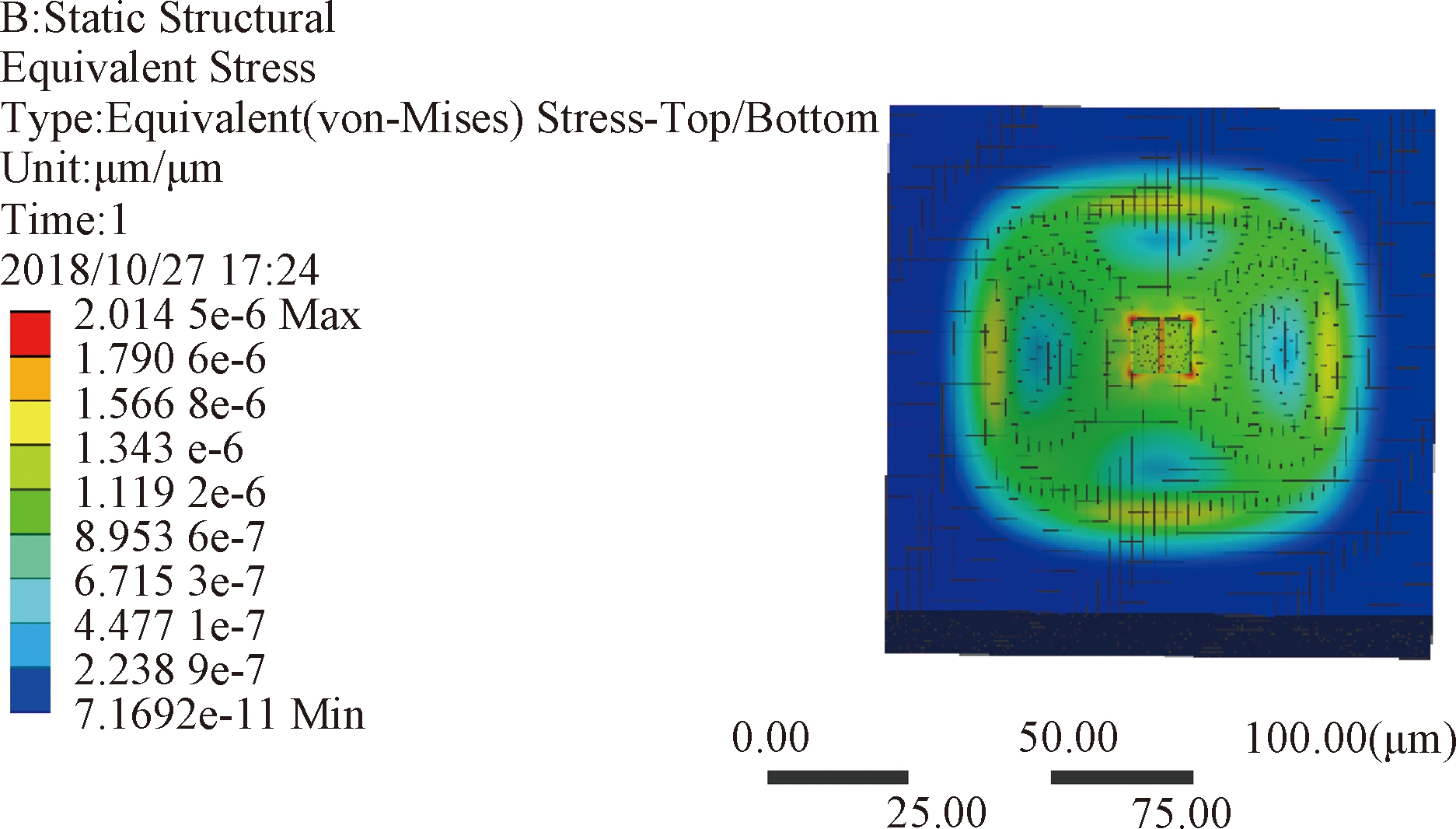
图5 谐振子等效应变分布
Fig.5 Resonator equivalent strain distribution
为了研究低压力下的谐振器的性能,所以对10 kPa以下的均布载荷进行有限元仿真,仿真结果如图6所示.石墨烯谐振梁的谐振频率随均布载荷的增加而增加,谐振频率随均布载荷呈非线性增加.在≤0.5 kPa情况下对数据进行线性拟合,系数R2=0.957 3;在(5 kPa,10 kPa]对数据进行线性拟合,决定系数R2=0.997 5,同时灵敏度达到81.30 Hz/Pa,高于传统的谐振式压力传感器的灵敏度[10].
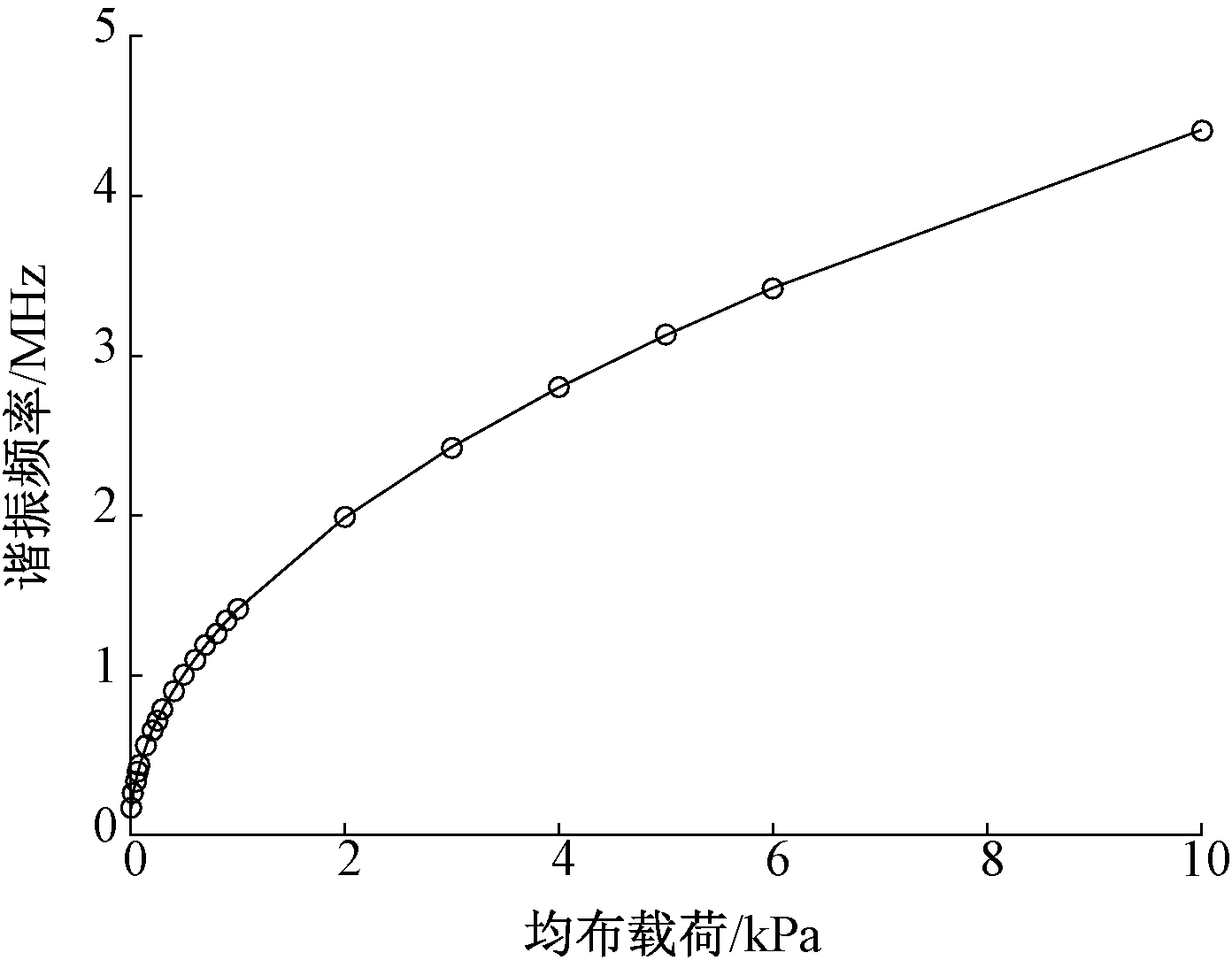
图6 石墨烯谐振频率随均布载荷变化关系
Fig.6 Graphene resonance frequency changes with pressure
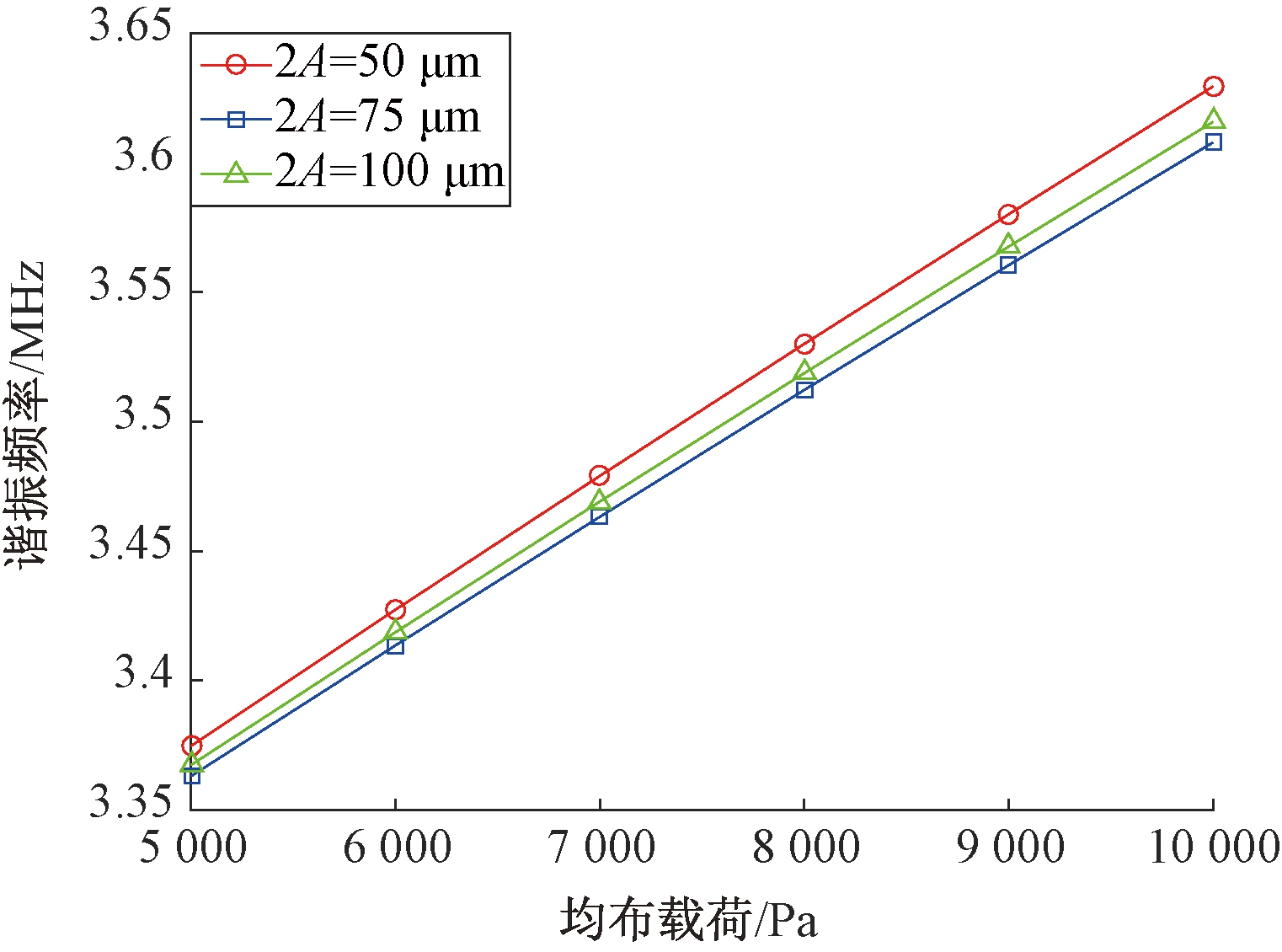
图7 硅膜边长对梁谐振频率影响
Fig.7 Effects of silicon membrane length on resonant frequency of beam
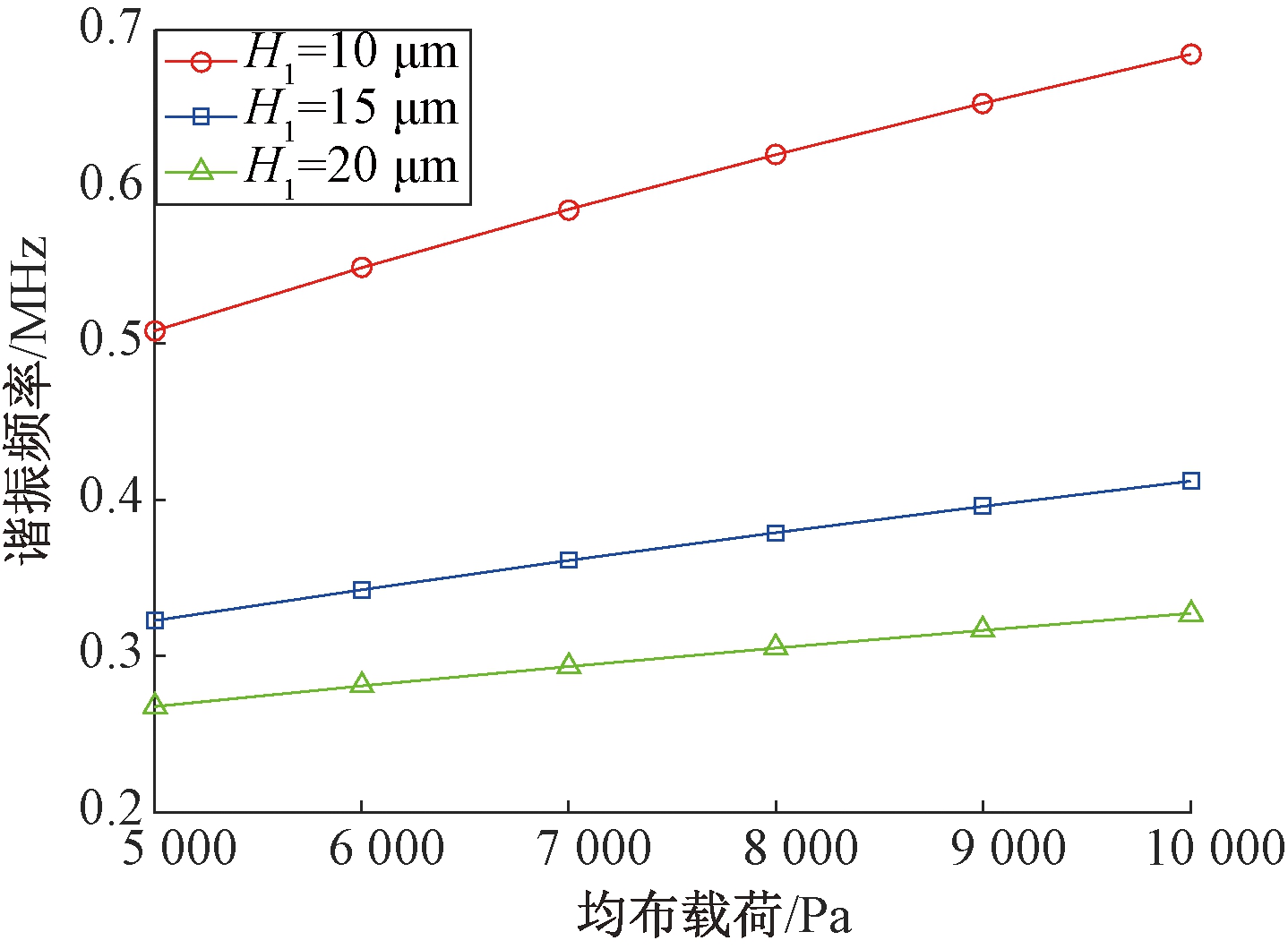
图8 硅膜厚度对梁谐振频率影响
Fig.8 Effects of silicon membrane thickness on resonant frequency of beam
3.2 结构参数分析
石墨烯谐振器的灵敏度受谐振器本身结构多个参数综合影响,为探究这些参数对于灵敏度的影响规律,独立地改变各参数量,进行仿真.
首先探究硅基底各参数对于灵敏度的影响.在石墨烯谐振子梁和凹槽尺寸参数不变的情况下,分别改变硅基底的边长和厚度,结果如图7、8所示.硅基底的边长分别取值为50、75、100 μm,随着硅基底边长增大,相同载荷下,边长为50 μm时石墨烯梁的谐振频率最高;边长为75 μm时石墨烯梁的谐振频率最低.不同边长情况下,谐振子的灵敏度(曲线的斜率)均没有明显变化.厚度方面,在保持硅基底半边A=50 μm,凹槽深度D=5 μm不变的情况下,硅膜厚度分别为10、15、20 μm进行有限元仿真,对应灵敏度为35.41、17.86、11.95 Hz/Pa;相应的线性拟和程度R2为0.997 8、0.998 6、0.998 8.结果表明:灵敏度随硅膜片厚度增加而降低,线性度随膜片厚度增加而增加.
其次探究凹槽的结构参数对于谐振器的影响.对凹槽边长的研究结果如图9所示.随着凹槽边长的提高,梁谐振频率增加,谐振器的灵敏度(曲线斜率)提高.对于凹槽深度D的探究,在硅膜厚度H1=20 μm情况下,分别取D=5、10、15 μm进行仿真,结果如图10所示.结果表明:谐振器灵敏度随着凹槽深度的增加而提高,相同均布载荷下,凹槽深度越深,梁的谐振频率越大,但同时非线性程度加深.
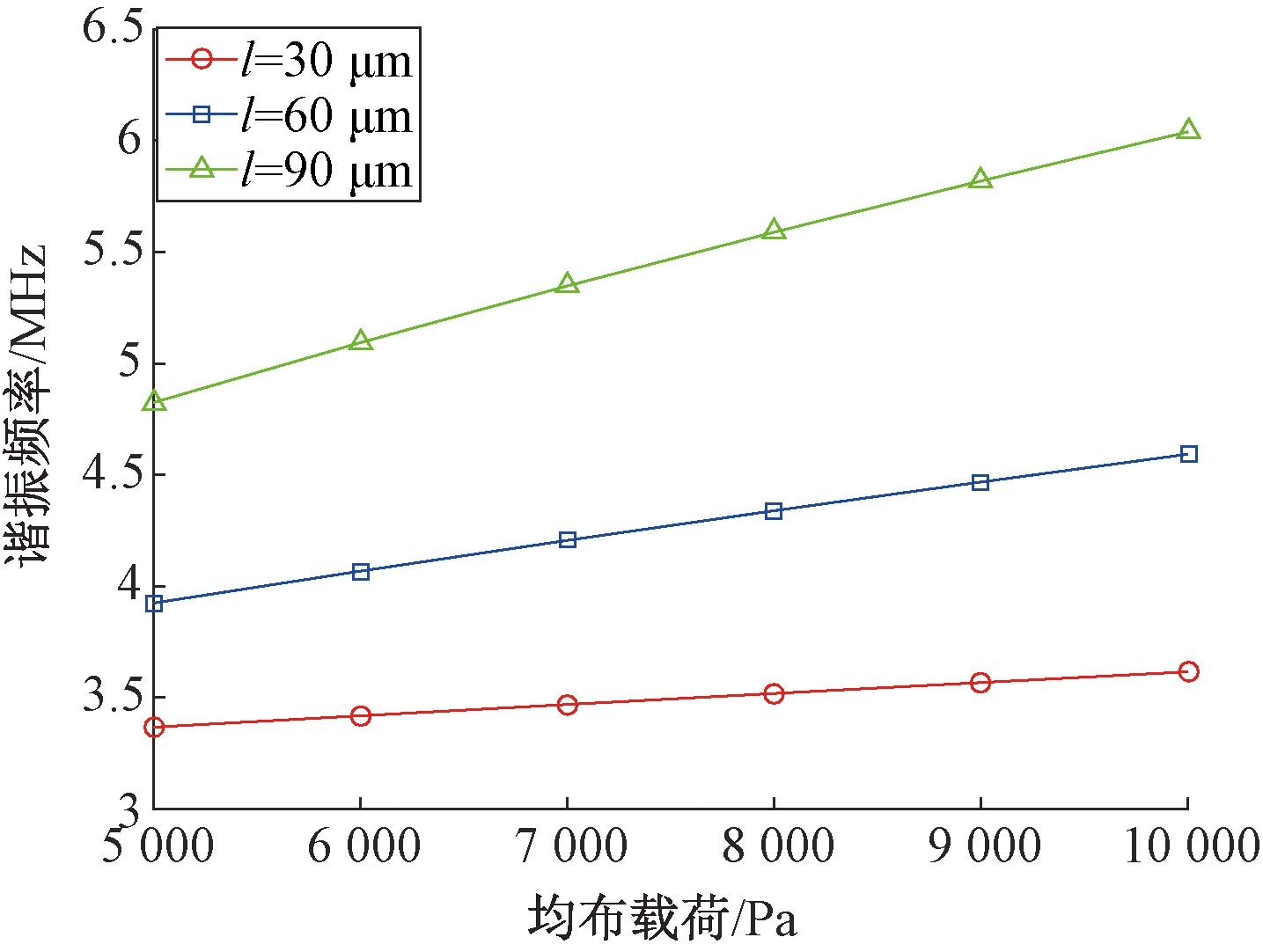
图9 凹槽边长对梁谐振频率影响
Fig.9 Effects of groove length on resonant frequency of beam
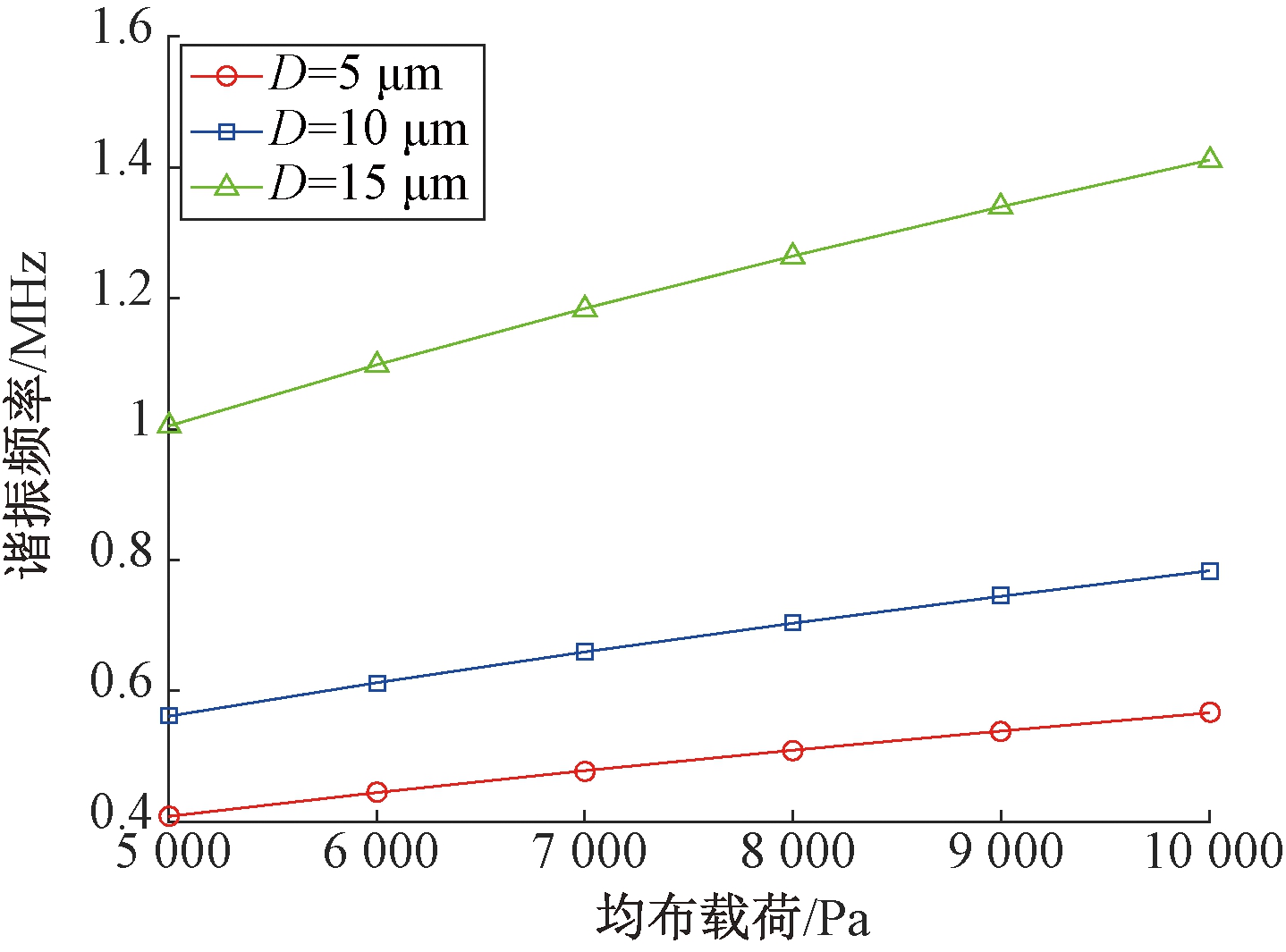
图10 凹槽深度对梁谐振频率影响
Fig.10 Effects of groove depth on resonant frequency of beam
最后研究石墨烯梁的位置和梁的结构参数对于谐振频率的影响.首先改变梁的位置,使其在二氧化硅绝缘层上沿图x轴正半轴进行平移即梁分别位于膜中心位置、膜1/4位置和膜边沿位置进行仿真,结果如图11所示.结果表明:梁位于中心位置时,相同载荷下谐振频率最高,压力灵敏度最大;梁位于1/4位置时,谐振频率随均布载荷增加而增大,压力灵敏度小于中心位置处;梁位于膜片边沿时,谐振频率随均布载荷无明显变化规律.
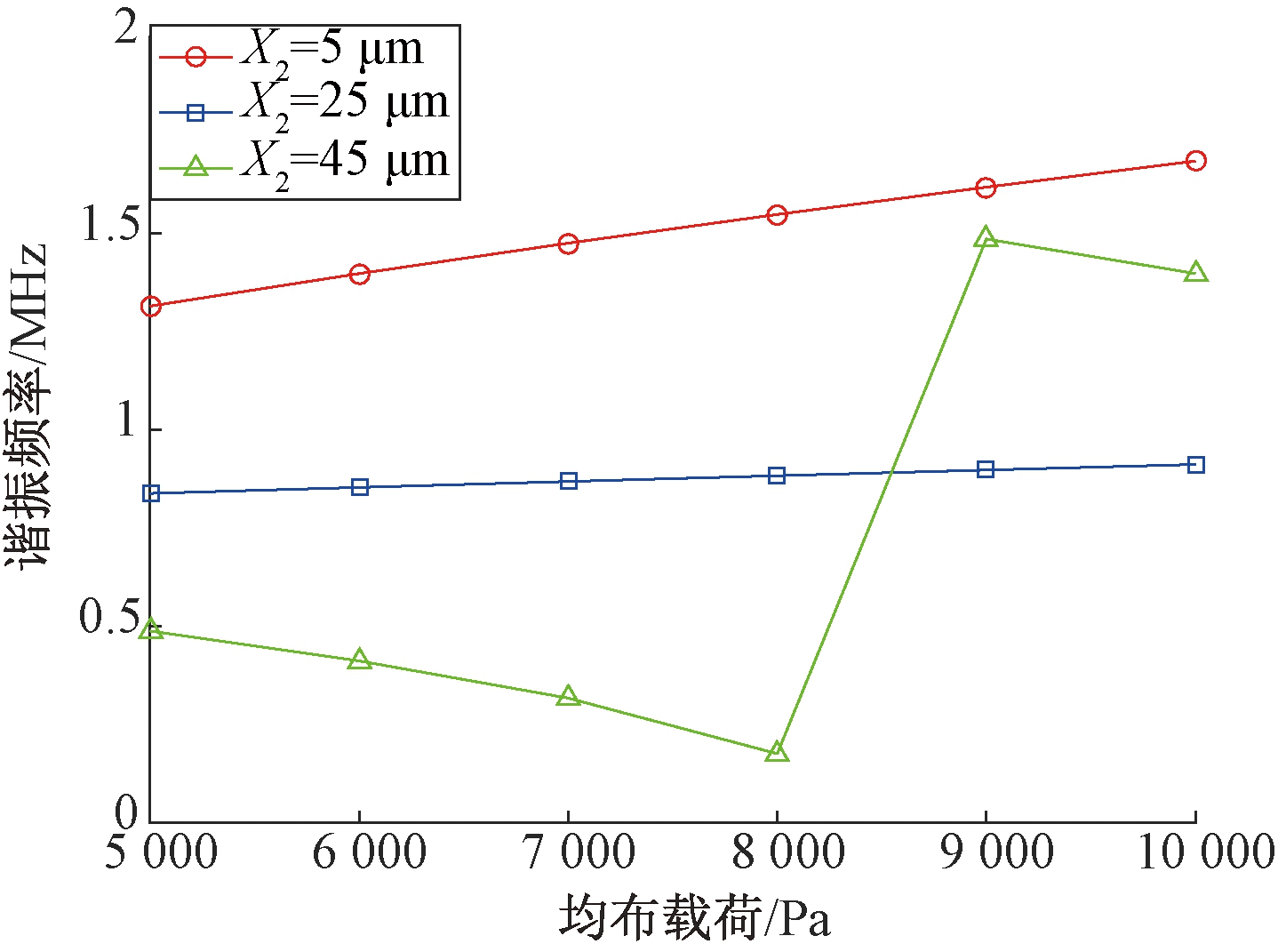
图11 梁的位置对梁谐振频率影响
Fig.11 Effects of beam position on resonant frequency of beam
其次研究梁的结构参数对于灵敏度的影响规律.石墨烯梁长度、宽度影响规律如图12所示.结果表明:长度不变,长宽比改变,均布载荷与梁谐振频率的曲线几乎重合,说明宽度对于谐振子灵敏度影响很小.宽度不变,长宽比增加,斜率下降,谐振器的灵敏度降低,非线性程度减小.在石墨烯梁长度与宽度均不变的情况下,改变梁的厚度进行仿真,结果如图13所示.结果表明:石墨烯单层厚度为0.34 nm,厚度增加,相同载荷下梁的谐振频率增加,灵敏度无明显变化.
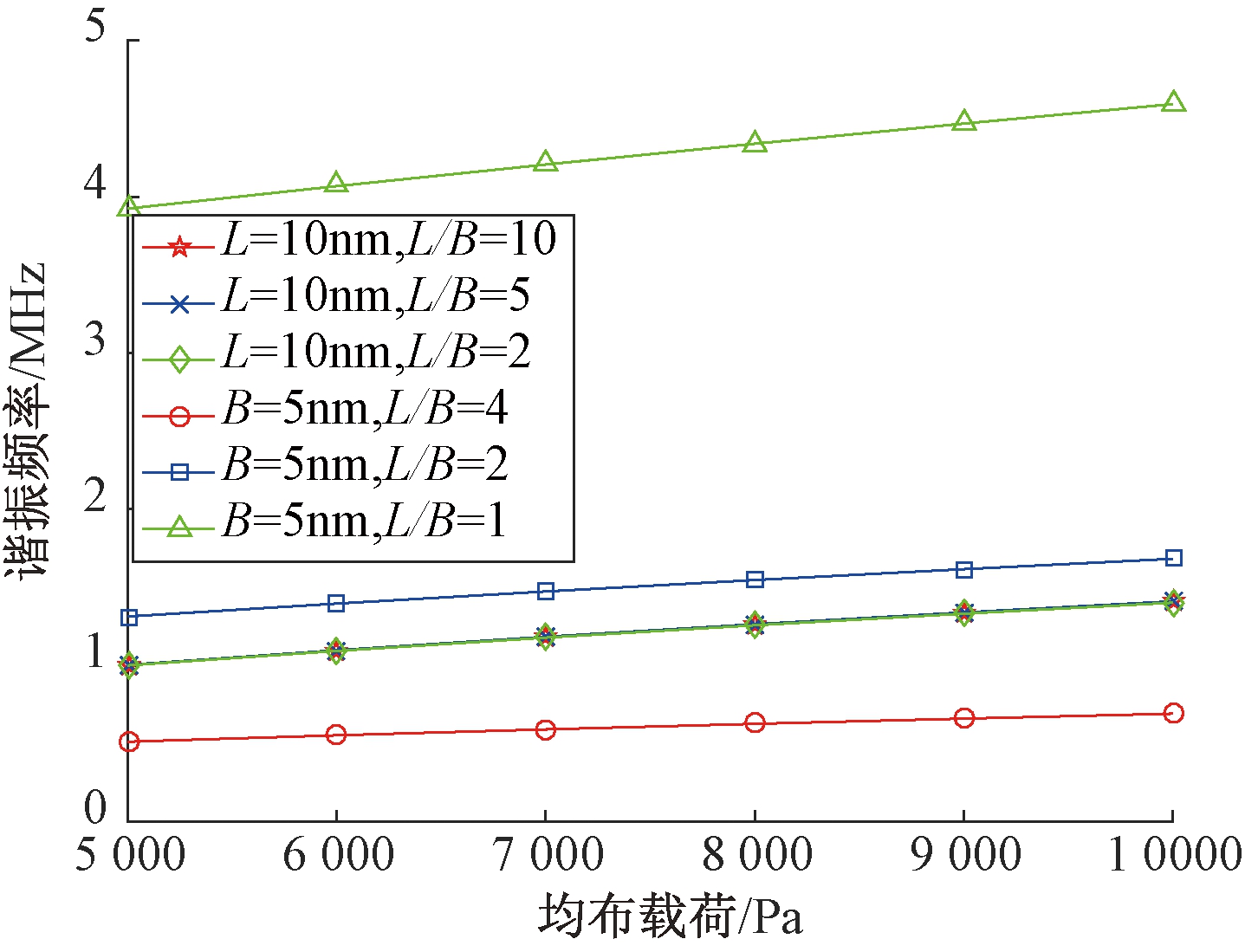
图12 梁的长、宽度对梁谐振频率影响
Fig.12 Effects of beam length and width on resonant frequency of beam
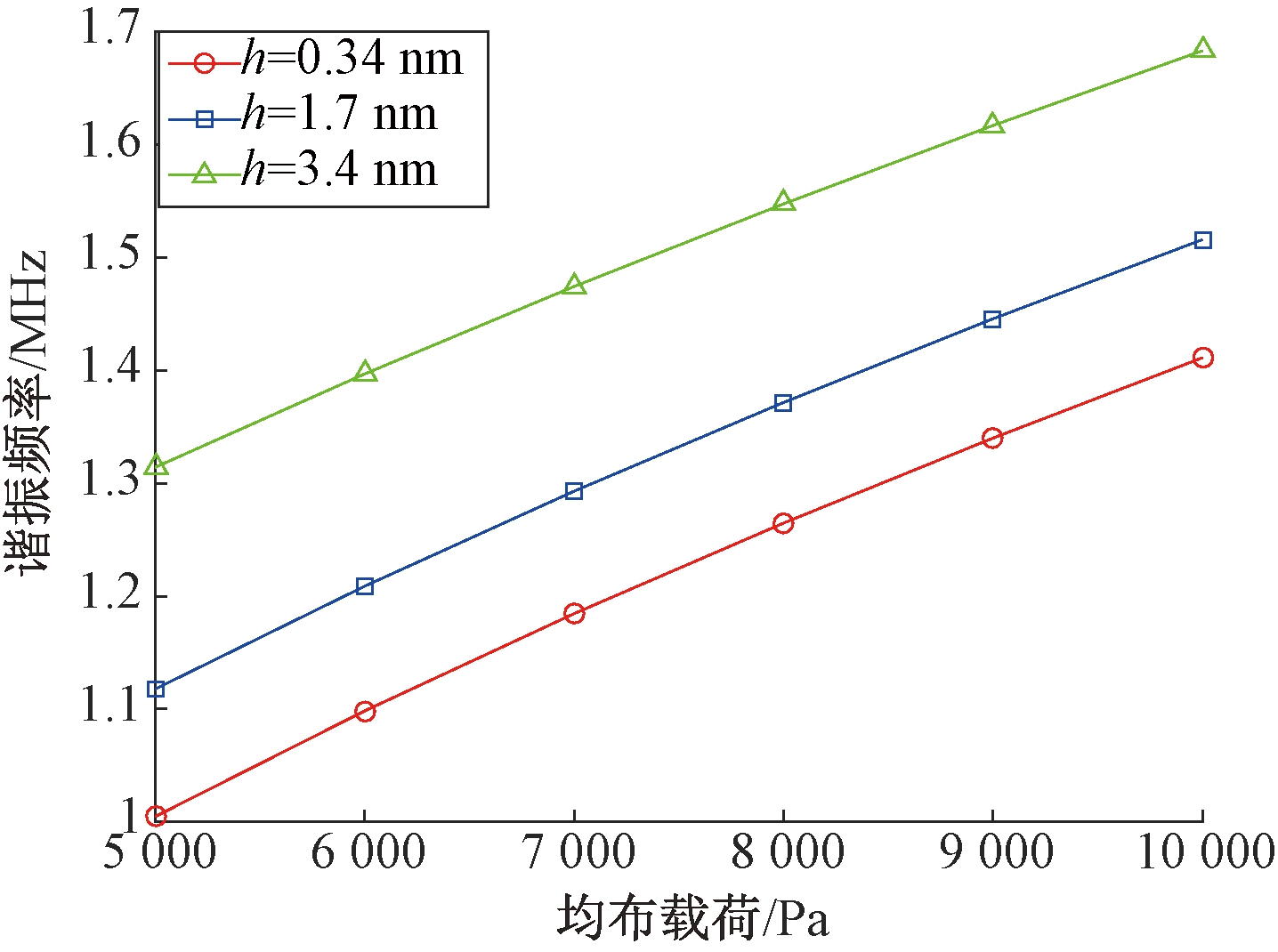
图13 梁的厚度对梁谐振频率影响
Fig.13 Effects of beam thickness on resonant frequency of beam
4 谐振子加工工艺
针对谐振子加工工艺,研究重点为石墨烯的制备、转移与吸附及石墨烯的高精度剪裁等相关技术.目前石墨烯制备采取的方法主要有微机械剥离法、外延生长法、氧化还原法和化学气相沉积法.
微机械剥离法是物体相对石墨烯运动,在施加外力的情况下,利用物体与石墨烯之间产生的摩擦力,使得石墨烯从表面剥离,获得石墨烯粉体.微机械剥离法获得的石墨烯一般质量较好,适合用于研究石墨烯的电学性能,但是该方法无法实现工业量产.
外延生长法是真空条件下,以1 200~1 600 ℃高温加热单晶SiC,由于硅的升华率高于碳,所以晶体上硅原子脱离而只留下碳原子,留下的碳原子经过结构重构形成了与SiC厚度相当的石墨烯薄膜.Shivaraman等[11]将化学机械抛光的4H-SiC在10-5 Torr的真空室中以1 400 ℃的高温加热1 h,得到了外延生长在4H-SiC的石墨烯.高温加热造成的碳原子重构往往结构复杂,存在表面缺陷,同时制备需要高温、真空等条件,不适合大规模制备.
氧化还原法是利用化学试剂将石墨氧化,使得石墨边沿连接一些官能团,在石墨层与层之间插入氧化物,从而扩大层与层之间的间距,减小层与层之间的引力,获得氧化石墨.然后通过水洗、干燥、剥离、膨胀等步骤的处理,氧化石墨被制作成为氧化石墨烯.最后利用还原剂将其还原,便得到了石墨烯.Luo D的实验[12]证明,使用两部还原法得到的石墨烯电学性能好,还原程度高.氧化还原法成本较低,操作简便,适合于大规模的制备对于品质要求不高的石墨烯,但是不同时间生产的石墨烯品质相差较大,互通性较差.
化学气相沉积法是利用含碳的有机气体在高温条件下进行化学反应,随后在基底表面进行气相沉积,从而获得石墨烯薄膜.Kim团队[13]成功地使用该方法制得了少层的石墨烯薄膜,且没有使用强烈的机械或化学方法就将其转移到了任意衬底上,保持了石墨烯样品的高结晶质量状态.化学气相沉积法是目前生产厚度薄、面积大的石墨烯薄膜最有效的方法.
综上所述,石墨烯的制备拟采用化学气相沉积法.利用Cu箔作为金属衬底,在高温反应炉中通入甲烷(乙烯)等碳氢化合物气体,利用H2、Ar为载气,可以制备得到大面积高质量的石墨烯材料,转移到含有二氧化硅绝缘层的硅片上.采用Raman谱仪和扫描隧道显微镜/扫描隧道镜对制备得到的石墨烯样品进行表征,得到其完整性、均一性、缺陷率、缺陷类型等相关信息.
单层和多层石墨烯薄膜采用干法转移的方法转移到工作界面上,可以减少转移过程中对石墨烯的污染.为了得到规则的形状和合适的尺寸,还需要对其进行剪裁加工,拟采用反应离子刻蚀工艺进行,根据需要刻蚀的材料和光刻胶的刻蚀比,选择不同的气源,刻蚀Si/SiO2选用CF4或CHF3等,刻蚀石墨烯的气体初步考虑O2,需根据实际效果进一步确定.吸附或刻蚀会改变石墨烯的状态,可采用Raman光谱、原子力显微镜等方法分析此时石墨烯样品的质量及内应力.
5 结论
笔者参照硅谐振式压力传感器,设计了一种以石墨烯为梁结构的谐振子.对新的谐振子进行了理论分析和有限元仿真,两者相互验证,新的谐振子在低压情况下(0~10 kPa)灵敏度可达到81.30 Hz/Pa.通过ANSYS仿真探究了硅基底结构参数、凹槽参数和梁几何尺寸对于梁谐振频率的影响,发现硅膜片厚度、凹槽深度和边长以及梁的长度对传感器的灵敏度都会产生影响.灵敏度随硅膜厚度、梁的长度增加而降低,随凹槽边长、深度的增加而提高.灵敏度的提高同时会导致曲线线性度的降低,这些规律为设计高性能石墨烯谐振式压力传感器提供理论依据.最后,初步拟定采用化学气相沉积法制备石墨烯,采用干法转移的方法转移石墨烯薄膜,利用反应离子刻蚀工艺进行剪裁加工.
[1] NOVOSELOV K S, GEIM A K, MOROZOV S V, et al.Electric field effect in atomically thin carbon films[J].Science, 2004, 306(5696): 666-669.
[2] NI Z H, WANG H M, KASIM J, et al.Graphene thic-kness determination using reflection and contrast spectroscopy[J].Nano letters, 2007, 7(9): 2758-2763.
[3] LEE C, WEI X, KYSAR J W, et al.Measurement of the elastic properties and intrinsic strength of monolayer graphene[J].Science, 2008, 321(5887): 385-388.
[4] BALANDIN A A, GHOSH S, BAO W, et al.Superior thermal conductivity of single-layer graphene[J].Nano letters, 2008, 8(3): 902-907.
[5] CHEN J, JANG C, XIAO S, et al.Intrinsic and Extrinsic performance limits of graphene device on SiO2[J].Nature nanotechnology, 2008, 3(4):206-209.
[6] BUNCH J S, ZANDE A M, VERBRIGE S S, et al.Electromechanical resonators from graphene sheets[J].Science, 2007, 315(5811): 490-493.
[7] ZANDE A V D, BARTON R A, ALDEN J S, et al.Large-scale arrays of single-layer graphene resonators[J].Nano letters, 2010, 10(12):4869-4873.
[8] HABIBI M, DARBARI S, RAJABALI S, et al.Fabrication of a graphene-based pressure sensor by utilising field emission behavior of carbon nanotubes[J].Carbon,2016,96:259-267.
[9] 樊尚春.传感器技术及应用[M].第3版.北京:北航航空航天大学出版社,2016:337-338.
[10] 苑伟政, 任森, 邓进军,等.硅微机械谐振压力传感器技术发展[J].机械工程学报, 2013, 49(20): 2-9.
[11] SHIVARAMAN S, BARTON R A, YU X, et al.Free-standing epitaxial graphene[J].Nano letters,2009,9(9):3100-3105.
[12] LUO D, ZHANG G, LIU J, et al.Evaluation criteria for reduced graphene oxide[J].Journal of physical chemistry C,2011,115(23):11327-11335.
[13] KIM K S, ZHAO Y, JANG H, et al.Large-scale pattern growth of graphene films for stretchable transparent electrodes[J].Nature,2009,457:706-710.