0 引言
磁场测量在资源勘探、国防安全、地震监测等领域都有着极为重要的应用,例如:在资源勘探及国防安全方面,磁场传感器可以用于监测潜艇等水下目标;在地震监测方面,磁场传感器可用于探索地震与磁异常信号之间的关系,从而实现地震预测.
鉴于在众多领域的广泛应用前景,多种性能和用途的磁场传感器已经被开发出来,如磁通门磁强计[1]、光泵磁强计[2]、质子旋进磁力仪[2]、超导量子干涉器件[3]和光纤磁场传感器[4]等.相比于电学类磁场传感器,光纤磁场传感器以光纤为传感和信号传输的磁场传感器,具有频带宽、灵敏度高、重量轻、抗干扰能力强、易于组成大规模阵列等特点.因此,光纤磁场传感器的研究受到了国内外的广泛关注.目前,研究的光纤磁场传感器从原理上大体分为四类:第一类基于法拉第效应[5];第二类基于磁流体[6];第三类是基于安培力[7];第四类是基于磁致伸缩效应[8].其中,基于磁致伸缩效应的光纤磁场传感器具有可靠性好、结构紧凑、不需供电等优点,是目前研究较多的一类光纤磁场传感器.
从传感器的传感机理上来看,基于磁致伸缩效应的光纤磁场传感器主要分为干涉型[9]、光纤激光型[10]和光纤光栅型[11]三个大类,其分类主要是根据利用的敏感元件不同.干涉型磁场传感器通过高灵敏度的光纤干涉仪技术,结合各种不同的增敏结构,将磁场信号转换成光信号,并通过光纤传至信号处理系统从而提取磁场信息,实现对磁场信号的还原.国外的科研单位早在八十年代就对这类传感器展开了研究[12],这类传感器可以在高频段达到较高的测量分辨率,但是在低频段(10 Hz~DC)的分辨率因受限于激光频率噪声而难以进一步提高[13].光纤激光器类型的传感器主要利用光纤激光器作为敏感元件[10],国内科研者受限于掺杂光纤制作技术和光栅刻写技术的发展,在光纤激光传感技术研究上起步较晚,制作的光纤激光器较差,激光频率噪声较高,无论是在高频段还是在低频段,这类传感器分辨率都较低[10].光纤光栅型主要利用光纤光栅作为敏感元件,这类传感器的核心优势在于结构简单、封装工艺简单、易于大规模复用,因而被普遍看好.但是,普通的光纤光栅线宽较宽,无论是在高频段还是在低频段,依其制成的光纤磁场传感器分辨率较差、动态范围小,是该项技术的一个弱点.综上所述,如何在低频段提高传感器的分辨率是目前研究的主要难点.
最近,一种光纤布拉格光纤光栅法布里-珀罗(FBG-FP)腔的光栅器件被提出用于高精度光纤光栅波长解调技术[8].与FBG[14]腔相比,FBG-FP腔的反射谱线宽更窄;与光纤F-P干涉仪相比,FBG-FP腔的选频特性更好.因此,采用FBG-FP腔,有望实现更高分辨率的磁场测量.
笔者提出了一种基于光纤布拉格光纤光栅法布里-珀罗(FBG-FP)腔和超磁致伸缩材料(Terfenol-D)的磁场传感器:采用FBG-FP腔作为传感元件、Terfenol-D材料作为磁场灵敏元件.将FBG-FP腔封装在其中,当磁场变化时,Terfenol-D材料就会产生伸缩,带动FBG-FP腔也产生伸缩.结合高精度的低频光纤光栅波长解调技术,可以实现静态微弱磁场信号的探测,且相比于普通的无源光纤光栅磁场传感器,信号探测能力可以提高几个数量级.
1 传感器设计方案
1.1 传感器设计
传感器结构如下图1所示,外筒长55 mm,直径35 mm,采用铝合金材质,上下两端有内螺纹,分别与顶盖和底盖上的外螺纹配合.Terfenol-D管材长40 mm,外径10 mm,一端嵌入底盖的凹槽中,另一端嵌入顶杆的凹槽中.FBG-FP穿过Terfenol-D管材,两端分别点胶固定在底盖和顶杆上.模具弹簧套在顶杆上.钕铁硼磁环长3 mm,外径15 mm,套在Terfenol-D棒外,用于提供偏置磁场.
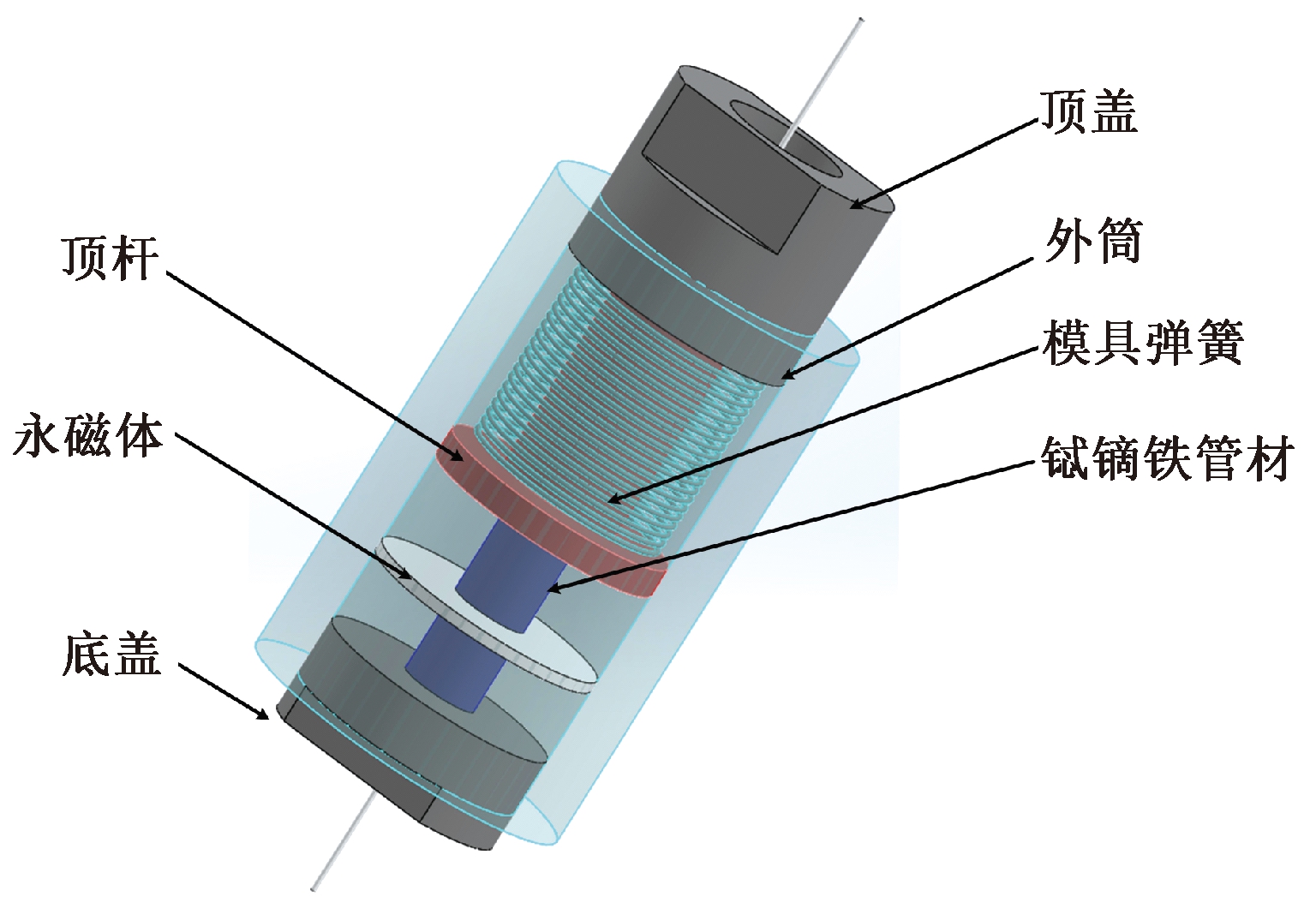
图1 传感器结构图
Fig.1 Schematic map of the sensor
当外加磁场作用在传感器上时,Terfenol-D管材伸长,通过顶杆使FBG-FP腔也伸长,使得FBG-FP腔反射谱谐振峰的峰值波长发生变化,通过检测峰值波长的变化,可以得出磁场的变化量.
1.2 高精度低频应变解调系统
本文中的光纤磁场传感器系统由光纤磁场传感器探头和高精度低频应变解调系统[15]组成.解调系统的示意图如图2所示.
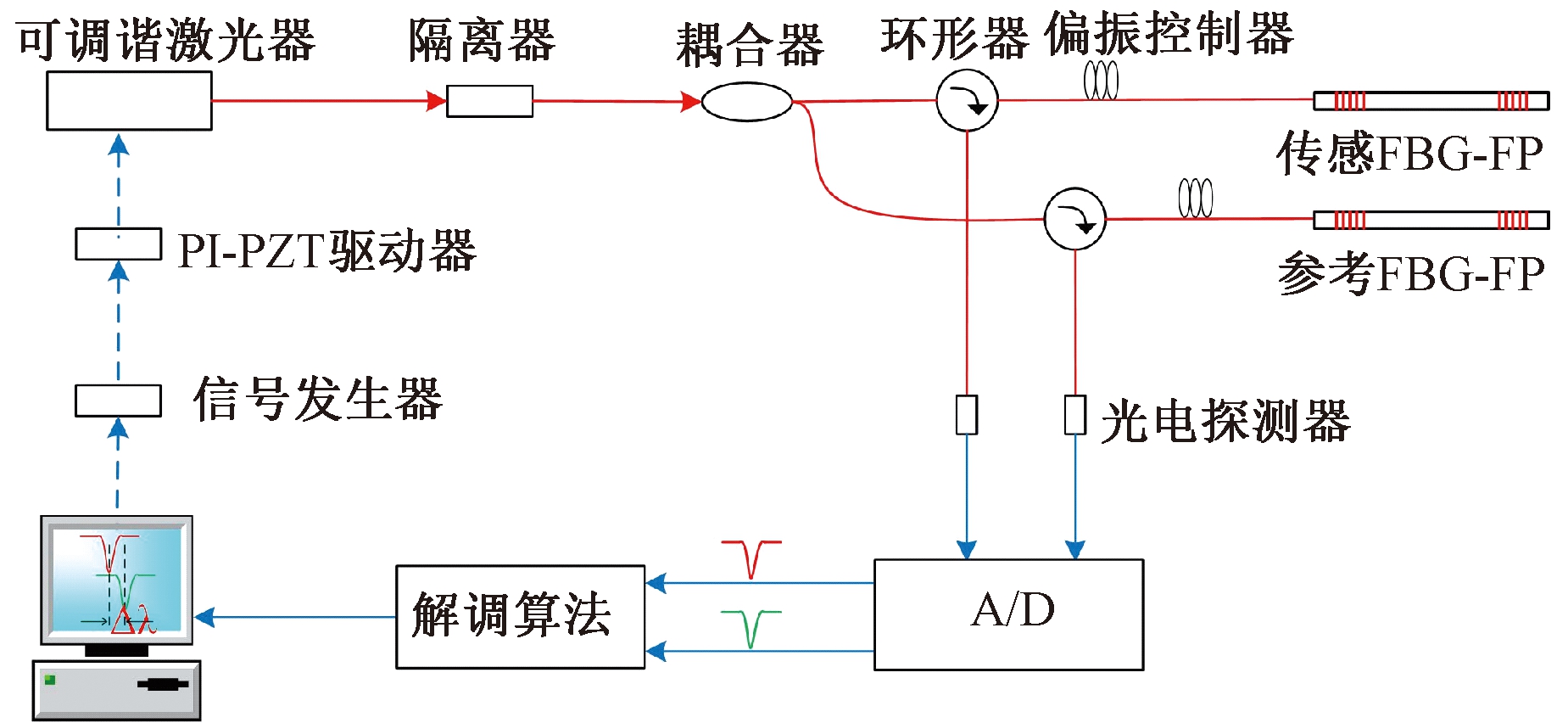
图2 解调系统原理图
Fig.2 Schematic map of the demodulation system
解调系统的工作原理是:首先,信号发生器产生扫描波形,将该信号送入PI-PZT驱动器.PI-PZT驱动器实际上是一个高精度电压放大器,将电压放大后,输出给可调谐的窄线宽激光器,来驱动激光器以固定的调谐方式输出光波,该光经过隔离器进入耦合器.耦合器将光分为两束,一束进入到环形器,经环形器入射到传感FBG-FP腔中,并按激光器的调谐方式扫描传感FBG-FP腔,扫描后返回的光再经过该环形器的另一个端口输出给光电探测器;另一束以相同的方式进入到参考FBG-FP腔并进行扫描,并将返回的光输出给另一个光电探测器.两光电探测器将得到的光信号转化为电信号,然后利用数据采集卡采集该信号,将模拟信号转化为数字信号便可以得到两路FBG-FP腔的反射谱.最后,在电脑中利用解调算法对反射谱进行解调处理,便可以得到静态应变的测量结果.当两个 FBG-FP腔传感器受到外界应变时,其反射谱的中心波长将发生漂移.由于两个传感器中,一个作为参考,另一个作为传感.当受到外界应变作用时,传感用FBG-FP腔除受外界应变作用的影响外,还受环境温度及其他环境因素的影响;而参考FBG-FP腔主要受环境温度及其他环境因素的影响.因此,两个FBG-FP腔的反射谱的中心波长漂移量会有所不同.基于这个原理,利用解调算法计算出两个FBG-FP腔传感器反射谱中心波长的差值,该差值既反应了所受外界应变量的大小,又在很大程度上进行了温度补偿并消除外界环境的干扰.
1.3 理论计算
当外加磁场作用在传感器上时,Terfenol-D管材伸长,产生的应变与外加磁场的关系表示为:
(1)
式中:εT为Terfenol-D管的应变量;ΔL为Terf-enol-D管的伸长量;L为Terfenol-D管的长度;Cf 为Terfenol-D管的磁致伸缩系数,该系数的取值随着偏置磁场的增大而增大;H为外加磁场的大小.
在外加磁场作用下,Terfenol-D管产生应变,使得传感FBG-FP腔也产生相应的应变,传感FBG-FP腔中心波长的变化量Δλ1与该应变值εT的关系为:
Δλ1=[(1-pe)εT+α1T]λc,
(2)
式中:pe为光纤的有效光弹系数;α1为Terfenol-D材料的热膨胀系数;λc为FBG-FP腔的中心波长值.
由于Terfenol-D材料的热膨胀系数与FBG-FP腔的热膨胀系数差别较大,当外界环境温度变化时,二者的热膨胀系数不同会使得附着在FBG-FP腔上的Terfenol-D材料形变量大于光纤,因此,需要引入测量误差,对传感器进行温度补偿.选用与Terfenol-D具有非常相近热膨胀系数的Monel-400合金,将该合金与参考FBG-FP腔耦合,采用与图1中相同的方式进行封装,进行温度补偿.参考FBG-FP腔峰值波长的变化量Δλ2与温度的关系为:
Δλ2=α2Tλc,
(3)
式中:α2为Monel-400合金的热膨胀系数;λc为FBG-FP腔的中心波长值.由于Monel-400合金与Terfenol-D材料的热膨胀系数非常相近,可以近似认为α1=α2=α.
结合式(1)~(3),可以得出传感FBG-FP腔峰值波长与参考FBG-FP腔的反射谱峰值波长差Δλ与外加磁场的关系为:
Δλ=Cf(1-pe)λcH2.
(4)
因此,传感器的磁场灵敏度可以表示为:
(5)
由上述表达式(5)可以看出,磁致伸缩系数Cf是影响传感器磁场灵敏度的主要因素.在该传感器的设计中,采用钕铁硼永磁体的方式提供偏置磁场,可以增大磁致伸缩系数,从而提高传感器的灵敏度.
2 测试结果分析与讨论
2.1 测试系统
采用的测试系统如图3所示.零磁空间采用高纯铝制材料铸造的正八角26面体骨架作为主体框架,包裹两层高纯铝板(电屏蔽层)和八层高磁导率的坡莫合金材料(磁屏蔽层),实现了对地磁场的“静态”屏蔽,零磁空间内部的剩余磁场小于20 nT,不到正常地磁场强度的万分之五.在零磁空间中放置有环型标准线圈,线圈的直径为60 cm,磁场的均匀区半径为20 cm.使用高精度恒流源可以调节线圈中电流的大小和方向,从而控制磁场的大小和磁场方向,线圈可以产生的磁场范围为-100 μT~100 μT.其中,符号代表磁场方向的两个轴向.磁场传感器放置在线圈的中心位置,加载在传感器上的磁场可以看做均匀的轴向磁场.
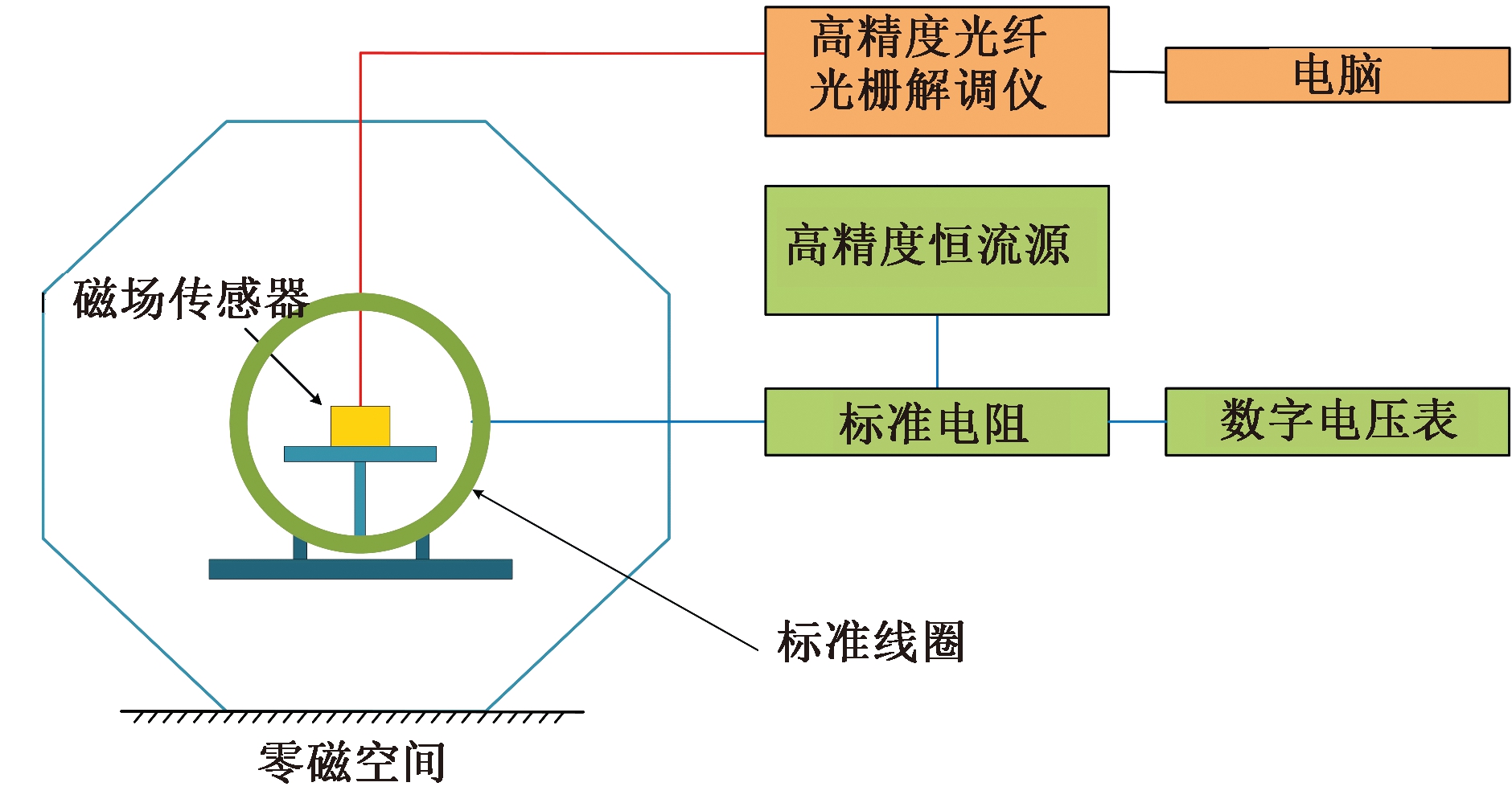
图3 测试系统示意图
Fig.3 Schematic map of the test system
2.2 测试内容及方法
(1)传感器的磁场灵敏度测试.将传感器放置在线圈中,Terfenol-D管的轴向与线圈的轴向一致;从-100 μT开始,步长20 μT,不断增大磁场,每次增大磁场并稳定后,连续记录30 s数据,取30 s内反射谱中心波长差的平均值作为中心波长差值,从而准确测定传感器响应的线性度以及轴向灵敏度.
(2)传感器的指向性测试.指向性是Terfenol-D材料的固有属性,即当磁场方向与Terfenol-D棒的易磁化方向一致时,磁致伸缩引起的波长变化量最大.观察Terfenol-D棒与线圈轴向夹角为0°~ 360°、步长10°时,传感器在100 μT轴向磁场作用下的响应,得出响应幅值与传感器和磁场夹角的关系.
2.3 测试结果及讨论
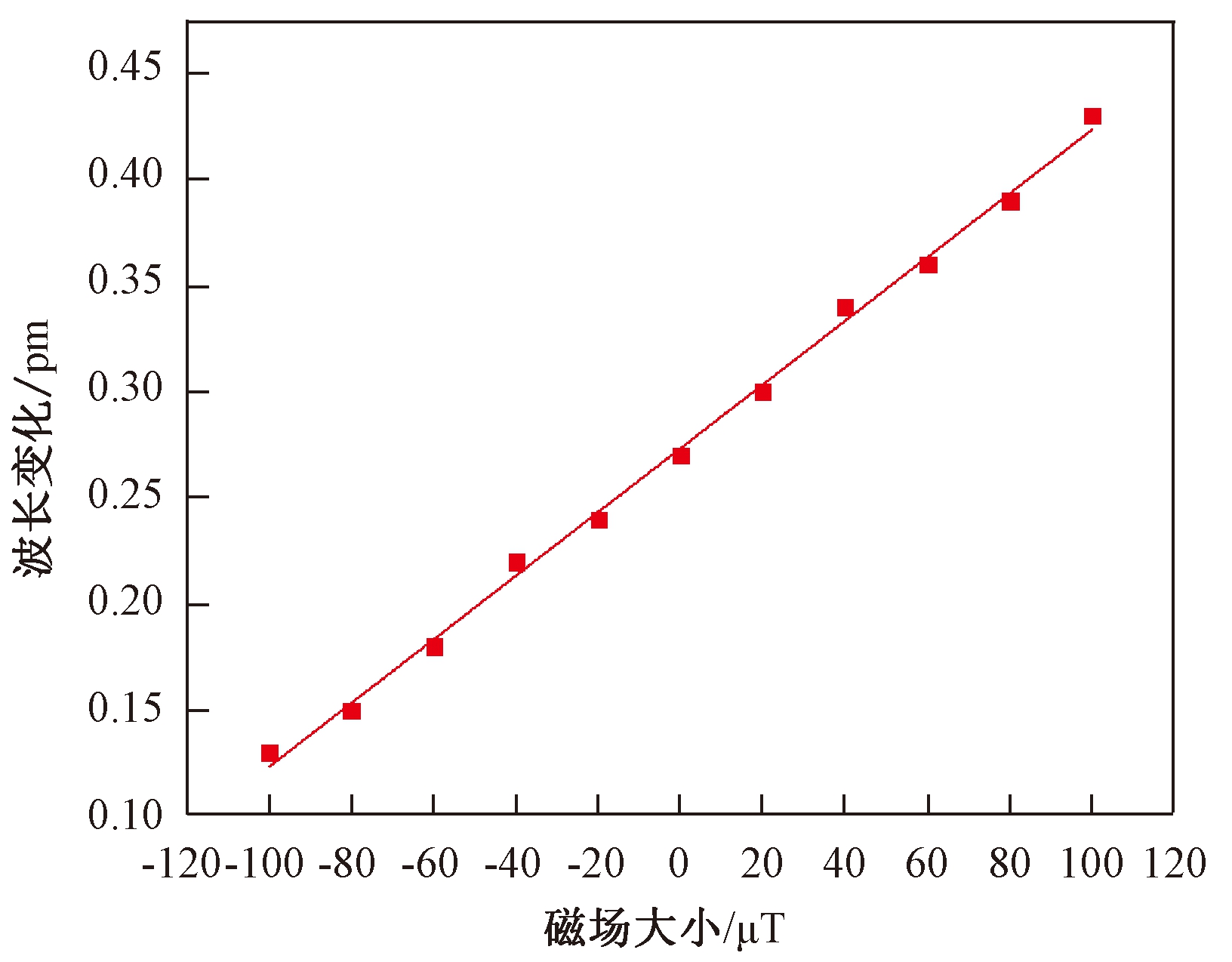
图4 磁场灵敏度测试图
Fig.4 Test of the magnetic field sensitivity
(1)磁场灵敏度测试.如2.2节中测试方法所述,测得的两FBG-FP腔波长差与环形线圈产生的磁场关系,如图4所示.图4中,红色点为测试点,红色曲线为线性拟合曲线,拟合得到相关系数为0.997,曲线的斜率即为传感器的磁场灵敏度,为1.5×10-3 pm/μT,高精度低频应变解调系统的波长分辨率为1.0×10-3 pm,因此,传感器的磁场分辨率为0.67 μT.
(2)传感器指向性测试.当磁场方向与Terfenol-D棒的易磁化有一定夹角时,满足如下规律:
Δλθ=Δλmax·cos θ,
(6)
式中:Δλθ是传感FBG-FP腔和参考FBG-FP腔的波长差值;Δλmax是当磁场方向与Terfenol-D棒轴向平行时,两FBG-FP腔波长的差值;θ是Terfenol-D棒轴向与磁场的夹角.
如图5所示,将传感器放置在线圈中心的旋转台上,磁场大小固定为100 μT,设置0°为磁场方向,保持该方向不变,以步长10°改变Terfenol-D棒与线圈轴向夹角,观察传感器的响应.
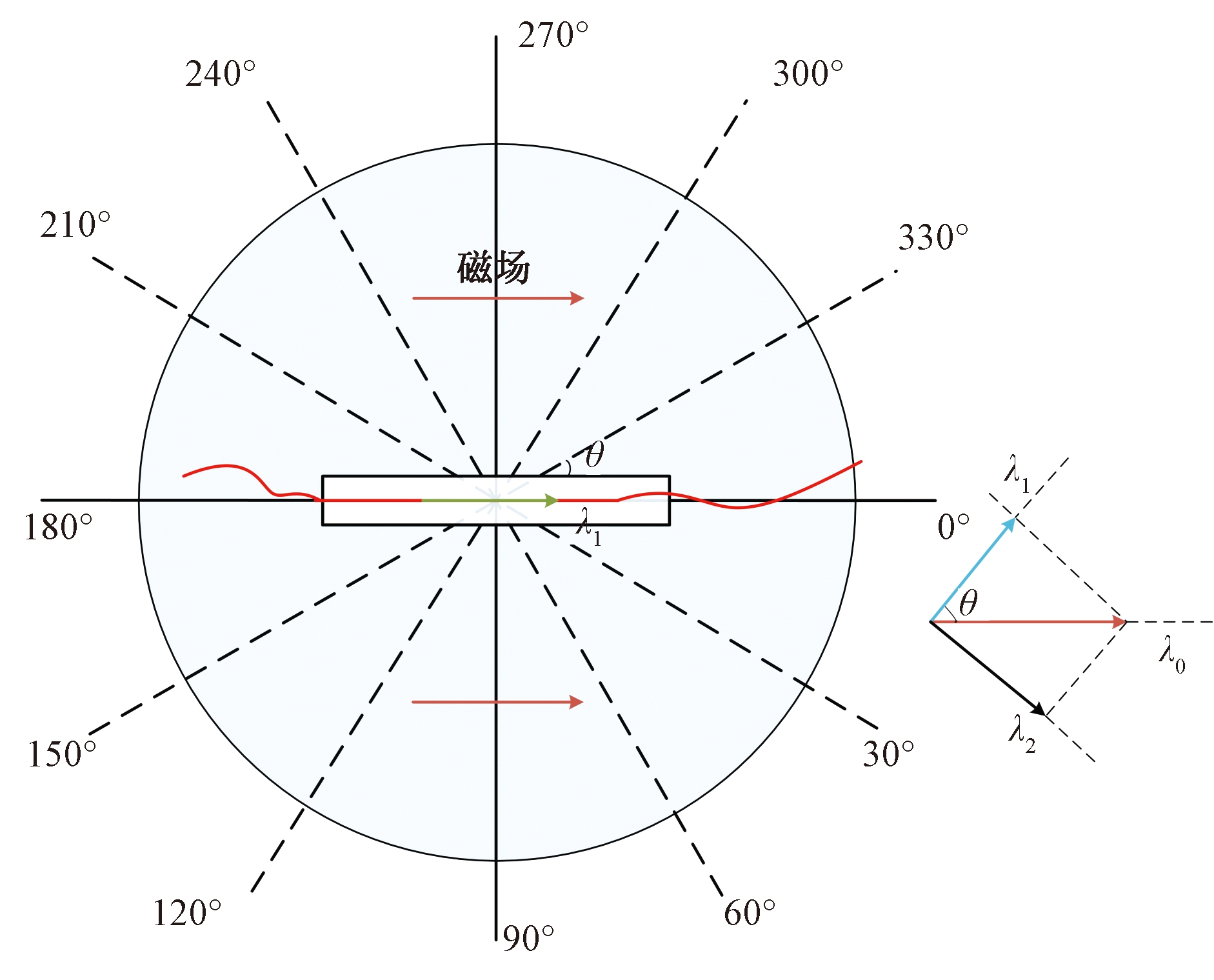
图5 传感器指向性测试图
Fig.5 Test of the directivity of the sensor
图6为传感器指向性的测试结果图.图6中,红色曲线是实际测量结果;黑色曲线是理论计算结果.0 dB代表当磁场方向与Terfenol-D棒轴向平行时,传感器具有最大的响应;同时,当传感器方向与磁场方向垂直时,其对磁场没有响应,凹点深度约为-20 dB,这与式(6)基本相符,满足余弦变化规律.
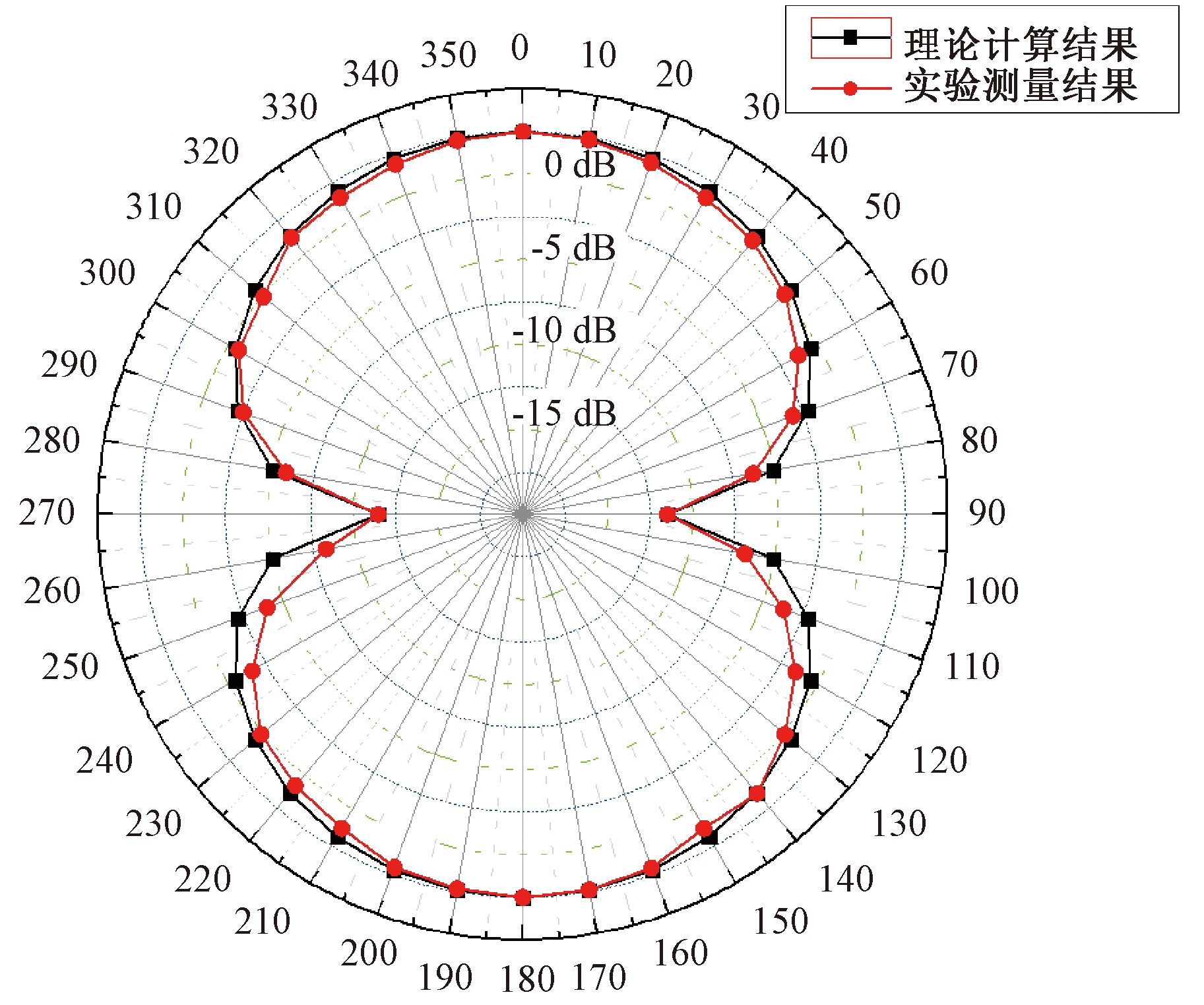
图6 传感器指向性测试结果图
Fig.6 Test result of the directivity of the sensor
实际的测量结果与理论值有一定差距,推测产生这一结果的原因有两种:(1)实验中人为手动调整旋转台,可能产生一定的误差;(2)在实验过程中,由于人不断靠近传感器,会对传感器周围的温度产生一定的影响,导致波长差发生变化.
3 结论
笔者研究了基于磁致伸缩效应的光纤磁场传感器,提出了一种基于光纤布拉格光纤光栅法布里-珀罗(FBG-FP)腔和超磁致伸缩材料(Terfenol-D)相结合的磁场传感器方案.该方案采用钕铁硼永磁体提供偏置磁场,将Monel-400合金与FBG-FP腔耦合,作为温度补偿元件,有效消除了温度的影响;介绍了高精度低频应变解调系统的解调原理,并对传感器的磁场灵敏度公式进行了理论推导,发现磁致伸缩系数是影响传感器灵敏度的重要因素.最后,通过实验对传感器的性能进行了测试,可知磁场灵敏度为1.5×10-3 pm/μT,磁场分辨率为0.67 μT,并且该传感器具有良好的指向性,因此,有望用于微弱静态磁场测量.
[1] 朱万华,底青云,刘雷松,等.基于磁通负反馈结构的高灵敏度感应式磁场传感器研制[J].地球物理学报, 2013, 56(11):3683-3689.
[2] 裴彦良,梁瑞才,刘晨光,等.海洋磁力仪的原理与技术指标对比分析[J].海洋科学, 2005, 29(12): 4-8.
[3] HIROTA M, NANAURA K, TERANISHI Y, et al.SQUID gradiometers for a fundamental study of underwater magnetic detection[J].IEEE transactions on applied superconductivity, 1997, 7(2): 2327-2330.
[4] 陈学岗,何兴道,邹文栋.光纤磁场传感器的磁场探头设计[J].仪表技术与传感器, 2004(2): 5-6.
[5] GUAN B O, HAN J, CHENG L, et al.Faraday-rotation-based miniature magnetic field sensor using polarimetric heterodyning fiber grating laser[J].Optics letters, 2013, 38(5):688-690.
[6] SONG B, MIAO Y, LIN W, et al.Loss-based magnetic field sensor employing hollow core fiber and magnetic fluid[J].IEEE photonics technology letters, 2014, 26(22): 2283-2286.
[7] CHENG L, GUO Z, HAN J, et al.Ampere force based magnetic field sensor using dual-polarization fiber laser[J].Optics express, 2013, 21(11): 13419-13424.
[8] CHEN F, JIANG Y.Fiber optic magnetic field sensor based on the TbDyFe rod[J].Measurement science & technology, 2014, 25(8): 085106.
[9] BUCHOLTZ F, VILLARRUEL C A, KIRKENDALL C K, et al.Fibre optic magnetometer system for undersea applications[J].Electronics letters, 1993, 29(11):1032-1033.
[10] HE W, CHENG L H, YUAN Q, et al.Magnetostric-tive composite material-based polarimetric heterodyning fiber-grating laser miniature magnetic field sensor[J].Chinese optics letters, 2015, 13(5):17-20.
[11] QUINTERO S M M, BRAGA A M B, WEBER H I, et al.A magnetostrictive composite-fiber Bragg Grating sensor[J].Sensors, 2010, 10(9):8119-8128.
[12] KERSEY A D, MARRONE M J, DANDRIDGE A, et al.Optimization and stabilization of visibility in interferometric fiber-optic sensors using input-polarization control[J].Journal of lightwave technology, 1988, 6(10):1599-1609.
[13] HUANG W, ZHANG W, ZHEN T, et al.A cross-correlation method in wavelet domain for demodulation of FBG-FP static-strain sensors[J].IEEE photonics technology letters, 2014, 26(16):1597-1600.
[14] 胡业发, 王彬, 张锦光, 等.基于FBG传感的CFRP层合板低速冲击响应监测[J].郑州大学学报(工学版), 2018,39(3):82-86.
[15] HUANG W Z, ZHANG W T, ZHEN T K, et al.π-phase-shifted FBG for high-resolution static-strain measurement based on wavelet threshold denoising algorithm[J].Journal of lightwave technology, 2014, 32(22):4294-4300.