0 引言
超声波流量计具有始动流量小、量程比大、寿命长等优点，因而被广泛应用于流量计量。超声波传感器(以下简称传感器)是超声波流量计的核心部件之一[1]。流量计量时，一只超声波流量计需要使用一对传感器，并共同使用一套信号收发电路。为保证获取的时间差准确，要求一对传感器转换效率及特性尽可能一致，而只有保证了谐振频率与反谐振频率、谐振阻抗与反谐振阻抗等参数的一致性，才有可能使得一对传感器的转换效率相互接近[2]。
基于阻抗特性的导纳圆图法是有效的测试手段之一，该方法具有精度较高、操作简便等优点，但是需要人工来判断谐振频率数值，并且需要通过手工计算传感器其他参数，所以不适用于在线测量[3]。针对传感器谐振频率等参数对结构和环境温度等变化比较敏感的问题，Ghasemi等[4]采用型号分别为TMS320F28355与AD9833的数字信号仪与可编程信号发生器搭建了传感器谐振频率的测试装置，利用测试电压电流的方法间接计算其阻抗，进而确定谐振频率。
ásek等[5]设计了一款基于ARM阻抗分析仪，其原理是通过测试自动平衡电桥的同步电压和电流获得传感器的阻抗，具有速度快、分辨能力强等特点。频率分辨力为1 Hz，频率测量范围为50～5 000 Hz。
如上所述，国内外学者对超声波传感器的研究更多的是偏向于对传感器单一参数测试方法，而对于流量计量而言，还需要有一种测试装置来在线评价一对传感器主要参数的一致性，作为其是否适用于一只流量计的判断依据[6]。
1 传感器特性与分析
1.1 谐振与反谐振特性分析
将超声波传感器串接到一个由激励信号源、采样电阻组成的测试回路中，当激励信号的频率变化时，采样电阻两端电压如图1所示。从图1的曲线可以看出，在频率变化范围内存在两个频率点fm、fn，且fm<fn。当激励信号频率为fm时电流最大，频率为fn时电流最小。
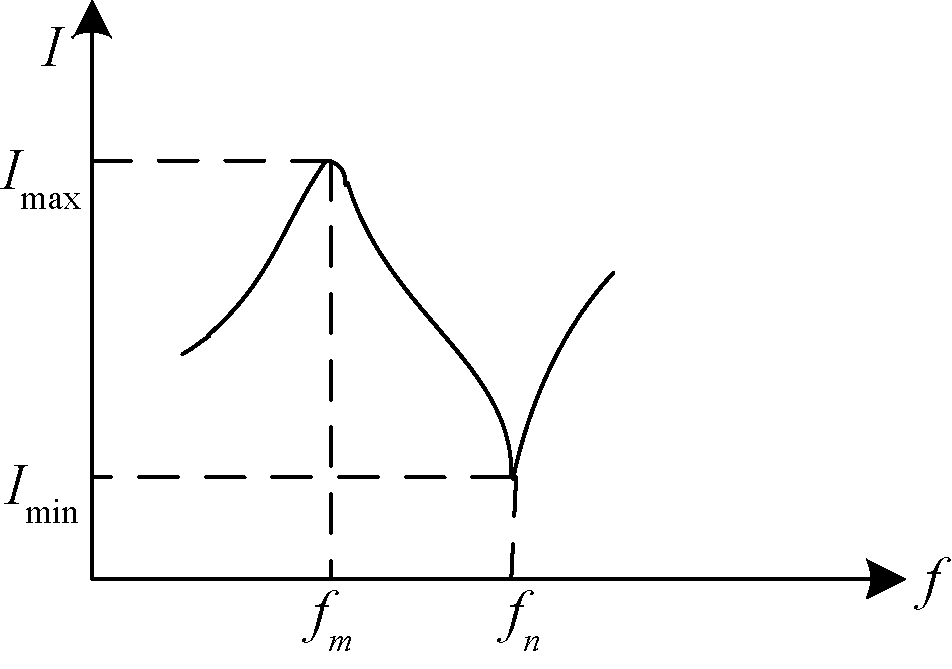
图1 电流随频率变化曲线示意图
Figure 1 The curve diagram of current varing with frequency
图2为等效阻抗随激励信号频率变化的曲线图。其中，fm称为最小阻抗频率，其附近会有超声波传感器的谐振频率fr； fn称为最大阻抗频率，其附近会有反谐振频率fa[7]。
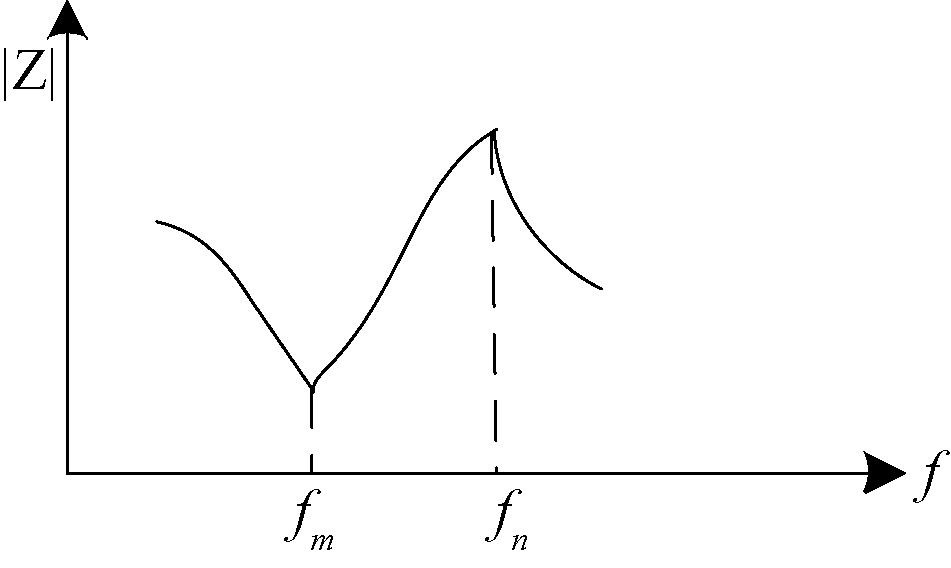
图2 阻抗随频率变化曲线示意图
Figure 2 The curve diagram of impedance varing with frequency
超声波传感器的机电等效电路如图3所示。其中，C0为传感器的静态电容;L1为传感器的等效电感；C1为传感器的等效电容；R1为传感器的等效电阻。由文献[8]可知，传感器的最小阻抗频率fm和最大阻抗频率fn分别为式(1)、(2)。
(1)
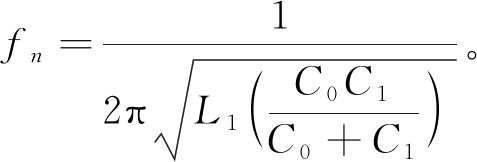
(2)
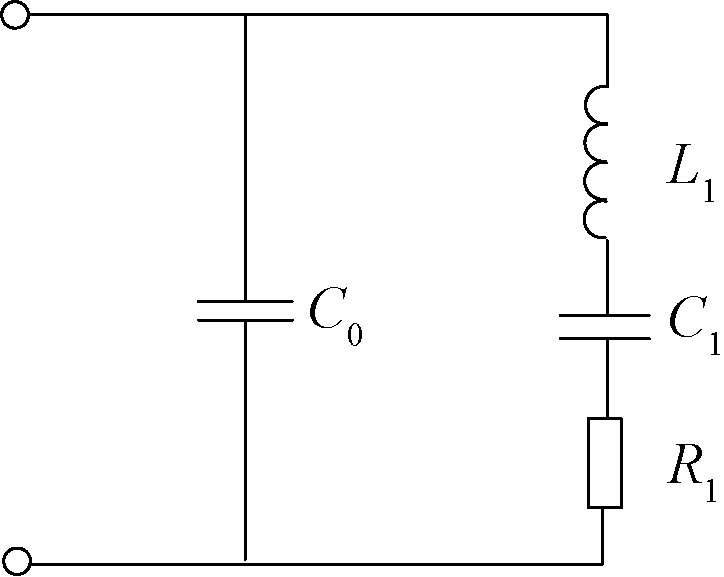
图3 超声波传感器的机电等效电路图
Figure 3 Electromechanical equivalent circuit of ultrasonic sensor
电路串联谐振现象产生于信号频率fs等于fm时，fs为串联谐振频率；电路并联谐振现象产生于信号频率fp等于fn时，fp为并联谐振频率。
当无机械损耗时：
fm=fs=fr； fa=fp=fn。
(3)
当有机械损耗时：
fm<fs<fr； fa<fp<fn。
(4)
1.2 主要参数对传感器压电效应的影响
压电式超声波传感器具有正压电效应与逆压电效应，无论是正压电效应还是逆压电效应，其转换效率高则说明转换过程中能量损耗小。流量计量过程中都期望正压电效应与逆压电效应转换效率尽可能高一些，即转换后信号幅值与转换前的信号幅值之比大，这样会更便于转换后小信号的识别，更能保证时间差的计算精确度。
(1)谐振频率对压电效应影响的分析。如图3所示，在谐振频率点，传感器等效电路右侧分支电路L1、C1、R1等效于一只纯电阻，则传感器等效为R1和C0的并联，传感器转换效率最高；偏离谐振频率点较远时，右侧分支电路L1、C1、R1中就会存在L1与C1，就会因为L1与C1的存在而产生无功功率、减少有功功率。P=U2/R可知，若阻值不变，功率减少，则R1压降就会减少，进而使传感器转换效率下降。
(2)静态电容对转换效率的影响。根据电路理论可知，随着传感器的静态电容的增加，无功功率也将随之而增加，而激励信号产生的总功率P=P有+P无是不变的，有功功率与无功功率是此消彼长的关系。由P=U2/R可知，传感器阻抗保持稳定时，有功功率的减少会导致输出电压降低，进而降低了传感器的转换效率。
1.3 声波收发特性分析
超声波传感器声波收发状态是动态的，振动特性和电信号的响应都是时间的函数，传感器的动态特性决定着传感器的转换效率。流量计量时，传感器是成对工作的，互为发送/接收信号，同时信号处理电路也对称使用，要求传感器的特性具有一致性，接收与发送信号互为交换后，呈现的特性具有较高的相似性，否则将会出现阈值偏差、相位偏差等现象，进而会产生较大的计量误差。
2 传感器的测试方法及设计
2.1 测试项目及整体结构设计
为保证传感器的一致性，要针对谐振频率与反谐振频率、谐振阻抗与反谐振阻抗、输出幅值、静态电容、转换效率等进行测试，保证用于同一流量计的一对传感器主要特性的一致性。图4为设计装置结构框图。
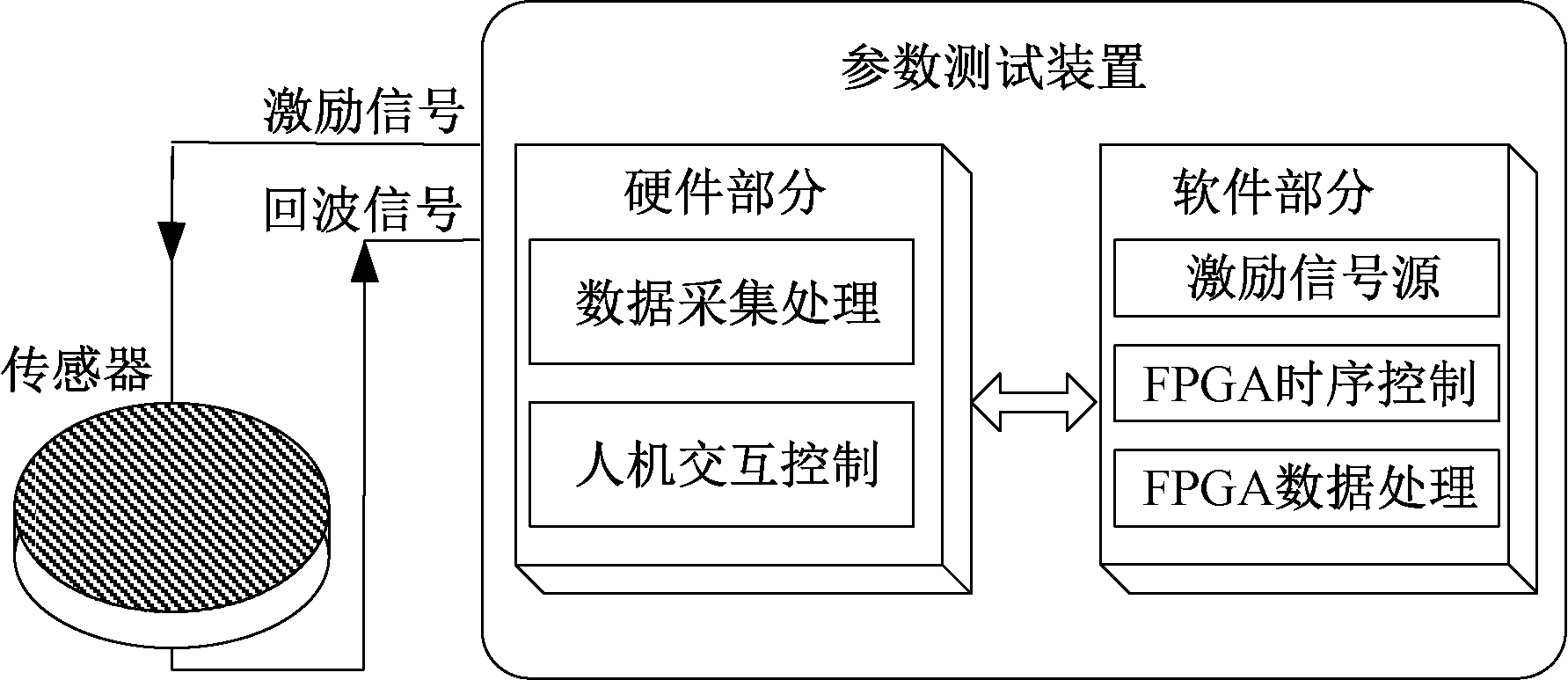
图4 参数测试装置整体结构框图
Figure 4 The overall structure diagram of parameter test device
针对谐振频率与反谐振频率的测试采用传输线路法，针对谐振阻抗与反谐振阻抗的测试采用替代法，针对传感器输出幅值的测试采用脉冲激励信号法，针对静态电容的测试采用交流容抗法。
2.2 信号调理电路设计
图5是传感器测试装置硬件总体框图。
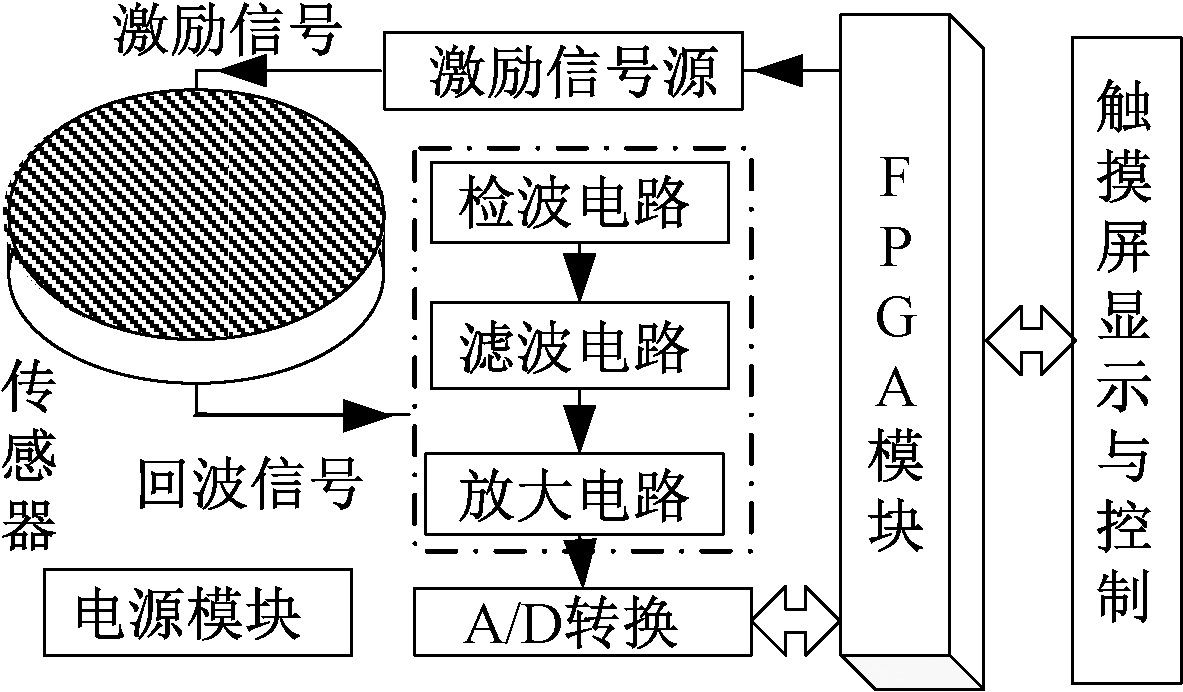
图5 测试装置硬件总体框图
Figure 5 Electromechanical equivalent circuit of ultrasonic sensor
2.2.1 检波电路
因为传感器信号衰减很大且很微弱，同时，接收到的电信号是含有被测量信息的调制信号，所以需要对再次接收到的电信号进行检波、滤波、放大等信号调理。频率、阻抗和幅值测试选用图6所示的全波检波电路1，静态电容测试选用图7所示的全波检波电路2。
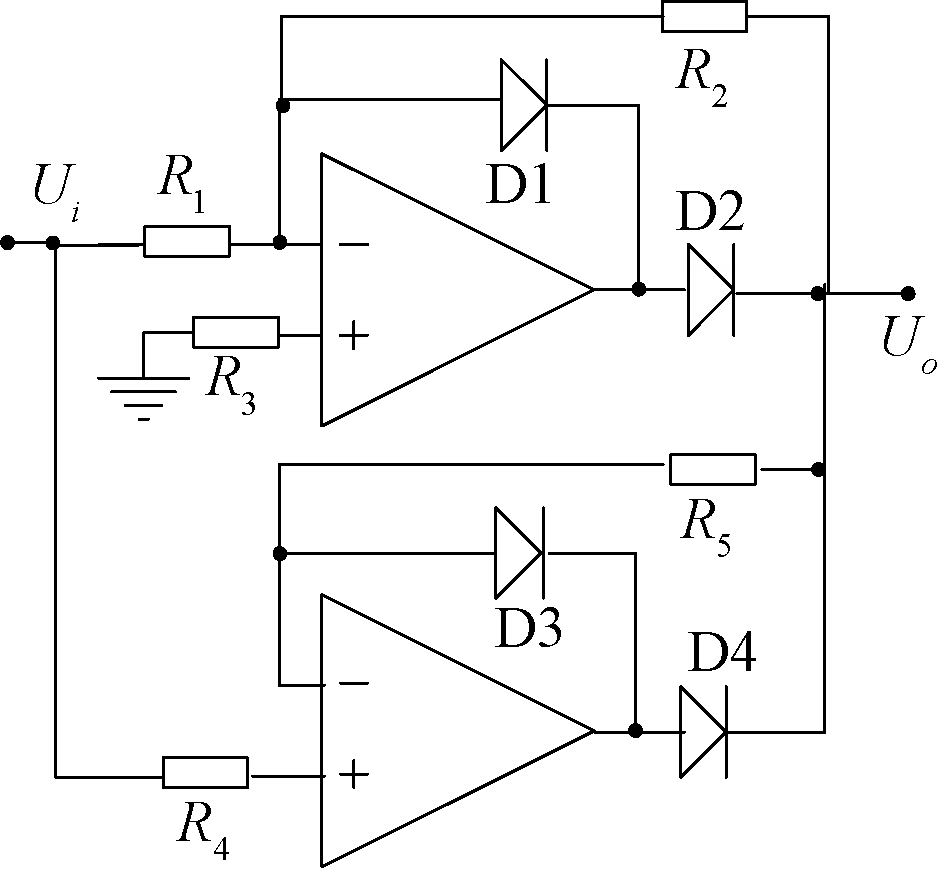
图6 全波检波电路1
Figure 6 Full wave detection circuit 1
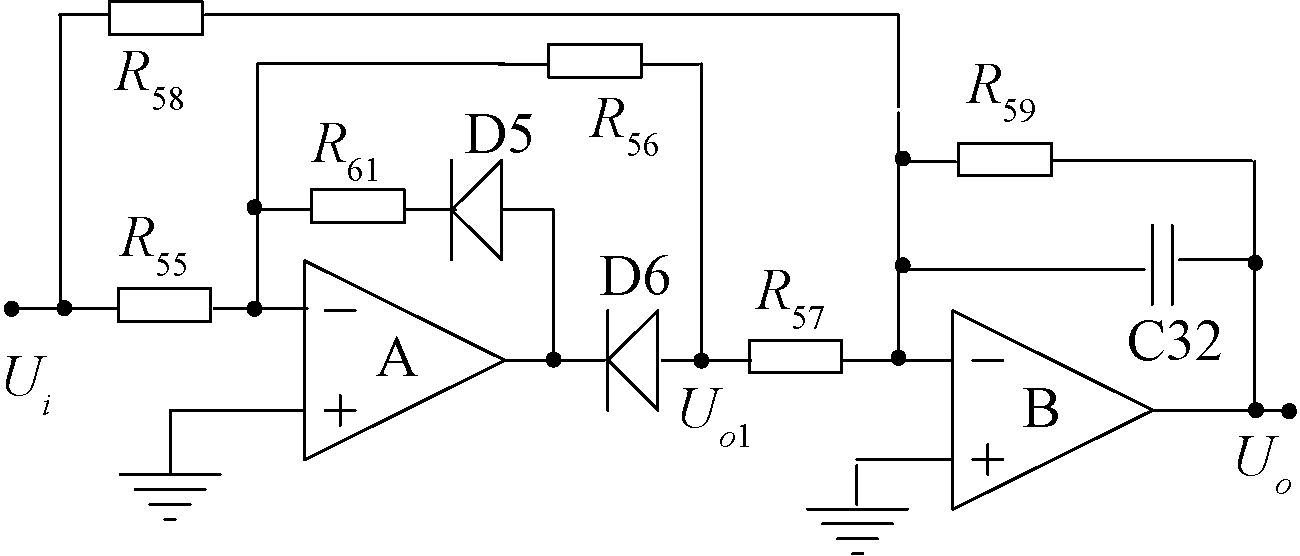
图7 全波检波电路2
Figure 7 Full wave detection circuit 2
要求装置产生频率在100 kHz～4.5 MHz，图6的运算放大器AD8063和二极管1N4148均为高速型。
图7中，运放A与二极管D5、D6以及电阻R55和R56构成半波整流部分，运放B与电阻R57、R58、R59共同组成一个信号加法器的结构。
2.2.2 滤波电路
滤波的目的是滤出检波后信号存在的高频干扰，提取待测传感器输出信号的低频部分。图8为二阶压控电压源型低通滤波器。
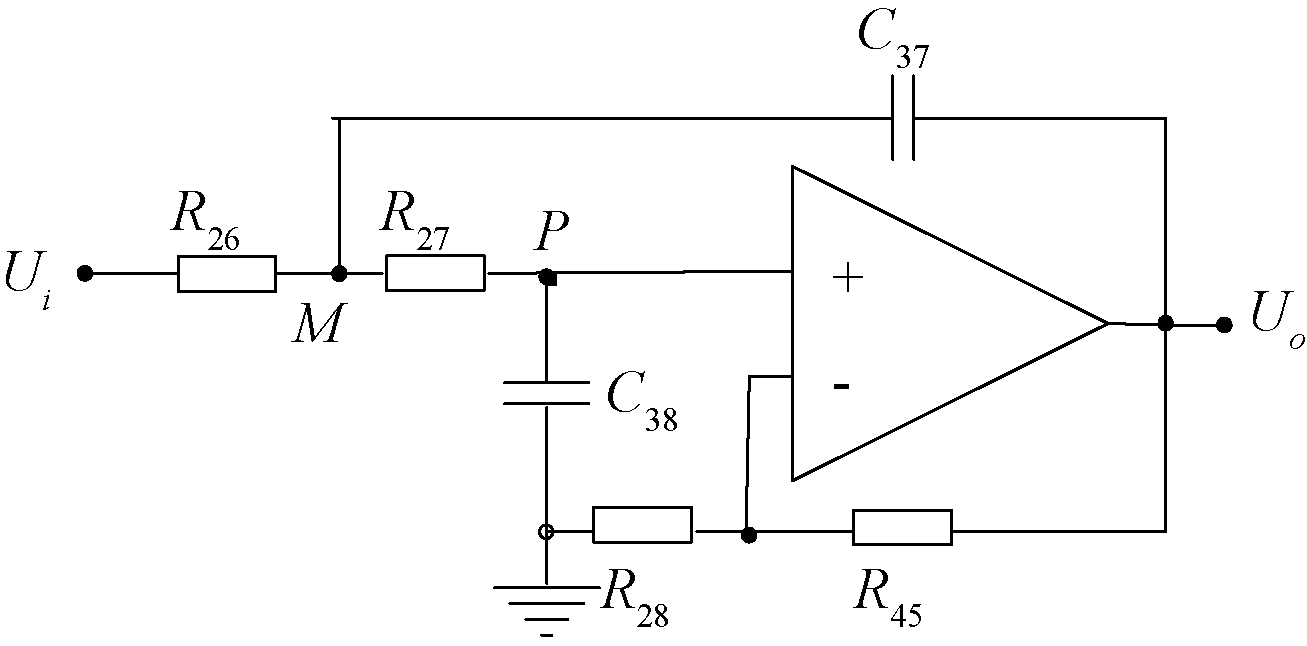
图8 二阶压控电压源型低通滤波器
Figure 8 Second order VCVS type low pass filter
根据基尔霍夫电流定律可知，M点的电流方程为式(5)：
(5)
P点的电流方程为式(6)：
(6)
联立公式(5)和(6)，可求得R27和R26：
(7)
(8)
电路中相关参数计算与选择结果如下：C37=1pF、C38=1nF、R26=R27=1.2 kΩ、R28=4.7 kΩ、R45=16.3 kΩ。
2.3 测试模块设计
2.3.1 频率测试模块
如图9所示，信号发生器给传感器输入幅值固定、频率可变的激励信号Ui，采样电阻R2将传感器工作电流转换为电压信号，谐振频率点的传感器工作电流最大、等效阻抗最小，反谐振频率点的传感器工作电流最小、等效阻抗最大。所以，通过测试图9输出电压值U0，就可以求得传感器的谐振频率与反谐振频率。
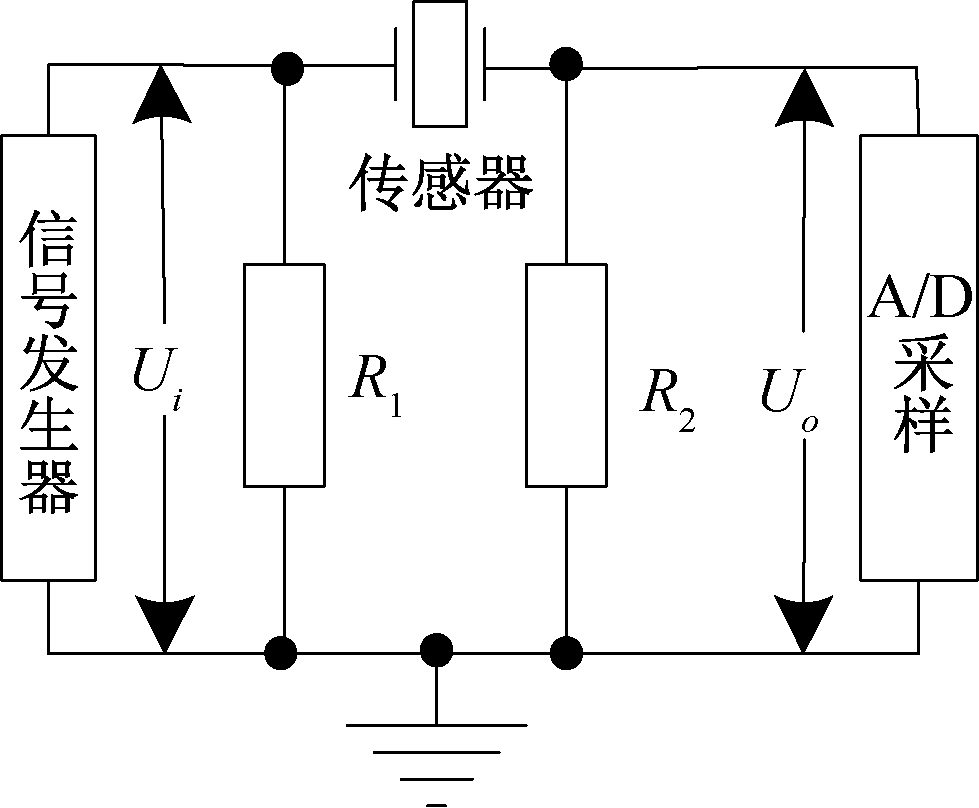
图9 传感器频率测试原理
Figure 9 The frequency testing principle of sensor
2.3.2 阻抗测试模块
如图10所示，采用替代法，首先让传感器与电阻R串联，利用固定幅值、固定频率的激励信号激励传感器并测试电阻R两端电压U，再让可调电阻Rx与电阻R串联，调整可调电阻Rx阻值使电阻R上的电压等于U，此时可调电阻的阻值即为传感器的阻值。
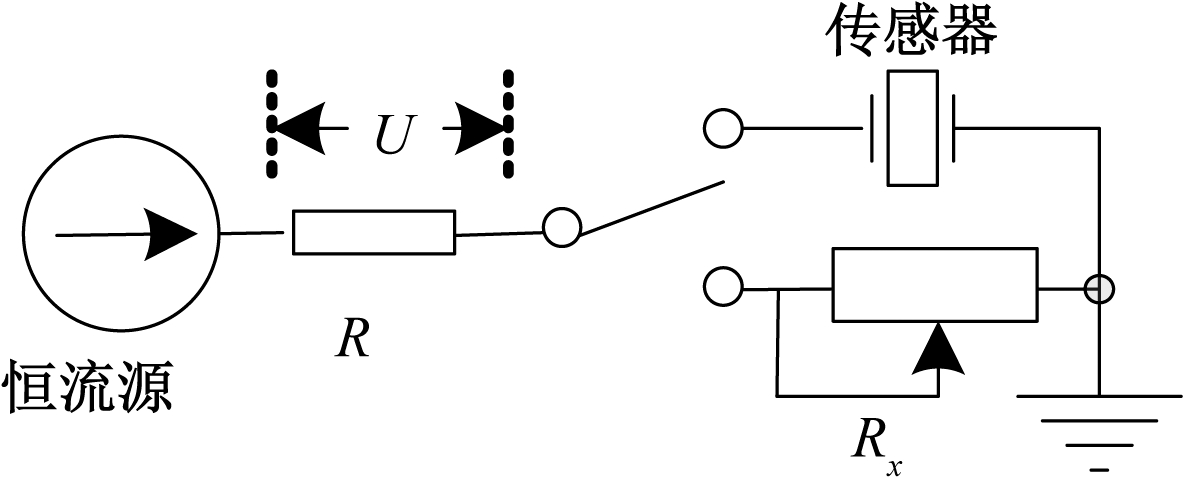
图10 传感器阻抗测试原理
Figure 10 The impedance testing principle of sensor
2.3.3 输出幅值测试
图11是一个模拟工况环境设计的测试单个传感器示意图，由具有一定光洁度的反射底板、能够固定安装传感器的顶板组成。测试时，把传感器面朝下放置在位于顶板的圆孔上，传感器经过逆压电效应与压电效应的两次转换实现了电信号(传感器发出)—机械波(介质中传输、底板发射)—电信号(传感器接收)的两次转换。
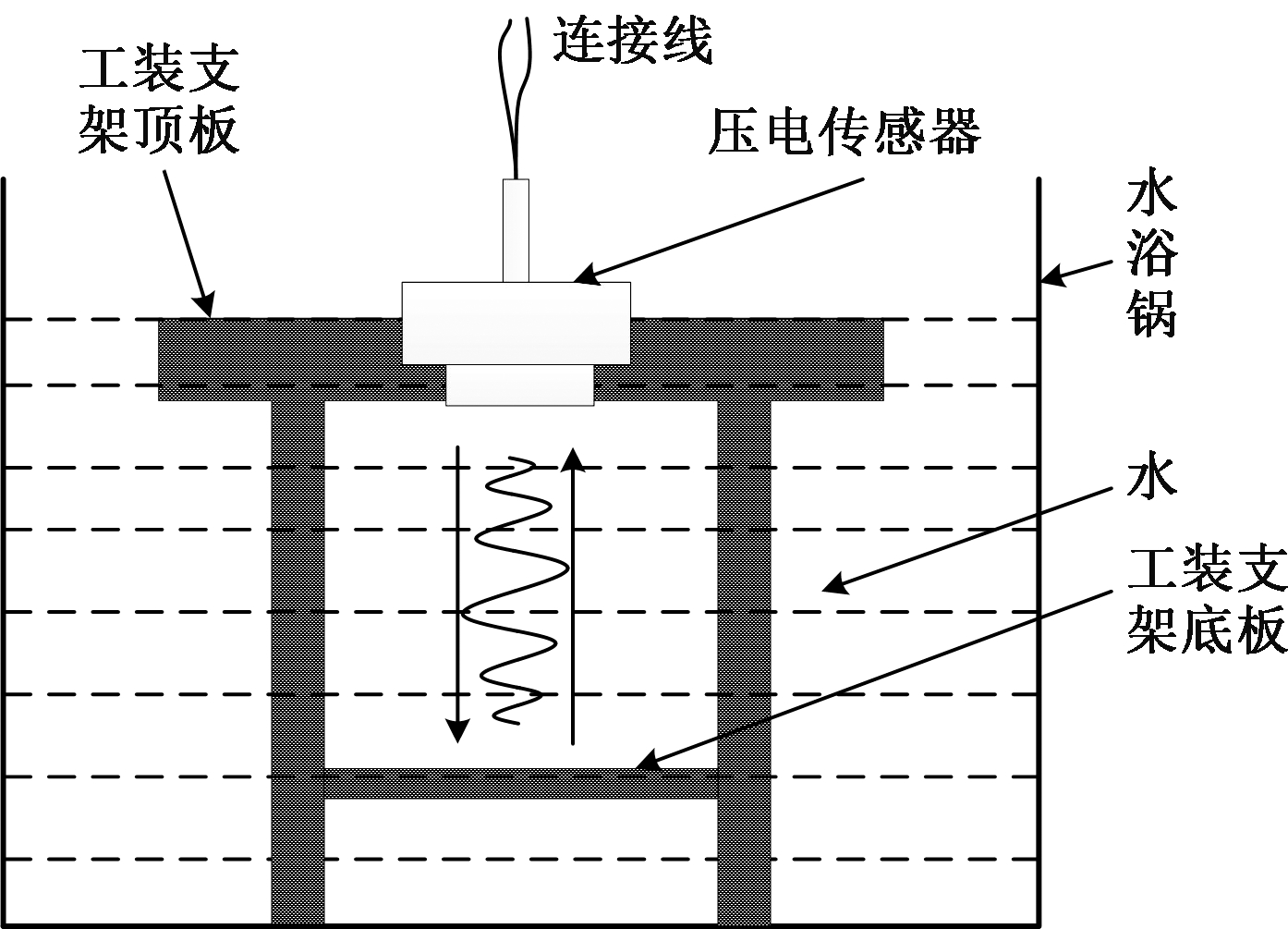
图11 传感器幅值测试示意图
Figure 11 The amplitude testing schematic of sensor
2.3.4 静态电容测试
压电式超声波传感器不加激励信号时等效为电容，在此条件下测试得到的电容值即为传感器的静态电容C0。给传感器加载低频激励信号，通过C/U转换电路把传感器静态电容值转换成与之成正比的电压值。
3 测试结果及分析
采用标准仪器与本设计的测试装置分别对传感器样品进行测试并比对分析。
(1)谐振频率与反谐振频率：采用频率特性测试仪作为标准仪器，型号为SA1005D；
(2)谐振阻抗与反谐振阻抗：采用电阻箱、示波器、函数信号发生器作为标准仪器，型号分别为ZX32D、TDS2012C、DG1022U；
(3)幅值测试：采用示波器、水浴锅等作为标准仪器，示波器型号为TDS2012C；
(4)静态电容：采用LCR测试仪、标准电容盒作为标准仪器，型号分别为TH2811C、ATCDB12。
3.1 谐振频率(阻抗)与反谐振频率(阻抗)
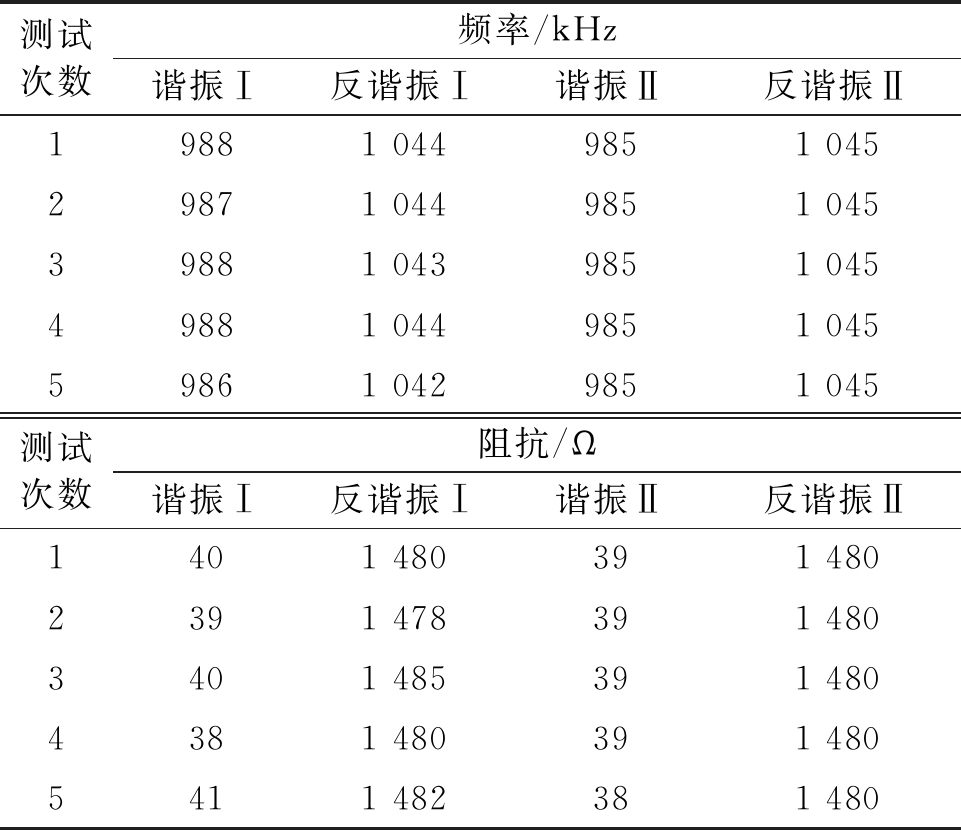
连续进行了5次测试实验，数据如表1所示。表中标准仪器测试数据记为I，设计装置测试数据记为Ⅱ。由表1可知，设计装置与标准仪器测试结果中，谐振频率的最大偏差值是3 kHz，出现在第1、3、4行数据中，最大相对误差为0.3%；反谐振频率的最大偏差值也是3 kHz，出现在第5行数据中，最大相对误差为0.29%。对比可知，设计装置读数稳定，测试结果一致性好，满足设计要求。
表1 谐振频率(阻抗)与反谐振频率(阻抗)实验数据
Table 1 The experimental data of resonant frequency (impedance) and anti-resonance frequency (impedance)
测试次数频率/kHz谐振Ⅰ反谐振Ⅰ谐振Ⅱ反谐振Ⅱ19881 0449851 04529871 0449851 04539881 0439851 04549881 0449851 04559861 0429851 045测试次数阻抗/Ω谐振Ⅰ反谐振Ⅰ谐振Ⅱ反谐振Ⅱ1401 480391 4802391 478391 4803401 485391 4804381 480391 4805411 482381 480
由表1可知，设计装置与标准仪器测试结果中，谐振阻抗的最大偏差值是3 Ω，出现在第5行数据中，最大相对误差为7.3%；反谐振阻抗的最大偏差值也是3 kHz，出现在第3行数据中，最大相对误差为0.34%。对比可知，设计装置输出值稳定，测试结果一致性好，满足设计要求。
3.2 静态电容
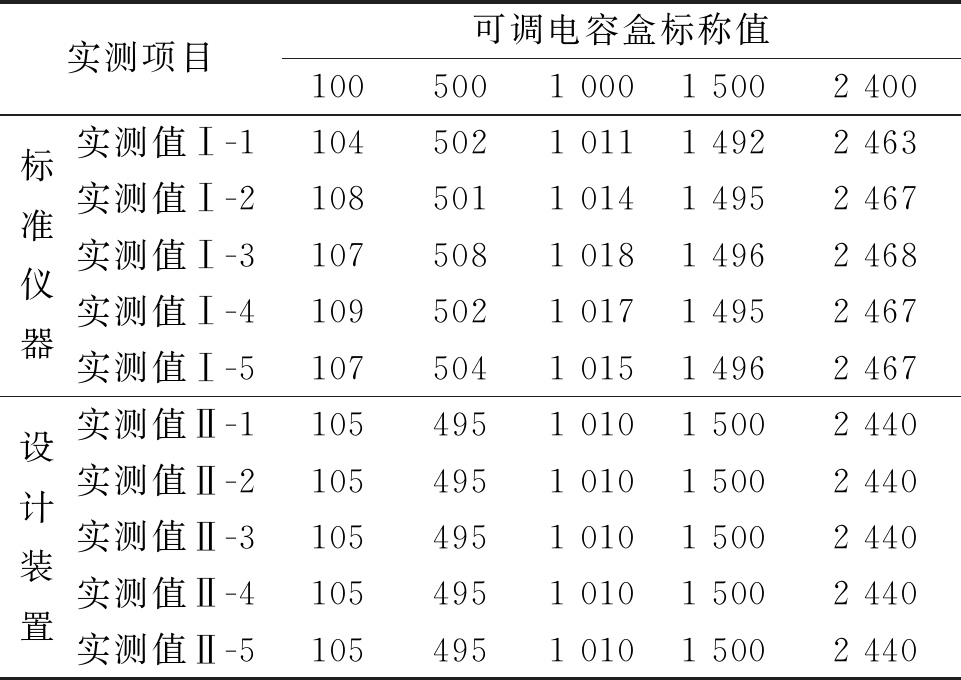
设计装置静态电容测试范围为100～2 400 pF，用标准电容盒作为标定设备，每隔100 pF测试一次结果、重复测试5次，测试数据如表2所示，为简化表格，选取100、500、1 500、2 000、2 400 pF 5个点的数据。由表2可知，设计装置与标准仪器测试结果中，针对电容盒的5个电容值(100、500、1 000、1 500、2 400 pF)，标准仪器实测电容的最大偏差值分别为9、8、18、8、68 pF，最大相对误差为9%，出现在第1列数据中；设计装置实测电容的最大偏差值分别为5、5、10、0、0 pF，最大相对误差为5%，也出现在第1列数据中。对比可知，设计装置输出值稳定，测试结果一致性好，满足设计要求。
表2 静态电容实验数据
Table 2 The experimental data of static capacitance pF
实测项目可调电容盒标称值1005001 0001 5002 400标准仪器设计装置实测值Ⅰ-11045021 0111 4922 463实测值Ⅰ-21085011 0141 4952 467实测值Ⅰ-31075081 0181 4962 468实测值Ⅰ-41095021 0171 4952 467实测值Ⅰ-51075041 0151 4962 467实测值Ⅱ-11054951 0101 5002 440实测值Ⅱ-21054951 0101 5002 440实测值Ⅱ-31054951 0101 5002 440实测值Ⅱ-41054951 0101 5002 440实测值Ⅱ-51054951 0101 5002 440
3.3 发射幅值与回波幅值
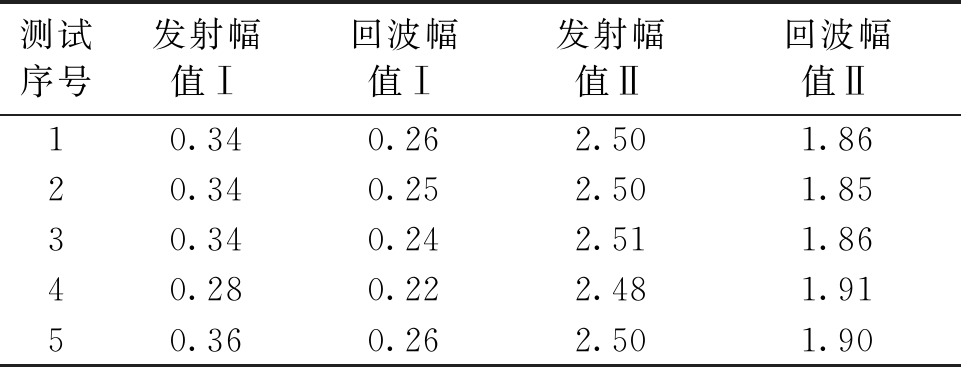
表3为发射与接收幅值的5次测试数据。从表3可以看出，因为对输出信号做了必要的调整，所以无论是输出信号的幅值还是信号的一致性，设计装置都有了很大的改善。设计装置对传感器输出信号进行整流滤波放大之后进行读数，因此测试数据相对较大。
表3 发射幅值与回波幅值实验数据
Table 3 The experimental data of the sending wave amplitude and the returned wave amplitude V
测试序号发射幅值Ⅰ回波幅值Ⅰ发射幅值Ⅱ回波幅值Ⅱ10.340.262.501.8620.340.252.501.8530.340.242.511.8640.280.222.481.9150.360.262.501.90
3.4 配对实验
实验方案如图11所示，以5只传感器为例，测试条件：1)将样品放置在设定温度的水浴锅中加热10 min，使两者温度达到一致；2)设定水浴锅在30 ℃～90 ℃温度范围内可调，测试数据取样间隔温度为10 ℃；3)测试对应温度的传感器输出幅值。
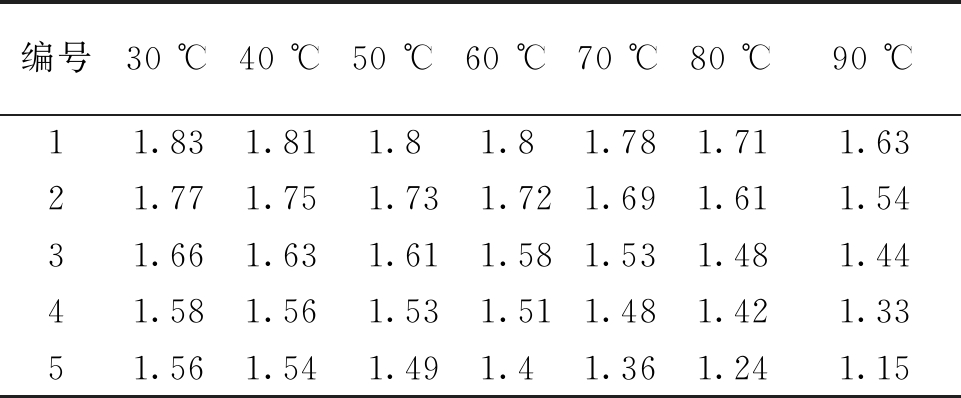
自收自发条件下传感器输出幅值的测试数据如表4所示，图12为自收自发测试数据曲线图。
由表4与图12可知，1号、2号传感器特性接近，3号、4号传感器特性接近。根据一收一发测试数据选择传感器配对的有效性，将1号与2号、3号与4号分别在工况条件下进行互为收发的配对实验，测试结果如表5所示。表中“1→2”表示1号传感器发送信号，2号传感器接收信号，图13为一收一发配对数据曲线图。
表4 自收自发传感器输出幅值测试结果
Table 4 The output amplitude test results of self-sending and self-receiving sensor V
编号30 ℃40 ℃50 ℃60 ℃70 ℃80 ℃90 ℃11.831.811.81.81.781.711.6321.771.751.731.721.691.611.5431.661.631.611.581.531.481.4441.581.561.531.511.481.421.3351.561.541.491.41.361.241.15
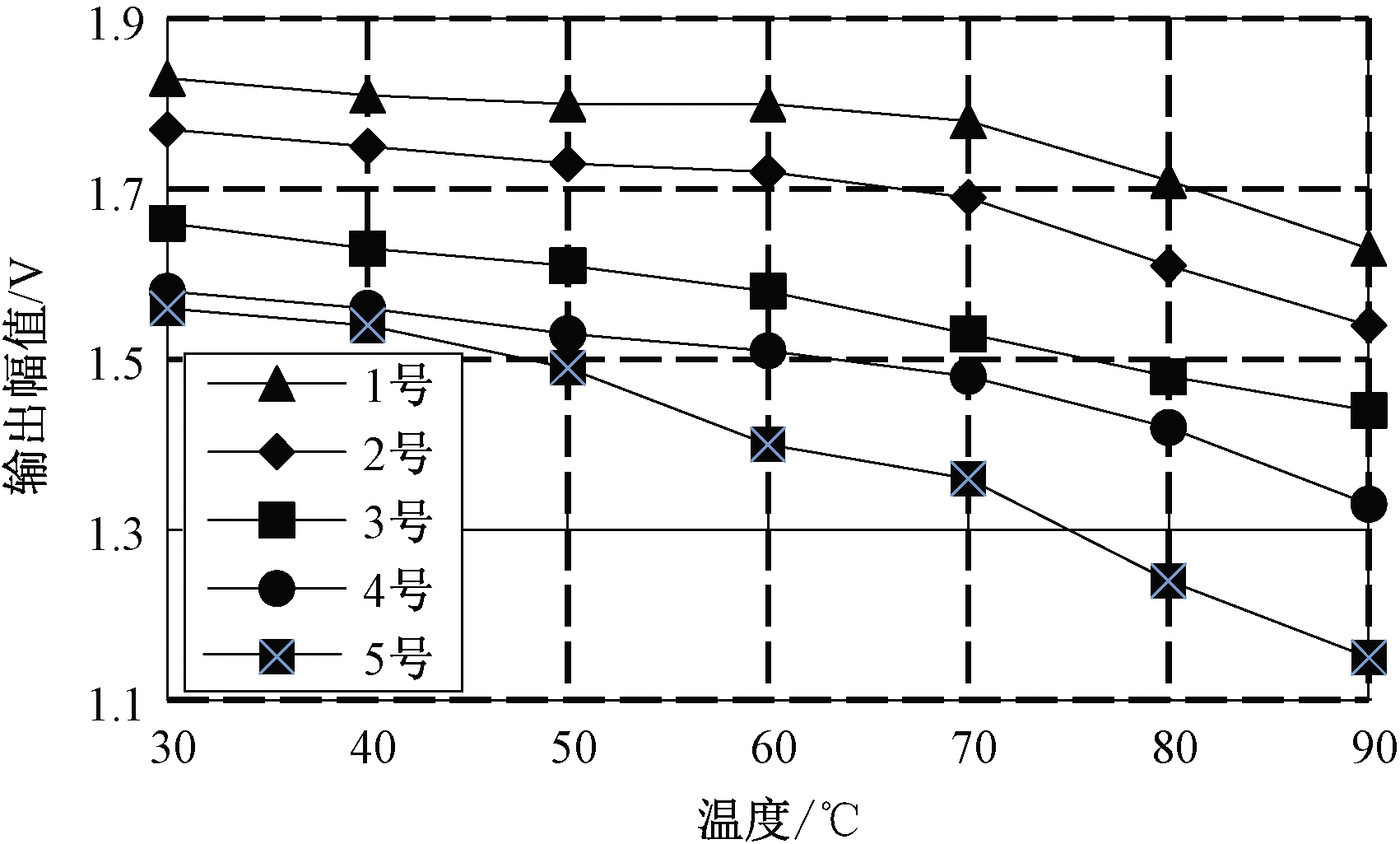
图12 自收自发数据曲线图
Figure 12 The data gragh of self-sending and self-receiving
表5 一收一发传感器输出幅值测试结果
Table 5 The output amplitude test results of sensors with one sending and one receiving V
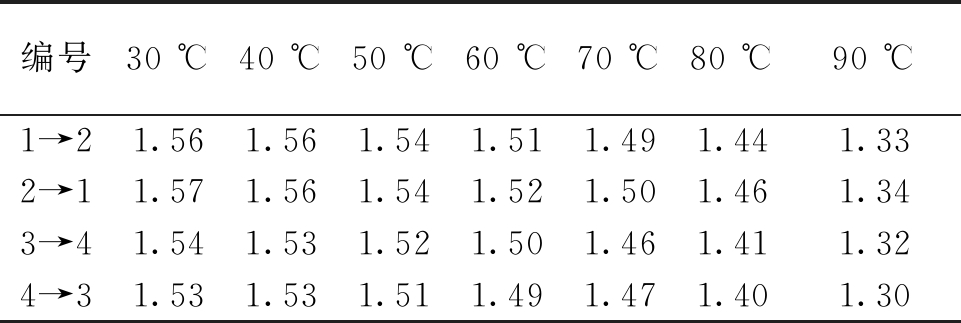
编号30 ℃40 ℃50 ℃60 ℃70 ℃80 ℃90 ℃1→21.561.561.541.511.491.441.332→11.571.561.541.521.501.461.343→41.541.531.521.501.461.411.324→31.531.531.511.491.471.401.30
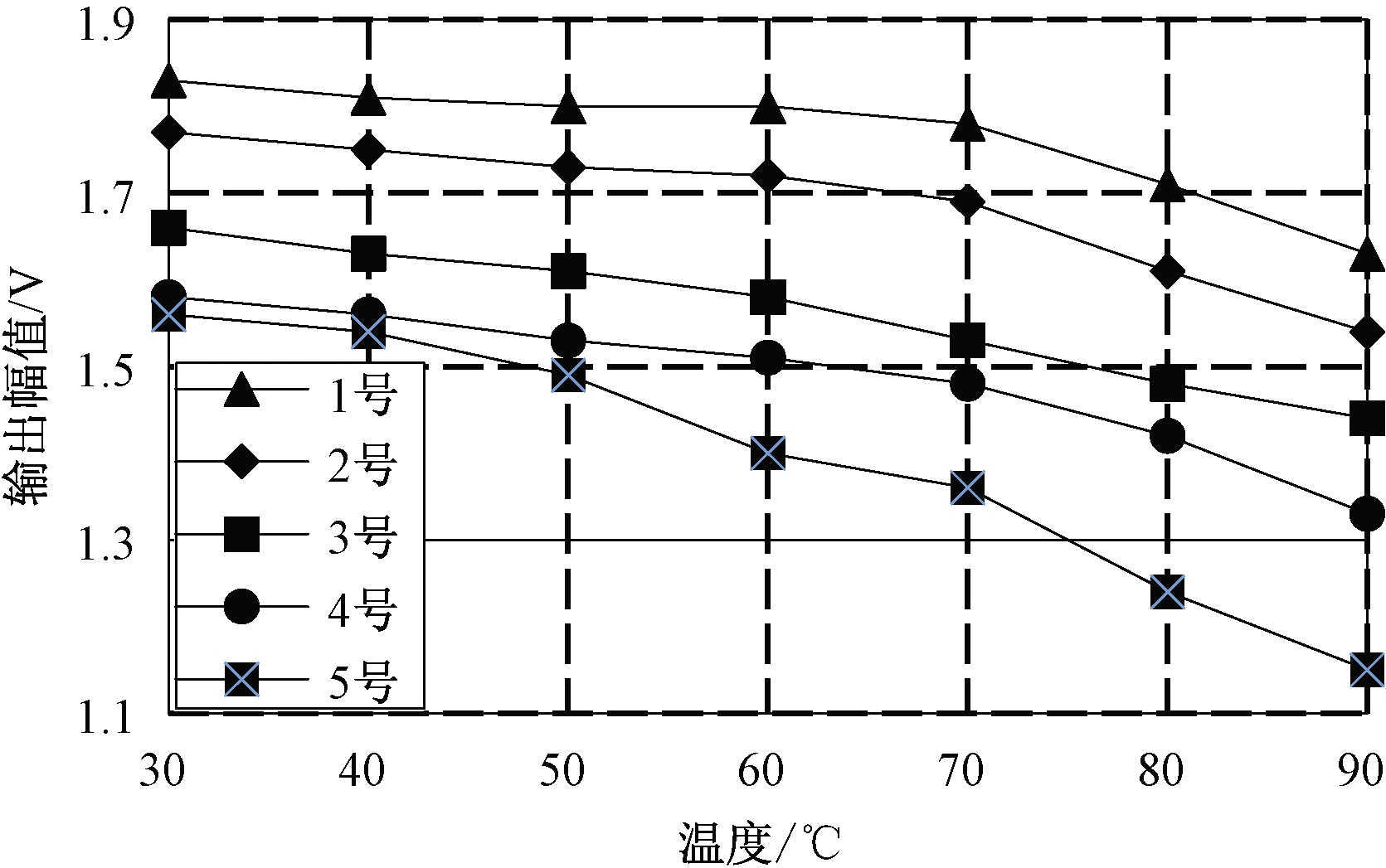
图13 一收一发数据曲线图
Figure 13 The data gragh of one sending and one receiving
由表5与图13数据分析可知，1号、2号传感器配对后收发特性接近，3号、4号传感器配对后收发特性接近，而特性接近的传感器转换效率也接近，信号传输过程中衰减也接近，信号处理电路中信号的上升率与相位移也接近，这样就可以更好地保证流量计量精确度。
需要说明的是，流量计量的精确度主要取决于传感器，但是与基表管段以及其他工艺条件也有很大关系。所以，两只配对传感器特性相似度的量化值，需要在确定的生产工艺、参数比较稳定的环境下做标定，将标定值作为检测参数用于生产实践中。
4 结束语
针对目前超声波流量计生产过程中存在的因传感器性能一致性差而带来的超声波流量计精确度不高、产品合格率低等问题，通过理论分析及大量实验，提出了一种可以用于同一支超声波流量计上的一对超声波传感器的测试方法，并给出传感器配对选择的依据，以及给出具体测试的关键电路设计方法。实验数据分析证明了理论分析与具体设计的有效性，该装置已经应用于生产实践，生产效率与成品率都有很大提高。
[1] 靳涛. 浅析能源计量在节能减排管理中的作用[J/OL]. 工程技术(全文版)，2017(5)：17[2019-03-06].http://www.cqvip.com/QK/72150X/201701/epub1000000667751.html.
[2] 侯春雷. 超声波换能器性能测试仪的设计与实现[D]. 哈尔滨：哈尔滨工业大学，2015.
[3] RAJITA G, MANDAL N. Review on transit time ultrasonic flowmeter[C]//2016 2nd International Conference on Control, Instrumentation, Energy & Communication. Kolkata. India: IEEE, 2016:88-92.
[4] GHASEMI N, ABEDI N, MOKHTARI G. Real-time method for resonant frequency detection and excitation frequency tuning for piezoelectric ultrasonic transducers[C]//2016 Australasian Universities Power Engine-ering Conference (AUPEC). Queensland，Australia: IEEE, 2016: 1-5.
J, VACLAVíK J, MARTON P. Fast and portable precision impedance analyzer for application in vibration damping[C]//IEEE International Work-shop of Electronics, Control, Measurement, Signals and their Application to Mechatronics. Liberec， Czech: IEEE, 2015: 1-5.
[6] 王翥，崔晓志，侯春雷. 超声波传感器接收信号强度非对称性分析与对策[J]. 传感技术学报，2015，28(1)：81-85.
[7] AMRI K, WIRANATA L F, SUPRIJANTO, et al. Fluid flow velocity measurement using dual-ultrasonic transducer by means of simultaneously transit time method[C]//International Conference on Instrumentation, Communications, Information Technology and Biomedical Engineering. Bandung，India: IEEE, 2015: 113-116.
[8] 刘春龙. 压电式超声波换能器测试方法的研究与设计[D]. 哈尔滨：哈尔滨工业大学，2017.