0 引言
近年来无人机(unmanned aerial vehicles, UAV)广泛应用于各个领域.在侦查和监视任务中,无人机需要依次飞越一系列目标,并利用机载探测装置对目标进行观测.规划无人机飞行航路时,应综合考虑无人机飞行性能和机载探测装置的可视范围,以满足任务的侦查要求.无人机航路规划是指搜索从起点到终点的最短路径,并满足环境因素、无人机飞行特性以及传感器性能等约束.目前的求解方法可分为确定性方法和启发式算法两类.
确定性的方法首先将优化问题进行离散化,通过搜索笛卡尔空间中的最短曲线以获得最优解.如Dijkstra算法[1-2],人工势场法[3]等基于图论的寻优算法被广泛地应用于无人系统最优系统路径的求解问题中.但这些方法往往基于局部信息搜索最优解,其所得路径的全局性较差[4].此外,如何选择合适的离散化尺度也缺乏理论依据,较大的尺度可以提高问题求解的效率,但所得解的精度较低而导致算法过早收敛[5].而过小的搜索尺度将使得计算复杂度急剧增加,发生维数灾难.
为解决基于图论搜索方法的固有局限性, 尹高扬等[6]提出了一种基于自适应边界快速扩展随机树(RRT)的求解方法,提高了基于概率搜索算法在处理复杂、大规模优化问题的效率.基于元启发式的优化方法,如遗传算法[7]、粒子群优化算法[8-9]在解决组合优化问题中表现出优越的性能.由于地表环境的遮挡目标可能无法始终处于探测装置的可视区域之内,Wang等[10]研究城市环境中的传感器可见区域,并提出以目标观测时间作为性能指标求解最优跟踪路径问题.邱华鑫等[11]提出了一种鸽群优化(pigeon inspired optimization, PIO)算法,并在无人机编队控制和图像配准问题中获得了成功的应用.但是,在用于离散优化问题时其求解效率和性能迅速下降.
目前,关于无人机航路规划的研究方法大多仅考虑环境威胁以及无人机飞行性能等约束,对目标可探测范围以及地表遮挡等因素的研究工作还不多见.因此,笔者针对复杂环境中的无人机侦查航路规划问题开展研究,提出了一种基于动态规划和鸽群优化框架的混合规划方法.
1 问题描述
1.1 无人机运动学模型
为了简化分析,假设无人机在设定高度以恒定速度飞行,并忽略无人机偏航角和俯仰角的影响,无人机的运动学特性可以表示为[10]:

(1)
式中:x(k)和y(k)表示在时刻k无人机的位置;φ(k)表示无人机的滚转角;φmax为滚转角最大值.
1.2 探测装置可视区域模型
假设无人机的飞行姿态与探测装置的视轴指向相互独立.给定探测装置的视场角和无人机的飞行高度,探测装置的理论最大可探测范围为可视锥体与地面的相交平面.但由于地表特征的遮挡,目标不能在任意角度被完整观测.
根据探测装置指向、视场参数、目标位置以及地面特征等条件,探测装置对地面目标的可视范围可以由视线传播算法(sight of line propagation, LoS Propagation)进行求解[10],即计算视点与理论最大可探测范围内任意一点的连线是否与地表特征相交.若不相交,则说明地表上点为可探测点,反之为不可探测点.
假设无人机在恒定高度飞行,给定探测装置的视场、视轴指向等参数,地面目标的最大可探测区域可以表示为以目标为中心的半球.在此范围内,通过分析探测装置与目标的相对位置以及地表遮挡条件,移除视图中被阻挡部分,目标的可探测区域为无人机飞行高度剖面与探测装置可视半球的相交平面,如图1(a)所示.因此,依次分析每个目标周围的地形特征,可以求解出各个目标的可被观测范围,如图1(b)所示.
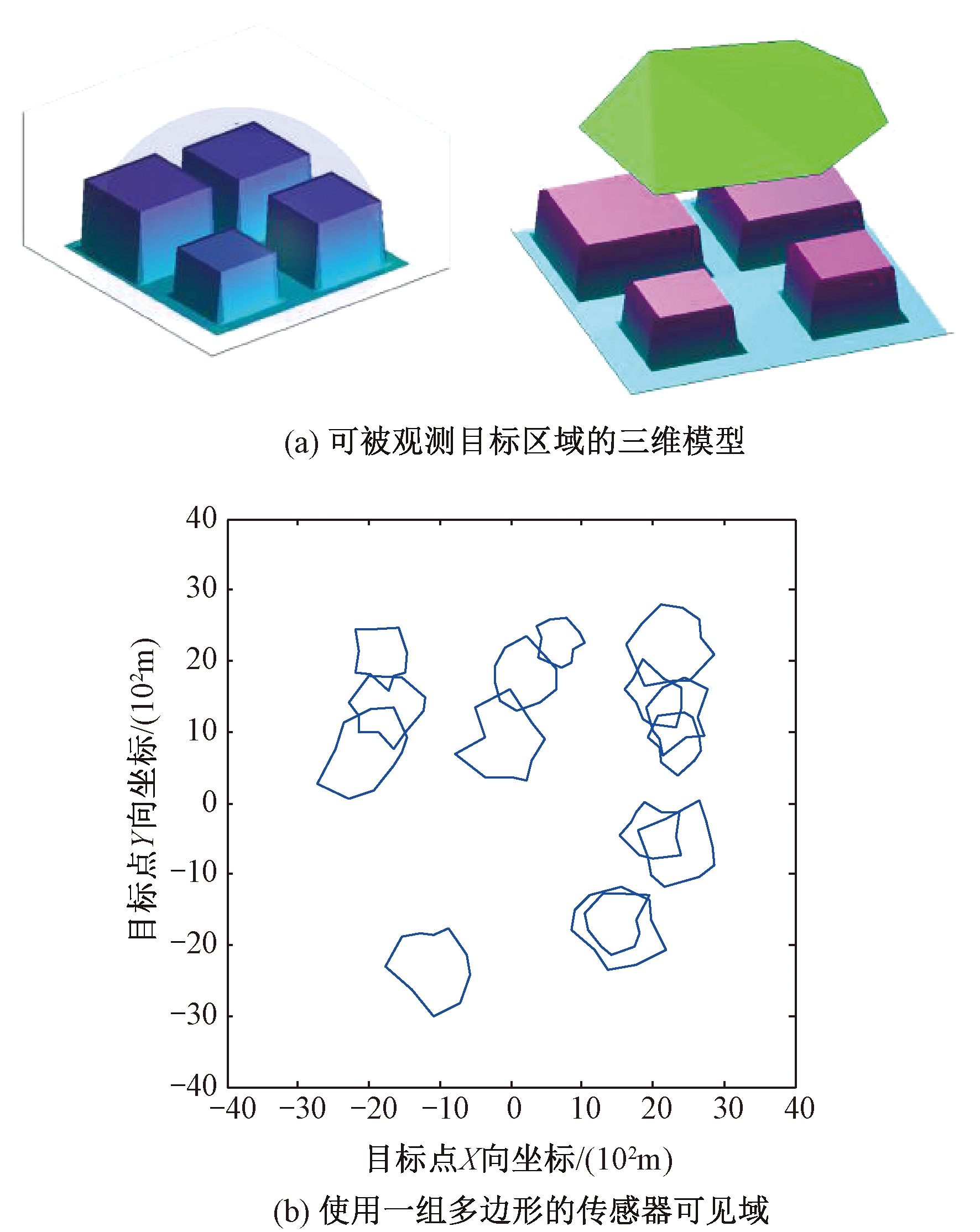
图1 目标可被观测区域简化模型
Fig.1 Simplifed model of the target′s visibility regions
为使得无人机探测装置能够有效观察目标,假设无人机在飞越目标附近空域时,必须至少接触可视范围内的任何一点.
2 基于鸽群优化的航迹优化方法
2.1 基于改进PIO算法的无人机航路规划方法
侦查任务的目的是以最小的时间代价获取所有目标区域的有效信息.如果无人机的速度和高度恒定,则该问题等价于求解旅行商问题(travelling salesmen problem, TSP).标准的PIO算法针对连续优化问题设计,由于目标侦查航路规划问题的离散性,使用标准的PIO方法进行求解效率较低且准确性差.为此,笔者提出了一种离散化的PIO改进方法,改善离散优化问题的性能.
由前文的分析可知,由于地表环境的遮挡,机载探测装置不能在所有角度观测到目标. 因此,在搜索最佳路径时应考虑探测装置的可视区域.为了解决这一问题,笔者提出首先根据目标的空间分布确定无人机飞越各个目标的顺序,得到初始航点.然后再根据目标的可视区域与无人机飞行性能的约束,基于动态规划方法对初始航点进行优化,以保证无人机能从适当的角度进入目标区域,实现对目标有效观测.
2.2 离散化地图和磁场算子
鸽群优化算法中,每个个体表示问题域中的一个可行解.在无人机侦查航路规划问题中,鸽群中个体的位置和速度矢量可表示为:
(2)
式中:i=1,2,…N表示鸽群的规模;xiD为整数,表示飞越目标的顺序;D是目标的编号;Vi是与位置矢量具有相同维数的速度矢量.根据量子行为的演化过程,改进的地图和磁场算子如下:
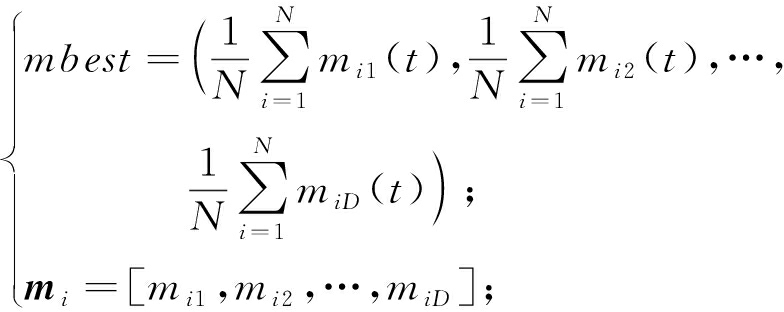
(3)
p=f1·pbesti+(1-f1)·gbest;
(4)
Xi(t+1)=p+β·|mbest-Xi(t)|·log(1/u)·
(exp(-R·NC))+Vi(t+1);
(5)
Vi(t+1)=Vi(t)·e-R·t+rand(gbest-Xi(t)),
(6)
式中:mi(t)是到第t次迭代时第i个鸽子的最优解;mbest表示N只鸽子的平均最佳位置;f1表示0和1之间的随机数;pbest是第i只鸽子的最优位置;gbest为所有个体的最优解;β是创造力系数;Xi(t+1)是(t+1)次迭代中第i只鸽子的相关位置信息;u是0和1之间的随机数.
基于连续鸽群优化的更新方式,所得解Xi(t+1)可能无法正确表示要访问目标的顺序,出现大量无效解,降低算法的寻优性能.为解决这一问题,笔者首先通过对初始解取整获得离散解.但由于舍入解决方案可能不包含所有目标的标记,因此将缺少的部分添加到位置初始解Xi(t+1)中,该向量由路径规划问题的有效解组成.采用“取整补全”方法对位置矢量进行离散化处理,第一步采用四舍五入取整法,将优化结果全部取整,筛选出超出所需离散范围以及重复出现的数,将不符合要求的位置矢量均置0;第二步对其补全,将遗漏的位置变量进行排列组合,并将所有排列组合一次放入遗漏的位置变量中,再挑选出适应值更优的排列方式,以完成对可行航迹优化路线的离散化处理.
2.3 离散化的地标算子
地标算子使得鸽群的整体运动向中心聚拢,从而加快算法的收敛速度,是一种局部搜索策略.当全局搜索不够充分,鸽群尚未到达最优解附近时,基于未改进的更新策略可能会使得算法陷入局部最小值中.为避免早熟收敛的问题,笔者采用次优解作为鸽群的地标,在实现鸽群总体向中心聚拢的同时,具有一定的全局搜索能力:
mbest=![]()
(7)
(8)
Xi(t+1)=Xi(t)+rand·(mbest-Xi(t)),
(9)
式中:Nc是地标算子中定义的种群大小.
2.4 代价函数
在第一步求解中,只需要确定无人机的航点排序,因此可以采用无人机航路的长度评估每个个体的适应度:
fc=dist(Xi),
(10)
式中:函数dist()用于计算给定目标顺序Xi的航路长度.用于优化侦察航迹的完整代价函数为:
fc=![]()
(1-f2)×(180-arccos(((yi+1-yi,n)2+
(xi+1-xi,n)2+(yi,n-yi-1)2+
(xi,n-xi-1)2-(yi+1-yi-1)2-
(11)
2.5 基于动态规划的航点优化
如前文所述,为实现对目标的有效观测,无人机应当根据探测装置的可视区域飞越目标.因此,无人机的飞行航点应至少位于各个目标可视范围的边界上.笔者基于动态规划策略,对所得的初步航点进行优化,如图2所示,考虑3个相邻的目标区域,固定飞越第i-1和i+1两个航点,通过PIO算法确定第i个目标可视范围的边界,从而得到满足目标观测要求和飞行性能约束的最优航点.无人机的转弯半径与飞行速度与滚转角约束有关,因此其最大可跟踪航路可由Dubins方法进行求解.
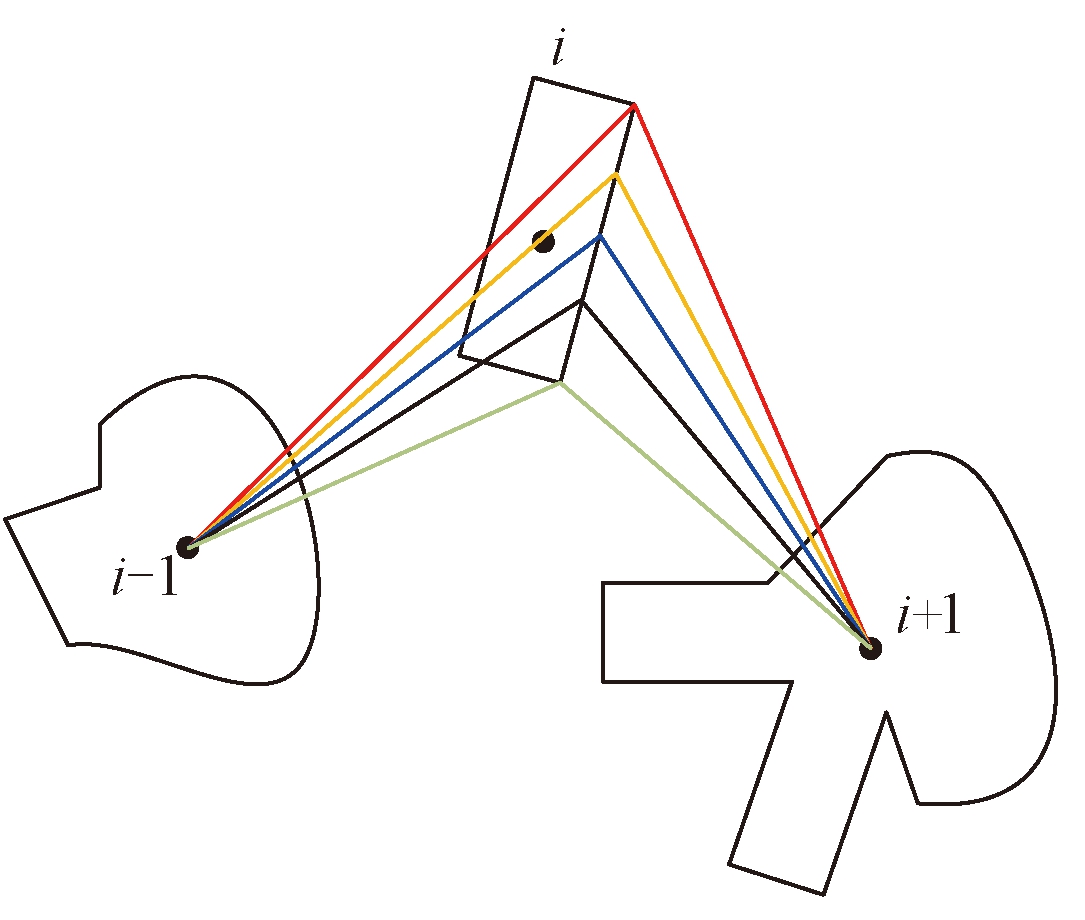
图2 基于动态规划的航点优化示意图
Fig.2 Schematic diagram illustrate the polygon point selection process
所得的优化航点除了满足对目标的有效观测外,还应当考虑无人机航程和机动性能的约束,因此所得航点的代价可以表示为:
fc=f2·d+(1-f2)×(180-A),
(12)
式中:f2是一个会影响所得路线长度和转角的权重因子.给定3个连续的多边形,距离和转角可以如图2计算.
3 仿真与分析
为了验证所提算法的有效性和准确性,笔者将其与标准PIO算法以及量子粒子群优化算法(quantum particle swarm optimization, QPSO)进行比较,用于解决复杂环境中的侦查路径优化问题.上述3种算法在个人计算机(Intel i7 3.6 GHz和16 GB内存)上使用MATLAB实现,可调参数根据相关文献和标准Benchmark数据集测试来确定.仿真针对复杂环境下的目标侦查航路规划问题,基本设计如下:随机生成15个多边形用于表示目标的可探测区域.对于PIO算法,以每个多边形的中心作为无人机需飞越的航点.初始参数设置及取值为R=0.1,N=100,D=15,C1=400, C2=600.
图3为采用标准PIO算法和笔者所提出方法所得到的最优飞行航路.从图3(a)可以看出,由于无人机转弯半径的约束,通过标准PIO算法获得的可跟踪路径不能够完成对所有目标区域的有效探测.如图3(b)所示,由于笔者所提出的航路优化算法同时考虑了对目标观测和无人机机动性能的约束,所得到的航路在满足对目标区域有效观测的同时,所得到的航线也更加平滑.
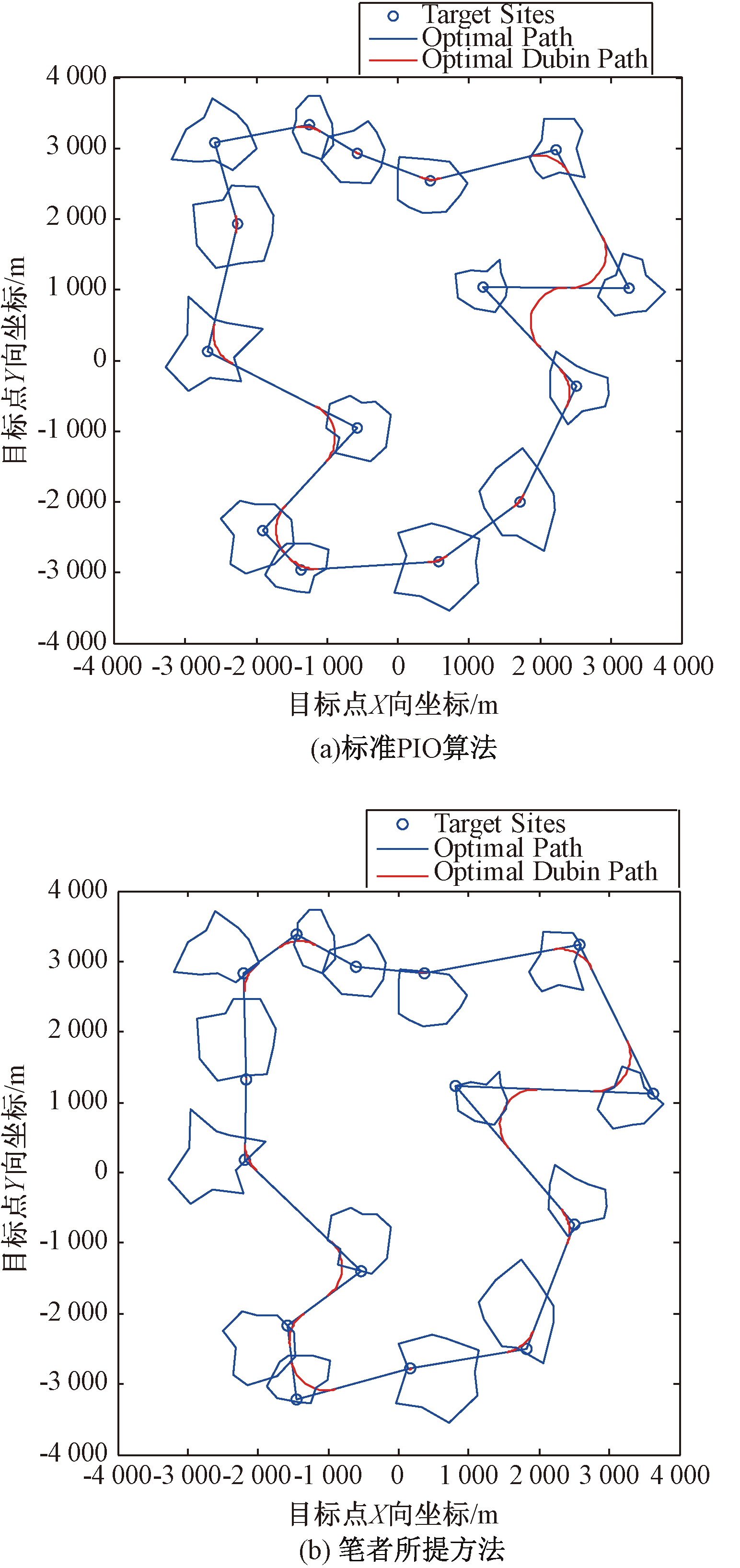
图3 标准PIO算法(a)和所提出的方法(b)产生的路径
Fig.3 The resulting path obtained through the standard PIO algorithm (a) and the proposed method (b)
从图4可以看到,笔者所提出方法具有更快的收敛速度和更好的寻优能力.这是因为对PIO算法的两种导航算子进行了离散化改进,提高了其用于解决非连续优化问题的能力.此外,所提出的方法利用改进的地标算子考虑到在最优性附近产生更多的解,从而进一步增加收敛速度.
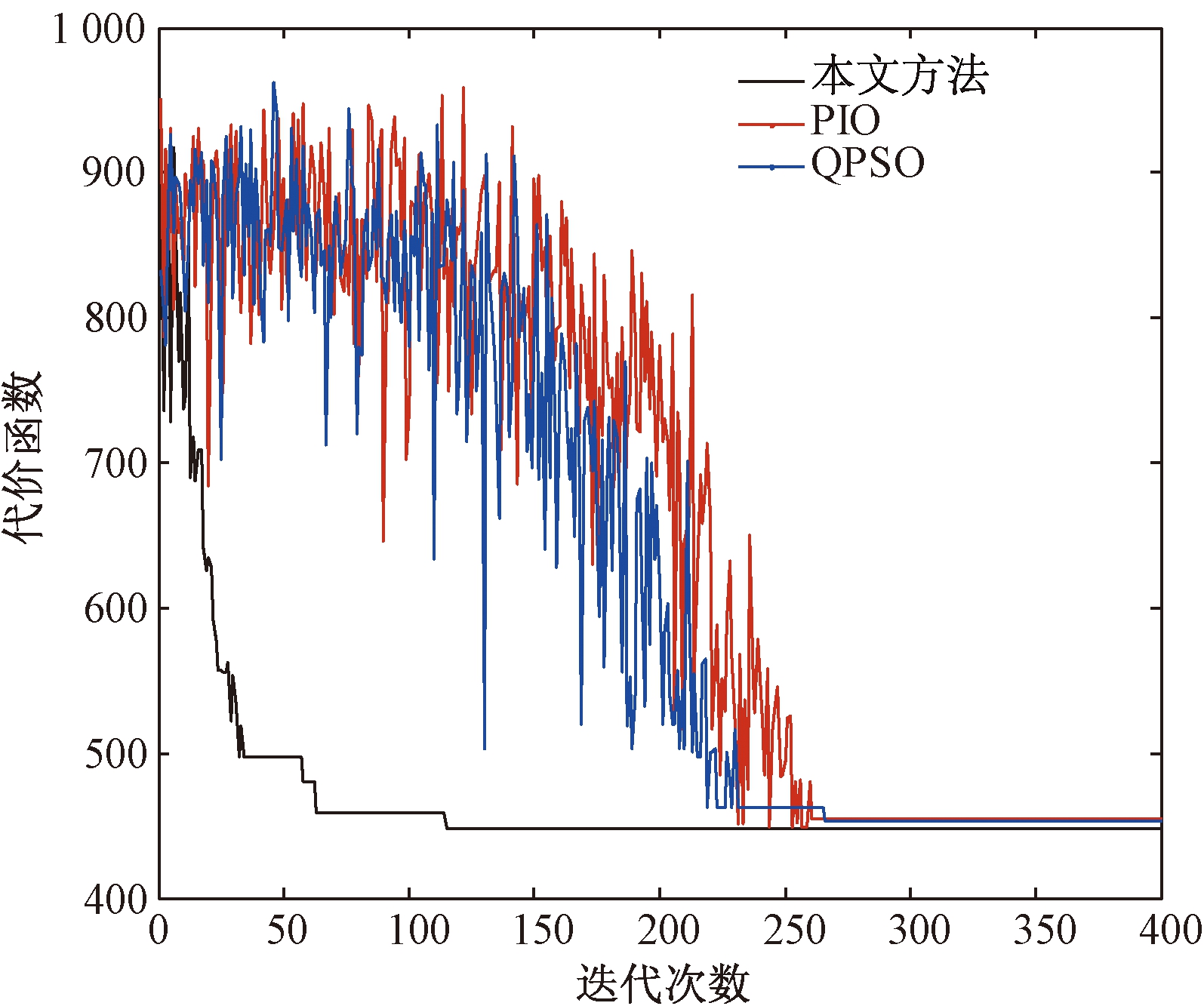
图4 不同算法的收敛曲线
Fig.4 Illustrate the convergence of different methods
为了验证所提方法面向大规模复杂问题中的性能, 进一步将上述算法应用于由1 000个目标组成的场景中.为了消除初始化的影响,所有算法都运行20次,这些方法的性能如表1~3所示.
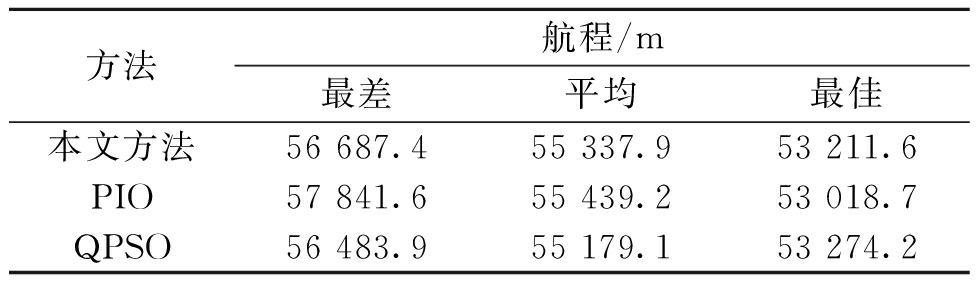
表1 使用不同方法的路径规划的航程比较
Tab.1 Comparison of the ranges for route planning using different methods
方法航程/m最差平均最佳本文方法56 687.455 337.953 211.6PIO57 841.655 439.253 018.7QPSO56 483.955 179.153 274.2
表2 使用不同方法的路径规划的未覆盖目标数量比较
Tab.2 Comparison of the number of uncovered targets for route planning using different methods

方法未覆盖目标的数量最差平均最佳本文方法000PIO329267137QPSO361248129
从表1可以看出,从所得到最优航路的航程上来看,所提出的方法比基于QPSO的规划方法稍差,略优于标准的PIO算法.这是因为基于QPSO的规划方法没有考虑目标的可探测性,而是仅以总的航程为最优指标对航路进行规划.
从表2中可以看出,标准PIO和QPSO这两种方法均未能实现对所有目标的有效探测,不能完整地完成目标侦查的任务.表3统计了3种规划算法的执行时间,可以看到笔者提出方法的总时间要高于另外两种算法(耗时增加约35%),这是因为笔者所研究算法综合目标可探测性和无人机机动性,对航点进行了进一步优化.从任务完成度和算法效率两方面综合考虑,方法的整体性能要优于标准PIO方法和基于QPSO的规划方法.
表3 使用不同方法的路径规划的平均运行时间比较
Tab.3 Comparison of the average running time for route planning using different methods

方法步骤平均运行时间/s本文方法PIOQPSO初始解15.3航点优化10.8总时间26.1总时间18.6总时间19.2
4 结论
笔者研究了复杂环境下的无人机侦查航路规划问题,针对机载探测装置与地表特征间的相对空间关系给出了目标可视范围模型,并将其作为被优化的要素用于求解最优航路.针对标准PIO算法不用直接用于求解非连续优化问题,笔者提出了离散化改进算法,改善了其用于离散优化问题的性能.仿真结果表明,与标准PIO算法和QPSO算法相比,笔者所提出的航路规划方法具有更快的收敛速度和寻优能力,并极大提高了侦查任务的完成度.
[1] 王树西,李安渝. Dijkstra算法中的多邻接点与多条最短路径问题[J]. 计算机科学, 2014, 41(6):217-224.
[2] 金婷,方欢,方贤文. 改进型Dijkstra算法的最短路径求解[J]. 软件导刊, 2016, 15(2):129-131.
[3] 丁家如,杜昌平,赵耀,等. 基于改进人工势场法的无人机路径规划算法[J]. 计算机应用, 2016, 36(1):287-290.
[4] FU Y G, DING M Y, ZHOU C P. Phase angle-encoded and quantum-behaved particle swarm optimization applied to three-dimensional route planning for UAV[J]. IEEE transactions on systems, man and cybernetics-Part A:Systems and humans, 2012, 42(2):511-526.
[5] BELKHOUCHE F. Reactive path planning in a dynamic environment[J]. IEEE transactions on robotics, 2009, 25(4):902-911.
[6] 尹高扬,周绍磊,吴青坡. 基于改进RRT算法的无人机航迹规划[J]. 电子学报, 2017, 45(7):1764-1769.
[7] 穆瑞杰. 基于遗传算法的地铁车站引导标识布点探析[J]. 郑州大学学报(工学版), 2018, 39(1):73-89.
[8] 李文,伍铁斌,赵全友,等. 改进的混沌粒子群算法在TSP中的应用[J]. 计算机应用研究, 2015, 32(7):2065-2067.
[9] 梁静,宋慧,瞿博阳,等.基于改进粒子群算法的路径优化问题研究[J].郑州大学学报(工学版),2014,35(1):34-38.
[10] WANG Y, CAO Y. Coordinated target tracking via a hybrid optimization approach[J]. Sensors, 2017, 17(3): 472.
[11] 邱华鑫, 段海滨, 范彦铭. 基于鸽群行为机制的多无人机自主编队[J]. 控制理论与应用, 2015, 32(10):1298-1304.