0 引言
由于图像数据量大、冗余度高，并且图像中相邻像素之间具有很强的相关性，所以传统的数据加密方法诸如AES、DES、IDEA和RSA等加密效率不高．为此，研究人员致力于寻找新的满足混淆和扩散要求的图像加密方法．
混沌系统因其运动轨迹的非周期性以及对初始条件极度敏感性、非线性、各态遍历性、不可预测性等特性被许多学者和专家所重视[1]．1998年，Fridrich首次将混沌系统应用于图像加密中，充分保证了算法的高效性[2]．随后，基于混沌系统的图像加密方法取得了一系列的研究成果[3-5]．但是，基于混沌系统的图像加密方法仍存在诸多不足，比如混沌退化、对基于明文的攻击方式防御能力低等．为此，将混沌系统与其他方法结合，成为目前的研究热点[6-9]．
遗传算法是一种以自然选择为原则的随机搜索最优化算法[10-12]．将遗传算法运用到信息加密中也是近几年加密领域中的研究前沿之一[13]．2014年，Wang等引入基因重组和交叉两种操作来扰动密钥，提出了一种基于基因重组思想和超混沌系统的图像加密算法[14]．同年，Enayatifar等提出了基于遗传算法和DNA序列的图像加密算法[15]．2018年，Pujari等结合DNA序列，给出一种基于混沌与遗传算法的图像加密算法[16]．这些方法多采用遗传算法的优化策略来实现图像的加密．
基于此，笔者利用Duffing、Logistic映射的伪随机性、遍历性和遗传算法的交叉变异算子来解决图像加密所遇到的安全威胁和效率低下问题．增强算法的混淆和扩散特性．
1 理论基础
1.1 混沌映射
(1) Logistic映射是研究动力系统、混沌、分形等复杂系统行为的一个经典模型，且具有良好的混沌特性,其数学描述如下：
xt+1=μxt(1-xt)，
(1)
式中：t为迭代时间步；μ为可调参数．当3.569 945 6<μ≤4时，Logistic映射处于混沌状态．
(2) Duffing映射(也称Holmes映射)是一个离散时间的动力系统，是Duffing方程的一个离散形式，其数学描述如下：
(2)
Duffing映射的两个常数a和b通常被设置为a=2.75和b=0.2，以产生混沌行为，如图1所示．它对初始值有极其敏感的依赖性．这里将其对初值的敏感性充分体现在加密算法对明文和密钥的扩散性与混乱性上．Duffing映射还具有优良的伪随机性，其轨道的演化是非周期、不收敛的，具有很好的随机性及不可预测性．已从理论上证实了Duffing映射可以产生统计特性优良的伪随机序列．
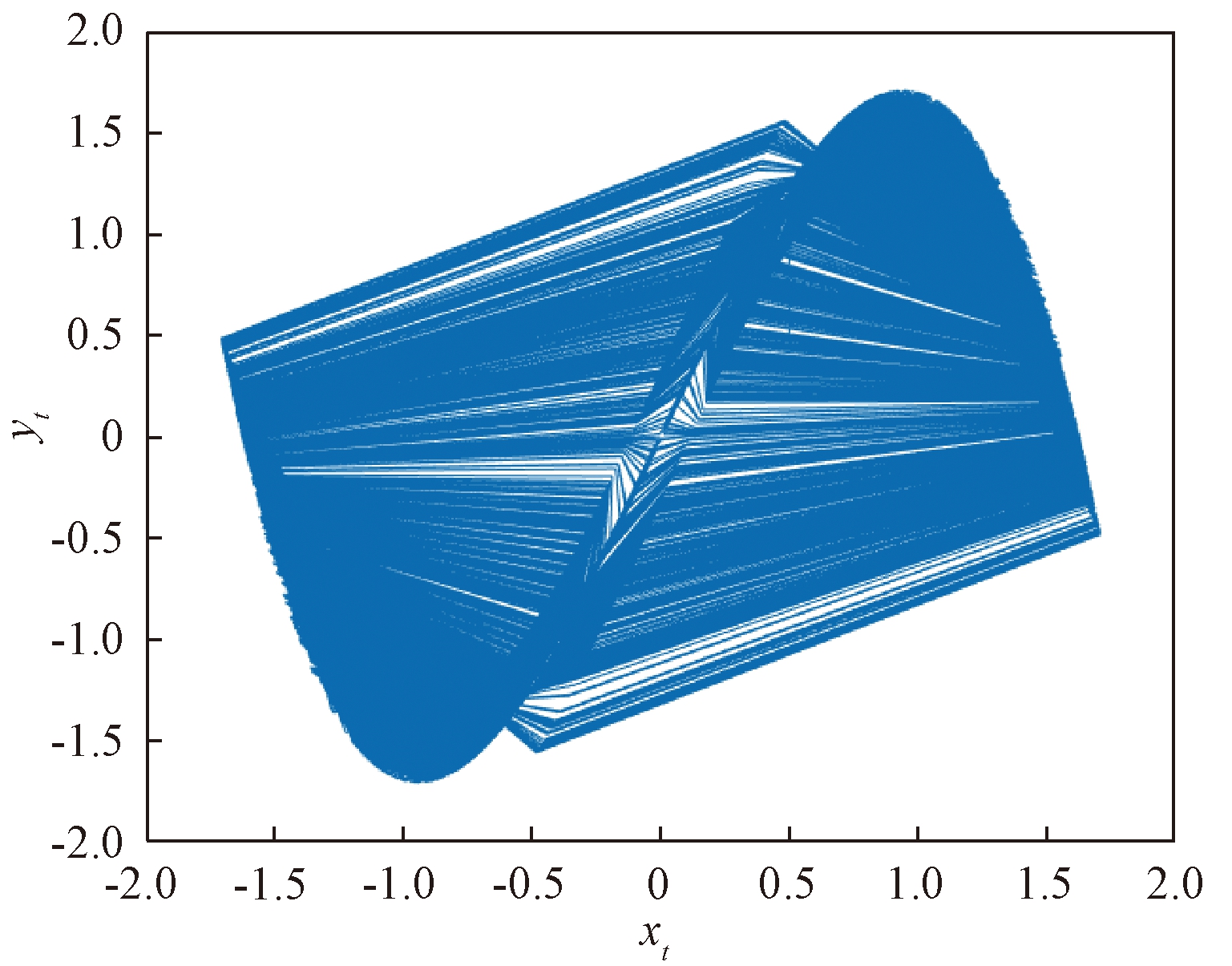
图1 处于混沌状态的Duffing映射
Fig.1 The duffing map in chaotic state
1.2 DNA编码
DNA分子是遗传信息的载体，由4种脱氧核苷酸组成，分别是腺嘌呤(A)、胞嘧啶(C)、鸟嘌呤(G)、胸腺嘧啶(T)．碱基的化学结构确定了碱基互补配对的原则，这一天然的四进制组合，正好与半导体通断所形成的二进制类似．因此，运用碱基的排列组合可以进行信息的存储和计算．
对于灰度图像来说，每个像素的灰度值可以用8位二进制数表示，如果采用DNA编码的话，则两位二进制编码一个碱基，只需4个碱基即可完成一个像素的编码．通过对每个像素进行DNA编码，将图像转换成DNA序列，可以将DNA序列的交叉变异操作用于图像加密．8种编码规则如表1所示．
表1 8种编码规则
Tab.1 Eight types of encoding rules.
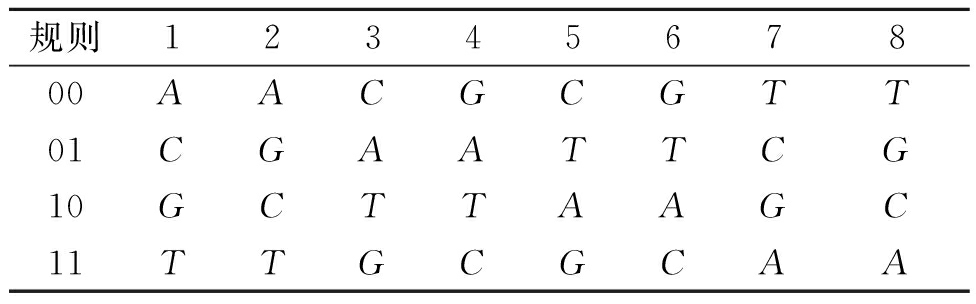
规则1234567800AACGCGTT01CGAATTCG10GCTTAAGC11TTGCGCAA
2 加密算法
2.1 密钥的产生
经典的数字图像加密中，密码仅受密钥控制，与明文无关，这种类型的图像密码系统易受选择明文攻击或已知明文攻击．如果相同的密钥，但不同的明文图像对应着不同的密码，将能有效抵抗选择明文攻击或已知明文攻击．
用给定密钥以及图像的哈希值作为混沌系统的初值和参数，实现加密的密码既与密钥有关，也与明文相关联．用Keccak算法生成明文图像的哈希值K，其长度为512 bit．将K分为64组，每组包含8个比特位，记K={k1，k2，k3，…，k64}．按照如下公式计算混沌系统的初值Key1、Key2、Key3、Key4：
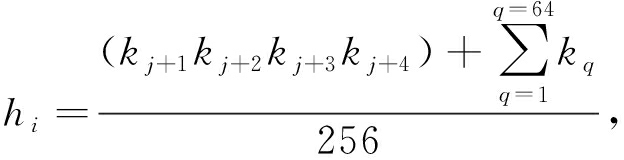
(3)
(4)
式中：
为给定值；j=4(i-1)；i=1、2、3、4．
2.2 遗传操作
给定大小为M×N的灰度图像，将单个像素看作一个“个体”．使用混沌映射产生的序列值作为个体在图像中的位置来选择个体，用遗传算子对个体进行交叉、变异操作．
选择：给定Duffing映射初值，迭代Duffing映射2 000次，以消除暂态效应带来的不良影响，以此为起点，继续迭代M×N次，产生两个序列U={u1，u2，…，uM×N}和V={v1，v2，…，vM×N}，并根据公式(5)和(6)进行处理后得到序列
和
确保U和V的每个元素取值大小在给定的范围内．
＾14·ui,256))；
(5)
＾14·vi,256))，
(6)
式中：i=1，2，…，M×N．
交叉：给定两个个体(像素)A和B，将其像素值用二进制表示．引入控制字C来控制两个个体的交叉操作．针对8位二进制的每一位，若控制字的当前位是0时，个体A和B的当前位保持不变，若控制字的当前位是1时，个体A和B互换当前位．最终得到新个体A′和B′．比如给定个体A、B和控制字C分别为10011001、00111100、01101001时，交叉后得到的新个体A′和B′为10111000和00011101，交叉过程如图2所示．
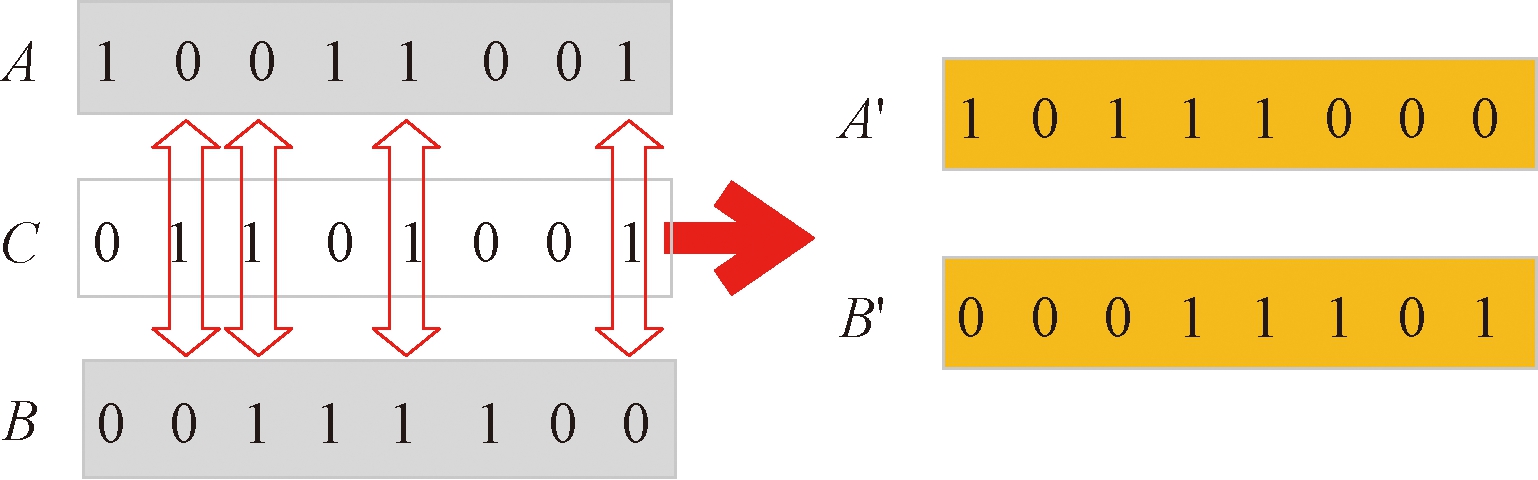
图2 个体10011001和00111100进行交叉操作
Fig.2 Crossover between individuals 10011001 and 00111100
变异：变异是生成新个体的辅助手段．这里用控制字来控制个体的变异．为增加密文的抗攻击特性，引入非线性扩散机制——DNA编码技术，实现DNA分子级别上的变异，也符合基因变异的本质．为此，选取核酸数据库中的某一核酸序列作为控制字．通过选择表1中的某种编码规则(也可以进行动态编码)将待转换的图像矩阵转换为DNA序列，借助于核酸数据库中的某一序列来控制明文图像DNA序列的变异．引入一个变异函数κ(x)，并进行如下约定：
(7)
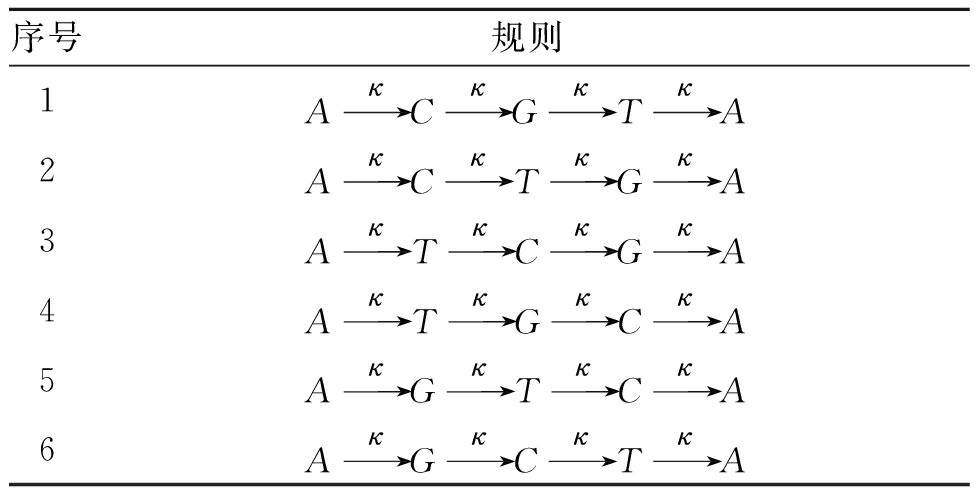
式中：x∈{A，C，G，T}．按照这个约定，有6种碱基变异规则，如表2所示．
表2 碱基变异规则
Tab.2 Base mutation rules
序号规则1Aκ→Cκ→Gκ→Tκ→A2Aκ→Cκ→Tκ→Gκ→A3Aκ→Tκ→Cκ→Gκ→A4Aκ→Tκ→Gκ→Cκ→A5Aκ→Gκ→Tκ→Cκ→A6Aκ→Gκ→Cκ→Tκ→A
在进行个体变异时，可以随机选择一种变异规则进行碱基变异，从而达到像素值扰乱的目的．这里随机选取基因库中某一个DNA序列，从中截取长度为4×M×N个碱基的序列，命名为序列Q={q1，q2，…，q4×M×N}，用于指导碱基的变异．控制变异的方法如下：
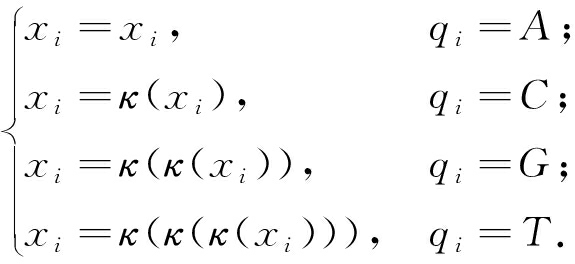
(8)
2.3 希尔置换
希尔置换(也称希尔加密)是基于矩阵论的一种替换密码．它通过采用线性代数中的矩阵乘法运算和逆运算，能够较好地抵抗频率分析，很难被攻破．希尔密码的关键在于加密矩阵，如果加密矩阵不可逆，密文将无法还原成明文．为避免加密矩阵元素之间强相关性，笔者使用混沌序列构造自逆加密矩阵来降低矩阵之间的相关性，从而使密文难于破解．
将待加密的图像每4个像素为一组，组成4×1的矩阵I4×1．通过构造4×4自逆矩阵W，对每组图像矩阵进行局部的希尔置换加密．置换加密公式如下：
E=(W×I)mod256,
(9)
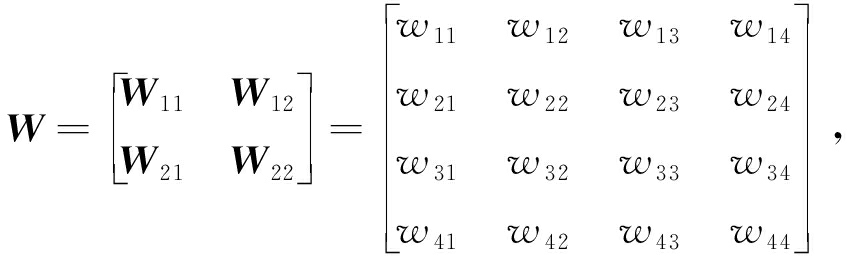
(10)
式中：
和W22类似．
使用W的乘法逆矩阵W-1=W，对密文进行解密：I=(W-1×E)mod256=(W×E)mod256．
将自逆矩阵W分成4部分，其构造过程如下：
(1)Logistic映射作为伪随机数发生器，给定初值和参数产生混沌序列，并对序列进行取模处理，然后依次选择混沌序列中的元素，填充W11子矩阵．
(2)根据W12=n×(I-W11)计算生成子矩阵W12，这里n取2．
(3)令子矩阵W22=-W11．
(4)根据W21=1/n×(I+W11)计算生成子矩阵W21．最后将生成的4个子矩阵W11、W12、W22、W21合并得到可逆加密矩阵W．
基于分块矩阵W11，生成的置换矩阵更具有鲁棒性，免去求解逆矩阵．
2.4 像素扩散
密文扩散操作使明文的微小变化可以扩散到整个密文，从而打乱明文图像与密文图像的关系，可以有效抵抗选择明文等攻击手段，实现密文扩散．将图像矩阵按照行优先的顺序转换为长度为M×N的一维序列S={s1，s2，…，sM×N}，给定的密码流C={c1，c2，…，cM×N}，设密文扩散后的序列为E={e1，e2，…，eM×N}，密文扩散的公式如下：
ei+1=si⊕eici.
(11)
初始化元素e(0)=127，i=1，2，…，M×N．扩散过程包括正向扩散和反向扩散．根据上述公式对一维序列S从左到右进行一次如公式(11)所示的运算，属于正向扩散，扩散效果是有限的，因此，需要将所得到的序列E赋值给S，然后再按照式(11)进行一次从右到左的反向扩散．
2.5 加密过程
本算法的加密结构，主要包括：像素位置置乱、希尔矩阵置换、对图像像素进行遗传操作和密文扩散操作．加密流程如图3所示．具体步骤如下：
输入：灰度图像和密钥．
输出：加密图像．
(1) 将灰度图像转换成大小为M×N的二维矩阵P1.
(2) 采用哈希函数计算图像矩阵P1的哈希值K，并根据式(3)和式(4)计算得到混沌初始化参数．
(3) 根据Logistic映射产生的序列L，升序排列得到置换索引序列L′，将L′按照每行M个值进行填充可得到置换矩阵，用其置乱图像矩阵P1得到置乱后图像矩阵P2．
(4) 采用Logistic映射产生的序列L，构造T=(M×N/4)个希尔加密矩阵KM1，KM2，…，KMT．对加密图像P2按照每4个像素一组，选择构造的希尔加密矩阵进行希尔置换，得到图像矩阵P3．
(5) 从GenBank数据库中下载ID号为NZ_LOZQ01000042的DNA序列．从起始位置r处截取长度为4×M×N个碱基的序列，作为序列Q．
(6) 根据Duffing映射产生的序列U和V，每次选择图像矩阵P3中的两个个体，将序列Q中的碱基进行DNA解码，每4个碱基解码后组成一个控制字，依次控制个体的交叉操作,得到图像矩阵P4．
(7) 将图像矩阵P4变换为一维向量，并对其进行DNA编码，得到一维DNA序列，采用给定的DNA序列Q，根据公式(8)，选择表2中的一种变异规则，对图像DNA序列的每个碱基实现变异操作．随后对变异后的图像DNA序列进行DNA解码，恢复成二维矩阵形式，得到图像矩阵P5．
(8) 根据前面描述的像素扩散技术，对每个像素实行正反扩散，Duffing映射产生的序列U作为正向扩散密码流，序列V作为反向扩散的密码流．扩散后得到图像加密矩阵P6，将其恢复成图像并输出，得到密文图像．
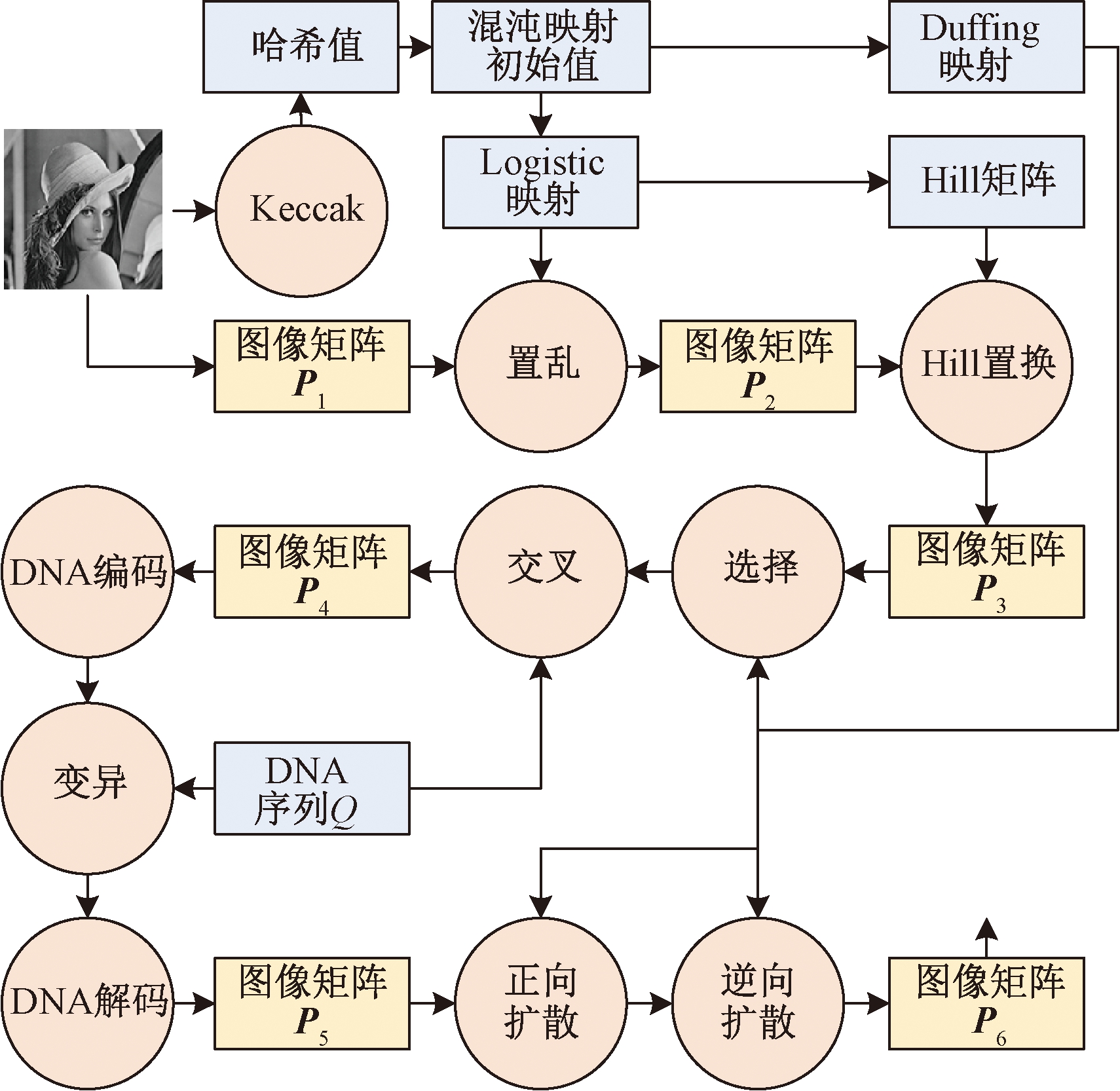
图3 加密流程图
Fig.3 Description of the encryption process
解密算法是上述过程的逆过程．这里不再阐述．本算法也适用于彩色图像的加密，只需将像素的值进行RGB分解处理即可．
3 实验结果及安全性分析
采用3幅大小为256×256的灰度图像Lena、Baboon和Pepper，使用Matlab软件来验证该算法的可行性和有效性．密钥给定值
核酸数据库的DNA序列ID号NZ_LOZQ01000042，起始位置r=1．初始值Key1和Key2作为Logistic映射的参数μ及初始状态值，初始值Key3和Key4作为Duffing映射的初始状态值．采用本算法对3幅图像进行加密．明文图像、加密图像和解密图像分别如图4(a)、4(b)和4(c)所示．
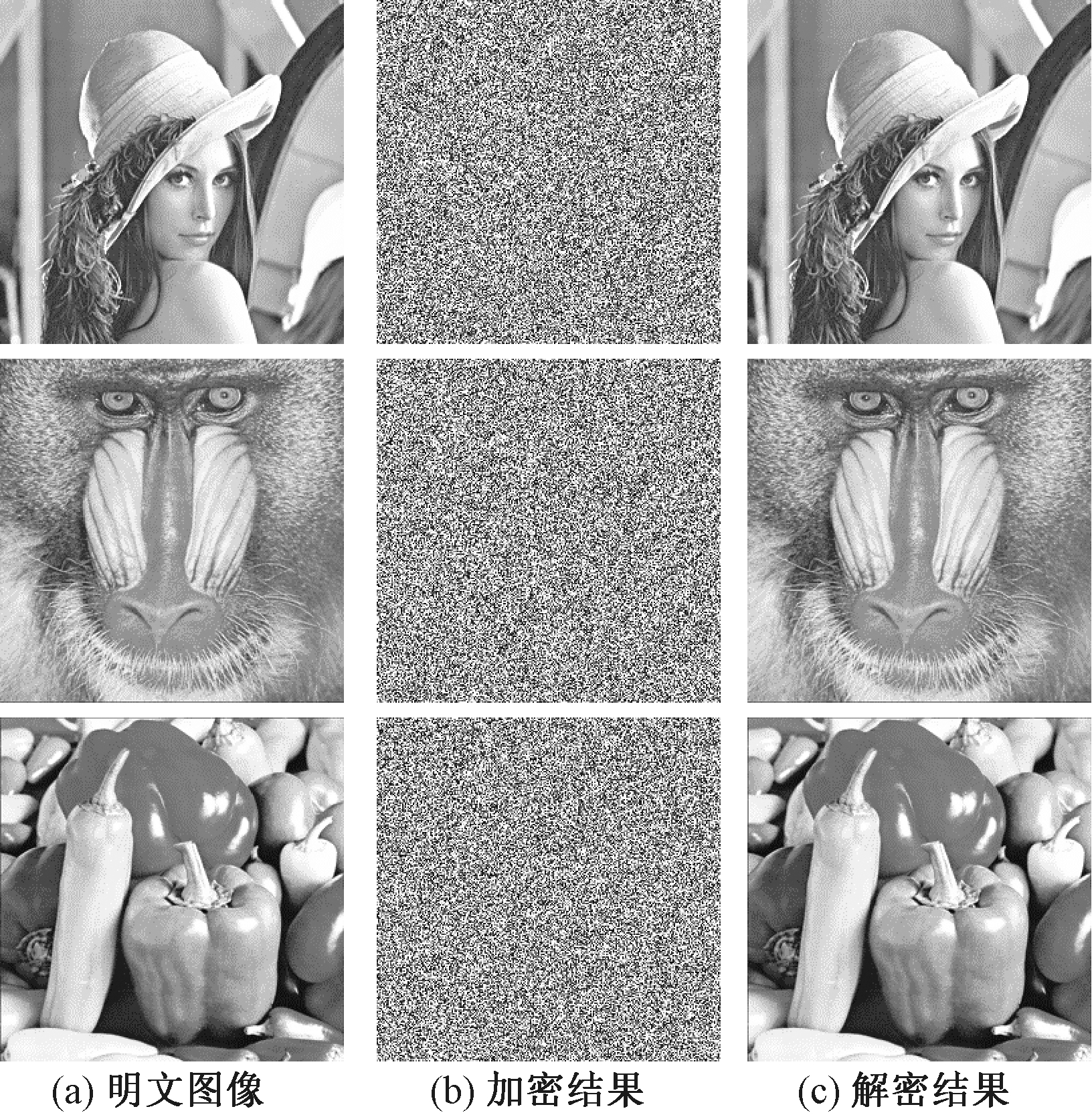
图4 加密与解密图像
Fig.4 Cipher and decryption images of Lena
3.1 密钥空间
算法涉及的密钥有Logistic映射的参数μ及状态值，Duffing映射的两个初值状态值，以及DNA序列ID．如果计算精度为10-15，密钥的空间总空间为1015×1015×1015×1015×1010=1070．可见本算法具有足够的空间来抵抗穷举攻击．
3.2 统计分析
(1)灰度直方图分析.直方图在一定程度上可以反映出图像灰度值的分布规律，能否改变明文图像的统计分布也是图像加密中至关重要的指标．图5为明文和密文图像Lena的直方图，直观上密文图像具有平坦的直方图，而明文图像的直方图跌宕起伏．
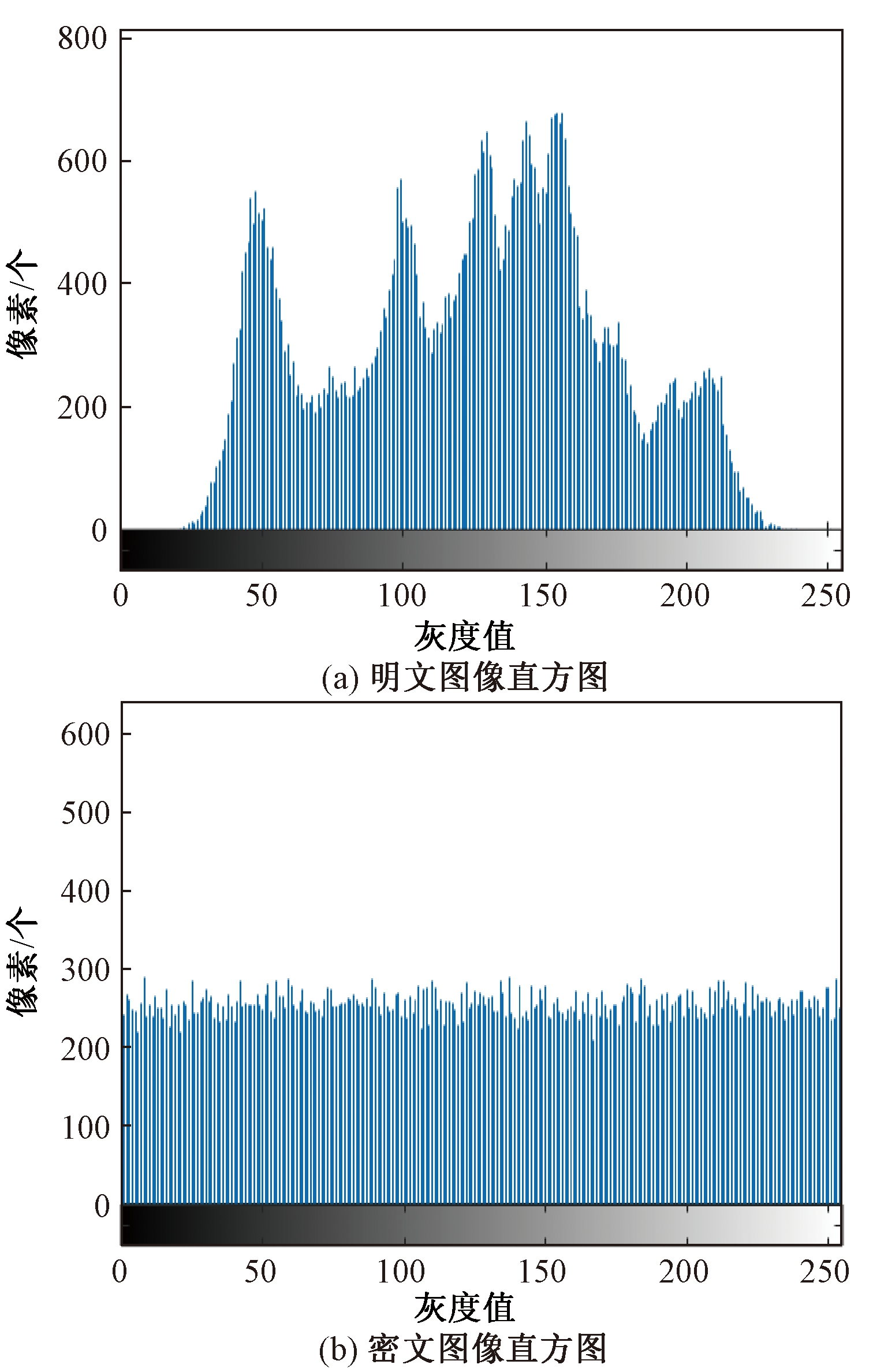
图5 直方图分析
Fig.5 The histograms analysis
进一步，引入直方图的χ2统计量在数量上衡量两者的差别[17]．对于灰度等级为256的灰度图像，χ2统计量计算公式如下：
(12)
式中：Oi为观测到的频数分布；ei为理论频数分布．对于灰度等级为256的灰度图像而言，给定大小为M×N的图像，假设直方图中每个像素灰度值的像素点频数Oi服从均匀分布，即ei=e=M/256，则式(12)服从自由度为255的χ2分布．当显著性水平α取0.05时，有
表3列出了χ2检验结果，3个明文图像的χ2检验结果明显大于
而3个密文图像的χ2检验结果均小于
可以认为密文图像近似均匀分布．
表3 χ2检验结果
Tab.3 Chi-square test results
图像LenaBaboonPepper本文算法文献[3]明文39 851.328 179 056.906 331 629.656 3密文240.296 9265.765 6270.742 2密文279.148 4——
(2)相关性分析.明文图像在相邻像素之间一般具有较强的相关性，为抵御统计分析攻击，必须降低相邻像素之间的相关性．利用式(13)，分别随机选取明文图像和密文图像各2 000对像素，测试其水平、垂直和对角方向的像素相关性，结果如表4所示．从表4中可以看出，密文图像像素之间相关性大大减少．这表明明文图像的统计特征已被扩散．图6给出了Lena图像的明文和密文在各个方向上的相关情况．
表4 图像的相关性分析
Tab.4 Correlation coefficients of the images
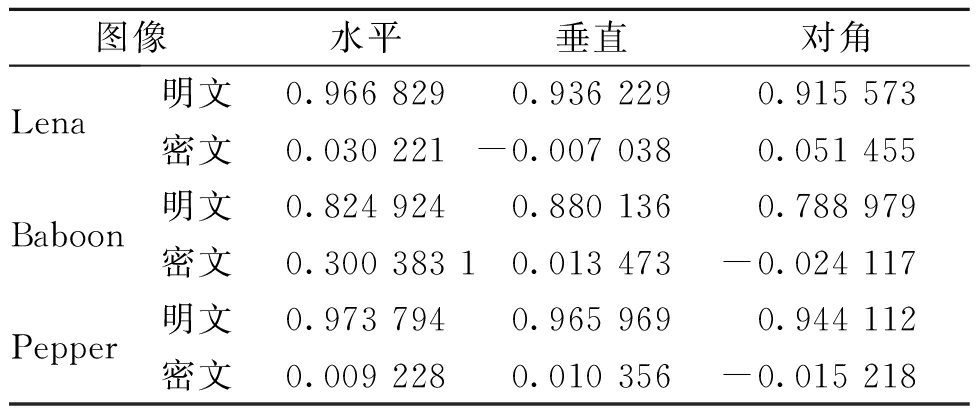
图像水平垂直对角LenaBaboonPepper明文0.966 8290.936 2290.915 573密文0.030 221-0.007 0380.051 455明文0.824 9240.880 1360.788 979密文0.300 383 10.013 473-0.024 117明文0.973 7940.965 9690.944 112密文0.009 2280.010 356-0.015 218
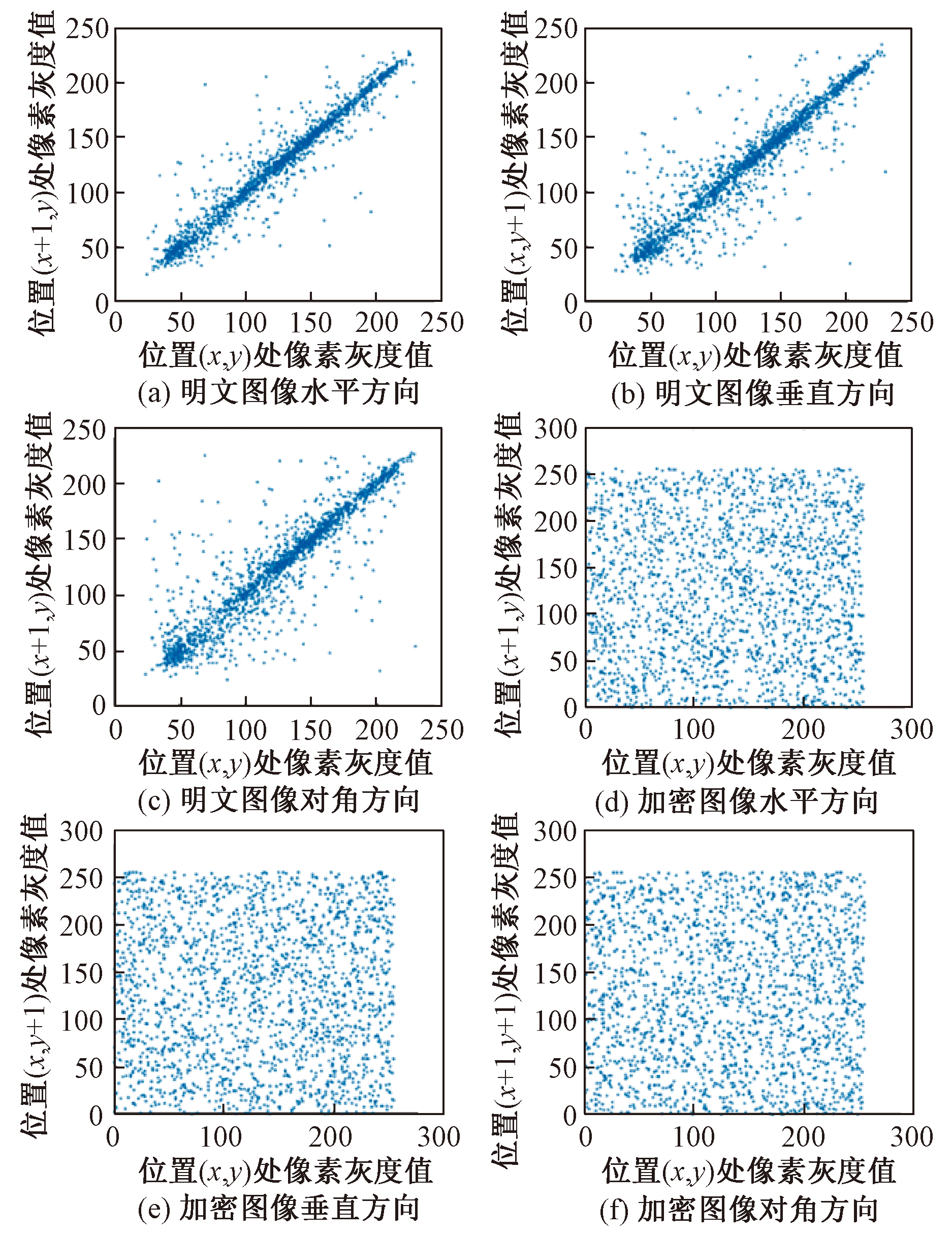
图6 明密文图像的相关性
Fig.6 Correlations of plain and cipher images
相关系数计算如下：
(13)
式中：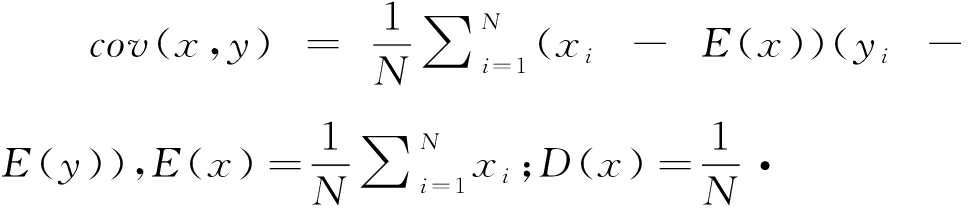
3.3 信息熵分析
信息熵反映了图像信息的不确定性．计算公式：
(14)
式中：p(i)表示信息i出现的概率．对于灰度图像来说，信息i有256种状态，最小值0，最大值为255．灰度图像信息熵的理论值为8．密文信息熵越大，信息越安全．Lena、Baboon和Pepper的密文图像的信息熵分别为7.989 7、7.989 4和7.989 5，各个密文图像的信息熵接近理论值．
3.4 敏感性分析
度量敏感性通常使用2个标准：像素数目改变率(NPCR)和平均强度变化率(UACI)．
(15)
(16)
式中：W和H分别代表图像的长度和宽度；C和C′表示两个密文图像．对于像素点(i，j)的像素值，如果C(i,j)≠C′(i,j)，则D(i,j)=1，否则D(i,j)=0．
(1)密钥敏感性.为测试密钥的灵敏度，将
的值增加0.000 000 01，在其他密钥不变的情况下,使用修改后的密钥解密被加密的Lena图像，无法解密出原图像．再者，利用修改后的密钥对图像重新加密，得到加密图像与图4(b)中相应的加密图像进行对比可知，两个密文图像之间对应像素点的不同率在99.65%以上，可见该算法具有较强的密钥灵敏性，且能抵抗暴力攻击，具有很好的密钥安全性．
(2)差分分析.差分分析是一种选择明文攻击即对明文图像做微小的改变后，再分别对原图像和改变后的图像进行加密．通过比较两幅被加密后的图像来获得原图像与加密图像之间的关系,从而破解加密系统．NPCR和UACI两个标准常用来衡量加密方法抵御差分攻击的能力．
这里将明文图像位置(100，100)的像素点的像素值增加50．针对Lena图像，算法的NPCR和UACI值如表5所示．明文微小的变化导致密文巨大的差异，因此算法具有很好的抗差分攻击能力．
表5 差分分析的NPCR和UACI值
Tab.5 The NPCR and UACI values of the Lena image %
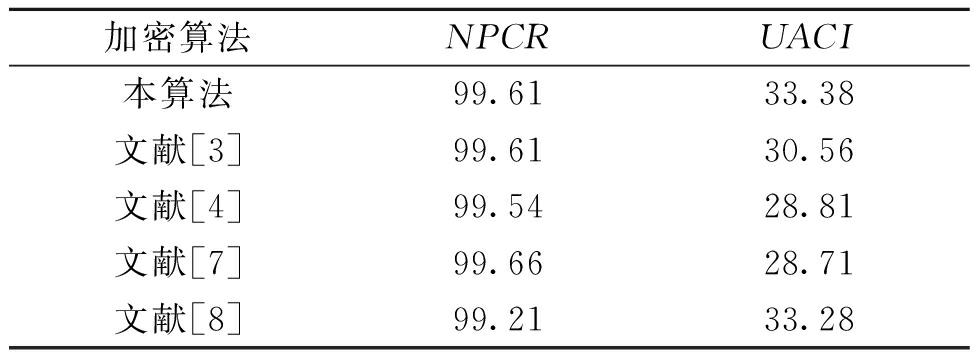
加密算法NPCRUACI本算法99.6133.38文献[3]99.6130.56文献[4]99.5428.81文献[7]99.6628.71文献[8]99.2133.28
3.5 复杂度分析
采用Matlab、Windows 10操作系统、Intel Core 2.6 GHz CPU和4 GB RAM计算机测试．测试为256×256的灰度Lena图像．本文算法的耗时主要集中在像素置换、置乱阶段，每一轮的置换、置乱均为M×N次，总共执行5轮的置换、置乱过程．因此整个算法的复杂度为O(M×N)．
4 结论
通过Logistic映射产生的混沌序列构造希尔矩阵，对图像进行置换与置乱，增强了混沌序列的随机性.希尔置换能实现局部的置乱，而无法满足全局置乱，这容易通过部分明文破解．进一步，结合Duffing映射与DNA编码技术，利用遗传操作实现像素的选择、交叉和变异来实现全局置乱与扩散．安全性分析表明该算法具有很好的安全性和抗攻击能力．
[1] DHALL S, PAL S K, SHARMA K. Cryptanalysis of image encryption scheme based on a new 1D chaotic system[J]. Signal processing, 2018, 146:22-32.
[2] FRIDRICH J. Symmetric ciphers based on two-dimensional chaotic maps[J]. International journal of bifurcation & chaos, 1998, 8(6): 1259-1284.
[3] ASKAR S S, KARAWIA A A, ALAMMAR F S. Cryptographic algorithm based on pixel shuffling and dynamical chaotic economic map[J]. IET image processing, 2018, 12(1): 158-167.
[4] SIVAKUMAR T, VENKATESAN R. Image encryption based on pixel shuffling and random key stream[J]. International journal of computer and information technology, 2014, 3(6): 1468-1476.
[5] OZKAYNAK F. Brief review on application of nonlinear dynamics in image encryption[J]. Nonlinear dynamics, 2018, 92(2): 305-313.
[6] 田海江, 雷鹏, 王永. 基于混沌和DNA动态编码的图像加密算法[J]. 吉林大学学报(工学版), 2014, 44(3):801-806.
[7] ZHANG J, FANG D X, REN H G. Image encryption algorithm based on DNA encoding and chaotic maps[J]. Mathematical problems in engineering, 2014(3):1-10.
[8] ZKAYNAK F, YAVUZ S. Analysis and improvement of a novel image fusion encryption algorithm based on DNA sequence operation and hyper-chaotic system[J]. Nonlinear dynamics, 2014, 78(2): 1311-1320.
[9] WEI X P, GUO L, ZHANG Q, et al. A novel color image encryption algorithm based on DNA sequence operation and hyper-chaotic system[J]. Journal of systems and software, 2012, 85(2): 290-299.
[10] 程适,王锐,伍国华,等.群体智能优化算法[J]. 郑州大学学报(工学版), 2018, 39(6): 1-2.
[11] 穆瑞杰. 基于遗传算法的地铁车站引导标识布点探析[J]. 郑州大学学报(工学版),2018,39(1): 73-77.
[12] TIN
S R, ZHAO L, CHICANO F, et al. Nk hybrid genetic algorithm for clustering[J]. IEEE transactions on evolutionary computation, 2018, 22(5): 748-761.
[13] RAJ R, SINGH P K, SINGH R S. Multi-image encryption using genetic computation[J]. CSI transactions on ICT, 2016, 4(2/4):95-101.
[14] WANG X Y, ZHANG H L. A novel image encryption algorithm based on genetic recombination and hyper-chaotic systems[J]. Nonlinear dynamics, 2016, 83(1/2):333-346.
[15] ENAYATIFAR R, ABDULLAH A H, ISNIN I F. Chaos-based image encryption using a hybrid genetic algorithm and a DNA sequence[J]. Optics & lasers in engineering, 2014, 56:83-93.
[16] PUJARI S K, BHATTACHARJEE G, BHOI S. A hybridized model for image encryption through genetic algorithm and DNA sequence[J]. Procedia computer science, 2018, 125:165-171.
[17] KWOK H S, TANG W K S. A fast image encryption system based on chaotic maps with finite precision representation[J]. Chaos solitons & fractals, 2007, 32(4): 1518-1529.