0 引言
正交异性钢桥面板在大跨径桥梁中得到了广泛的运用[1]。在服役过程中,桥梁的疲劳问题一直是困扰其发展的主要问题之一[2-4]。循环荷载作用下,顶板-U肋焊缝较易产生疲劳裂纹。该类裂纹维修和检测难度大,影响桥面系的耐久性和桥梁安全运营。因此有必要对顶板-U肋焊缝的疲劳特性进行研究,提出合理的疲劳寿命评估方法,为该类细节的抗疲劳设计提供参考。
目前针对顶板-U肋焊缝细节,国内外学者开展了大量的研究工作。其中疲劳寿命评估多采用基于名义应力或热点应力的S-N曲线,并结合线性累积损伤理论的单轴疲劳评估方法。如Ya等[5]对顶板-U肋局部截断试件进行了疲劳试验,通过焊趾处的名义应力拟合S-N曲线,对比分析了80%熔透焊缝与全熔透焊缝疲劳强度的差异;Yamada等[6]采用1 mm法确定热点应力,通过试验结果拟合了顶板-U肋细节的S-N曲线;张呈奕等[7]开展了顶板-U肋细节的弯曲疲劳试验,基于名义应力和热点应力对不同钢材强度下的疲劳寿命进行了评估。吉伯海等[8]根据实桥监测得到了顶板-U肋焊趾处的名义应力,结合BS5400规范中S-N曲线对该细节疲劳寿命进行了评估。实桥运营中,车轮分布具有随机性,考虑结构的非对称性,顶板-U肋焊缝实际发生多轴疲劳。基于名义应力或热点应力的单轴评估法多采用垂直于焊缝方向的正应力作为疲劳评估的基准,具有简单高效的特点,但不能全面反映实桥焊缝处的多轴疲劳效应。因此,分析顶板-U肋焊缝处的多轴疲劳效应,定量给出该细节单、多轴疲劳评估的差异,对多轴疲劳寿命的评估工作的开展具有重要意义。
为了评估顶板-U肋焊缝多轴疲劳效应,基于弹性力学理论对比单、多轴疲劳应力,笔者提出了合理的多轴疲劳评判依据。建立钢桥面板节段模型与细节子模型,对细节处的多轴疲劳变形和应力进行了评估。通过多轴比例加载试验获取了多轴疲劳强度S-N曲线,定义了应力幅偏差值δ与单多轴疲劳寿命比R,理论分析得R=Aδ3的相关关系,定量评估了单、多轴疲劳评估的差异。
1 有限元模型与多轴疲劳评估准则
1.1 有限元模型
以某悬索桥正交异性钢桥面板为工程背景,其顶板厚12 mm,U肋尺寸为300 mm×280 mm×6mm,U肋间距为600 mm,横隔板厚8 mm,横隔板间距3 200 mm。钢材采用Q345qD,顶板与U肋采用80%熔透焊缝连接。钢桥面板中顶板-U肋焊缝细节分为两类,分别为横隔板处细节和横隔板间细节。
采用ABAQUS分别建立总体节段模型与局部细节子模型。节段模型纵向包括5道横隔板,横向包括7道U肋[9];采用C3D8R六面体单元划分,网格尺寸为20 mm;边界条件设为约束顶板,U肋和铺装的所有平动自由度以及横隔板的所有平动加转动自由度。子模型横向位于节段模型中部,横隔板间细节纵向位于No.2号和No.3号横隔板正中,横隔板处细节纵向位于No.3号横隔板正上方。横隔板间细节子模型横向取300 mm,纵向取200 mm,竖向取342 mm。横隔板处细节子模型竖向取258 mm。采用C3D8R六面体单元和C3D10四面体单元进行网格混合划分,非焊缝区域采用20 mm六面体网格划分,焊缝区域采用1 mm六面体网格细化,过渡区域采用四面体网格。钢材弹性模量取2.06×105 MPa,铺装弹性模量为1 000 MPa,泊松比均取0.3。有限元模型如图1所示。
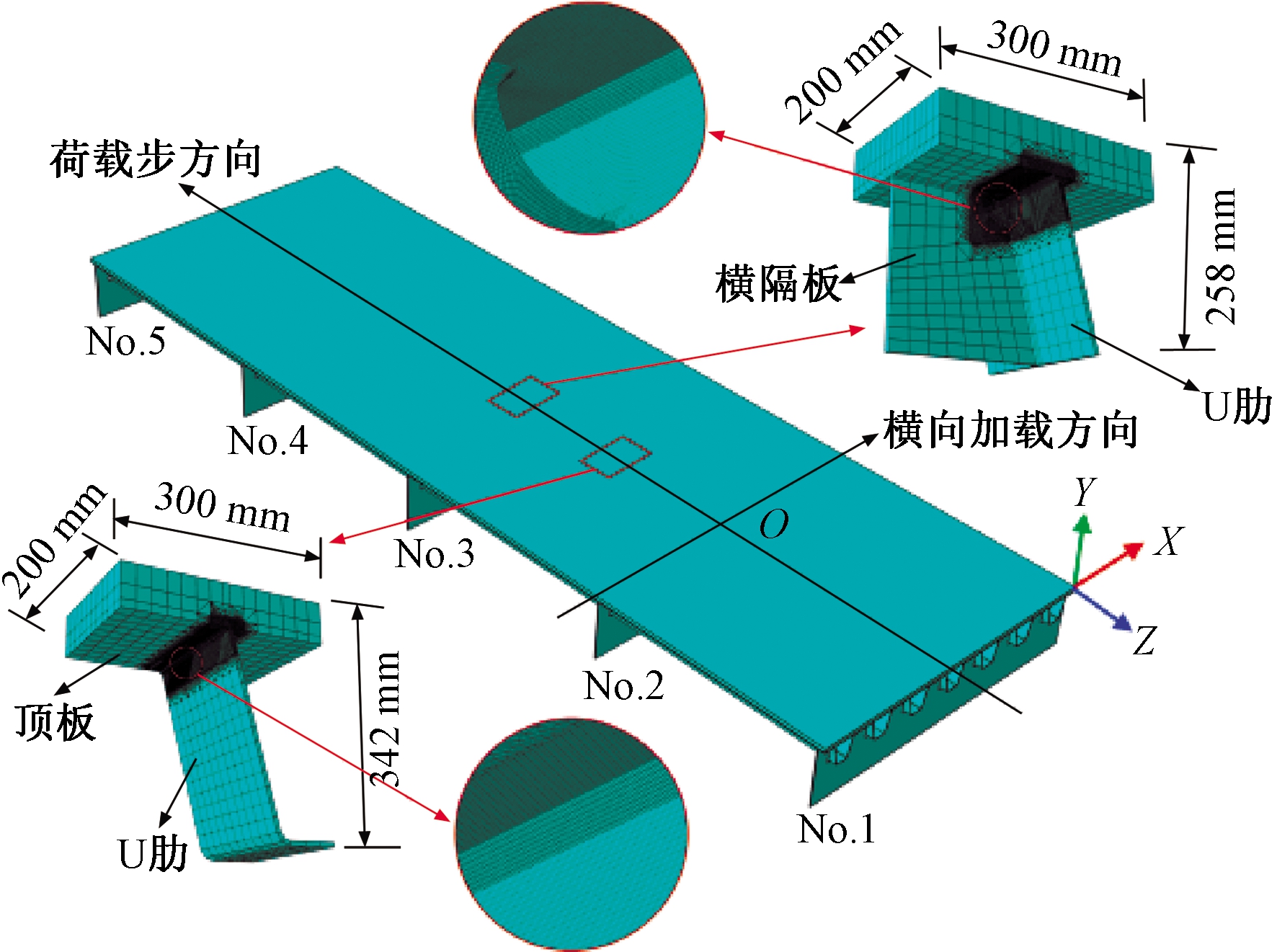
图1 有限元模型
Figue 1 Finite element model
参考《公路钢结构桥梁设计规范》[10],取单侧双轮加载面积为600 mm×200 mm,荷载集度为0.5 MPa。考虑顶板-U肋焊缝细节所处的位置,以No.2号横隔板中点为原点,横桥向分为11种加载工况,加载间距为150 mm。在纵桥向上,车轮从No.2号横隔板移动至No.4号横隔板,加载间距取200 mm,共计33个荷载步。加载工况如图2所示。
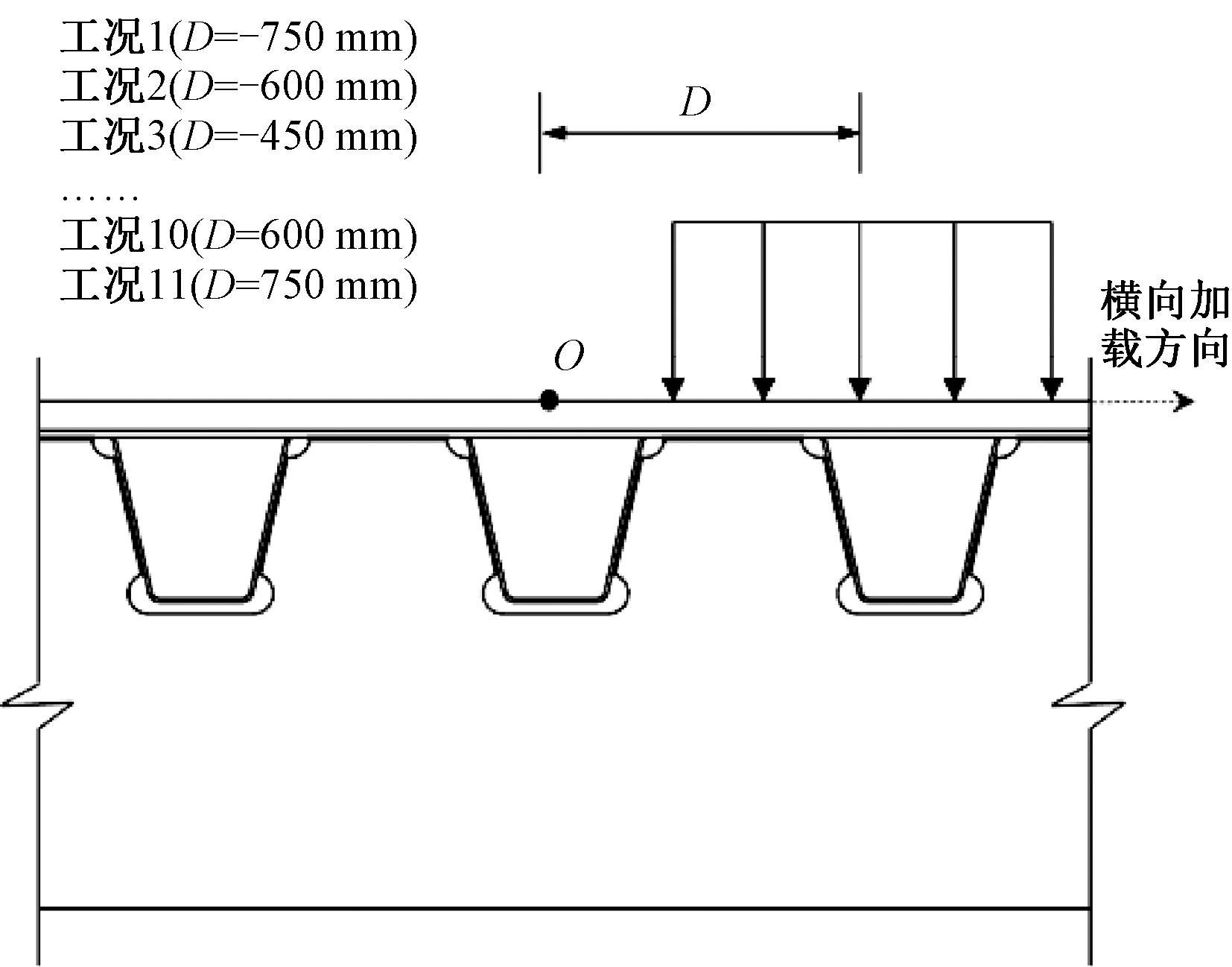
图2 加载工况示意图
Figue 2 Schematic diagram of loading cases
1.2 多轴疲劳评估准则
对易损细节进行多轴疲劳效应评估之前,需要提出一套合理可靠的评估准则。针对细节的疲劳研究常以某种坐标系为基准,基准坐标系的设置一般使某坐标轴与实际裂纹大致垂直。定义沿坐标轴向的应力分量中幅值最大的正应力为主要应力分量,例如以图1坐标系为基准,顶板-U肋焊缝处的主要应力分量为σx。一般情况下,裂纹的扩展方向与主应力方向垂直[11],当主应力为主要应力分量时,扩展方向与主要应力分量垂直。而多轴疲劳效应是引起主应力与主要应力分量不一致的主要原因之一。由此可知,主应力及主要应力分量与疲劳开裂关系密切,并且两者的偏差与多轴疲劳效应存在联系。因此考虑对比主要应力分量与主应力的量值以评估细节处的多轴疲劳效应。由于主应力类别中绝对值最大的主应力较能反映细节承受交变应力循环作用的实际情况,故主应力采用绝对值最大的主应力。
钢板面板在疲劳开裂前处于弹性工作状态,由弹性力学公式可知,三维问题中某一点主应力求解公式为:
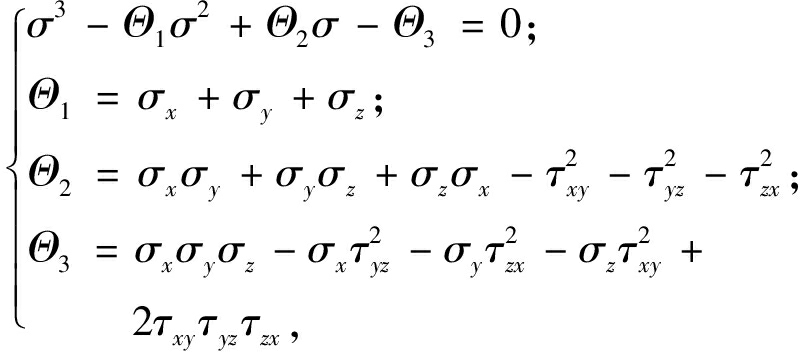
(1)
式中:σ为主应力大小;Θ1~Θ3为应力张量不变量。
绝对值最大的主应力与主要应力分量间的关系,不仅包括两者量值的大小,也包含两者方向间的关系。弹性力学中某一点主应力方向余弦的求解公式为:
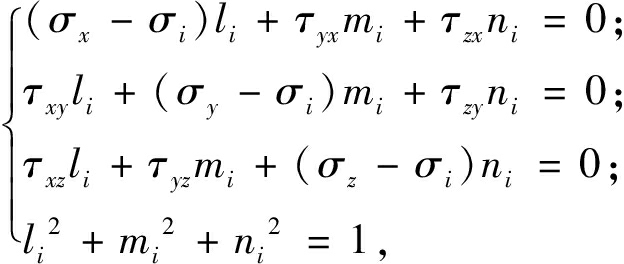
(2)
式中:li、mi、ni为主应力σi的方向余弦,其中i=1~3。
单轴荷载下的钢试件只承受单向正应力或单向切应力[12]。取试件某一点微元,绘制其应力状态如图3所示。
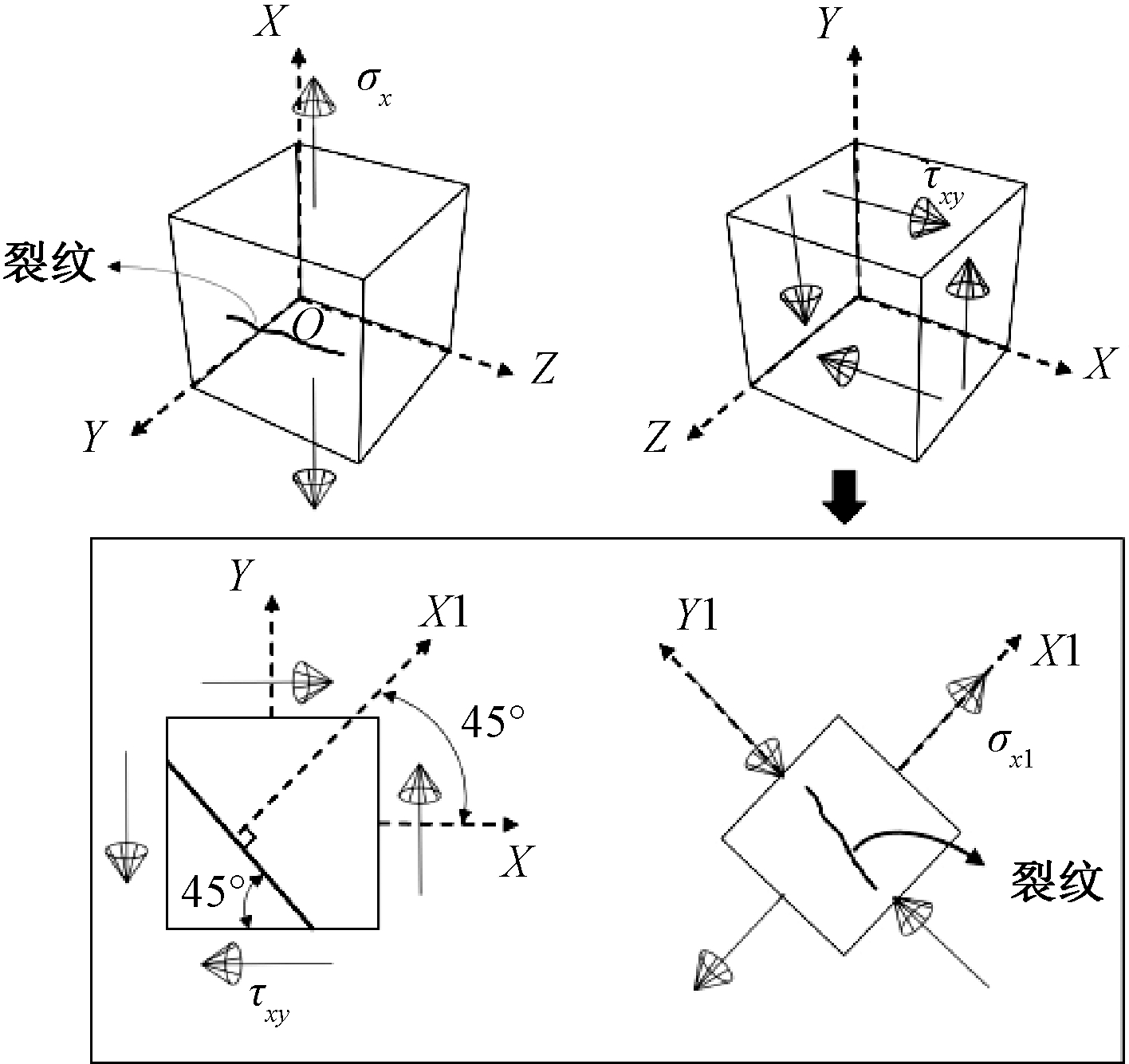
图3 应力状态
Figue 3 Stress state
对于只承受正应力的情况,不妨设该正应力为σx,此时σx即为主要应力分量。将σx≠0代入式(1),得3个主应力分别为σx、0、0,此时绝对值最大的主应力大小等于σx。将σi=σx代入式(2),得绝对值最大的主应力对应的方向余弦为±1、0、0,此时绝对值最大的主应力即为主要应力分量。
对于只承受切应力的情况,即纯剪状态,不妨设该切应力为τxy。此时主要应力分量应为基于坐标系的σx1,经坐标变换后得σx1的大小等于τxy,方向沿X1轴。将τxy≠0代入式(1),得3个主应力分别为τxy、0、-τxy,此时绝对值最大的主应力大小等于τxy。将σi=τxy代入式(2),得绝对值最大的主应力对应的方向余弦为![]() 和
和![]() 此时绝对值的最大主应力即为主要应力分量。
此时绝对值的最大主应力即为主要应力分量。
多轴荷载下的钢试件承受多向应力,6个应力分量中至少有2个独立分量不为0,最大主应力与主要应力分量不再相等。为此,需要给出一个参数定量两种应力的偏差程度。一段应力时程中应力幅Δσ的最大值对疲劳损伤的贡献最大,故采用应力幅最大值的比值量化两者的偏差,且定义偏差值δ:
(3)
式中:Δσn为各级主要应力幅最大值;Δσm为各级绝对值最大的主应力幅最大值。由δ定义可知,δ与1相差越大,σm与σx的偏差程度越大,当δ=1时,σm与σx的应力循环曲线重合,对应于单轴疲劳。
综合上述分析结果可知,单轴荷载下,一点的绝对值最大的主应力即为主要应力分量。多轴荷载下,一点的绝对值最大的主应力与主要应力分量存在偏差,偏差越大,多轴疲劳效应越显著。偏差程度与疲劳效应显著程度的关系在下文给出证明。
2 多轴疲劳变形分析与应力分析
2.1 变形分析
开裂前细节的疲劳分析主要基于弹性理论,弹性理论中构件的宏观变形与细节处应力应变直接相关。从钢桥面板构造来看,顶板受到U肋与横隔板的纵横向加劲,该加劲分布是非均匀的,因而钢桥面板的刚度分布不均匀且有突变。从整体来看,在车轮荷载作用下,钢桥面板发生纵横向挠曲。从局部区域来看,考虑几何构造引起的刚度不足和突变以及车轮荷载局部作用特点,部分区域将产生较大变形,从而引起顶板-U肋焊缝细节较大的应力集中。
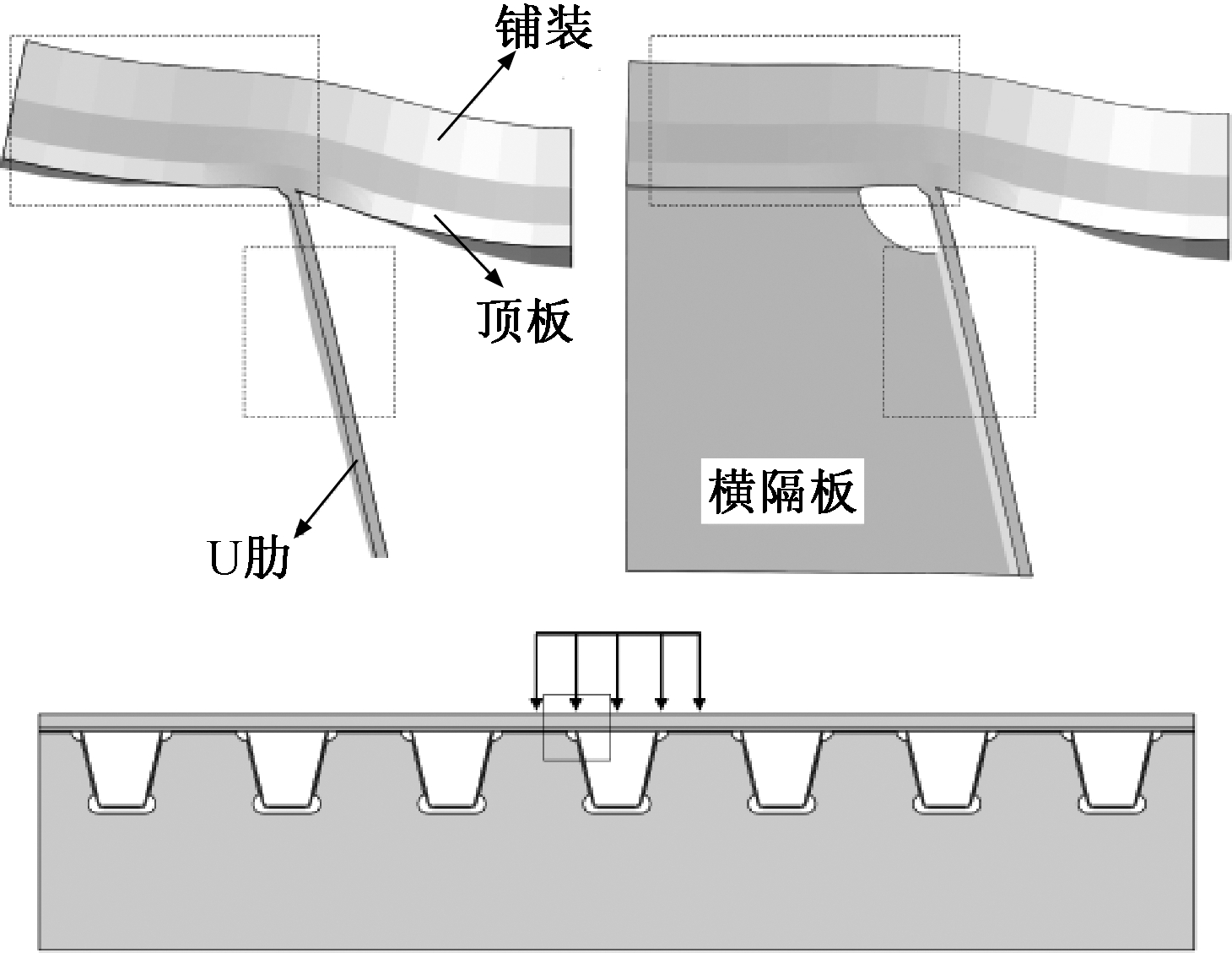
图4 局部变形示意图
Figue 4 Schematic diagram oflocaldeformation
轮载作用下顶板-U肋焊缝细节的局部变形如图4所示。横隔板处细节由于横隔板的约束,其变形小于横隔间细节。车轮直接作用在顶板上产生较大的弯曲效应,顶板的变形以面外变形为主。以荷载位于细节正上方为例,横隔板间细节开裂截面的膜应力为-1.8 MPa,弯曲应力为-136.6 MPa,膜应力仅为弯曲应力的1.3%。横隔板处细节的膜应力为-10.5 MPa,弯曲应力为-109.4 MPa,膜应力为弯曲应力的9.6%。从膜应力的占比来看,横隔板的约束减小了顶板的面外变形。
2.2 应力分析
应力状态分析是细节疲劳评估的基础。考虑横向加载工况下应力分布的相似性,分别提取两类焊缝在工况6、8、10下的应力状态,绘制成如图5所示的应力循环曲线。
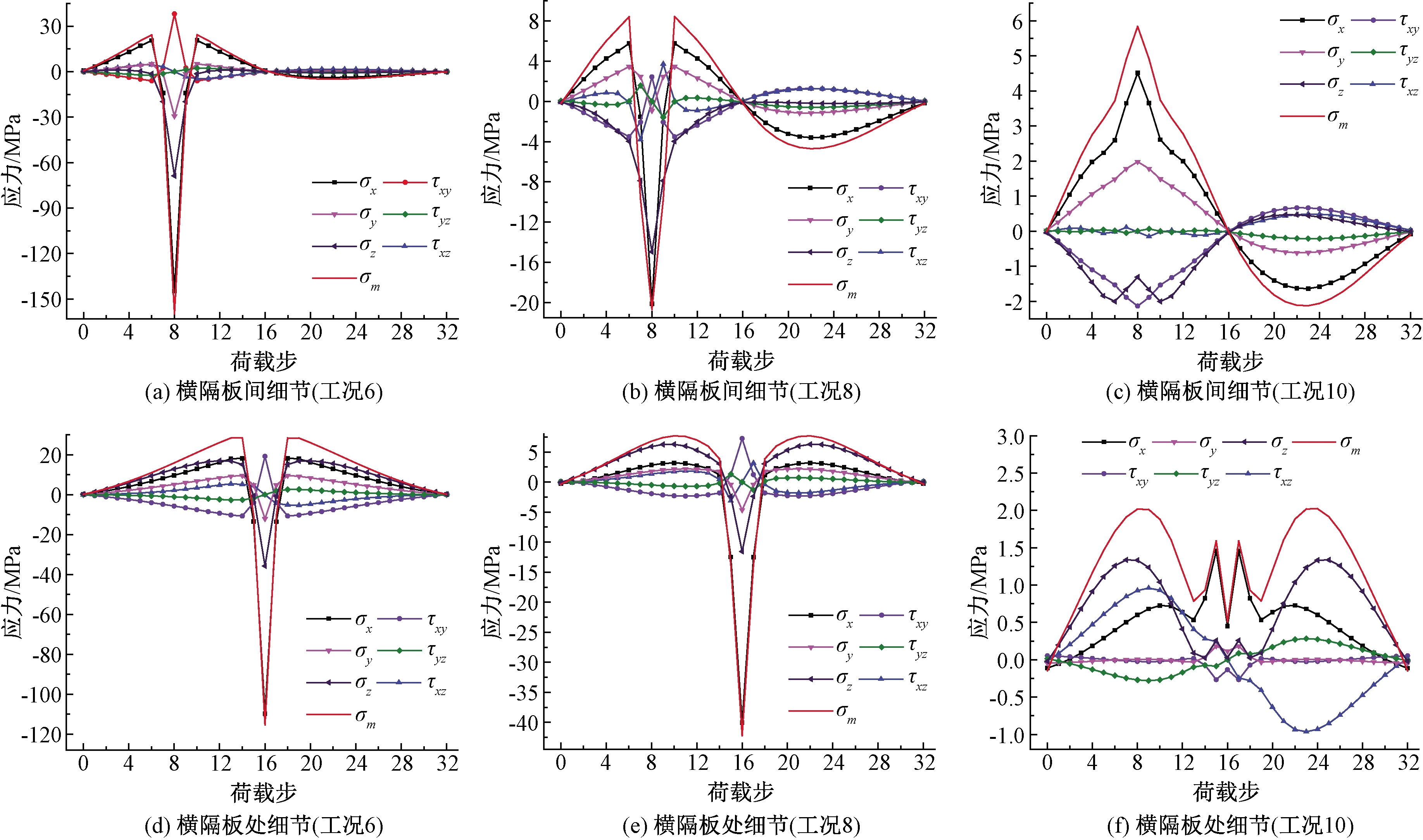
图5 焊趾应力循环曲线
Figue 5 Stress cycles of weld toe
由图5可知,由于顶板-U肋焊缝主要承受车轮弯曲荷载,横桥向正应力σx变化最为明显,应力水平远大于其他应力分量。σx对疲劳开裂的贡献最大,实际裂纹扩展方向与σx接近垂直。其他应力分量的存在是引起扩展方向不垂直于σx的重要原因。其中纵桥向正应力σz的水平接近于σx,这与U肋简支于横隔板承受纵桥向弯矩的受力形式一致。σz以压应力为主,对X方向的裂纹张开具有促进作用。车轮的局部冲切使得切应力τxy的水平也较高。从开裂机理来看,切应力是疲劳损伤的主要原因,τxy对裂纹扩展的驱动作用亦不可忽略[11]。对于横隔板间细节,当车轮作用于细节正上方时,正应力σz达到了σx的47.5%,切应力τxy达到了σx的26.4%。
图5中绝对值最大的主应力σm与正应力σx的循环曲线变化趋势基本一致,且σm总体外包σx。应力幅偏差值δ的计算结果显示,各工况下横隔板处细节σm与σx的偏差大于横隔板间细节。以图5中工况10为例,横隔板处细节的应力幅偏差值δ=0.72,横隔板间细节的δ=0.77。这是由于横隔板造成顶板-U肋焊缝局部约束条件发生改变,进而导致多轴应力状态变得显著。随着车轮横向偏离细节距离D的增大,σm与σx的偏差程度变大。以横隔板间细节为例,当距离D=0 mm(工况6),应力幅偏差值δ=0.90;当D=300 mm(工况8),δ=0.89;当D=600 mm(工况10),δ=0.77。该现象表明,随着荷载中心线逐渐偏离细节,顶板-U肋焊缝处的多轴疲劳效应越发显著。
3 单、多轴疲劳寿命评估对比分析
3.1 ...曲线
如果能量化单、多轴疲劳寿命评估的差异,采用单轴疲劳评估方法对细节的多轴疲劳寿命近似估量,为实际工程提供简单可靠的参考,将具有重要意义。2.2节结果表明,正应力σx变化显著且量值最大,故实际工程中常采用σx与Miner损伤理论相结合,并基于S-N曲线对顶板-U肋焊缝进行单轴疲劳评估。2.2节结果还反映出正应力σz和切应力τxy对疲劳损伤具有贡献。同时1.2节中指出绝对值最大的主应力σm与正应力σx的偏差能反映细节的多轴疲劳效应,且主应力具有使裂纹突破裂尖阻滞作用继续扩展的作用。结合σm正负交替变化的特性,采用σm与Miner损伤理论相结合的方法对顶板-U肋焊缝细节进行多轴疲劳评估。
为了得到基于绝对值最大的主应力的多轴疲劳强度,针对顶板-U肋焊缝细节制作疲劳试件,开展多轴比例加载试验,得到不同主应力幅作用下的疲劳寿命,拟合Δσm-N曲线。
参照文献[5]的试验,选取疲劳试件为顶板-U肋焊缝细节截断足尺模型,共设计制作6个试件,编号SJ1~SJ6。试件采用Q345qD钢,顶板尺寸为600 mm×300 mm×12 mm,顶板与U肋采用熔透率为80%的单面坡口焊缝连接,通过振动疲劳试验机对试件进行弯扭加载,试件几何及加载如图6所示。通过改变悬臂长度a和偏心距b实现多轴比例加载,a、b取值见表1。采用名义应力法,在距离焊趾10 mm处布置应变花,如图7所示。参照文献[13],将裂纹深度达到顶板厚度70%作为试件破坏准则,整理各测点此时应力数据,得到绝对值最大的主应力幅与疲劳寿命,如表2所示。SJ5由于应变花损坏,实测数据缺失,视为失效试件。

图6 疲劳加载
Figue 6 Fatigue loading
表1 试件加载参数
Table 1 Loading parameters for specimens mm

试件编号悬臂长度a偏心距bSJ117540SJ217580SJ322540SJ422580SJ527540SJ627580
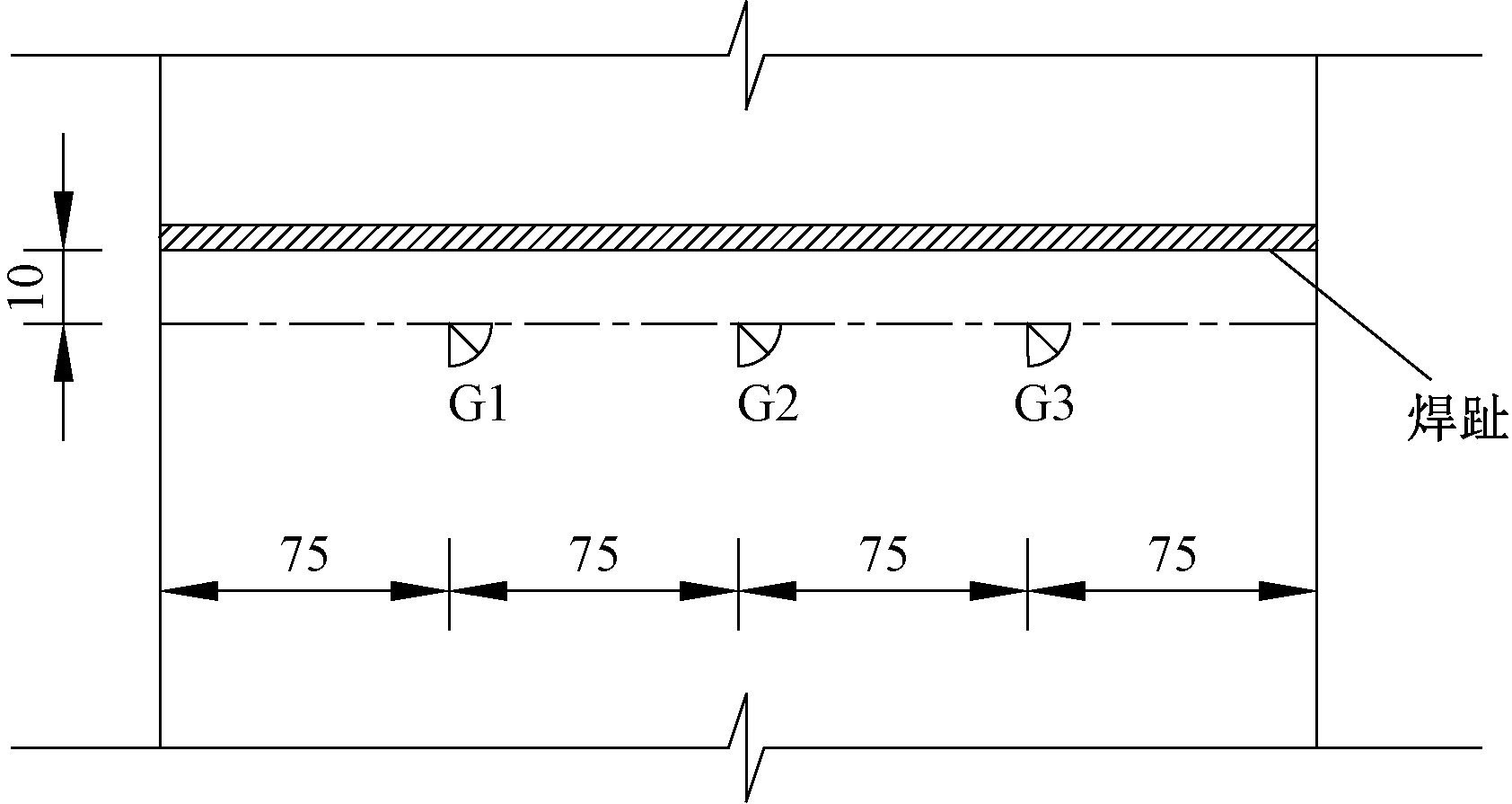
图7 测点布置示意图(单位:mm)
Figue 7 Schematic diagram of measuring point arrangement(unit: mm)
将各试件的疲劳试验结果绘制于双对数坐标,线性拟合后得到基于绝对值最大的主应力的疲劳强度S-N曲线,如图8所示。考虑97.7%的保证率,减去两个标准差,得到的曲线方程为:
lg N=11.877 5-3lg Δσm。
(4)
表2 试件疲劳试验结果
Table 2 Fatigue test results of specimens
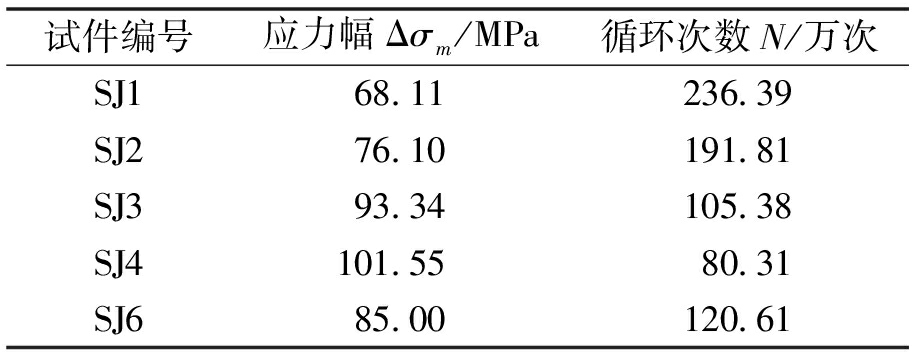
试件编号应力幅Δσm/MPa循环次数N/万次SJ168.11236.39SJ276.10191.81SJ393.34105.38SJ4101.5580.31SJ685.00120.61

图8 Δ....曲线
Figue 8 Δ.... curve
以循环200万次作为疲劳失效基准,得到基于绝对值最大的主应力的疲劳强度为72.25 MPa。
3.2 寿命评估的差异
由数值模拟或实桥监测可得顶板-U肋焊缝处的应力时程。经雨流计数后,可得各工况下各级应力幅及其循环次数。根据《公路钢结构桥梁设计规范》[10]确定顶板-U肋焊缝细节的正应力幅疲劳强度曲线,并结合试验所得的绝对值最大的主应力幅疲劳强度曲线,按照Miner线性损伤累积理论分别进行单、多轴疲劳评估,疲劳损伤度可通过式(5)得出。
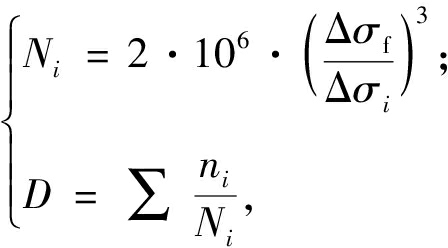
(5)
式中:Δσi表示各级应力幅;Δσf为200万次对应的疲劳强度;ni为雨流计数得到的Δσi的循环次数;Ni为疲劳失效时Δσi对应的循环次数。对于当前工程背景,单轴疲劳评估Δσf取70 MPa,多轴疲劳评估Δσf取72.25 MPa。
为了量化单、多轴疲劳评估的差异,提出寿命比R:
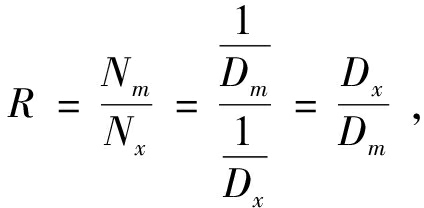
(6)
式中:Nm为多轴疲劳评估所得寿命;Nx为单轴疲劳评估所得寿命;Dm为多轴疲劳评估对应的损伤度;Dx为单轴疲劳评估对应的损伤度。由R定义可知,R越接近1,单、多轴疲劳评估的差异越小。
将疲劳强度和各级应力幅及其循环次数代入式(5),可得单、多轴疲劳评估的损伤度Dx与Dm,式(6)可进一步表示为:
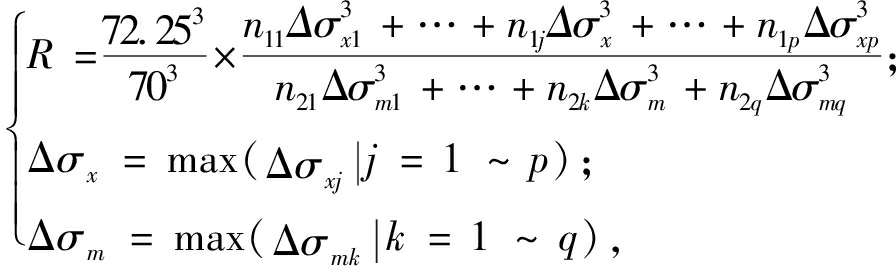
(7)
式中:Δσxj为第j级正应力幅;n1j为该级正应力幅对应的循环次数,其中j=1~p;Δσmk为第k级绝对值最大的主应力幅;n2k为该级主应力幅对应的循环次数,其中k=1~q。
对雨流计数结果进行分析,在筛除幅值较小的应力幅后,存在以下规律:①各级应力幅对应的循环次数相等;②正应力幅级数p与绝对值最大的主应力幅级数q相等;③各级应力幅中的最大值远大于其他应力幅。根据以上规律,将式(7)上下同除以![]() 寿命比R可进一步简化为:
寿命比R可进一步简化为:
(8)
式中:δ为2.2节定义的应力幅偏差值;A为差异系数。
从式(8)可以看出,疲劳寿命比R与应力幅偏差值δ的三次方成正比,从而也论证了1.2节中偏差程度越大,多轴疲劳效应越明显的论断。
3.3 差异系数
以当前工程背景为例,对差异系数A的确定给出示例,具体确定过程如下:①采用雨流法对有限元结果进行计数统计,得各工况下的应力幅及对应的循环次数;②将疲劳强度等相关参数代入式(5),得各工况下单、多轴疲劳损伤度;③分别按照式(3)和式(6)计算各工况下的应力幅偏差值δ和疲劳寿命比R;④以δ为横坐标,R为纵坐标,将各工况的结果绘制于图9;⑤利用函数R=Aδ3对图9中的散点进行拟合,从而得差异系数A的具体量值。
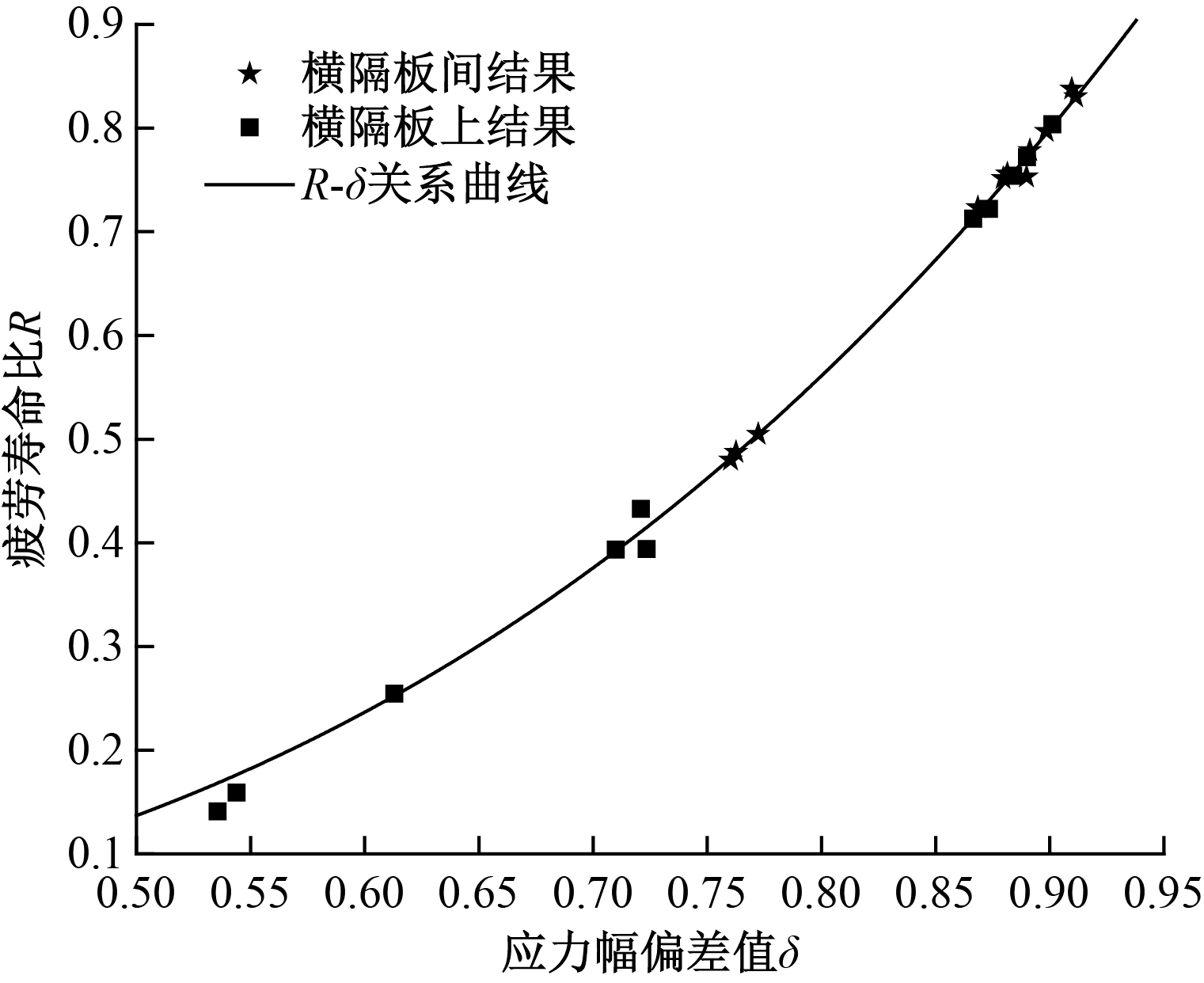
图9 ...关系曲线
Figue 9 ... relationship curve
由图9可知,曲线R=Aδ3拟合结果良好(可决系数为0.997 5),由此说明3.2节的理论推导具有合理性。针对当前工程背景,拟合得A=1.095 77,疲劳寿命比R与应力幅偏差值δ的关系为:
R=1.095 77δ3,
(9)
A=1.095 77仅针对当前工程背景得出。若能对国内大桥采样,在细节位置选取和应力时程获取等过程中运用概率论与数理统计知识,最终给出差异系数A的分布规律,将对钢桥面板多轴疲劳评估工作的开展具有重要理论意义。
4 结论
(1)在单轴荷载下,绝对值最大的主应力等于坐标轴向幅值最大的正应力。在多轴荷载下,绝对值最大的主应力与坐标轴向幅值最大的正应力存在偏差,偏差越大,多轴疲劳效应越显著。
(2)对于顶板-U肋焊缝,多轴疲劳效应随荷载中心线偏离焊缝位置越发显著,横隔板处顶板-U肋焊缝的多轴应力状态更为明显。
(3)定义了疲劳寿命比R与应力幅偏差值δ,理论推导得R与δ3成正比,该关系为在单轴疲劳评估的基础上进行多轴疲劳寿命评估提供参考。
[1] 丁楠, 邵旭东.轻型组合桥面板的疲劳性能研究[J].土木工程学报, 2015, 48(1):74-81.
[2] 黄祖慰, 雷俊卿, 桂成中,等.斜拉桥正交异性钢桥面板疲劳试验研究[J].浙江大学学报(工学版), 2019, 53(3):1-12.
[3] YAN F, CHEN W Z, LIN Z B.Prediction of fatigue life of welded details in cable-stayed orthotropic steel deck bridges[J].Engineering structures, 2016, 127:344-358.
[4] 詹健, 邵旭东, 曲宛桐,等.钢-STC轻型组合桥面结构多参数分析[J].公路交通科技, 2018, 35(5):73-81.
[5] YA S, YAMADA K, ISHIKAWA T.Fatigue evaluation of rib-to-deck welded joints of orthotropic steel bridge deck[J].Journal of bridge engineering, 2011, 16(4):492-499.
[6] YAMADA K, SAMOL Y.Plate bending fatigue tests for root crack of trough rib of orthotropic steel deck[J].Journal of structural engineering,A, 2008, 54A:675-684.
[7] 张呈奕, 傅中秋, 吉伯海,等.钢材强度对钢桥面板焊缝疲劳强度的影响[J].工业建筑, 2017, 47(5):12-16.
[8] 吉伯海, 程苗, 傅中秋,等.基于实测应变的钢桥面板疲劳寿命分析[J].河海大学学报(自然科学版), 2014, 42(5):422-426.
[9] YA S, YAMADA K.Fatigue durability evaluation of trough to deck plate welded joint of orthotropic steel deck[J].Structural engineering/earthquake engineering, 2008, 64(3):603-616.
[10] 中华人民共和国交通运输部.公路钢结构桥梁设计规范: JTGD64—2015[S].北京:人民交通出版社, 2015:10.
[11] SCHIJVE J.Fatigue of structures and materials(second edition)[M].Berlin:Springer, 2009.
[12] 尚德广, 王德俊.多轴疲劳强度[M].北京:科学出版社, 2007.
[13] SAMOL Y, YAMADA K, ISHIKAWA T.Fatigue durability of trough rib to deck plate welded detail of some orthotropic steel decks[J].Journal of structural engineering, A, 2010, 56A:77-90.