0 引言
经过漫长的时间演化,大自然造就了很多奇妙的现象,令人叹为观止的同时也给人们为解决问题带来了无限的启发.人们从各种现象中汲取智慧.例如,根据自然界的生物进化按“适者生存,优胜劣汰”这一规律提出了遗传算法(GA)[1];受生物免疫系统启发而设计的人工免疫算法(AIS)[2];受到即兴创作音乐作品的启发而提出的和声搜索算法(HS)[3];根据金属的退火过程提出模拟退火算法(SA)[4].根据动物的觅食行为,众多学者提出了很多智能算法,包括粒子群算法(PSO)[5]、蚁群算法(ACO)[6]、萤火虫算法(FA)[7]、蝙蝠算法(BA)[8]、狼群算法(WPA)[9]、细菌觅食优化算法(BFA)[10]、布谷鸟算法(CS)[11]、人工鱼算法(AFSA)[12]、蛙跳算法(SFLA)[13]、人工蜂群算法(ABC)[14]、鸡群算法(CSO)[15]、天牛须算法(BAS)[16]等.这样的元启发式算法成为解决许多棘手优化问题的有效方法.由于这些算法都具有某些优点和缺点,很多学者针对其缺点不断进行改进,并应用于合适的领域中[17].因此,从自然界中获取新启发,为解决优化问题等提供新思路仍然具有意义.
笔者根据海岛上植物的生长位置随着海平面的上升及海岛面积的缩小,越来越集中于最高点的现象,提出一种新的元启发式算法,即海岛算法(IA).海岛算法通过不断升高海平面的同时,维持植物总数不变,从而来寻找最佳点位置.通过实验,与已经广泛应用的粒子群算法进行对比.实验表明,相比于粒子群算法,海岛算法在CEC2013函数集上,总体上保持优势.
1 海岛算法
海岛算法是一种新的元启发式算法.海岛算法分为3个阶段:淘汰阶段、海平面上升阶段、平衡阶段.
1.1 淘汰阶段
该阶段是为迭代的海平面上升阶段做准备,主要的任务是根据范围的变化量来产生本次迭代需要淘汰植物的个数.因为至少需要2个植物才能定义海岛的范围,所以淘汰后,未被淘汰的植物个数至少为2,即最大的淘汰个数要小于总量数减2.该阶段的任务由淘汰函数完成.淘汰函数的自变量为范围的变化量,函数值为淘汰个数.当范围变化量比较大时,为了避免陷入局部解,应减少淘汰个数来减小下一次的范围变化量;当范围变化量比较小时,为了加快算法收敛,应增加淘汰个数来增大下一次的范围变化量.故函数满足以下两点要求:
(1)范围变化量为零时,淘汰个数为最大淘汰个数.
(2)淘汰函数为一个递减函数,随着范围变化量的增大,淘汰个数将减小.
采用既满足以上两点要求又较为简单的负指数函数:
fout(h)=[(Am-Al)·e-h]+Al,
(1)
式中:h为范围变化量,由上次迭代中海平面上升阶段产生;Am为最大淘汰个数;Al为最小淘汰个数.
1.2 海平面上升阶段
海平面上升阶段将根据淘汰阶段产生的淘汰个数来提升海平面.海平面的提升表现为海岛范围的缩小.该阶段的主要任务是产生新的海岛范围以及海岛范围变化量.其中,新的海岛范围为接下来的平衡阶段做准备,范围变化量为下次迭代中淘汰阶段做准备.
海岛的新范围由未被淘汰的植物所生长的范围所决定.新范围由每一维度的最大值Xmax和最小值Xmin表示.为了避免由于收敛过快,易陷入局部最优位置,将范围通过公式2和3进行扩展.
(2)
(3)
海岛范围变化量由公式4表示:
(4)
式中:![]() 和
和![]() 分别是上一次迭代中包含每一维度的最大值和最小值的向量;Xmax和Xmin分别是当前迭代中包含每一维度的最大值和最小值的向量;
分别是上一次迭代中包含每一维度的最大值和最小值的向量;Xmax和Xmin分别是当前迭代中包含每一维度的最大值和最小值的向量;![]() 和Xmax-Xmin分别表示上次迭代和当前迭代的海岛范围大小.norm为求取向量2范数的函数.算法开始运行时,范围变化量由初始化产生.初始化范围变化量h为1.
和Xmax-Xmin分别表示上次迭代和当前迭代的海岛范围大小.norm为求取向量2范数的函数.算法开始运行时,范围变化量由初始化产生.初始化范围变化量h为1.
1.3 平衡阶段
平衡阶段的主要任务是在海平面上升的同时,维持植物的总量不变,并根据位置高度进行排序.具体的实现是在海平面上升阶段产生的新范围内,产生A个新植物,替换种群中最差的植物,从而使植物总量不变.
为了加快搜索速度,提高搜索精度,将每一个新植物通过式(5)朝着全局最优植物处移动,然后评估该植物,若优于全局最优植物,则将两者的位置和适应度值进行交换.
x(j,:)=x(j,:)+2·rand(1,D)·
(x(1,:)-x(j,:)),
(5)
式中:x(j,:)为在新范围内产生的第j个新植物位置;x(1,:)为全局最优位置;D为维度;2为参数,使移动后的位置在当前位置向最优位置方向上以2倍的距离均匀分布.
移动和评估完所有新植物后,所有植物根据适应度值进行排序.在程序中,测试函数的适应度值即为植物的位置高度,当按照从大到小排序时,即求解测试函数最大值;当按照从小到大排序时,即求解测试函数最小值.3个阶段相互依存,关系如图1所示.每一次的迭代包含该3个阶段.
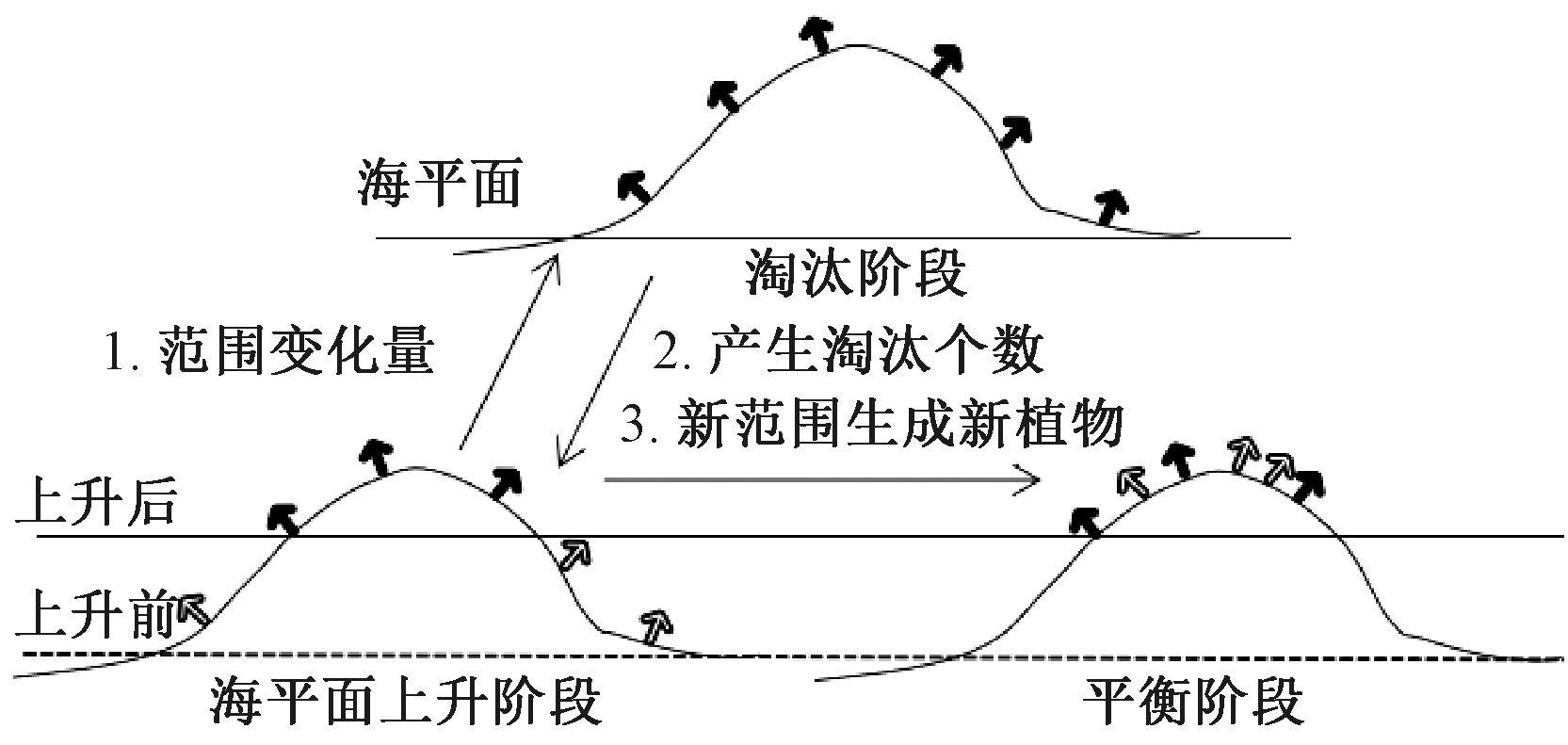
图1 3个阶段关系图
Fig.1 Three-stage relationship
1.4 算法流程
基本海岛算法的步骤如下.
步骤1 参数初始化:设最大评估次数E,海岛的维度D,淘汰个数的最大最小值分别为Am,Al,范围变化量h,植物总量N,植物的生长位置为xi (i=1,2,…,N),海岛范围Xmax,Xmin.
步骤2 进入淘汰阶段,根据式(1)生成淘汰个数.
步骤3 进入海平面上升阶段,记录上次迭代的海岛范围,产生新的海岛范围,根据式(2)和(3),对新范围进行扩展,根据式(4)产生海岛范围变化量h.
步骤4 进入平衡阶段,在新的海岛范围内根据淘汰个数产生新植物,并对植物种群中最差的植物进行淘汰.
步骤5 每一个新植物向最优植物处移动,求解新植物的适应度值,若优于最优植物,则进行交换,最后对所有植物进行排序.
步骤6 若达到终止条件,输出结果,终止算法.否则,转入步骤2,进入下一次的迭代.
算法伪代码如下所示.
输入:初始化N、Al、Am、h、D、E,
Xmax=100·ones(1,D),Xmin=-100·ones(1,D),
x=ones(N,1)·Xmin+ones(N,1)·(Xmax-Xmin)·rand(N,D);
获取每一个植物对应的适应度值,并排序
输出:最优值位置x(1,:),最优值适应度值fit(1)
1:while(结束条件)
2: 淘汰阶段
3: 根据式(1)生成淘汰个数;
4: 海平面上升阶段
![]()
6: Xmax=max(x(1:N-taotai,:));
7: Xmin=min(x(1:N-taotai,:));
8: 对新的海岛范围使用式(2)和式(3)进行扩展;
9: 根据式(4)产生范围变化量;
10: 平衡阶段
11: 在新范围内产生A个新植物,替换最差的A个植物;
12: for j=N-A+1:N;
13: 根据式(5)进行移动;
14: if(达到最大评估次数)
15: 输出结果,算法结束
16: else
17: fit(j)=Fun(x(j,:)); 评估次数加一;
18: 判断是否优于最优植物,是则进行交换
19: end
20: end
21: [fit,index]=sort(fit); x=x(index,:);
22:end
2 算法分析及对比
2.1 算法分析
相比于粒子群算法、蝙蝠算法、蜂群算法等,海岛算法在每次的迭代中,并未对每一个植物进行位置的更新和评估,而是只更新最差的植物,个数为淘汰阶段产生的淘汰个数.这样不仅可以在每一次迭代中减少计算量,而且也保留了相对较好的位置信息,其信息将在接下来多次的迭代中被利用,直到该位置被淘汰.因此,算法对每一个位置信息都有着充分的利用.这也是海岛算法能体现优越性的关键原因.
当求解的函数存在连续梯度很小或很大区域,即存在连续平坦或有尖锐峰或谷的区域,如图2所示,将不适合算法的求解.
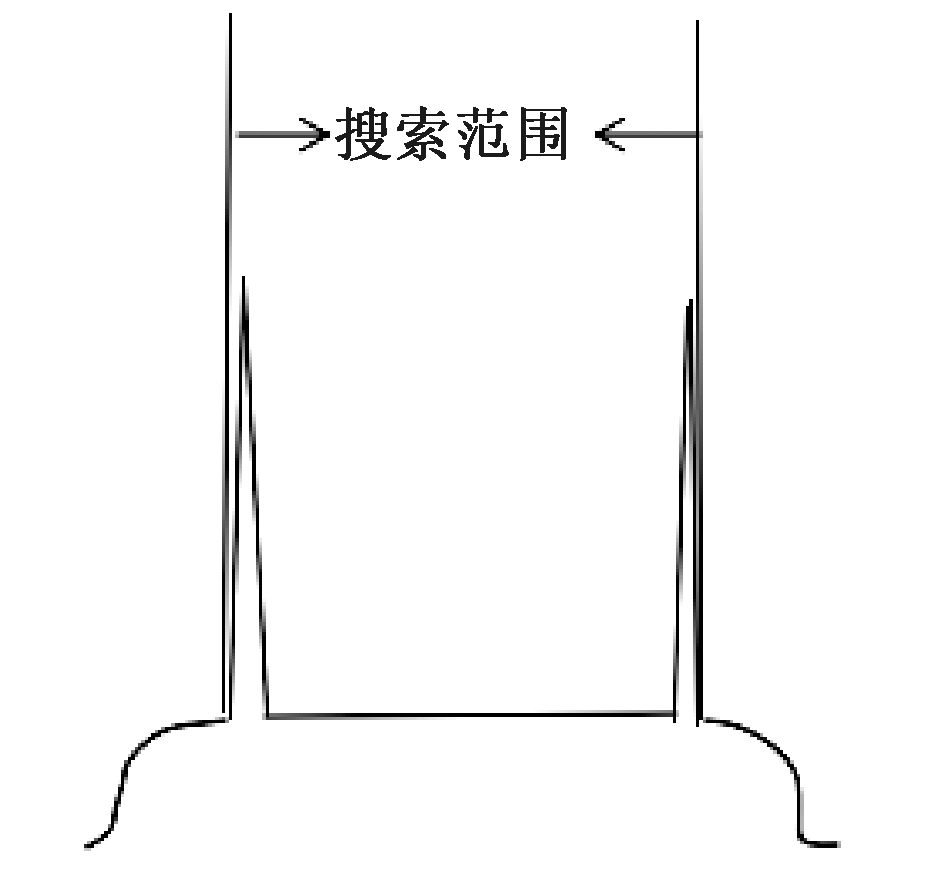
图2 不利情况
Fig.2 Unfavorable situation
由于搜索范围内存在很大的平坦区域,新增的植物位于平坦区域的概率很高,因此,海平面上升阶段,海岛的范围变化不大,甚至为0,不利于算法的收敛.但通过淘汰阶段产生更多的淘汰个数,最终使其跳出局部解.最极端的情况下,只保留2个植物,其余全部淘汰.据此,也可以预测出,该算法不适合求解具有众多尖锐的峰,且峰周围区域较为平坦的函数.典型函数如f8函数.
在求解函数的整个求解区域内,梯度相对适中,即没有连续平坦和尖锐峰或谷的区域,如图3所示,将适合算法的求解.
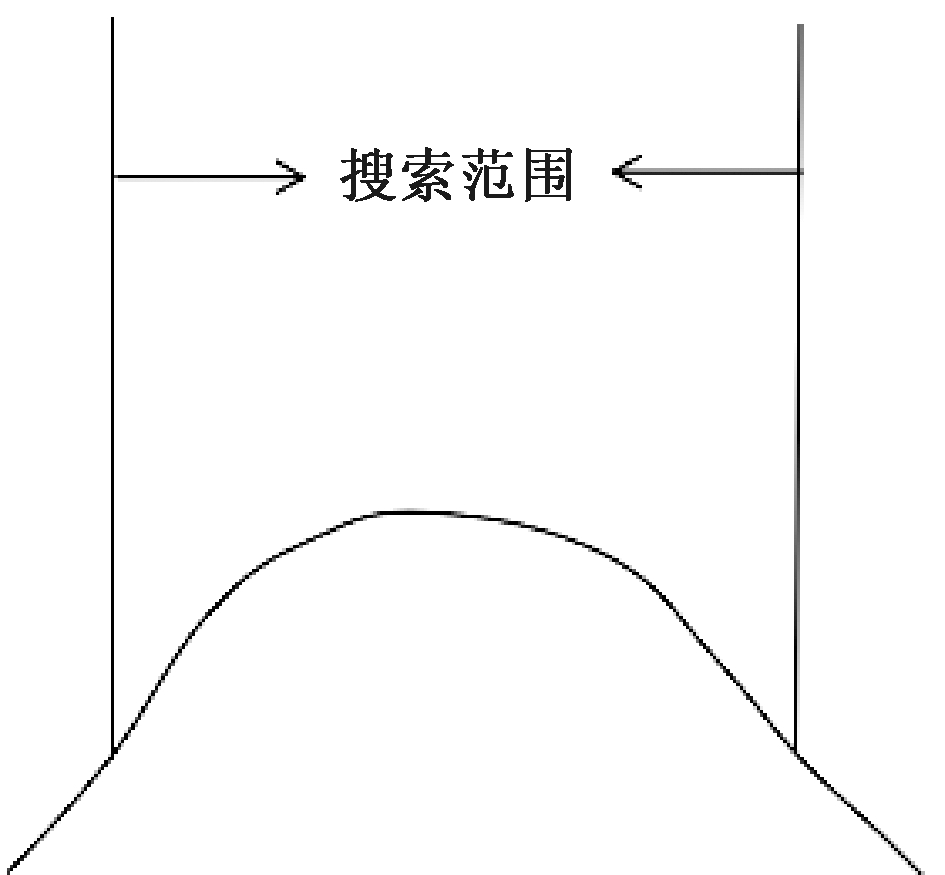
图3 有利情况
Fig.3 Favorable situation
在该搜索区域范围内,新增的植物更易处于不同的高度,这将有利于算法往最优位置处收敛.典型函数如f1函数.
由于植物随机分布在搜索范围内,在算法初期,搜索范围较大,仅通过范围的缩小来使算法收敛,相较于单个粒子根据其他信息寻找最优位置的算法如粒子群优化算法,收敛速度慢,但将新植物向最优植物处移动,大大提高了算法的收敛速度,而通过对新范围的扩展,使算法又尽可能避免因收敛过快而陷入局部最优位置;在算法后期,随着搜索范围逐渐缩小,整个种群在一个小范围内寻找最优位置,加速了收敛速度,从而达到更好的精度.海岛算法是整个种群通过淘汰方式逐渐缩小搜索范围来寻找最优区域,相较于单个粒子寻找最优位置的算法,具有更强的鲁棒性.
若取每次迭代的平均评估次数为(Am+Al)/2,则公式及排序操作的次数为2E/(Am+Al),与最大评估次数成线性关系,故算法的计算复杂度为O(n).
2.2 算法对比
有些元启发式算法在新粒子生成方式上,基于粒子的当前位置,根据其他信息调整步长及方向进行移动来生成新粒子,一般都具有惯性权重系数.如粒子群算法利用个体认知和社会认知信息,蝙蝠算法利用回声定位信息.在收敛方式上,这些信息调整的步长和方向将会引导种群收敛于最优值.
有些元启发式算法在新粒子生成方式上,是在整个搜索区域内,通过应用某种策略来产生新粒子.如遗传算法通过选择、交叉和变异3种算子来产生新粒子,人工蜂群算法通过侦察蜂随机搜索、采蜜蜂采蜜、观察蜂跟随3种方式来产生新粒子.在收敛方式上,遗传算法采用适者生存的原则,人工蜂群算法采用贪婪准则来更新差粒子,通过不断更新差粒子来实现种群朝着最优值收敛.很多元启发式算法从某种程度上讲,都是通过迭代,不断地生成新粒子和更新差粒子,使种群朝着最优值收敛.
IA算法在新粒子生成和收敛方式上与上述两种不同.新粒子采用最简单的随机搜索策略生成于不断缩小的搜索范围内,通过更新最差个体使搜索范围缩小,再通过不断缩小搜索范围来使算法收敛.
3 实验仿真分析
3.1 实验设计
为了验证本文海岛算法的性能,通过解决CEC2013测试集中测试函数来分析所提算法的性能.CEC2013测试集中包含28个函数,其中f1~f5为单峰函数,f6~f20为多模态函数,f21~f28为组合函数,搜索范围均为[-100,100].如表1所示.
实验环境是在Windows 10系统Matlab R2014a软件,CPU为i5-3470 3.20 GHz,RAM为4 GB.
海岛算法的参数设置如表2所示.
为了体现算法的优越性,在相同的条件下,与已经被广泛使用的粒子群算法进行对比.两个算法的种群大小一致.粒子群算法的社会认知系数为1.5,个体认知系数为1.5,惯性权重系数为0.8.
表1 测试函数
Tab.1 Test function

函数函数名称最优值f1Sphere Function-1 400f2Rotated High Conditioned Elliptic Function-1 300f3Rotated Bent Cigar Function-1 200f4Rotated Discus Function-1 100f5Different Powers Function-1 000f6Rotated Rosenbrock's Function-900f7Rotated Schaffers F7 Function-800f8Rotated Ackley's Function-700f9Rotated Weierstrass Function-600f10Rotated Griewank's Function-500f11Rastrigin's Function-400f12Rotated Rastrigin's Function-300f13Non-Continuous Rotated Rastrigin's Function-200f14Schwefel's Function-100f15Rotated Schwefel's Function100f16Rotated Katsuura Function200f17Lunacek Bi_Rastrigin Function300f18Rotated Lunacek Bi_Rastrigin Function400f19Expanded Griewank's plus Rosenbrock's Function500f20Expanded Scaffer's F6 Function600f21Composition Function 1 (n=5,Rotated)700f22Composition Function 2 (n=3,Unrotated)800f23Composition Function 3 (n=3,Rotated)900f24Composition Function 4 (n=3,Rotated)1 000f25Composition Function 5 (n=3,Rotated)1 100f26Composition Function 6 (n=5,Rotated)1 200f27Composition Function 7 (n=5,Rotated)1 300f28Composition Function 8 (n=5,Rotated)1 400
表2 参数设置
Tab.2 Parameter settings
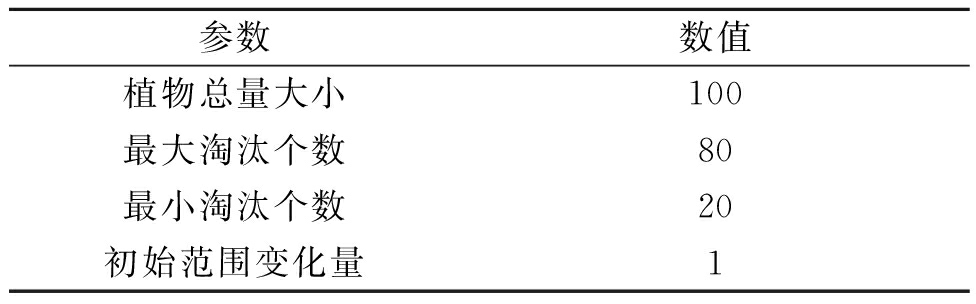
参数数值植物总量大小100最大淘汰个数80最小淘汰个数20初始范围变化量1
针对每一个函数,两个算法分别在搜索维度为10、30和50上独立运行51次,并将计算结果进行对比分析.由于海岛算法每次迭代中,对测试函数的评估次数无法确定,故通过比较相同的评估次数下计算结果的精度,来比较算法的性能.
3.2 实验结果及分析
两个算法分别在搜索维度为10、30和50上,分别对测试函数评估100 000、300 000、500 000次.将51次中所得最优误差值、最差误差值、中间误差值、平均误差值和其标准差作为算法精度和鲁棒性的衡量指标,如果小于10-8,则认为0.10维运行结果如表3~4所示,20维和30维运行结果如图4~5所示.
表3 10维f1~f7
Tab. 3 10 dimensional f1~f7
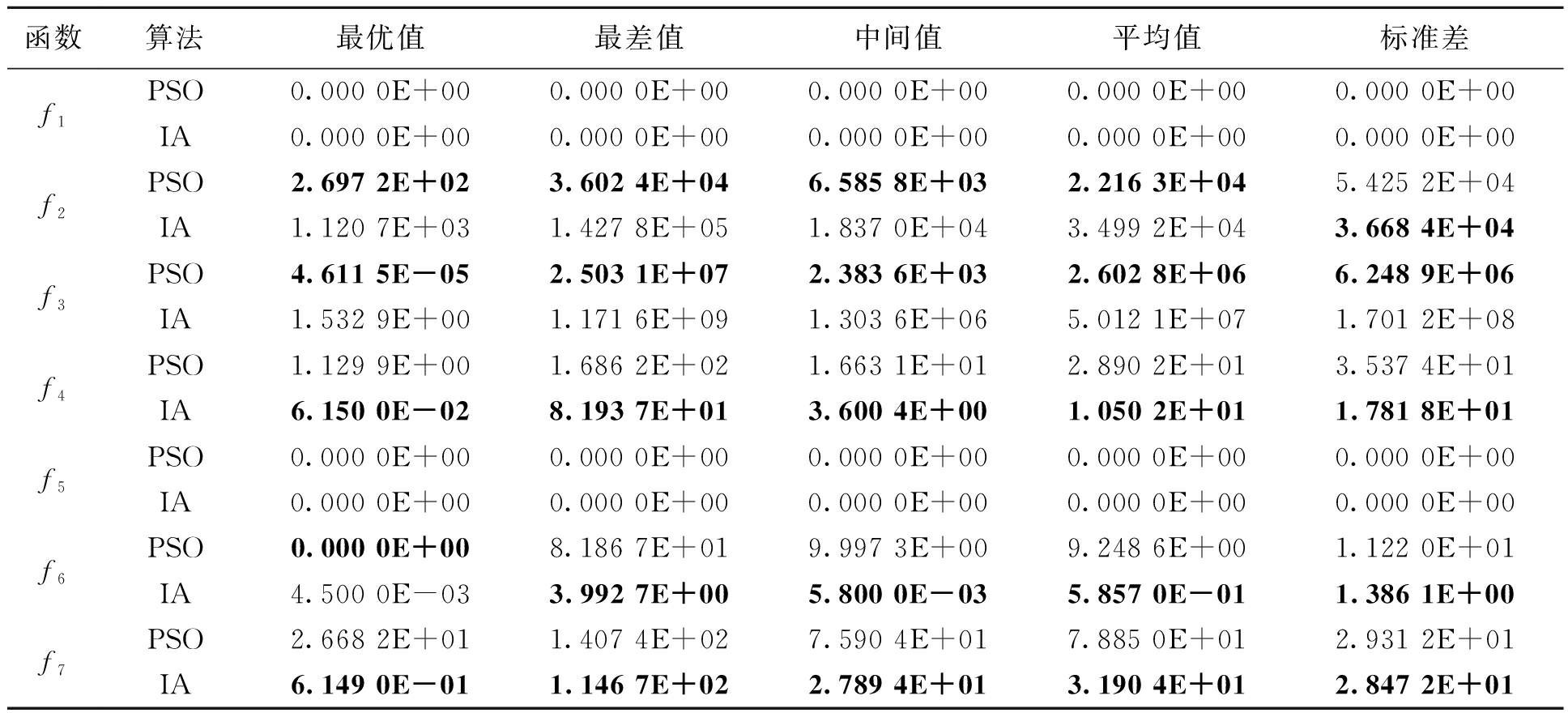
函数算法最优值最差值中间值平均值标准差f1f2f3f4f5f6f7PSO0.000 0E+000.000 0E+000.000 0E+000.000 0E+000.000 0E+00IA0.000 0E+000.000 0E+000.000 0E+000.000 0E+000.000 0E+00PSO2.697 2E+023.602 4E+046.585 8E+032.216 3E+045.425 2E+04IA1.120 7E+031.427 8E+051.837 0E+043.499 2E+043.668 4E+04PSO4.611 5E-052.503 1E+072.383 6E+032.602 8E+066.248 9E+06IA1.532 9E+001.171 6E+091.303 6E+065.012 1E+071.701 2E+08PSO1.129 9E+001.686 2E+021.663 1E+012.890 2E+013.537 4E+01IA6.150 0E-028.193 7E+013.600 4E+001.050 2E+011.781 8E+01PSO0.000 0E+000.000 0E+000.000 0E+000.000 0E+000.000 0E+00IA0.000 0E+000.000 0E+000.000 0E+000.000 0E+000.000 0E+00PSO0.000 0E+008.186 7E+019.997 3E+009.248 6E+001.122 0E+01IA4.500 0E-033.992 7E+005.800 0E-035.857 0E-011.386 1E+00PSO2.668 2E+011.407 4E+027.590 4E+017.885 0E+012.931 2E+01IA6.149 0E-011.146 7E+022.789 4E+013.190 4E+012.847 2E+01
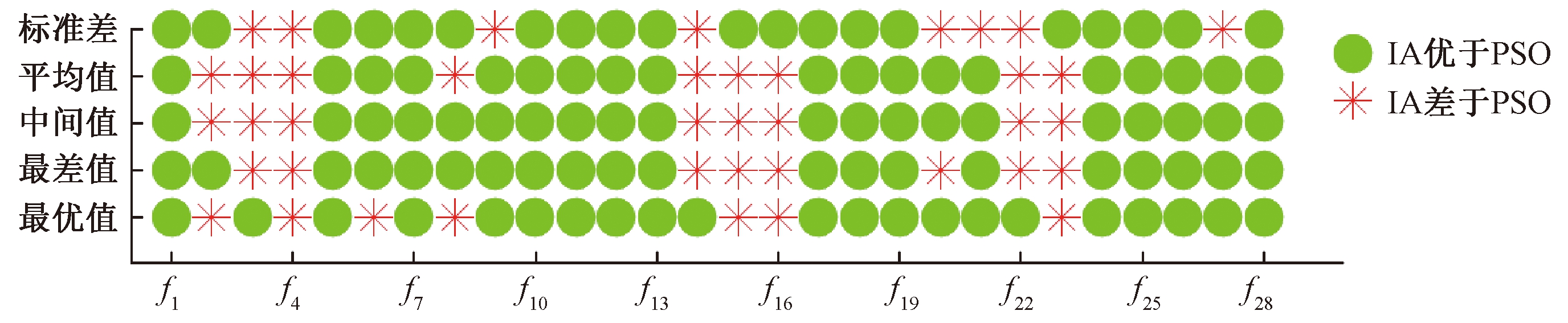
图4 30维运行结果
Fig.4 Operation results of 30 dimensional
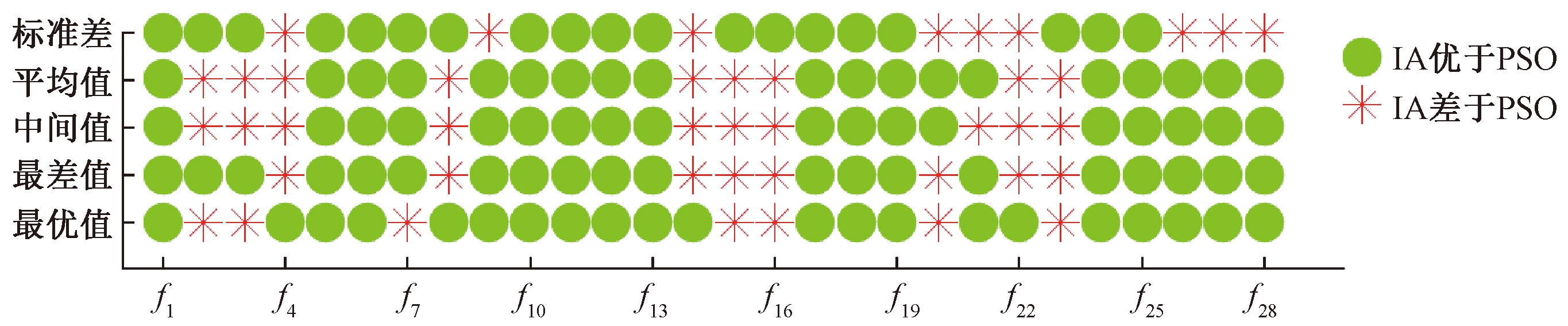
图5 50维运行结果
Fig.5 Operation results of 50 dimensional
f8函数是指数函数叠加上适度放大的余弦而得到的连续性测试函数,其特征是一个几乎平坦的区域由余弦波调制形成一个个孔或峰,从而使曲面起伏不平,有着较为平坦的区域和陡峭的峰,同样有此特点的函数还有f2、f3、f4函数.f14、f15、f16、f22和f23有非常密集的陡峭的峰和谷形成的众多局部最优位置,从对算法的分析中可知,海岛算法并不适用于求解具有此类特点的函数.
在51次独立运行的结果中,28个函数中有5个函数f2、f3、f8、f15、f16,在10、30、50维度上均差于PSO算法,f4、f14、f22和f23在30、50维度上均差于PSO算法.其余函数在3个维度中均优于PSO算法,验证了算法的分析及算法的有效性.从总体上看,海岛算法在CEC2013函数集中的大部分函数中表现优异,相同条件下海岛算法的精度和鲁棒性普遍优于已被广泛应用的粒子群算法.
表4 10维f8~f28
Tab. 4 10 dimensional f8-f28
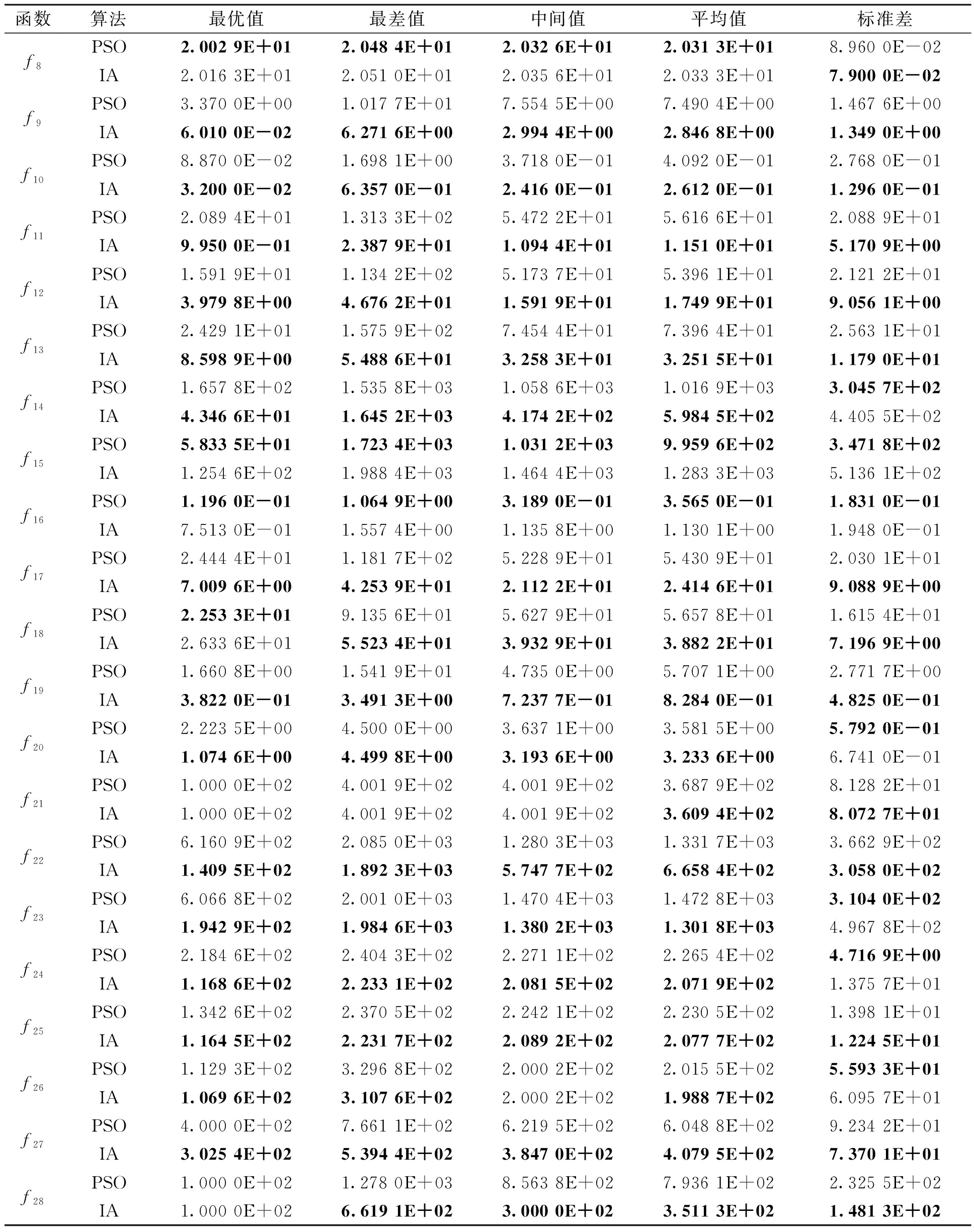
函数算法最优值最差值中间值平均值标准差f8f9f10f11f12f13f14f15f16f17f18f19f20f21f22f23f24f25f26f27f28PSO2.002 9E+012.048 4E+012.032 6E+012.031 3E+018.960 0E-02IA2.016 3E+012.051 0E+012.035 6E+012.033 3E+017.900 0E-02PSO3.370 0E+001.017 7E+017.554 5E+007.490 4E+001.467 6E+00IA6.010 0E-026.271 6E+002.994 4E+002.846 8E+001.349 0E+00PSO8.870 0E-021.698 1E+003.718 0E-014.092 0E-012.768 0E-01IA3.200 0E-026.357 0E-012.416 0E-012.612 0E-011.296 0E-01PSO2.089 4E+011.313 3E+025.472 2E+015.616 6E+012.088 9E+01IA9.950 0E-012.387 9E+011.094 4E+011.151 0E+015.170 9E+00PSO1.591 9E+011.134 2E+025.173 7E+015.396 1E+012.121 2E+01IA3.979 8E+004.676 2E+011.591 9E+011.749 9E+019.056 1E+00PSO2.429 1E+011.575 9E+027.454 4E+017.396 4E+012.563 1E+01IA8.598 9E+005.488 6E+013.258 3E+013.251 5E+011.179 0E+01PSO1.657 8E+021.535 8E+031.058 6E+031.016 9E+033.045 7E+02IA4.346 6E+011.645 2E+034.174 2E+025.984 5E+024.405 5E+02PSO5.833 5E+011.723 4E+031.031 2E+039.959 6E+023.471 8E+02IA1.254 6E+021.988 4E+031.464 4E+031.283 3E+035.136 1E+02PSO1.196 0E-011.064 9E+003.189 0E-013.565 0E-011.831 0E-01IA7.513 0E-011.557 4E+001.135 8E+001.130 1E+001.948 0E-01PSO2.444 4E+011.181 7E+025.228 9E+015.430 9E+012.030 1E+01IA7.009 6E+004.253 9E+012.112 2E+012.414 6E+019.088 9E+00PSO2.253 3E+019.135 6E+015.627 9E+015.657 8E+011.615 4E+01IA2.633 6E+015.523 4E+013.932 9E+013.882 2E+017.196 9E+00PSO1.660 8E+001.541 9E+014.735 0E+005.707 1E+002.771 7E+00IA3.822 0E-013.491 3E+007.237 7E-018.284 0E-014.825 0E-01PSO2.223 5E+004.500 0E+003.637 1E+003.581 5E+005.792 0E-01IA1.074 6E+004.499 8E+003.193 6E+003.233 6E+006.741 0E-01PSO1.000 0E+024.001 9E+024.001 9E+023.687 9E+028.128 2E+01IA1.000 0E+024.001 9E+024.001 9E+023.609 4E+028.072 7E+01PSO6.160 9E+022.085 0E+031.280 3E+031.331 7E+033.662 9E+02IA1.409 5E+021.892 3E+035.747 7E+026.658 4E+023.058 0E+02PSO6.066 8E+022.001 0E+031.470 4E+031.472 8E+033.104 0E+02IA1.942 9E+021.984 6E+031.380 2E+031.301 8E+034.967 8E+02PSO2.184 6E+022.404 3E+022.271 1E+022.265 4E+024.716 9E+00IA1.168 6E+022.233 1E+022.081 5E+022.071 9E+021.375 7E+01PSO1.342 6E+022.370 5E+022.242 1E+022.230 5E+021.398 1E+01IA1.164 5E+022.231 7E+022.089 2E+022.077 7E+021.224 5E+01PSO1.129 3E+023.296 8E+022.000 2E+022.015 5E+025.593 3E+01IA1.069 6E+023.107 6E+022.000 2E+021.988 7E+026.095 7E+01PSO4.000 0E+027.661 1E+026.219 5E+026.048 8E+029.234 2E+01IA3.025 4E+025.394 4E+023.847 0E+024.079 5E+027.370 1E+01PSO1.000 0E+021.278 0E+038.563 8E+027.936 1E+022.325 5E+02IA1.000 0E+026.619 1E+023.000 0E+023.511 3E+021.481 3E+02
4 结论
笔者提出一种新的元启发式算法即海岛算法.通过对海岛算法分析,找出该算法优缺点,并对算法的收敛特点、鲁棒性及计算复杂度进行探讨.最后在CEC2013函数集上进行实验分析,结果表明,总体上,海岛算法的寻优能力强于粒子群算法.下一步将研究不同的淘汰函数及海岛范围变化量的表达方式对算法的影响.
[1] HONDA M. Application of genetic algorithms to modelings of fusion plasma physics[J]. Computer physics communications, 2018, 231:94-106.
[2] SCHMIDT B, AL-FUQAHA A, GUPTA A, et al. Optimizing an artificial immune system algorithm in support of flow-based internet traffic classification[J]. Applied soft computing, 2017, 54(C):1-22.
[3] GAO K Z, SUGANTHAN P N, PAN Q K, et al. Discrete harmony search algorithm for flexible job shop scheduling problem with multiple objectives[J]. Journal of intelligent manufacturing, 2016, 27(2):363-374.
[4] LEITE N, MELICIO F, ROSA A C. A fast simulated annealing algorithm for the examination timetabling problem[J]. Expert systems with applications, 2019, 122:137-151.
[5] 夏星宇,高浩,王创业. 均衡策略粒子群算法在图像分割中的应用[J]. 郑州大学学报(工学版), 2018, 39(1):59-66.
[6] 常玉林,汪小渟,张鹏. 改进蚁群算法在交通分配模型中的应用[J]. 郑州大学学报(工学版), 2017, 38(2):41-44.
[7] TIGHZERT L, FONLUPT C, MENDIL B. A set of new compact firefly algorithms[J]. Swarm and evolutionary computation, 2018, 40:92-115.
[8] 崔志华,张春妹,时振涛,等. 基于蝙蝠算法的观测矩阵优化算法[J]. 控制与决策, 2018, 33(7):1341-1344.
[9] SIMON F, DEB S, HANNE T, et al. Eidetic wolf search algorithm with a global memory structure[J]. European journal of operational research, 2016, 254(1):19-28.
[10] 李珺,党建武. 改进细菌觅食算法在高维优化问题中的应用[J]. 计算机科学, 2017, 44(4):269-274.
[11] 朱浩亮,李光平. 基于改进布谷鸟搜索算法的图像分割[J]. 计算机工程与设计, 2018,39(5):1428-1432.
[12] 邓记才,耿亚南. 基于人工鱼群优化SVM的声磁标签信号检测研究[J]. 郑州大学学报(工学版), 2017, 38(4):35-38.
[13] ZHAO Z Z, XU Q S, JIA M P. Improved shuffled frog leaping algorithm-based BP neural network and its application in bearing early fault diagnosis[J]. Neural computing and applications, 2016, 27(2):375-385.
[14] 金叶,孙越泓,王加翠,等. 基于单纯形的改进精英人工蜂群算法[J]. 郑州大学学报(工学版), 2018, 39(6):36-42.
[15] 孔飞,吴定会. 一种改进的鸡群算法[J]. 江南大学学报(自然科学版), 2015, 14(6):681-688.
[16] JIANG X Y, LI S. BAS: beetle antennae search algorithm for optimization problems[J]. International journal of robotics and control. 2018, 1(1):1-3.
[17] 林诗洁,董晨,陈明志,等. 新型群智能优化算法综述[J]. 计算机工程与应用, 2018, 54(12):1-9.