0 引言
商用车载重大、强度高、时间久、速度快等特点对商用车操纵稳定性提出了更高的要求[1],同时操纵稳定性是车辆动力学性能中较为复杂的一项性能,因此对商用车操纵稳定性的影响因素研究就显得尤为重要。得益于计算机技术的大量应用,众多学者对汽车操纵稳定性进行了相关仿真研究[2-4]。文献[5]通过Adams建立整车模型,并利用遗传算法有效提高了商用车的操纵稳定性;文献[6]利用Carsim-Simulink联合仿真研究了汽车的操稳性;文献[7]基于Trucksim对整车操纵稳定性进行了仿真分析研究,但缺少参数对性能影响的量化研究;文献[8]利用Matlab/Simulink建立电动助力转向系统控制策略,改善了商用车的操纵稳定性。商用车结构参数的设计对其操纵稳定性有较大影响,因此,笔者利用Trucksim建立整车及道路模型,结合汽车操纵稳定性的客观定量评价指标和综合客观评价指标,定量分析商用车结构参数的变化对整车操纵稳定性的影响。通过改变商用车结构参数,建立商用车操纵稳定性与自身结构参数之间的量化关系,并结合蛛网图对整车操纵稳定性影响参数进行综合评价,为商用车在设计阶段提供部分数据上的参考依据。
1 系统建模
1.1 整车建模
基于Trucksim的友好用户界面及快速化建模特性,笔者基于大运某款轻型载货汽车基本参数进行整车动力学模型的建立。该模型主要由整车外形、轮胎参数、转向系统、动力传动系统、制动系统和悬架系统等几部分组成[9],由于在仿真中仅涉及到整车操纵稳定性的仿真,因此模型是以speed control通过PID控制来调节车速,不需要详细的动力传动系统参数,只需提供发动机功率限制最高车速。仿真车辆参数见表1所示,建立仿真模型如图1所示。
1.2 道路建模
笔者采用Trucksim 中的3维平整路面作为道路模型,仿真道路的几何线形根据仿真工况的国家标准确定,设置相应的环境参数和路面参数。
在相关研究中,通过采用双移线仿真(double lane change,DLC)试验,可以对汽车操纵稳定性进行全面评价。根据GB/T 6323—2014《汽车操纵稳定性试验方法》[10]的规定,并考虑实车情况,设定本文中的仿真条件:在试验过程中不施加制动力,只有转向操作;试验车速按汽车最高车速的70%的整数倍确定,试验的初速度取85 km/h。仿真采用驾驶员转向模型来控制车辆动作,在Trucksim中输入双移线轨迹坐标数据如表2所示,采用3次样条插值得到轨迹如图2所示,仿真距离为150 m。
表1 仿真车辆主要参数
Table 1 Main parameters of simulation vehicle
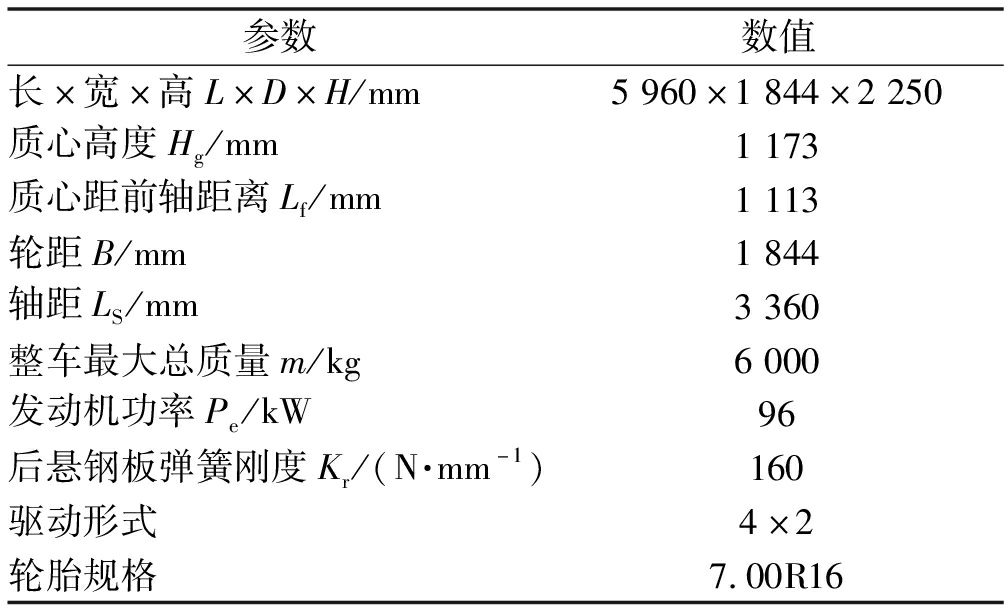
参数数值长×宽×高L×D×H/mm5960×1844×2250质心高度Hg/mm1173质心距前轴距离Lf/mm1113轮距B/mm1844轴距LS/mm3360整车最大总质量m/kg6000发动机功率Pe/kW96后悬钢板弹簧刚度Kr/(N·mm-1)160驱动形式4×2轮胎规格7.00R16

图1 轻型载货汽车仿真模型
Figue 1 Simulation model of light truck
表2 双移线坐标参数
Table 2 Coordinate parameters of double shift line m
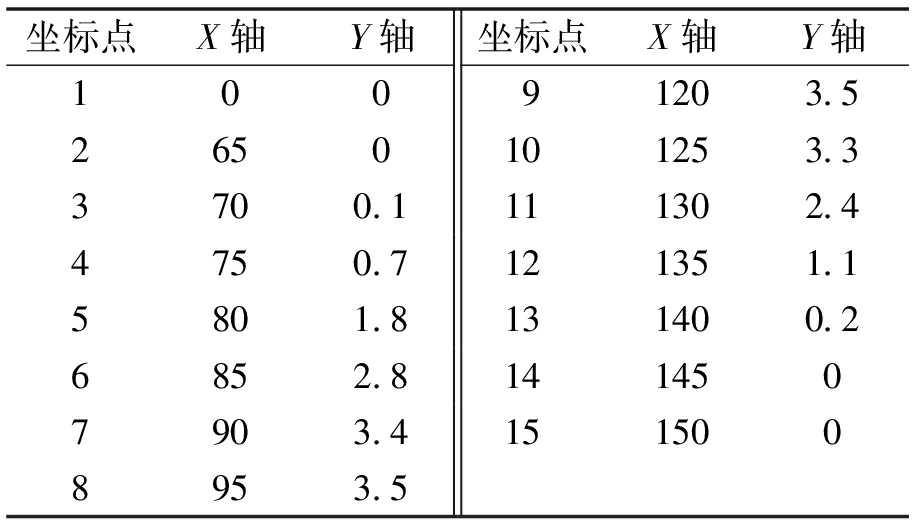
坐标点X轴Y轴坐标点X轴Y轴10091203.52650101253.33700.1111302.44750.7121351.15801.8131400.26852.81414507903.41515008953.5
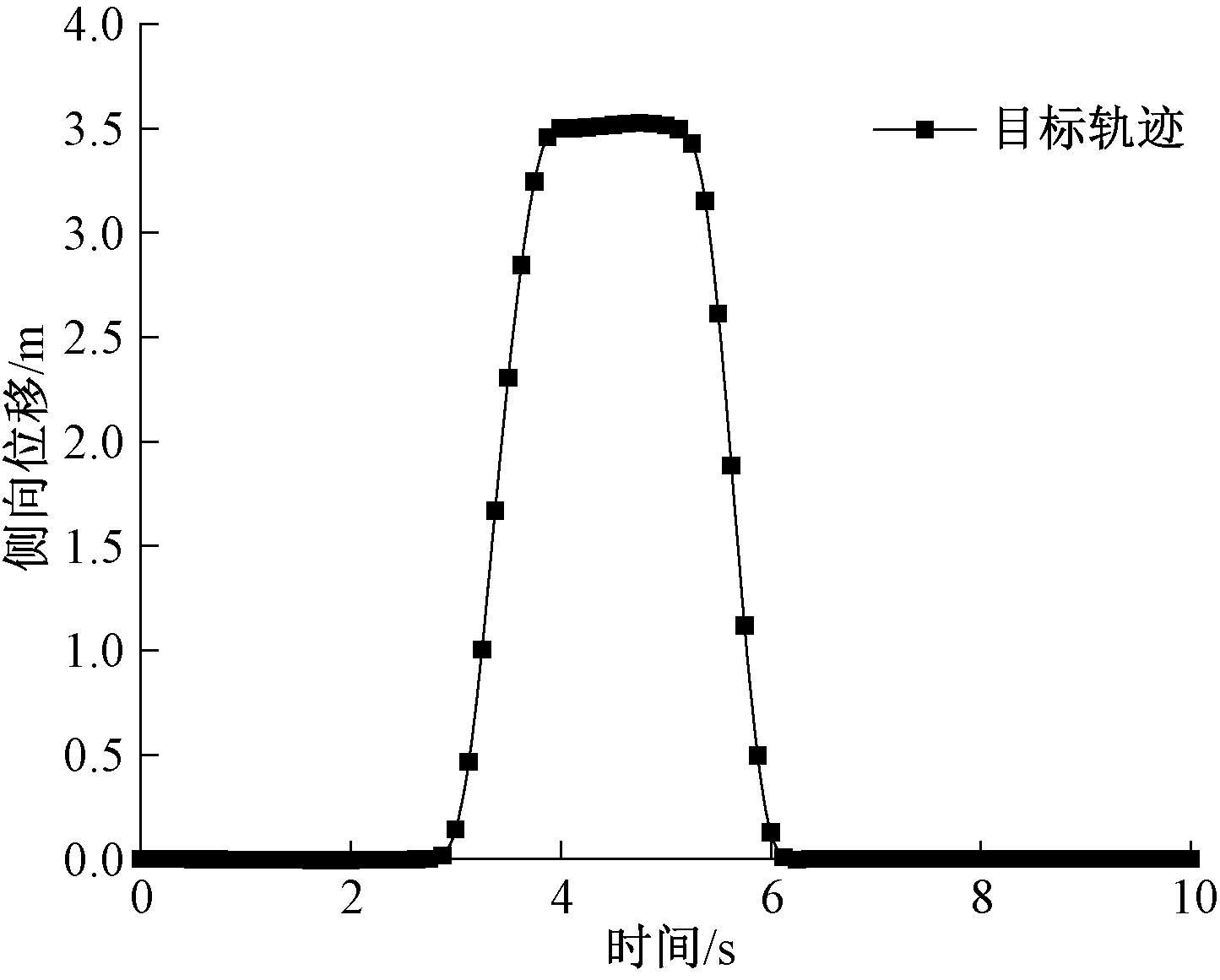
图2 双移线试验驾驶员模型输入与时间关系
Figue 2 Between driver model input and time relationship under double-shift test
2 汽车操纵稳定性客观评价指标
汽车操纵稳定性受汽车结构参数、环境条件和人为感觉等多种因素的影响,使得对其评价变得错综复杂。考虑到多种因素,笔者采用轨道跟踪好坏、翻车危险、侧滑危险等几种评价指标,该评价方法与驾驶员主观评价的相关性达到99%以上,具体评价指标包括以下几种。
2.1 轨道跟踪好坏的指标
(1)轨道误差指标。汽车轨道跟踪的好坏直接影响其主动安全性,因此,轨道误差的总方差对于汽车主动安全性是一个重要指标,其标准化后表达式为:
(1)
式中:f(t)为期望路径;![]() 为轨迹误差标准门槛值;y(t)为试验时汽车目标轨迹;tn为试验时间。
为轨迹误差标准门槛值;y(t)为试验时汽车目标轨迹;tn为试验时间。
(2)方向误差指标。侧向加速度ay=v+uωr,汽车纵向速度与横摆角速度的乘积uωr是非稳态量,影响汽车的行驶方向,因此将其作为方向误差考虑。标准化后总方差表达式为:
(2)
式中:ωr为汽车质心横摆角速度;![]() 为横摆角速度标准门槛值。
为横摆角速度标准门槛值。
2.2 翻车危险性指标
(1)侧向加速度。侧向加速度是操纵稳定性中最重要的汽车响应参数和评价指标,它代表汽车的侧向行驶性能。侧向加速度ay的总方差表达式为:
(3)
式中:![]() 为侧向加速度标准门槛值。
为侧向加速度标准门槛值。
(2)侧倾角。从驾驶员的角度考虑,车身侧倾角也代表翻车危险性,可以间接反映驾驶员的紧张程度,但与侧向加速度所表示的意义又有所不同,其标准化的总方差表达式为:
(4)
式中:φ为汽车的侧倾角;![]() 为汽车的侧倾角标准门槛值。
为汽车的侧倾角标准门槛值。
2.3 侧滑危险指标
汽车前、后轮的侧滑是实际行驶中经常遇到的情况,它直接影响汽车的行驶安全性及驾驶员的安全感。因此,汽车的侧滑是影响驾驶员主观评价的一个因素。当汽车前、后轮的侧向力大于地面附着力,地面附着力不足以提供汽车所需要的侧向力时,汽车将产生侧滑,其标准化的总方差表达式为:
(5)
式中:i=1、2、3、4分别表示左前、左后、右前、右后4个轮胎;Fyi(t)为车轮侧向力;Fzi(t)为车轮垂直载荷;![]() 为Fyi(t)/Fzi(t)的标准门槛值。
为Fyi(t)/Fzi(t)的标准门槛值。
2.4 综合客观评价指标
将上述各单项评价指标加权组合并取其加权平均值,建立一个考虑因素全面的表征汽车主动安全性的客观评价指标:
(6)
式中:W1、W2、W3、W4、W5为加权值。为了调整权系数,Wi均取为1,所有门槛值取文献[12]标准门槛值。
3 不同结构参数对商用车操纵稳定性的影响
商用车的操纵稳定性能是由各结构参数共同决定的,其中整车质量、轴距、轮距、质心位置是车体最重要的特性参数,钢板弹簧刚度是商用车悬架特性参数,这些结构参数与商用车的操纵稳定性息息相关。文献[11]研究了不同结构参数对操纵稳定性影响程度,笔者在此基础上以整车质量、轴距、轮距、后悬钢板弹簧刚度、质心高度及质心距前轴距离这6个结构参数作为试验的仿真变量,根据文献[11]将每个因素分为3种情况,分别为原车参数的0.9倍、1.0倍和1.1倍,通过此方案得到18种不同参数的商用车,采用控制变量法,结合客观评价指标定量考察此6个结构参数变化的对整车操纵稳定性的影响,具体参数变化如表3所示。
表3 仿真参数
Table 3 Simulation parameters
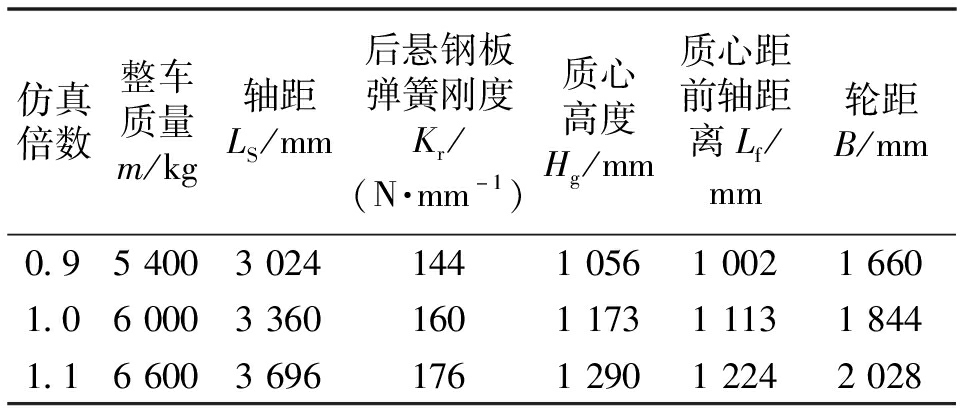
仿真倍数整车质量m/kg轴距LS/mm后悬钢板弹簧刚度Kr/(N·mm-1)质心高度Hg/mm质心距前轴距离Lf/mm轮距B/mm0.9540030241441056100216601.0600033601601173111318441.166003696176129012242028
3.1 整车质量的影响
根据式(5)将各车轮上的垂向力和侧向力通过计算得到侧滑危险指标,最后根据上述5个指标计算得到综合客观评价指标如表4所示。通过表4可以看出,随着整车质量的增加,其各项指标均有所变大,表征车辆操纵稳定性变差,更易出现危险工况,因此在实际交通运输中应避免超载。
根据表1参数,仅改变仿真模型中商用车的整车质量,进行双移线试验,其他仿真参数与原始参数一致。通过试验得到的侧向偏移量、横摆角速度、侧向加速度、侧倾角与时间的关系曲线如图3所示。
从仿真曲线可以看出,整车质量的变化对轨道误差影响较小,但随着质量的变大,整车惯性变大,导致侧倾角变大,表明车辆出现侧翻危险的可能性随整车质量的增加而增加。
3.2 轴距的影响
根据表1参数,仅改变模型中商用车轴距,保持其他仿真试验参数与原始参数一致,进行双移线试验。通过试验得到的侧向偏移量、侧偏角速度、侧向加速度、侧倾角与时间的关系曲线分别如图4所示。对比分析商用车轴距对其各项操纵稳定性指标的影响。
从仿真曲线可以看出,轴距对各项操稳性指标影响比较明显,随着轴距的增大,所有指标的峰值都有一定程度的减少。表明商用车操纵稳定性随轴距的增大而提升。
表4 不同整车质量下仿真结果
Table 4 The simulation results under different vehicle mass

整车质量/kg轨道误差指标Je1方向误差指标Je2侧向加速度指标Jr1侧倾角指标Jr2侧滑指标JS综合指标J54003.9243381454.934.8312.3267.958650.68160004.0269821468.684.8713.3038.362656.83266004.1772371488.594.9364.5988.896665.739
将各车轮上的垂向力和侧向力通过计算得到侧滑危险指标,各项指标以及客观综合评价指标具体数值如表5所示。从表5可以看出,随轴距的增大,各项指标都随之降低,尤其体现在轴距由3 024 mm增大到3 360 mm时最为明显,表明车辆轴距的减小会导致操纵稳定性变差,因此从整车操纵稳定性方面考虑,在满足设计要求的情况下,应尽量选取较大轴距。
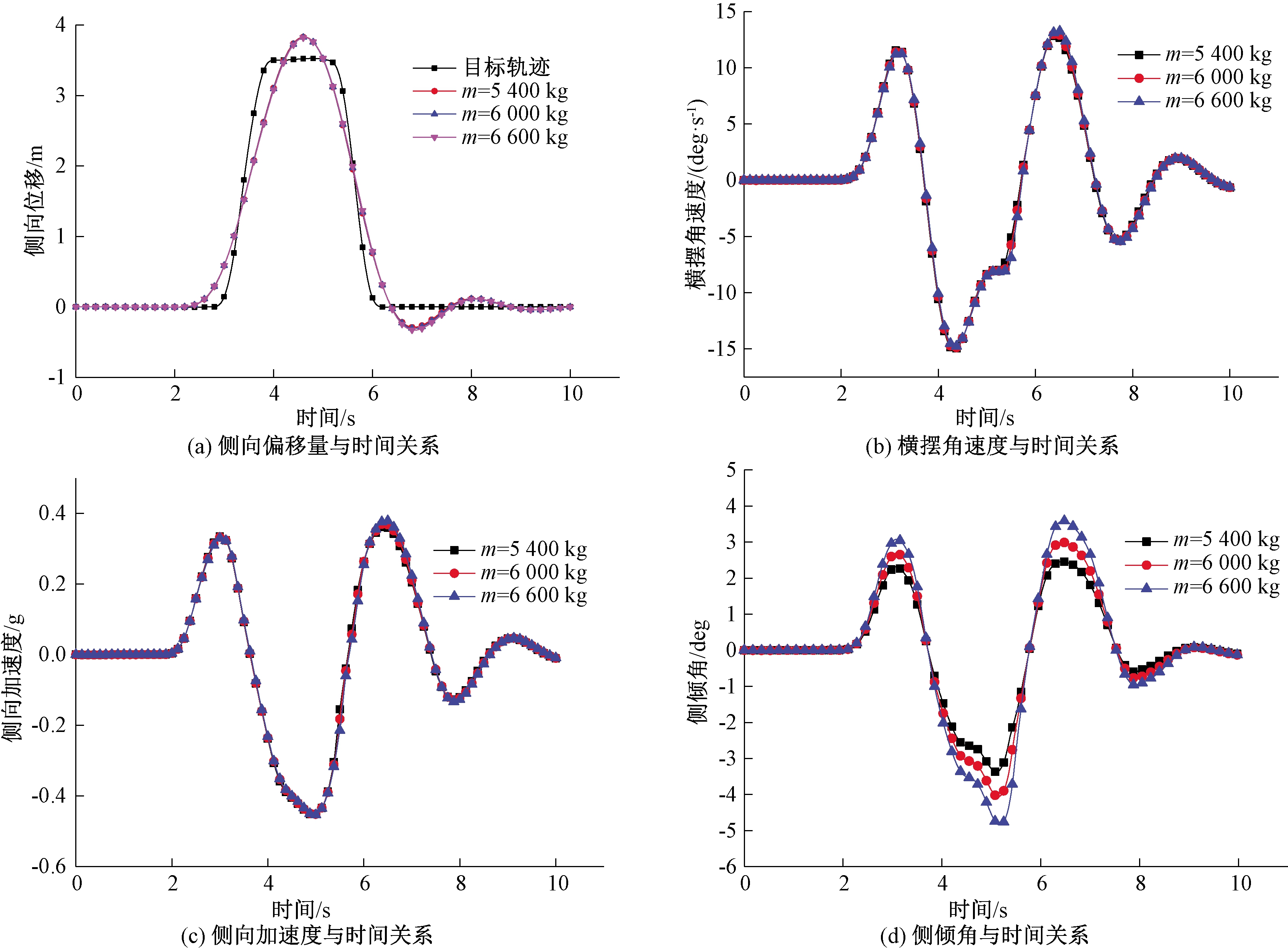
图3 整车质量改变下仿真曲线图
Figue 3 Simulation curves change with vehicle mass
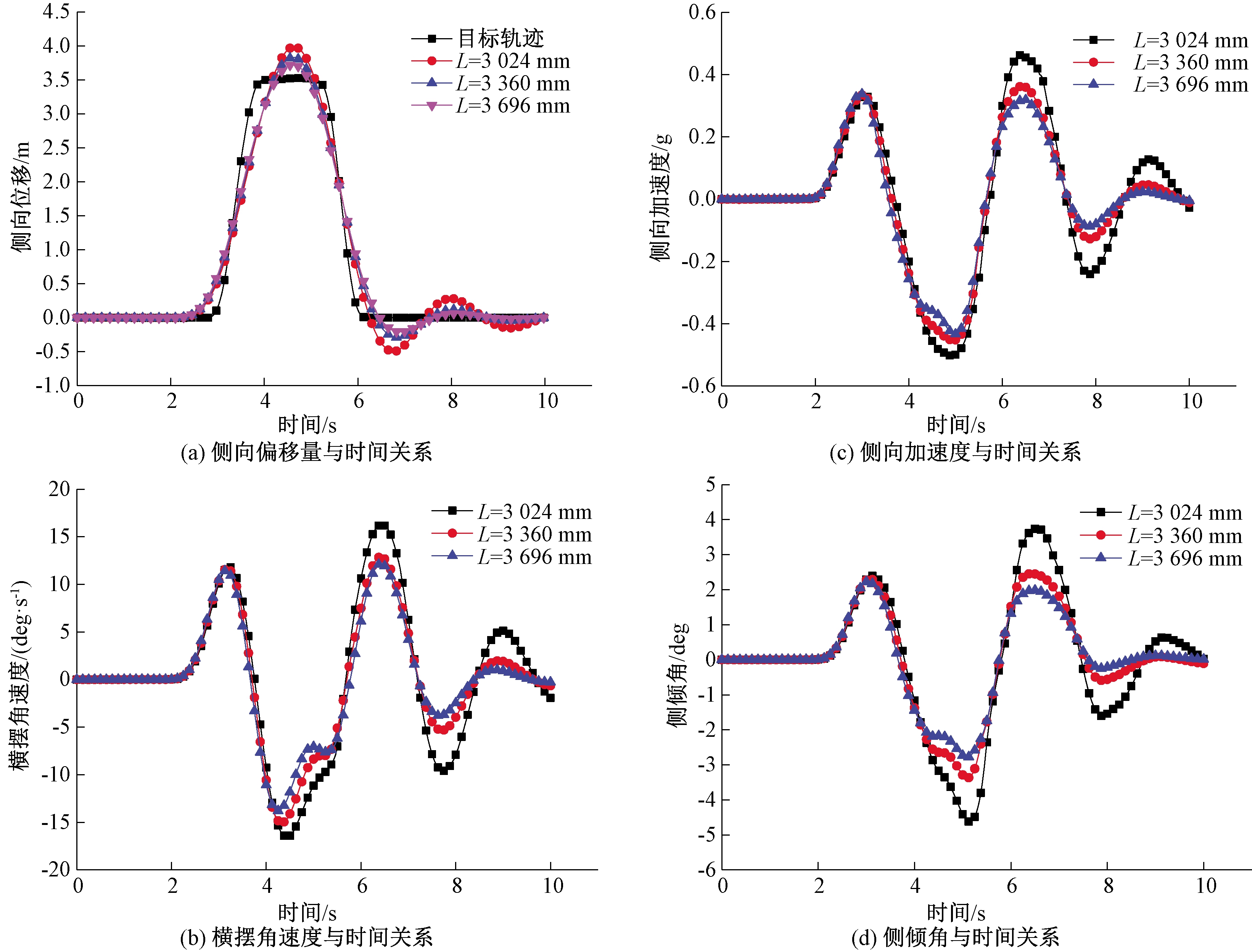
图4 轴距改变下仿真曲线图
Figue 4 Simulation curves change with vehicle wheelbase
表5 不同轴距下仿真结果
Table 5 The simulation results under different vehicle wheelbase

轴距/mm轨道误差指标Je1方向误差指标Je2侧向加速度指标Jr1侧倾角指标Jr2侧滑指标JS综合指标J30244.94162168.586.587414.07719210.108110969.83833603.95811454.934.831002.3265417.958148650.68136963.91641222.864.150851.7434897.256446546.896
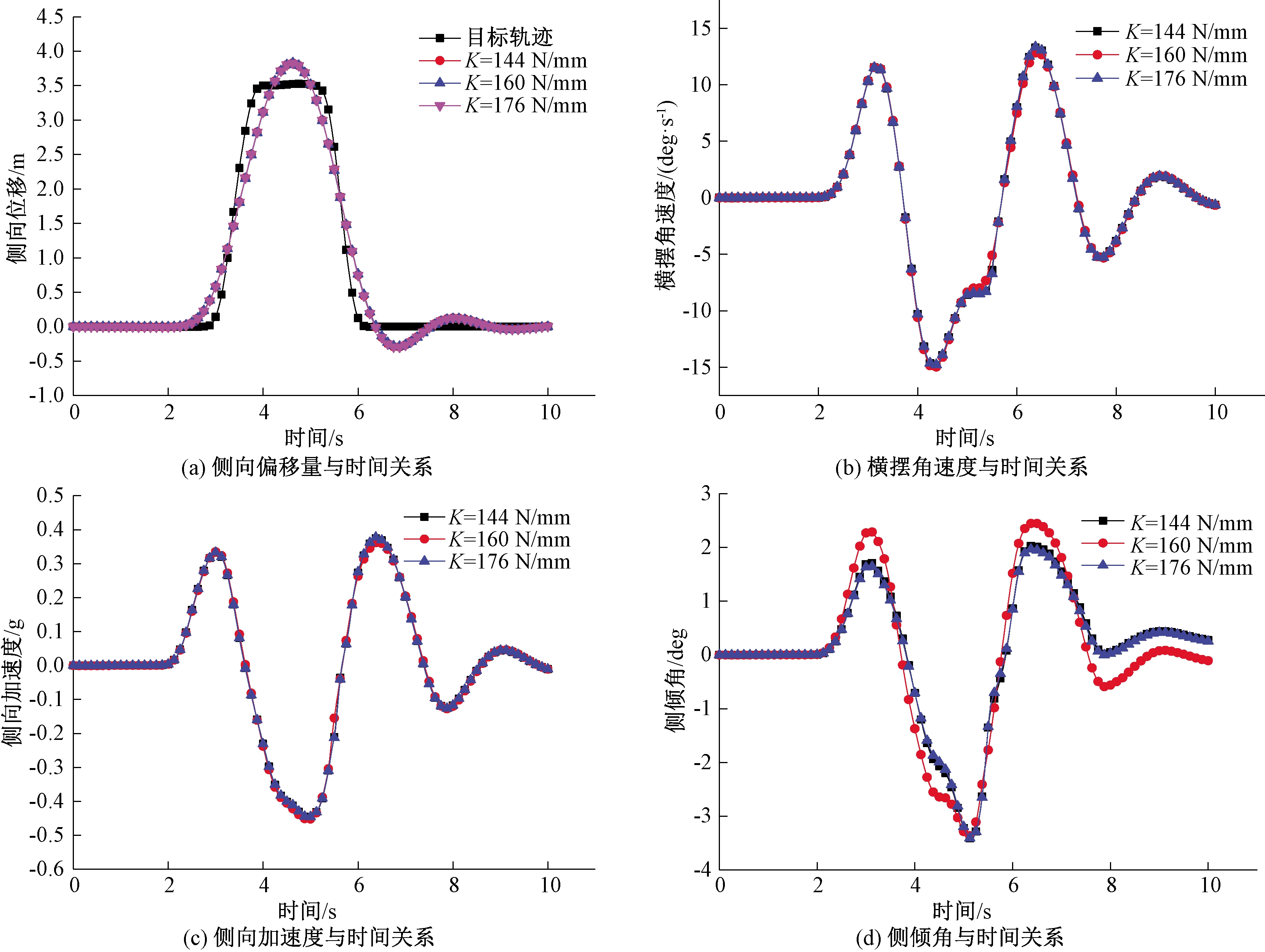
图5 后悬钢板弹簧刚度改变的仿真曲线图
Figue 5 Simulation curves change with vehicle stiffness change of back suspension leaf spring
3.3 后悬钢板弹簧刚度
根据表1改变模型中商用车的后悬钢板弹簧刚度,进行双移线试验,其他仿真参数与原始参数一致。通过试验得到的侧向偏移量、侧偏角速度、侧向加速度、侧倾角与时间的关系曲线如图5所示。对仿真结果曲线进行对比,分析商用车后悬钢板弹簧刚度对其操纵稳定性各项指标的影响。
分析图5仿真结果各参数变化可知,后悬钢板弹簧刚度的变化对4项指标影响较小,因此从图像上难以说明后悬钢板弹簧刚度的变化对操纵稳定性的影响。
根据式(5)将各车轮上的垂向力和侧向力通过计算得到侧滑危险指标Js。表6是根据汽车操纵稳定性综合客观评价指标计算不同装载质量下双移线试验的结果。从数值结果上可以看出,当商用车后悬钢板弹簧刚度K=160 N/mm时,其综合客观评价指标最小,因此,在商用车后悬钢板弹簧刚度设计时,应考虑一个最优设计值,过大或者过小都会影响其操纵稳定性。
对于表3另外3个结构参数:质心高度、质心距前轴距离及轮距,其仿真过程与整车质量、轴距以及后悬钢板弹簧刚度的仿真过程类似,不再赘述,仅在表7中给出最终仿真综合客观评价指标的数值,可从综合评价指标中得到质心高度、质心距前轴的距离及轮距的变化对整车操纵稳定性影响的变化趋势。
表6 不同后悬钢板弹簧刚度下仿真结果
Table 6 The simulation results under different vehicle stiffness of back suspension leaf spring

后悬钢板弹簧刚度/(N·mm-1)轨道误差指标Je1方向误差指标Je2侧向加速度指标Jr1侧倾角指标Jr2侧滑指标Js综合指标J1443.837271480.484.83581.73398.0805662.1071603.932061454.934.83102.32657.9581650.6811763.833601483.604.84261.65758.0899663.502
4 蛛网图
为综合对比不同结构参数对横向稳定性的影响,笔者借助蜘蛛网图构建出结构参数对商用车操纵稳定性影响模型。蛛网图的基本原理是根据评价系统需求确定主要的评价指标,并将评价指标数据进行无量纲化处理,转化为具有可比性的数值。仿真所得综合评价指标如表7所示。以6个结构参数仿真变量及综合客观评价指标J建立蛛网图模型如图6所示。分析表7中不同结构参数的变化可知,整车操纵稳定性随整车质量、质心高度的变大而变差,随轴距、质心距前轴的距离及轮距的变大而提升。
表7 不同结构参数的综合评价指标
Table 7 Comprehensive evaluation index of different structural parameters

仿真参数倍数整车质量/kg轴距/mm后悬钢板弹簧刚度/(N·mm-1)质心高度/mm质心距前轴距离/mm轮距/mm0.9650.6809946969.8377006662.1068556664.1064749692.5559752732.19683791.0656.8320514650.6810363650.6810046676.8320641656.8320641653.75655021.1665.7390302546.8957566663.5021177709.9666627645.9287287586.4122427
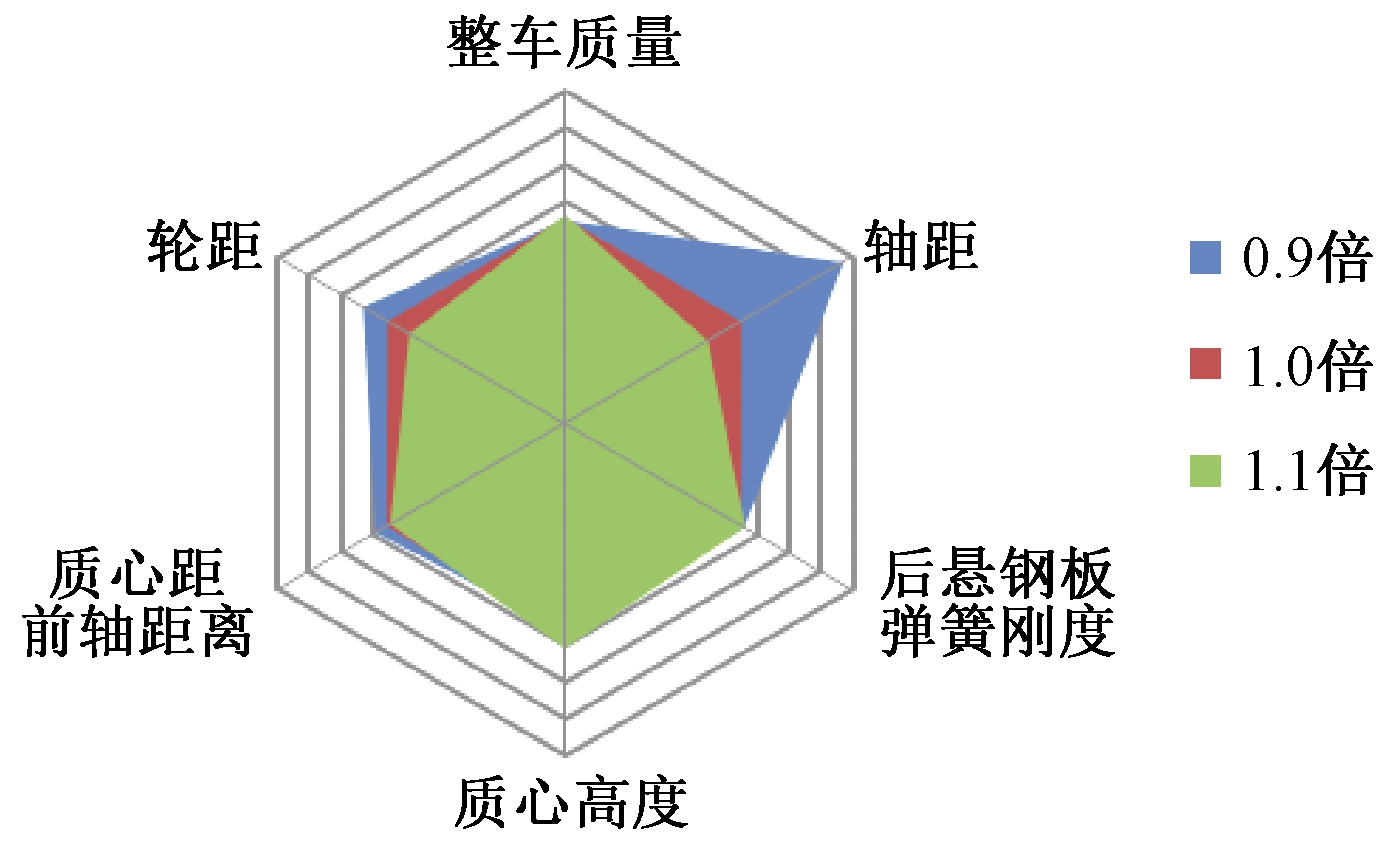
图6 不同结构参数操纵稳定性的蛛网图
Figue 6 Spider chart with different structural parameters
从图6可以看出,轴距对商用车操纵稳定性的影响最明显,而另外4个参数的改变对其影响较小。具体来说,随着整车质量的增大,综合客观评价指标变差,商用车操纵稳定性降低,但这种变化并不明显;而随着轴距、质心距前轴距离和轮距的变大,综合客观评价指标变好,表明商用车操纵稳定性在提升。
5 结论
(1)随着整车质量的变大,商用车操纵稳定性的各项指标变差,综合客观评价指标也变差,表明商用车的操纵稳定性降低。
(2)随着整车轴距、质心距前轴距离和轮距的变长,商用车操纵稳定性的各项指标变好,综合评价指数也变好,表明商用车操纵稳定性随轴距的增大而提升。
(3)后悬钢板弹簧的刚度及质心高度的变化对整车操纵稳定性的影响不大。
(4)在实际商用车设计阶段,上述变化关系为商用车参数的设计提供了部分数据上的参考依据。
[1] 陈可际,过学迅,裴晓飞.基于多工况匹配的商用车侧翻预警方法[J].中国机械工程,2016,27(20): 2822-2827.
[2] JIN X J, YU Z T, YIN G D, et al.Improving vehicle handling stability based on combined AFS and DYC system via robust Takagi-Sugeno fuzzy control[J].IEEE transactions on intelligent transportation systems, 2018, 19(8):2696-2707.
[3] 郑睿.某重型商用车平顺性和操纵稳定性优化[D].合肥:合肥工业大学, 2018.
[4] 孙勇,郭魁元,许志光.商用车电子稳定性控制系统测试评价方法研究[J].汽车技术,2018(4):52-57.
[5] 张召振,许凯,曾发林.基于Adams的某重型商用车操纵稳定性优化研究[J].广西大学学报(自然科学版),2017,42(2):452-460.
[6] HUANG F H, FU C Y, TANG X L, et al.Study on stability and handling characteristics and control of four-wheel-drive electric vehicles[J].Advances in mechanical engineering, 2017, 9(12): 1-15.
[7] 章雪华,石柏军,李岩.基于Trucksim整车操纵稳定性仿真分析研究[J].机械设计与制造工程,2017,46(2):30-34.
[8] 张硕,余强,闫光辉,等.商用车EPS助力控制策略的研究[J].汽车工程,2013,35(9):812-816.
[9] 吴涛,焦静,范学琼,等.基于Trucksim的整车动力性能仿真分析[J].汽车实用技术,2016(6): 63-65.
[10] 全国汽车标准化技术委员会.汽车操纵稳定性试验方法:GB/T 6323—2014[S].北京:中国标准出版社,2014.(这个不会查)
[11] 崔丽楠.重型载货汽车建模、仿真及总成特性对性能影响的分析[D].长春:吉林大学,2011.