0 引言
随着智能物联网的快速发展,需要对部署在室内的众多设备或人员定位,且定位精度要求也日益提高[1]。然而,现有定位方法主要依托无线信号,受复杂室内环境、障碍物和噪声影响严重,定位精度存在误差。
常用的室内定位方法主要包括红外线定位、超声波定位、蓝牙定位、射频识别定位、激光定位和超宽带定位[2]等。其中,红外线定位易受障碍物干扰,且通信距离较短[3];超声波定位受室内环境中存在的多径效应影响大,且定位距离较短[4];蓝牙定位对室内噪声敏感,且定位误差较大、定位距离短[5];射频识别定位速度快、安全性强,但是定位距离短、系统兼容性差[6];超宽带定位采用带宽大于500 MHz的纳秒级脉冲信号,穿透性强、时间分辨率高、定位精度高,信号在传输过程中抗干扰能力强[1]。然而,采用超宽带实现目标位置标定,是根据测定距离,基于一组非线性定位方程组,通过最小二乘法(least square method, LS)[7]、直接法[8]或Taylor级数迭代算法[9-10]进行方程求解获得。其中,采用最小二乘法和直接法进行方程求解,获得的定位精度较差;Taylor级数迭代算法的求解精度高,但是对初始值具有较强的依赖性,可能出现目标定位偏离实际值且不收敛的情况。
基于此,笔者针对超宽带室内定位方法,提出一种融合差分进化算法和Taylor级数迭代算法的新型定位解算方法。该算法以定位误差作为优化目标,采用差分进化算法对目标点实现全局定位,然后以差分进化算法获得的最优定位点作为初始值,采用Taylor级数迭代算法对定位点进行局部寻优。通过这种定位解算方法克服传统Taylor级数迭代算法对初始值的依赖性,从而获得高精度的目标定位。进而将所提方法用于煤矿掘进巷道这一复杂室内场景下,掘进支护移动支架的超宽带定位解算。
1 超宽带定位原理
超宽带技术不是利用传统的载波来传输数据,而是通过发送和接收具有纳秒及纳秒以下的极窄脉冲来传输数据,从而具有GHz量级的带宽[2]。美国联邦通信委员会对超宽带的定义为:
![]() 或fH-fL≥500 MHz,
或fH-fL≥500 MHz,
(1)
式中:fH和fL分别为相对于峰值功率下降10 dB时对应的高频和低频值;fC为载波的中心频率。
采用超宽带定位方法对目标点进行位置标定时,通常相对于目标点设置多个基站,如图1所示。通过K个基站依次对目标点进行超宽带测距,进而依据测距信息,构建定位方程组,解算获得目标点位置坐标。
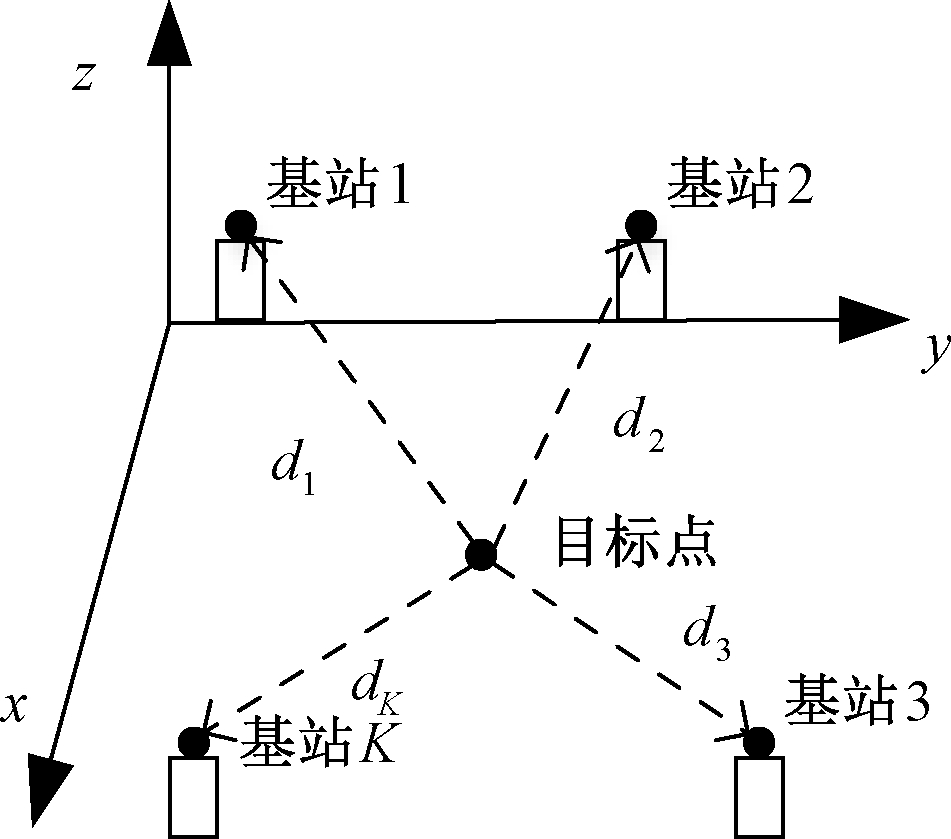
图1 超宽带定位原理
Figue 1 Positioning principle of ultra-wideband
超宽带定位通常采用基于接收信号强度、基于信号到达角度和基于信号到达时间[11]。相比而言,采用到达时间测距方法具有较高的测距精度,但是单向测距需要基站和目标点之间时钟严格同步,这一要求很难保证,而采用双向测距不需要时钟同步,有效提高了测距精度[12]。
基于双向测距的接收信号时间法原理如图2所示。针对第i(i=1,2,…,K)个基站,目标点在Ti0时刻发送含有时间标记信息的数据包给基站i,基站i收到此数据包,并延时时间Ti delay后,回送一个信号给目标点,目标点根据接收到的信号来确定传播时间。假设Ti为信号在目标点和基站i之间传输所用时间,Ti0为信号从目标点发出的时刻,Ti1为目标点收到返回信号的时刻,c为光速,则目标点和基站i之间的测定距离为:
di=Tic;
(2)
(3)
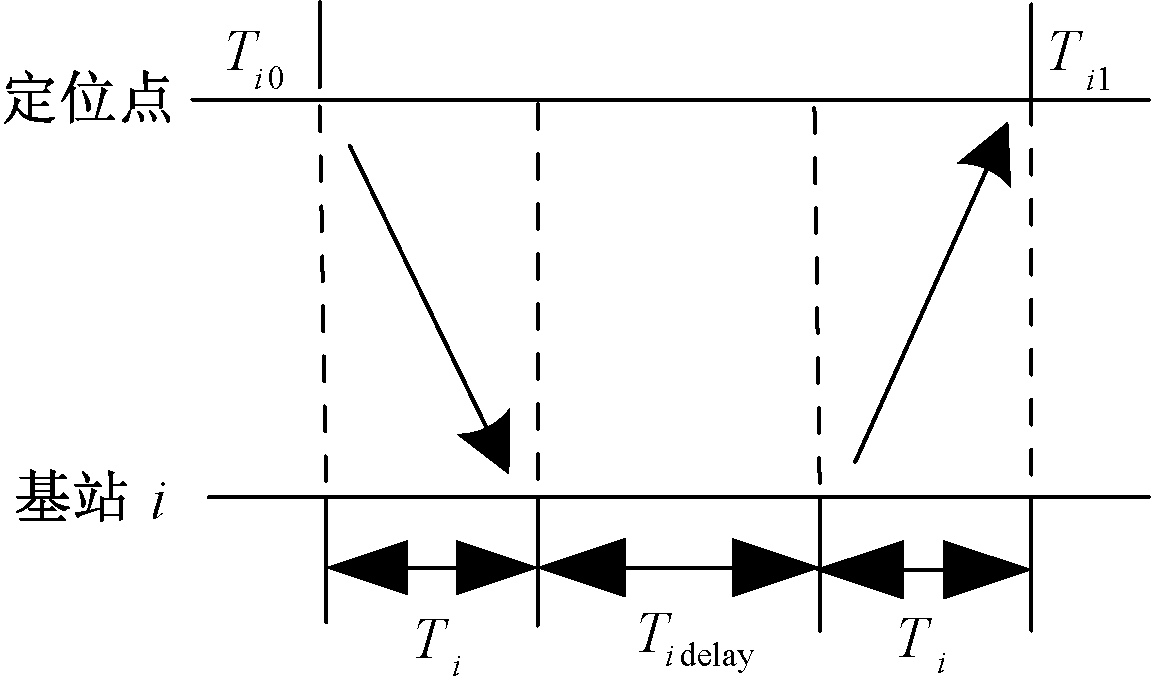
图2 基于双向测距的接收信号时间法原理
Figue 2 Principle of received signal time method based on two-way ranging
假设第i个基站的坐标为(xi,yi,zi),目标点坐标为(xs,ys,zs),则根据所有基站与目标点之间的到达时间构建超宽带定位解算模型为:
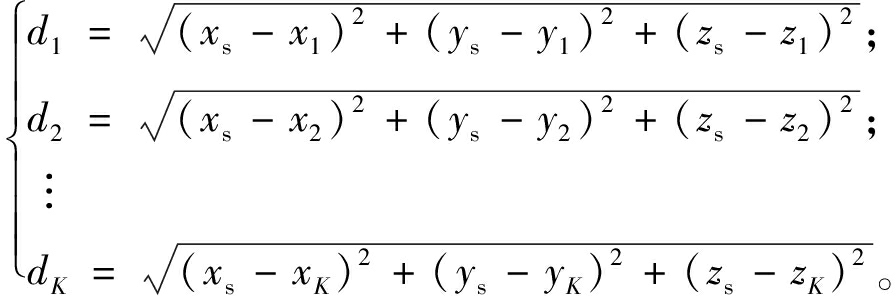
(4)
解算上述定位方程组,就可以获得目标点位置,记为![]()
2 融合差分进化和Taylor级数的定位解算方法
Taylor级数迭代算法求解超宽带定位方程组可以获得精确的定位结果,但是该算法对初始值具有较强的依赖性。选取不当的初始值,可能导致获得的目标位置偏离实际值较远,甚至不收敛的情况。基于此,研究人员提出直接法[11]、LS算法[12]用于选取Taylor级数迭代算法的初始值。但是,LS算法中逆矩阵的求解耗时,且定位精度不高。基于此,笔者引入差分进化算法这一基于群体的高效启发式全局优化算法,对目标点实现全局定位,将获得的最优定位点作为Taylor级数迭代算法初始值进行局部寻优,从而获得高精度的目标定位。
2.1 基于差分进化算法的全局定位
差分进化算法(differential Evolution,DE)由Rainer Storn和Kenneth Price于1997年提出,是一种基于种群的启发式进化优化方法[13]。DE算法结构较简单且易于实现,调控参数少,时间复杂度低。为提高DE算法的搜索能力,目前已有一些改进,如JADE[14]、SHADE[15]算法等,相比于DE算法, JADE、SHADE算法整体上具有较快的收敛速度和收敛精度,同时表现出较好的稳定性。
以目标点位置坐标(xs,ys,zs)作为差分进化个体,且个体中各个变量满足xs∈[xs min,xs max],ys∈[ys min,ys max],zs∈[zs min,zs max]。记第i个超宽带基站到目标点的测量距离为di,则超宽带定位解算模型转化为如下单目标优化问题:
f(xs,ys,zs)=
(5)
采用DE算法实现超宽带定位方程解算,具体算法流程如下。
Step1:初始化种群,设种群规模为N,初始化种群中的每个解记为xi(0),i=1,2,…,N。
Step2:评价种群中每个个体的适应值。
Step3:在第t次迭代中,对第i个个体进行变异操作,从种群中随机选择3个个体xp1(t)、xp2(t)、xp3(t),且p1≠p2≠p3≠i,记为:
(6)
式中:F∈[0,2]为加权因子。
Step4:对于![]() 将其与xi(t)进行交叉,生成的交叉后个体为:
将其与xi(t)进行交叉,生成的交叉后个体为:
(7)
式中:CR∈[0,1]是交叉概率;j=1,2,…,M;jrand为随机整数,jrand∈[1,M],M为个体的变量维数。
Step5:比较![]() 与xi(t)的适应值,满足以下条件的个体,被选择进入下一代,
与xi(t)的适应值,满足以下条件的个体,被选择进入下一代,
(8)
Step6:判断是否达到最大进化代数,若是,则终止进化,将得到最优个体作为目标点位置输出;若否,则跳转到Step2。
2.2 基于Taylor级数迭代算法的局部定位
Taylor级数迭代算法是一种递归算法。它基于定位初始值,通过反复迭代,获得目标点的最优坐标[10]。假设目标点的真实坐标为(xs,ys,zs),位置初始值为(xs0,ys0,zs0),真实目标点坐标与解算后目标点坐标满足以下关系:
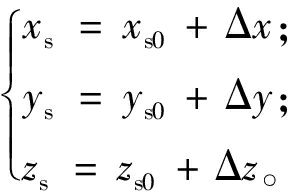
(9)
在初始坐标(xs0,ys0,zs0)处,对超宽带定位方程组进行Taylor级数展开,并忽略二阶以上分量:
Δ=(.T.)-1.T.,
(10)
式中:

.=
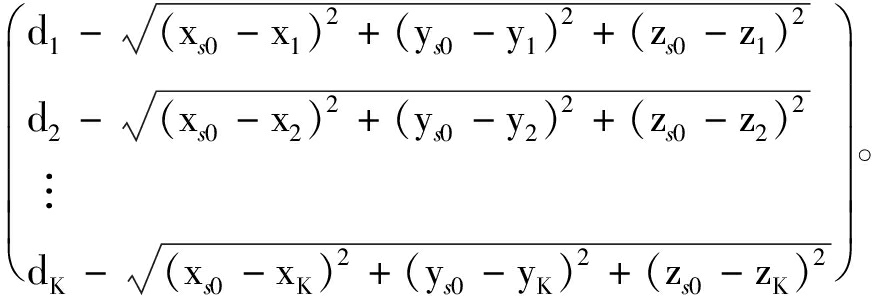
根据定位误差,修正解算后的目标点坐标,重复迭代上述过程,直到满足|Δx|+|Δy|+|Δz|≤ε或达到最大迭代代数,最终获得的目标点位置坐标为![]() 其中,ε为预先设定的误差阈值。
其中,ε为预先设定的误差阈值。
基于DE算法和Taylor级数迭代算法的室内超宽带定位解算方法的步骤如下。
Step1:目标点依次向各个基站发起一次测距,根据公式(2)和(3),计算每次测量的距离值,对每一个基站进行1 000次测距,取其平均值作为目标点与这个基站的距离,记为d1,d2,,…,dk。
Step2:根据目标点与各个基站之间的距离,列出定位方程解算模型。
Step3:以公式(5)作为适应度函数,采用DE算法求取目标点的最优位置坐标(xs0,ys0,zs0),作为Taylor级数迭代的初始值。
Step4:将(xs0,ys0,zs0)代入.和.,依据公式(10)进行迭代计算,直到满足|Δx|+|Δy|+|Δz|≤ε。
Step5:若条件成立,则把(xs0,ys0,zs0)作为最优目标点定位输出;若不成立,则计算公式(9),并返回Step4。
3 实验分析与结果说明
为充分验证所提定位解算方法的合理性和有效性,将所提方法用于煤矿掘进巷道这一复杂室内场景,对掘进支护移动支架进行超宽带定位解算。
3.1 测试环境和参数设置
假设巷道为矩形,宽4.2 m、高3.9 m、长100 m。采用4个基站进行定位,且4个基站的坐标分别为(0,0,0)、(2,4,0)、(-2,4,0)、(0,0,3.8)。每隔10 m,掘进支护支架上的目标点依次对4个基站进行超宽带测距,一般测距误差服从均值为0、标准差为2 cm的正态分布[12]。在上述定位环境下,目标点对每个基站进行1 000次测距,取其均值作为距离估计值。
DE算法中个体的搜索范围取决于巷道尺寸,即xs∈[-2.1,2.1],ys∈[10,100],zs∈[0,3.9]。选取种群规模为30,最大迭代次数为100,Taylor级数迭代算法中的误差阈值ε=0.01。
假设第k次运行后得到的解算目标点坐标为![]() 真实定位点坐标为(xs,ys,zs),L为运行次数,则定义平均定位误差为:
真实定位点坐标为(xs,ys,zs),L为运行次数,则定义平均定位误差为:
(11)
3.2 所提定位解算方法对参数敏感性分析
笔者结合已有文献分析DE算法参数对解算结果的影响。文献[16]设置加权因子F=0.5,交叉概率CR=0.9或CR=0.1;文献[17]设置加权因子F=0.5,交叉概率CR=0.5;文献[18]设置加权因子F=0.9,交叉概率CR=0.9;文献[19]设置加权因子F=1.0,交叉概率CR=0.9。面向不同测量距离,分别采用以上DE算法参数,进行500次独立运行后的定位误差均值如图3和图4所示。
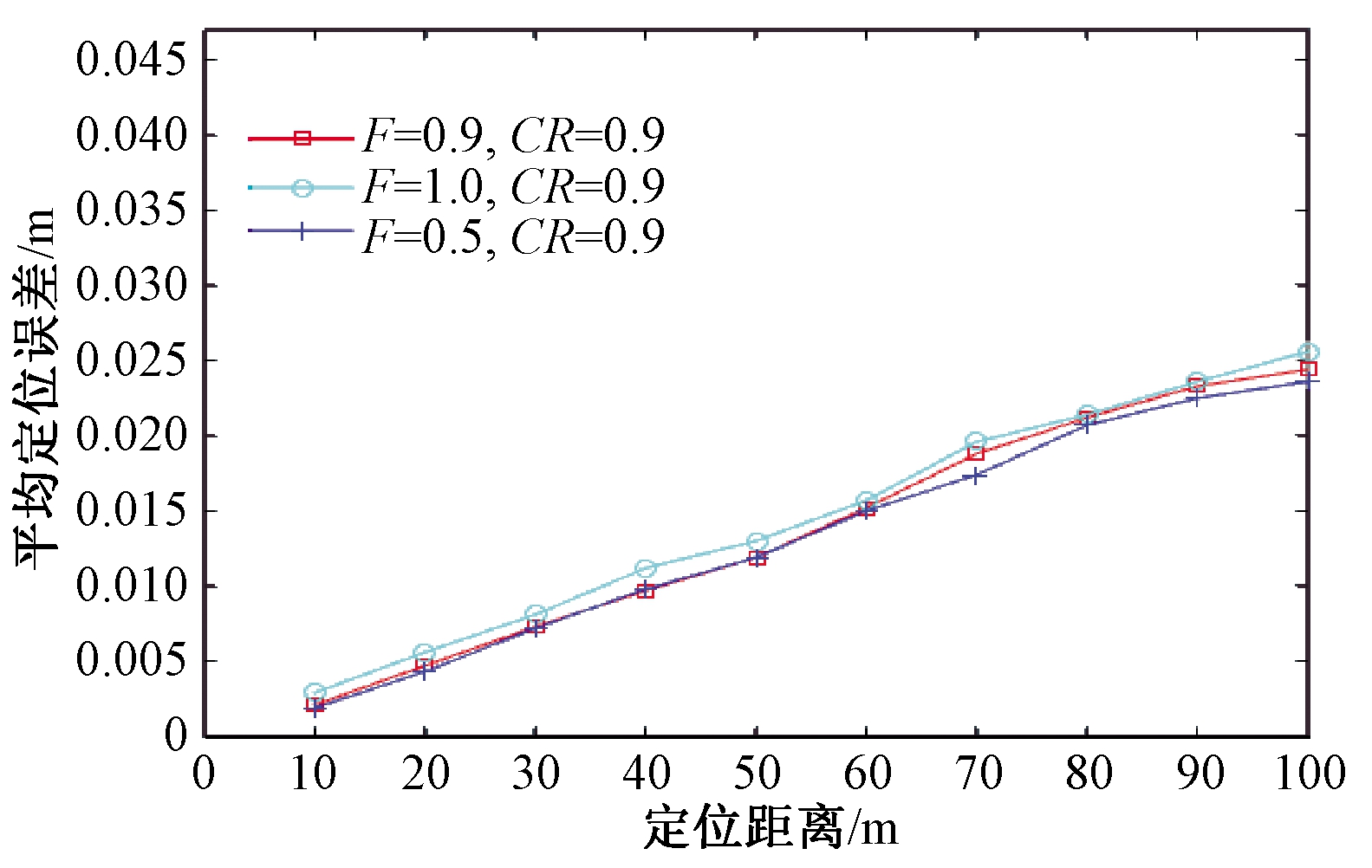
图3 不同加权因子时定位解算方法的平均定位误差
Figue 3 Average positioning error of positioning solution method with different weighting factors
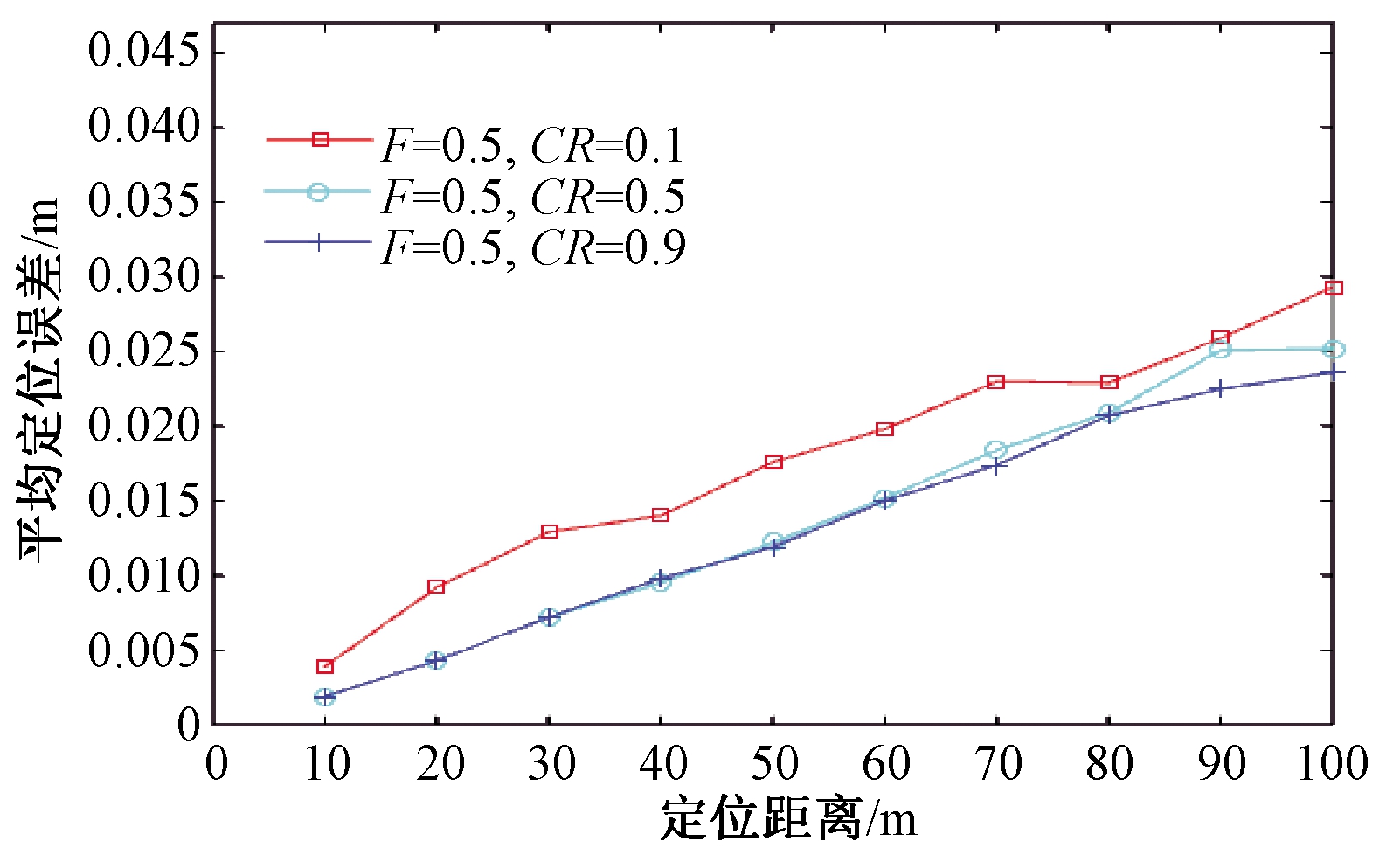
图4 不同交叉概率时定位解算方法的平均定位误差
Figue 4 Average positioning error of positioning solution method with different crossover probabilities
对比图3可知:加权因子对于定位解算方法的影响较小。其中,定位解算方法在加权因子F=0.5时,取得较好的效果,在F=1和F=0.9时的平均定位误差稍大于F=0.5时的平均定位误差,但是差别不明显。对比图4可知:交叉概率对于定位解算方法的影响较大。其中,定位解算方法在交叉概率CR=0.1时,平均定位误差明显大于CR=0.5和CR=0.9时的平均定位误差;在CR=0.9时的平均定位误差稍小于CR=0.5时的平均定位误差。在以下实验中,设置加权因子F=0.5和交叉概率CR=0.9。
3.3 不同定位解算方法性能对比分析
分别用LS算法[9]、直接法[10]、直接-Taylor算法[11]、LS-Taylor算法[12]和笔者提出的DE-Taylor算法,实现对掘进支护移动支架超宽带定位方程组的解算。面向不同测量距离,进行500次独立运行后的定位误差均值和方差如表1所示;相应的定位误差均值和boxplot图,如图5和图6所示。
表1 噪声环境下5种解算方法的平均定位误差和方差
Table 1 Average positioning error of five solution methods in noisy environment
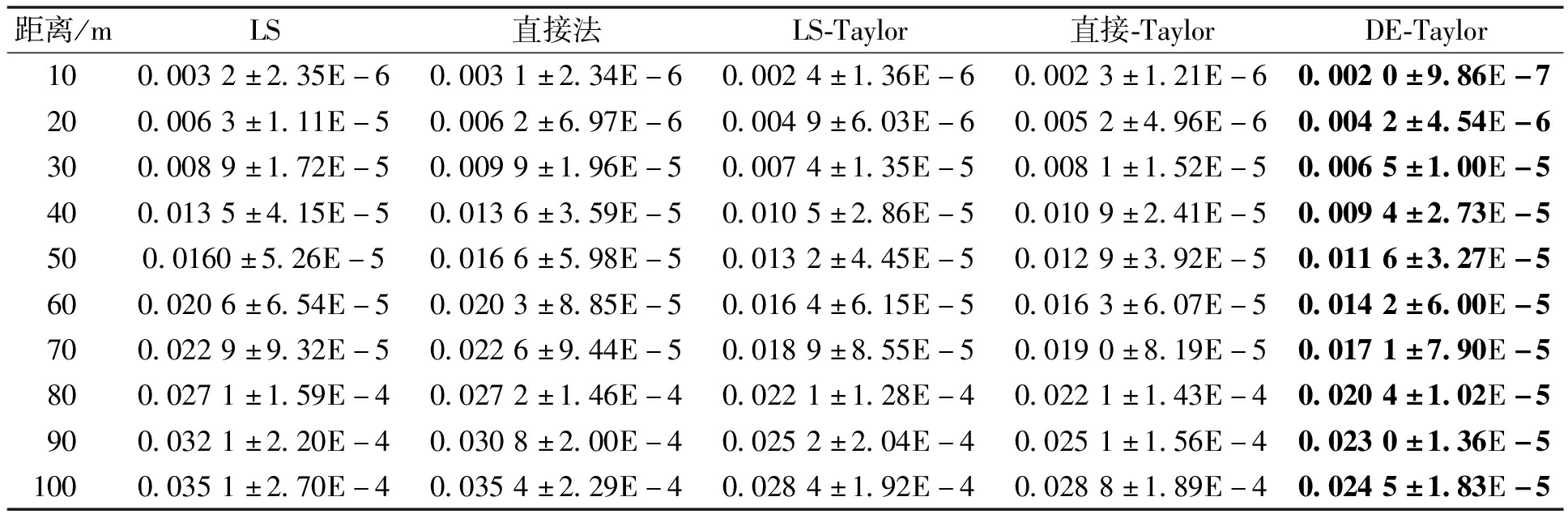
距离/mLS直接法LS-Taylor直接-TaylorDE-Taylor100.0032±2.35E-60.0031±2.34E-60.0024±1.36E-60.0023±1.21E-60.0020±9.86E-7200.0063±1.11E-50.0062±6.97E-60.0049±6.03E-60.0052±4.96E-60.0042±4.54E-6300.0089±1.72E-50.0099±1.96E-50.0074±1.35E-50.0081±1.52E-50.0065±1.00E-5400.0135±4.15E-50.0136±3.59E-50.0105±2.86E-50.0109±2.41E-50.0094±2.73E-5500.0160±5.26E-50.0166±5.98E-50.0132±4.45E-50.0129±3.92E-50.0116±3.27E-5600.0206±6.54E-50.0203±8.85E-50.0164±6.15E-50.0163±6.07E-50.0142±6.00E-5700.0229±9.32E-50.0226±9.44E-50.0189±8.55E-50.0190±8.19E-50.0171±7.90E-5800.0271±1.59E-40.0272±1.46E-40.0221±1.28E-40.0221±1.43E-40.0204±1.02E-5900.0321±2.20E-40.0308±2.00E-40.0252±2.04E-40.0251±1.56E-40.0230±1.36E-51000.0351±2.70E-40.0354±2.29E-40.0284±1.92E-40.0288±1.89E-40.0245±1.83E-5
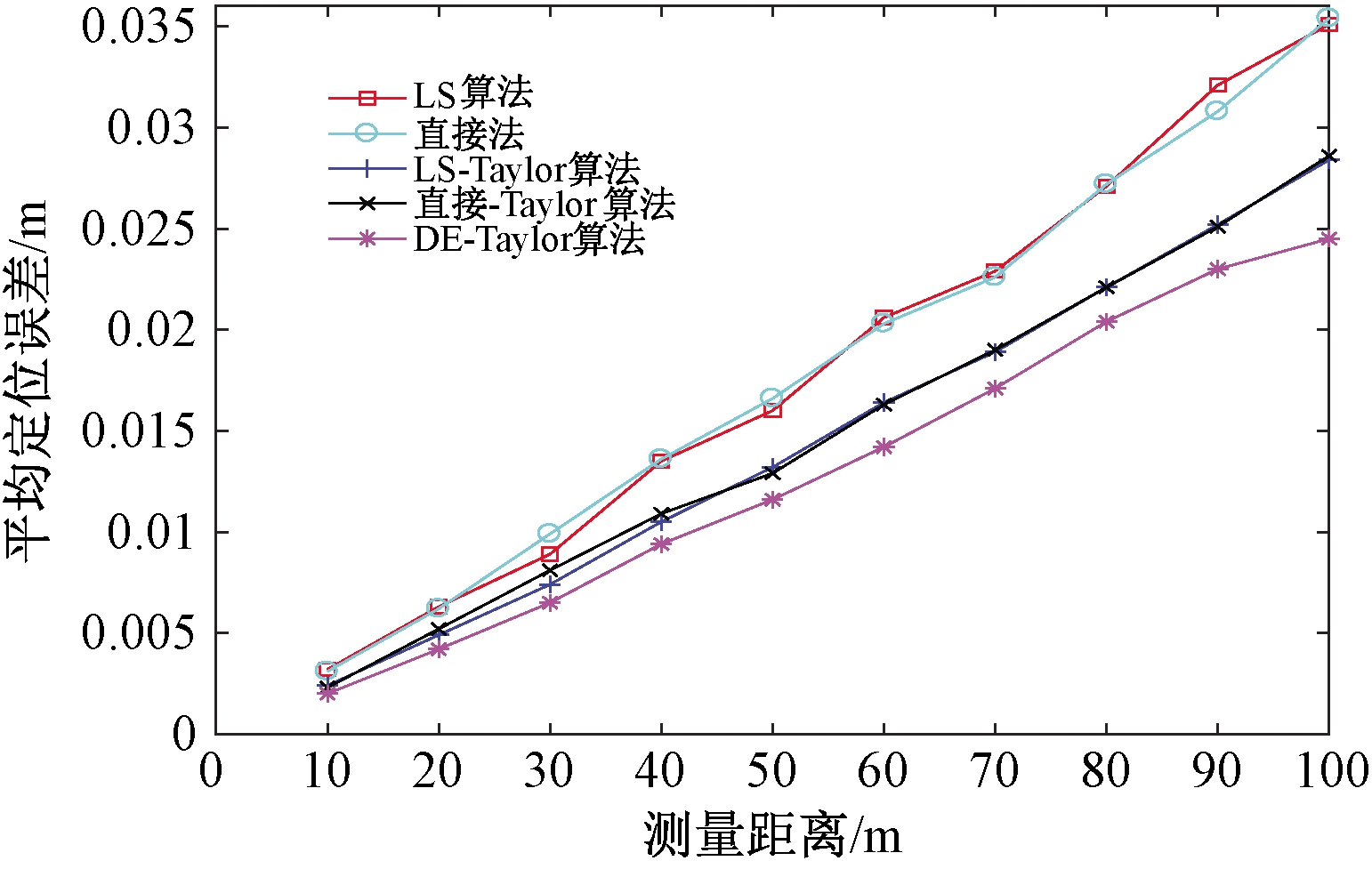
图5 5种算法的平均定位误差
Figue 5 Average positioning error of five algorithms
对比5种算法的平均定位误差,可知:随着目标点距离基站位置的增加,无论何种算法,其定位误差都逐渐变大,且呈线性增加。在相同的定位距离下,LS算法和直接法作为全局定位方法,具有相对较大的定位误差。在融合Taylor级数迭代这一局部定位算法后,上述算法的定位精度显著提高。采用DE算法作为全局定位方法后,笔者所提出的DE-Taylor定位解算方法具有最好的定位精度。
图6为5种算法的定位误差分布图,由图6可知:在相同的定位距离下,LS算法和直接法的误差分布较分散,定位误差均值比较大。融合Taylor级数迭代算法后,3种算法的定位误差分布较紧密,定位误差均值有一定程度的减小,其中DE-Taylor算法的定位误差分布最紧密且具有最小的定位误差均值。由表1可以看出:DE-Taylor算法的平均定位误差和方差都最小(表1加黑部分)。
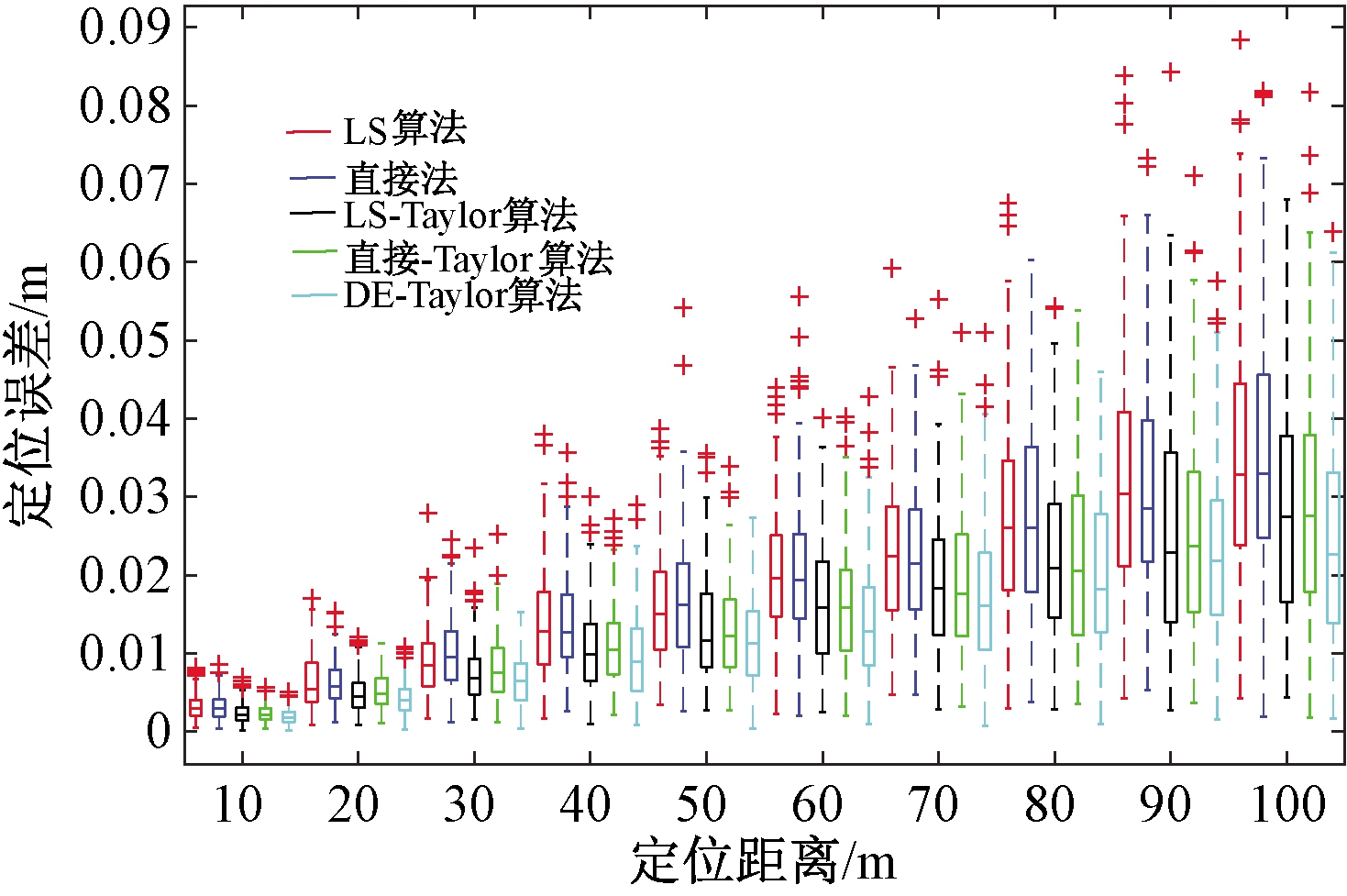
图6 5种算法定位误差分布图
Figue 6 Positioning error boxplot diagram of five algorithms
4 结论
用于室内设备或人员定位的超宽带定位方法,其传统的定位模型解算采用Taylor级数迭代算法,对初始值存在较强依赖性。基于此,笔者提出一种融合差分进化算法和Taylor级数迭代的新型超宽带定位解算方法,通过差分进化算法获得的全局最优值作为Taylor级数迭代的初始值,实现更准确的目标定位。针对煤矿掘进巷道这一复杂室内场景,采用所提方法实现掘进支护移动支架的超宽带定位解算,实验结果表明,所提方法比LS算法、直接法、LS-Taylor算法和直接-Taylor算法具有更高的定位精度和更强的鲁棒性。
[1] 张忠娟.基于UWB的室内定位技术研究[D].天津:天津大学, 2011.
[2] 林传分.基于超宽带的室内定位算法研究[D].乌鲁木齐:新疆大学, 2014.
[3] 张春香.基于RFID技术的室内定位系统的研究[D].南昌:南昌大学, 2017.
[4] 李冰.超声波室内定位导航装置的设计与实现[D].哈尔滨:哈尔滨理工大学, 2017.
[5] 王益健.蓝牙室内定位关键技术的研究与实现[D].南京:东南大学, 2015.
[6] 石雪军, 纪志成.基于射频识别的室内定位系统算法研究[J].系统仿真学报, 2015, 27(6): 1294-1300.
[7] 李晨阳.基于相位的无源超高频射频识别定位研究[D].南京:东南大学, 2017.
[8] 魏培,姜平,贺晶晶,等.基于内三角形质心算法的超宽带室内定位[J].计算机应用, 2017, 37(1): 289-293.
[9] CHEHRI A, FORTIER P, TARDIF P M.UWB-based sensor networks for localization in mining environments[J].Ad hoc networks, 2009, 7(5):987-1000.
[10] YU K G, MONTILLET J P, RABBACHIN A, et al.UWB location and tracking for wireless embedded networks[J].Signal processing, 2006, 86(9):2153-2171.
[11] 蒋文美,王玫.一种基于TOA的UWB直接-Taylor复合定位算法[J].桂林电子工业学院学报, 2006, 26(1):1-5.
[12] TALOM F T, DENIS B, KEIGNART J, et al.Uwb positioning experiment in a typical snowy environment[C]// 2007 4th Workshop on Positioning, Navigation and Communication.Hannover:IEEE, 2007:65-70.
[13] 杨洲,汪云甲,陈国良,等.超宽带室内高精度定位技术研究[J].导航定位学报, 2014,2(4):31-35.
[14] 熊海良.超宽带无线通信与定位关键技术研究[D].西安:西安电子科技大学通信工程学院, 2011.
[15] 梁久祯.无线定位系统[M].北京:电子工业出版社,2013.
[16] 符世琛,李一鸣,成龙,等.几何布局对掘进机位姿检测精度的影响分析[J].工矿自动化, 2017, 43(5):46-49.
[17] 朱晓东, 刘冲, 郭雅默.基于烟花算法与差分进化算法的模糊分类系统设计[J].郑州大学学报(工学版), 2015, 36(6):47-51.
[18] 廖雄鹰,李俊,罗阳坤,等.基于自适应变异算子的差分进化算法[J].计算机工程与应用, 2018,54(6):128-134.
[19] ZHANG J Q, SANDERSON A C.JADE: adaptive differential evolution with optional external archive[J].IEEE Transactions on evolutionary computation, 2009, 13(5): 945-958.