0 引言
随着互联网技术的进步,传统的由企业或组织内部完成的某项任务,可以借助于网络平台,转交给专业或者非专业的大众完成[1],成功实现目标者获取报酬,这种合作创新形式,称为“众包”[2].
传统的外包[3]则必须借助于专业性较强的公司或者个人利用专业装备才能完成[4],如测量河道、软件制作等.但是很多任务并不需要通过专业装备或者算法实现,而且相对来说这种任务粒度更为细小,比如给图像打标签、语言翻译[5]、市场调查[6-7]、reCAPTCHA[8]等,这些就可以借助众包来完成.而随着智能设备以及信息技术的发展,基于现实的地理位置的空间众包[9]应用场景也越来越广泛,如某个地方拍摄照片或者从附近取某样东西送到某地等.而随着互联网经济的深入发展,空间众包也面临着越来越广阔的应用前景,同时空间众包也是个年轻的行业,随着进一步发展,空间众包也将开始进行变革,笔者以组织绩效为主要关注点,包括效率(最快)、效能(质量)、费用(任务定价).过往研究表明[10],低技能劳动的任务定价与行业的高速增长对于组织绩效造成了较大影响,笔者希望通过某劳务众包平台的实际数据研究绩效提升模型,对低技能劳动这种空间众包模型的组织绩效提供策略性建设.
Liu等[11]通过使用Taskcn进行随机现场实验,研究结果表明高的任务价格更能刺激接包方参与和提交高质量的结果.Singer等[12]通过对亚马逊的Mechanical Turk(亚马逊2005年建立的众包市场,又称土耳其机器人)市场的研究,提出了恒定竞争激励相容的机制,以最大限度地增加预算下的任务数量,并将给定的任务数量最小化.Mao等[13]通过调研TopCoder最大的软件开发众包平台,分析了5 910个软件开发任务,引入16个成本驱动因素并使用4种流行的绩效指标评估12种预测定价模型来解决任务定价问题.
现有的相关文献大多数集中在对众包任务定价策略以及参与动机对绩效影响的定性研究,笔者以某劳务众包平台(拍摄某地照片)空间众包的实际数据,研究绩效提升模型.笔者在分析原有定价规律的基础上,建立基于多目标规划的任务定价模型,通过TOPSIS等级评价法对不同定价方案进行综合选择.
1 空间众包任务及定价影响因素
众包任务通常可以按照其复杂度、难度和粒度进行相应的划分[14],笔者所采用的实例为目前应用最广的微观任务即Human Intelligence Task(HIT),同时对于任务搜索采用由工人主动查找相关任务的方法,研究相应定价方法.
1.1 影响因素定义
(1)任务密度.为形象地表示某任务点O四周其他任务点以及会员的基本信息,定义此任务点为等效任务代表点.以等效任务代表点所在位置为圆心,半径为r的圆形区域为该任务点的代表范围,如图1所示.
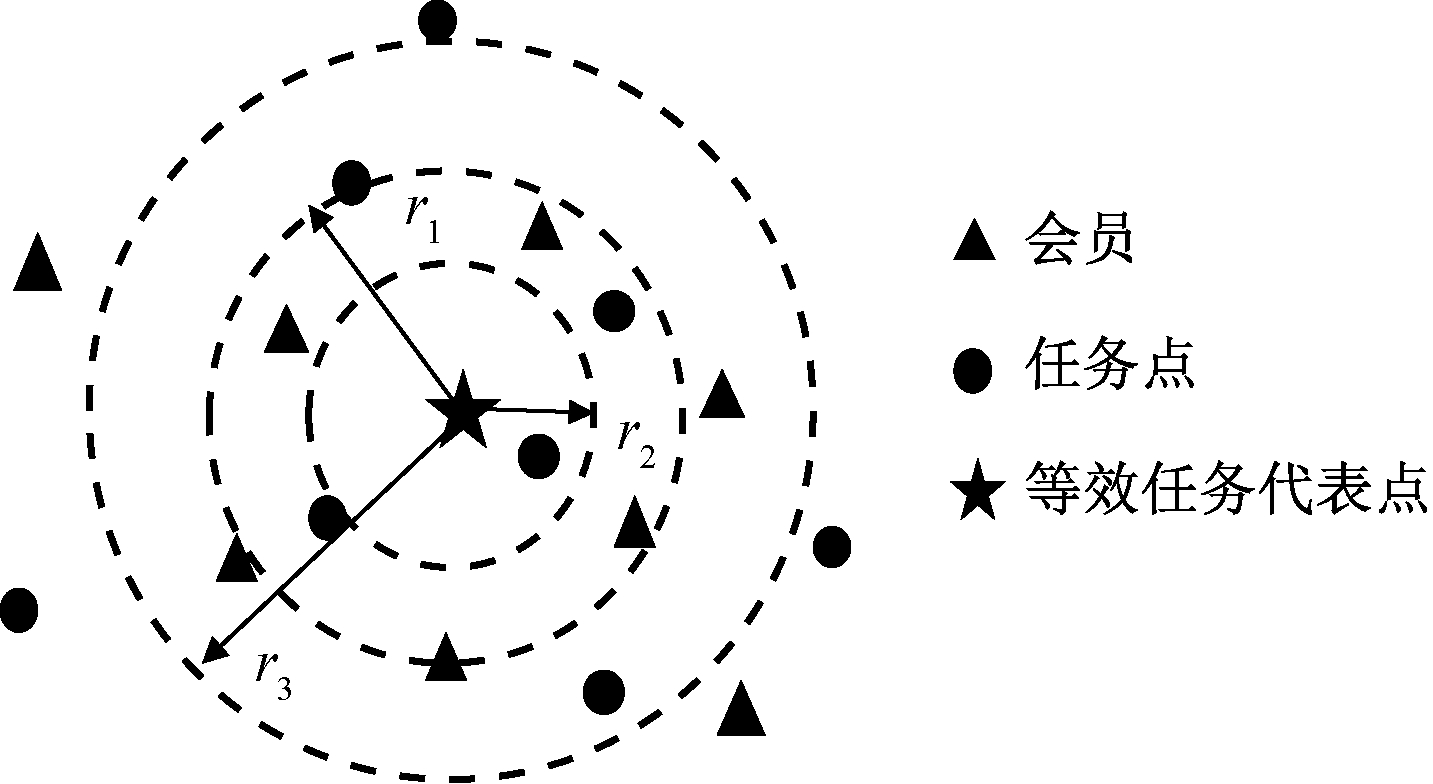
图1 等效任务代表点示意图
Fig.1 Equivalent representative point of task
设W为全体等效任务代表点的集合:
W={w1,w2,…,wi,…,wN},
式中:wi为所研究的第i个等效任务代表点,N为全体任务的总数,对某一研究点wi而言,wij为该任务点的响应范围中第j个任务.此时集合wi即为该圆形区域中的所包含的其他任务的基本信息:
wi={wi1,wi2,…,wiB},
式中:B为圆形区域中所包含的其他任务的总的个数,也即任务密度.不同的代表范围会有不同的任务密度,如图1所示,r1、r2、r3 对应了不同的代表半径和任务密度.
(2)会员密度.定义hij为第i个等效任务代表点的圆形区域中的第j个会员.此时集合hi即为圆形区域中所包含的会员的基本信息:
hi={hi1,hi2,…,hiK},
式中:K为该包围圈中的总的会员人数,也即为该任务的会员密度.
(3)会员平均信誉度.设第i个等效任务代表点的代表范围中第j个会员的信誉度为aij,则集合ai可反映圆形区域中会员的信誉度的基本情况:
ai={ai1,ai2,…,aiK},
为刻画该区域中会员信誉度的整体情况,定义会员平均信誉度![]() 来反映该代表范围中的会员接单后完成任务的可信程度:
来反映该代表范围中的会员接单后完成任务的可信程度:
(4)最邻近可达距离.定义任意等效任务代表点wi到其最近的会员之间的距离为最邻近可达距离asi:
asi=min{di1,di2,…,dij,…,diU},
式中:dij为第i个任务与第j个会员间的距离;U为总的会员数,本文中U=1 874.
1.2 任务定价与各因素的关系
首先,选取代表半径r=10 km,其次选取任务密度、会员密度、会员平均信誉度、最邻近可达距离4个因素,根据任务完成情况以及会员信息数据,从4个角度分别探讨任务定价与其的关系.
(1)定价与任务密度的关系.首先计算某任务点O代表范围内的任务密度,其次将相同任务密度的任务点的定价取平均值,绘制任务密度wi与任务平均定价pi的散点图,见图2.
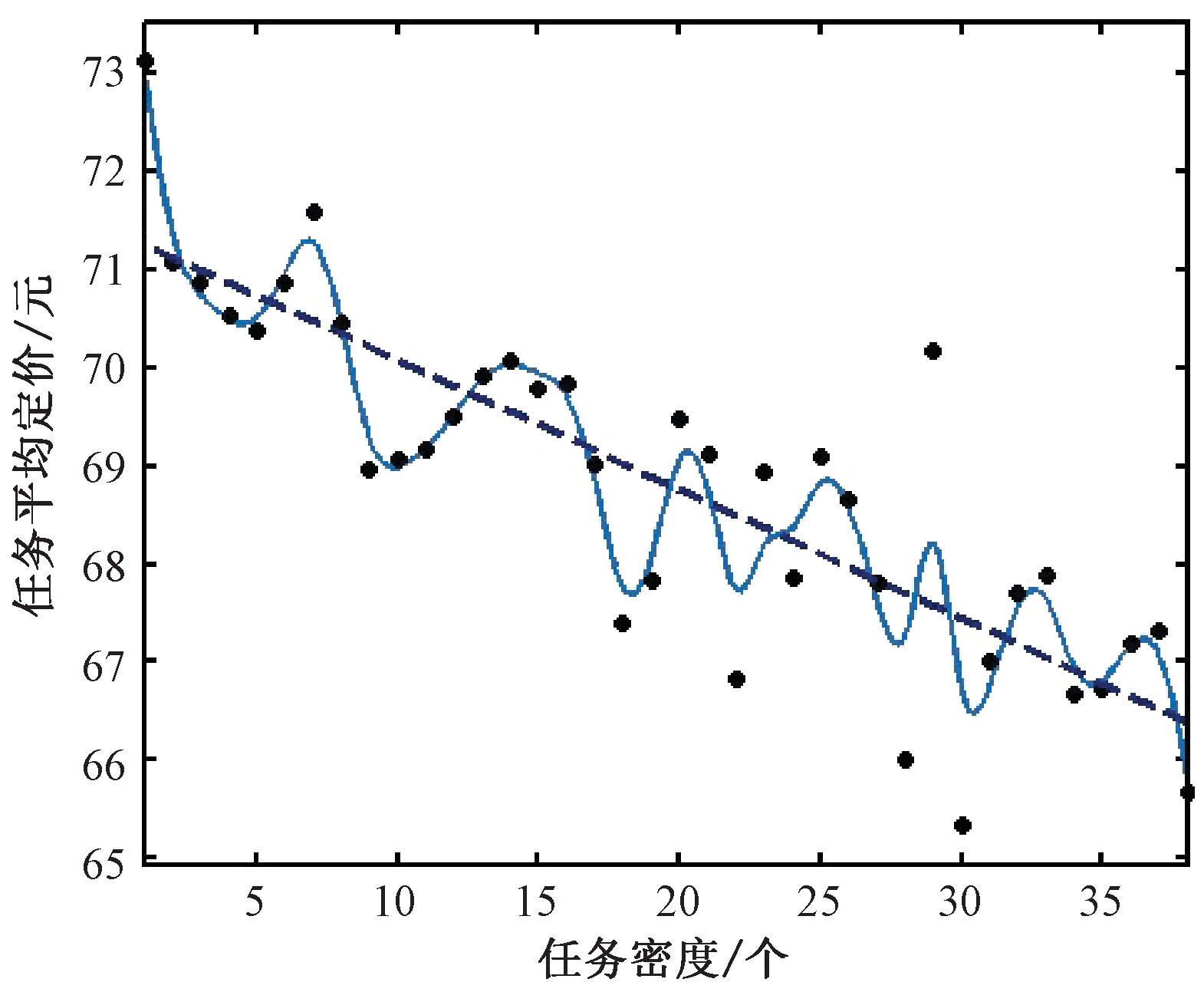
图2 任务定价与任务密度的关系
Fig.2 Relationship between task pricing and task density
从图2可以看出任务平均定价随着任务密度的增加整体呈现下降趋势,且在下降的过程中存在着波动.对其进行最小二乘线性拟合,先假设两者关系如下:
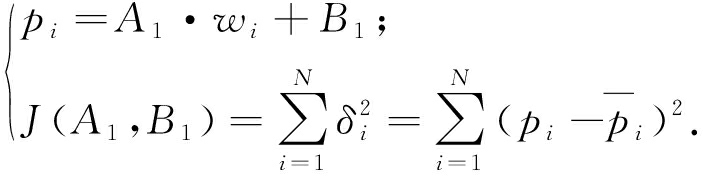
(1)
为求系数A1、B1 使得J达到最小[10],只需利用极值的必要条件∂J/∂A1=0以及∂J/∂B1=0,得到关于A1、B1的线性方程组:
![]()
![]()
Q=[A1,B1]T;
P=[p1,p2,…,pN],
则方程(1)可以表示为:
RTRQ=RTP.
(2)
因为{w1,w2,…,wN}线性无关,R列满秩,RTR可逆,于是方程(2)具有唯一解:
Q=(RTR)-1RTP
最终解得:A1=0.131 8,B1=71.39,其拟合优度为 69%,可以认为任务定价与任务密度之间的线性关系比较明显,得到wi与pi之间的线性关系为:
pi=-0.131 8wi+71.39.
这说明对于任一任务点O来说,其周围的任务数越多,会员可花费越少的时间和精力成本来赚取酬金,以数量来吸引会员完成任务,因此任务定价较低.而处在比较偏远位置的任务,其周围的任务量较少且距离较远,为避免这些任务无人问津,众包平台会通过提高任务定价来吸引客户,因此这种线性关系是符合实际的.
(2)定价与会员密度的关系.同样,首先计算某任务点O代表范围内的会员密度,其次将相同会员密度的任务点的定价取平均值,绘制会员密度hi与任务平均定价pi的散点图,见图3.
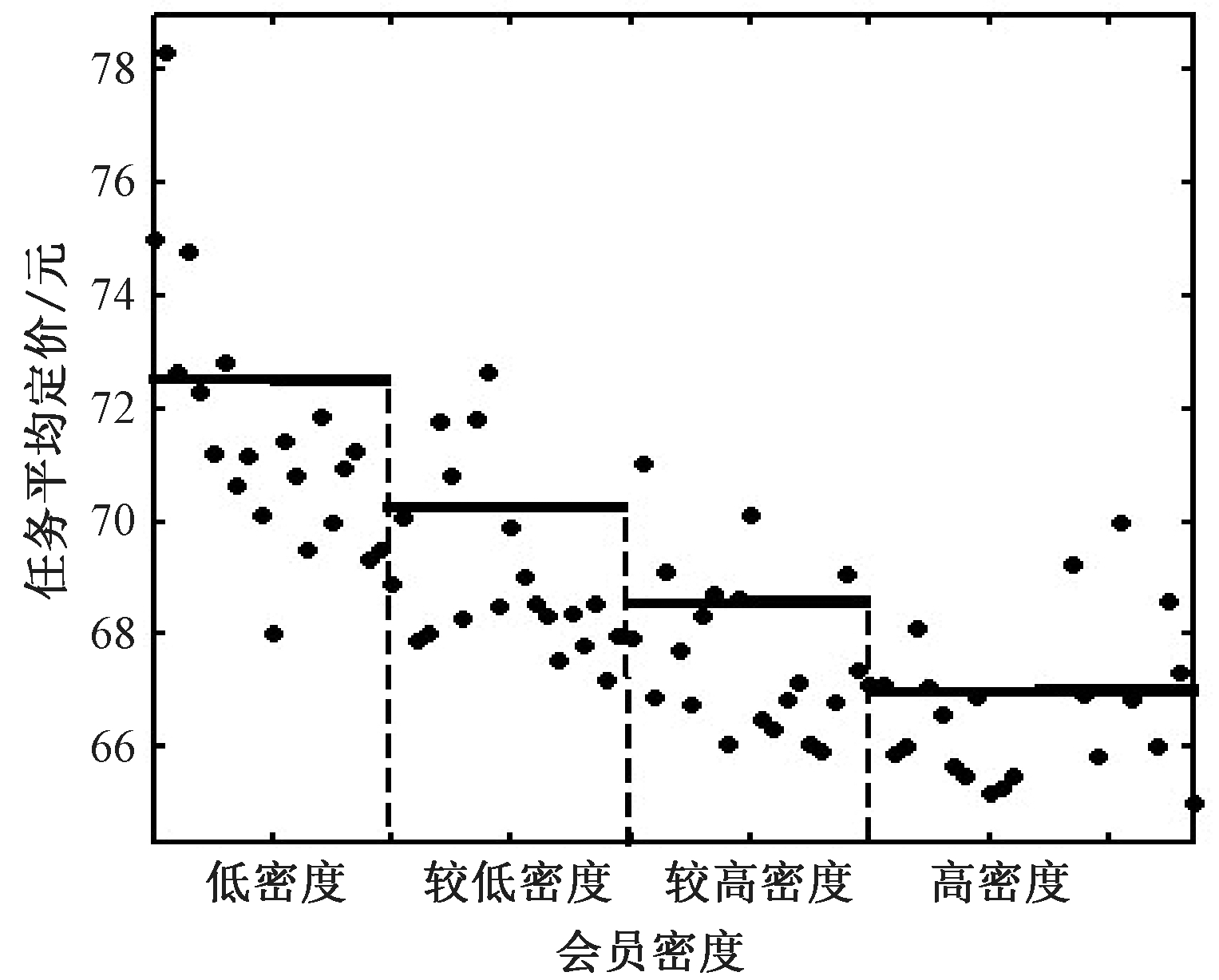
图3 任务定价与会员密度的关系
Fig.3 Relationship between task pricing and membership density
从图3中可以看出任务平均定价与会员密度并非完全线性,因此对其进行指数拟合:
pi=A2·exp(-B2hi).
最终得到:A2=71.9,B2=0.001,即会员密度hi与pi之间的关系服从指数分布:
pi=71.9exp(-0.001hi).
这表明任务定价随着会员密度的增加,先快速下降后趋势平缓.当会员密度越低时,平台就越需要以高价发布任务,以补偿低密度地区会员完成任务的时间与精力成本.当会员密度非常大时,任务定价将稳定在一个较低水平.
(3)定价与会员平均信誉度的关系.对会员平均信誉度与任务定价的关系进行分析,将会员平均信誉度分段求得任务平均定价,绘制两者关系的柱状图,如图4所示.
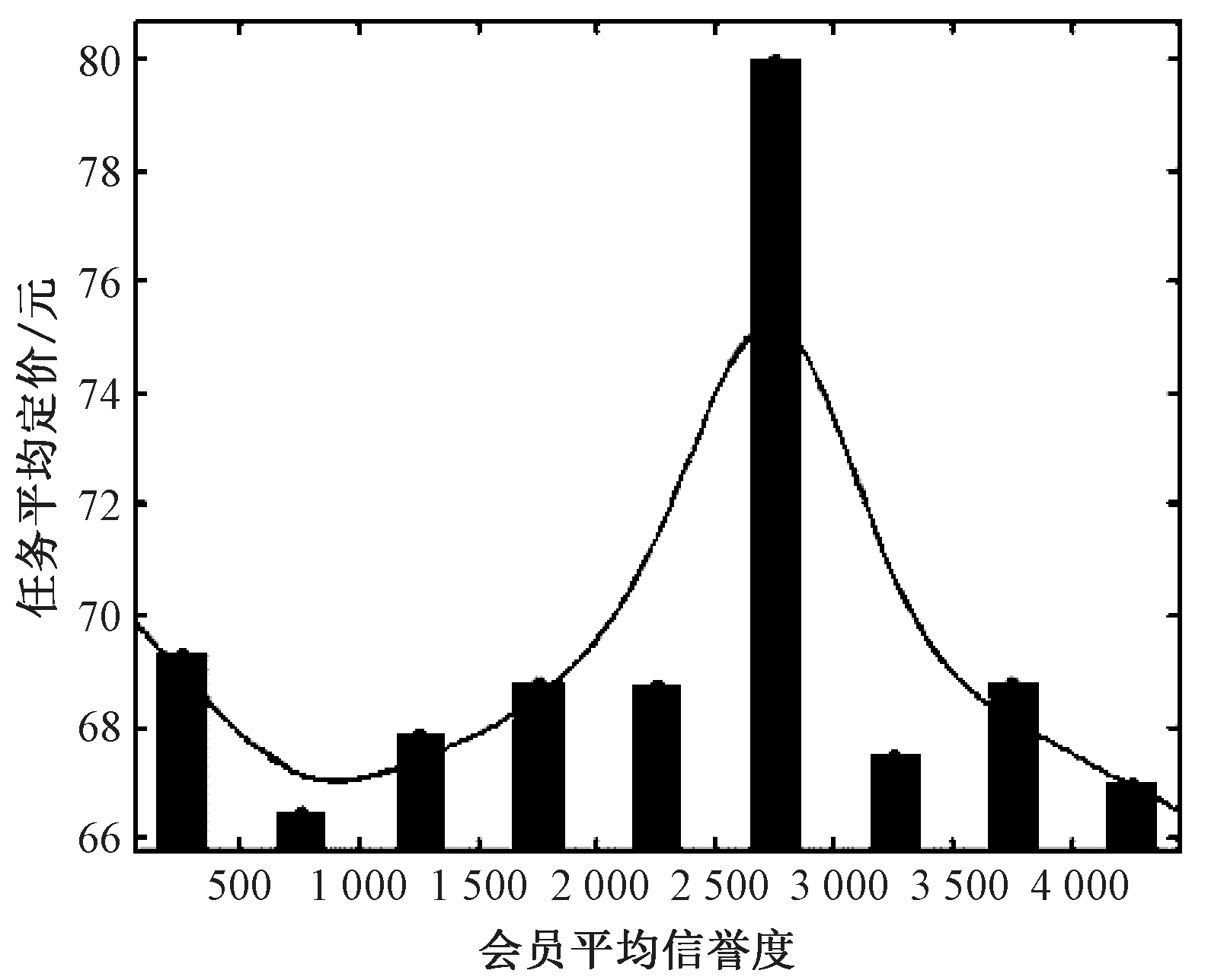
图4 任务定价与会员平均信誉度的关系
Fig.4 Relationship between task pricing and average member credit
该图表明:在会员平均信誉度低的时候,任务平均定价随着会员平均信誉度增加而震荡明显;而后随着会员平均信誉度的增加,任务平均定价会先上升,在2 500~3 000 的区间内达到峰值,之后任务平均定价会随着会员平均信誉度的上升而下降.
(4)定价与最邻近可达距离的关系.对最邻近可达距离与任务定价的关系进行分析,将最邻近可达距离分段求得任务平均定价,绘制两者关系的柱状图,如图5所示.
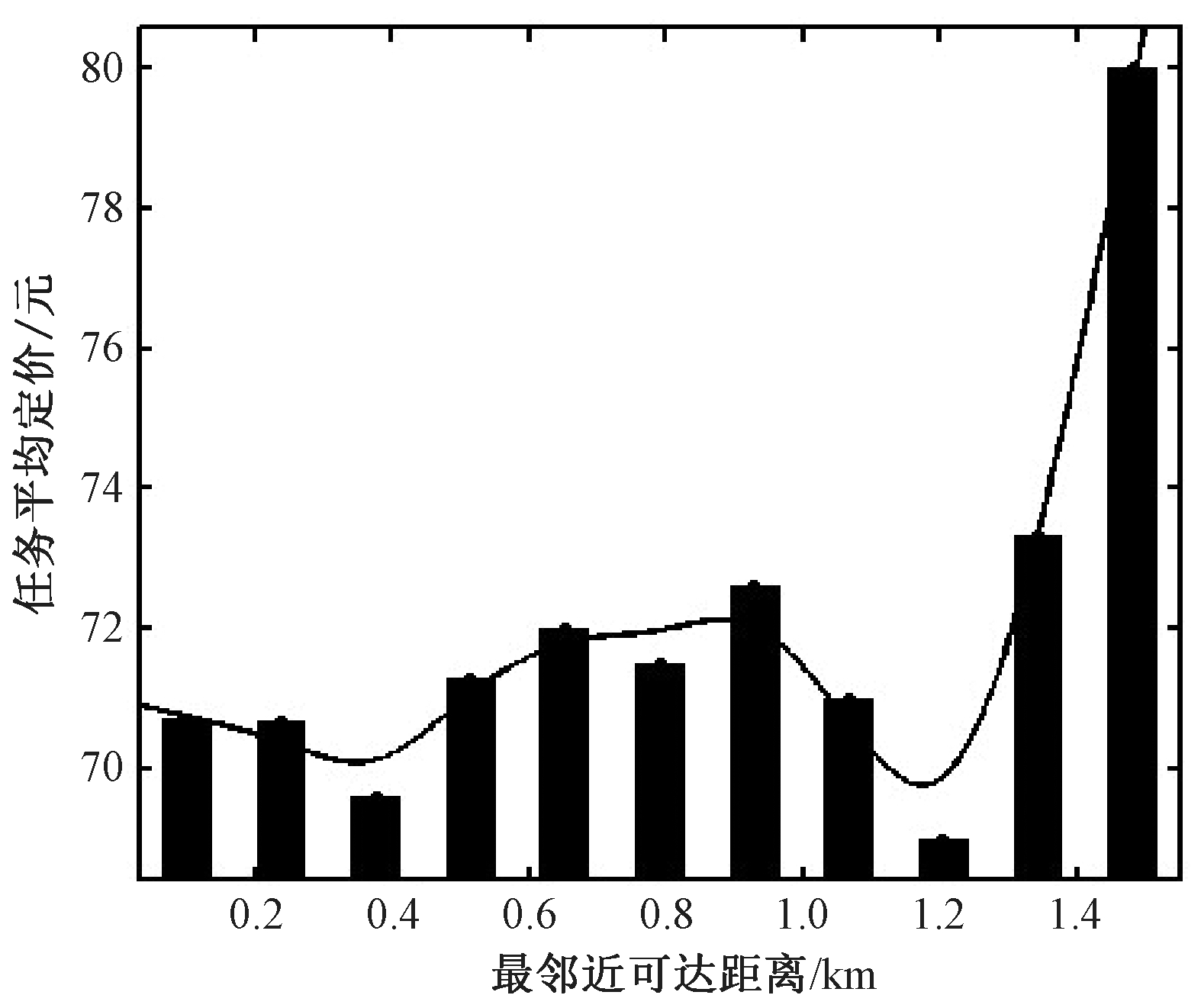
图5 任务定价与最邻近可达距离的关系
Fig.5 Relationship between task pricing and nearest neighbor reach distance
图5表明在最邻近可达距离较小时,任务定价与最邻近可达距离并无明显关系,而当最邻近可达距离达到 1.2 km 时,任务定价随邻近可达距离的上升而快速攀升.从实际意义考虑,当一个任务的最邻近的会员较远时,该任务完成的困难度较高,成本也较高,因此平台会开出相对高价来促使该任务完成.
2 任务定价数学描述及模型建立
发包方发布相应的任务价格后,一旦任务预定开始时间开启,众包平台的接包方(即会员)开启抢单模式进行抢单.每一轮抢单完成后该平台对被预定的任务进行分配,然后各个领取到任务的会员便可以执行相应任务获取酬金,该流程如图6所示.
图6 任务实现流程
Fig.6 Task implementation process
2.1 多目标的任务定价模型
对于发包方来说,设pij为分配给会员j的任务i的定价,则发包方的总成本为∑j∑ipij.设n为所有会员完成的任务的总数,则单位任务的成本![]() 为:
为:
(3)
对于众包平台,任务的完成率越高,平台就更具竞争优势,因而取平台任务的完成率C作为一个评价指标:
(4)
式中:N为总的任务数.
对于接包方(会员)来说,个人平均效益∑j∑ipij/∑j达到最大,而单位信誉值![]() 所能够转化的酬金更多,会员满意度越高.
所能够转化的酬金更多,会员满意度越高.
综合上述3个角度,可以得到式(5)所示任务定价的目标函数,寻取最优定价,使得发包方单位任务成本最小,平台发布的任务完成率最高,接包方个人平均效益最大,且信誉效益转化率最高.
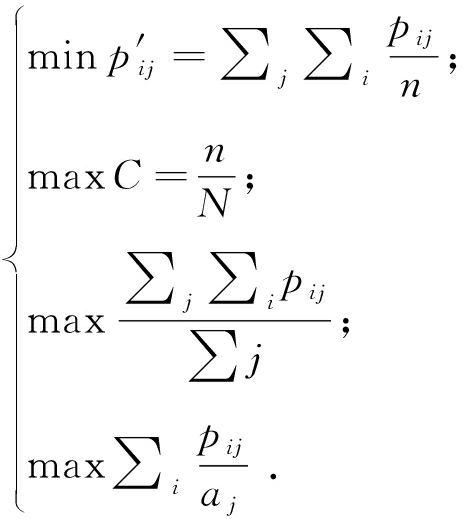
(5)
由于任务密度wi、会员密度hi、会员平均信誉度![]() 均为制约型因素,即其值越小,任务所需定价越高;而最邻近可达距离asi为效益型因素,即其值越小,任务所需定价越低.取最邻近可达距离的倒数usi 作为任务定价的一个影响因子,usi=1/asi,称其为距离指数.
均为制约型因素,即其值越小,任务所需定价越高;而最邻近可达距离asi为效益型因素,即其值越小,任务所需定价越低.取最邻近可达距离的倒数usi 作为任务定价的一个影响因子,usi=1/asi,称其为距离指数.
考虑不确定因素对任务酬金产生影响,引入随机扰动项ε作为任务初始定价的扰动因子.假设ε是服从标准正态分布的.
在原有任务定价的基础上设计新的任务定价模型:
(6)
其中,假定4个影响因子对任务的初始定价的影响的重要性是相同的,因此取相同的权重![]() 为随机扰动项的系数,其值应与任务原始定价有关,此处选择原始定价的标准差作为σ的数值,计算可得σ=4.5.
为随机扰动项的系数,其值应与任务原始定价有关,此处选择原始定价的标准差作为σ的数值,计算可得σ=4.5.
2.2 会员动态抢单模型
任务预定开始时间从06:30开始,至08:00结束,每隔3 min开启一轮新的任务预定.对于会员来说,任务预定存在空间约束问题,假设该会员在以他所在位置为中心,r′为半径的圆域内活动,即
dij≤r′.
(7)
当任务距离较远时,该会员不会预定该任务.此外,即使某任务在可达范围内,倘若该任务的酬金很低,又处在可达范围的边缘地带时,会员预定此任务的可能性会较低,需要定义路径效益因子γij:
(8)
式中:γ0为路径效益临界值,只有在任务i对会员 j的路径效益大于等于γ0时,该会员才会开始抢单模式,预定此任务.
当预定任务开始时间满足时,结合式(7)、式(8)建立动态抢单模型:

(9)
式中:vji表示会员j选择的第i个任务;vj max表示会员j的预定任务限额,该会员可事先预定的任务数必须在该限额之内.pi为第i个任务的定价,在vj max满足的情况下,会员会优先挑使自己利益最大化的任务.
2.3 任务分配模型
任务分配根据预定限额所占比例进行配发,即每一轮任务分配时,对被预定的任务而言,在预定该任务的会员当中,优先选择已抢得的单数vjm与任务预定限额vjmax之比较小的会员,建立任务分配模型:
min vjm/vjmax.
(10)
定义会员的任务饱和度uj=vjm/vjmax,倘若分配某任务时,出现多个会员任务饱和度相同的情况,优先选择信誉度aj最大的会员.
2.4 任务完成概率预测模型
设某一被预定的任务的完成概率为φij,其值与会员信誉值aij以及路径效益因子γij有关.
对于aij,根据会员信誉值的基本数据对其进行分级:
表1 会员信誉度分级表
Tab.1 Rate of member credit

指标等级一级二级三级…六级信誉度[0,1](1,5](5,20]…>500指数[0,20](20,40](40,60]…100
即建立会员信誉指数λij与会员信誉度aij之间的关系为:
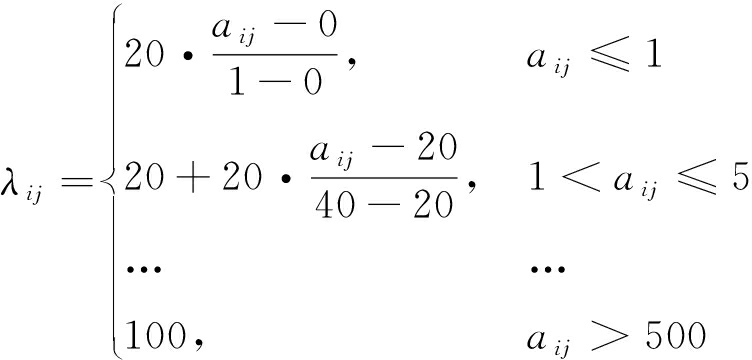
(11)
由式(5)可知,会员信誉度越高,会员信誉指数越大,会员信誉效益转化率越高,但会员是否选择完成该任务还与路径效益因子γij的大小有关.
对于γij,单位路程获得的酬金越多,对会员激励作用越大,完成此任务的积极性也越高.
根据λij和γij建立任务完成概率模型:
(12)
式中:F和(1-F)分别为λij和γij的权重;γimax和γimin分别表示第i个代表范围内被分配任务中路径效益因子的最大值和最小值.
结合管理学中“经济人”与“自我实现人”的人性假设,假定会员信誉和路径效益因子对会员完成任务概率的影响效果一样,取权重F=1/2.当大于 50%时,认为分配到该任务的会员会完成此任务.
3 模型求解与分析
3.1 最优任务定价方案求解
首先由于任务各个影响因子的具体数值相差较大,需要将它们进行规范化,设多属性决策问题的决策矩阵B=(bij)m×n,求得的规范化决策矩阵C=(cij)m×n为:
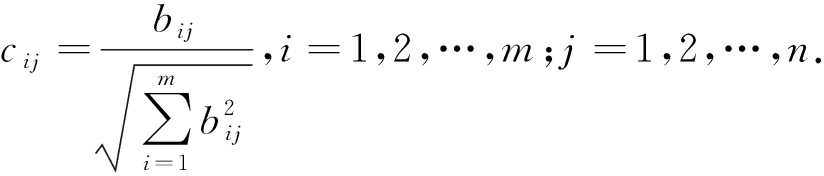
其次,选取100个代表点,部分任务代表点的数据经规范化处理后如表2所示.
表2 数据经规范化后的属性值
Tab.2 Normalized attribute value of data
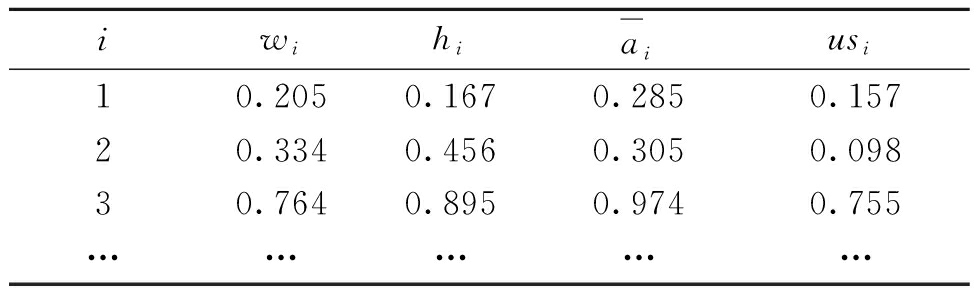
iwihiaiusi10.2050.1670.2850.15720.3340.4560.3050.09830.7640.8950.9740.755……………
由表2和公式(6)、(9)、(10)、(11),运用 TOPSIS 法解得正理想解E*=[0.564,0.627,0.608,0.755],负理想解E0=[0.105,0.098,0.285,0.043].
再者,计算各方案到正负理想解的距离.到正理想解的欧氏距离![]()
到负理想解的欧氏距离![]() 为:
为:
其中,eij为任务定价方案里各属性值,进而计算任务定价方案的综合评价指数:
最后,对任务定价方案进行排序,φi的值越大,任务定价方案的整体效果越好,选择其中最优的任务定价方案,部分如表3所示.
表3 最优任务定价方案
Tab.3 Optimal task pricing scheme
任务编号A0001A0002A0003A0004…A0835任务定价/元82.076.575.384.5…80.7
3.2 优化前后各目标值对比分析
将优化前后各目标值进行对比,如表4所示.在原有定价方案下,任务的完成率约为 62.5%,新设计的定价方案中单位任务定价相较于原方案提升了8.7%,而任务完成率大幅提升至84.3%,平台获取了竞争优势,众包绩效显著提升.
表4 优化前后目标值对比
Tab.4 Target value comparison before and after optimization
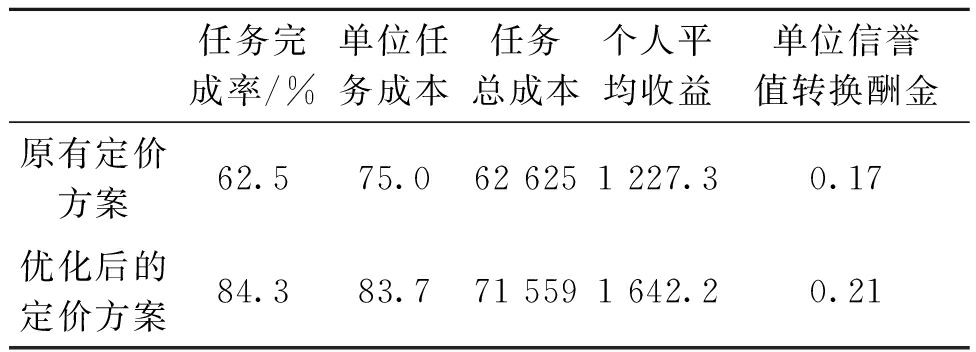
任务完成率/%单位任务成本任务总成本个人平均收益单位信誉值转换酬金原有定价方案62.575.062 6251 227.30.17优化后的定价方案84.383.771 5591 642.20.21
4 结论
笔者针对空间众包绩效问题,基于某自助式劳务众包平台的会员与任务的实际数据,从任务定价这一研究方向出发,首先研究了任务密度、会员密度、会员平均信誉度、最邻近可达距离4个影响因子与平台任务定价的关系,在此基础上建立了基于多目标规划的任务定价模型,并结合实际数据,运用TOPSIS法对新的任务定价方案进行评价排序,得到最优定价方案,根据结果证明该任务定价方案能显著提升众包绩效,对提升众包绩效的研究具有一定借鉴意义.
[1] BRABHAM D C. Crowdsourcing as a model for problem solving: an introduction and cases[J]. Convergence, 2008, 14(1): 75-90.
[2] HOWE J. The rise of crowdsourcing[J]. Wired magazine, 2006, 14(6): 1-5.
[3] 张利斌, 钟复平, 涂慧. 众包问题研究综述[J]. 科技进步与对策, 2012, 29(6): 154-160.
[4] ZHAO Y X, ZHU Q H. Evaluation on crowdsourcing research: current status and future direction [J]. Information systems frontiers, 2014, 16(3): 417-434.
[5] ZAIDAN O F, CALLISON-BURCH C. Crowdsourcing translation: professional quality from non-professionals[C]// Proceedings of the 49th Annual Meeting of the Association for Computational Linguistics: Human Language Technologies.Portland,Oregon:Association for Computational Linguistics,2011: 1220-1229.
[6] BEHREND T S, SHAREK D J, MEADE A W, et al. The viability of crowdsourcing for survey research[J]. Behavior research methods, 2011, 43(3): 800-813.
[7] GADIRAJU U, KAWASE R, DIETZE S, et al. Understanding malicious behavior in crowdsourcing platforms: the case of online surveys[C]//Proceedings of the 33rd Annual ACM Conference on Human Factors in Computing Systems. Seoul:ACM,2015: 1631-1640.
[8] VON AHN L, MAURER B, MCMILLEN C, et al. recaptcha: Human-based character recognition via web security measures[J]. Science, 2008, 321: 1465-1468.
[9] ALT F, SHIRAZI A S, SCHMIDT A, et al. Location-based crowdsourcing: extending crowdsourcing to the real world[C]// Proceedings of the 6th Nordic Conference on Human-Computer Interaction: Extending Boundaries. 2010: 13-22.
[10] 刘善仕, 周巧笑, 晁罡. 高绩效工作系统与组织绩效: 中国连锁行业的实证研究[J]. 中国管理科学,2005,13(1):141-148.
[11] LIU T X, YANG J, ADAMIC L A, et al. Crowdsourcing with all-pay auctions: a field experiment on taskcn[J]. Management science, 2014, 60(8): 2020-2037.
[12] SINGER Y, MITTAL M. Pricing mechanisms for crowdsourcing markets[C]//Proceedings of the 22nd International Conference on World Wide Web.Rio de Janeiro,Brazil:ACM,2013: 1157-1166.
[13] MAO K, YANG Y, LI M S, et al. Pricing crowdsourcing-based software development tasks[C]// 35th International Conference on Software Engineering. San Francisco:IEEE,2013: 1205-1208.
[14] 冯剑红, 李国良, 冯建华. 众包技术研究综述[J]. 计算机学报, 2015, 38(9): 1713-1726.