0 引言
近年来全断面岩石掘进机TBM在深埋长大隧道及超千米深部巷道掘进施工中,得到越来越广泛的应用。双护盾TBM在深部挤压性地层施工时极易因围岩挤压大变形而出现卡机事故[1-2]。Ramoni和Anagnostou[3]对挤压地层中3种类型TBM掘进性能的控制性影响因素进行了探讨,并提出了相应的对策。两位学者在2011年研究了均质挤压地层中护盾、围岩、支护之间的相互作用[4]。Zhao等[5]在考虑护盾与围岩不均匀间隙的基础上建立了三维数值模型,研究了TBM、衬砌与围岩之间的相互作用。刘泉声等[1]采用FLAC3D 研究了挤压性地层卡机机理,并提出TBM卡机判据。温森等[6]在考虑围岩流变效应的基础上,建立了停机和连续掘进两种工况下的卡机状态判断模型,并初步研究了卡机控制措施。Hasanpour等[7-8]运用FLAC3D对双护盾TBM与围岩的相互作用机理进行了研究,详细探讨了施工速度、扩挖间隙等对卡机控制的影响。程建龙等[9] 运用FLAC3D研究了扩挖量、护盾锥度、护盾长度、侧压系数等对双护盾TBM与围岩相互作用的影响。黄兴等[10]针对引大济湟工程 TBM 掘进围岩挤压大变形和卡机事故进行计算分析。
以上研究成果主要集中在双护盾TBM卡机机理及扩挖量、护盾长度等因素对卡机控制的影响等方面。研究表明[11-13],侧压系数(水平应力与自重应力的比值)是影响围岩变形、应力分布等重要因素;同时,衬砌与围岩之间的回填层参数对隧道整体稳定性的影响也不容忽略。目前开展侧压系数与回填层材料参数对双护盾TBM卡机控制影响的研究仍较少。基于此,笔者采用3DEC探讨侧压系数与回填层材料参数对双护盾TBM卡机控制的影响。
1 模型的建立及卡机状态判断
1.1 参数的选取
选取里昂-都灵隧道作为研究背景。该隧道埋深600 m,自重应力15.9 MPa,岩体弹性模量、泊松比、黏聚力、内摩擦角、剪胀角分别为942 MPa、0.25、0.61 MPa、28°、8°[14]。
1.2 模型建立与模拟步骤
根据完整模型的轴对称特点,计算模型选取完整模型的一半,尺寸为75 m×100 m×150 m,如图1所示。根据Hasanpour等[7]的研究结果,为避免模型边界效应造成的误差,软弱围岩的开挖深度应大于4倍隧道断面直径,故本文模型中隧道沿轴线方向开挖深度为50 m。
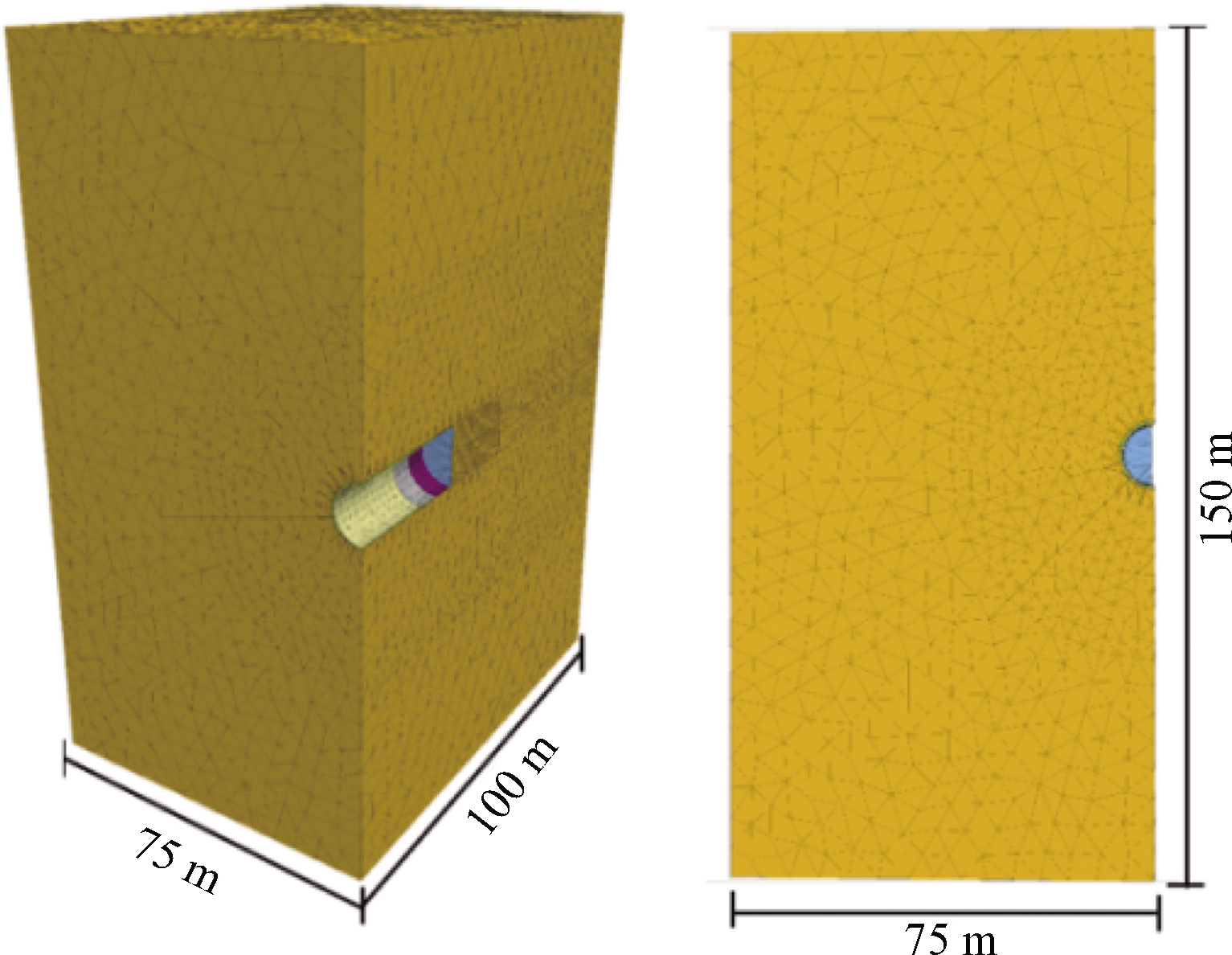
图1 模型的几何尺寸
Figure 1 Geometric dimensions of models
图2为双护盾TBM纵向剖面图,图中反映出TBM的几何构造、各部件尺寸以及护盾的锥度(即阶梯状减小的护盾直径)。双护盾TBM主要组成的几何尺寸如表1所示。图中软填充阶段是指回填层靠近TBM后盾尾部附近的新浇筑阶段,其硬化时间较短因而强度也较低;而硬填充阶段则指回填层硬化时间较长,强度也较高的阶段。
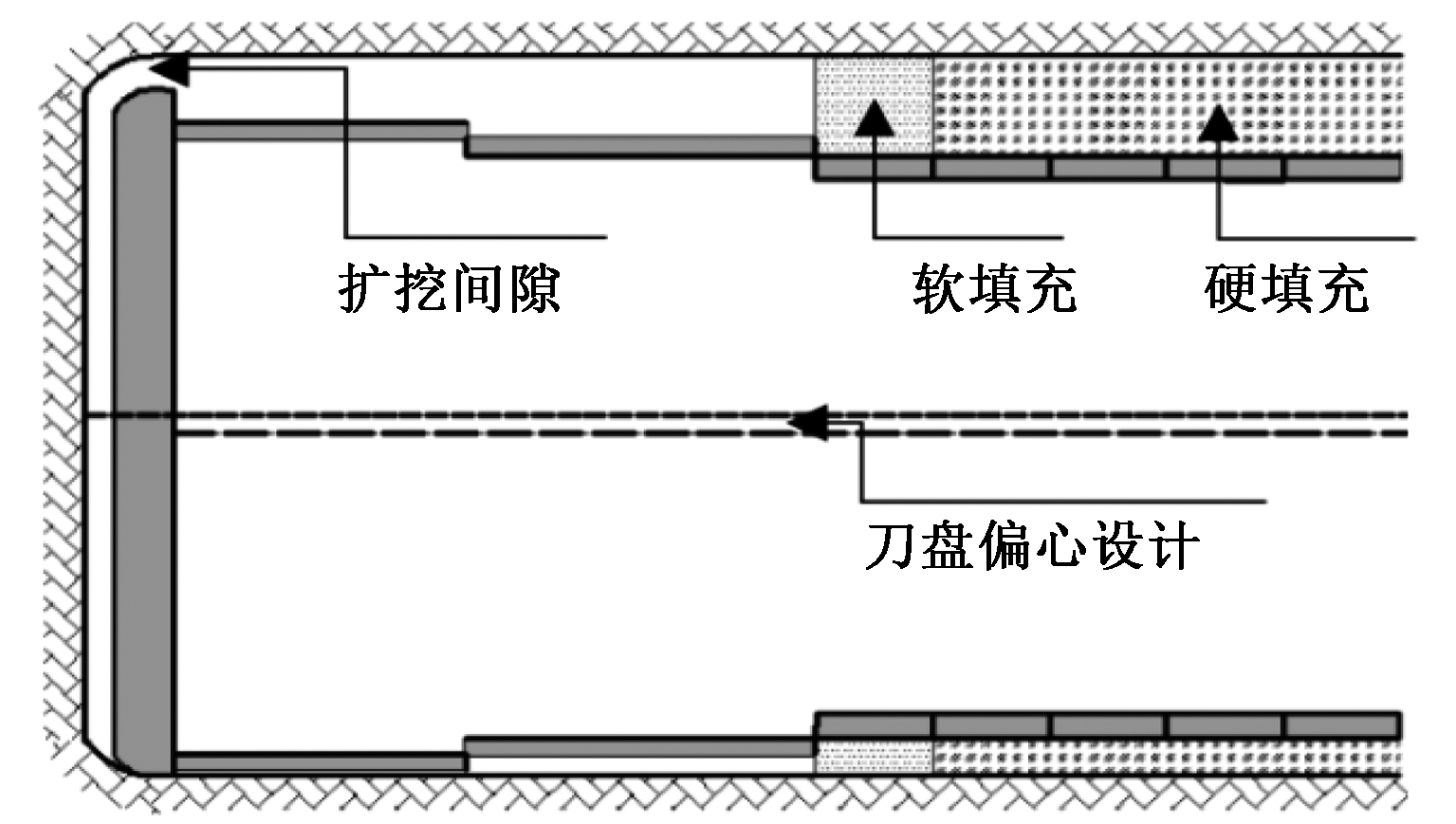
图2 双护盾TBM纵向剖面图
Figure 2 The longitudinal profile of the DS-TBM
表1 双护盾TBM的主要构件几何尺寸
Table 1 Geometric dimensions for main DS-TBM components
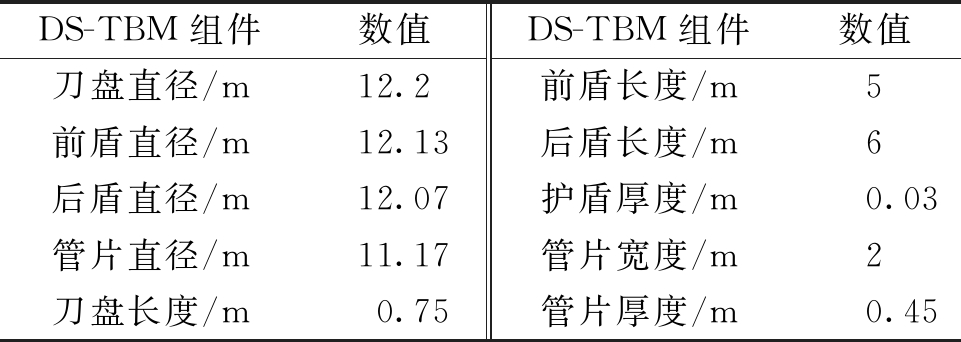
DS-TBM组件数值DS-TBM组件数值刀盘直径/m12.2前盾长度/m5前盾直径/m12.13后盾长度/m6后盾直径/m12.07护盾厚度/m0.03管片直径/m11.17管片宽度/m2刀盘长度/m0.75管片厚度/m0.45
选取3DEC 内置改进的burgers蠕变模型(CVISC)模拟岩体的黏弹塑性特性。模型中蠕变参数[14]详见表2。
建模时考虑到TBM自重,将其除以模型中各部件的体积换算出各部件的等效密度[9]。TBM刀盘及前后盾的材料为钢,预制衬砌管片为混凝土材料,回填材料为豆砾石灌浆。材料的物理力学参数详见表3[7]。
表2 岩体蠕变本构参数
Table 2 Creep constitutive parameters of rock mass

参数数值Maxwell剪切模量GM/MPa0.566Maxwell黏度系数ηM/(MPa·a)27.98Kelvin剪切模量GK/MPa498.1Kelvin黏度系数ηK/(MPa·a)4.26抗拉强度σt/MPa0.008 5
表3 主要部件及衬砌物理力学参数
Table 3 Physical and mechanical properties of main components and lining
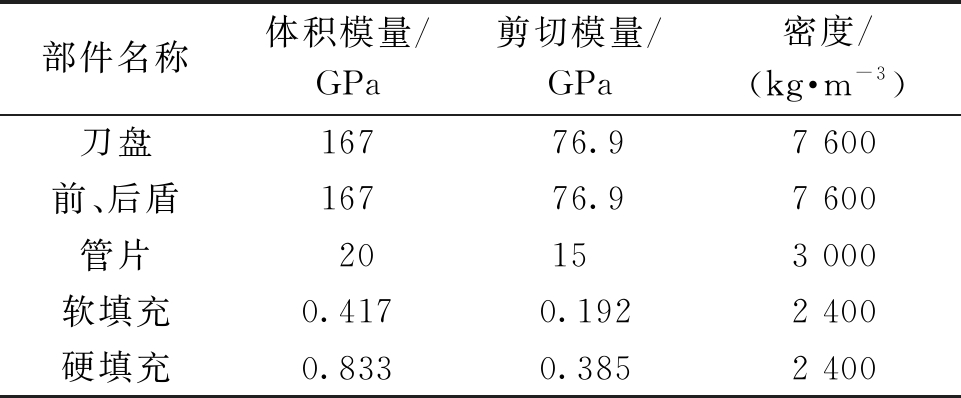
部件名称体积模量/GPa剪切模量/GPa密度/(kg·m-3)刀盘16776.97 600前、后盾16776.97 600管片20153 000软填充0.4170.1922 400硬填充0.8330.3852 400
由于刀盘直径为12.2 m,4倍隧道断面直径接近50 m,计算中每个开挖步的步长设置为1 m,选取50个开挖步。详细模拟步骤如图3所示。
1.3 卡机状态判断
若TBM总阻力大于额定推力FI,TBM则被卡住,卡机状态可用式(1)判断。
Rp(t)+RW+Fr>FI,
(1)
式中:Rp(t)为TBM上围岩压力产生的阻力;Rw为TBM自重产生的阻力;Fr 为TBM保持正常连续掘进所需的推力。
Rp(t)可以通过式(2)计算得到。
Rp(t)=Rs(t)·μ·β,
(2)
式中:Rs(t) 为TBM上的围岩压力;μ为TBM与围岩间的摩擦系数;β为有效折减系数。
Rs(t)可通过编写FISH语言从数值模拟的TBM刀盘、前后盾与围岩的接触单元中提取。μ的取值范围为0.15~0.30[8],本文取μ =0.30。β为刀盘半径或前盾半径或后盾半径r与隧道半径R的比值[7],分别为0.988、0.983与0.978。
Rw可以通过式(3)计算得到。
RW=μW,
(3)
式中:W 为TBM自重。
2 侧压系数及回填材料的影响分析
2.1 侧压系数对TBM卡机控制的影响
大量的地质调查结果和地应力实测统计资料表明,λ大多数处于0.8~1.5。为了探讨不同λ对双护盾TBM施工的影响,分别计算λ=0.6、0.8、1.0、1.2、1.4和1.6时的情况,探讨不同λ对TBM接触压力和总阻力的变化规律。参考已有研究,模拟中设定施工速度分别为AR=12、24 m/d,扩挖间隙Δr依次为10、18 cm。
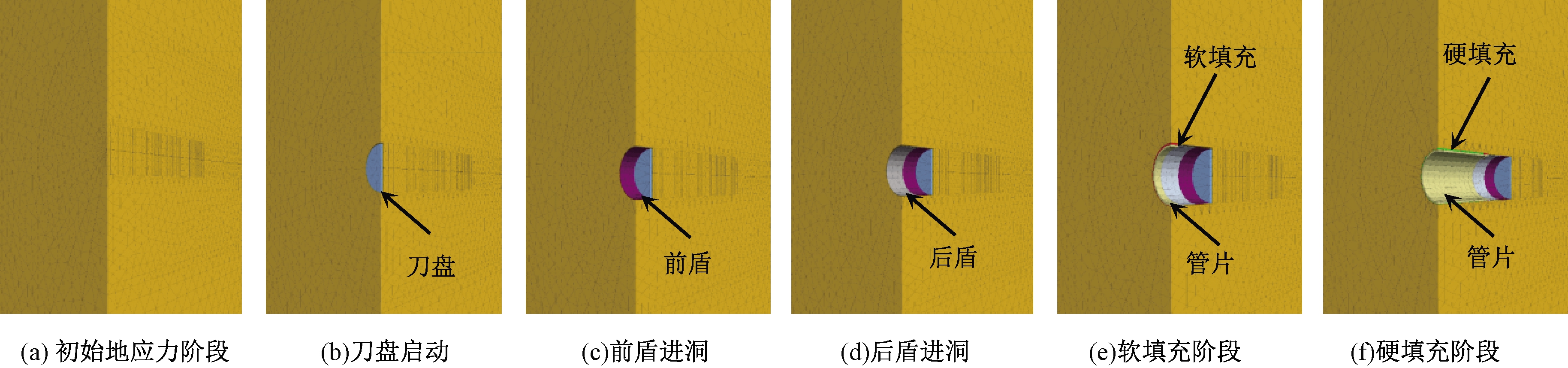
图3 双护盾TBM掘进模拟步骤
Figure 3 The modelling steps of DS-TBM Tunneling
图4是TBM接触压力和λ的关系图。图4显示,随着λ的增大,TBM接触压力不断增大。且随着λ的增加接触压力递增趋势逐渐变大,即λ越大对TBM掘进越不利。
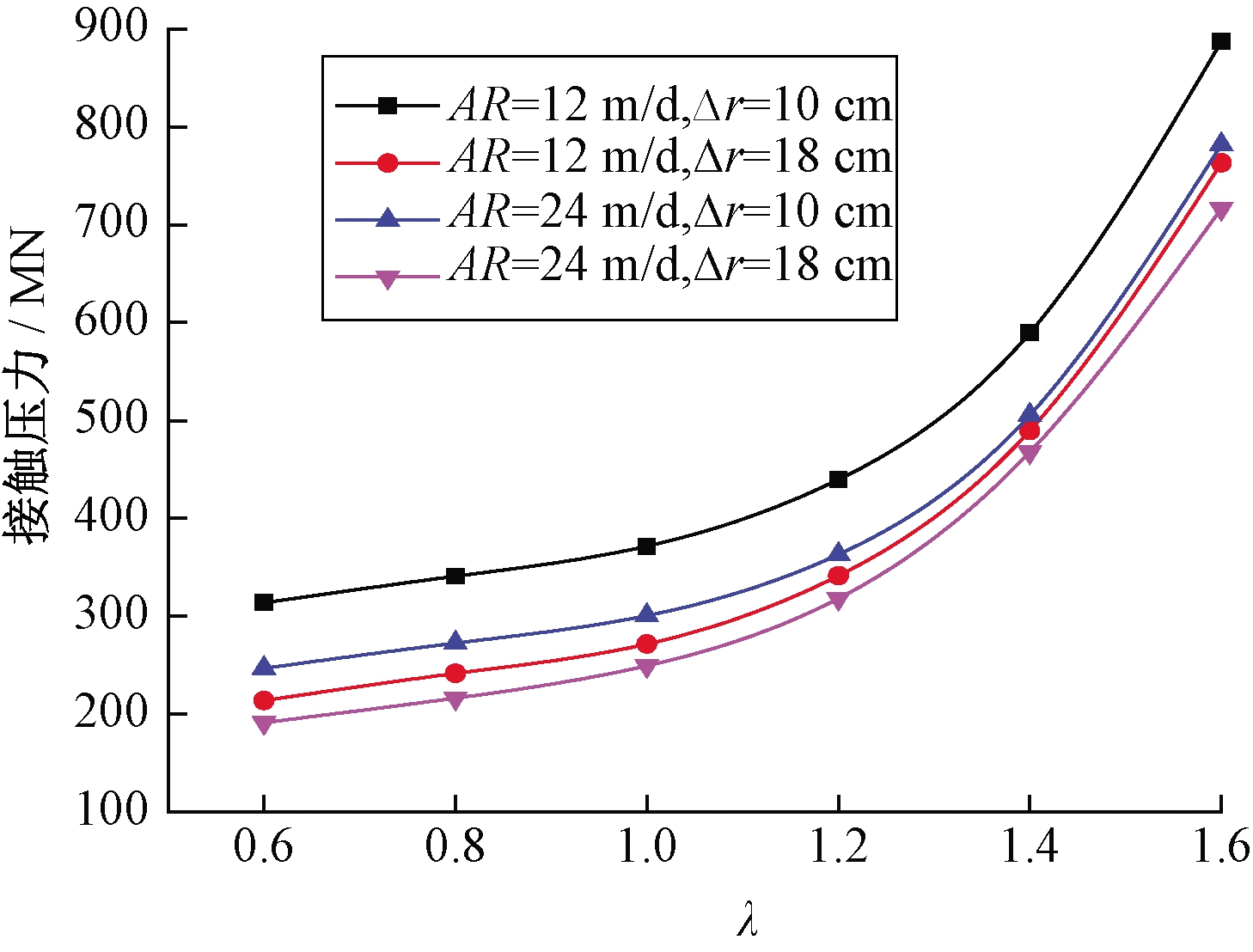
图4 λ对TBM接触压力的影响
Figure 4 The impact of λ on the contact force
根据由式(1)~(3)计算不同λ的TBM总阻力,绘制图5。图5显示,随着λ的增大,TBM的总阻力不断增大。表4给出了5个不同范围λ(每个范围λ变化均为0.2)下的TBM总阻力的增长比例。
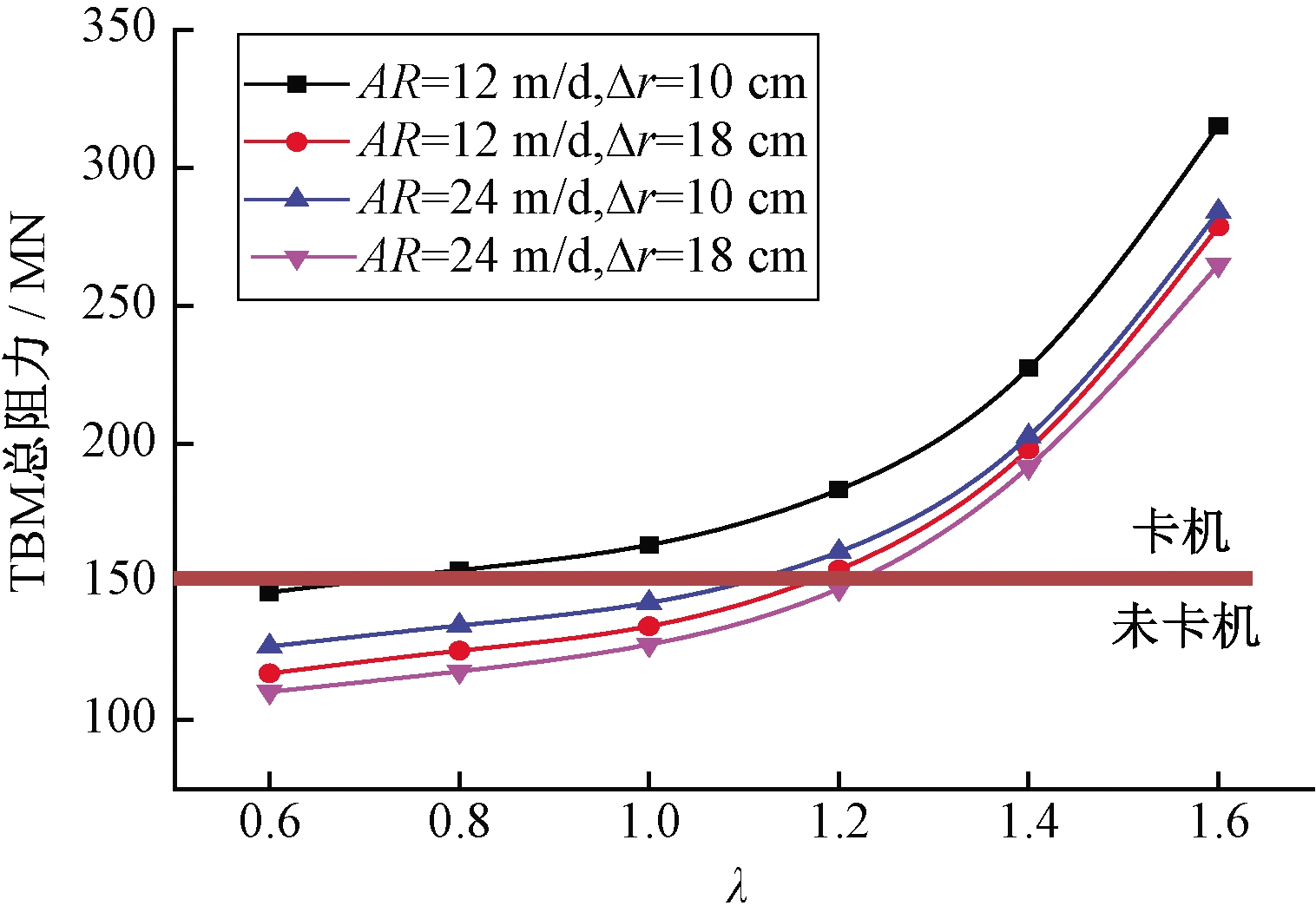
图5 λ对TBM总阻力的影响
Figure 5 The impact of λ on the total resistance
由图5与表4可得,当λ≤1时,总阻力的曲线趋势较为平缓,其增长比例也相对较小;当1<λ≤1.2时,TBM总阻力增长比例约为λ≤1时的2倍;当λ>1.2时,TBM总阻力急剧增长,其增长比例约为λ≤1的3~4倍,此时λ的增大对TBM总阻力影响较大。
由此说明,λ的增大对TBM的卡机控制产生了不利的影响。图5中给出了卡机状态分界线,不同的掘进速度和扩挖间隙卡机临界状态时的侧压系数并不相同。但是不管掘进速度和扩挖间隙多大,λ的增加对TBM施工越来越不利。
表4 不同范围λ下的TBM总阻力增长比例
Table 4 The extended rate of the total resistance among different internals of λ
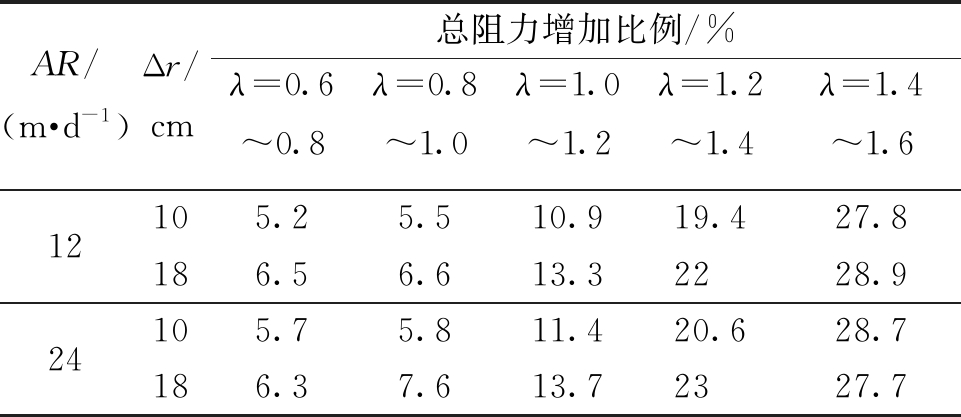
AR/(m·d-1)Δr/cm总阻力增加比例/%λ=0.6~0.8λ=0.8~1.0λ=1.0~1.2λ=1.2~1.4λ=1.4~1.61224105.25.510.919.427.8186.56.613.32228.9105.75.811.420.628.7186.37.613.72327.7
2.2 回填材料变形参数对TBM卡机控制的影响
假定管片衬砌支护体系处于弹性工作状态,以下针对回填材料的弹性模量E和泊松比μ对 TBM掘进的影响进行探讨。假设回填材料的E大小处于围岩与预制管片之间;根据一般回填层材料性质确定其μ、ρ值,如表5所示。
表5 围岩、回填层与预制管片的物理力学参数
Table 5 The physical and mechanical parameters of surrounding rock、backfill layer and segment

项目E/GPaμρ/(kg·m-3)围岩0.9420.252 650回填层[1,36]0.2,0.25,0.32 400预制管片360.23 000
图6和图7是在AR=12 m/d,Δr=10 cm的掘进条件下,回填层E=1、12、24GPa时TBM总接触压力、总阻力与μ的关系曲线。图中显示,TBM总接触压力与TBM总阻力均随回填材料μ的增大而减小,但其降低比例很小,例如,μ从0.2增加至0.3时,TBM总接触压力最大降低了3.1%,TBM总阻力最大降低了1.2%。由此可见μ的改变对TBM总阻力影响很小。因此,后续研究假定μ为定值0.3,只考虑E值变化对TBM掘进的影响。
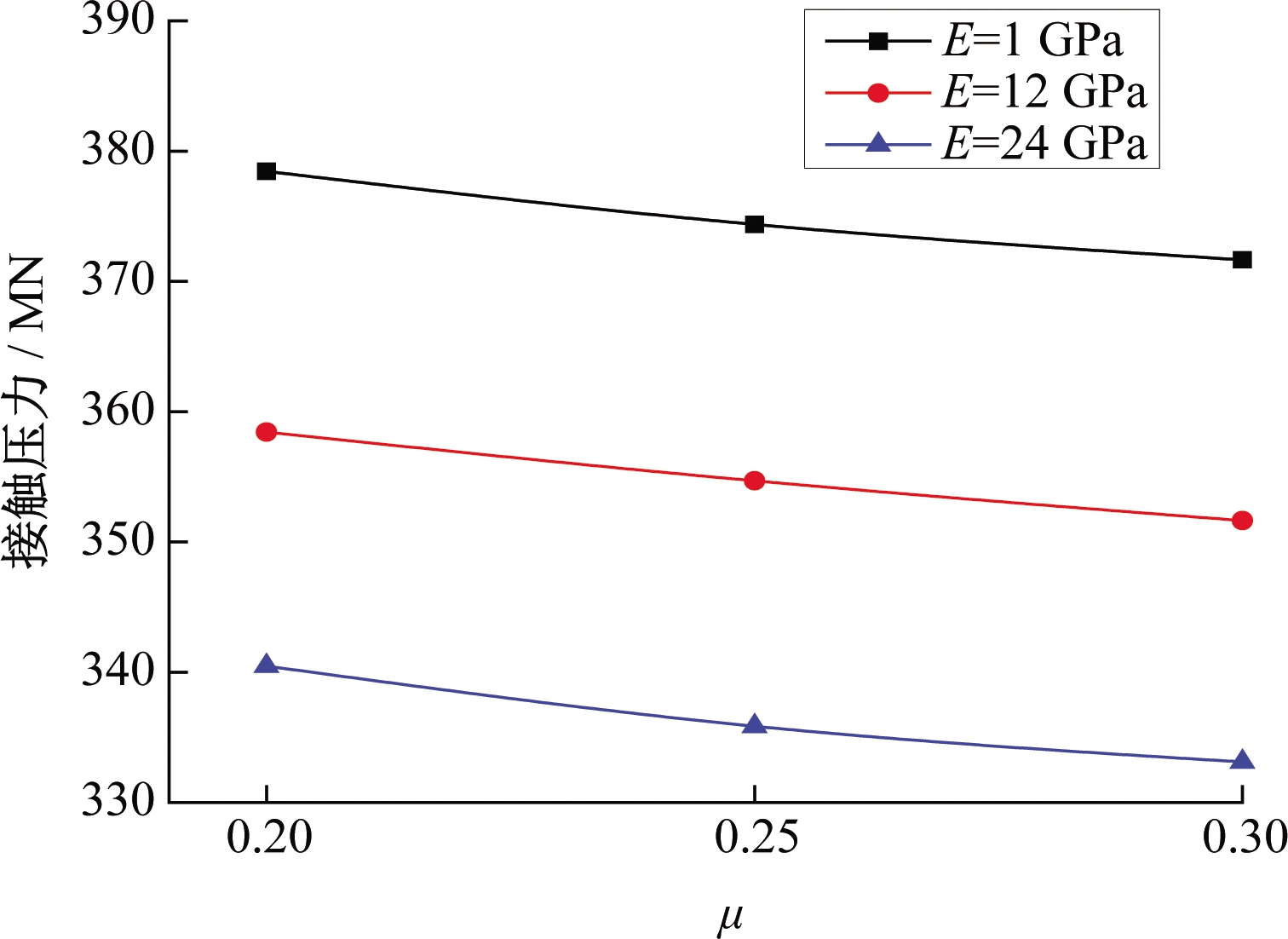
图6 TBM总接触压力、与μ关系图
Figure 6 The relationship of contact force and μ
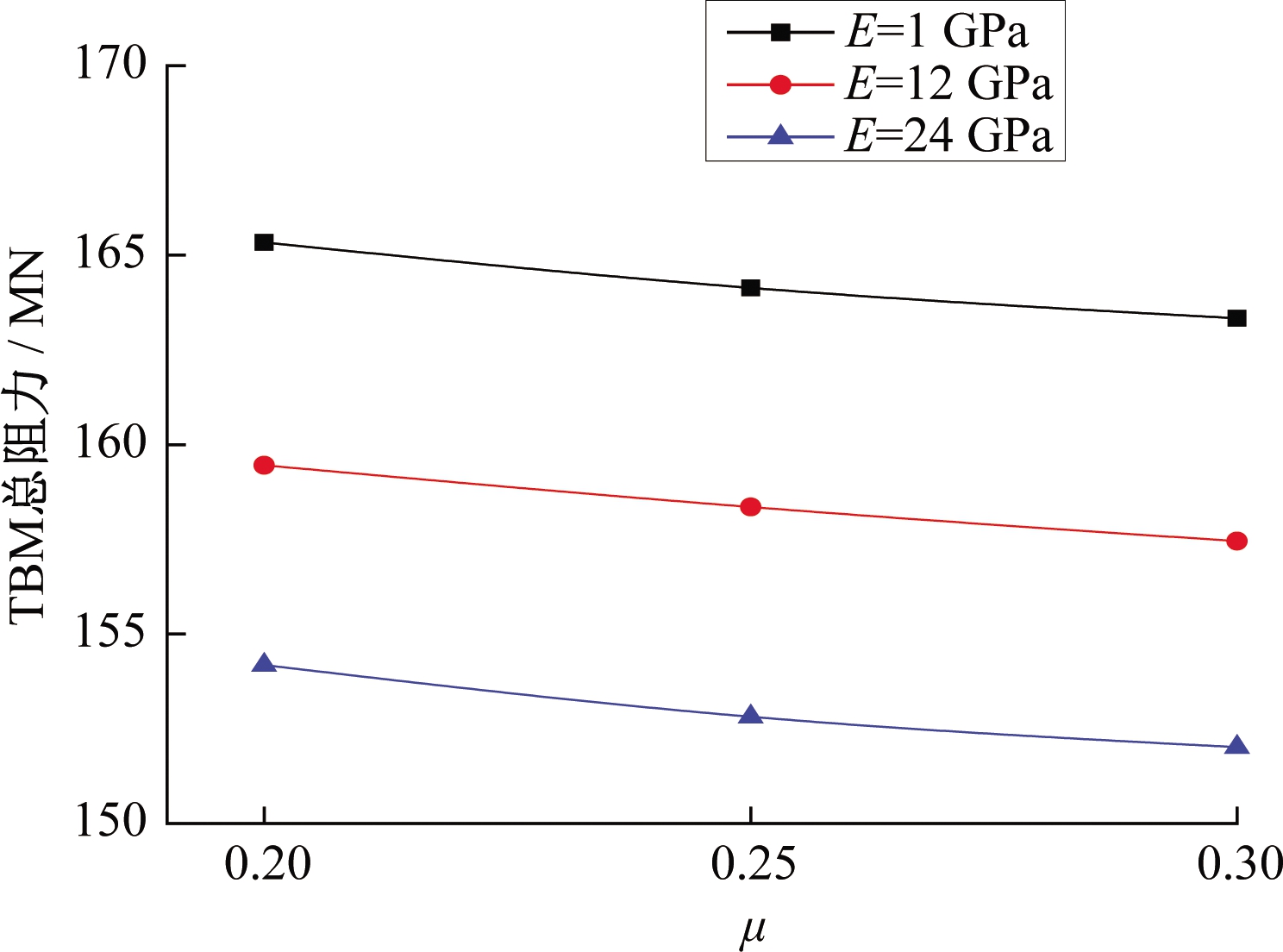
图7 TBM总阻力与μ关系图
Figure 7 The relationship of the total resistance and μ
讨论回填材料E的影响时,设定AR=12 m/d、24 m/d和扩挖间隙分别为Δr=10 cm、18 cm。计算中E取值为:E=1、6、12、18、24、30和36 GPa。
图8为不同掘进条件下,回填材料E与TBM刀盘、护盾的接触压力关系曲线。从图中可见,4种不同的TBM掘进条件下,E的改变均对TBM各部件产生了不同程度上的影响。其中刀盘上的接触压力受到的影响最小,这是因为刀盘距掌子面较近,受掌子面效应的影响最大,且刀盘距离回填衬砌段又相对较远;对于前盾和后盾而言,随着E的增加前后盾上的接触压力均呈减小趋势。同时受到前盾、后盾与围岩间隙阶梯型降低的影响,在各个掘进条件下均呈现出前盾接触压力大于后盾的规律。由于回填部位紧邻后盾尾部,随着E的增大,后盾的接触压力降低趋势最为明显。
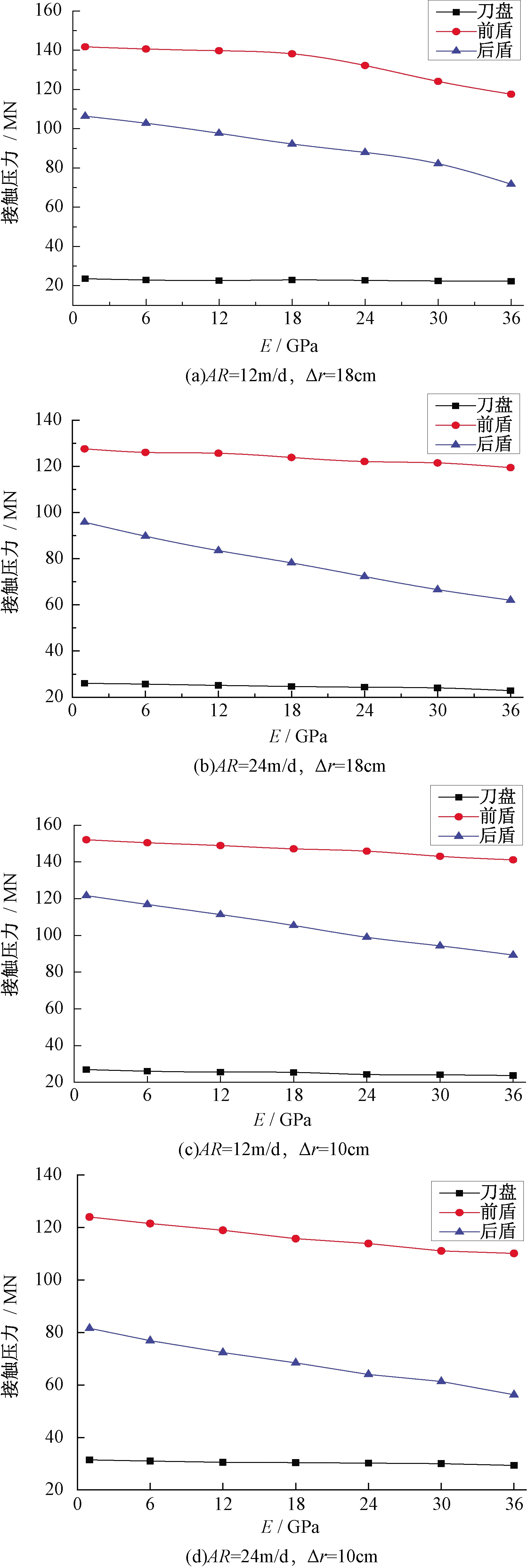
图8 不同回填材料E与TBM的接触压力关系图
Figure 8 The relationship of E and the contact pressure
图9为各掘进条件下的不同回填材料E与TBM总阻力的关系图,为清晰反映各掘进条件下的TBM总阻力降低情况,计算不同回填材料E下的TBM总阻力增长比例,如表6所示。图9和表6均显示出在4种不同的掘进条件下,随着E的不断增大,TBM的总阻力呈现降低趋势。
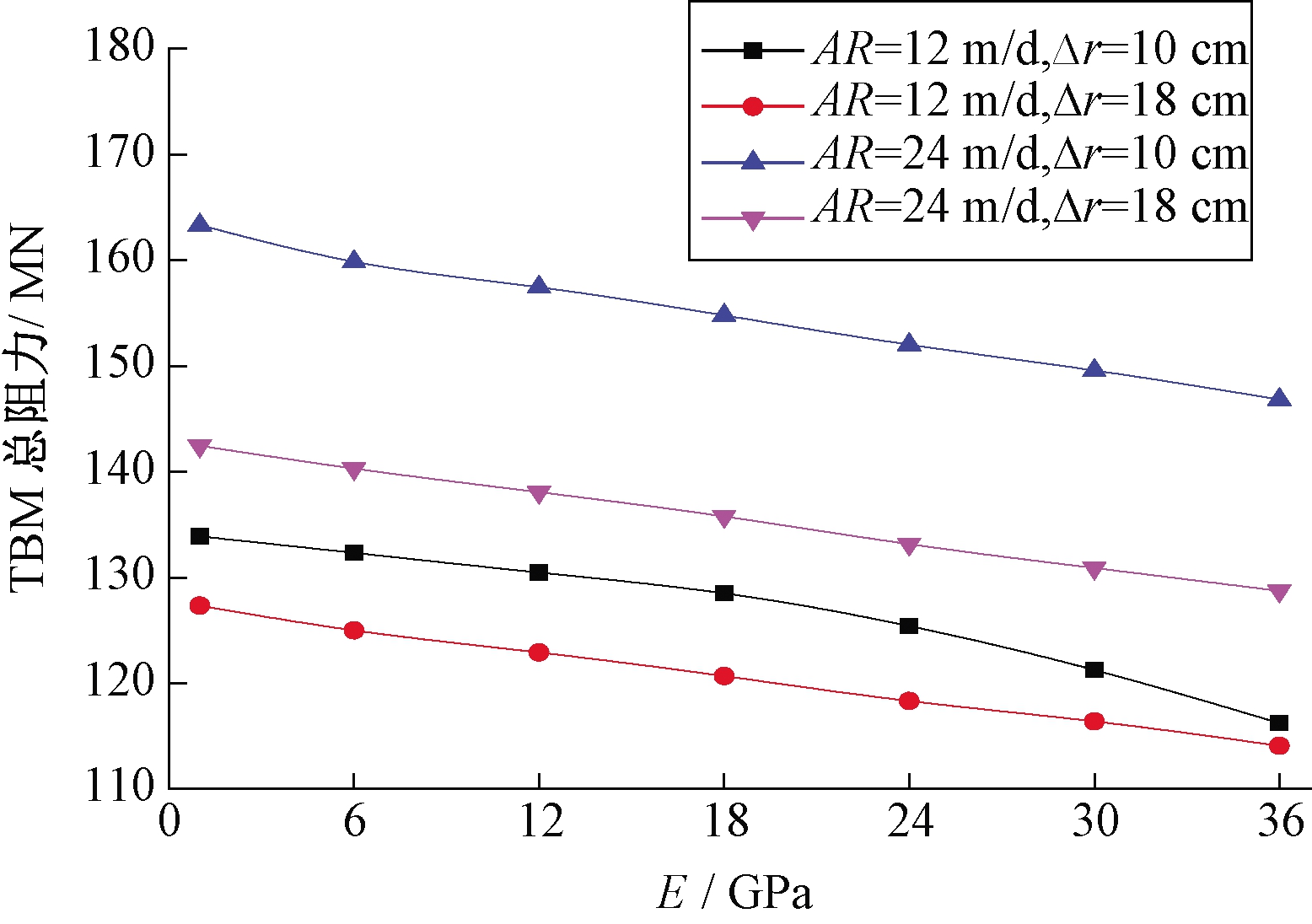
图9 不同回填材料E与TBM总阻力关系图
Figure 9 The relationship of E and the total resistance
表6 不同E下的TBM总阻力降低比例
Table 6 The extended rate of the total resistance by increasing E
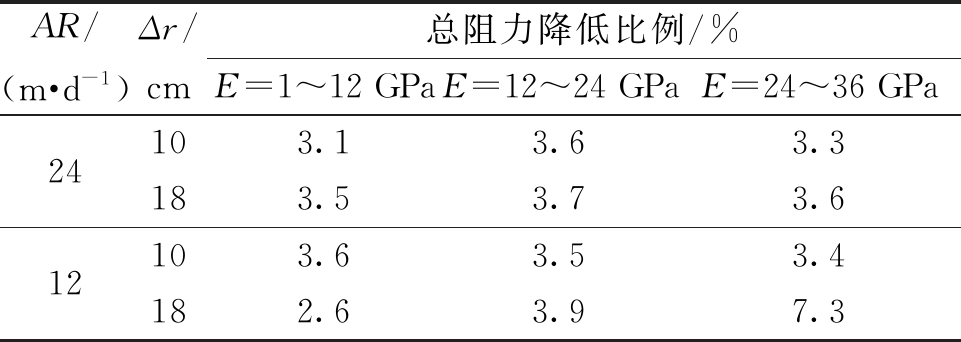
AR/(m·d-1)Δr/cm总阻力降低比例/%E=1~12 GPaE=12~24 GPaE=24~36 GPa2412103.13.63.3183.53.73.6103.63.53.4182.63.97.3
注:1~12表示E从1 GPa增加至12 GPa。
由图8和图9可知,回填材料的E越大其力学传递性能越好,对围岩的稳定性也越好,对TBM卡机控制产生有利影响。因此在TBM施工中可据此规律选择弹性模量较大的回填材料,更好的发挥回填层对围岩的稳定作用,同时降低TBM卡机概率。
2.3 软填充长度对TBM卡机控制的影响
图10为回填层软、硬填充阶段的局部示意图。众多研究中[5-8, 14]常将软填充阶段的长度假定为2 m,其弹性模量为硬填充阶段的一半,但工程中软填充长度取决于TBM施工速度和回填浆液的硬化速度。目前未见对回填层软填充长度Lr讨论的文献。
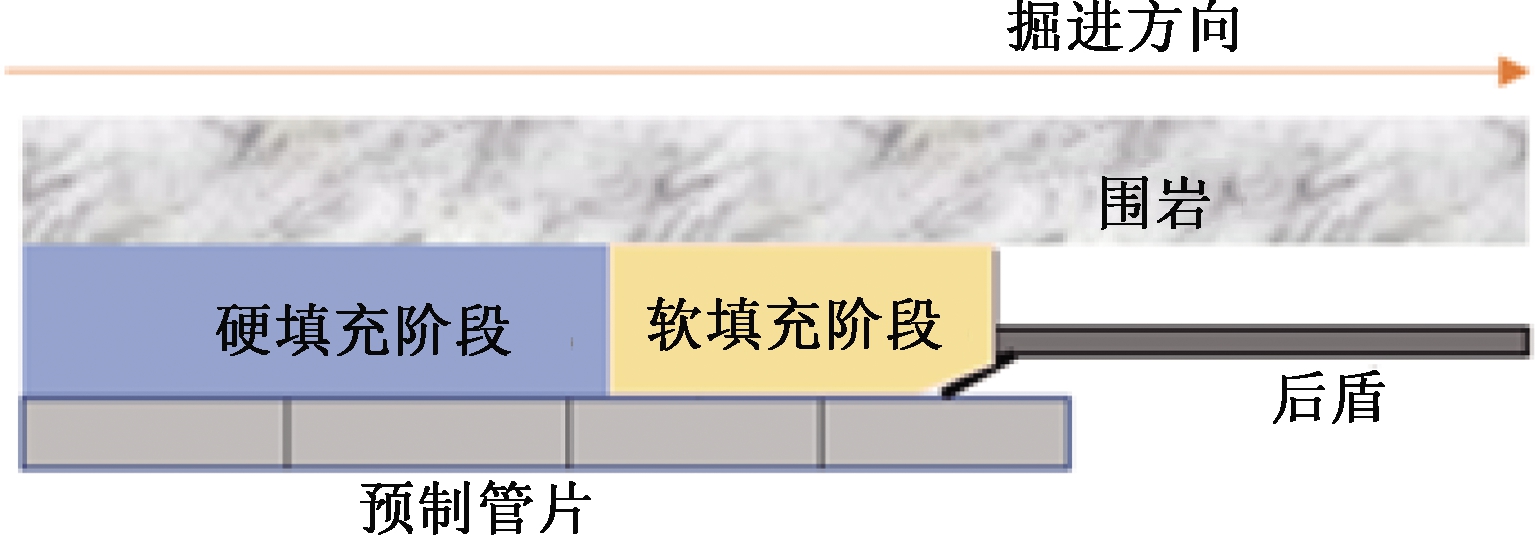
图10 回填层软、硬填充阶段的局部示意图
Figure 10 The local schematic diagram of soft and hard filling stage
研究中,分别计算Lr为2、5、8、10、12 m的情况。回填材料的E分别取6、12、18GPa,施工速度和扩挖间隙分别取12 m/d和10 cm。
图11为不同E时,Lr与TBM总阻力关系图。图中显示,不论E多大,Lr的增加均造成TBM总阻力不断增大。E分别为6、12、18 GPa时,当Lr从2 m增加至12 m,TBM总阻力分别增长了13.3%、13.7%、14.1%。由此可见,Lr的增加,显著增加了TBM卡机的概率。
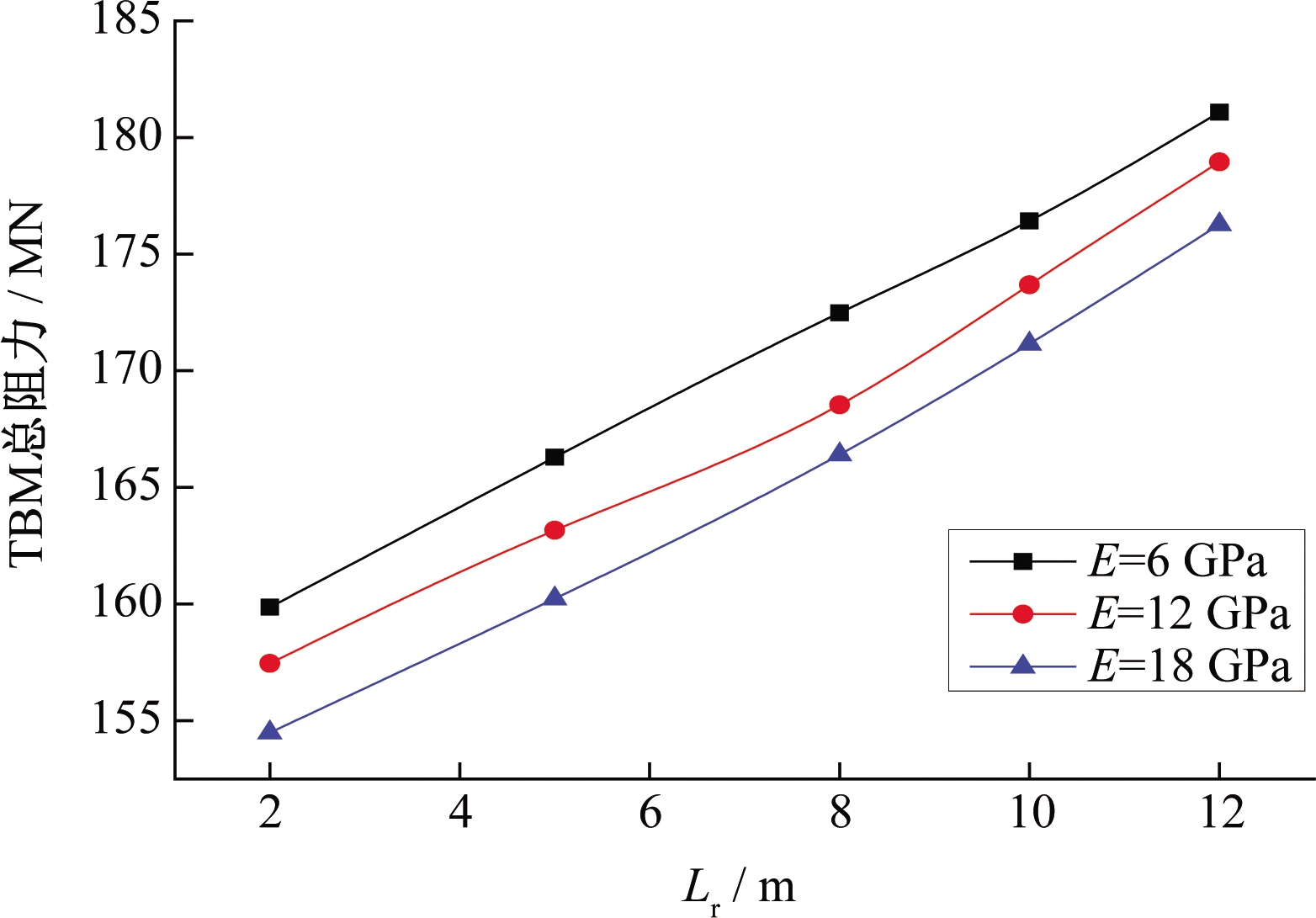
图11 Lr与TBM总阻力关系图
Figure 11 The relationship of Lr and the total resistance
在同一施工速度和扩挖间隙下,较长的Lr代表着回填灌浆物的硬化时间长、早期强度低,对TBM掘进不利。为了对TBM施工更有利,合理控制回填浆液的硬化速度很有必要。此外,TBM施工中回填需要大量的输送设备,而TBM内部的操作空间又相对比较狭小,常会出现因施工工序不协调,施工组织管理不完善而造成回填灌浆严重滞后的现象。由上可知,滞后的回填层施工将对卡机控制带来不利影响。为了避免或降低TBM掘进过程中卡机概率,因此,回填施工过程中,可选择合理的添加剂,达到回填浆液早强和快硬的目的;也可通过制定合理的施工组织方案等措施,避免回填层施工严重滞后于TBM掘进。
3 结论
(1)λ越大,对TBM卡机控制越不利。当λ<1时,其对TBM接触压力和总阻力的影响较小;当λ≥1时,增加λ对TBM接触压力和总阻力的影响较为明显,而当λ≥1.2时,TBM接触压力和总阻力随λ的增加而急剧增大,对TBM卡机控制极为不利。
(2)回填材料E越大TBM的总接触压力和总阻力越小。选择弹性模量较大的回填材料更有利于TBM的卡机控制。
(3)其他条件一定时,Lr越大TBM掘进总阻力越大。
[1] 刘泉声,黄兴,时凯,等. 超千米深部全断面岩石掘进机卡机机理[J].煤炭学报,2013,38(1):78-84.
[2] 张银霞,江志强,段留洋,等. TBM 盘形滚刀破岩过程的数值研究[J].郑州大学学报(工学版),2016,37(1):75-78.
[3] RAMONI M,ANAGNOSTOU G. Tunnel boring machines under squeezing conditions [J]. Tunneling and underground space technology,2010,25(2):139-157.
[4] RAMONI M,ANAGNOSTOU G. The interaction between shield,ground and tunnel support in TBM tunneling through squeezing ground[J]. Rock mechanics & rock engineering,2011,44(1):37-61.
[5] ZHAO K,JANUTOLO M,BARLA G. A completely 3D model for the simulation of mechanized tunnel excav-ation [J]. Rock mechanics and rock engineering,2012,45(4):475-497.
[6] 温森,杨圣奇,董正方,等. 深埋隧道TBM卡机机理及控制措施研究[J].岩土工程学报,2015,37(7):1271-1277.
[7] HASANPOUR R,ROSTAMI J,BARLA G. Impact of advance rate on entrapment risk of a double-shielded TBM in squeezing ground[J].Rock mechanics and rock engineering,2015,48(3):1115-1130.
[8] HASANPOUR R,ROSTAMI J,ÖZÇELIK Y. Impact of overcut on interaction between shield and ground in the tunneling with a double-shield TBM [J]. Rock mechanics and rock engineering,2016,49(5):2015-2022.
[9] 程建龙,杨圣奇,李学华,等. 挤压地层双护盾TBM与围岩相互作用影响因素分析[J].采矿与安全工程学报,2016,33(4):713-720.
[10] 黄兴,刘泉声,彭星新,等.引大济湟工程TBM挤压大变形卡机计算分析与综合防控[J].岩土力学,2017,38(10):2962-2972.
[11] BROWN E T,HOEK E. Trends in relationships between measured in-situ stress and depth [J]. International journal of rock mechanics and mining sciences & geomechanics abstracts,1978,15(4):211-215.
[12] 景锋,边智华,陈昊,等. 不同岩性侧压系数分布规律的统计分析[J].长江科学院院报,2008,25(4):48-52.
[13] 钱舟. 不同围岩级别下隧道回填材料合理工程参数分析[D].重庆:重庆交通大学,2016.
[14] BARLA G,BONINI M,DEBERNARDI D. Time dependent deformations in squeezing tunnels[J]. International journal of geoengineering case histories,2010,2(1):40-65.