0 引言
采用率失真(rate-distortion optimization, RDO)[1]是HEVC编码复杂度高的重要因素之一，而如何有效对其进行优化来降低计算量成为难题.
针对上述问题，研究人员已经从率失真计算的预测过程出发，在率失真函数和编码器编码单元的层面进行了优化，通过降低函数本身的运算量来提升HEVC编码器的性能，并以此达到优化编码时间的目的.文献[2]提出了离散余弦转换系数和基于全零块率失真优化量化跳过算法，提升了编码效率.文献[3]通过训练传输集合后选择最合适的传输模式来分类传输变换系数，从而降低视频比特率.文献[4]提出了变换编码传输约束条件实现了简化率失真代价计算的效果.文献[5]提出了一种基于运动特性的编码块分割算法，有效加快了帧内编码的速度.文献[6]提出了主动选择变换编码块的率失真优化量化(rate-distortion optimized quantization, RDOQ)的决策算法，得到了较好的编码增益.文献[7]使率失真优化量化代价计算随着标准测试模型中的量化值变化，实现了压缩率的提高.文献[8]采用一种基于自由量化框架的快速RDO算法，该算法在帧内、帧间预测过程都很有效，明显地降低了率失真计算复杂度.文献[9]利用感知特征引导率失真优化算法来改善视频编码中编码效率低的问题，提出通过空域中梯度幅值率特征和时域中梯度相似度偏差率特征来描述相关性，从而自适应地选择RDO编码过程中拉格朗日乘子来提升编码性能.文献[10]对编码块复杂度进行了分类，并根据分类情况对编码单元快速分割，有效地判决了编码块深度，提升了编码效率.文献[11]简化35种帧内编码模式到11种模式后，增加最有可能模式组成候选预测集，从而有效减少率失真优化过程中需计算代价值的模式数量，以此来降低计算复杂度.文献[12]介绍了对编码块和对应视频帧中已编码的编码块进行分类的压缩方法，改变了遍历计算的方式.但是，这些算法都是针对量化过程中的率失真计算进行的优化，忽略了应根据编码块特点来选择低计算复杂度量化器的方式.
基于此，笔者针对HEVC中可以使用不同的量化方法对变换系数进行量化的特点，提出了量化器判决条件，实现了标量量化和率失真优化量化的自适应选择，从而减少遍历计算量，缩短编码器编码时间.实验表明，笔者基于量化过程的自适应判决方法在全帧内(all intra, AI)实验条件下可以节省大约10.52%的编码时间，同时仅约有0.04%的码率上升和0.0 071 dB的信噪比下降.
1 均匀标量量化与率失真优化量化技术特征分析
均匀标量量化(uniform scalar quantizer)的量化步长Qs可以由输入信号变化区间和重建值数量决定：
(1)
式中:m和n分别表示信号的最大值和最小值；M表示重建值数量.则量化后输出：
(2)
其中，xi和xi+1分别是对应区间端点对应的映射值.假设输入值服从均匀分布，则以EMS衡量的量化误差为：
(3)
式中：
为重建值；M为重建个数.传统上HEVC使用的标量量化是
(4)
式中：
表示输入信号量化后的值；floor表示向下取整；Di是DCT系数；Qs是量化步长；f是偏移值控制舍入关系，根据IPB帧的分类原则取值为1/3或者1/6[13-14].均匀标量量化的特点在于失真小，量化过程简单，计算量低，尤其是对均匀变化范围的量化，能够在保证精度的情况下降低计算复杂度.
RDOQ在HEVC编码器中的计算需要不断利用RDO准则.以官方测试平台HM为例分析.首先，需要确定候选的量化值，公式如下：
(5)
式中：ci为变换块系数；li为系数量化后的值[15-16]；round为舍入关系.
首先，根据变换块系数及每个候选量化值计算所有候选量化值的代价，利用RDO遍历计算所有系数包含的所有候选值的代价值，并选取它们较低代价值对应的量化值作为最优量化值.
然后，还需要利用RDO准则来遍历搜索每一个系数块组(coefficient group，CG)是否量化为全零组，以达到较好的量化效果.最后，量化过程还需要确定最后一个非零系数的位置，通过确定熵编码中的该位置信息来解决拖尾零系数造成的编码比特升高问题.因此，与标量量化相比，RDOQ虽然提高了编码器的性能，但由于利用了RDO准则，需要遍历计算候选量化值以及全零组、最后一个非零系数位置等率失真代价值，因此，总的编码时间大约增加了10%～15%.
2 高效的率失真优化量化判决算法
2.1 均匀标量量化和率失真量化判决
对于变换块，如何自适应地合理分配标量量化和率失真优化量化，对变换过程降低计算复杂度至关重要.量化是对变换系数进行量化，根据其量化水平可以对量化器合理有效地判决.然而在下列两个条件下，两种量化器都将无法有效提升编码性能.
(1)变换系数量化为零；
(2)变换系数RDOQ量化水平等于变换系数均匀标量量化水平.
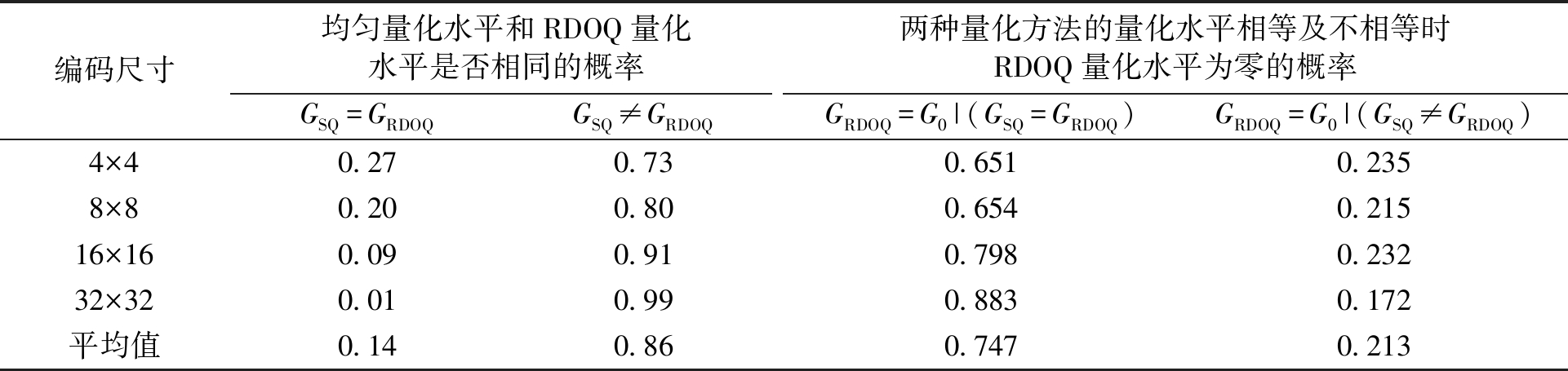
为此，我们对同一帧图像变换块变换系数进行RDOQ量化和标量量化后量化水平相等的概率进行了分析，如表1所示.其中，G0表示量化水平为零；GSQ表示均匀量化水平;GRDOQ表示RDOQ量化水平.通过对不同尺寸编码块在两种量化模式下量化为零或有相同量化水平的可能性分析进行第一步的筛选.当量化水平为零或相同时不需量化器选择，不同时则进行下一步的量化器选择判决.从表1可以看出，大约有14%的变换块系数在进行量化时，无论是使用标量量化还是率失真优化量化，量化水平都相同，两种方法编码效率也一样，不需进行量化模式选择.而在GSQ=GRDOQ和GSQ≠GRDOQ两种情况下，又分别有74.7%和21.3%的变换块系数量化为零，零变换块不需进行量化.所以，在GSQ=GRDOQ或量化水平为零或变换块变换系数近似为零时，两种量化方法对视频编码效率并没有较大的影响.此时，对变换块进行量化时，采用传统的标量量化或者RDOQ任一种即可.在进行视频编码时跳过笔者提出的量化器模式选择过程.但是，在GSQ≠GRDOQ且RDOQ量化水平不等于零时，大约86%中仍然有78.7%的变换块系数需要进一步判定量化方法.为此，继续分析了不同尺寸变换块变换系数进行RDOQ后量化水平的平均和，如表2所示.
表1 两种量化方法系数量化水平之间的关系
Tab.1 The corrlation of quantization level of coefficients between two quantization methods
编码尺寸均匀量化水平和RDOQ量化水平是否相同的概率两种量化方法的量化水平相等及不相等时RDOQ量化水平为零的概率GSQ=GRDOQGSQ≠GRDOQGRDOQ=G0|(GSQ=GRDOQ)GRDOQ=G0|(GSQ≠GRDOQ)4×40.270.730.6510.2358×80.200.800.6540.21516×160.090.910.7980.23232×320.010.990.8830.172平均值0.140.860.7470.213
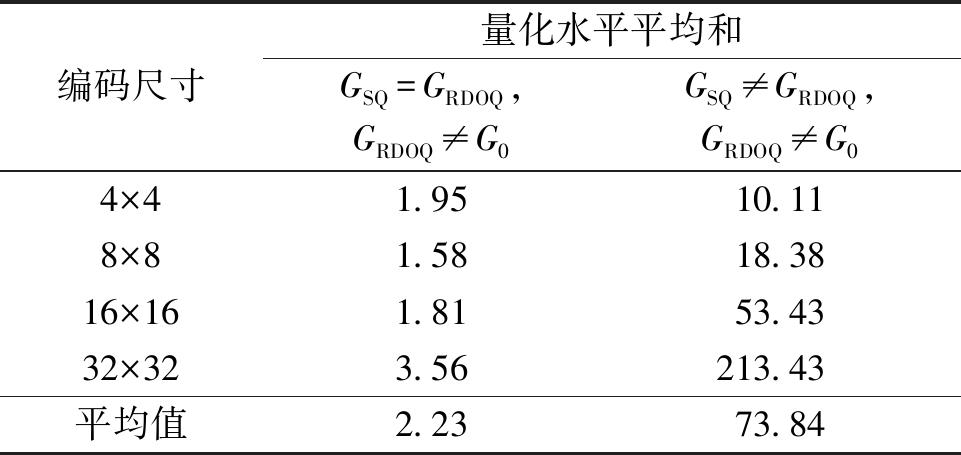
表2 系数量化水平不为零时RDOQ量化水平平均和
Tab.2 The mean sum of quantization level after RDOQ when quantization level of coefficients not equal to zero
编码尺寸量化水平平均和GSQ=GRDOQ,GRDOQ≠G0GSQ≠GRDOQ,GRDOQ≠G04×41.9510.118×81.5818.3816×161.8153.4332×323.56213.43平均值2.2373.84
表2中，在变换系数量化水平不为零，且量化水平和小于平均量化水平平均和(2.23)时，可以直接将变换系数量化为零，不再进行RDOQ量化.在变换系数量化水平不为零且GSQ≠GRDOQ情况下，若量化水平和小于最小尺寸4×4变换块对应的10.11，则RDOQ量化相对于计算复杂度带来的编码时间增高并没有较大幅度的比特率节省，编码器将选择均匀标量量化方法.
为了进行以上量化方法的选择，需要计算变换系数量化水平和，如式(6)所示：
⎣
+f」≅
(6)
式中：lm表示m级量化水平；cm表示未量化系数；N表示系数总量；f表示量化补偿.
所以，根据表2实验结果设定阈值T为10.11，并进行以下判决：
≅
(7)
判断条件(7)可以进一步简化为：
(8)
即GSQ≠GRDOQ且量化水平不为零时，若
小于阈值T时将不再进行RDOQ量化.
所以，在进行HEVC视频编码时，变换系数量化水平和若满足条件式(8)，量化过程将跳过RDOQ，直接进行均匀标量量化；否则，HEVC进行RDOQ量化.HEVC编码器通过笔者提出的判决条件进行量化器的选择，可以在保证在失真较低的条件下较大地降低量化过程中的计算复杂度.
2.2 算法流程
步骤1提取当前需编码变换块变换系数.
步骤2确定变换系数的RDOQ量化候选值，当GSQ=GRDOQ或量化水平为零时，变换块变换系数选择标量量化或者RDOQ并无区别，此时跳出此量化器选择算法，直接采用标准的RDOQ方法进行量化过程.否则需要进行下一步的选择判决.
步骤3根据式(6)计算变换系数量化水平和.若量化水平和小于平均量化水平平均和2.23时，则直接将变换系数量化为零，不再进行RDOQ量化；否则需要进行下一步判断.
步骤4设定10.11为阈值T，根据判决条件式(8)进行量化模式判决.若量化水平和满足判决条件(8)则使用均匀标量量化；否则则使用RDOQ，判决结束.
步骤5进行下一变换块的量化模式判决.
2.3 算法时间复杂度
从以上分析可知，采用了该选择判决算法后，由于大约有14%的变换块系数在进行量化时GSQ=GRDOQ;有86%的变换块系数在进行量化时GSQ≠GRDOQ.而在GSQ≠GRDOQ条件下，21.3%的变换块系数量化为零，所以大约有14%+86%×21.3%=32.32%的变换块系数在步骤2后跳出量化器选择算法，直接采用标准的RDOQ方法进行量化过程，在此种情况下并没有减少时间复杂度；而大约有86%×(1-21.3%)=67.68%的变换块系数需要进行步骤3以下的判断.当其量化水平和小于平均量化水平平均和(2.23)时，直接将变换系数量化为零，不再进行RDOQ量化.接下来当量化水平和小于10.11时，则判断需要使用均匀标量量化，不再进行RDOQ量化.该算法在这两种情况下均不再进行遍历计算候选量化值以及全零组、最后一个非零系数位置等率失真代价值，减少了编码时间.
3 实验结果
实验使用HEVC官方测试(HEVC Test Model,HM)16.0平台，在AI、随机接入(random access, RA)、低延迟(low delay, LD)3种条件下分别对不同分辨率和纹理变化特性的视频测试序列进行测试.
笔者提出的算法较HEVC编码器的平均节省时间(average saving time, AST)的百分率AST计算如下：
(9)
式中:tA是HEVC编码时间；tP是本文算法的编码时间.所以，AST值越高，性能较HEVC编码器越好.
3.1 与HEVC编码标准及其他改进算法的比较
试验在设定的标准测试条件下以峰值信噪比变化(bjontegaard delta peak signal-to-noise rate)RBDPSN和码率变化(bjontegaard delta bit rate)RBDB判定编码性能，以AST节省的时间多少表示编码复杂度降低程度，试验结果如表3所示.
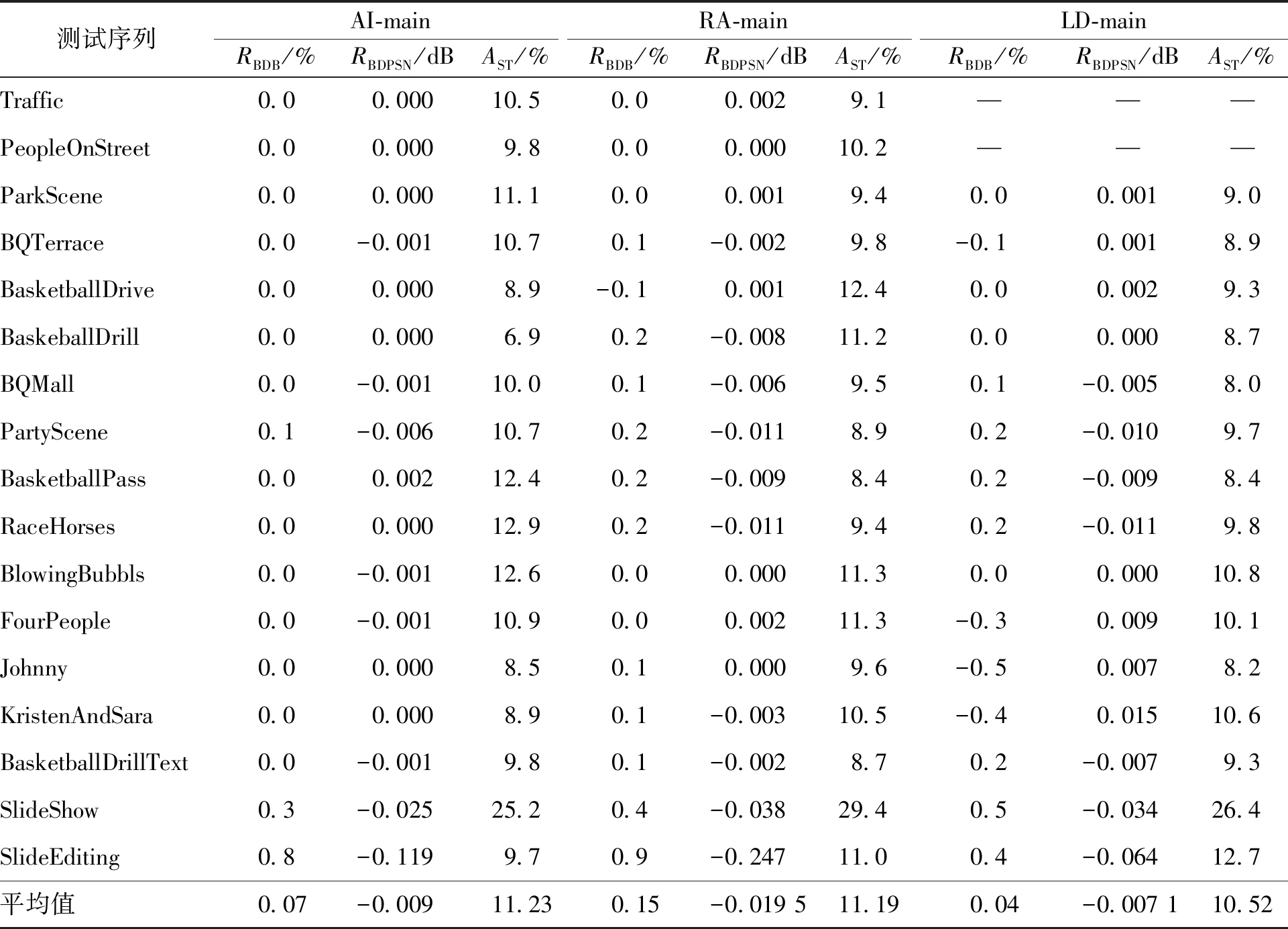
表3 提出的算法与原始HEVC编码器的结果比较
Tab.3 Comparison results between the proposed algorithm and the original HEVC encoder
测试序列AI-mainRA-mainLD-mainRBDB/%RBDPSN/dBAST/%RBDB/%RBDPSN/dBAST/%RBDB/%RBDPSN/dBAST/%Traffic0.00.00010.50.00.0029.1———PeopleOnStreet0.00.0009.80.00.00010.2———ParkScene0.00.00011.10.00.0019.40.00.0019.0BQTerrace0.0-0.00110.70.1-0.0029.8-0.10.0018.9BasketballDrive0.00.0008.9-0.10.00112.40.00.0029.3BaskeballDrill0.00.0006.90.2-0.00811.20.00.0008.7BQMall0.0-0.00110.00.1-0.0069.50.1-0.0058.0PartyScene0.1-0.00610.70.2-0.0118.90.2-0.0109.7BasketballPass0.00.00212.40.2-0.0098.40.2-0.0098.4RaceHorses0.00.00012.90.2-0.0119.40.2-0.0119.8BlowingBubbls0.0-0.00112.60.00.00011.30.00.00010.8FourPeople0.0-0.00110.90.00.00211.3-0.30.00910.1Johnny0.00.0008.50.10.0009.6-0.50.0078.2KristenAndSara0.00.0008.90.1-0.00310.5-0.40.01510.6BasketballDrillText0.0-0.0019.80.1-0.0028.70.2-0.0079.3SlideShow0.3-0.02525.20.4-0.03829.40.5-0.03426.4SlideEditing0.8-0.1199.70.9-0.24711.00.4-0.06412.7平均值0.07-0.00911.230.15-0.019 511.190.04-0.007 110.52
由表3可知，笔者提出的算法具有较好的量化效果，在3种配置条件下分别实现了11.23%、11.19% 和 10.52% 的编码时间节省.其中，AI条件下SlideShow最高实现了25.2%的时间节省，BaskeballDrill序列也降低了6.9%的编码时间；RA条件下SlideShow最高实现了29.4%的时间降低;BasketballPass也降低了8.4%的编码时间；LD条件下SlideShow序列实现了26.4%的时间降低；BQMall序列实现大约8.0%的时间节省.同时，3种条件下分别平均有0.07%、0.15%、0.04%的码率上升和0.009、0.0 195、0.0 071 dB的峰值信噪比降低.实验结果中，SlideShow视频测试序列因为具有较为单调的背景和较为复杂前景的特点，在提出的判决条件下进行编码，量化过程更多地选择了均匀标量量化，从而节省了大量的编码时间.与此同时，序列复杂也造成了较高的峰值信噪比(peak signal-to-noise rate)RPSN下降，但是仍在可接受范围内；而且，不同分辨率和运动特性的测试序列几乎都保持了较好的编码质量，RPSN和比特率(bit rate)RB在提出的算法中较HEVC编码器分别下降和升高得并不明显，如图1所示为测试视频序列率失真(rate distortion,RD)曲线图.可见，无论是RBDPSN还是RBDB，其变化都是非常微小的.在时间节省方面，文献[5]基于运动特性的编码块分割算法节省了4.7%的编码时间；文献[7]中基于代价值计算的RDOQ优化算法节省大约为3.74%编码时间；文献[10]基于编码块复杂度分类情况进行的编码单元快速分割算法节省了大约9.11%的编码时间，均低于本文算法的10.5%的时间节省.
因此，基于实验分析，笔者提出的本文算法能够在保证视频质量的同时还能节省编码时间，具有良好的编码性能.
3.2 试验结果主观质量分析
图2显示了编码后图像及其红色矩形区域的局部放大图.对比可知，笔者提出的量化判决方法能有效地对均匀量化和率失真优化量化进行自适应选择，量化器选择更加合理.采用本文算法进行编码后，图像局部放大图仍然保留了图像结构信息以及细节，表明该算法在降低了编码器的计算复杂度的同时，仍然能保持图像质量；同时可以看出，虽然本文算法理论上会造成一定的失真(如图1所示，视频RPSN值有轻微降低)，但从主观上看，对视频质量的影响却是有限的.
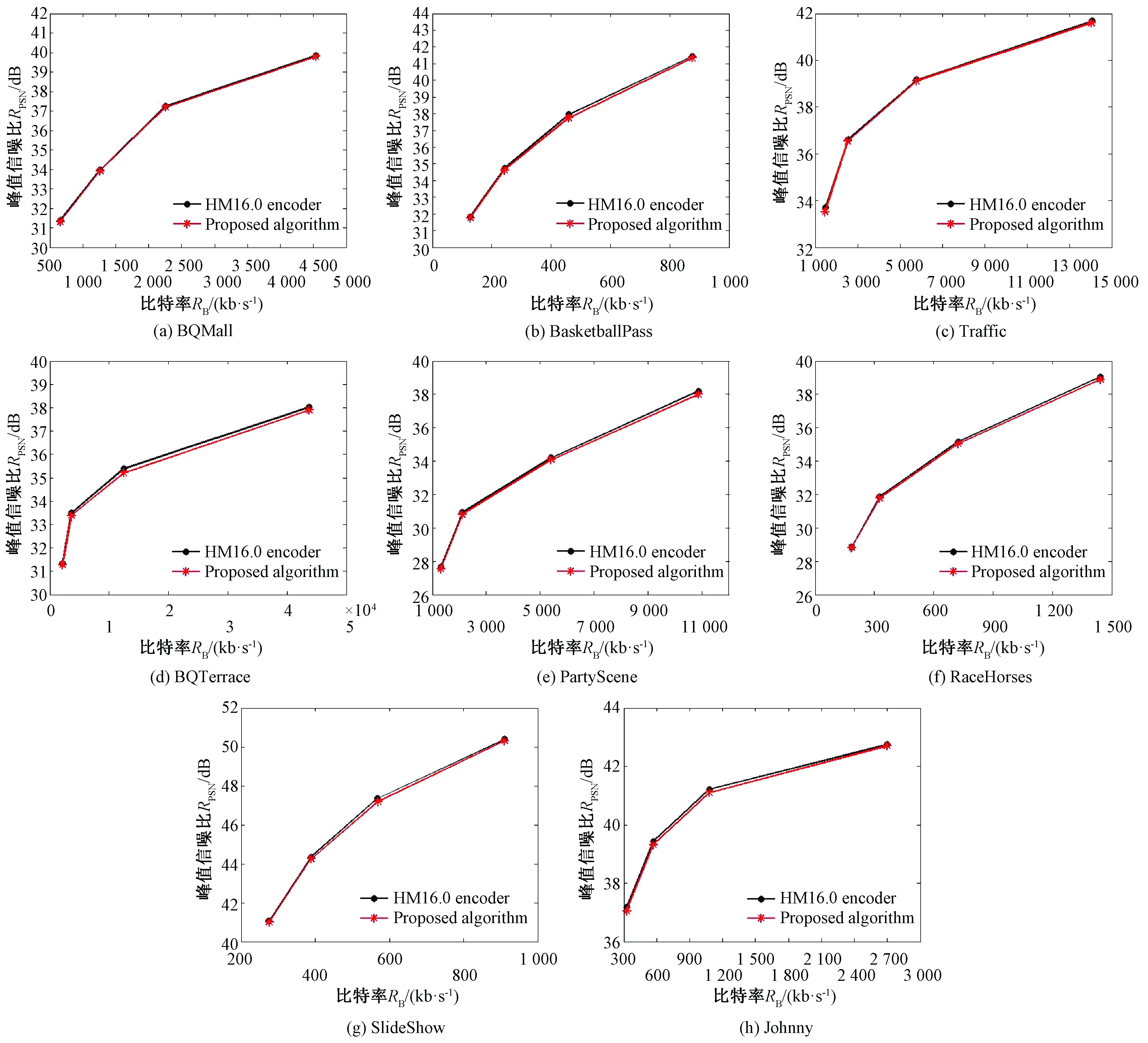
图1 测试视频序列RD曲线图
Fig.1 The RD curve of test sequences
图2 主观质量对比
Fig.2 The comparison of video subjective qualitys
4 总结
笔者对比分析了视频编码标准中均匀标准量化与率失真优化量化的不同特性，提出了一种基于量化水平的量化器自适应分配方法，通过对不同区域的特征分析自适应地选择合适的量化器.提出的算法不仅能降低HEVC编码复杂度，而且实现了较好的编码效果.实验表明，使用本文算法较HEVC编码器能节省大约10.52%左右的编码时间，同时保持了较好的编码质量.
[1] TECH G, CHEN Y, MÜLLER K, et al. Overview of the multiview and 3D extensions of high efficiency video coding[J]. IEEE transactions on circuits and systems for video technology, 2016, 26(1):35-49.
[2] ZHANG Y F, TIAN R, LIU J G, et al. Fast rate distortion optimized quantization for HEVC[C]// Visual Communications and Image Processing. Singapore: IEEE,2015:1-4.
[3] ZOU F, AU O C, PANG C, et al. Rate-distortion optimized transforms based on the Lloyd-type algorithm for intra block coding[J]. IEEE journal of selected topics in signal processing,2013,7(6):1072-1083.
[4] ARRUFAT A, PHILIPPE P, DÉFORGES O. Rate-distortion optimised transform competition for intra coding in HEVC[C]//IEEE Visual Communications and Image Processing Conference. Valletta, Singapore:IEEE,2014:73-76.
[5] XU Z, MIN B, CHEUNG R C C, et al. A fast inter CU decision algorithm for HEVC[J]. Signal processing image communication, 2018, 60:211-223.
[6] LEE H, YANG S, PARK Y, et al. Fast quantization method with simplified rate-distortion optimized quantization for an HEVC encoder[J]. IEEE transactions on circuits & systems for video technology, 2016, 26(1):107-116.
[7] STANKOWSKI J, KORZENIEWSKI C, DOMANSKI M, et al. Rate-distortion optimized quantization in HEVC: performance limitations[C]// Picture Coding Symposium. Cairns, Australia：IEEE, 2015:85-89.
[8] YANG A S, ZENG H Q, CHEN J, et al. Perceptual feature guided rate distortion optimization for high efficiency video coding[J]. Multidimensional systems and signal processing, 2017,28(4):1249-1266.
[9] ZHANG M M, ZHAI X J, LIU Z. Fast and adaptive mode decision and CU partition early termination algorithm for intra-prediction in HEVC[J]. Eurasip journal on image and video processing,2017(1):86.
[10] FERN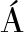
NDEZ D G, BARRIO A A D, BOTELLA G, et al. Complexity reduction in the HEVC/H265 standard based on smooth region classification[J]. Digital signal processing, 2017, 73:24-39.
[11] ORTEGA A, RAMCHANDRAN K. Rate-distortion methods for image and video compression[J]. IEEE signal processing magazine, 1998, 15(6):23-50.
[12] SEZER O G, HARMANCI O, GULERYUZ O G. Sparse orthonormal transforms for image compression[C]//2008 15th IEEE International Conference on Image Processing. Sun Diego, CA:IEEE, 2008:149-152.
[13] RAMEZANPOUR M, ZARGARI F. Fast HEVC I-frame coding based on strength of dominant direction of CUs[J]. Journal of real-time image processing, 2016, 12(2):397-406.
[14] RAHMANI F, ZARGARI F. Compressed domain visual information retrieval based on I-frames in HEVC[J]. Multimedia tools & applications, 2017, 76(5):7283-7300.
[15] LI X, OERTEL N, HUTTER A, et al. Laplace distribution based lagrangian rate distortion optimization for hybrid video coding[J]. IEEE transactions on circuits & systems for video technology,2009,19(2):193-205.
[16] GONZ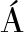LEZ-DE-SUSO J L, MART
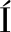NEZ-ENR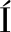QUEZ E, DAZ-DE-MARA F. Adaptive lagrange multiplier estimation algorithm in HEVC[J]. Signal processing: image communication, 2017, 56:40-51.