0 引言
网络控制系统(networked control system，NCS)由通信技术、网络技术和计算机技术等组成[1]。 NCS具有低耗、安装简便和高可靠性的优点，是研究复杂系统的重要工具[2]。 NCS的应用很多，例如深度神经网络[3]、内视镜检查[4]以及无线传感网络[5]。在数据传输的过程中不可避免会产生时变时延和丢包，给系统带来不利影响，甚至破坏其稳定性[6-7]。 与Kalman滤波相比，H∞滤波器具有较好的鲁棒性，引起人们的广泛关注[8]。
在控制系统中，时延经常出现会导致系统的性能降低[9]。数据包丢失也会影响系统性能。文献[10-11]讨论了带有数据包丢失的网络控制系统H∞滤波问题。在鲁棒滤波的早期研究中，基于二次稳定性引入李雅普诺夫方程，以保证该未知系统的鲁棒性能[12]。文献[13]利用伯努利变量描述丢包问题，并建立带丢包的NCS模型，设计了H∞滤波器。文献[14]利用变采样周期的方式，建立网络控制系统，并证明其满足均方指数稳定性。
此外，Middleton等[15]建立了Delta算子方法。 Delta算子具有如下优势：Delta算子方法将连续与离散系统进行统一处理，在快速采样下Delta算子具有更好的数字特性，运用Delta算子离散化模型便于观察和分析不同采样周期下的系统性能[16]。
1 问题描述
笔者研究了具有双边丢包和混合随机时延的Delta算子描述网络控制系统的H∞滤波问题。 使用马尔科夫链建立滤波误差系统，通过李雅普诺夫泛函证明系统的渐近稳定性和H∞性能。
Delta算子定义[15]如下：
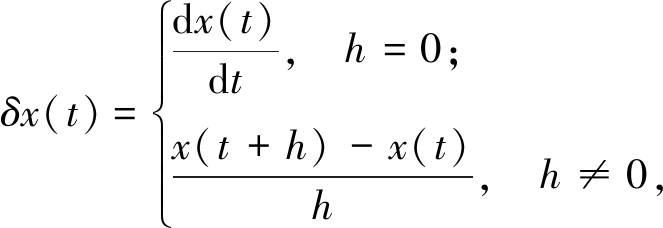
式中:h为采样周期。
考虑下面的Delta算子系统：
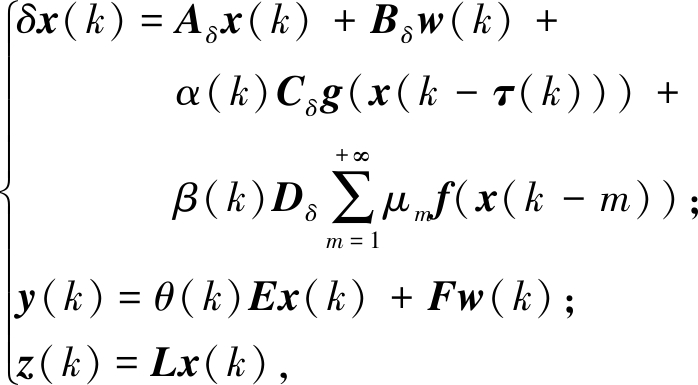
(1)
式中：x(k)∈Rn，表示系统状态向量；τ(k)为有界时变时延且是正整数，满足τm≤τ(k)≤τM，τm、τM分别为时延下界和上界；y(k)∈Rr，为系统输出；z(k)∈Rp，为要估计的信号；w(k)∈Rs，为外部扰动，且属于L2[0,∞)；g(x(k))=[g1(x(k)),…,gn(x(k))]T，f(x(k))=[f1(x(k)),…, fn(x(k))]T，为具有适当维数的非线性矩阵。
假设τ(k)取值于有限集合，发生概率如下：
Prob{τk}=λj，j=1,2,…，q，
(2)
式中：λj是一个正的标量，且
注1:网络控制系统由网络将传感器、控制器和执行器连接，形成分散式闭环反馈控制系统，用于远程操控。网络传输可能受到外部非线性因素的影响。
注2:系统(1)包含无限分布时滞项
它可看成
k(t-s)f(x(s))ds的离散化形式[9]。
式(1)中随机变量α(k)、β(k)、θ(k)相互独立，并符合Bernoulli 分布，满足：
Prob{α(k)=1}=α0；
Prob{β(k)=1}=β0；
Prob{θ(k)=1}=θ0，
其中，θ(k)=1代表传感器至控制器的数据传输正常；θ(k)=0代表数据包丢失。
考虑如下形式的滤波器:
(3)
式中：xf(k)∈Rn为滤波器状态；
为滤波器输入，
为信号z(k)的估计；Af、Bf、Lf为待定的滤波器矩阵。
存在通信序列矩阵：
Πi=diag{g(i-1),g(i-2),…,g(i-q)},
i∈{1,2,…,q},
(4)
式中：
表示k时刻控制器到执行器进行通信的节点，在k时刻成功发送数据，
存在数据包丢失时，令
进行处理[8]，可得同时含有马尔科夫链和通信序列的滤波器输入：
(5)
定义向量
e(k)=z(k)-zf(k)。
由式(1)～(5)可以推出滤波误差系统模型：
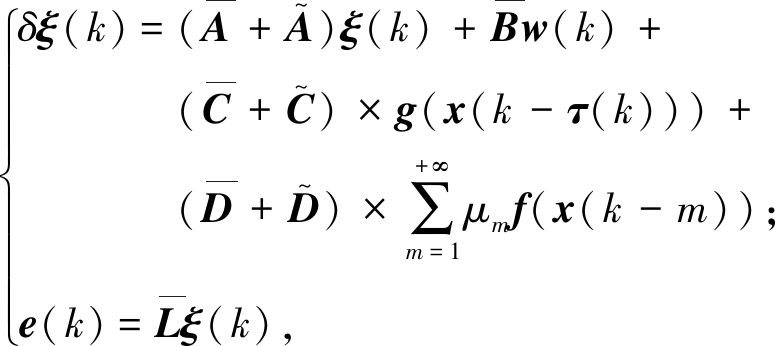
(6)
式中：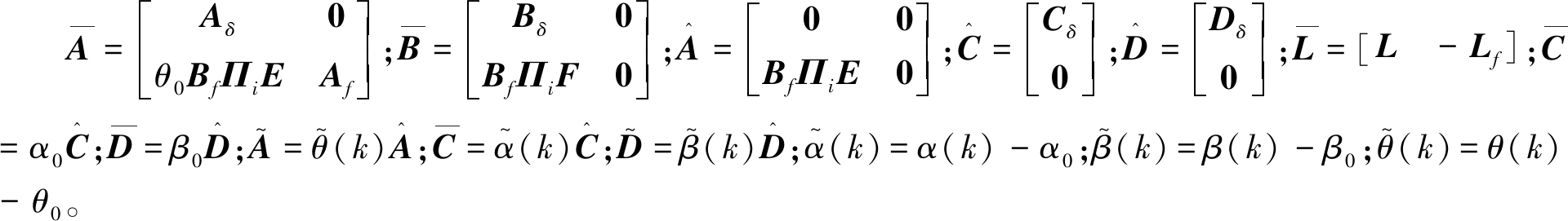
由此笔者考虑的问题转化成在马尔科夫跳跃系统(6)中滤波器的设计问题。
引理1[9] 设M∈Rn×n是半正定矩阵，xi=Rn，ai≥0(i=1,2,…)。若相关序列是收敛的，则以下不等式成立：
(7)
现对非常数g(·)和f(·)进行假设:
假设1 g(·)和f(·)向量有界，且
g(0)=f(0)。
假设2 矩阵g(·)和f(·)是连续的，且对于∀x,y∈Rn，有
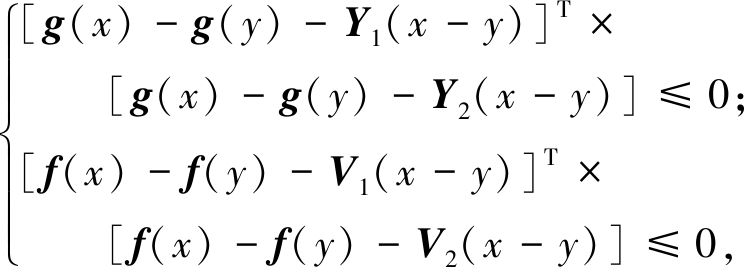
(8)
式中：Y1、Y2、V1和V2为常数矩阵。
2 主要结果
定义1[8] 当w(k)=0时，滤波误差系统是均方渐近稳定的，如果对于任意初始条件，下式成立：
(9)
定理1 对于离散网络控制系统(1)，当w(k)=0时，如果存在正定矩阵P,Qj 和Zj(j=1,2,…,q)，使得
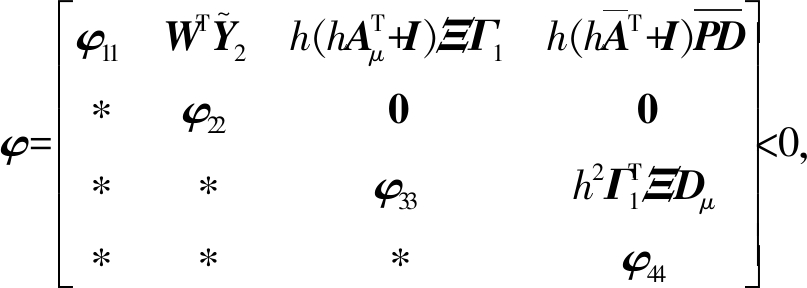
(10)
则滤波误差系统是均方渐近稳定的。式中对称矩阵中的对称项表示为*。
diag{Q1,Q2,…,Qq}；
Ξ=diag{P,P,…P}，σα=(1-α0)α0；
σθ=(1-θ0)θ0，σβ=(1-β0)β0；
证明：构造Delta域Lyapunov泛函：
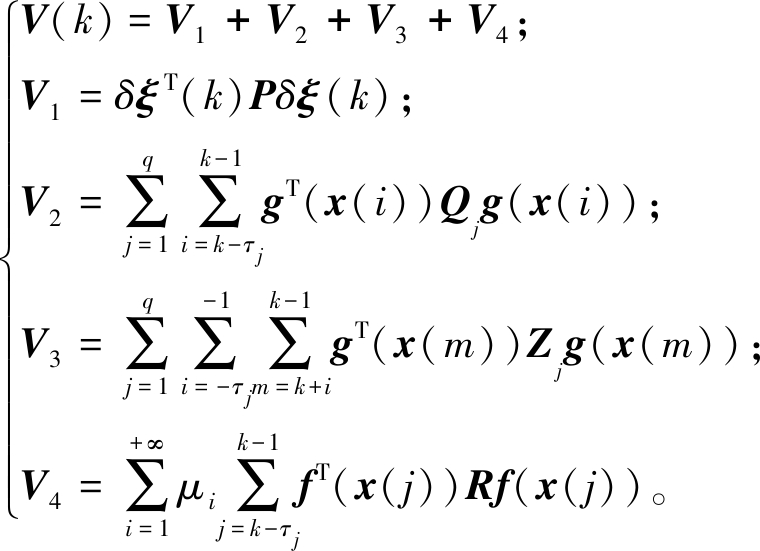
(11)
当w(k)=0时，
E{ΔV1}=E{δξT(k+1)Pδξ(k+1)-
(12)
类似地，
gT(x(k-τj))Qjg(x(k-τj))))=
gT(x(k-τj))Qjg(x(k-τj))，
(13)
gT(x(k+i))Zjg(x(k+i)))}≤
(14)
(x(k-m)))T×
(15)
由假设1和假设2可直接得到：
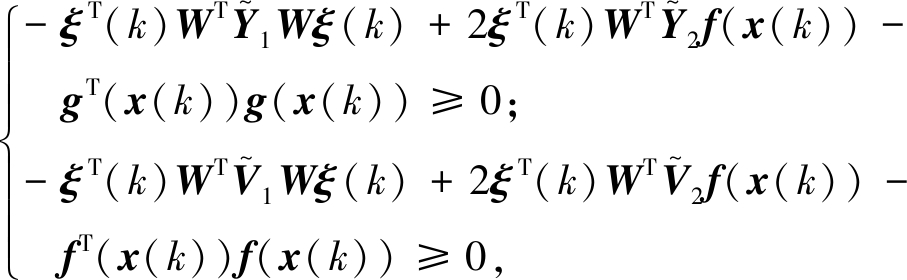
(16)
式中：
令
可以得出：
(17)
由Lyapunov稳定性理论可知，系统均方稳定。
定义2[8] 给定标量 γ>0，滤波误差系统是渐近稳定的且满足H∞性能γ，如果在零初始条件下，对于一切非零的w(k)∈L2[0,∞)，系统渐近稳定，并且滤波误差e(k)满足：
(18)
定理2 给定参数Af，Bf和Lf，设γ是一个正常数，且当w(k)=0时滤波误差系统是均方稳定的，则在零初始条件下，对于任意非零w(k)∈L2[0,∞)，如果存在正定矩阵P、Qj、Zj(j=1,2,…,q)、R，使得：
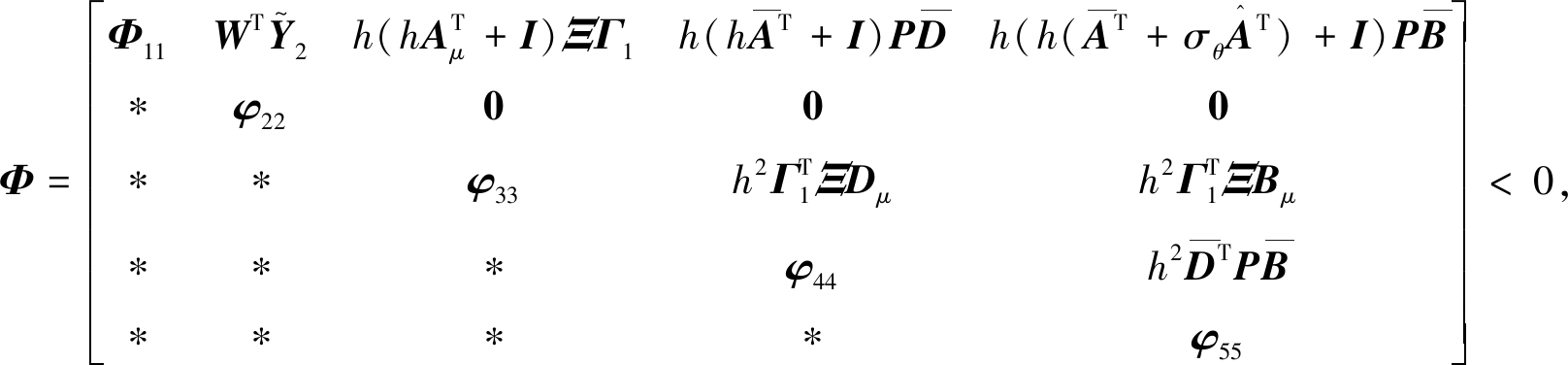
(19)
则滤波误差系统渐近稳定并具有H∞性能。式中：
φ22、φ33 和φ44由式(10)给出。
证明：易证明当Φ<0 时φ<0，由定理1可知，当w(k)=0时滤波误差系统是均方渐近稳定的。 为研究其在零初始条件下的H∞性能，由此引入性能指标：
(20)
构造与定理1相同的Lyapunov泛函，进行类似的处理，可得
(21)
则由式(20)～(21)可得
式中:
根据式(19), 可推出J(n)≤0，则 n→∞时可得
定理3 对于离散网络控制系统，给定常数γ>0，如果存在矩阵P>0，R>0，Qj>0，Zj>0，j=1,2,…,q，X和Lf满足：
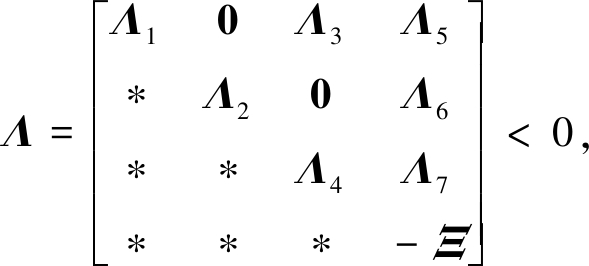
(22)
式中:
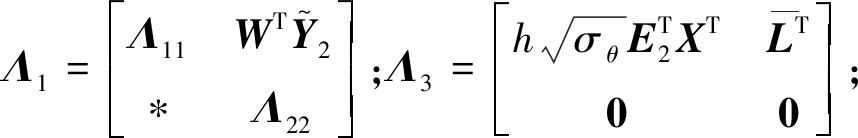
Λ2=diag{Λ33,Λ44};
Λ4=diag{-γ2I,-P,-I};
Λ11=
U1=A0TP+E1TXT;
若以上条件有可行解，则满足条件的H∞滤波器参数可由X和Lf得到：
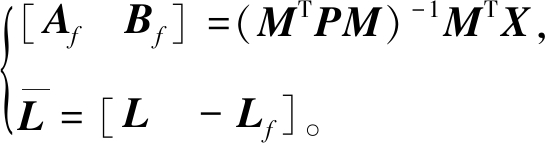
(23)
证明： 令
则式 (19) 等价于：
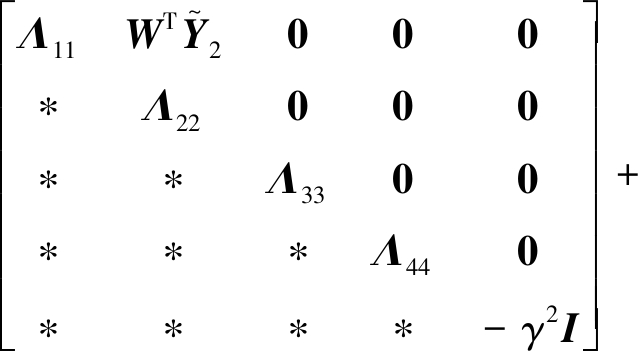
Γ1TΞ-1Γ1+Γ2TP-1Γ2+Γ3TΓ3<0。
应用 Schur 补引理[16],得
其中,
定理2中的参数可以写成如下形式:
证毕。
3 数值仿真
为验证本文方法的可行性，选取如下参数：
情形1：随机变量 α(k)、β(k)和θ(k)分别为
α0=0.8；β0=0.6；θ0=0.5。
利用MATLAB的LMI工具箱，通过计算求得γ=1.641,滤波器参数为：
通过计算得到：
情形2：随机变量 α(k)、β(k)和θ(k)分别为
α0=0.5；β0=0.7；θ0=0.5。
利用MATLAB的LMI工具箱，通过计算求得γ=1.507，滤波器参数为：
通过计算得到：
注3：由情形1、情形2可知，丢包率的改变在一定程度上影响系统的H∞性能。当参数取值α0=0，β0=0，θ0=1时，可得文献[8]中的结果。
系统的待估信号、滤波器估计信号和滤波误差状态曲线分别如图1、2所示。由图可以看出，原系统的待估计信号能很好地被滤波器估计，且因为
证明系统具有H∞性能，仿真结果可以表明本文方法的可行性。
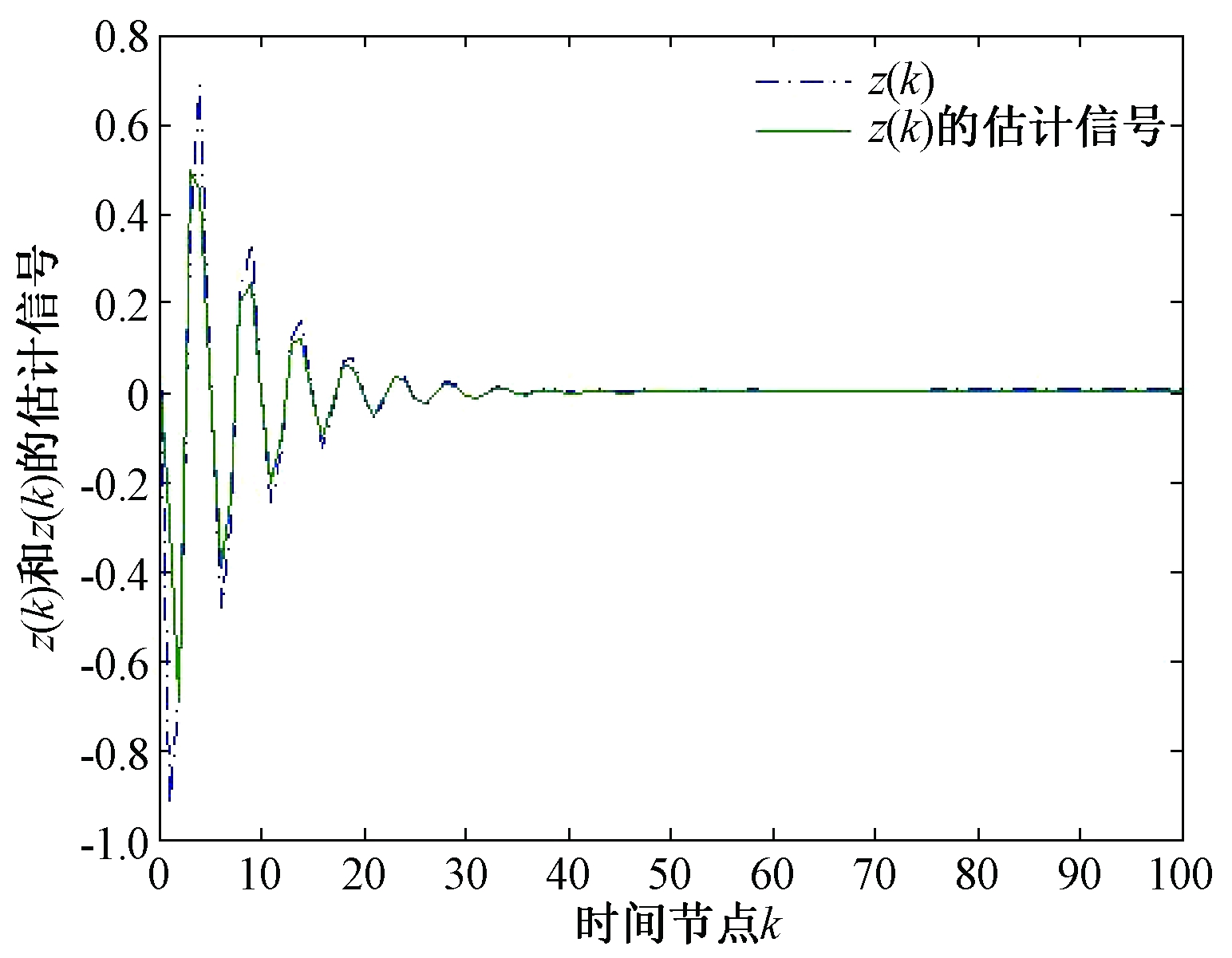
图1 z(k)和z(k)的估计信号
Figure 1 z(k) and estimated signal of z(k)
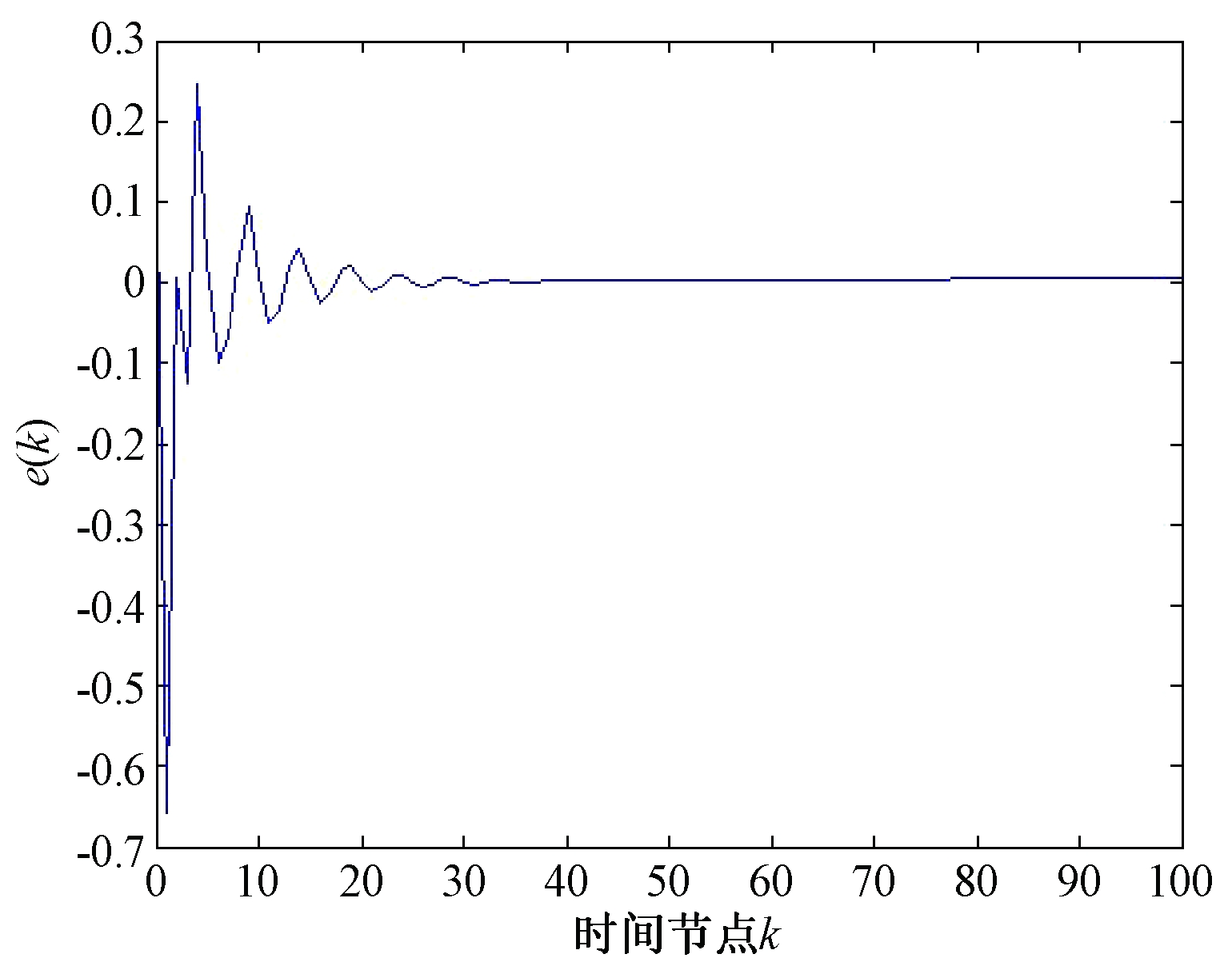
图2 滤波误差e(k)
Figure 2 Filtering error response e(k)
4 结论
研究了具有混合随机时延和双边丢包的Delta算子网络控制系统的H∞滤波问题。通过马尔科夫随机过程，构造基于Delta算子的滤波误差系统，采用Lyapunov泛函方法，证明该系统的渐近稳定性，并给出滤波器的设计方法。数值算例表明了所提方法的有效性。
[1] PAN Y N，YANG G H. Novel event-triggered filter design for nonlinear networked control systems [J]. Journal of the franklin institute, 2018，355(3):1259-1277.
[2] 齐迹，李艳辉. 带宽受限随机网络控制系统的量化H∞滤波[J].计算机仿真，2014，31(7):287-290.
[3] XIN W, WANG J Y, LI X. A feed-forward wavelet neural network adaptive observer-based fault detection technique for spacecraft attitude control systems [J]. Chinese journal of electronics, 2018, 27(1): 102-108.
[4] CASTRO C A, ALQASSIS A, SMITH S, et al. A wireless robot for networked laparoscopy [J].IEEE transactions on biomedical engineering, 2013, 40(4):930-936.
[5] MA D X, MA J, XU P M. An adaptive clustering protocol using niching particle swarm optimization for wireless sensor networks [J]. Asian journal of control, 2015, 17(4):1435-1443.
[6] 张端金，刘雪，范鑫. 基于Delta算子时变时延网络控制系统的H∞滤波[J]. 郑州大学学报(工学版)，2016，37(2):10-14.
[7] 刘义才，刘斌，张永，等. 具有双边随机时延和丢包的网络控制系统稳定性分析[J].控制与决策，2017, 32(9):1565-1573.
[8] GAO X B, ZHANG D J.H∞ filtering for networked control systems with limited communication via delta operator[C]∥2016 the 12th World Congress on Intelligent Control and Automation(WCICA).Guilin, China: IEEE, 2016:339-343.
[9] MATHIYALAGAN K, PARK J H, SAKTHIVEL R,et al. Robust mixed H∞ and passive filtering for networked Markov jump systems with impulses[J].Signal processing, 2014，101: 162-173.
[10] SHEN H, WU Z G, PARK J H. Reliable mixed passive and H∞ filtering for semi-Markov jump systems with randomly occurring uncertainties and sensor failures[J]. International journal of robust and nonlinear control, 2015, 25(17):3231-3251.
[11] 周颖，郑凤，何磊. 具有时变时延和丢包的网络控制系统H∞控制 [J].计算机技术与发展，2017，27(5):164-169.
[12] CHANG X H, XIONG J，PARK J H. Resilient H∞ filtering for discrete-time systems[J]. Signal processing, 2016,127: 71-79.
[13] 李明扬，张玲，褚东升，等. 一类随机不确定网络控制系统的H∞滤波器设计[J].中国海洋大学学报(自然科学版)，2018，48(4):134-139.
[14] 刘艳红，杨东伟. 基于观测器的网络控制系统均方指数稳定控制器设计[J].郑州大学学报(工学版)，2018，39(3):10-14.
[15] MIDDLETON R H, GOODWIN G C. Improved finite word length characteristics in digital control using delta operators[J]. IEEE transaction on automatic control, 1986, 31(11):1015-1021.
[16] YANG H J, XIA Y Q, SHI P,et al. Analysis and synthesis of delta operator systems[M]. Berlin: Springer, 2012.