0 引言
目前,国内外水污染溯源问题的研究较多,其本质是水质模型参数的识别。 参数识别方法主要有马尔科夫链蒙特卡罗算法(Markov chain Monte Carlo,MCMC)[1-7]、微分进化算法[8-11]、遗传算法[12-13]和最小二乘算法[14]等。陈海洋等[3]运用经典MCMC算法实现了水体污染源项的识别,得到了污染源强度、污染源位置和污染源排放时长3个未知参数的估计值。闵涛等[11]利用遗传算法求解对流-扩散方程源项识别反问题。这些算法可分为确定性方法和不确定性方法,其中确定性方法未考虑误差因素,得到参数确定的估计值,但容易丢掉“真值”；不确定性方法具有较强的随机性,收敛速度慢,计算量随着参数的增多而呈指数增长,得到待估参数的一个小的可靠范围。其中,MCMC方法应用较为广泛。Metropolis算法[13-14]是一种经典的MCMC方法,应用非常广泛。大多数MCMC算法都是通过改进Metropolis算法得到的,比如延迟拒绝算法(delayed rejection, DR)[15-16]、自适应Metropolis算法(AM)[17]、延迟拒绝自适应Metropolis算法(DRAM)[18]等。DRAM算法是一种高效自适应MCMC算法,其本质是把DR算法和AM算法二者组合起来。DR算法保证了马尔科夫链的局部自适应,AM算法采用全局自适应调整策略,因此DRAM算法能够对MCMC链条进行全局和局部的自适应,DRAM算法抽样效率优于DR算法和AM算法各自单独使用的情况[19]。但是Metropolis算法和DRAM算法都只有一条链,容易陷入到局部最优值[19-20],计算结果给决策者造成一定的负面影响。
运用二维地下水水质对流-扩散方程,通过贝叶斯公式建立水体污染源识别模型,得到污染源强度、排放位置(x,y)和排放时长4个未知参数的后验概率密度函数,并运用拉丁超立方抽样方法[21]优化DRAM算法,实现参数反演过程中准确性与效率的双提高,为突发性水污染反问题研究提供借鉴。
1 研究方法
1.1 贝叶斯公式
贝叶斯公式[22-23]如下：
(1)
式中：α为模型的未知参数；d为实测数据；p(α|d)为参数的后验概率密度函数；p(α)为参数的先验概率密度函数；p(d|α)为条件概率密度函数；p(d)为归一化的积分常数。
假设模型中未知参数共有m个,则α=(α1,α2,…,αm)。环境水力学的模型参数都分布在一个特定的范围内,可以认为每个参数都服从均匀分布,且α1,α2,…,αm相互独立。模型参数αi的先验概率密度函数可定义为：
(2)
总的先验分布p(α)可表示为：
(3)
假设模型中实测值共有n个,即d=(d1,d2,…,dn)。di表示第i个实测数据,Ci(x,y,t|α)表示相应的第i个预测值,则εi=di-Ci(x,y,t|α)为测量误差,i=1,2,…,n。假设测量误差服从均值为0、标准偏差为σ的正态分布,且相互独立,则条件概率密度函数p(d|α)可表示如下：
(4)
联合式(1)～(4),可得后验概率密度函数p(α|d)为：
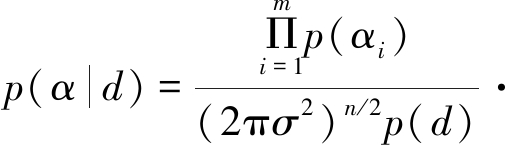
(5)
由于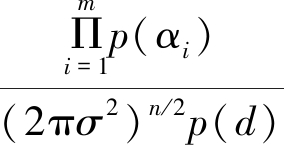
是与参数α的选取无关的固定数,可记为λ。故式(5)可写为：
(6)
在实测数据d固定的条件下,式(6)是关于参数α的函数。式(6)通过积分求解参数α的概率分布,计算较为复杂,难以得出明确的解析表达式。并且随未知参量维数的增加,数值积分算法的计算量将呈指数增长,实现复杂且难度较大。
1.2 延迟拒绝自适应Metropolis算法
式(6)一般可采用马尔科夫链蒙特卡罗方法(MCMC)近似求解。MCMC方法的核心是Monte Carlo模拟方法和Markov Chain抽样方法。当“概率事件”样本点足够多时,频率可以近似代表概率,这是Monte Carlo模拟方法的本质,而Markov Chain抽样方法能够保证Markov链花更多的时间在概率大的区域,节省Monte Carlo模拟方法的工作量。
Metropolis算法是一种经典的MCMC算法,应用非常广泛,具体算法参见文献[13-14],其提议分布一旦设定便保持不变,当提议分布远离目标分布时,马尔科夫链收敛速度会变慢。为了提高马尔科夫链收敛效率,Haario等[18]将DR算法和AM算法结合提出了高效自适应DRAM算法,其具体步骤如下。
1.2.1 非自适应阶段
(1)在模型未知参数α先验范围内随机产生初始的参数样本Xt(t=1),非自适应阶段迭代次数为N0,提议分布为高斯分布qt=N(Xt,C0),其中C0为协方差矩阵,要求C0满足对称正定条件,并且高斯分布满足对称随机游走。
(2)从提议分布N(Xt,C0)中抽取一个参数样本X*;产生[0,1]上的随机数u;计算接受概率
其中p(X*|d)与p(Xt|d)由式(6)计算得到。如果
接受X*,即Xt+1=X*;否则,拒绝X*,即Xt+1=Xt。
(3)重复过程(2),直至达到迭代次数N0。
1.2.2 自适应阶段
(1)通过步骤(1)已抽取到样本点X1,X2,…,XN0,此时t=N0。下一步提议函数
式中
表示参数α的维数,sm=2.38/m2[18];ε表示一个很小的正数,可取为10-6,目的是保证Ct1为正定矩阵;Im是一个m维单位矩阵。自适应阶段迭代次数为N。
(2)马尔科夫链的当前状态为Xt,从提议分布qt+1中抽取一个样本
计算接受概率
产生[0,1]上随机数u1。
如果
接受
即
转入过程(3)。
如果
设定
从
中抽取一个样本
计算接受概率
产生[0,1]上随机数u2;如果
接受
即
转入(3)。
如果
从
中抽取一个样本
计算接受概率
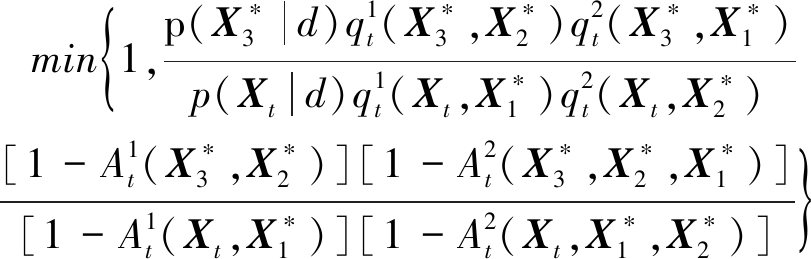
产生区间[0,1]上随机数u3;如果
接受
即
转入过程(2)。
(3)重复过程(2),直至达到迭代次数N。
1.3 拉丁超立方抽样
采用Metropolis算法和DRAM算法求解多维参数反演问题,Markov Chain容易受到样本初始点的影响,可能在局部最优处达到稳定或者产生难以收敛的问题。
为了保证样本初始点的随机性和均匀性,本研究基于拉丁超立方抽样方法[21]对DRAM算法进行改进。拉丁超立方抽样方法是一种多维分层随机抽样方法,具有良好的散布均匀性和代表性。假设要在m维模型参数α先验范围[Ai,Bi](i=1,2,…,m)内抽取q组样本,具体步骤如下：
(1)把m维模型参数的m个先验范围[Ai,Bi](i=1,2,…,m)都均分成q个小区间,小区间可记为[Aij,Bij](i=1,2,…,m;j=1,2,…,q),总共产生m×q个小区间。
(2)在任一小区间[Aij,Bij]中随机抽取一个数,记为αij,总共产生m×q个数,组成矩阵为
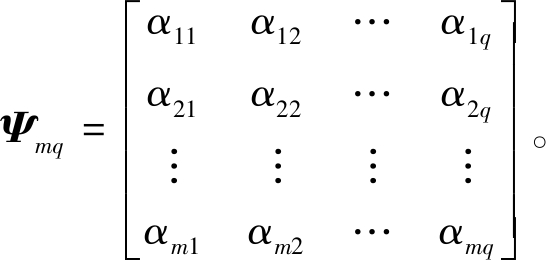
(3)对矩阵Ψmq中行向量[αi1,αi2,…,αiq](i=1,2,…,m)进行随机排序，所得向量记为[βi1,βi2,…,βiq](i=1,2,…,m);由此得到矩阵
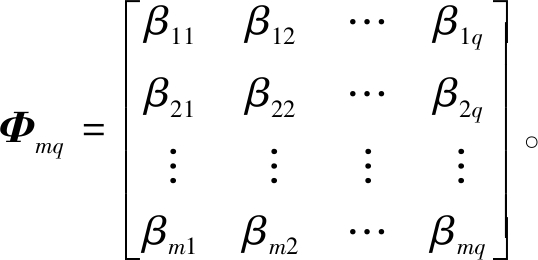
(4) 矩阵Φmq中每个列向量是一组样本,共抽取得到q组样本。
1.4 改进型多链DRAM算法
改进型多链DRAM算法具体步骤：
(1)运用拉丁超立方抽样方法,在模型参数先验范围内随机抽取q组初始样本。
(2)分别以q组初始样本作为初始点采用DRAM算法进行迭代运算,得到q条Markov Chains。
(3)对上面q条Markov Chains求平均值作为最终结果。
2 算例应用
2.1 算例概述
均质各向同性地下含水层中,二维地下水水质对流-扩散方程[24-25]可以表述为：
(7)
式中:C为测点(x,y)在t时长的污染物的质量浓度,mg/L；t为污染物排放后开始预测的时长,d；Dx、Dy分别为纵向、横向的弥散系数, m2/d；u为地下含水层水流平均流速, m/d。
对于污染物瞬时点源排放模式,方程的解析解可表示为：
(8)
式中:M为污染物的排放量,g；h为含水层的厚度,m；x、y分别为预测点距排放点的纵向、横向距离,m；k为含水层的有效孔隙率。
假设研究区域为均质各向同性地下含水层(建立坐标系，如图1)。含水层厚度为h=1 m, 孔隙率k=0.3，x轴代表含水层中水流的方向, 水流速度为u=5 m/d；纵向弥散系数为1.5 m2/d, 横向弥散系数为0.3 m2/d。待求参数真值:污染物泄漏点坐标为(X0=200 m, Y0=200 m), 污染源强度M=1 000 g, 污染源排放时长T0=110 d。观测点D坐标为(X1=800 m, Y1=215 m)。
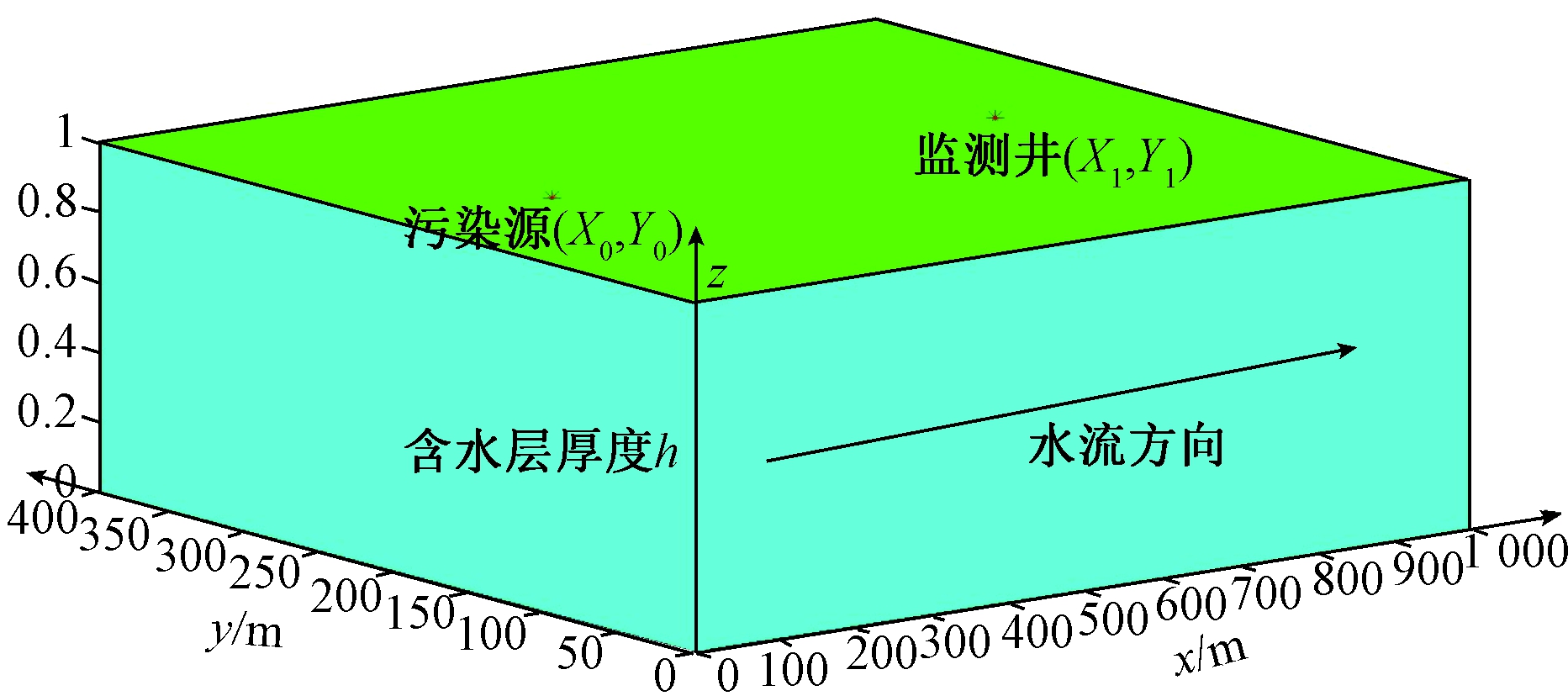
图1 算例模型示意图
Figure 1 Sketch of example model
2.2 监测数据
以构建的算例模型的计算值作为观测值, 设定2017年5月1日上午10∶00点作为初始监测时间,其后每隔2 d测量一次,直至2017年5月21日上午10∶00点结束,将研究区水文地质参数代入式(8),可计算得出观测点D的污染物浓度di,以此作为观测点D的污染物的观测值,如表1所示。
表1 观测点D处污染物观测浓度序列
Table 1 Sequence value of pollutant concentration at observation point D
时刻5月1日5月3日5月5日5月7日5月8日5月10日质量浓度/(mg·L-1)0.014 800.061 200.179 60.381 10.594 00.690 7时刻5月12日5月15日5月17日5月19日5月21日质量浓度/(mg·L-1)0.608 00.410 60.215 50.088 900.029 16
2.3 结果及比较
根据先验信息,污染源强度M、污染源位置坐标(X0,Y0)和污染源排放时长T0 4个待求参数的取值范围分别为：400 g≤M≤1 600 g, -200 m≤X0≤600 m, 185 m≤Y0≤215 m, 60 d≤T0≤160 d。运用MATLAB软件编程,对比分析不同算法的求解结果。
2.3.1 Metropolis算法求解结果
采用经典Metropolis算法构建马尔科夫链对模型进行求解,马尔科夫链选取初始点不同,4个待估参数M、X0、Y0、T0的迭代曲线差别很大。以待估参数M为例,随机选取两组不同初始样本,如样本点1:(M,X0,Y0,T0)=(827.44,592.05,190.59,80.77)；样本点2:(M,X0,Y0,T0)=(687.50,141.15,213.89,146.97),待估参数M迭代曲线见图2。
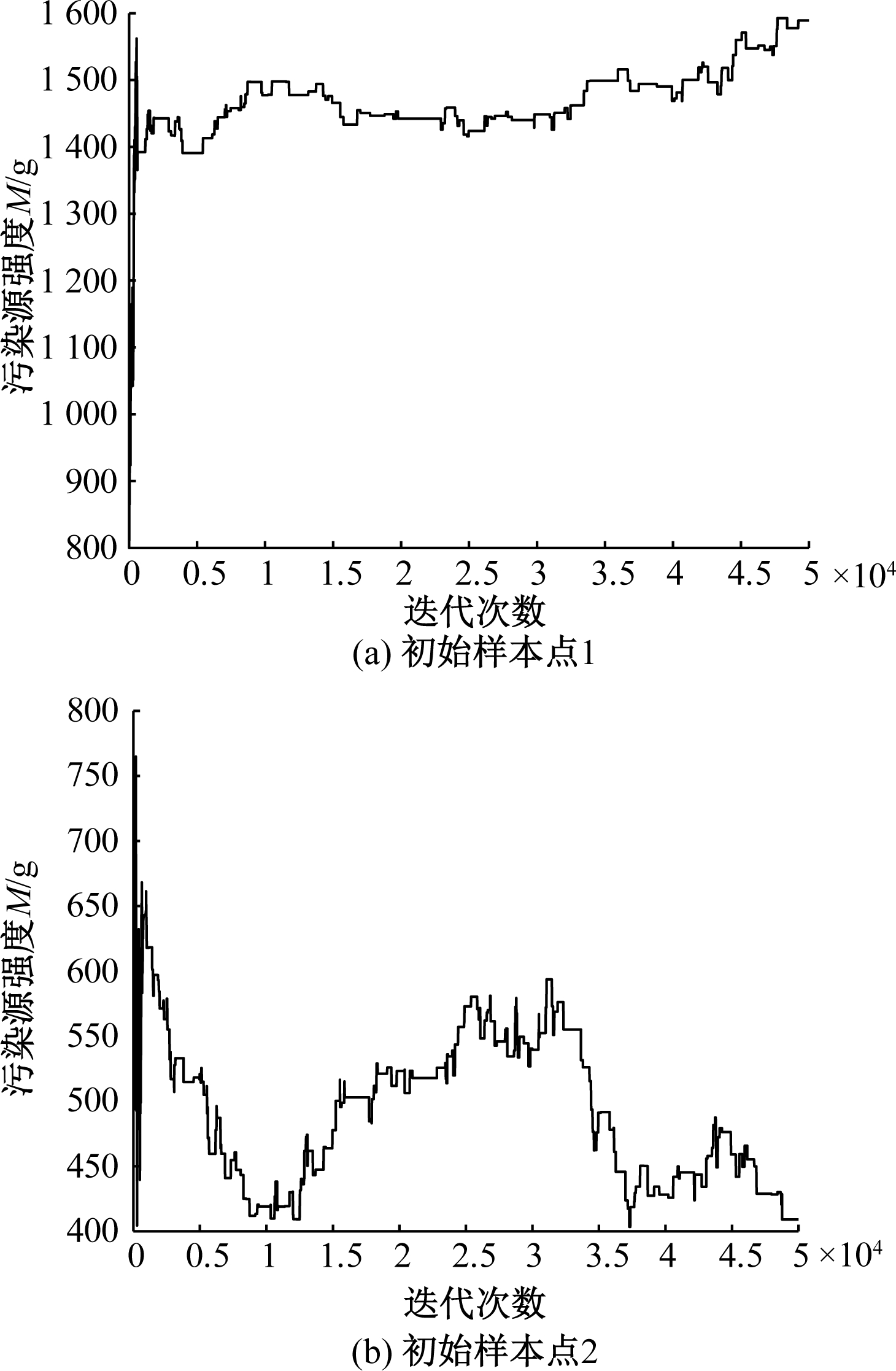
图2 基于Metropolis算法的不同初始点模型参数M迭代曲线图
Figure 2 Iterative curves of model parameter M based on Metropolis algorithm with different initial values
由图2(a)可知,在初始样本点为M1=827.44 g Metropolis算法迭代到5 000次时,参数M值逐渐趋于稳定,并最终在M=1 450 g处收敛,但是该值与真值(M=1 000 g)相差较大,误差达45%。另由图2(b)可知,在样本初始点为M2=687.50 g,Metropolis算法迭代到50 000次时,参数M值仍未收敛。因此运用Metropolis算法求解污染源强度时,求解结果受样本初始点的影响较大,容易出现局部最优或者难以收敛的问题。同理,在求解另外3个待求参数X0、Y0、T0时也会出现类似问题。
2.3.2 多链Metropolis算法求解结果
为防止反演结果的局部最优,构建基于拉丁超立方抽样的多链Metropolis算法求解算例(设定40条链, 单链长度为50 000)。污染源强度M、污染源位置坐标(X0,Y0)和污染源排放时长T0的反演迭代曲线见图3。
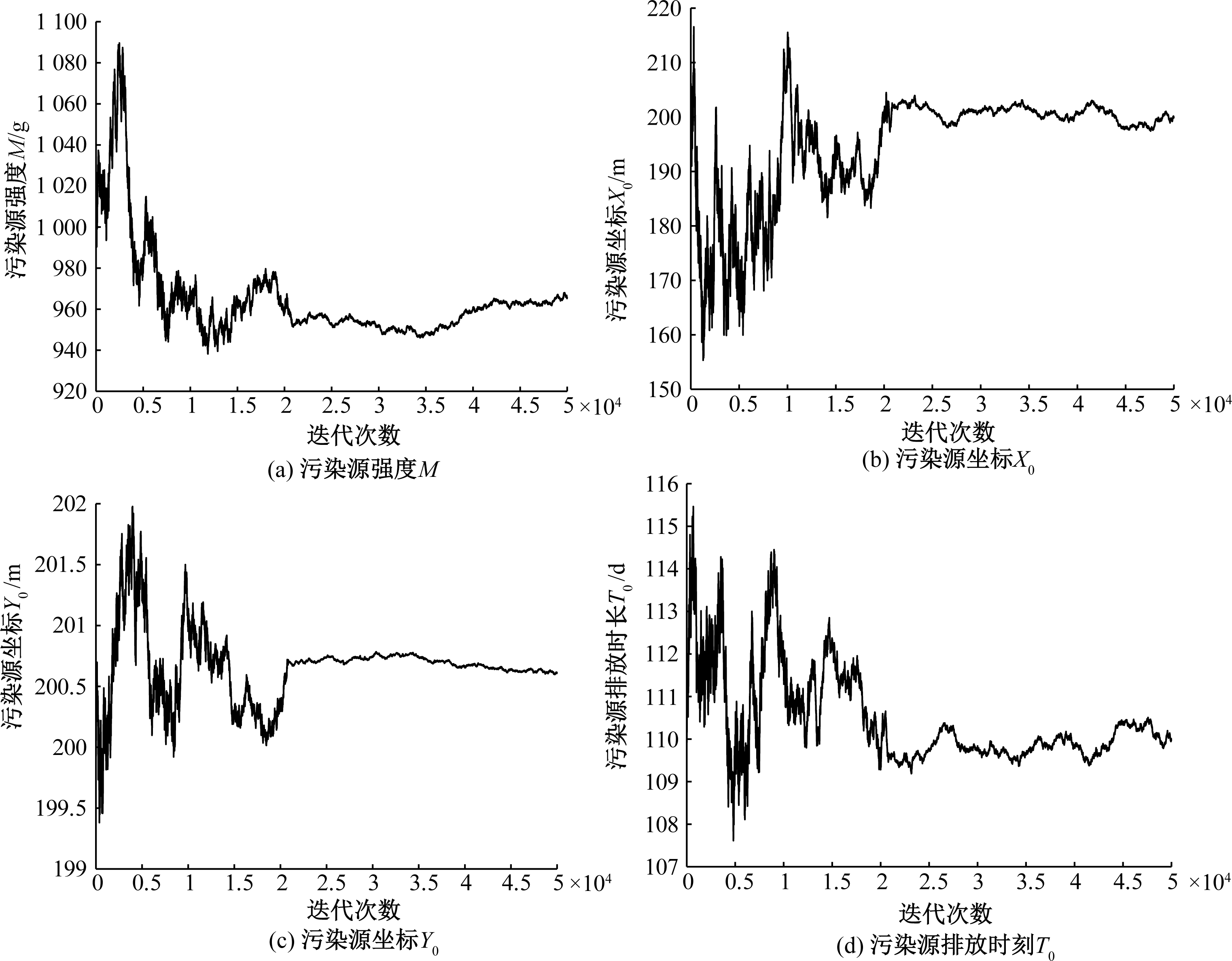
图3 基于多链Metropolis算法的模型参数迭代曲线
Figure 3 Iterative curves of model parameters based on multi-chain Metropolis algorithm
由图3可知, 当基于拉丁超立方抽样的多链Metropolis算法迭代到25 000次时,4个参数反演结果均基本在真值处达到稳定且收敛,而且通过程序验证迭代结果不受样本初始点选取的影响,有效解决了经典Metropolis算法受初始点的影响导致不收敛或局部最优的问题,表明该算法具有较强的稳定性。剔除前25 000次不稳定结果,对剩余的25 000次计算结果进行后验统计分析,见表2。
由表2可知,基于拉丁超立方抽样的多链Metropolis算法得出的4个待估参数M、X0、Y0、T0的均值与真值的误差分别为4.36%、0.18%、0.35%、0.08%,中值误差分别为4.30%、0.15%、0.35%、0.06%,表明基于拉丁超立方抽样方法的Metropolis算法可实现计算结果的全局最优,有效提高反演结果的准确性。
表2 基于多链Metropolis算法的模型参数后验统计结果
Table 2 Posterior statistical results of model parameters based on multi-chain Metropolis algorithm
参数均值均值误差/%中值中值误差/%污染源强度M/g956.384.36957.024.30污染源坐标X0/m200.360.18200.290.15污染源坐标Y0/m200.690.35200.690.35泄漏时间距离首次监测时间T0/d109.910.08109.930.06
2.3.3 改进型多链DRAM算法求解结果
多链Metropolis算法虽然有效提高了反演结果的准确性,但是迭代次数需达到25 000次时才能收敛,反演效率相对偏低,为此笔者构建基于拉丁超立方抽样的多链DRAM算法(设定40条链，单链长度为12 000)进行参数求解。 4个参数的反演遍历均值图见图4。
由图4可知,改进型多链DRAM算法迭代到8 000次时,4个参数取值均基本达到稳定,与基于拉丁超立方抽样的多链Metropolis算法(25 000次时迭代稳定且收敛)相比,速率提高68%,并且通过程序验证迭代结果不受样本初始点的影响,表明基于拉丁超立方抽样的DRAM方法具有较高的反演效率及稳定性。
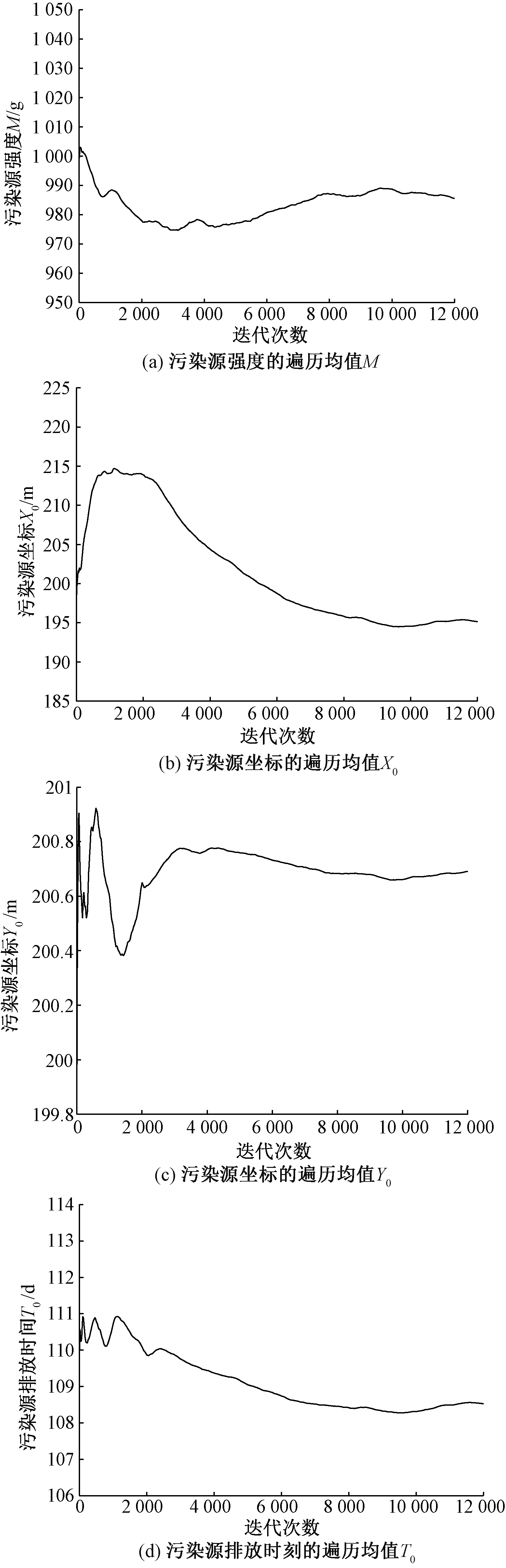
图4 基于改进型多链DRAM算法的模型参数遍历均值图
Figure 4 Ergodic mean plots of model parameters based on improved multi-chain DRAM algorithm
对于改进型多链DRAM算法的反演结果,剔除前10 000次不稳定结果,对剩余的2 000次模型参数进行后验统计分析,见表3。由表3可知,该算法在提高反演效率的前提下,同样可保证反演结果的准确性。
表3 基于改进型多链DRAM算法的模型参数后验统计结果
Table 3 Posterior statistical results of model parameters based on improved multi-chain DRAM algorithm
参数均值均值误差%中值中值误差%污染源强度M/g969.933.011 013.832.62污染源坐标X0/m197.991.01186.770.93污染源坐标Y0/m200.840.42200.380.41泄漏时间距离首次监测时间T0/d109.600.37107.370.35
3 结论
(1)利用Bayesian公式以概率语言解决突发性地下水污染反问题,可有效获取污染源信息(污染源强度、污染源位置和污染源排放时长)。
(2)运用经典Metropolis算法求解污染源信息时,求解结果受样本初始点的影响较大,容易出现局部最优或者难以收敛的问题,反演得到的未知参数估计值误差较大。
(3)基于拉丁超立方抽样的Metropolis算法可实现反演结果的全局最优,有效提高反演结果的准确性,但是效率相对低下。 基于拉丁超立方抽样的DRAM算法在保证反演结果准确性的前提下,可显著提高反演效率,其可靠性和稳定性均优于经典Metropolis算法。
[1] HAARIO H, SAKSMAN E, TAMMINEN J. An adaptive Metropolis algorithm [J]. Bernoulli, 2001, 7(2): 223-242.
[2] ZENG L Z, SHI L S, ZHANG D X, et al. A sparse grid based Bayesian method for contaminant source identification[J]. Advances in water resources, 2012, 37: 1-9.
[3] 陈海洋,腾彦国,王金生,等. 基于Bayesian-MCMC方法的水体污染识别反问题[J]. 湖南大学学报(自然科学版),2012,39(6): 74-78.
[4] 杨海东,肖宜,王卓民,等. 突发性水污染事件溯源方法[J]. 水科学进展, 2014, 25(1): 122-128.
[5] 顾文龙,卢文喜,张宇,等. 基于贝叶斯推理与改进的MCMC方法反演地下水污染源释放历史[J]. 水利学报,2016, 47(6): 772-779.
[6] 朱嵩,毛根海,刘国华,等. 改进的MCMC方法及其应用[J]. 水利学报,2009,40(8)：1019-1023.
[7] RUZEK B, KVASNICKA M. Differential evolution algorithm in the earthquake hypocenter location [J]. Pure and applied geophysics, 2001, 158(4): 667-693.
[8] 牟行洋.基于微分进化算法的污染物源项识别反问题研究[J].水动力学研究与进展(A辑),2011,26(1):24-30.
[9] 张双圣, 强静, 刘喜坤, 等. 基于贝叶斯-微分进化算法的污染源识别反问题 [J]. 山东大学学报(工学版),2018,48(1):131-136.
[10] HOLLAND J H. Adaptation in natural and artificial systerms [M]. Ann Arbor, MI: University of Michigan Press, 1975.
[11] 闵涛,周孝德,张世梅,等. 对流-扩散方程源项识别反问题的遗传算法 [J]. 水动力学研究与进展(A辑),2004,19(4): 520-524.
[12] 王秀峰,卢桂章. 系统建模与辨识[M]. 北京：电子工业出版社,2004.
[13] METROPOLIS N, ROSENBLUTH A W, ROSENB-LUTH M N, et al. Equation of state calculations by fast computing machines[J]. The journal of chemical physics, 1953, 21(6):1087-1092.
[14] HASTINGS W K. Monte Carlo sampling methods using Markov chains and their applications[J]. Biometrika, 1970, 57(1):97-109.
[15] TIERNEY L, MIRA A. Some adaptive Monte Carlo methods for bayesian inference[J]. Statistics in medicine, 1999(17/18):2507-2515.
[16] MIRA A. Ordering and improving the performance of Monte Carlo Markov chains[J]. Statistical science, 2001,16(4): 340-350.
[17] HAARIO H, SAKSMAN E, TAMMINEN J. An adaptive Metropolis algorithm[J]. Bernoulli, 2001,7(2):223-242.
[18] HAARIO H, LAINE M, MIRA A, et al. DRAM: Efficient adaptive MCMC [J]. Statistics and computing, 2006, 16(4): 339-354.
[19] 张江江. 地下水污染源解析的贝叶斯监测设计与参数反演方法 [D]. 杭州: 浙江大学, 2017.
[20] VRUGT J A. Markov chain Monte Carlo simulation using the DREAM software package: theory, consepts, and MATLAB implementation [J]. Enviromental modeling & software, 2016,75:273-316.
[21] 戴英彪. 基于拉丁超立方试验设计的事故再现结果不确定性分析[D]. 长沙:长沙理工大学, 2011.
[22] 师黎,王艺. 基于贝叶斯估计的初级视皮层光栅朝向编码研究 [J]. 郑州大学学报(工学版),2012,33(6): 1-4.
[23] 刘厂,赵俊翔,胡海. 基于双贝叶斯估计的动态威胁运动状态估计 [J]. 郑州大学学报(工学版),2017,38(2): 55-60.
[24] 陈崇希,李国敏. 地下水溶质运移理论及模型 [M]. 武汉：中国地质大学出版社,1996.
[25] 郑春苗,BENNETT G D. 地下水污染物迁移模拟[M].2版. 北京：高等教育出版社,2009.