0 引言
一般将图像融合过程由低到高分为3个层次：像素级融合、特征级融合、决策级融合[1].目前，空间域和变换域是主要的两种在像素级别基础上的融合方法.空间域算法主要包括基于区域斯能量和加权[2]、基于核范数最小化[3]等融合算法.而变换域算法主要采用多尺度几何变换进行图像融合[4]，例如文献[5]提出的基于轮廓波变换(contourlet transform, CT)的图像融合算法；文献[6]提出的基于非下采样轮廓波变换(non-subsampled contourlet transform，NSCT)与脉冲耦合神经网络(pulse coupled neural network，PCNN)图像融合算法；文献[7]提出的基于剪切波变换(shearlet transform, ST)与PCNN的图像融合算法.目前，处于主流位置的是变换域融合算法，其中应用最为广泛的为CT和ST.与CT相比，ST符合紧框架理论，可以有效地对图像的特征信息进行提取，同时其离散形式很容易实现[8].因此，ST在图像融合中得到了广泛的应用[9-10].为了克服ST不具有平移不变性的缺点，也为了更好地利用图像的空间连续性，文献[10]利用文献[11]提出的基于两尺度向导滤波的融合算法思想，在复剪切波变换(complex shearlet transform，CST)域中引入图像的空间连续性.虽然该算法明显地提升了融合后图像的视觉效果，但是在图像数据保留方面还可以提升，也就是低频部分的融合规则还可以进行改进.
近年来，由于深度学习理论的研究逐步深入并在相关领域取得了较好的研究成果[12-13]，因此CNN也被应用于多聚焦图像融合中，如文献[12]提出的一种采用CNN的多聚焦图像融合规则.虽然该算法获得很好的图像融合效果,但是在图像融合的过程中，该方法并没有对图像进行高低频的划分，这显然不符合人眼的视觉规律.因此，笔者结合该融合规则提出了基于NSST域的多聚焦图像融合算法.
1 非下采样剪切波变换原理
设Shearlet变换的基函数为：
ψj,l,k(x)=|detA|j/2ψ(BlAjx-k),
(1)
式中：j≥0；l=-2j～2j-1；k∈Z2；ψ∈L2(R2)；Aj表示伸缩变换矩阵；Bl表示保区域的几何变换矩阵.
因此函数f的ST可表示为：
Sψ=〈f,ψj,l,k〉.
(2)
NSST[8]是ST的扩展，能够很好地克服图像的下采样操作，因而具备图像变换的平移不变性.在进行图像融合时，能够使融合图像中拥有更多源图像的信息特征，使整体的融合图像效果得到极大的改善.
2 基于卷积神经网络的图像融合规则
在基于CNN的图像融合算法中，图像融合中决策图的生成通常被看作分类问题进行分析.文献[12]给出了基于CNN的一种多聚焦图像融合算法，将图像融合的主要任务转变成设计CNN的网络架构.而活动水平测量和融合规则可以通过大量的图像数据进行CNN模型训练生成[12].
文献[12]采用了文献[14]中提出的Siamese结构的CNN模型，如图1所示.由图1可知，网络中的每个分支具有3个卷积层和1个最大池化层.笔者设置图像块的大小为16×16，每个卷积核大小和步幅分别设置为3×3和1，最大池化层的缩放因子和跨度分别设置为2×2和2.
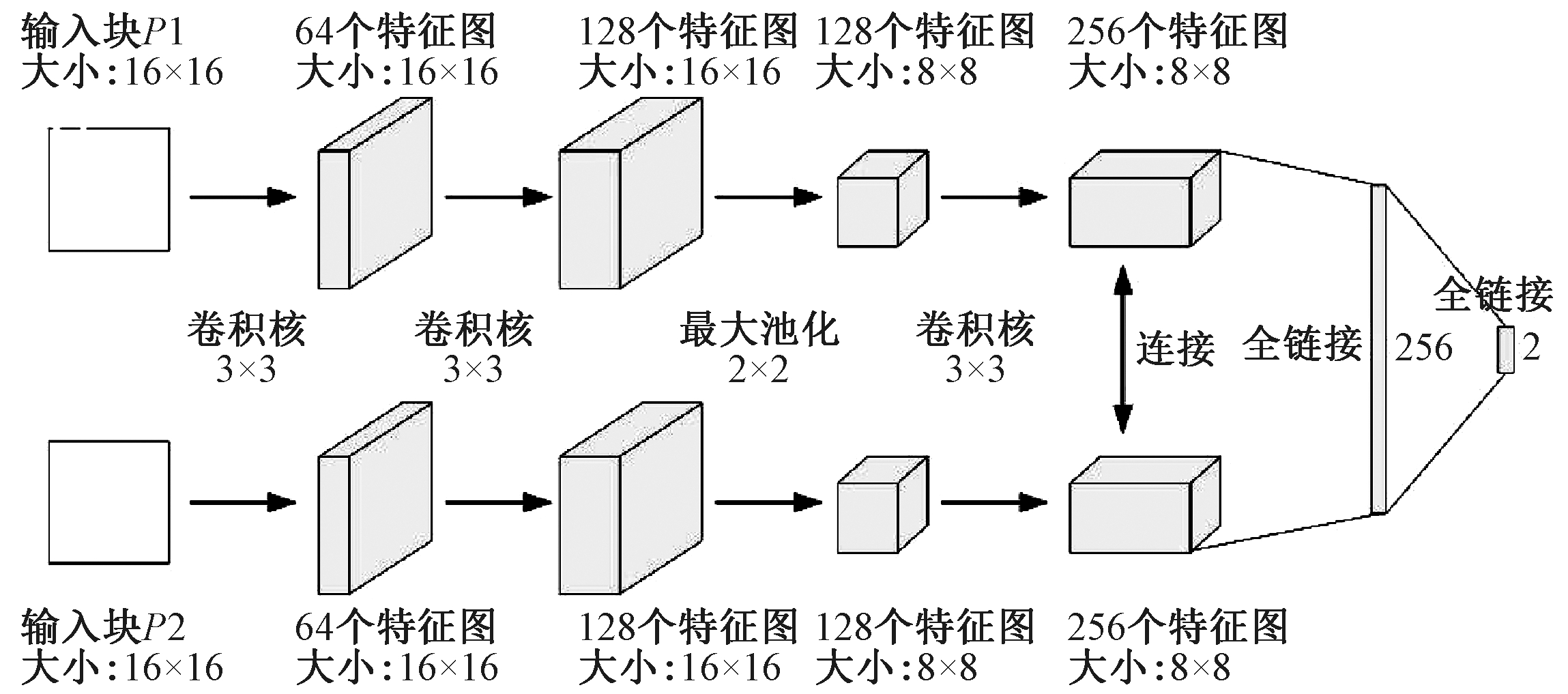
图1 CNN网络模型
Fig.1 The model of CNN
将CNN用于多聚焦图像融合算法的计算过程：首先，将两个源图像输送到预训练的CNN模型以输出得分图；其次，通过对重叠区域块求平均值，从得分图中获得具有与源图像相同大小的焦点图；再次，将焦点图以0.5为阈值分割成二进制图；然后，使用小区域去除和向导滤波[15]来精细化二进制分割图以生成最终决策图；最后，使用逐像素加权平均策略并利用最终决策图生成融合图像.
通过上述图像融合的步骤可知：在图像融合过程中，该方法并没有对图像进行高低频的划分，这显然是不符合人眼的视觉规律的.因此，笔者结合该融合规则提出了一种基于NSST域的多聚焦图像融合方法.
3 向导滤波
向导滤波对图像的边缘保持具备很好的效果.设向导图为I，输入图像为p，而输出图像为q[15].其中I与p可以是同一张图像.向导滤波的关键部分就是假设一个线性模型，即向导图I与输出图q之间存在局部线性模型：
qi=akIi+bk,∀i∈ωk，
(3)
式中：i为模型的像素索引；a、b为模型的线性系数；ωk为以向导图I中一点k为中心，长宽为(2r+1)的正方形窗.
图像的边缘保持滤波问题则转换为如下的最优化问题：
(4)
式中：ε表示归一化因子.可以使用线性回归求解公式(4)的解[15]：
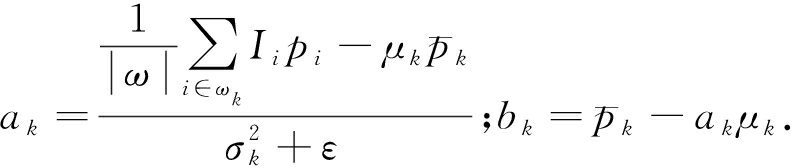
(5)
式中：μk和
表示向导图局部窗口中的均值和方差;
表示p在窗口ωk中的均值;|ω|表示窗口内的像素数.为了更简单直观地表示，在本文中使用Gr,ε(p,I)代表上述的向导滤波算法.
4 基于CNN的NSST域图像融合
笔者采用NSST进行图像分解，该变换可以很好地抑制伪吉布斯效应.文献[5]提出的改进的拉普拉斯能量和(sum of Laplace energy, SML)是一种能更好地表示图像边缘细节信息的区域能量函数，在选择高频变换域系数中具有很好的效果，笔者在此基础上对图像融合中的拉普拉斯能量加上所对应的权值，并对高频选择系数图用向导滤波来进行平滑处理.设输入具有不同聚焦点的两幅源图像A和B，经过融合后得到图像F.
首先，对两幅多聚焦的图像A和B采用相应NSST变换进行分解获得相应高频系数和低频系数为
和
(若没有下标则表示任一图像的分解系数)，其中l和d分别表示NSST分解的尺度和方向，当l为0的时候表示低频系数，否则为其相应的高频系数.
其次，对于源图像分解得到的低频系数采用基于CNN的图像融合算法进行图像融合.利用文献[12]对不同的图像训练集训练得到的CNN网络模型获得图A和B的融合决策图m，然后归一化并进行NSST来获取相应的低频系数决策图mL，则根据决策图获得的低频系数可由下式计算：
(6)
然后，对高频系数(l大于0)进行融合的规则为采用基于向导滤波的IWSML取大进行处理.
定义像素点的拉普拉斯能量如下：
Ml,d(x,y)=
|2Sl,d(x,y)-Sl,k(x-1,y)-Sl,k(x+1,y)|+
|2Sl,k(x,y)-Sl,k(x,y-1)-Sl,k(x,y+1)|.
(7)
由于高频图像的权值主要是由距离的大小和子带的方向所决定的，所以定义相应的权值公式：
ω(x,y)=ω0(x,y)+θd(x,y)，
(8)
其中，ω0(x,y)=
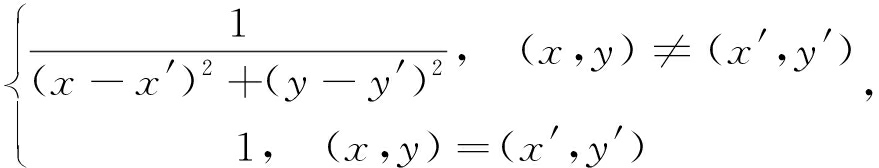
而θd中的θ表示距离的大小，d表示NSST分解方向，其作用对ω(x,y)的d方向数据进行翻倍.
因此，IWSML的定义式为：
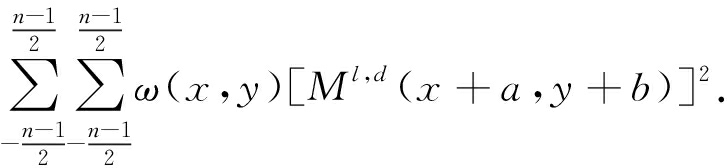
(9)
计算高频系数的IWSML值，可得
和
其中k=(x,y))，则计算高频决策图为：
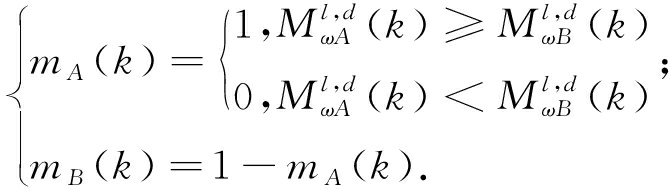
(10)
然后，对mA和mB进行向导滤波来加强高频系数的空间联系性，如式(11)所示：
(11)
随后，再将mA和mB进行数值的归一化规则处理，再通过式(12)能够获得最终所需要的高频部分系数
(12)
最终，将经过笔者提出的融合规则获得的低频系数
和高频系数
经过NSST重构获得最后所需要的目标图F.经过上述的描述，所确定的本文的融合算法表示过程如图2所示.
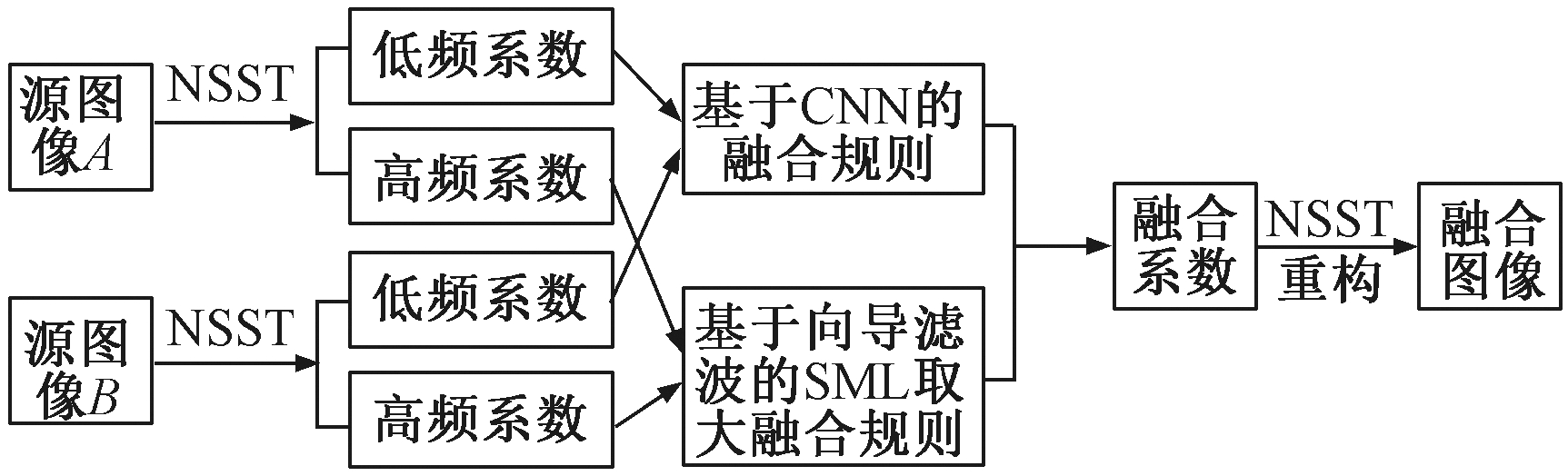
图2 基于CNN的NSST域图像融合框架
Fig.2 The diagram of multi-focus image fusion algorithm based on CNN in NSST domain
5 实验结果
为了有效地评估该算法在不同聚焦程度图像中的融合性能，利用在不同图像融合中常用的融合测试图像所提出的算法，并且从主观和客观两方面与文献[5]中所提出的CT-SML图像融合方法、文献[6]提出NSCT-PCNN图像融合方法、文献[7]提出的ST-PCNN图像融合方法、文献[10]中提出的CST-GF图像融合方法和文献[12]提出基于CNN的图像融合方法进行对比.客观性能评价指标采用5种不同的方法，如图像方差(standard deviation，Std)、图像平均梯度(average gradient，Avg)[10]、图像QAB/F度量[5]、图像的互信息(mutual information，MI)[10]和图像空间频域度(spatial frequency，SF)[10].这5个指标测试值越大，表明图像融合的评价指标越高，融合的图像越清晰，越符合人类的视觉系统.本文算法在实验过程中NSST的分解层数设置为4层，每层方向滤波器设置为有6、10、10、18个方向子带，CNN参数选择与文献[12]相同，高频融合规则中的r=3,ε=1.
首先对多聚焦图像进行图像融合的测试，图3(a)、(b)为经典的多聚焦图像融合测试图Clock 的左侧部分聚焦和右侧部分聚焦的图像.然后采用所述的不同方法对多聚焦图像进行融合，所得融合图像及与原测试图像的差图见图3(c)～(t).
图3 Clock原图像和各融合算法的融合效果
Fig.3 Fusion effect of each fused method and Clock original image
在实验结果中，不同算法的融合结果不同，上图的融合结果中大表的左上角部分和大表中数字8附近的区域，能够发现本文的算法能够更清晰地表达图像，更符合人眼的视觉特性.与CNN相比，本文的算法在多聚焦图像融合中这些区域稍差一些，但是本文的算法在图像的灰度层次呈现中更为清晰明显，这归功于NSST的应用.从上述各种融合图像实验结果与图3(a)的差图对比能够发现，本文算法得到融合图像的实验效果图是最好的，这说明了本文的算法在图像的细节信息保留方面是很有效的，这主要归功于CNN融合策略的引入.综合上述来看，从不同融合图像差图对比中可以明显地看出在视觉效果方面本文的算法是最好的，人造纹理产生的最少，这主要是由于引入向导滤波使图像的空间连续性得到很大的提升，从而有效地抑制了融合图像中人造纹理的产生.
表1给出了各融合算法相应的客观评价指标.由表1可知，本文所提出的融合算法在各项评价指标所取得的结果值都是最好的.这表明本文所提出的融合算法可以有效地提取源图像的聚焦信息并且较好地保留空间信息.最后从计算时间上看，虽然在数据的计算时间上本文的算法用时比较长，但是可以看到与其他融合算法相比，本文采用的NSST变换具有更好的时频特性，而与CNN相比，笔者提出的融合规则能充分地利用图像的统计信息.
然后对空拍图像进行融合测试.图4(a)、(b)为不同聚焦图像，各算法融合效果如图5(c)～(t)所示.
从实验结果中可以发现，融合结果中上下飞机前面和后面邻近的区域，与图3中的融合结果视觉效果类似，能够发现本文的算法在图像的融合质量和层次的清晰度表达上，更容易使人眼系统接受到更好视觉的图像信息特征，并且本文算法充分地利用了图像的空间连续性从而克服了其他融合算法在融合图像中引入的一些人造纹理.
同样，表2给出了各融合算法的客观评价指标.由表2可知，本文算法具有最好的客观评价标准.这也说明本文算法不但可以充分地提取源图像中的细节信息，很好地抑制了最终融合图像中人造纹理的产生，并且对于不同种类的图像融合具有鲁棒性，所以综合来看,本文所提出融合规则是一种比较好的在图像融合中的方法.
表1 图3中各个融合算法融合效果的客观评价指标
Tab.1 Objective evaluation index of each fusion algorithm in Figure 3
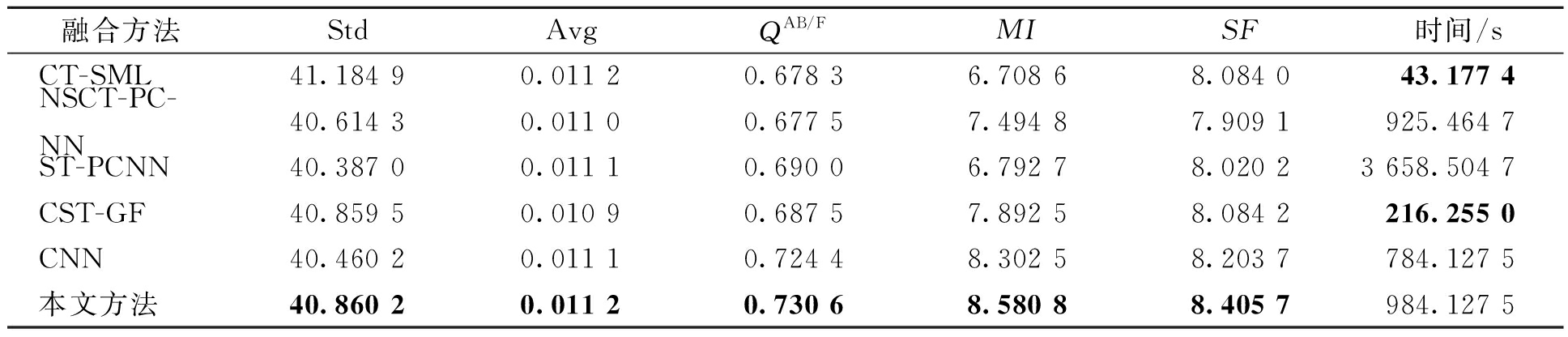
融合方法StdAvgQAB/FMISF时间/sCT-SML41.184 90.011 20.678 36.708 68.084 043.177 4NSCT-PC-NN40.614 30.011 00.677 57.494 87.909 1925.464 7ST-PCNN40.387 00.011 10.690 06.792 78.020 23 658.504 7CST-GF40.859 50.010 90.687 57.892 58.084 2216.255 0CNN40.460 20.011 10.724 48.302 58.203 7784.127 5本文方法40.860 20.011 20.730 68.580 88.405 7984.127 5
表2 图4中各个融合算法融合效果的客观评价指标
Tab.2 Objective evaluation index of each fusion algorithm in Figure 4
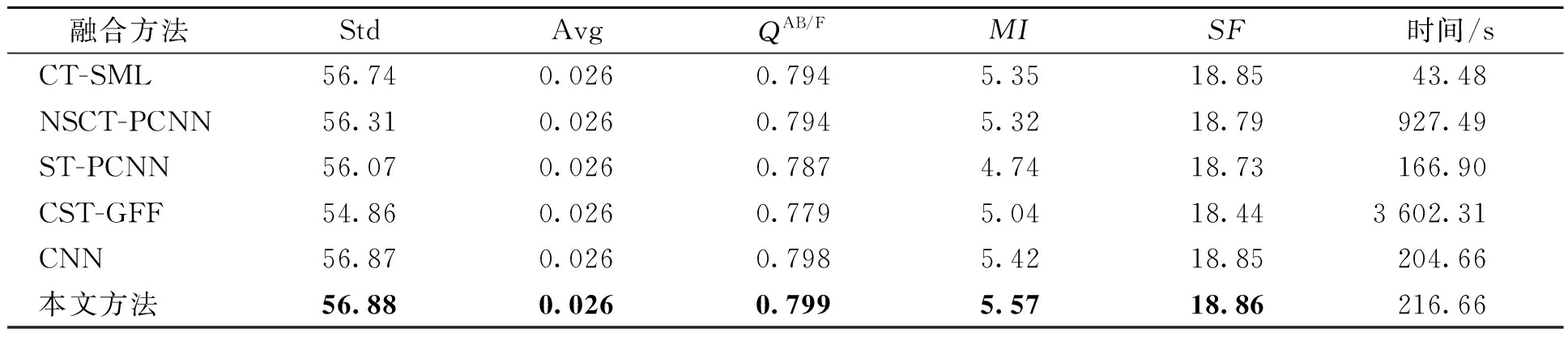
融合方法StdAvgQAB/FMISF时间/sCT-SML56.740.0260.7945.3518.8543.48NSCT-PCNN56.310.0260.7945.3218.79927.49ST-PCNN56.070.0260.7874.7418.73166.90CST-GFF54.860.0260.7795.0418.443 602.31CNN56.870.0260.7985.4218.85204.66本文方法56.880.0260.7995.5718.86216.66
图4 飞机原图像和各融合算法的融合效果
Fig.4 Fusion effect of each fused method and Airplane original image
6 结论
笔者提出了一种基于CNN的NSST变换域图像融合方法.该方法有效利用NSST变换域优良的时频变换特性又充分应用了CNN图像融合规则较好的能量保持特点，并通过向导滤波使对融合过程中的高频图像进行平滑处理，进而更好地提高了图像的空间连续性，使图像的融合质量进一步增强.综合上述的实验表明，该方法具有更好的图像特征表达性能，不管是在图像的整体效果还是在客观性能指标上都要更优于文中所描述的目前的图像融合算法.
[1] LI S T, KANG X D, FANG L Y, et al. Pixel-level image fusion: a survey of the state of the art [J]. Information fusion, 2017, 33:100-112.
[2] LIU S Q, ZHAO J, SHI M Z. Medical image fusion based on improved sum-modified-Laplacian [J]. International journal of imaging systems & technology, 2015, 25(3):206-212.
[3] LIU S Q, ZHANG T, LI H L, et al. Medical image fusion based on nuclear norm minimization [J]. International journal of imaging systems & technology, 2015, 25(4):310-316.
[4] GENG P, HUANG M, LIU S, et al. Multifocus image fusion method of ripplet transform based on cycle spinning [J]. Multimedia tools & applications, 2016, 75(17):10583-10593.
[5] 屈小波,闫敬文,杨贵德.改进拉普拉斯能量和的尖锐频率局部化Contourlet域多聚焦图像融合方法[J].光学精密工程,2009,17(5): 1203-1212.
[6] QU X B, YAN J W, XIAO H Z, et al. Image fusion algorithm based on spatial frequency-motivated pulse coupled neural networks in nonsubsampled contourlet transform domain [J]. Acta automatica sinica, 2008, 34 (12):1508-1514.
[7] GENG P, WANG Z Y, ZHANG Z G, et al. Image fusion by pulse couple neural network with shearlet [J]. Optical engineering, 2012, 51(6): 067005-1-067005-7.
[8] LIM W Q. The discrete shearlet transform: a new directional transform and compactly supported shearlet frames [J]. IEEE transactions on image processing, 2010, 19(5): 1166-1180.
[9] 石智，张卓，岳彦刚. 基于Shearlet变换的自适应图像融合算法[J]. 光子学报, 2013, 42(1): 115-120.
[10] LIU S Q, SHI M Z, ZHU Z H, et al. Image fusion based on complex-shearlet domain with guided filtering [J]. Multidimensional systems & signal processing, 2017, 28(1):207-224.
[11] LI S T, KANG X D, HU J W. Image fusion with guided filtering [J]. IEEE transactions on image processing, 2013, 22(7): 2864-2875.
[12] LIU Y, CHEN X, PENG H, et al. Multi-focus image fusion with a deep convolutional neural network [J]. Information fusion, 2017, 36:191-207.
[13] 李章晓，宋微，田野. 基于深度学习和进化计算的外汇预测与投资组合优化[J]. 郑州大学学报(工学版), 2019, 40(1): 92-96.
[14] NAIR V, HINTON G E. Rectified linear units improve restricted boltzmann machines[C]//Proceedings of the 27th International Conference on International Conference on Machine Learning. Haifa: Omnipress, 2010:807-814.
[15] HE K M, SUN J, TANG X O. Guided image filtering [J]. IEEE transactions on pattern analysis & machine intelligence, 2013, 35(6):1397-1409.