0 引言
齿轮在进行机加工以及热处理时,温度变化不均、材料相变不均以及材料的塑性变形等会使齿轮表面产生残余压应力。在齿轮工作过程中齿面承受弯曲应力和接触应力,承受弯曲应力时,齿面一侧受拉,另一侧受压,工艺过程中产生的残余压应力可以抵消一部分齿轮轮齿的工作拉应力,对延长齿轮寿命、避免轮齿疲劳断裂有积极影响。但齿轮轮齿表面层的残余压应力对轮齿疲劳寿命的影响情况定量分析尚不完善[1-4]。笔者基于ANSYS平台,对不存在残余压应力的齿轮以及因渗碳淬火存在残余压应力的齿轮,分别进行了弯曲强度及寿命分析,得到了残余压应力对齿轮弯曲疲劳寿命的影响规律,为齿轮的抗疲劳设计提供了参考。
1 算例描述
1.1 减速器基本参数
以单向运转直齿圆柱齿轮减速器为例,基本参数如下:小齿轮齿数为21,大齿轮齿数为75,大齿轮齿宽为51 mm,输入转矩为905.95 N·m,齿轮模数为3,齿轮材料为20CrMnTi渗碳淬火。
1.2 齿面残余应力随深度变化情况
通过剥层方法X射线应力检测可知,20CrMnTi齿轮经过渗碳淬火处理后,轮齿表面层存在较大的残余压应力。残余应力值随其距表面的深度而变化,实测残余应力随深度的变化如图1所示。其中径向为齿面法线方向,切向为齿面切向方向,轴向为齿轮轴线方向。最大残余压应力出现在距表面层0.4 mm处。
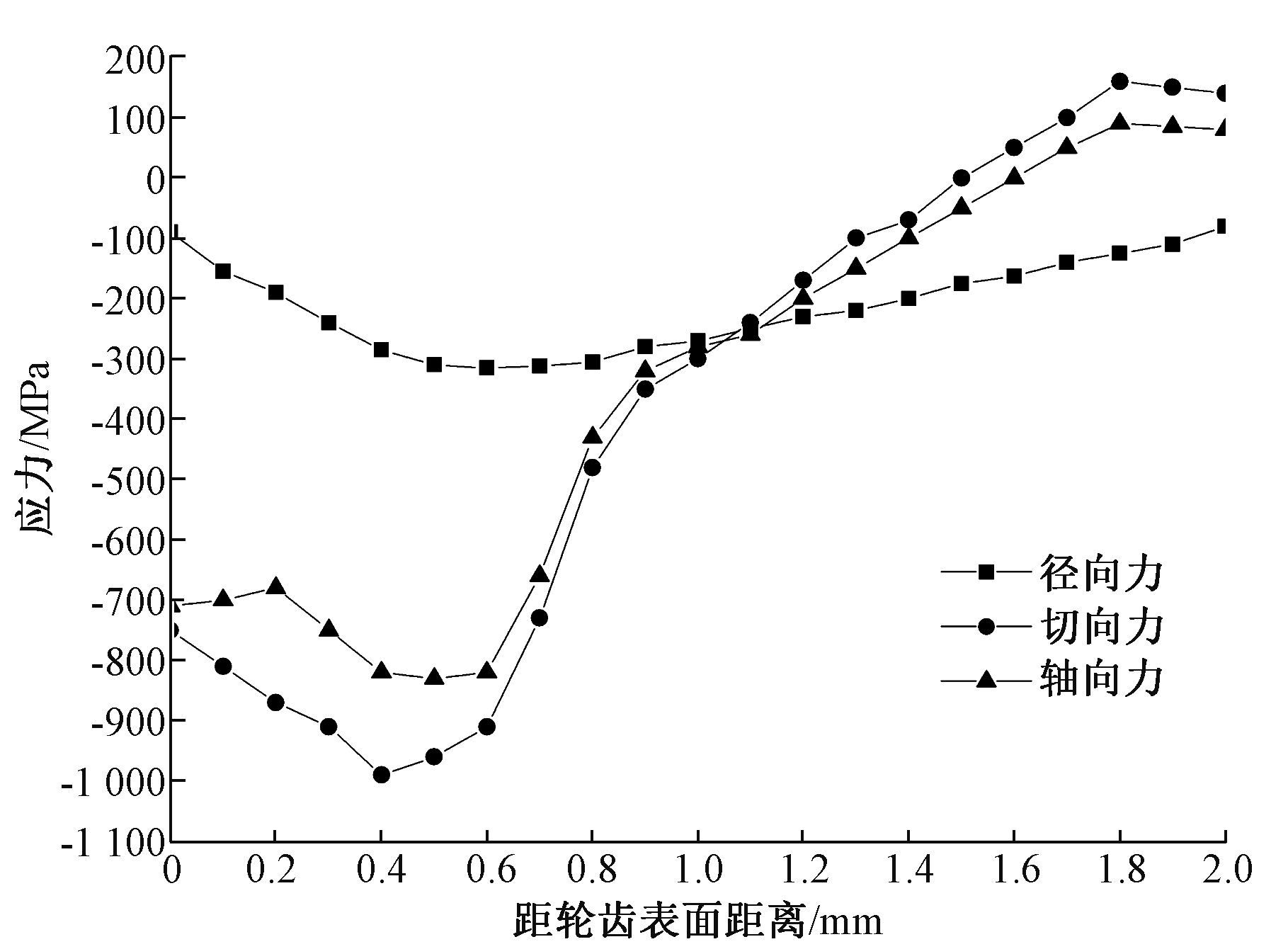
图1 残余应力值随深度变化情况
Figure 1 The variation of residual stress with depth
2 零件的疲劳寿命估计
呈周期性变化的载荷作用于机械零件上,使得零件内部产生交变应力应变,导致裂纹产生于零件内部,随着载荷的不断作用,裂纹逐渐从内部扩展,致使零件出现损坏、断裂等现象。
疲劳寿命即为零件从开始工作到疲劳失效时所经历的交变应力循环次数[5]。
2.1 疲劳寿命分析方法
目前疲劳寿命分析方法有:名义应力法、局部应力应变法和应力场强法。名义应力法根据零件的S-N曲线,结合参考结构危险部位的名义应力,通过疲劳累积损伤理论分析零件的疲劳寿命,能够估算出弹性范围内的高周疲劳寿命。直齿圆柱齿轮减速器在工作过程中长期承受交变载荷,属于高周疲劳,故选用名义应力法来完成减速器齿轮轮齿疲劳寿命预测[6-8]。
线性疲劳累积损伤理论的思想:材料在应力作用下的疲劳损伤是相互独立的;且材料所受损伤是能够线性累加的。该理论未考虑各应力间的相互作用,导致疲劳寿命的计算值偏高,但形式简单,使用方便,在工程中应用最广[9]。笔者采用线性损伤理论的代表——Miner法则对齿轮疲劳寿命进行研究。
Miner法则认为,根据线性累积损伤理论和S-N曲线,材料在应力σ1作用下循环N1次达到破坏,那么经过n1循环,材料损伤为n1/N1,在应力为σ1,σ2,σ3,…,σn时,经受n1,n2,n3,…,nn次循环,各损伤累积之和等于1,即:
(1)
此时材料发生疲劳破坏。
2.2 疲劳寿命理论计算
传动齿轮20CrMnTi钢材料特性如表1所示。
表1 20CrMnTi材料属性
Table 1 Material property of 20CrMnTi

弹性模量/MPa泊松比抗拉强度σb/MPa屈服强度σs/MPa脉动循环疲劳极限/MPa2.07×1050.31 080850350
减速器齿轮的S-N曲线:
lg N=27.795 2-8.174 014 lg S,
(2)
式中:S为材料所承受的某一应力值;N为材料在S应力下循环工作的次数。
3 算例分析
3.1 几何模型的建立
以ANSYS有限元软件为工具,对齿轮进行建模,由于齿轮是轴对称模型,考虑到计算效率,仅建立部分齿模型。齿轮在渗碳淬火处理之后,齿面层残余压应力随轮齿表面深度的变化而变化。为了在分析时更好地模拟残余压应力,得到准确的齿轮受载后的应力及位移分布,将齿轮轮齿进行分层建模,每层厚0.2 mm,将图1中残余应力值,以预应力形式施加在每层模型中[10]。齿轮轮齿模型如图2所示。
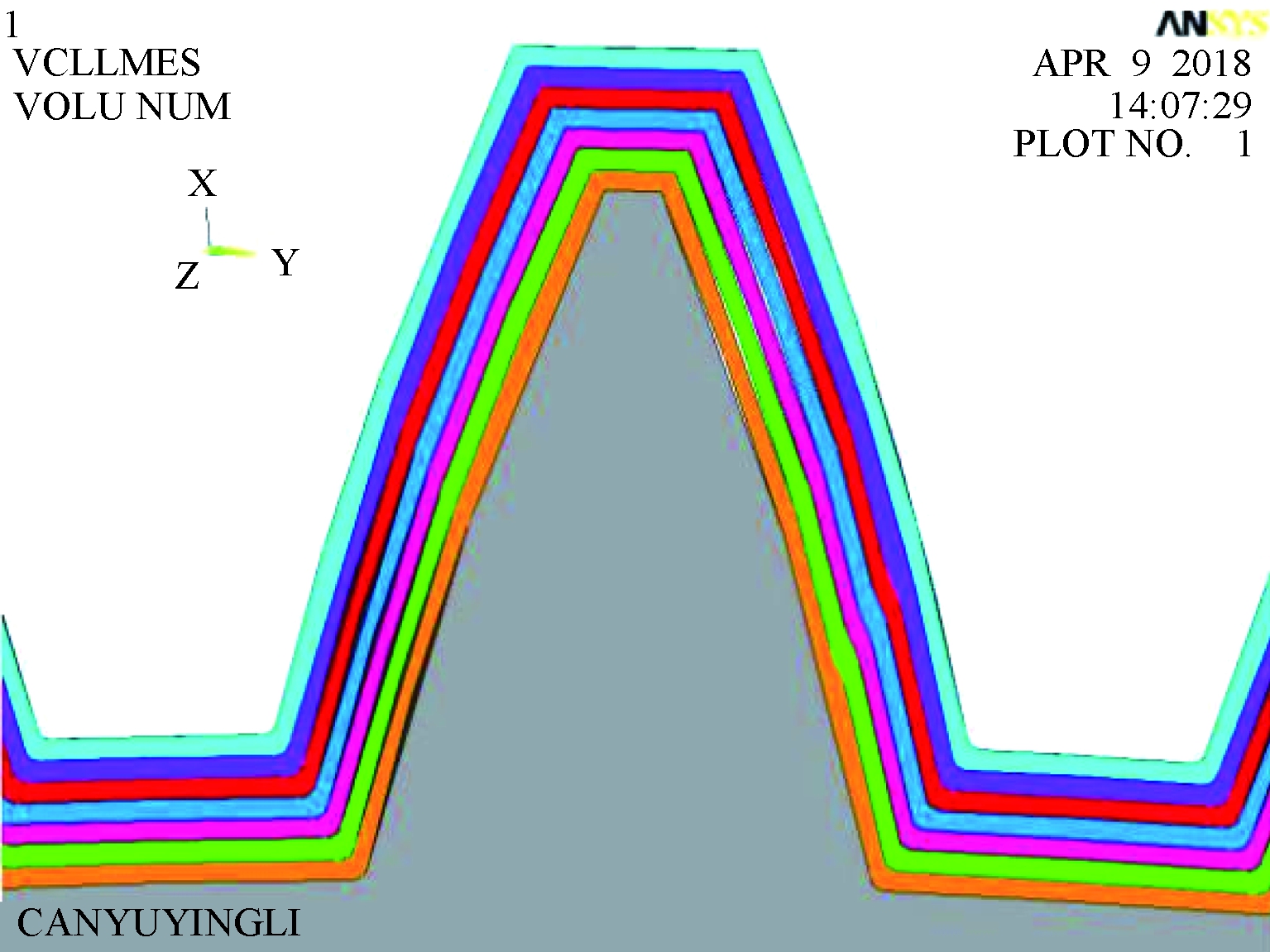
图2 齿轮轮齿模型
Figure 2 Gear tooth model
3.2 网格划分及边界条件的施加
选择SOLID185三维单元对模型进行网格划分,对中心孔表面施加全约束[11]。本文分析模型为3个齿模型,对齿侧断面施加固定约束。
齿轮在双齿啮合状态下,虽然啮合点在齿顶,弯曲力臂大,但此时由两对轮齿分担载荷,齿根处的弯曲应力未达到最大;齿轮在单齿啮合状态下,只有一对轮齿承担载荷,因此在单齿啮合区上界点(图3中C点)[12],齿根处弯曲应力最大,该点为齿轮单齿啮合承载最大点。
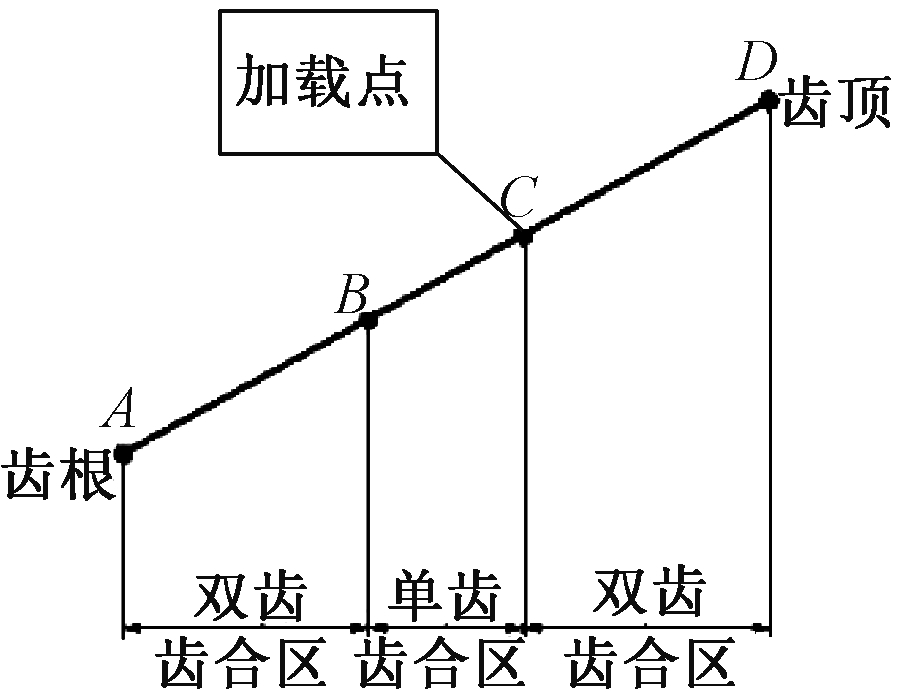
图3 齿轮轮齿啮合状态
Figure 3 Gear teeth meshing state
通过在单齿啮合承载最大点周围0.1mm宽的范围内施加均布载荷,来模拟该点实际所承受载荷。
3.3 齿轮弯曲强度计算结果及分析
将经过渗碳淬火、存在残余压应力的齿轮称为模型1,将未经渗碳淬火、不存在残余压应力的齿轮称为模型2。
对齿轮进行弯曲强度仿真分析计算得到合成应力云图,如图4、5所示。图4中,模型1在啮合力作用下齿根处最大的拉应力为567 MPa,位于齿根处端面附近,弯曲应力主要集中在载荷作用点以下到齿根部分的齿面一定深度范围内,其余位置应力较小。图5中,模型2齿根处最大应力为650 MPa,弯曲应力主要集中在近齿根处齿面及齿底一定深度范围,应力随深度增加而减小,其余位置应力较小。
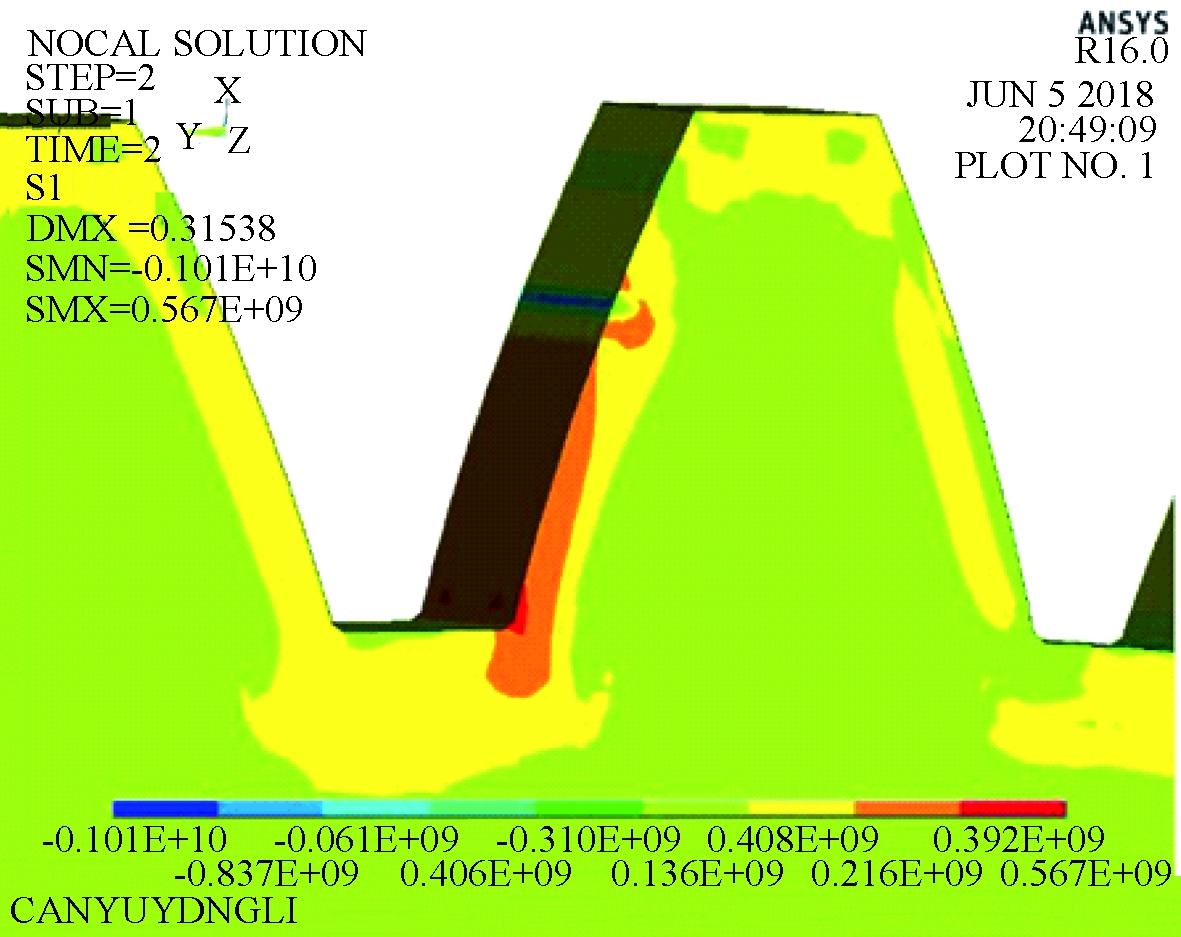
图4 模型1的弯曲应力云图
Figure 4 The bending stress cloud of model 1

图5 模型2的弯曲应力云图
Figure 5 The bending stress cloud of model 2
为了对残余压应力在轮齿受载后的应力分布有更加深入的了解,在齿宽中心剖面处做应力云图,如图6、7所示。图6中,模型1应力主要集中在齿面中下部一定深度范围内,应力随齿面深度的增加由450 MPa迅速减小,然后又稍稍增大。图7中,模型2应力主要集中在齿底部及齿面中下部一定深度,应力由650 MPa逐渐减小。
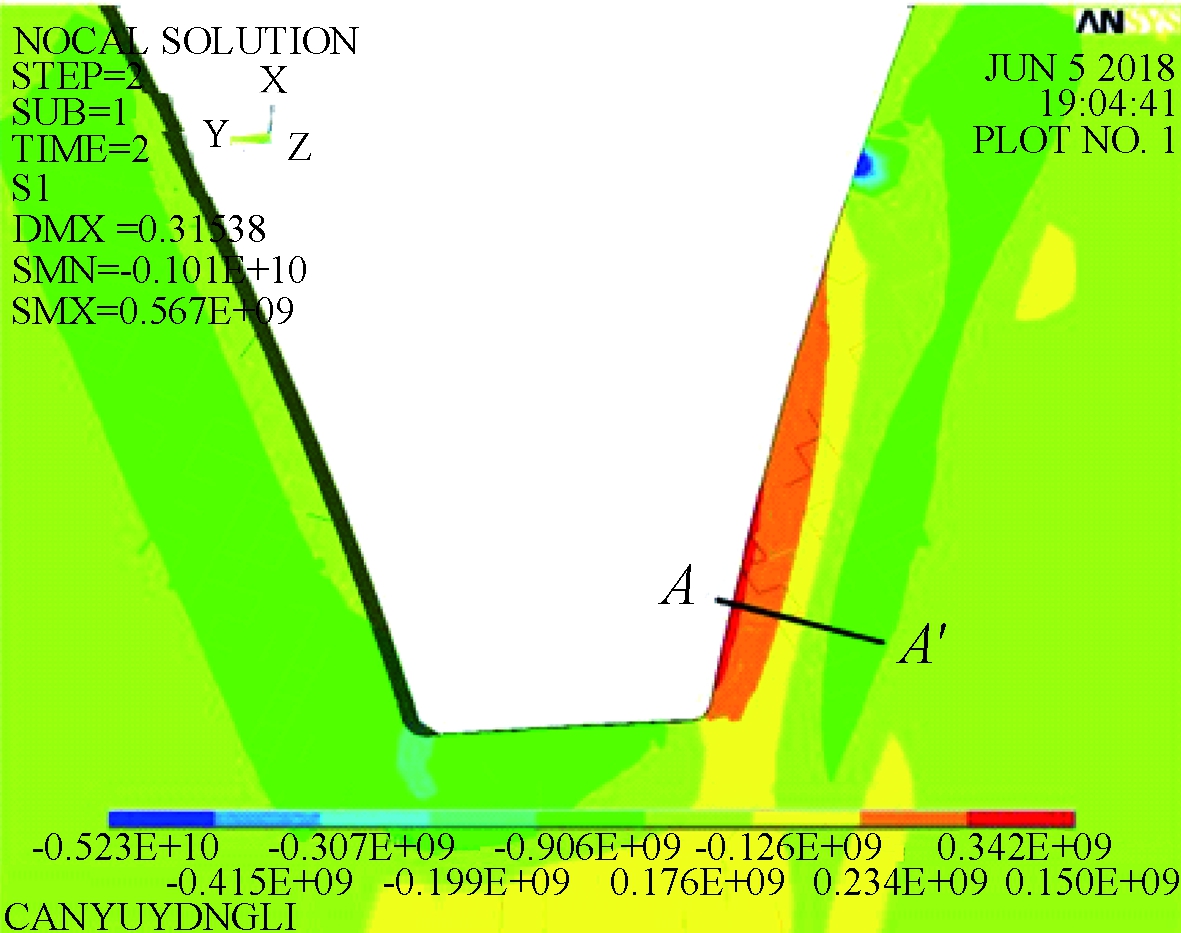
图6 模型1的剖面应力云图
Figure 6 The profile stress cloud of model 1
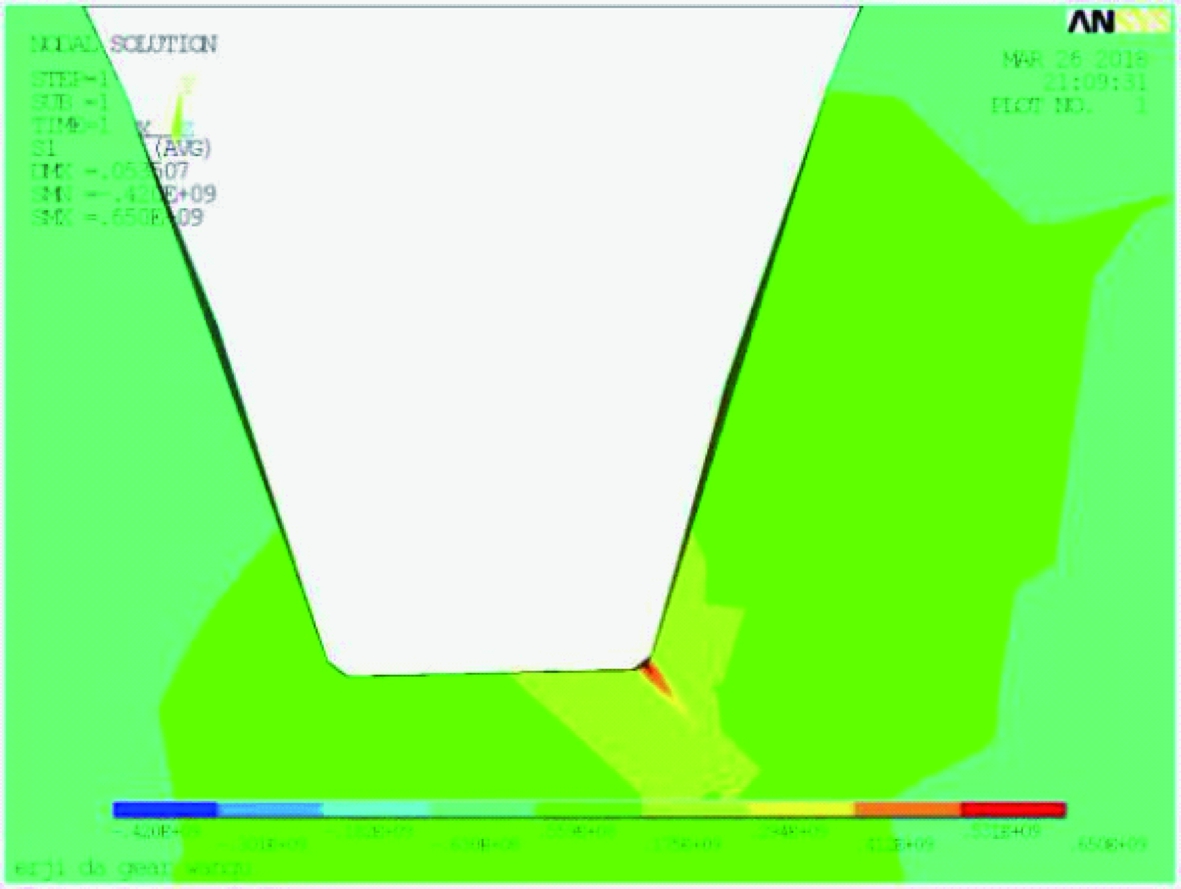
图7 模型2的剖面应力云图
Figure 7 The profile stress cloud of model 2
图8为模型1齿宽中心剖面AA′处应力随深度变化曲线图。由图8可知,径向应力由351 MPa减小到-30.9 MPa;切向应力由10.8 MPa减小到-51.2 MPa;轴向应力由-244.4 MPa先减小后增大到-77.2 MPa;合成应力由364 MPa减小到-20.4 MPa。图9为最大应力处应力随深度变化曲线图。由图9可知,径向应力由471 MPa减小到-55.2 MPa;切向应力由64.2 MPa减小到-156.4 MPa;轴向应力在0 MPa附近波动;合成应力由508 MPa减小到-10 MPa。
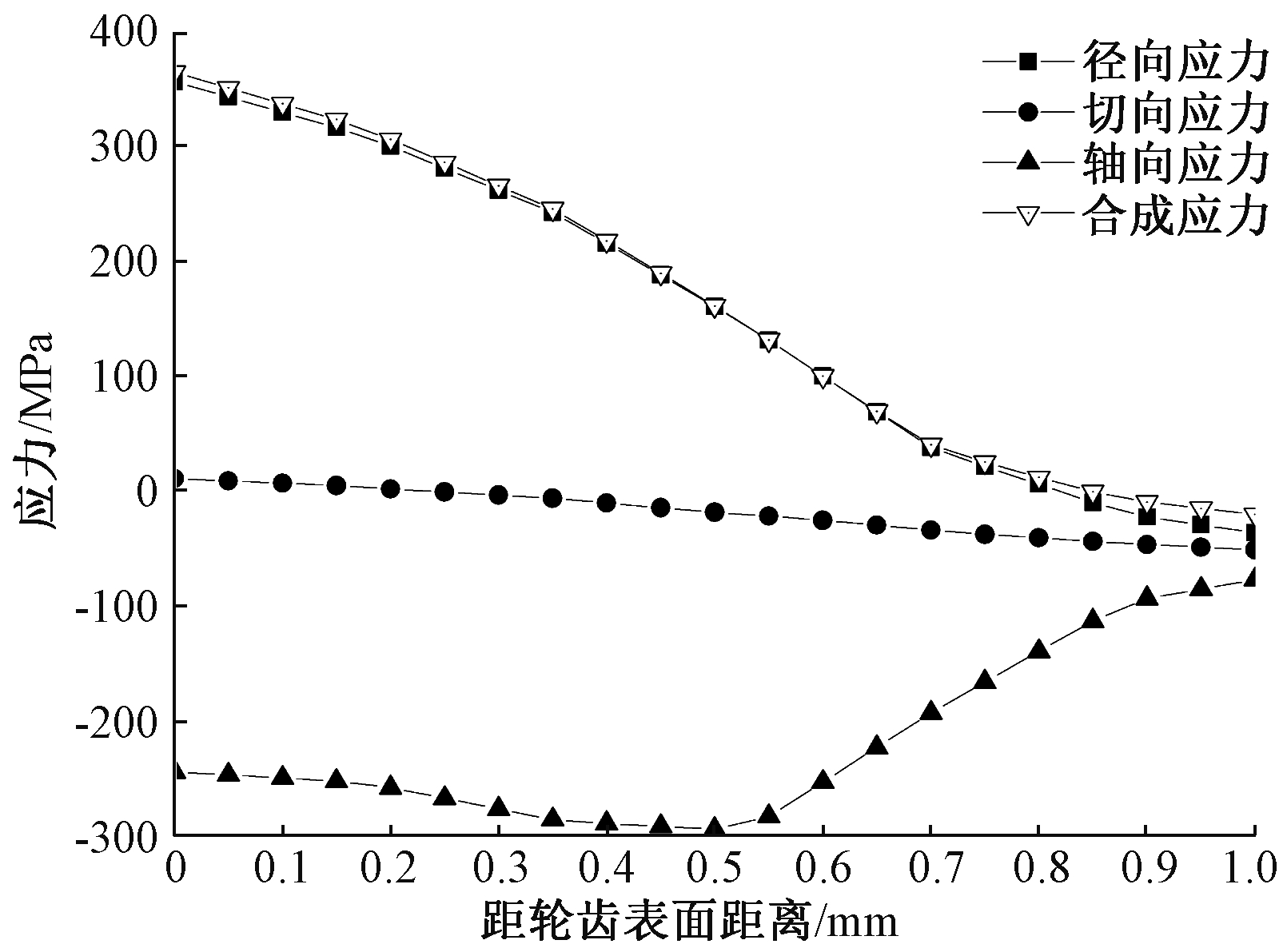
图8 模型1齿宽中心剖面AA’处应力随深度变化曲线
Figure 8 Curve of stress - depth at AA’ in the profile of the tooth width center of model 1
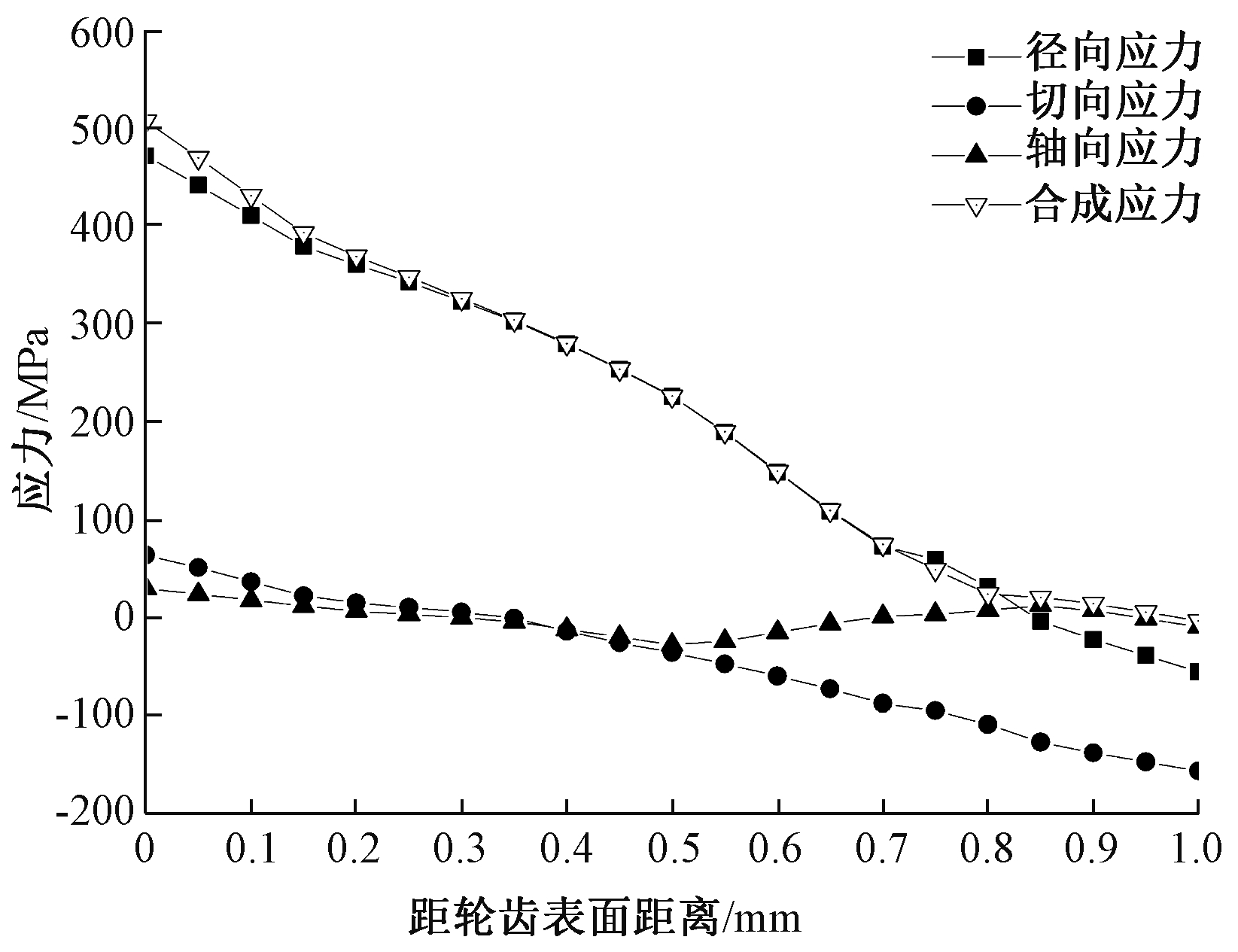
图9 模型1最大应力处应力随深度变化曲线
Figure 9 Curve of stress - depth at maximum stress of model 1
通过对比可知,存在残余压应力的齿轮齿根处弯曲应力相对于不存在残余压应力的齿轮要小,且轮齿表层弯曲应力随深度减小快。因为轮齿表层存在残余压应力,可以抵消一部分工作拉应力,而残余压应力值随深度先增大后减小,故弯曲应力在一定深度后会稍微增大。
3.4 齿轮弯曲疲劳寿命计算分析
根据式(2)分别对两模型进行理论疲劳寿命计算,得到模型1疲劳寿命为1.11×107次,模型2疲劳寿命为1.5×105次。
ANSYS疲劳分析是基于Miner法则进行的,以弯曲强度分析结果为基础,在疲劳计算模块中,设置应力作用位置、循环次数以及载荷,实现疲劳寿命计算。根据3.3节两模型的弯曲强度分析结果,设定应力位置为齿根弯曲应力最大处,齿轮疲劳循环次数设为10 000次,分别对其进行疲劳寿命分析,模型1弯曲疲劳寿命为1.5×107次,模型2疲劳寿命为4.396×105次。
对比结果可知,残余压应力的存在提高了轮齿的抗弯曲疲劳性能。理论计算值较仿真值小,其原因在于理论计算时将载荷全部加载在轮齿齿顶,且未考虑齿根圆角的影响。因此,仿真计算结果更符合实际工作情况,计算结果更精确,具有可信度。
4 结论
采用施加预应力的方法来实现对齿轮经渗碳淬火产生的残余压应力的模拟,并对存在及不存在残余压应力的齿轮分别进行分析。由分析可知:存在残余压应力的齿轮最大拉应力为567 MPa、不存在的为650 MPa,从定量角度证明了齿面残余压应力的存在对轮齿强度提高有益。在此基础上分别对两者进行了疲劳寿命分析,结果表明,存在残余压应力齿轮的疲劳寿命约为不存在残余压应力齿轮的30倍。相对于简化理论计算,仿真方法计算结果更精确、更符合齿轮实际工作状态,减轻了疲劳试验的工作量,同时硬齿面齿轮的仿真计算方法为减速器部件、整机强度及疲劳寿命仿真分析提供了参考。
[1] 陈毅. 20CrMnMo齿轮齿根残余应力理论及试验研究[D]. 重庆:重庆大学, 2013.
[2] 谢俊峰. 喷丸对渗碳齿轮的变质层形成及弯曲疲劳寿命的影响研究[D]. 郑州:郑州大学, 2017.
[3] LI Z C, FREBORG A M, HANSEN B D, et al. Modeling the effect of carburization and quenching on the development of residual stresses and bending fatigue resistance of steel gears[J]. Journal of materials engineering & performance, 2013, 22(3):664-672.
[4] 王广生. 金属热处理缺陷分析及案例[M]. 北京:机械工业出版社,1997:84-90.
[5] 李舜酩. 机械疲劳与可靠性设计[M]. 北京:科学出版社,2006:11-13.
[6] 夏云清. 装载机差速器齿轮的非线性接触与疲劳寿命分析[D]. 杭州:浙江理工大学,2010.
[7] 杨忠炯,董栋.振动对TBM液压泵泵轴受力及疲劳寿命影响分析[J].郑州大学学报(工学版),2016,37(4):6-10.
[8] 张剑雄,王良模,夏汉关,等. 变速器倒挡齿轮疲劳寿命的有限元分析[J]. 机械传动,2013,37(9):110-112,117.
[9] 马朋朋. 基于随机有限元法的行星传动装置疲劳可靠性分析[D]. 郑州:郑州大学,2016.
[10] 杨志强. 渗碳圆柱齿轮淬火过程的数值模拟[D]. 秦皇岛:燕山大学,2010.
[11] 刘竹丽,赵敏敏,马朋朋,等. 基于ANSYS的斜齿轮副接触分析与可靠性分析[J]. 郑州大学学报(工学版),2015,36(2):6-9.
[12] 鲍洪,安琦. 渐开线直齿轮轮齿载荷及应力计算方法[J]. 华东理工大学学报(自然科学版),2012,38(1):116-122.