0 引言
现代大型变电站中常用的变电构架和避雷针是钢管结构,它具有构造简单、受力明确、轻质高强[1-2]等特点,尤其适合标准化生产和制作。其中构架避雷针是由法兰将各段钢管连接而成的单管构件,高度一般在20~50 m[3],属于典型的高耸结构,在风荷载作用下,避雷针各段连接处易产生振动累积损伤,在薄弱位置甚至可能发生断裂。近年来,在役构架避雷针断裂事故时有发生[4],如元江220 kV 变电站、东屿220 kV 变电站和宁夏某750 kV 变电站。2014年12月,河南某500 kV变电站构架避雷针出线侧发生折断事故,断口位于避雷针和横梁的相贯T型节点处,表现为避雷针底座钢管横梁撕裂。
迄今为止,关于构架避雷针断裂原因的分析主要是从材料化学成分、金相组织等方面进行[4],对于避雷针及其相贯节点的受力特性尤其是风致动力响应等方面的研究较少,使得标准化设计制作的构架避雷针仍不能较好地反映其在实际复杂应力状态下的受力特点。为此,采用ANSYS软件建立典型构架避雷针结构的有限元模型,按照DL/T5457—2012《变电站建筑结构设计技术规程》[5]推荐的设计方法,将风荷载等效为静力作用施加在结构上,分析典型构架避雷针结构在设计荷载工况下的承载特点和薄弱环节,在此基础上对结构进行风致动力响应分析并提出加固建议,以期为类似构架避雷针结构的优化设计和日常维护提供依据。
1 构架避雷针结构的有限元模型
以河南省某500 kV高压变电站中的出线侧变电构架[6]为研究对象,按照原设计图纸可得到其整体构架避雷针的计算模型和部分构件尺寸,如图1所示。该变电构架共六跨,中间和右边跨各设一根避雷针,材料为Q235B,避雷针由6段圆钢管连接而成,自下而上各段钢管规格分别为:D1D2(φ325×8)、D2D3(φ325×10)、D3E1(φ(325/220)×6)、E1E2(φ140×4)、E2E3(φ89×5)、E3E4(φ48×3.5),各段长度及标高如图1所示。构架横梁采用Q345B圆钢管,规格为φ480×6,每跨横梁中都有3个位置留有挂导线孔;同时,在未设置避雷针的各构架柱上部还设有悬挂地线的地线柱,地线柱亦采用Q235B圆钢管,规格为φ325×8。构架柱为人字形,两端沿y向分别设置侧向支撑,同时沿柱高方向设置两道横撑;构架柱和支撑杆件均采用Q235B钢材,除最上层横撑(如C1C2)采用L89×7角钢外,其他杆件均采用φ325×8圆钢管。构架跨度及支柱间距详见图1。
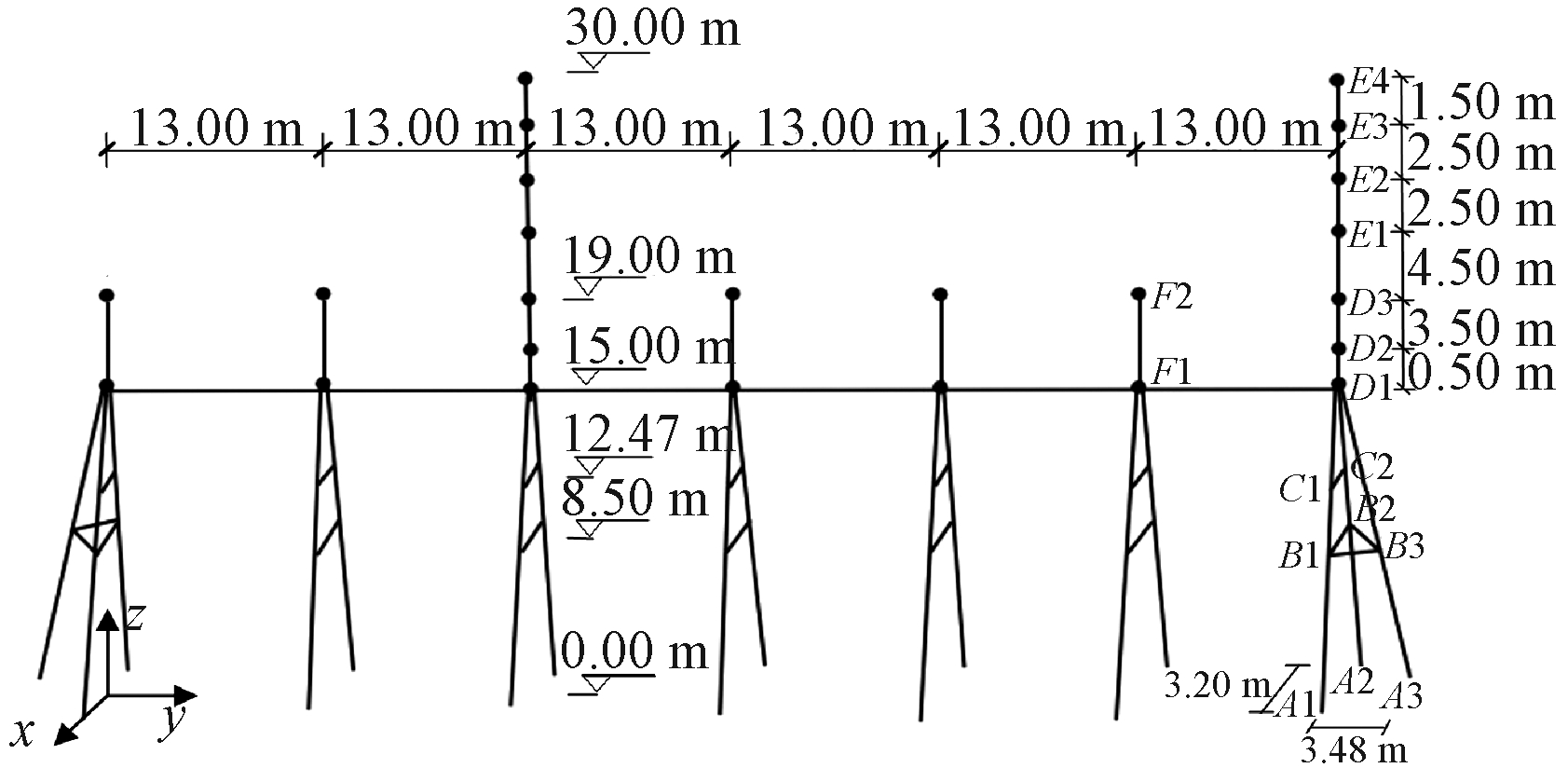
图1 变电构架避雷针结构计算模型示意图
Figure 1 Schematic diagram of a substation framework with lightning rods
选用Beam188单元[7]模拟构架杆件,取双线性随动强化模型BKIN模拟Q235B 和Q345B钢材本构关系,屈服强度分别为 235 MPa 和345 MPa,弹性模量和泊松比分别为2.06×105 MPa 和0.3,强化模量取0.02倍弹性模量。最终建立的有限元模型如图2所示,共有 3 418 个节点和3 310 个单元,所有杆件均采用刚性连接,各构架柱底部均采用固定端约束。

图2 变电构架避雷针结构的有限元模型图
Figure 2 Finite element model of the substation framework with lightning rods
2 构架避雷针结构的设计荷载工况及静力承载力分析
2.1 设计荷载工况
根据规范[5]的规定,设计变电构架时,应考虑结构可能同时出现的不同荷载,并按各工况下的最不利效应组合进行设计。由于该变电构架所在地的基本风压w0=0.35 kN/m2,根据风压和风速的换算关系,可换算出10 m 高处的设计风速v=23.66 m/s。安装和检修时取风速v=10 m/s,对应的基本风压为w0=0.0 625 kN/m2,该值小于规范[5]规定的最小基本风压0.30 kN/m2,故静力设计时仍选用最小基本风压。由此可列出构架避雷针结构在承载能力极限状态时的以下5种荷载效应组合工况:
①大风工况:1.2恒荷载+1.3导(地)线荷载(大风条件)+1.4结构风压(取v=23.66 m/s);
②最大覆冰工况:1.2恒荷载+1.3导(地)线荷载(覆冰情况)+1.4结构风压(取v=10 m/s);
③温度工况:1.2恒荷载+1.3导(地)线荷载(最高温度)+1.0温度作用+1.4结构风压(取v=10 m/s);
④安装工况:1.2恒荷载+1.2导(地)线荷载(安装条件)+1.4结构风压(取v=10 m/s);
⑤检修工况:1.2恒荷载+1.2导(地)线荷载(检修条件)+1.4结构风压(取v=10 m/s)。
进行荷载工况组合时,结构自重可在ANSYS软件中通过施加重力加速度的方式自动计入。由于导(地)线本身细且柔,对结构整体的刚度影响很小,因此建模时只在构架相应位置施加导(地)线的三相荷载,具体数值见表1。由表1知,导(地)线的张力有3种类型:水平张力、垂直荷重和侧向张力,分别对应于模型的x、z和y向。
根据表1,可判断设计最大风速工况、检修上人三相各100 kg和检修上人单相150 kg工况为结构的不利工况。按照上述参数和不利工况条件,对结构进行设计荷载组合效应下的静力承载力分析,结果如表2所示。可以看出,避雷针根部到中间变截面处(标高15~15.5 m)的应力值较大;总体上看设计最大风荷载垂直构架长度方向(x向)作用时为最不利工况组合。因此本文以设计风速x向作用为例对构架避雷针进行承载性能分析。
表1 变电构架导(地)线张力设计参数
Table 1 Parameters of the conductor (ground line) tensions of the substation framework kN

导线型号荷载条件最高温度最大风速覆冰安装检修上人三相各100 kg检修上人单相150 kgR1.4463.492.0121.4501.9502.200LGJ-500/45Z0.8210.8210.8210.8210.8210.821H4.271107.4395.07310.02212.642地线张力R=1.13Z=0.64H=5.0
注:表中R指垂直荷重,Z指侧向风压,H指水平张力。
表2 3种最不利组合工况下避雷针各段连接点处的应力
Table 2 Stress at each connection point of the lightning rod subjected to wind loads under three working conditions MPa

高度/m节点号风荷载垂直构架长度方向(x向)风荷载顺构架长度方向(y向)工况①工况⑤(三相)工况⑤(单相)工况①工况⑤(三相)工况⑤(单相)23.5N243114.88103.98103.97114.91104.00104.0019.0N21348.7343.5943.5948.7443.6043.6015.5N183142.95134.80134.80107.79102.02102.0315.0N182156.61149.90149.90119.91113.63113.63
2.2 设计风荷载下构架避雷针的静力承载力
在设计风速x向作用下,构架避雷针不同高度处的风荷载可按式(1)计算[5]:
wk=βzμzμsw0,
(1)
式中:wk为风荷载标准值;w0为基本风压值;βz为高度z处的风振系数;μz为风压高度变化系数;μs为风荷载体型系数,对于圆形独立单杆,可按如下规定计算[5]:当μzw0d2≤0.002时,μs=1.2,当μzw0d2≥0.015时,μs=0.6,中间按线性插值计算,其中w0按kN/m2计算,d为单杆直径,按m计算。
(1)构架避雷针的应力和位移响应。为了分析地线对避雷针受力的影响,本节分别考虑避雷针上是否悬挂地线两种情况,计算结果如图3所示。
由图3可知,在设计风速等效静载作用下,边跨和中间跨构架避雷针下部的应力较大,顶端的位移较大;悬挂地线时,避雷针底部应力和顶部位移较没有地线时增加较多,最大应力为82 MPa,最大位移为173.92 mm,均在规范[5]许可范围内。由于地线张力施加在避雷针底部附近,因此挂线时,避雷针根部附近的应力增加较多,地线张力的影响不可忽视。对比边跨和中间跨避雷针的响应可知,相同情况下中间避雷针的应力和位移均比边跨避雷针对应节点的值大,说明中间避雷针受力更为不利,结构设计时应予以关注。
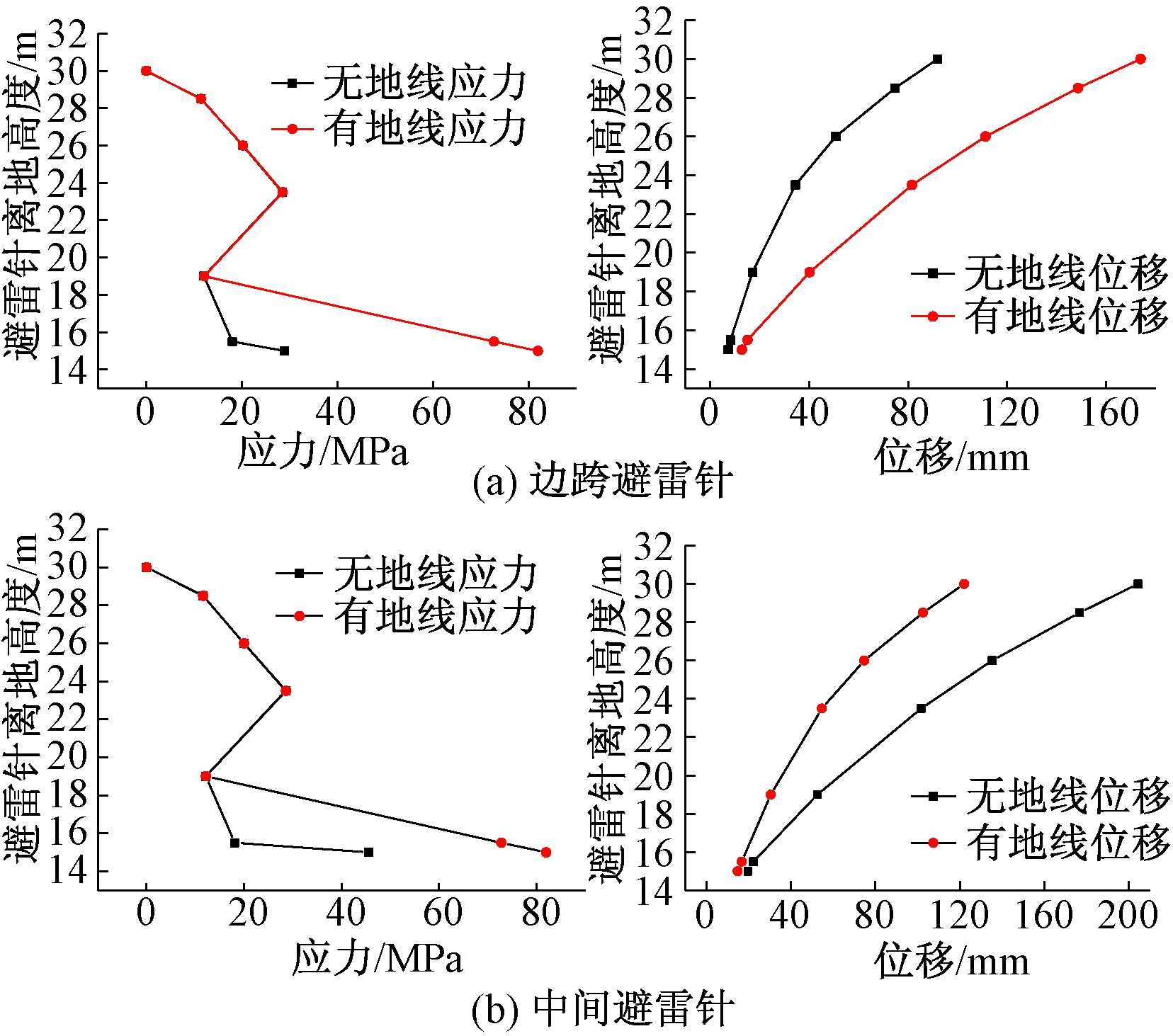
图3 构架避雷针有无地线时节点应力及位移对比
Figure 3 Comparison of the stress and displacement results for the lightning rods with and without ground wire
(2)构架避雷针相贯节点的受力特点及加固分析。由于实际中构架避雷针断裂多发生在避雷针与横梁的T型相贯节点处。为进一步了解该部位的应力分布,进而提出合适的加固方案,本节以中间避雷针为例,采用Shell 93单元建立典型相贯节点的精细化有限元模型,避雷针各段之间通过创建刚性区连接,横梁两端的法兰盘和加劲肋对称设置,构架柱底部设置为固结,建模时各部件采用切分和搭接命令形成整体。在前述结构自重、地线张力和风荷载作用下,相贯节点处的应力分布如图4(a)所示。可以看出,在设计荷载作用下避雷针和横梁交接处应力水平较高,虽然总体上仍处于安全范围,但在相贯节点根部出现了明显的应力集中现象,最大拉应力达到398.30 MPa。该值已超过了钢材的屈服强度(345 MPa),说明上述避雷针相贯节点构造不够合理,在随时间不断变化的风荷载等因素作用下易发生脆断事故。
为改进上述构造的不足,考虑在避雷针和横梁T型相贯节点处设置加劲肋,对其进行加固。具体方案如下:在横梁中部设置3道竖向加劲肋,厚度为12 mm,间隔100 mm。采用和未加固避雷针相同的方式对加固后的结构进行静力加载分析,结果如图4所示。
由图4可知,当在横梁上设置加劲肋后,相贯节点区域的应力明显减小,最大值为120.07 MPa,出现在中部竖向加劲肋和横梁相贯位置处,该值远小于钢材屈服强度。这说明笔者建议的加固方式可以有效缓解构架避雷针相贯节点区域的应力集中现象,是一种较为可行的加固方案。
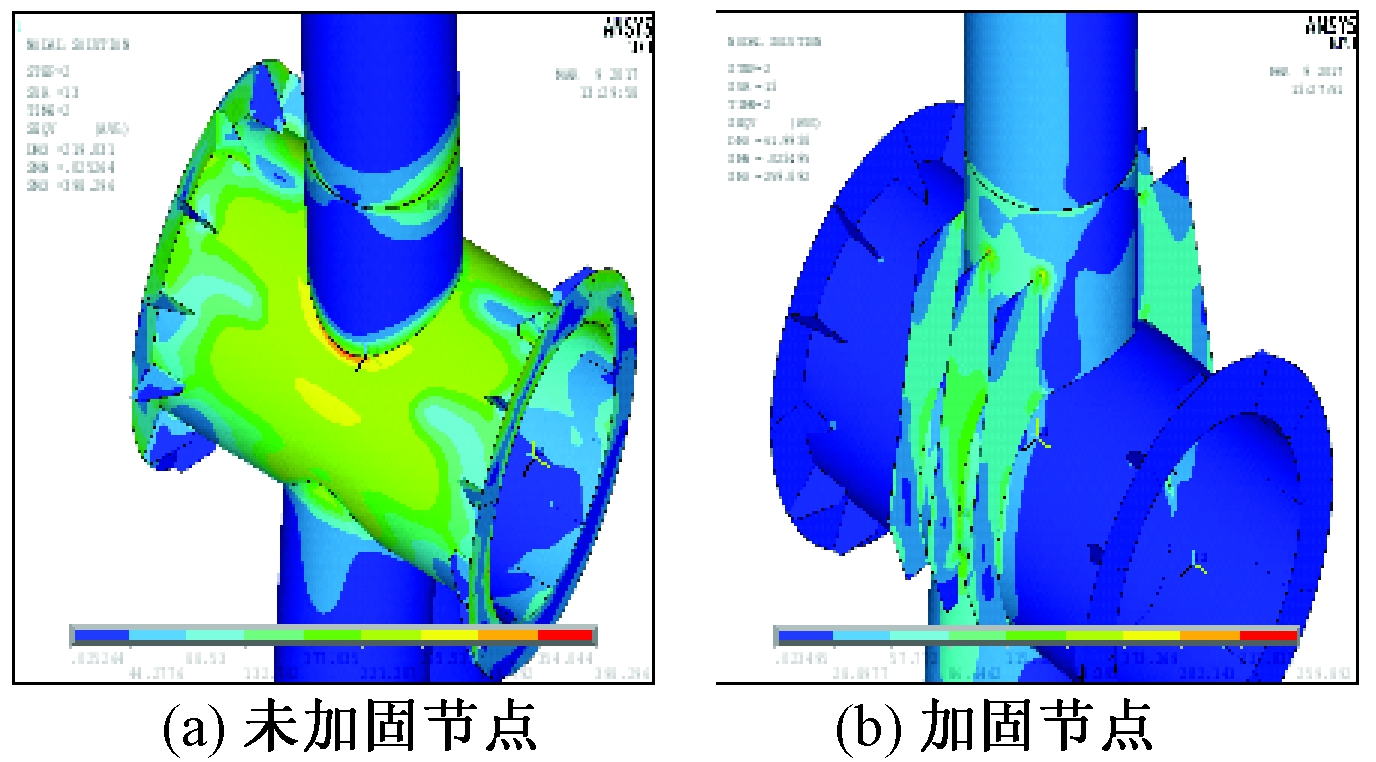
图4 加固前后构架避雷针相贯节点应力云图
Figure 4 Stress of the unreinforced and reinforced tubular joint of the lightning rod
3 构架避雷针的风致动力响应分析
考虑到构架避雷针结构具有高度高、刚度小的特点,在脉动风作用下极易发生振动。因此,对其进行设计风速作用下的动力响应分析,了解其受力特点,进而提出合理的设计建议,这对于预防类似断裂事故的发生具有较大的实际意义。
3.1 脉动风速时程模拟
由于缺乏可靠的实测风速数据,采用谐波叠加法[8]模拟构架避雷针结构的风场,将模拟结果作为结构的输入荷载来进行风振响应分析。谐波叠加法是采用一系列余弦波加权叠加以实现风速模拟的,具有计算简单、数据稳定且精度较高的优点。基于多维随机过程样本模拟理论,谐波叠加法模拟的随机过程为:
bjm(l)sin[ωlt-φjm(ωl)]},j=1,2,…,n。
(2)
式中:![]()
|Ijm(ωl)|ξm;ηm和ξm是相互独立的标准差为1、均值为0的高斯随机数;Δω=(ωb-ωa)/N是圆频率的增量;φjm(ωl)是处于不同位置处的相位角。
由于变电构架各跨的间距较大,相邻构架相关性较弱,模拟时只需考虑结构竖向的风速相关性。模拟采用的各参数见表3。 限于篇幅,这里仅以中间避雷针顶部节点42(标高为30 m)和中部节点39(标高为23.5 m)为例,给出模拟的风速时程曲线,同时将模拟所得的脉动风速功率谱和目标谱进行比较,结果如图5所示,二者吻合较好。因此,笔者模拟的脉动风荷载时程样本,可用于构架避雷针结构的风振响应分析。在获得了各节点位置处的脉动风时程后即可依据体型系数按照准定常理论[10]建立节点脉动风荷载。
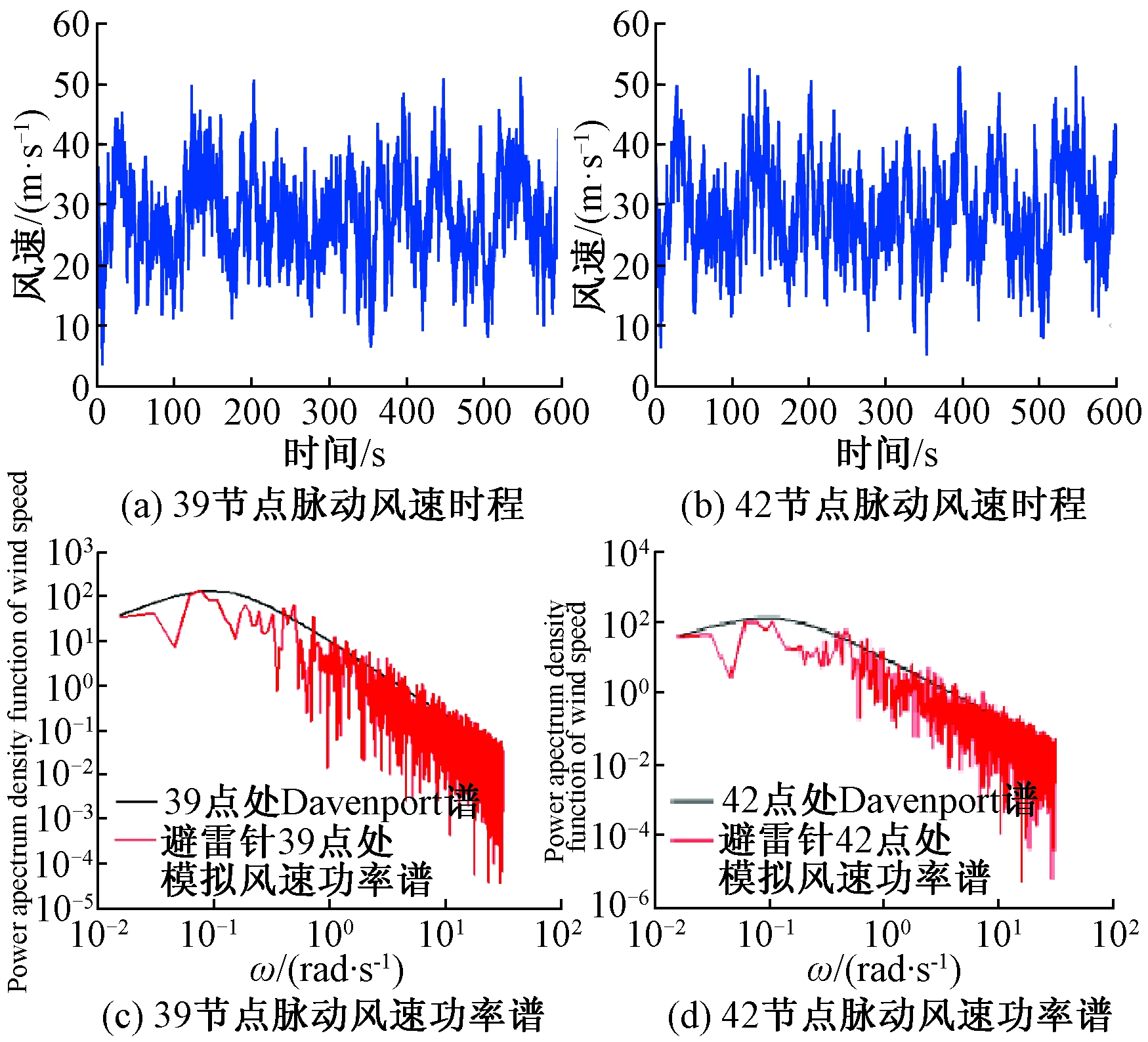
图5 避雷针代表点处的脉动风速时程及其功率谱
Figure 5 Wind speed time history curve and power spectrum at each representative points of the lightning rod
表3 风速时程模拟各参数
Table 3 Parameters of the wind speed time simulation

参数模拟方法平均风速模型基本风压/(N·m-2)地面粗糙度类别、系数脉动风速谱模拟点数风速时程总时间/步长频率采样点数上限频率/Hz取值谐波叠加对数律0.35B类、0.16Davenport[9]56600 s/0.12 04810
3.2 构架避雷针的风致动力响应
3.2.1 未加固构架避雷针的风振响应
首先分析未加固的构架避雷针的风振响应,结果如图6所示。由图6可以看出,设计风速作用下,构架避雷针的应力和位移动力响应均较静力时有较大增加。为更清楚地了解避雷针在动、静力荷载作用下的响应特点,笔者还计算了两种情况下中间避雷针主要节点的应力响应比值,如表4所示。
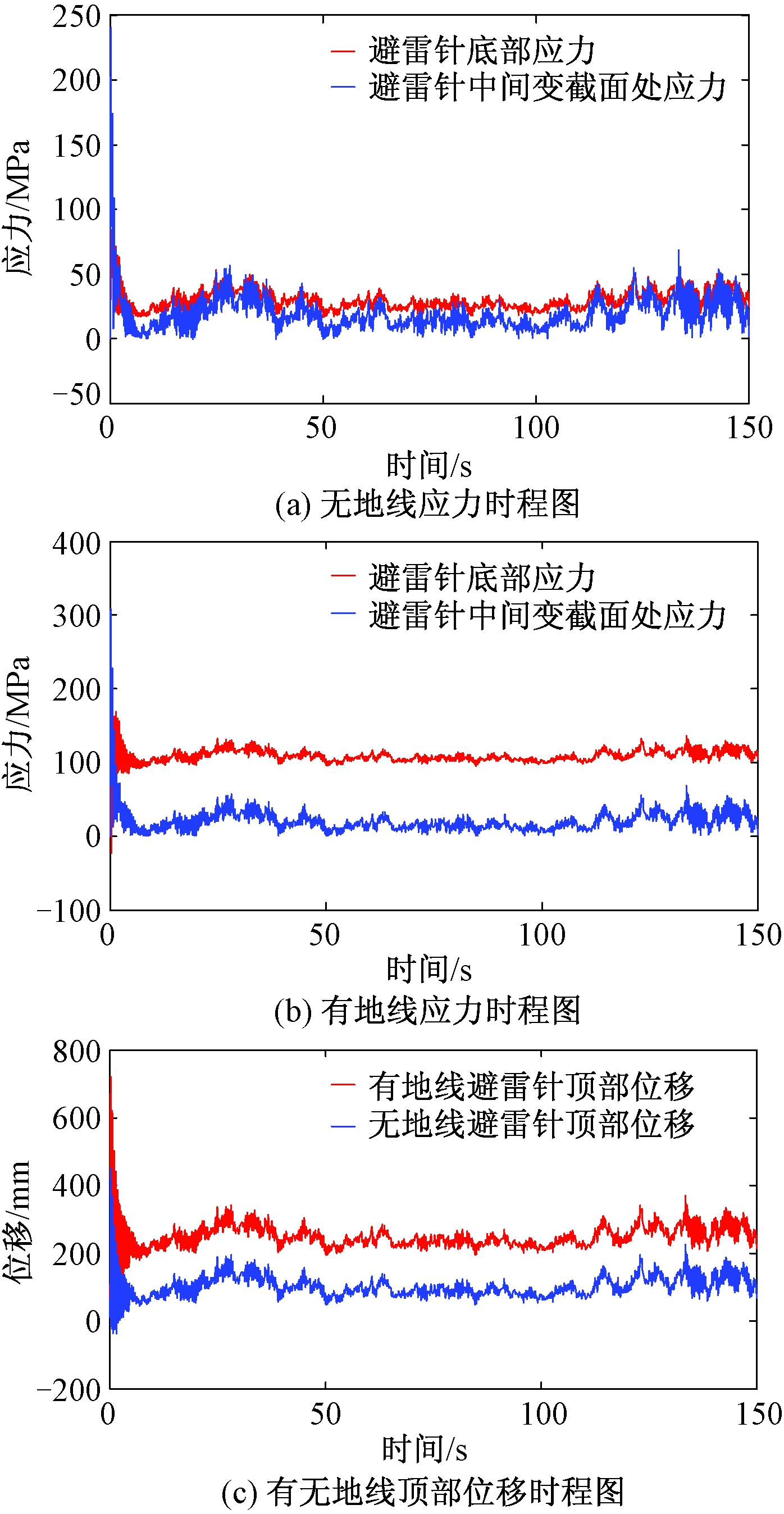
图6 构架避雷针底部和变截面处应力及顶部位移时程
Figure 6 Time history of the stress at the bottom and the variable cross-section and the displacement at the top of the lightning rod
对比表4中结果可知,考虑脉动风的影响时,避雷针主要节点的应力响应均大于静力情况,就具体数值来看,避雷针底部应力水平较高,为受力最不利截面,动静力应力比值为1.57,说明按照现行规范拟静力方法设计的构架避雷针对于脉动风的动载效应考虑不全面,结果偏于不安全。再结合表4还可以看出,避雷针中间变截面应力发生了突变,说明其构造不合理。建议实际设计时将设计风速下的拟静力分析结果乘以相应的动力放大系数δ(就本文算例工况而言,建议取δ≥1.6)以考虑脉动风对结构的不利影响。同时采用均匀渐变的圆钢管截面避雷针形式,避免截面的突变引起应力集中等不利影响。
表4 设计风速作用下构架避雷针的动、静力应力响应对比
Table 4 Comparison of the dynamic and static stress of the middle lightning rod under the design wind speed
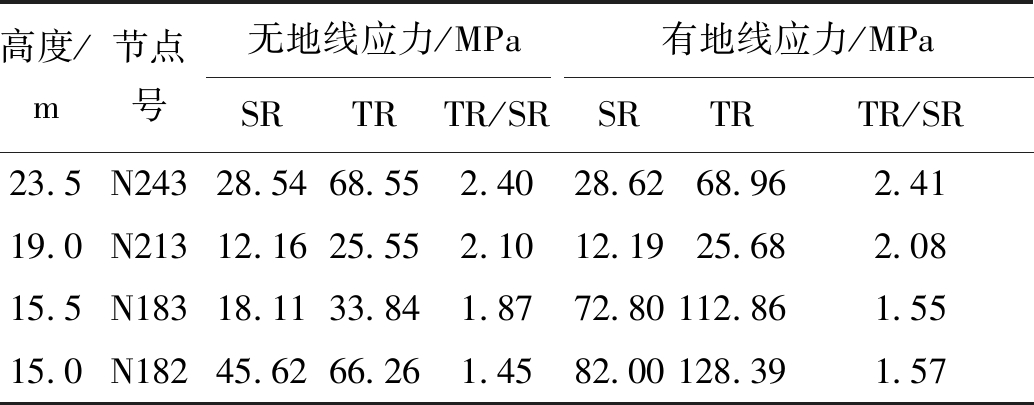
高度/m节点号无地线应力/MPa有地线应力/MPaSRTRTR/SRSRTRTR/SR23.5N24328.5468.552.4028.6268.962.4119.0N21312.1625.552.1012.1925.682.0815.5N18318.1133.841.8772.80112.861.5515.0N18245.6266.261.4582.00128.391.57
注:SR表示静力计算结果,TR表示动力计算结果,下同。
3.2.2 构架避雷针相贯节点区域的风振响应
前文分析表明,构架避雷针相贯节点区域较为薄弱。因此,本节重点考察脉动风作用下相贯节点区域的应力。为了反映脉动风对避雷针相贯节点区域应力的影响,同时对加固效果进一步评价,本节计算了加固前后构架避雷针相贯节点区域的最大拉应力时程曲线,如图7所示。
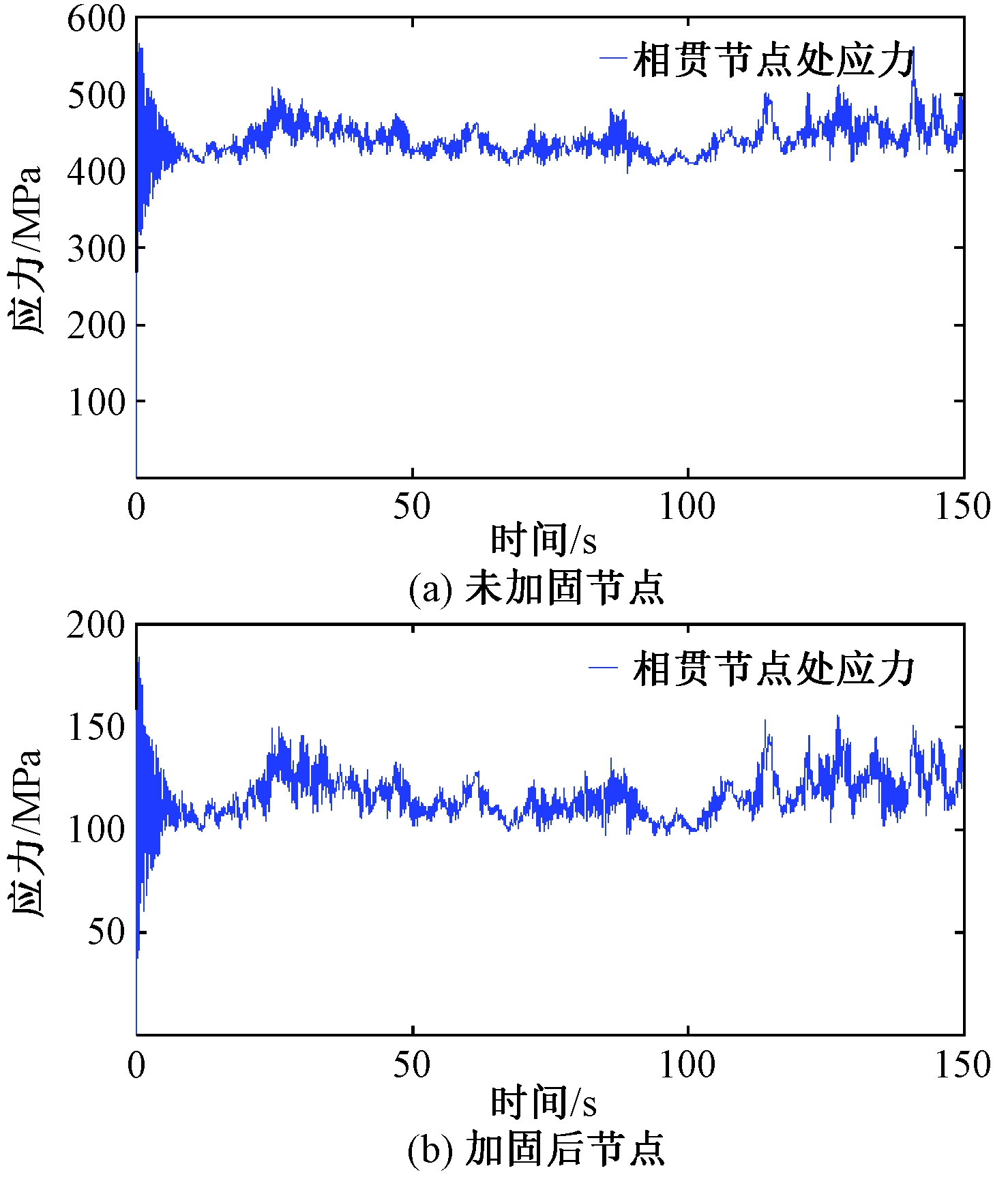
图7 加固前后构架避雷针相贯节点区域最大拉应力时程
Figure 7 Time history of the maximum tensile stress of the unreinforced and reinforced tubular joint of the lightning rod
从图7可以看出,在脉动风作用下加固前相贯节点区域最大拉应力达到了560.15 MPa,远超过横梁钢材屈服强度;而加固后最大拉应力仅为155.21 MPa,仍在弹性范围之内。为了更清楚地对比加固前后构架避雷针动、静力响应,笔者还计算了悬挂地线时避雷针各代表高度处的应力值,结果如表5所示。由表5可知,当在横梁上设置加劲肋后,各代表位置处的动、静应力值都明显减小,尤其是相关节点和中间变截面处的动、静力应力比值也明显减小,分别为1.29和1.81。这说明设置加劲肋可以有效缓解结构的应力集中现象,是较为可行的加固方式,但脉动风引起的动力放大效应仍然不能忽略。
表5 加固前后构架避雷针有地线时的应力对比
Table 5 Comparison of the dynamic and static stress of the unreinforced and reinforced lightning rod with ground wire
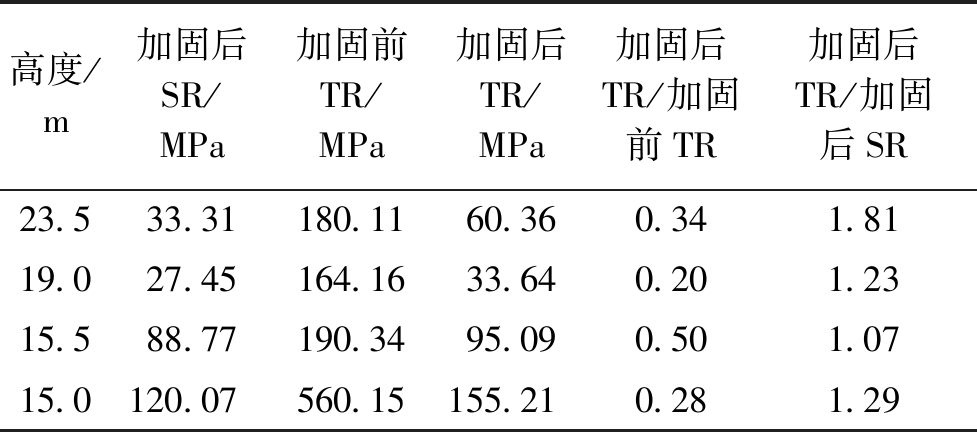
高度/m加固后SR/MPa加固前TR/MPa加固后TR/MPa加固后TR/加固前TR加固后TR/加固后SR23.533.31180.1160.360.341.8119.027.45164.1633.640.201.2315.588.77190.3495.090.501.0715.0120.07560.15155.210.281.29
4 结论
对现代大型变电站中常用的构架避雷针结构进行了设计风荷载作用下的静力和风致动力响应分析,了解了结构的整体受力特点和薄弱环节,并根据分析结果提出了加固设计建议。
(1)目前常用的变电构架避雷针结构中,避雷针和横梁T型相贯节点区域构造不合理,容易出现应力集中现象。通过在该区域设置加劲肋的方式可显著降低相贯节点区的应力水平,有效缓解应力集中,建议工程中参考使用。
(2)在变电构架避雷针结构的标准化设计中,按照现行规范拟静力方法设计的结果是偏于不安全的。实际设计时建议将规范拟静力方法得到的结果乘以相应的动力放大系数δ(就本文算例工况而言,建议取δ≥1.6)以考虑脉动风对结构的不利影响。
(3)当前标准化设计中典型构架避雷针中间采用变截面形式连接不够合理。建议在实际中采用均匀渐变的圆钢管截面避雷针形式,避免截面突变引起的局部应力增大等不利影响。
[1] VANDERBILT M D,CRISWELL M E. Analysis and design of single-pole transmission structures [J]. Computers & structures, 1988, 28(4):551-562.
[2] 李天,袁征,郑德乾,等. 应用高等分析理论分析人字形电力构架[J].郑州大学学报(工学版),2006,27(1):15-18.
[3] 张劲光,王朝华,库永恒,等. 高压变电站构架避雷针结构抗震性能分析[J].世界地震工程,2017,33(3):192- 201.
[4] 丁国君,郭磊,董曼玲,等.构架避雷针折断原因分析及对策[J].河南电力,2015,43(4):6-9.
[5] 国家能源局.变电站建筑结构设计技术规程:DL/T 5457—2012[S].北京:中国计划出版社,2012.
[6] 陈怡文.变电构架避雷针结构的风致动力响应分析[D].郑州:郑州大学,2017.
[7] 王新敏,李义强,许宏伟.ANSYS结构分析单元与应用[M].北京:人民交通出版社,2011.
[8] RICE S O. Mathematical analysis of random noise [J]. The bell system technical journal, 1944, 23(3):282-332.
[9] DAVENPORT A G. The spectrum of horizontal gustiness near the ground in high winds [J].Quarterly journal of the royal meteorological society, 1961, 87(372): 194-211.
[10] DYRBYE C, XHANSEN S O. Wind loads on structures [M]. New York: John Wiley & Sons Ltd, 1996.