0 引言
最优化问题分为传统优化方法和启发式优化方法.传统优化方法大多利用目标函数的梯度(或导数)信息实现单可行解的惯序、确定性搜索;启发式优化方法以仿生算法为主,通过启发式搜索策略实现多可行解的并行、随机优化.启发式搜索算法不要求目标函数连续、可微等信息,具备较好的全局寻优能力,因而成为最优化领域的一个研究热点[1-2].
多启发式算法众多,有基于蚂蚁觅食提出的蚁群算法(ant colony optimization,ACO)[3],基于蜜蜂采蜜提出的人工蜂群算法(artifical bee colony,ABC)[4],基于细菌捕食提出的细菌捕食算法(bacterial forging optimization,BFO)[5],差分进化算法 (different evolution,DE)[6],头 脑 风 暴 算 法(brain storm optimization,BSO)[7-8]等.作为一种经典的启发式算法——粒子群优化算法(particle swarm optimization algorithm,PSO)是对鸟群捕食行为的模拟[9-10].PSO概念简单,易于实现,目前已广泛运用于函数优化、神经网络训练、模糊系统控制以及其他的科学和工程应用领域[11-15].
原始的粒子群算法易陷入局部最优.为解决原始粒子群算法早熟的缺点,笔者根据人类社会中领袖任期机制提出一种周期性最优机制,同时引入周期性的学习策略,提出聚类分组变异方法来改进粒子群从而提高种群的多样性,避免陷入局部最优,同时保障种群的收敛速度.
1 标准粒子群算法
在PSO中,每个解被称为“粒子”(particle),所有的粒子都有一个适应度值(fitness value),每个粒子还有一个速度向量决定他们的运动方向,粒子通过不断更新运动方向搜索解空间.算法的数学描述为:在Q维空间中有n个粒子在进行搜索,粒子的位置表示为 Xi=(xi1,xi2,…,xiQ),粒子对应的速度可以表示为Vi=(vi1,vi2,…,viQ),粒子在搜索时要考虑两个因素:①单个粒子搜索到的个体历史最优值 Pbi,Pbi=(pbi1,pbi2,…,pbiQ),i=1,2,3,…,n;②全部粒子搜索到的全局历史最优值Pgb,Pgb=(pgb1,pgb2,…,pgbQ),i=1,2,3,…,n.
各粒子的速度和位置按如下公式进行更新:
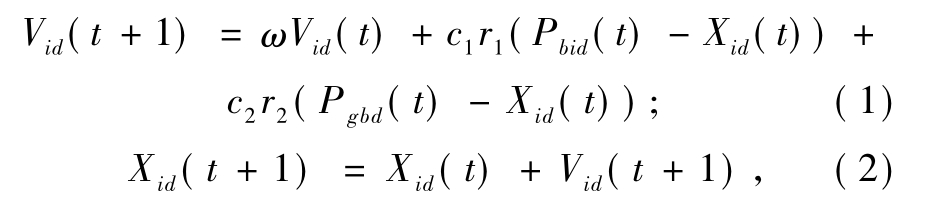
式中:d为粒子的维度;ω是保持原来速度的系数,即惯性权重;c1、c2是粒子跟踪自己和群体历史最优值的权重系数;r1、r2是[0,1]均匀分布的随机数.
2 基于学习理论的改进粒子群优化算法
为避免早熟,提高种群的多样性,笔者引入了周期性学习策略,分别提出周期性最优机制、聚类分组变异机制以及分类预测评估机制.周期性最优机制通过为全局最优粒子设定数据,全局最优粒子陷入局部更新,避免整个种群陷入局部最优.聚类分组变异机制通过聚类划分种群,再选取不同类的粒子产生竞争粒子.分类预测评估机制通过依照以往若干代竞争粒子与全局最优粒子的进化结果构建分类器,预测竞争粒子是否能够替换全局最优粒子,确保全局最优粒子的优越性.
2.1 周期性最优机制
在自然界中,每个群居生物种群都有对应的领袖带领种群前行,无论是动物还是人类都是如此.Kubota等[16-17]将这个概念运用到遗传算法设计.在包含老年化机制的遗传算法中,每个个体都被分配一个年龄.当它的年龄达到一个预定义的寿命时,该个体会被移除.Chen等[18]同样引入衰老机制到粒子群算法中,以此提高粒子群的多样性.
笔者借鉴这种思想,针对粒子群算法中全局最优粒子提出一种限制条件——周期性,即周期性地改变粒子群中的全局最优粒子,从而避免种群在全局最优粒子陷入局部最优而导致整个群体也陷入局部最优.
2.2 聚类分组变异机制
为了周期性地生成新的全局最优粒子,笔者首先生成一个竞争粒子来尝试替换这个全局最优粒子.
聚类可以用于寻找数据内在的分布结构,因此研究者提出将聚类分析应用到多目标演化计算中[19-21].笔者提出一种聚类分组变异机制,借助聚类的思想对粒子群依照其个体分布情况进行分组[22].当全局最优粒子存在的时间超过周期限制时,对粒子群采用K-means.依据粒子间的欧氏距离进行分组,最后随机选择2个组依照公式(3)进行变异产生竞争粒子,
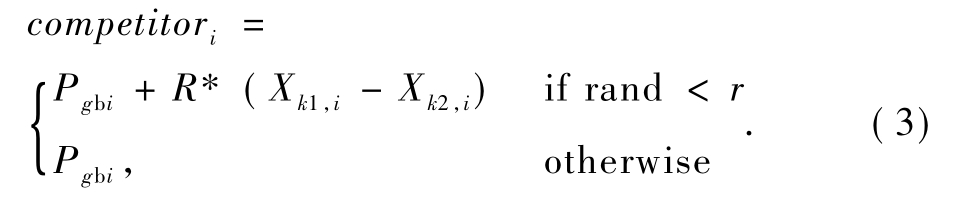
笔者提出的改进粒子群算法流程如图1所示.
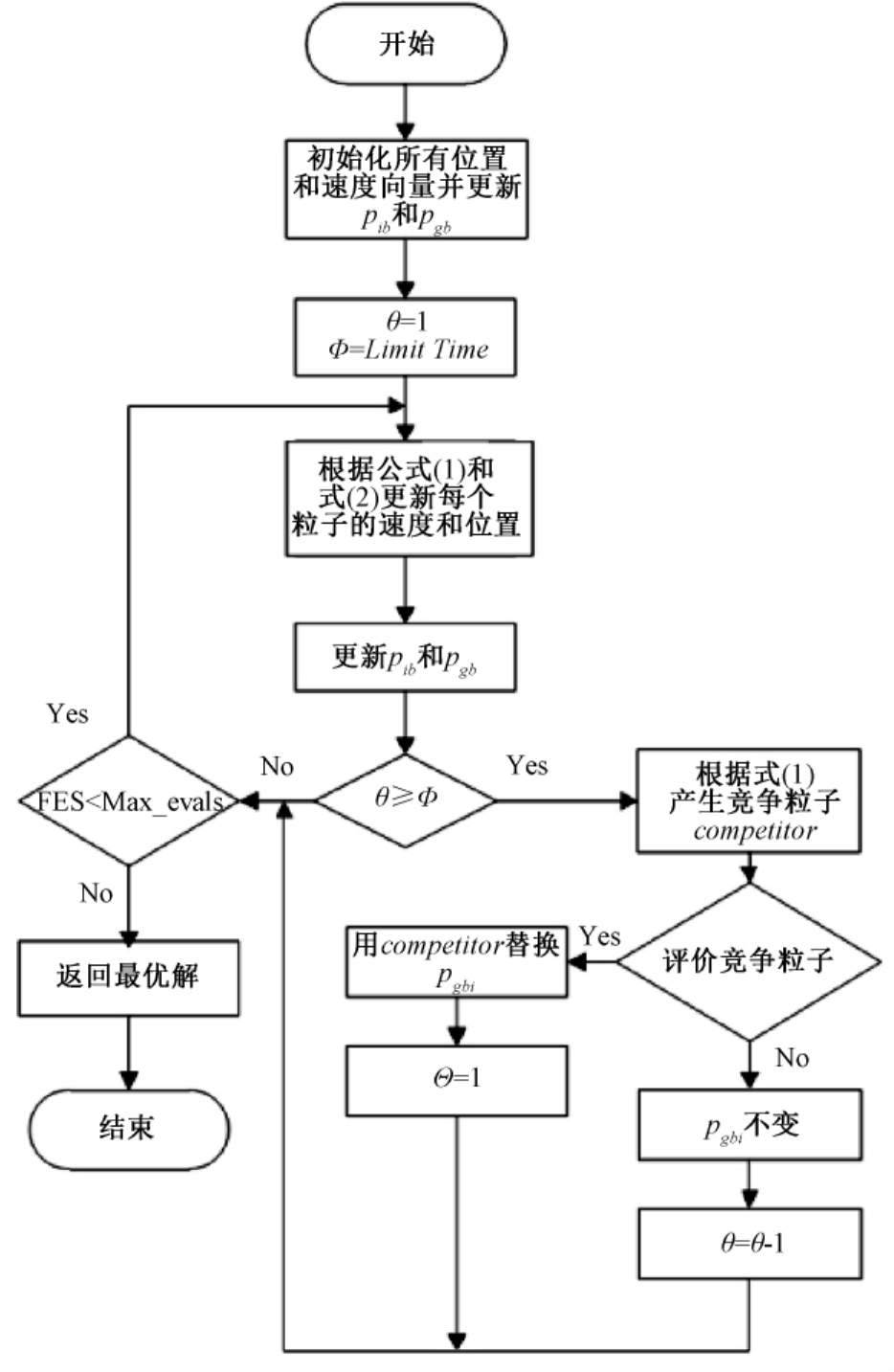
图1 L-PSO算法流程框图
Fig.1 Flowchart of L-PSO
3 参数设置
笔者提出的L-PSO算法引入了3个主要参数.包括聚类的分组个数SET、产生竞争粒子时的变异概率r以及Pgb的周期限制tenure.
聚类分组中较大的SET将加重算法的时间复杂度;反之,聚类分组后无法从个体在决策空间的分布上看出个体间的差异,因此,为平衡时间复杂度和方法的有效性,我们在文中将 SET设置为3.
产生竞争粒子时的变异概率为 r.因为当前的Pgb粒子仍然是已知的最优粒子,因此 Pgb的解在不同维度上的值是具有参考价值的.因此,r值设置为1/n,n是解的维度大小.这样,生成的竞争粒子在极大程度上保持Pgb解结构的同时,在每一个维度上都有相同的产生变异的机率.这样,即保证了生成的竞争粒子质量,也有很大机会生成有较好进化潜能的新粒子.
此外,为了衡量tenure值的变化对算法性能的影响,我们从所选择的22个测试函数如表1所示.选择了单峰函数 f1,从 CEC2013中选择了一个多峰函数(在本文编号为 f22)做参数测试,统计结果如图2.可以看出,当tenure设置为10时,L-PSO在解决单峰和多峰函数时能显示出较好的性能,因此,在实验中我们将tenure的值取为10.
表1 标准测试函数
Tab.1 Basic test functions

编号 测试函数 N 搜索范围 最优值f1 Sphere 30 [-100,100]0 f2 Schwefel’s P2.22 30 [-10,10]0 f3 Quadric 30 [-100,100]0 f4 Rosenbrock’s 30 [-10,10]0 f5 Step 30 [-100,100]0 f6 Schwefels 30 [-500,500]-12 569.5 f7 Rastrigin 30 [-5.12,5.12]0 f8 Noncontinuous Rastrigin 30 [-5.12,5.12]0 f9 Ackley 30 [-32,32]0 f10 Griewank 30 [-600,600]0 f11 Penalized 1 30 [-50,50]0 f12 Penalized 2 30 [-50,150]0
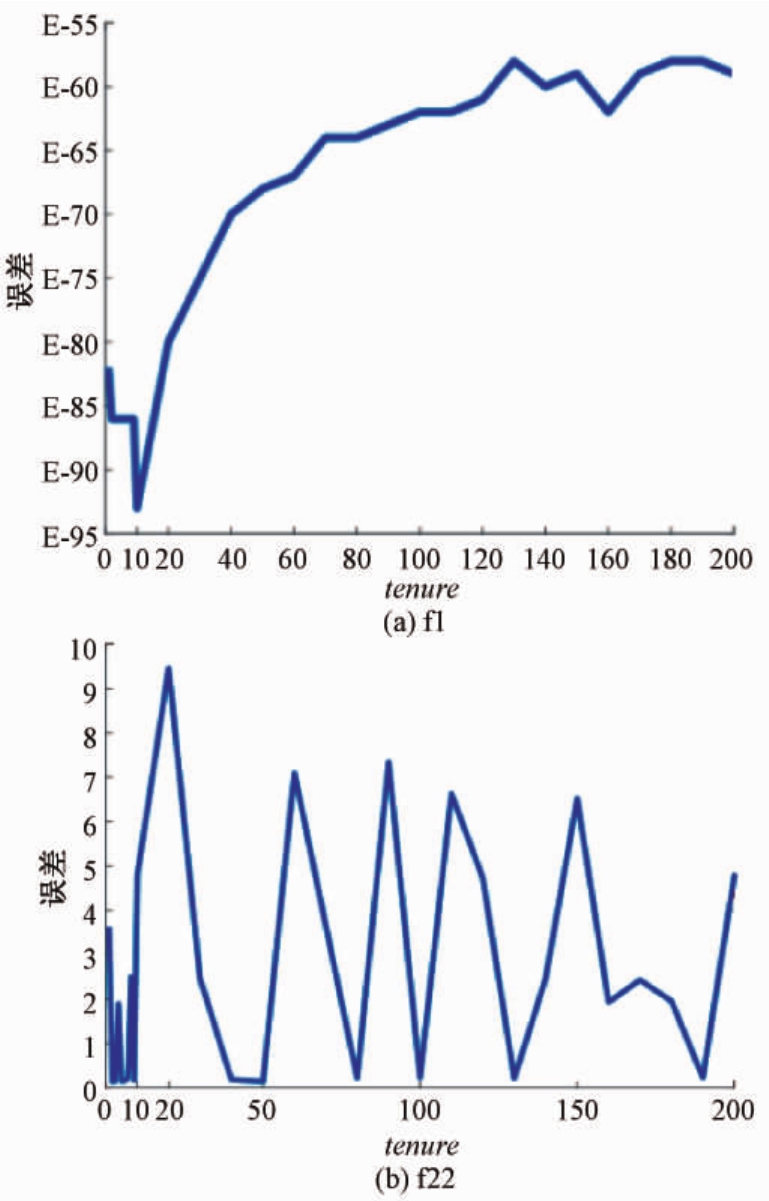
图2 f1和f22上不同tenure值L-PSO的算法性能
Fig.2 Performance of the L-PSO under different tenure values on f1 and f22
4 对比实验
4.1 测试函数和对比算法
为了验证本文所提策略的有效性,笔者选择了22个测试函数来评估L-PSO的性能.前12个为表1所示的基本函数,其余函数为CEC2013中的前十个测试函数,在本文中编号为f13~f22.
为了比较算法性能,笔者选择了4个有代表性的改进的 PSO算法作为对比算法,包括 ALCPSO、DMS-PSO、GPSO和线性权重递减版本的GPSO.所有算法的参数设置与原文献中相同,具体设置如表2所示.此外,L-PSO中公式(3)的R值为生成竞争粒子的控制参数,设置为0.5.为保证实验结果准确,每一个算法都在各个测试函数上独立地运行20次并求取平均值.每个测试函数的维度N设置为30,算法种群大小设置为20,算法迭代的停止条件为最大函数评估次数Max_evals=200 000.
表2 对比算法及参数设置
Tab.2 Parameters settings for algorithms

算法名称 参数设置ALC-PSO c1=2,c2=2,ω =0.4,T=2,ω=60 DMS-PSO χ=0.729 8,c1=c2=1.494 45,M=4,R=0.4线性权重递减的 GPSO c1=2,c2=2,ω∈[0.4,0.9]=10 GPSO c1=2,c2=2,ω/n L-PSO c1=2,c2=2,ω =0.4,SET=3,tenure=10,r=1
4.2 数值结果对比
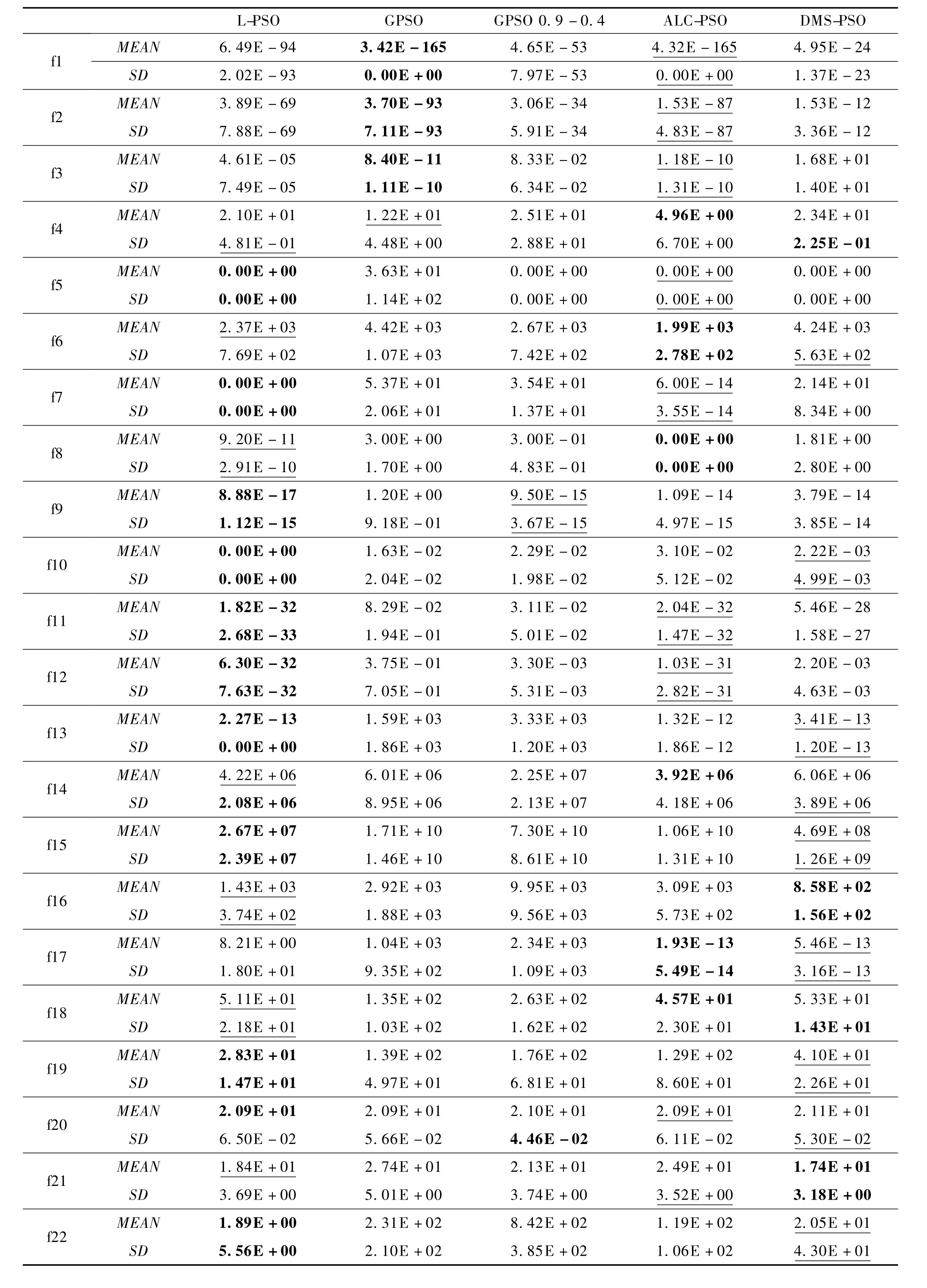
各个算法20次独立运行后的平均误差值MEAM以及标准差SD的统计结果如表3所示.最好的结果用粗体表示,次优的结果用下划线表示.
从表3中可以看出L-PSO算法在22个测试函数中的 f5、f7、f9、f10、f11、f12、f13、f15、f19、f20和 f22 上取得了最好的结果.在 f6、f8、f14、f16、f18和f21上取得了次优的结果.此外,L-PSO在解决多峰函数时,展现出了优越的性能,在 f6~f12,f18~f22这12个多峰函数的试验中,L-PSO在其中的8个函数上取得了最优解,综合所有函数最后的结果可以看出,基于学习理论的改进粒子群算法在性能上具有一定的优越性.
4.3 算法收敛比较
图3为L-PSO算法与其他算法的比较结果.其中横坐标为函数评估次数,纵坐标为误差值.由于篇幅限制,只展示部分有代表性的结果.从收敛曲线可以看出,L-PSO保持了较好的收敛性可
见L-PSO在解决本文中的测试函数时显现出了较好的性能.
表3 对比实验结果
Tab.3 Results comparison on all test functions
L-P S O G P S O G P S O 0.9-0.4 A L C-P S O D M S-P S O f 1 M E A N 6.4 9 E-9 4 3.4 2 E-1 6 5 4.6 5 E-5 3 4.3 2 E-1 6 5 4.9 5 E-2 4 S D 2.0 2 E-9 3 0.0 0 E+0 0 f 2 7.9 7 E-5 3 0.0 0 E+0 0 1.3 7 E-2 3 M E A N 3.8 9 E-6 9 3.7 0 E-9 3 3.0 6 E-3 4 1.5 3 E-8 7 1.5 3 E-1 2 S D 7.8 8 E-6 9 7.1 1 E-9 3 f 3 5.9 1 E-3 4 4.8 3 E-8 7 3.3 6 E-1 2 M E A N 4.6 1 E-0 5 8.4 0 E-1 1 8.3 3 E-0 2 1.1 8 E-1 0 1.6 8 E+0 1 S D 7.4 9 E-0 5 1.1 1 E-1 0 f 4 6.3 4 E-0 2 1.3 1 E-1 0 1.4 0 E+0 1 M E A N 2.3 4 E+0 1 S D 2.1 0 E+0 1 1.2 2 E+0 1 2.5 1 E+0 1 4.9 6 E+0 0 f 5 M E A N 0.0 0 E+0 0 3.6 3 E+0 1 0.0 0 E+0 0 0.0 0 E+0 0 0.0 0 E+0 0 S D 0.0 0 E+0 0 f 6 1.1 4 E+0 2 0.0 0 E+0 0 0.0 0 E+0 0 0.0 0 E+0 0 M E A N 2.3 7 E+0 3 4.4 2 E+0 3 2.6 7 E+0 3 1.9 9 E+0 3 4.2 4 E+0 3 S D 7.6 9 E+0 2 1.0 7 E+0 3 7.4 2 E+0 2 2.7 8 E+0 2 f 7 5.6 3 E+0 2 M E A N 0.0 0 E+0 0 5.3 7 E+0 1 3.5 4 E+0 1 6.0 0 E-1 4 2.1 4 E+0 1 S D 0.0 0 E+0 0 f 8 2.0 6 E+0 1 1.3 7 E+0 1 3.5 5 E-1 4 8.3 4 E+0 0 M E A N 1.8 1 E+0 0 S D 9.2 0 E-1 1 3.0 0 E+0 0 3.0 0 E-0 1 0.0 0 E+0 0 f 9 2.9 1 E-1 0 1.7 0 E+0 0 4.8 3 E-0 1 0.0 0 E+0 0 2.8 0 E+0 0 M E A N 8.8 8 E-1 7 1.2 0 E+0 0 9.5 0 E-1 5 1.0 9 E-1 4 3.7 9 E-1 4 S D 1.1 2 E-1 5 f 1 0 9.1 8 E-0 1 3.6 7 E-1 5 4.9 7 E-1 5 3.8 5 E-1 4 M E A N 0.0 0 E+0 0 1.6 3 E-0 2 2.2 9 E-0 2 3.1 0 E-0 2 2.2 2 E-0 3 S D 0.0 0 E+0 0 f 1 1 2.0 4 E-0 2 1.9 8 E-0 2 5.1 2 E-0 2 4.9 9 E-0 3 M E A N 1.8 2 E-3 2 8.2 9 E-0 2 3.1 1 E-0 2 2.0 4 E-3 2 5.4 6 E-2 8 S D 2.6 8 E-3 3 f 1 2 1.9 4 E-0 1 5.0 1 E-0 2 1.4 7 E-3 2 1.5 8 E-2 7 M E A N 6.3 0 E-3 2 3.7 5 E-0 1 3.3 0 E-0 3 1.0 3 E-3 1 2.2 0 E-0 3 S D 7.6 3 E-3 2 f 1 3 7.0 5 E-0 1 5.3 1 E-0 3 2.8 2 E-3 1 4.6 3 E-0 3 M E A N 2.2 7 E-1 3 1.5 9 E+0 3 3.3 3 E+0 3 1.3 2 E-1 2 3.4 1 E-1 3 S D 0.0 0 E+0 0 f 1 4 1.8 6 E+0 3 1.2 0 E+0 3 1.8 6 E-1 2 1.2 0 E-1 3 M E A N 4.2 2 E+0 6 6.0 1 E+0 6 2.2 5 E+0 7 3.9 2 E+0 6 6.0 6 E+0 6 S D 2.0 8 E+0 6 f 1 5 8.9 5 E+0 6 2.1 3 E+0 7 4.1 8 E+0 6 3.8 9 E+0 6 M E A N 2.6 7 E+0 7 1.7 1 E+1 0 7.3 0 E+1 0 1.0 6 E+1 0 4.6 9 E+0 8 S D 2.3 9 E+0 7 f 1 6 1.4 6 E+1 0 8.6 1 E+1 0 1.3 1 E+1 0 1.2 6 E+0 9 M E A N 1.4 3 E+0 3 2.9 2 E+0 3 9.9 5 E+0 3 3.0 9 E+0 3 8.5 8 E+0 2 S D f 1 7 3.7 4 E+0 2 1.8 8 E+0 3 9.5 6 E+0 3 5.7 3 E+0 2 1.5 6 E+0 2 M E A N 8.2 1 E+0 0 1.0 4 E+0 3 2.3 4 E+0 3 1.9 3 E-1 3 5.4 6 E-1 3 S D 1.8 0 E+0 1 9.3 5 E+0 2 1.0 9 E+0 3 5.4 9 E-1 4 f 1 8 3.1 6 E-1 3 M E A N 5.3 3 E+0 1 S D 5.1 1 E+0 1 1.3 5 E+0 2 2.6 3 E+0 2 4.5 7 E+0 1 f 1 9 2.1 8 E+0 1 1.0 3 E+0 2 1.6 2 E+0 2 2.3 0 E+0 1 1.4 3 E+0 1 M E A N 2.8 3 E+0 1 1.3 9 E+0 2 1.7 6 E+0 2 1.2 9 E+0 2 4.1 0 E+0 1 S D 1.4 7 E+0 1 f 2 0 4.9 7 E+0 1 6.8 1 E+0 1 8.6 0 E+0 1 2.2 6 E+0 1 M E A N 2.0 9 E+0 1 2.0 9 E+0 1 2.1 0 E+0 1 2.0 9 E+0 1 2.1 1 E+0 1 S D 6.5 0 E-0 2 5.6 6 E-0 2 4.4 6 E-0 2 f 2 1 6.1 1 E-0 2 5.3 0 E-0 2 M E A N 1.8 4 E+0 1 2.7 4 E+0 1 2.1 3 E+0 1 2.4 9 E+0 1 1.7 4 E+0 1 S D f 2 2 3.6 9 E+0 0 5.0 1 E+0 0 3.7 4 E+0 0 3.5 2 E+0 0 3.1 8 E+0 0 M E A N 1.8 9 E+0 0 2.3 1 E+0 2 8.4 2 E+0 2 1.1 9 E+0 2 2.0 5 E+0 1 S D 5.5 6 E+0 0 2.1 0 E+0 2 3.8 5 E+0 2 1.0 6 E+0 2 4.3 0 E+0 1 4.8 1 E-0 1 4.4 8 E+0 0 2.8 8 E+0 1 6.7 0 E+0 0 2.2 5 E-0 1
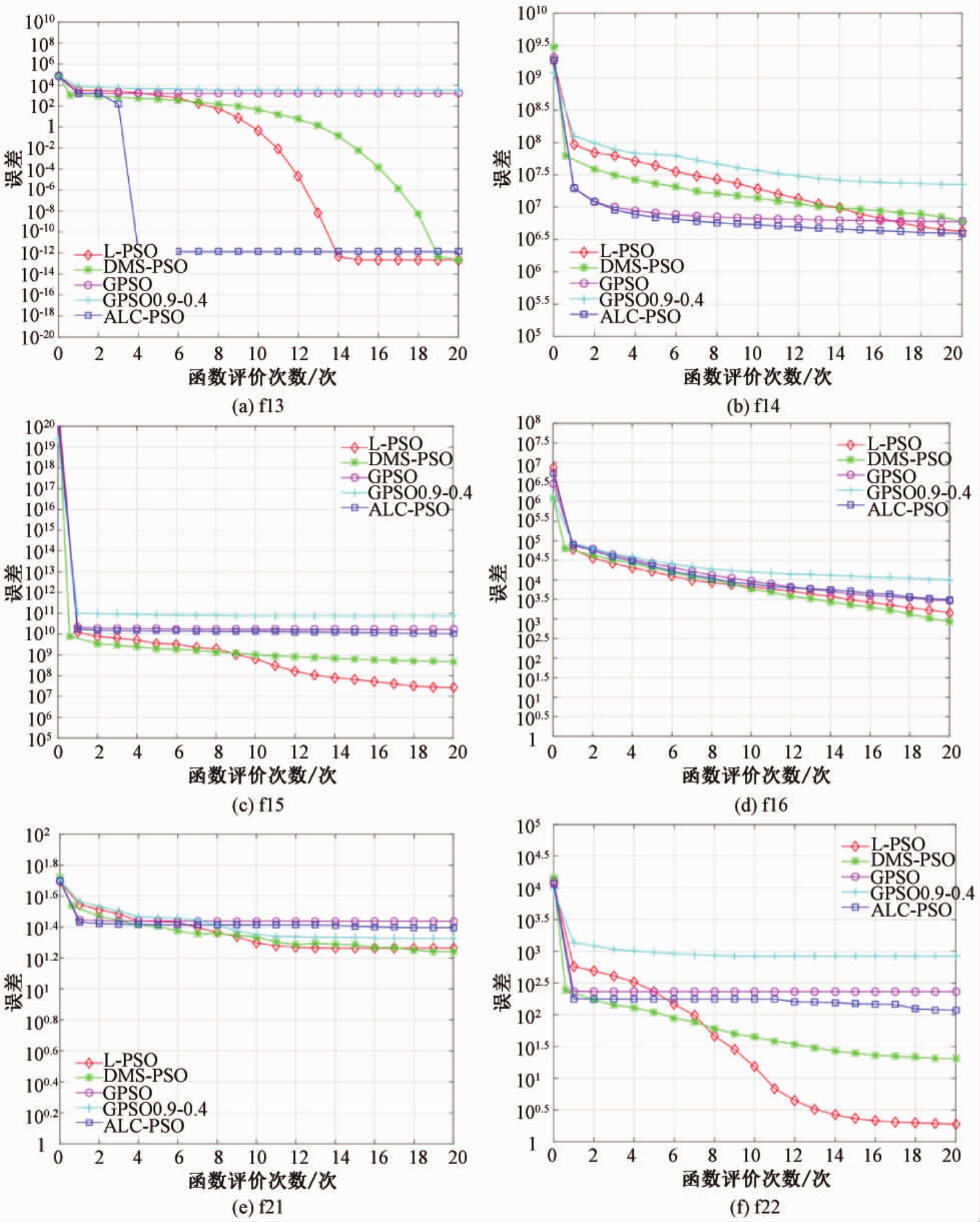
图3 收敛过程对比图
Fig.3 Comparrsion of convergencemap
5 结论
引入周期性学习策略,提出了周期性最优机制以及聚类分组变异机制对标准粒子群进行改进,提出基于学习理论的改进粒子群算法.该算法有效克服了标准粒子群优化及一些经典演化算法的缺陷,能够快速寻优,避免陷入局部最优,在单峰和多峰函数上都能较好地求解.下一步将尝试应用该算法到大规模的实际应用问题上进行优化求解.
[1]XUE B,ZHANG M,BROWNE W N,et al.A survey on evolutionary computation approaches to feature selection[J].IEEE transactions on evolutionary computation,2016,20(4):606-626.
[2]梁静,刘睿,瞿博阳,等.进化算法在大规模优化问题中的应用综述[J].郑州大学学报(工学版),2018,39(3):15-21.
[3]DORIGO M, MANIEZZOV, COLORNIA.Ant system:optimization by a colony of cooperating agents[J].IEEE transactions on systems,man,and cybernetics,part B:cybernetics,1996,26(1):29-41.
[4]KARABOGA D.An idea based on honey bee swarm for numerical optimization[R].Technical report-tr06,Erciyes university,engineering faculty,computer engineering department,2005.
[5]PASSINO K M.Biomimicry of bacterial foraging for distributed optimization and control[J]. Control systems,IEEE,2002,22(3):52-67.
[6]STORN R,PRICE K.Differential evolution —— a simple and efficient heuristic for global optimization over continuous spaces[J].Journal of global optimization,1997,11(4):341-359.
[7]SHI Y.Brain storm optimization algorithm[M]∥Advances in Swarm Intelligence.Springer Berlin Heidelberg,2011:303-309.
[8]程适,陈俊风,孙奕菲,等.数据驱动的发展式头脑风暴优化算法综述[J].郑州大学学报(工学版),2018,39(3):22-28.
[9]KENNEDY J.Particle swarm optimization[M]∥Encyclopedia ofMachine Learning. SpringerUS,2010:760-766.
[10]SHI Y,EBERHART R.A modified particle swarm optimizer[C]∥ Evolutionary Computation Proceedings,1998.IEEE World Congress on Computational Intelligence,The 1998 IEEE International Conference on.IEEE,1998:69-73.
[11]严晶晶,阎新芳,冯岩.WSN中基于梯度和粒子群优化算法的分集簇算法[J].郑州大学学报(工学版),2016,37(2):33-36.
[12]SHANG R,DAI K,JIAO L,et al.Improved memetic algorithm based on route distance grouping for multiobjective large scale capacitated arc routing problems[J].IEEE transactions on cybernetics,2017,46(4):1000-1013.
[13]LIANG J J,QIN A K,SUGGANTHAN P N,et al.Comprehensive learning particle swarm optimizer for global optimization of multimodal functions[J].IEEE transactions on evolutionary computation,2006,10(3):281-295.
[14]赵新超,刘国莅,刘虎球,等.基于非均匀变异和多阶段扰动的粒子群优化算法[J].计算机学报,2014,37(9):2058-2070.
[15]YE W,FENG W,FAN S.A novel multi-swarm particle swarm optimization with dynamic learning strategy[J].Applied soft computing,2017(61):832-843.
[16]KUBOTA N,FUKUDA T.Genetic algorithms with age structure[J].Soft computing,1997,1(4):155-161.
[17]GHOSH A,TSUTSUI S,TANAKA H.Individual aging in genetic algorithms[C]∥Intelligent Information Systems,1996., Australian and New Zealand Conference on.IEEE,1996:276-279.
[18]CHEN W N,ZHANG J,LIN Y,et al.Particle swarm optimization with an aging leader and challengers[J].IEEE transactions on evolutionary computation,2013,17(2):241-258.
[19]KOTINIS M.Improving a multi-objective differential evolution optimizerusingfuzzyadaptation and K-medoids clustering[J].Soft computing,2014,18(4):757-771.
[20]ZHANG H,ZHOU A,SONG S,et al.A self-organizing multiobjective evolutionary algorithm[J].IEEE transactions on evolutionary computation,2016,20(5):792-806.
[21]AES F G G,WANNER E F,TAKAHASHI R H C.A quality metric for multi-objective optimization based on hierarchical clustering techniques[C]∥Evolutionary Computation, 2009.CEC'09.IEEE Congresson.IEEE,2009:3292-3299.
[22]LU X F,TANG K.Classification-and regression-assisted differentialevolution forcomputationally expensive problems[J]. Journalofcomputerscience and technology,2012,27(5):1024-1034.