0 引言
随着城市交通出行方式的多样化，出行者的出行模式从单一的交通方式出行转变为多交通方式的组合出行，如停车换乘(P&R，park and ride)出行方式。相比单一出行方式，组合出行更能刻画出行者的实际出行行为。Fernández等最早建立了固定需求下的组合出行交通分配模型[1]，在此基础上，国内外学者进行了相应的扩展研究，主要包括混合交通分配模型[2]、弹性交通分配模型[3]、随机交通均衡分配模型[4]和动态交通分配模型[5]。这些组合出行模型与单一出行方式的模型相比，不仅能够分析出行者的广义路径选择行为，同时还能研究出行者的换乘站点选择行为，为网络换乘站点的规划提供理论支持。然而，上述研究均是在确定性网络中展开的，并没有考虑交通网络的不确定性。
交通系统是典型的不确定性系统[6]，比如受天气、交通事故的影响，路网通行能力将会衰减，考虑该种不确定性，孟梦等[7]研究了降级路网下组合出行交通流分配模型与算法。但是除了交通系统的不确定性外，出行者本身还存在观测误差和非完全理性行为，因此并非所有出行者均会选择实际费用最小的路径[8]。累积前景理论是Tversky和Kahneman[9]在一系列心理学实验基础上提出的，用于描述经济行为主体面临不确定条件时的决策行为过程。研究者们通过一系列实证调研，发现累积前景理论能够很好地描述出行者在不确定环境下的路径选择行为，并将其应用于交通网络分配和路径优化等问题[10-11]。
为了定量分析随机组合网络中出行者的交通选择行为和网络均衡状态，在现有文献的基础上，引入累积前景理论，采用前景值描述出行者在不确定交通网络中的选择效用，基于随机效用理论分析了网络随机用户均衡条件，并建立了相应的变分不等式模型。该模型同时考虑了交通系统不确定性、组合出行方式、出行者观测误差和风险决策行为，可以更加精确地描述出行者的交通选择行为和网络均衡状态。
1 基本符号和理论
1.1 基本符号
定义交通网络G=(N,A)，N为节点的集合，A为路段集合，W为OD对集合。R和D分别代表城市道路路段集合和地铁路段集合，它们之间由换乘路段集合E进行连接，R∪D∪E=A。M为交通方式集合，包含小汽车和地铁两种方式，用1和2表示。w为一个OD对，qw为OD对w的出行需求，Kw为OD对w的所有路径集合，
为OD对w之间路径k∈Kw的流量，xa为路段a上的流量，
为路段-路径关联变量，若路段a在路径k上则
否则
为路段出行时间预算，
为OD对w之间路径k的出行时间预算，
为OD对w之间路径k∈Kw的前景值。
1.2 累积前景理论
累积前景理论将风险的前景和不确定性因素纳入前景理论中，用决策权重函数替换决策概率值，分别考虑损失和收益，主要包含了3个基本观点：①收益和损失是相对于参考点而言的；②面对收益人们倾向于风险规避，面对损失人们倾向于风险偏好；③人们会高估小概率事件发生的可能，而低估大概率事件发生的概率。
在累积前景理论框架下，每条可行路径对应着相应的价值函数和决策权重函数，它们的乘积为路径前景值。根据累积前景理论，出行者将路径的前景值作为路径选择依据。计算路径的前景值，需要3个基本要素，分别为路径的价值函数、参照点和决策权重函数。
(1)路径的价值函数与参照点密切相关，可以由下式表示：
(1)
式中：参数m>0，n≤1，表示出行者对价值收益和损失的敏感程度；λ≥1表示出行者对损失的规避系数；uw为参照点。
(2)采用内生的方式确定参考点[12]，即该OD对所有路径中出行时间预算的最小值：
(2)
(3)为了确保权重函数是关于到达概率的单调递增函数，采用Prelec给出决策权重函数的形式[13]：
w(p)=exp[-(-ln p)γ],0<γ<1。
(3)
沿用Connors的推导过程[14]，令
为的概率分布函数，从而得到路径的前景值为：
(4)
式中:
和
分别为出行时间预算的下界和上界，上下界的取值会对前景值的计算造成影响，比较合理的取值方法为：
为路径自由出行时间，
2 模型建立
2.1 路径出行时间预算
小汽车网络路段出行时间采用BPR(Bureau of Public Road)函数，即
(5)
式中：
为路段自由走行时间；xa为路段流量；Ca为路段实际通行能力；α和β为参数，通常取α=0.15，β=4。
降级路网条件下，路段通行能力会在外部条件干扰下衰减，此时Ca为一个变量。令Ca服从
上的均匀分布，其中
为路段a的设计通行能力，θa为其通行能力的降级系数。经推导，可以得到小汽车网络路段出行时间的均值和方差[15]，分别为：
(6)
(7)
换乘时间通常由步行时间和等待时间组成。步行时间由换乘点到地铁站点的距离la,a∈E和步行速度vwalk决定，等待时间与发车间隔tf相关，假设其服从[0,tf]的均匀分布。则换乘时间的均值和方差为：
(8)
(9)
地铁运行时间相对比较平稳，几乎不受路段上流量的影响，因此可假设地铁网络的路段出行时间为一个常数定值Ta,a∈D。
假设路段出行时间相互独立，根据中心极限定理，路径的出行时间总是服从正态分布，则路径k的均值和方差为：
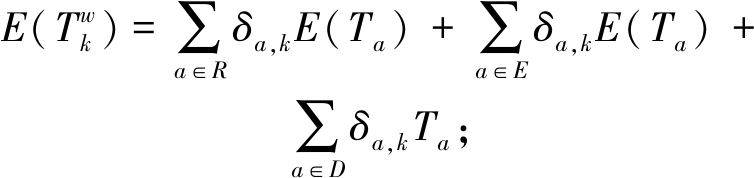
(10)
(11)
若给定到达概率p，则路径k的出行时间预算为：
(12)
式中：Φ-1(·)为标准正态分布反函数。
2.2 随机用户均衡条件
考虑出行者的观测误差，则出行者的感知路径前景值为一个随机变量，它由实际前景值和一个随机误差项
组成：
(13)
假设观测误差项服从独立同Gumbel分布，根据随机效用理论，选择路径k的概率为
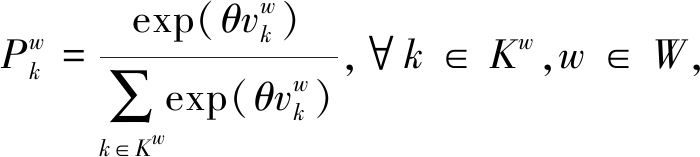
(14)
式中：θ>0,为参数，反映出行者对路网的熟悉程度。
根据网络均衡条件，达到随机用户均衡状态时应满足如下条件：
(15)
(16)
(17)
qw≥0；
(18)
(19)
式(15)为随机用户均衡条件，式(16)为流量守恒约束，式(17～18)为流量非负约束，式(19)为路径-路段流量关系。
2.3 变分不等式模型
将随机用户均衡条件转化为等价的变分不等式模型，对模型解的存在性和等价性进行证明。
首先定义期望最小费用[16]，其表达式为：
(20)
令Ω为所有可行路径流量集f的集合，随机用户均衡模型的解等价于寻找一个可行的路径流量集f *∈Ω，使得
满足如下变分不等式：
(21)
(1)等价性证明。根据变分不等式定理，变分不等式等价于如下的互补松弛条件：
(22)
(23)
(24)
当
时，由上式(22～24)可知：
(25)
对式(25)进行等价变换，即可得到：
(26)
不难看出，式(26)等价于随机用户均衡条件，从而得证变分不等式模型(21)等价于随机用户均衡条件(14～19)。
(2)存在性证明。由约束条件(16～19)可知，可行路径集Ω是由一系列线性约束构成，因此为紧致凸集，由式(12)和式(20)可知和S(vw)是关于
的连续函数，从而
是关于的连续函数，根据变分不等式定理[17]，模型至少存在一个解。
3 求解算法
如前文所述，出行者将路径的前景值作为路径选择依据，采用基于路径的相继平均算法MSA对模型进行求解，其具体步骤如下：
step 0 初始化：设定有效路径集合Kw，初始化参数，计算路径初始时间预算和前景值
采用式(26)对交通需求qw在路网上进行随机用户均衡加载，得到路径初始流量
和初始路段流量
step 1 更新路径前景值：根据路段流量，由式(6)～(12)更新路径出行时间，再由式(1)～(4)更新路径前景值
step 2 确定方向：基于路径前景值对交通需求qw在路网上进行随机用户均衡加载，得到辅助路径流量
得到路径流量更新方向
step 3 更新路径和路段流量：
由路径路段关联矩阵得到路段流量
step 4 收敛检验：
当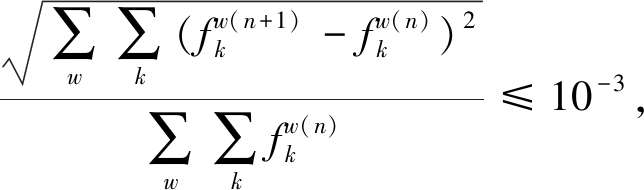
算法结束，否则n=n+1，返回第一步。
4 算例
引入“超级网络”的概念[18]，将交通网络表达为包含多个交通方式子网络的超级网络，同时在各子网络节点间添加虚拟弧段表示交通方式之间的换乘。图1展示了一个传统网络转换为超级网络的过程。
现实中，根据地铁站和出行者目的地位置，可能会出现两种情况：(1)地铁出行不能直接到达目的地，这时节点
和节点12位置不一致，两节点之间需添加一段步行弧；(2)地铁出行能直接到达目的地，即节点和节点12位置一致。沿用前人研究中网络的设置方法[2-4]，本文考虑第二种情况，采用图1网络进行算例分析。
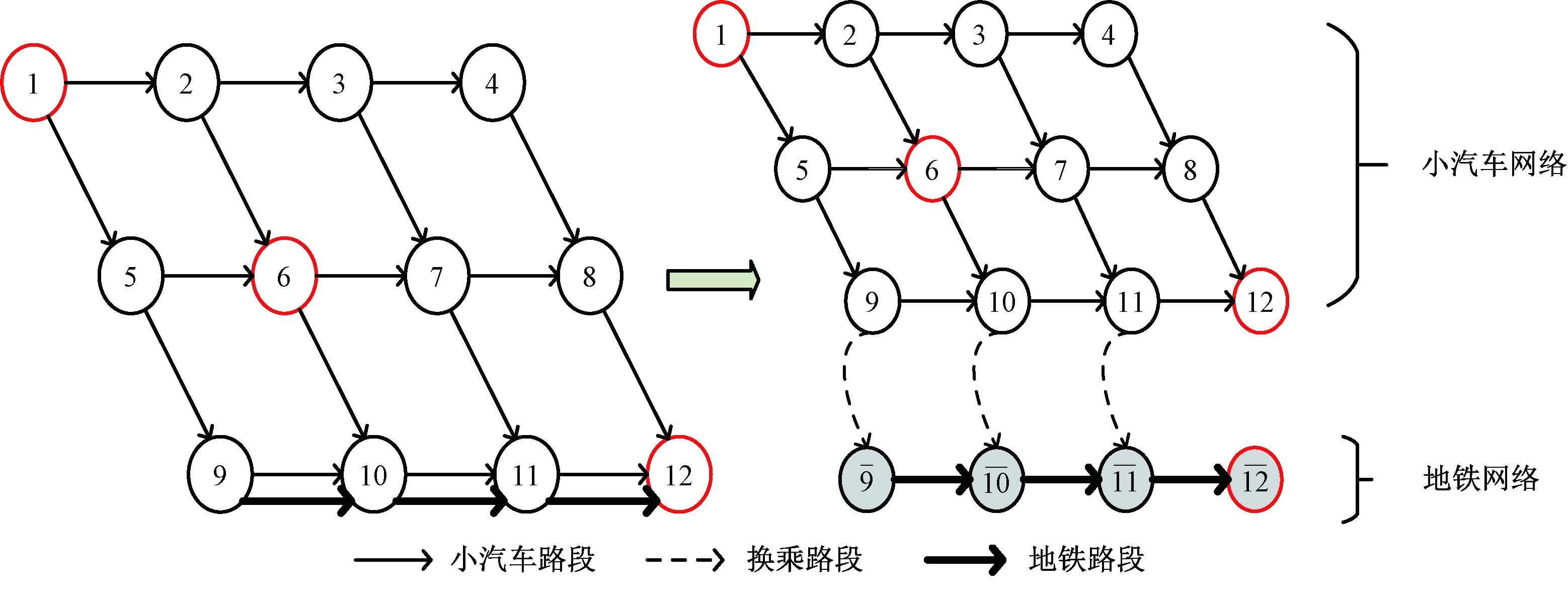
图1 超级网络
Figure 1 Super network
如图1所示，网络中包含小汽车网络和地铁网络两个子网络，包含16个节点，共两个OD对(1,12)和(6,12)，它们的交通需求分别为q1=1 500 pcu/h，q2=1 200 pcu/h。网络中共23条路段，其中17条小汽车网络路段，3条换乘路段
和3条地铁路段
小汽车网络、换乘网络和地铁网络的路段参数如表1和表2所示。
表1 小汽车网络路段参数
Table 1 Parameters for links in network of cars
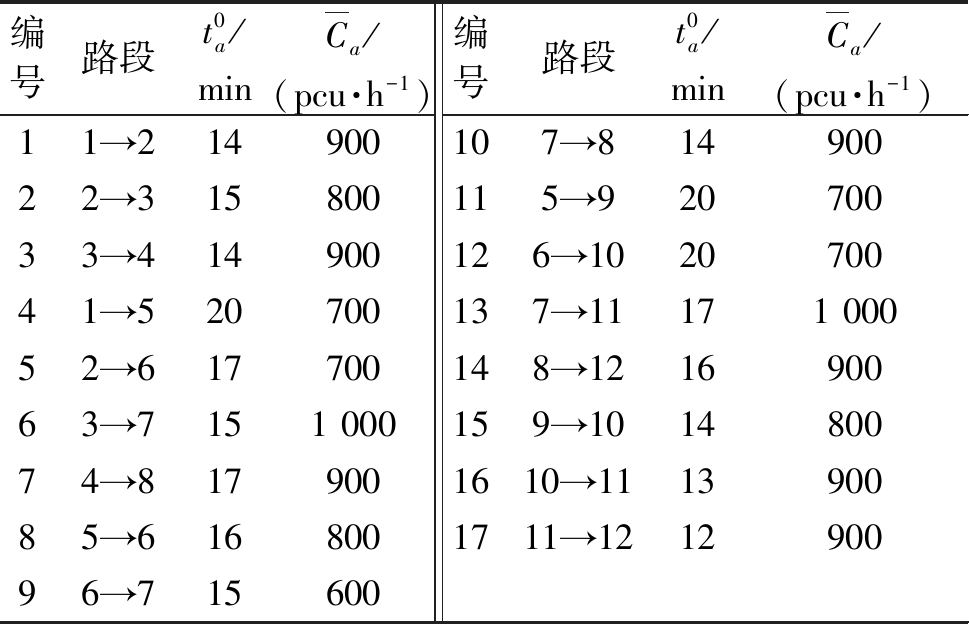
编号路段t0a/minCa/(pcu·h-1)编号路段t0a/minCa/(pcu·h-1)11→214900107→81490022→315800115→92070033→414900126→102070041→520700137→11171 00052→617700148→121690063→7151 000159→101480074→8179001610→111390085→6168001711→121290096→715600
表2 换乘和地铁网络路段参数
Table 2 Parameters for links in network of transfer and metro
编号换乘路段la/mvwalk/(m·min-1)tf/min编号地铁路段t0a/min189→9300606219→10141910→103006062210→11142011→113006062311→1214
对于组合出行下的分配结果，相比路径流量，本文更加关注每个OD对中选择小汽车出行和换乘出行的流量，以及每个换乘站点的流量。下面将分析参数变化对均衡条件下出行者交通选择行为的影响。
(1)路网降级程度和到达概率。其他参数的设置情况为，路径价值函数(1)中m=n=0.88，λ=2.25，决策权重函数(3)中γ=0.74。同时对到达概率和通行能力降级系数进行参数敏感性分析。设置高中低3种到达概率，分别对应p=0.8,p=0.5,p=0.3 3种情况；设置高中低3种通行能力降级系数，分别对应θa=0.8，θa=0.7，θa=0.6，a∈R，综合下来，共9种情形。其结果如表3所示。
由表3可知，随着路网降级程度越严重，选择P&R出行方式的出行者越多，这是因为随着θa的减小，小汽车网络出行费用均值和方差都将变大。此外，出行者更加倾向于选择离终点较远的地铁站点进行换乘，这是因为出行者换乘距离越长，获得地铁出行费用稳定性的优势越大。
表3 不同参数下出行选择结果
Table 3 Results of travel mode under different parameters pcu/h
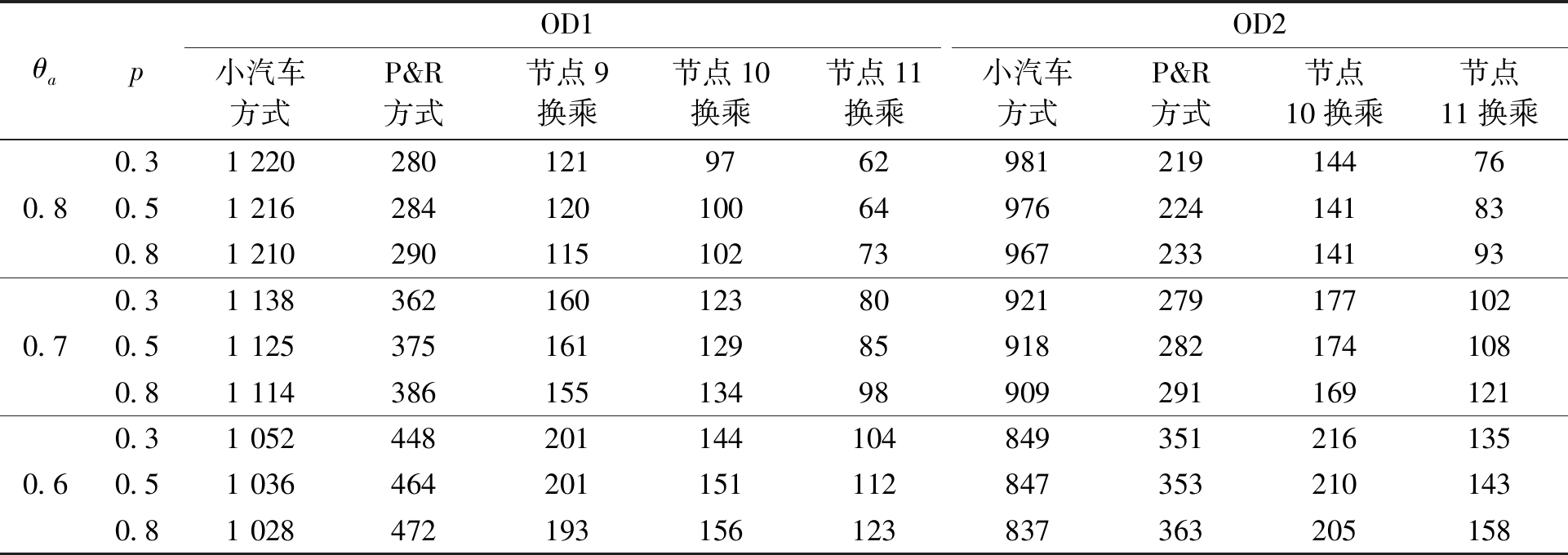
θapOD1OD2小汽车方式P&R方式节点9换乘节点10换乘节点11换乘小汽车方式P&R方式节点10换乘节点11换乘0.80.70.60.31 2202801219762981219144760.51 21628412010064976224141830.81 21029011510273967233141930.31 138362160123809212791771020.51 125375161129859182821741080.81 114386155134989092911691210.31 0524482011441048493512161350.51 0364642011511128473532101430.81 028472193156123837363205158
此外，随着到达概率增加，选择P&R出行方式的出行者会增多，但并不显著。由式(2)和(12)可知，参照点会随到达概率p的取值变化而不同，对比参考文献[12]中累积前景理论下出行者的路径选择行为，出行者交通方式和换乘节点的选择行为参考点依赖效应并不显著。
(2)收益和损失的敏感性m和n。令p=0.8，θa=0.7，λ=2.25，其他参数固定不变。设置m=n，取值由低到高为0.4, 0.5, 0.6, 0.7, 0.8和0.88。由表4可知，出行者对于收益和损失的敏感性，对出行模式选择具有一定影响，且OD间距离(即OD2)越小，影响越大，其具体表现为：出行者对收益和损失越敏感，那么两种出行方式中，流量大的将越大，流量小的将越小。
表4 不同m和n下的交通方式选择结果
Table 4 Results of mode choice with variation of m and n pcu/h
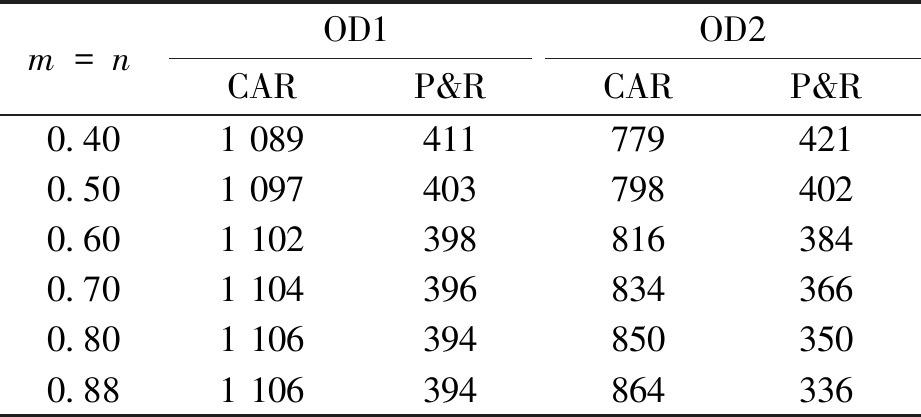
m=nOD1OD2CARP&R CARP&R0.401 0894117794210.501 0974037984020.601 1023988163840.701 1043968343660.801 1063948503500.881 106394864336
(3)出行者损失规避程度λ。令p=0.8，θa=0.7，m=n=0.88，其他参数固定不变。设置λ取值由低到高为1, 1.25, 1.5, 1.75, 2和2.25。由表5可知，出行者损失规避程度对于出行模式选择影响程度较弱，但从中也能发现：出行者损失规避程度越大，两种出行方式中，流量大的将越大，流量小的将越小，这与出行者对于收益和损失的敏感性参数分析结论是一致的。
表5 不同λ下的交通方式选择结果
Table 5 Results of mode choice with variation of λ pcu/h
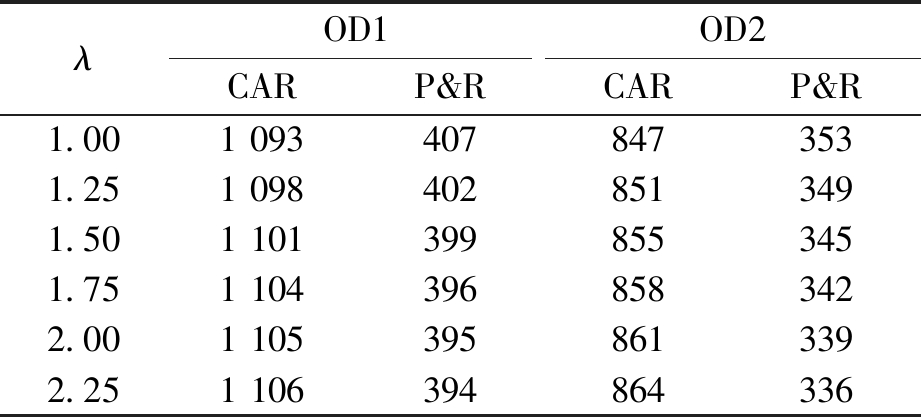
λOD1OD2CARP&R CARP&R1.001 0934078473531.251 0984028513491.501 1013998553451.751 1043968583422.001 1053958613392.251 106394864336
综上所述，累积前景理论框架下出行方式的选择规律，与现有文献中路径选择规律有着一定的相似性，这是因为出行方式选择是广义路径选择的集计过程。此外，组合交通出行模型还能够辨析出行者的交通方式和换乘节点的选择行为，比单一交通出行模型具有更广泛的应用价值。
5 结论
对组合出行网络交通分配模型和算法进行了研究。为了考虑不确定环境下，组合出行网络中出行者的观测误差和风险决策行为，基于累积前景理论和随机用户均衡条件，构建了相应的变分不等式模型，对模型解的存在性和等价性进行了分析，并提出了求解算法。最后通过构建包含小汽车网络和地铁网络的超级网络作为算例，对模型的参数进行了敏感度分析。算例结果表明:模型能够有效地描述出行者的交通方式和换乘站点的选择行为，此外，路网降级系数和出行者风险态度均会影响网络的均衡分配结果。本文的研究工作为城市多模式交通规划提供了理论支持，能够应用到交通方式划分，停车换乘选址及停车场容量规划等工作中。
[1] FERNANDEZ E, DE CAE J, FLORIAN M, et al. Network equilibrium models with combined modes [J]. Transportation science, 1994, 28(3): 182-192.
[2] 黄海军, 李志纯. 组合出行方式下的混合均衡分配模型及求解算法[J]. 系统科学与数学, 2006, 26(3): 352-361.
[3] 李志纯, 黄海军. 弹性需求下的组合出行模型与求解算法[J]. 中国公路学报, 2005, 18(3): 94-98.
[4] 李先进, 张国平, 张杰, 等. 组合出行模式下的随机交通平衡分配模型及算法[C]//第25届中国控制与决策会议论文集. 沈阳：控制与决策编辑部，2013.
[5] 孟梦, 邵春福, 曾靖静, 等. 考虑出发时间的组合出行动态路径选择模型[J]. 中南大学学报(自然科学版), 2014, 45(10): 3676-3684.
[6] 马庚华, 杜牧青, 张小丽. 不确定因素下的综合运输网络容量可靠性分析[J]. 郑州大学学报 (工学版), 2018, 39(1): 1-6.
[7] 孟梦, 邵春福, 曾靖静, 等. 降级路网组合出行交通流分配模型与算法[J]. 中南大学学报(自然科学版), 2014, 45(2): 643-649.
[8] SIMON H A. A behavioral model of rational choice [J]. Competition policy international, 2010, 6(1): 241-258.
[9] TVERSKY A,KAHNEMAN D. Advances in prospect theory: Cumulative representation of uncertainty [J]. Journal of risk and uncertainty, 1992, 5(4): 297-323.
[10] 潘晓锋, 左志, 赵胜川. 基于前景理论的改进多路径交通分配模型[J]. 交通运输系统工程与信息, 2014, 14(2): 162-167.
[11] 崔岩, 张子祥, 时新, 等. 考虑顾客时间紧迫的生鲜电商配送路径优化问题[J]. 郑州大学学报 (工学版), 2017, 38(6): 59-63.
[12] XU H L, LOU Y Y, YIN Y F, et al. A prospect-based user equilibrium model with endogenous reference points and its application in congestion pricing [J]. Transportation research part B: methodological, 2011, 45(2): 311-328.
[13] PRELEC D. The probability weighting function [J]. Econometrica, 1998,66(3): 497-527.
[14] CONNORS R D,SUMALEE A. A network equilibrium model with travellers’ perception of stochastic travel times [J]. Transportation research part B: methodological, 2009, 43(6): 614-624.
[15] SUN C, CHENG L, ZHU S L, et al. Multiclass stochastic user equilibrium model with elastic demand: considering systematic and accidental delays [J]. Transportation research record: journal of the transportation research board, 2015 (2497): 1-11.
[16] SHEFFI Y. Urban transportation networks equilibrium analysis with mathematical programming methods[M]. Englewood Cliffs, NJ: Prentice-Hall, 1985.
[17] XIE C, WANG T G, PU X T, et al. Path-constrained traffic assignment: modeling and computing network impacts of stochastic range anxiety [J]. Transportation research part B: methodological, 2017, 103: 136-157.
[18] LIAO F X, ARENTZE T, TIMMERMANS H. Application of supernetworks in modelling activity-travel behavior [J]. Journal of the university of Shanghai for science and technology, 2011, 33(3): 279-286.