0 引言
在控制系统中，测量噪声对系统的控制品质有着重要的影响.在控制系统的数学模型和噪声统计特征已知的情况下，可以利用卡尔曼滤波器对系统输出进行滤波，降低测量噪声的干扰［1］.但在实际系统中很难得到精确的数学模型和噪声的统计特征，控制系统的噪声特征完全未知或者部分未知，错误的噪声统计特征可能降低卡尔曼滤波器的滤波精度，甚至使滤波器发散从而导致滤波失败.为了解决此问题，Sage和Husa提出了一种在线计算系统噪声Q和测量噪声R的自适应卡尔曼滤波算法，并在非线性和复杂系统的滤波处理中得到了应用.然而，由于每次滤波都需要对Q或者R进行在线估计，滤波的复杂度增加，在实际使用时无法保证滤波结果的实时性［3］.
韩京清提出的自抗扰控制技术具有较强的抗干扰能力和解决不确定性问题的能力［4］，在不依赖控制系统数学模型的情况下依靠扩张状态观测器(extended state observer，ESO)降低测量噪声和系统扰动对控制系统的影响.自抗扰控制技术已经在许多实验系统和实际工程中得到了检验［5-7］，受到了研究人员的广泛重视.
自抗扰控制技术包括跟踪微分器(tracking differentiator，TD)、ESO 和非线性 PID 3 部分［8］，其中ESO是自抗扰控制技术的核心部分.非线性ESO将系统的扰动扩张成系统的一阶新的状态，根据“大误差小增益，小误差大增益”的原则，利用特定的非线性误差反馈对原系统进行状态观测.适当地选择扩张状态观测器的参数可以得到包括系统总干扰信息在内的所有系统状态观测值.进一步的研究表明，根据经典控制论中的极点配置方法将扩张状态观测器的误差反馈线性化［9］，设计出线性扩张状态观测器(linear ESO，LESO)，可以在保证观测能力的情况下减少参数个数，降低参数调整的复杂度，便于工程应用［10］.
宋金来等［11］将带测量噪声的系统输出进行积分作为新的状态建立扩张状态观测器，即积分型扩张状态观测器(integral ESO，IESO)，对系统进行滤波和状态估计.但扩张的积分状态值随着时间的增长而增加，可能出现存储溢出等问题.Bai等［12］通过设计扩张状态观测器的反馈增益矩阵增强扩张状态观测器对系统输出噪声的抑制能力，取得了一定的效果.
LESO对测量噪声具有一定的抑制性，且不依赖于系统模型.笔者根据LESO的特点，设计了一种将观测带宽ωo和调节参数τ作为调节参数的离散线性扩张状态观测滤波器，通过仿真和应用研究，对其滤波性能进行分析和验证.
1 扩张状态观测器(ESO)
扩张状态观测器是自抗扰控制技术中的核心部分，目的是利用观测器原理对控制系统状态及未建模部分和系统扰动进行观测，其中未建模部分和系统扰动作为一个扩张的系统状态对待.扩张状态观测器不依赖系统的精确数学模型，而仅利用系统的阶次进行扩张状态观测器设计［6］.
考虑一类单输入单输出的非线性时变系统，数学描述为［6］:
其中，y是系统的输出；u为系统输入；w为系统的外界干扰；b为非零的输入增益；f(y(n-1)，y(n-2)，…，y，w)表示系统的非线性时变动态描述.
建立式(1)对应的状态方程:
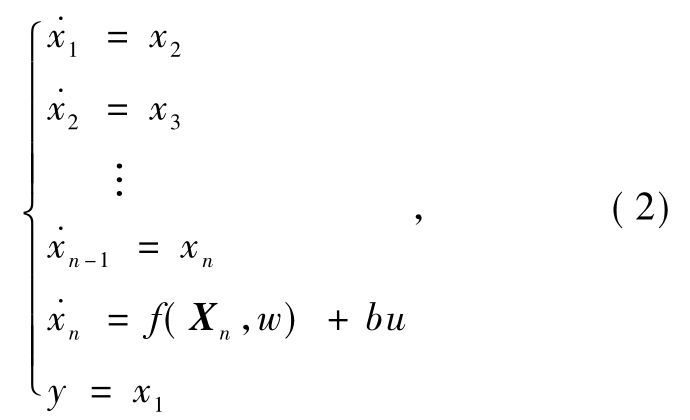
式中:Xn= ［x1，…，xn］T；f(Xn，w) 表示系统动态和系统干扰的总和.为了表示方便将f(Xn，w)用f表示，并假定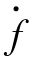
=h.因此可以构建系统的扩张状态观测器，
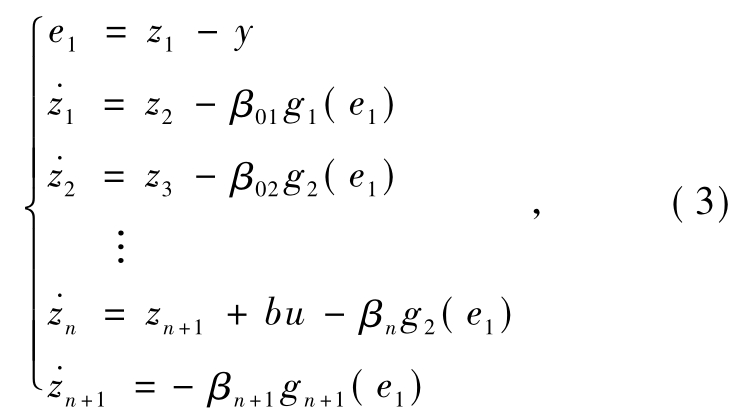
式中:zi是观测状态；e1表示观测误差；gi(e1)是关于 e1的非线性函数；且e1·gi(e1)≥0.如果取gi(e1)=e1的线性形式，则扩张状态观测器变为线性的，称为线性扩张状态观测器.线性扩张状态观测器的估计能力在文献［13］中得到了证明.
以上扩张状态观测器的分析建立在系统只有扰动的基础上.如果系统存在测量噪声，系统的状态方程表达为:
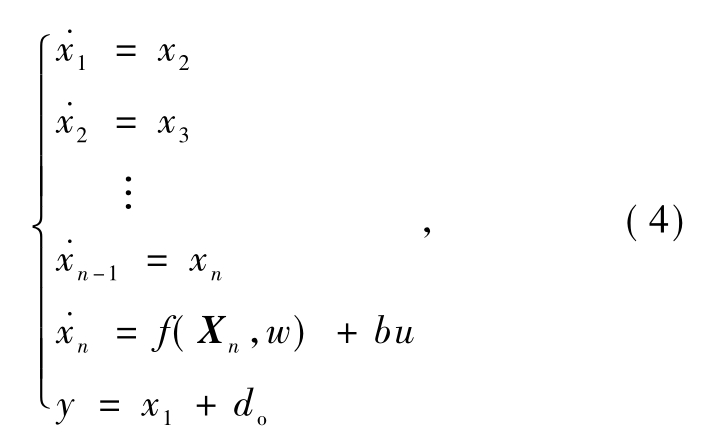
式中:do表示系统的测量噪声.带测量噪声的扩张状态观测器误差表达式改为e1=z1-y=
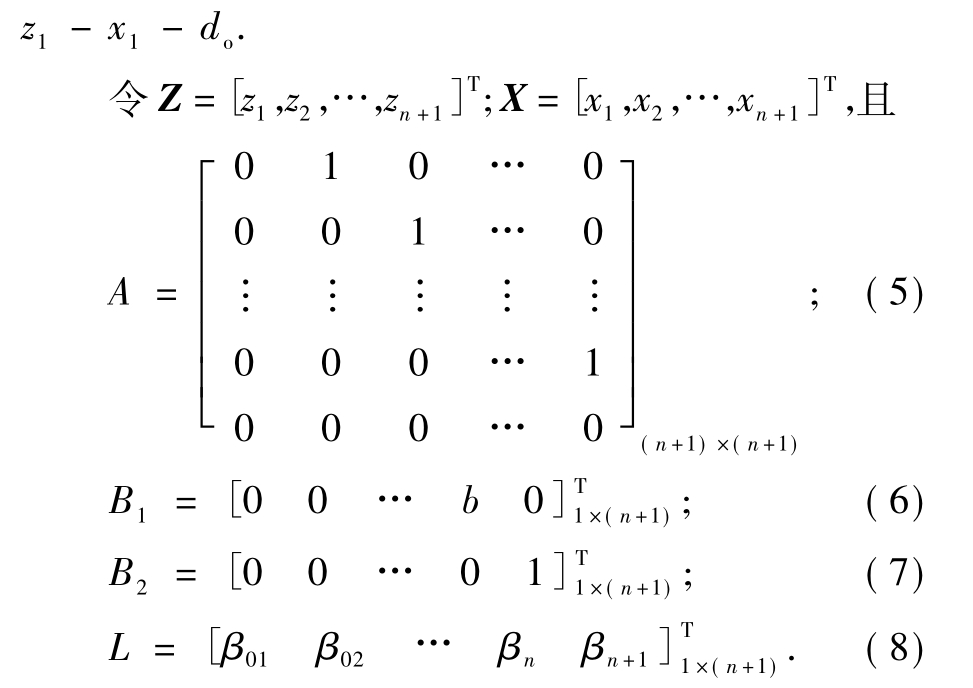
则系统状态方程和线性扩张状态观测器方程表示为:
记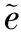
~=X-Z；A1=A-L，观测误差表达式为:可以得到如下结论.
定理1：假设总干扰的导数h(Xn，w)和do是有界的，即存在正数M1使
，存在正数M2使
，则总有线性扩张观测器对带测量噪声的系统的状态观测误差是有界的.即存在正数M3使
证明：取正数 λi ＜ λj，(i ＜ j；i，j=1，2，…，n+1)，使得
此时存在可逆矩阵T，使得
则有
当t＞0时，对式(13)取m∞范数，可得，
其中，α为常数.由式(10)得到观测误差的解为
综合可得
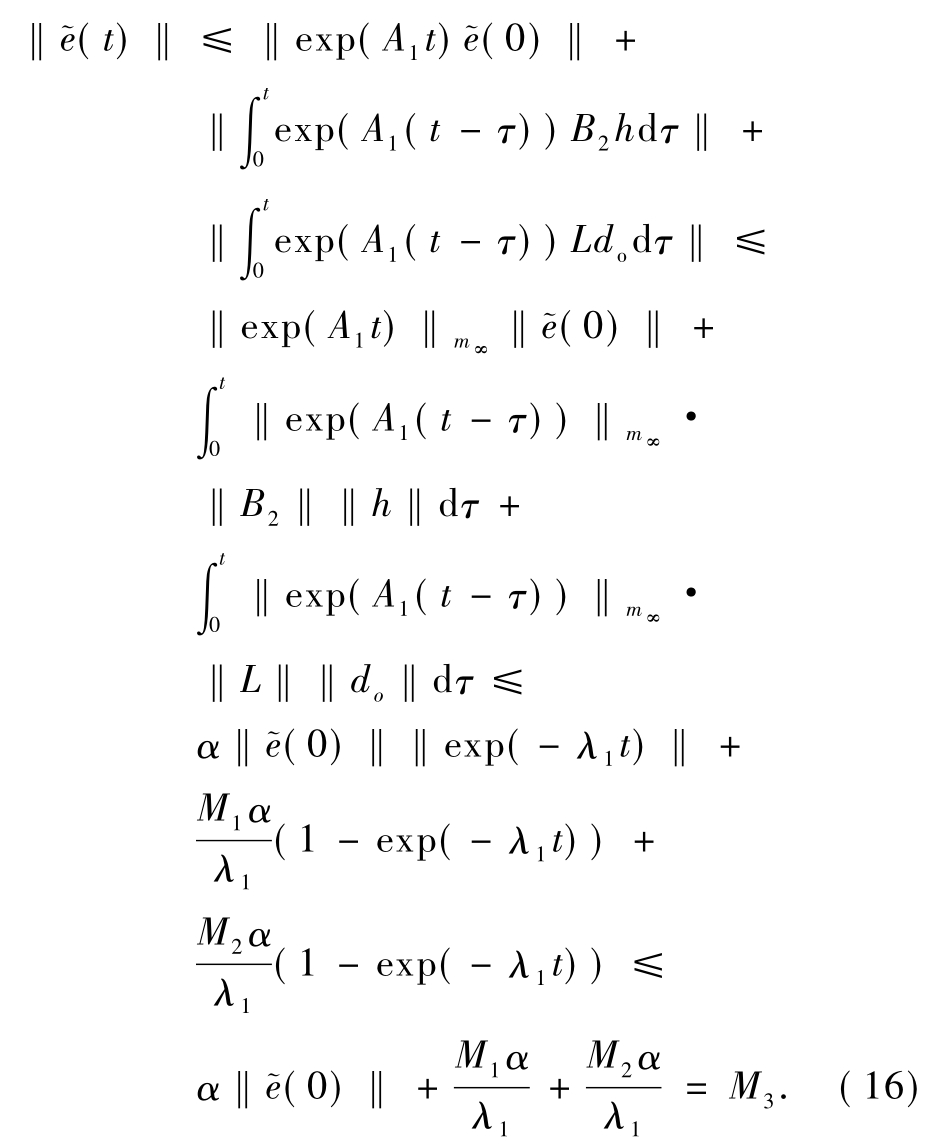
证毕.
2 线性扩张状态观测滤波器设计
根据定理1，线性扩张状态观测器在对带有测量噪声的被控系统进行观测时，选择适当的观测器参数可以得到理想的观测效果，因此，可以设计适当的扩张状态观测器作为滤波器使用.
2.1 线性扩张状态观测器离散化
对于数字控制系统，控制器对系统输出的采样和处理都是以离散的形式进行［14］.以二阶扩张状态观测器为例，对应的控制系统的扩张状态表达式为
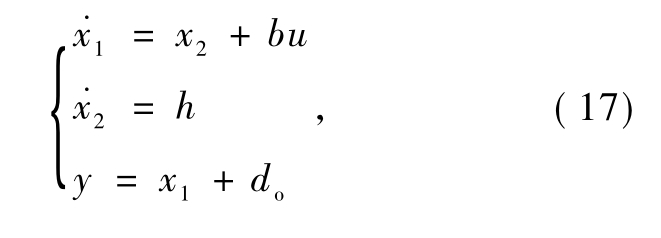
取
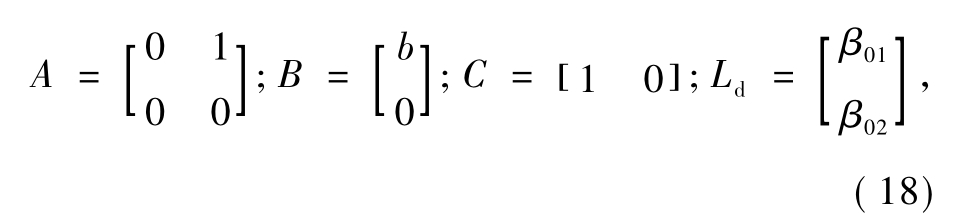
则式(17)对应的线性扩张状态观测器设计为
式中:Z= ［z1，z2］T；e1=z1-y.线性扩张状态观测器离散化后得
设离散后的误差增益Ld=ΦLc，则有
为了简化设计，通过设置 Lc将系统极点配置到
其中，β =exp(-ωoTd)，ωo和Td分别表示线性扩张状态观测器的带宽调节系数和系统采样周期.
根据连续系统离散化理论，得到
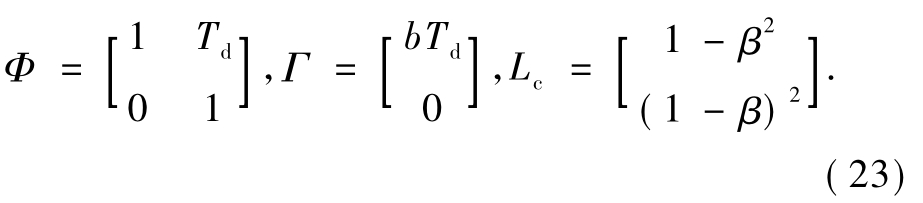
式中:X= ［x1，x2］T.式(24)所示的系统可以直接根据式(20)设计离散形式的线性扩张状态观测器.
2.2 线性扩张状态观测滤波器设计
对于任意带噪声系统输出信号序列y(k)，都可以写成如下形式
式(17)所示系统的离散形式为
式中:x(k)表示系统实际状态；x'(k)表示两次采样间隔时间内控制系统状态的变化率；d(k)表示测量噪声.
式(25)中 x'(k)是一个动态变化量，将x'(k)看作可以通过ESO估计的系统总扰动，同时考虑到滤波器的作用是对系统输出进行准确观测，不需要总扰动的准确值，所以可以将式(25)中的T设计为可调参数，并用τ代替，从而根据观测器的设计原理设计式(25)对应的扩张状态观测滤波器
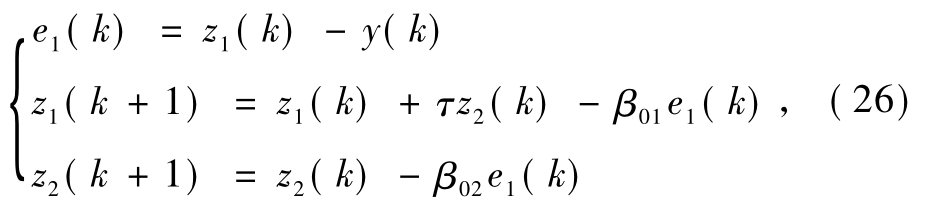
式中:τ是设置的类似采样周期的可调滤波参数.根据扩张状态观测器离散方法，式(26)中有
其中，
线性扩张状态观测滤波器可表示为
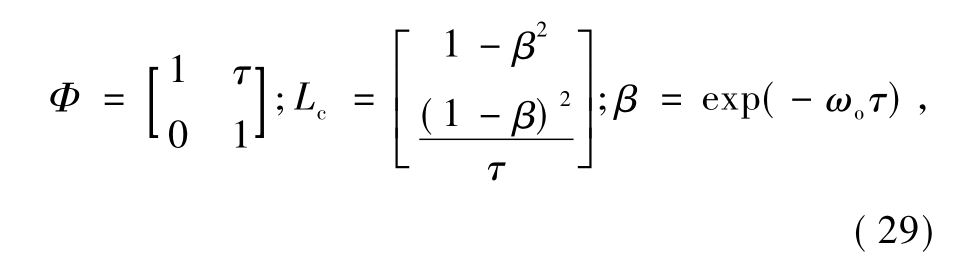
式中:ωo和τ是扩张状态观测滤波器的滤波调节参数.
3 仿真分析与应用研究
为说明线性扩张状态观测滤波器的滤波效果，加入了应用广泛的卡尔曼滤波算法作为对比.在卡尔曼滤波算法中，系统状态方程和测量方程为［15-16］
式中:Xk为状态矩阵；Φk|k-1为k-1时刻到k时刻的状态转移矩阵；Γk-1为k-1时刻的噪声转移矩阵；Wk-1为系统噪声；Zk为系统测量向量；Hk为系统测量矩阵；Vk表示系统噪声.其中噪声特征描述为 E(Wk)=q；E(Vk)=r；E(Wk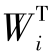
) =Qδi，E(Vk
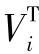)=Rδi.δi为 Kronecker函数.在对比中假定噪声的统计特征均为已知的.卡尔曼递推更新算法表示为
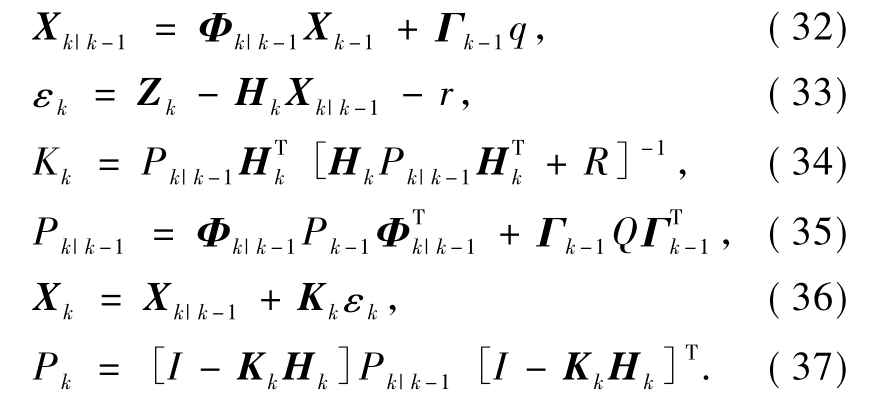
3.1 仿真分析
在仿真分析中，设置带测量噪声的传感器输出序列的采样周期为100 Hz，这满足一般工业传感器的实际采样频率.
在二阶的线性扩张状态观测滤波器中，有两个可调参数，ωo和τ均与测量输出的采样频率无关.在参数调节中，一般考虑调节ωo、τ改变 β的值实现线性扩张状态观测滤波器的极点配置，参数调整方式与线性扩张状态观测器的调参方式相同［7］.ωo的值越大收敛速度越快，相应的噪声也同样放大；ωo的值越小滤波器滤波效果也好，但会带来较大的相位偏差，造成时间上的滞后.τ的取值影响滤波精度，仿真实验表明，一般取τ∈［0.1，1］时滤波效果比较理想.
以控制系统输出周期为10 s，幅值为1的正弦波和三角波为例，采样间隔0.01 s，加入幅值为正弦波10%的高斯白噪声，测量结果与实际值的对比如图1所示.y(k)为实际输出序列；z1(k)为y(k)的带噪声测量序列.控制系统的传递函数为
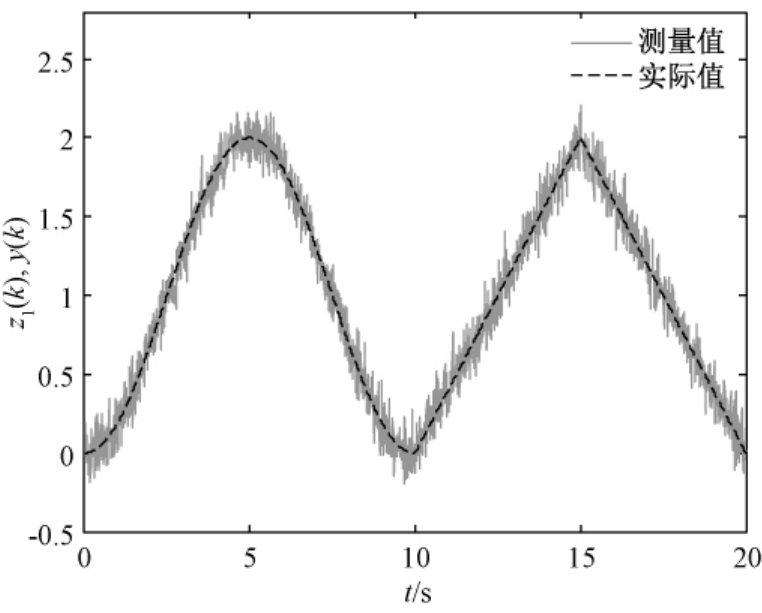
图1 系统实际输出与测量值
Fig.1 Actual and measured output of system
线性扩张观测滤波器参数选择τ=0.5，分别对 ωo=0.01、0.1、0.5 进行滤波分析.分别用zA1(k)，zB1(k)和 zC1(k) 表示 ωo取 0.1、0.01 和0.5时滤波器的输出，用zD1(k)表示噪声统计特征已知时卡尔曼滤波器的输出.滤波器输出结果与y(k)的对比结果如图2.
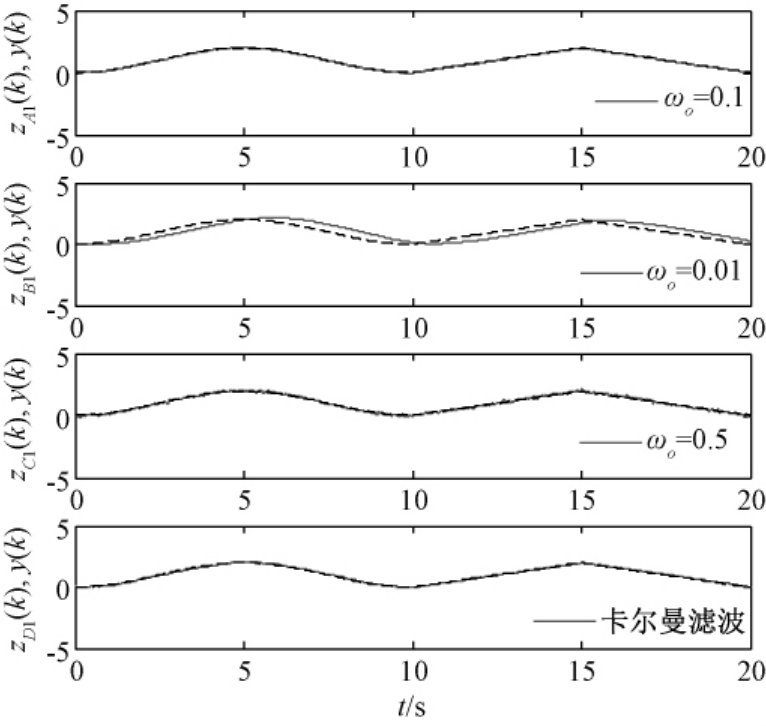
图2 滤波器输出与系统实际输出比较
Fig.2 Comparisons between filter output and source data
线性扩张状态观测滤波器不同参数取值与卡尔曼滤波器滤波效果的数值特征统计如表1所示.卡尔曼滤波器根据式(25)描述的系统进行设计，取 R=0.1，Q=0.001 .
从表1可以看出，线性扩张状态观测滤波器的总计算时间在0.011 s左右，仅为卡尔曼滤波器计算时间的40%.在算法实现中，卡尔曼滤波器需要进行求逆矩阵运算，对于单片机尤其是低位宽、低频率的嵌入式系统来说实现比较困难，计算周期比较长，可能影响实时性，自适应卡尔曼滤波器等需要在线辨识噪声统计特征的滤波算法则运算效率更低.线性扩张状态观测滤波器结构简单，计算效率更高.
从平均绝对误差和误差方差指标的对比中可以看出，在 ωo取0.1时，扩张状态观测滤波器滤波性能优于卡尔曼滤波器；当 ωo取0.5时，扩张状态观测滤波器的滤波性能有所下降，与卡尔曼滤波器效果接近.从图2中的zB1(k)与y(k)对比中可以得出，当 ωo取0.01时滤波器输出序列zB1(k)趋于平滑，但相对y(k)出现了相位偏差，因此平均绝对误差和误差方差均有所增大.
从以上比较中可以得出结论，线性扩张状态观测滤波器比卡尔曼滤波器具有更高的计算效率，算法结构简单便于实现，通过调整 ωo和 τ可以使线性扩张状态观测滤波器得到更好的滤波效果，而且不存在因噪声统计特征未知而出现的滤波发散等问题.ωo和τ都是与测量信号的采样频率无关的参数，因此扩张状态观测滤波器对测量信号的来源系统和传感器参数不做要求.
表1 滤波结果对比
Tab.2 Comparison of filtering results
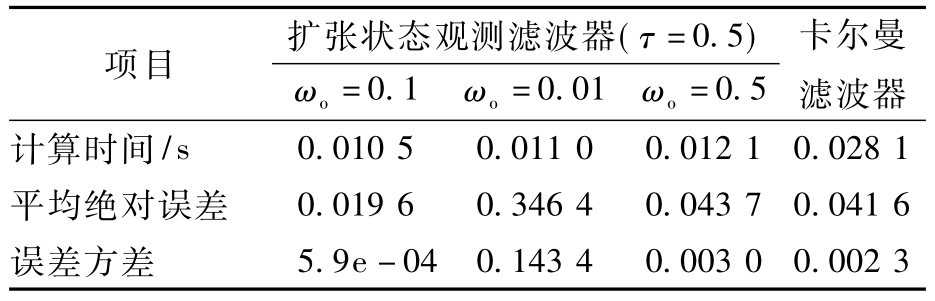
卡尔曼项目 扩张状态观测滤波器(τ=0.5)ωo=0.1 ωo=0.01 ωo 滤波器计算时间=0.5/s 0.010 5 0.011 0 0.012 1 0.028 1平均绝对误差 0.019 6 0.346 4 0.043 7 0.041 6误差方差5.9e-04 0.143 4 0.003 0 0.002 3
3.2 动力翼伞风场辨识中的滤波器应用
本节以动力翼伞系统空投风场的风速风向辨识为例，对线性扩张状态观测滤波器的应用效果进行分析.
翼伞是一种由轻质材料制作的可操纵降落伞［17-18］，由于质量轻，在飞行过程中非常容易受到风场的干扰，因此在动力翼伞系统轨迹规划、轨迹跟踪、雀降着陆等操作中需要获得风场信息［19］，其中最主要的是风向信息.
动力翼伞系统通过其对地速度、对空气速度和风速之间的矢量关系求解风速和风向［20-21］.风场辨识原理如图3所示.
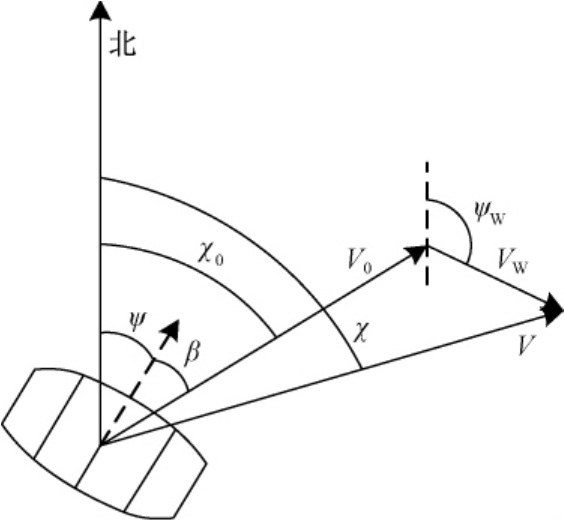
图3 动力翼伞系统速度矢量关系图
Fig.3 Velocity vector diagram of powered parafoil system
图3 中，ψ代表欧拉偏航角；β代表侧滑角；V0代表动力翼伞系统相对于空气的速度，即空速；VW代表风速；V代表动力翼伞系统相对于大地的速度，即地速.从图3中可以看出，V0、VW和V组成一个速度矢量三角形，χ0、χ和 ψW 分别是 V0、VW 和V与正北方向的夹角.动力翼伞系统的地速V是可由GPS测得的实际速度，空速V0和风速VW在辨识过程中保持不变［20］.
由于GPS存在一定的定位误差，动力翼伞系统通过GPS获得的定位信息都是带有测量误差的含噪声信号，所以在进行风场辨识之前需要对GPS数据进行滤波处理.在系统中加入线性扩张状态观测滤波器对GPS数据进行滤波处理.
通过对动力翼伞系统进行建模和仿真获得动力翼伞系统的飞行轨迹，模拟 GPS获得采样信息，并添加与GPS模块定位精度相等的白噪声作为定位干扰.在对仿真环境添加 VW=(1，2)m/s的稳定风场时，动力翼伞系统在单下偏控制时的飞行轨迹和风场辨识结果如图4和图5所示.风场辨识过程中GPS的采样频率为4 Hz，线性扩张状态观测滤波器的结构根据式(28)进行设计，滤波参数取 τ=0.2，ωo=0.23.
图4 单下偏作用下动力翼伞水平轨迹
Fig.4 Horizontal trajectory of the powered parafoil system with unilateral bias
从图4中可以看出，动力翼伞系统的轨迹在单下偏控制时受风场作用沿风向发生偏移，即风场影响动力翼伞的运动状态.
图5表示风场辨识的迭代更新结果.因为递推最小二乘法的初值设置为0，所以前期的估计结果为无效值，未在图中给出.风向角的辨识结果最大误差为 6.48°，绝对平均误差为 2.67°，风速值的辨识结果中最大误差值为0.45 m/s，平均误差为0.17 m/s，而且随着迭代步数的增加，辨识结果接近真实数值.结果表明经过GPS信号滤波后的风场辨识结果在风速和风向上均有较高的辨识精度.
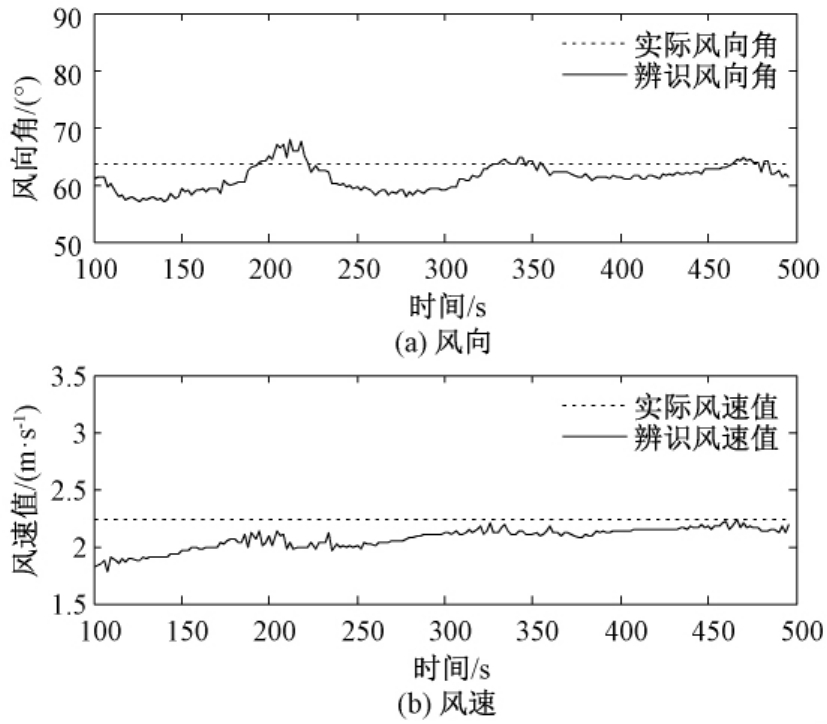
图5 单下偏作用下风场辨识结果
Fig.5 Wind identification result of the powered parafoil system with unilateral bias
4 结论
线性扩张状态观测器可以对带有测量噪声的信号进行准确的观测，具有一定的滤波能力.将扩张状态观测器的滤波能力作为主要指标进行设计，提出了一种线性扩张状态观测滤波器.线性扩张状态观测滤波器设计中对参数τ的引入可以实现滤波器对采样频率未知或者变化系统输出的滤波处理，扩大了滤波器的应用范围.仿真对比结果显示，线性扩张状态观测滤波器比卡尔曼滤波器具有更快的计算速度.同时，线性扩张状态观测滤波器不需要测量噪声的统计特征，因而更实用.线性扩张状态观测滤波器在动力翼伞系统风场辨识中的应用结果也表明其具有良好的滤波效果，风场辨识结果中风向的辨识精度足以保证动力翼伞系统雀降时的迎风对准和着陆.
［1］丁国强，张铎，熊明，等.SINS姿态估计的 HoMMUKF模型算法［J］.郑州大学学报(工学版)，2017，38(4):39-45.
［2］王晓东，马磊，韦宗毅.基于 Sage-Husa方法的旋翼姿态控制［J］.计算机工程与设计，2015，36(7):1747-1751.
［3］李明，许川佩，李翔.基于 UD分解的 Sage-Husa自适应滤波算法［J］.计算机仿真，2017，34(11):285-289.
［4］韩京清.自抗扰控制器及其应用［J］.控制与决策，1998，13(1):19-23.
［5］周宜然，甘屹，陶益民，等.基于改进遗传算法的伺服系统自抗扰控制研究［J］.机械工程与自动化，2015(1):159-161.
［6］刘一莎，杨晟萱，王伟.四旋翼飞行器的自抗扰飞行控制方法［J］.控制理论与应用，2015，32(10):1351-1360.
［7］FENG G，LIU Y F，HUANG L P.A new robust algorithm to improve the dynamic performance on the speed control of induction motor drive［J］.IEEE transactions on power electronics，2004，19(6):1614-1627.
［8］HAN J Q.From PID to active disturbance rejection control［J］.IEEE transactions on industrial electronics，2009，56(3):900-906.
［9］GAO Z Q.Scaling and bandwidth-parameterization based controller tuning［C］∥ Proceedings of the American Control Conference.Colorado:2003(6):4989-4996.
［10］周宏，谭文.线性自抗扰控制的抗饱和补偿措施［J］，控制理论与应用，2014，31(11):1457-1463.
［11］宋金来，甘作新，韩京清.自抗扰控制技术滤波特性的研究［J］.控制与决策，2003，18(1):110-113.
［12］BAI W，XUE W，HUANG Y，et al.The extended state filter for a class of multi-input multi-output nonlinear uncertain hybrid systems［C］∥Conference on computational complexity.Nanjing，2014:2608-2613.
［13］陈增强，孙明玮，杨瑞光.线性自抗扰控制器的稳定性研究［J］，自动化学报，2013，39(5):574-580.
［14］MIKLOSOVIC R，RADKE A，GAO Z Q，et al.Discrete implementation and generalization of the extended state observer［C］∥ American control conference.Minneapolis，2006:2209-2214.
［15］VENKATARAMAN V，FAN G，HAVLICEK J P，et al.Adaptive kalman filtering for histogram-based appearance learning in infrared imagery［J］.IEEE transactions on image processing，2012，21(11):4622-4635.
［16］GAO X D，YOU D Y，KATAYAMA S.Seam tracking monitoring based on adaptive Kalman filter embedded elman neural network during high-power fiber laser welding ［J］.IEEE transactions on industrial electronics，2012，59(11):4315-4325.
［17］ZHU E L，SUN Q L，TAN P L，et al.Modeling of powered parafoil based on Kirchhoff motion equation［J］.Nonlinear dynamics，2015，79(1):617-629.
［18］TAO J，SUN Q L，TAN P L，et al.Autonomous homing control of a powered parafoil with insufficient altitude［J］.Isa transactions，2016(65):516-524.
［19］檀盼龙，孙青林，陈增强.自抗扰技术在动力翼伞轨迹跟踪控制中的应用［J］.浙江大学学报(工学版)，2017，51(5):992-999.
［20］檀盼龙，孙青林，高海涛，等.动力翼伞系统空投风场的辨识与应用［J］.航空学报，2016，37(7):2286-2294.
［21］高海涛.翼伞系统自主归航航迹规划与控制研究［D］.天津:南开大学计算机与控制工程学院，2014.