0 引言
齿轮由于其结构简单、传动平稳等优点而被广泛应用于工程机械中[1]。齿轮的传动是通过与轴的配合实现的。其中,轴-齿轮过盈配合因其结构简单、承载能力大、对中性好、抗冲击性强等优点而被普遍用于传动精度高、低振动的设备中[2-3]。国内外学者针对过盈配合进行了大量的研究,目前针对轴-齿轮过盈配合的研究主要集中在结合面的应力分布状态的计算方法[4-9]、过盈量的确定[10-12]和过盈配合对轴、齿轮疲劳寿命及磨损的影响[13-15]等方面,所采用的方法大多为有限元法,研究的重点为轴-齿轮过盈配合接触面处的变形和应力。
然而,过盈装配的实质是在装配结合面发生弹性变形,这种变形不仅可以影响到装配结合面,还会影响到齿轮的齿形。过盈配合后齿形的变化会对齿轮副侧隙、啮合线、接触应力等产生影响,而以上参数的变化又会导致齿轮的传递特性和疲劳寿命发生改变。随着齿轮传动系统高速化的发展,齿形变化带来的影响越来越明显。因此,有必要建立轴-齿轮过盈装配后齿形变化的精确计算模型。
综上分析,笔者拟基于渐开线方程和弹性力学中的拉美公式,研究轴-齿轮过盈装配的齿形变化规律,并通过MATLAB编写了过盈配合装配应力应变计算系统,准确获得齿形上任意位置的变形,为齿轮过盈装配后齿形计算提供精确模型。
1 理论基础
1.1 齿轮与轴过盈装配的应力、位移理论计算
轴-齿轮过盈配合面可简化为图1,其中轴径为2Ra,齿轮齿顶圆直径为2Rt,过盈配合产生的内应力为p。
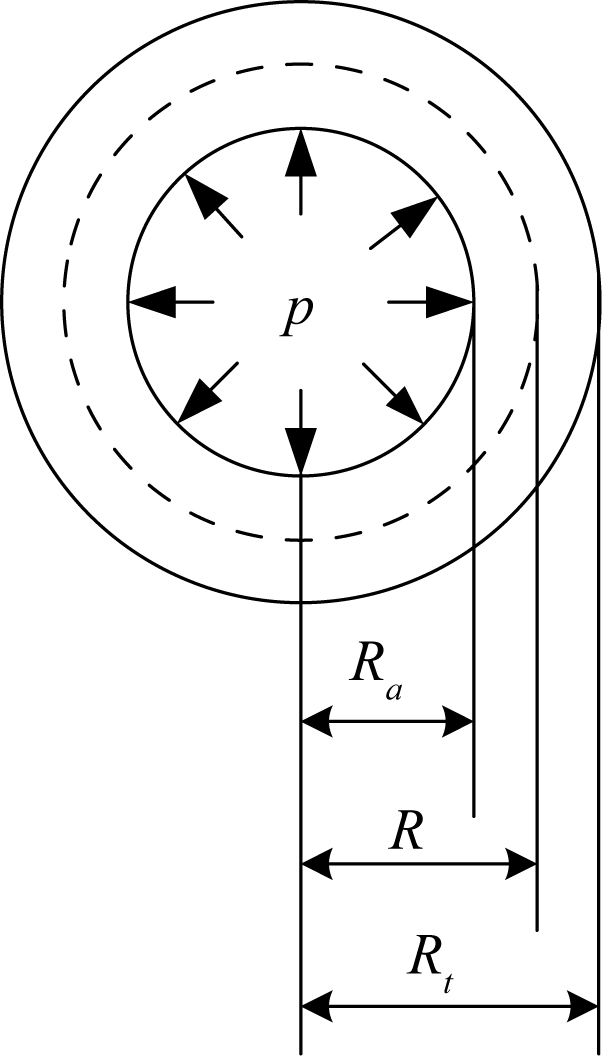
图1 轴-齿轮过盈简化模型
Figure 1 The theoretical model of peg-in-hole
齿轮应力分量与位移为[11]:
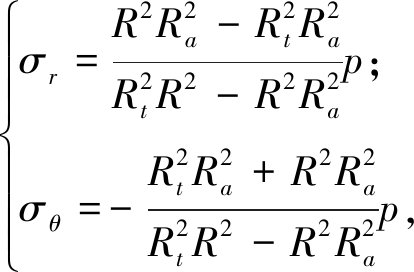
(1)
式中:σr为径向应力;σθ为周向应力。
![]()
(2)
同理可得轴任意位置处的径向位移[11]:
(3)
式中:μ为材料的泊松比;E为弹性模量;R为接触半径到齿顶圆直径之间的任意半径。
1.2 轴-齿轮过盈量的确定
由于过盈量的存在,轴在过盈装配后受到压力从而在表面产生压应力,而此时齿轮与轴的配合孔会产生拉应力,这会使轴与齿轮内孔径产生径向位移,总的位移为[11]:
Δ=u1+u2,
(4)
式中:u1、u2分别为齿轮与轴的径向变化量。
由式(2)、(3)可知在接合面处,齿轮、轴的径向位移分别为:
(5)
(6)
轴-齿轮过盈装配必须保证装配接合面始终在弹性变形范围内。因此,装配接合面处的接触应力必须小于材料的许用应力,过盈配合接触面的二维应力状态为[11]:
(7)
式中:τrθ=βp,β为摩擦系数。
将σr、σθ代入式(8),可得
(8)
式中:[σ]为材料的许用应力。由式(1)、(2)、(7)、 (8)可得最大的接触应力为:
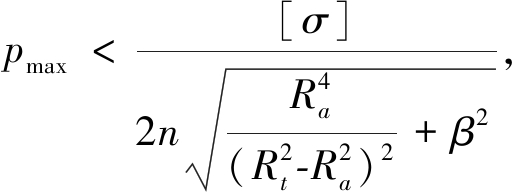
(9)
将式(5)、(6)和(9)代入式(4),可得最大过盈量Δ为:
(10)
1.3 齿形变形量计算
轴-齿轮过盈装配会导致齿形发生改变。若要求解齿形的变化量,首先要建立过盈装配前齿形的计算模型。由于渐开线齿形具有易加工、承载能力大等优点,因此本节选用渐开线齿形为研究对象。
图2为渐开线示意图,齿轮渐开线方程为:
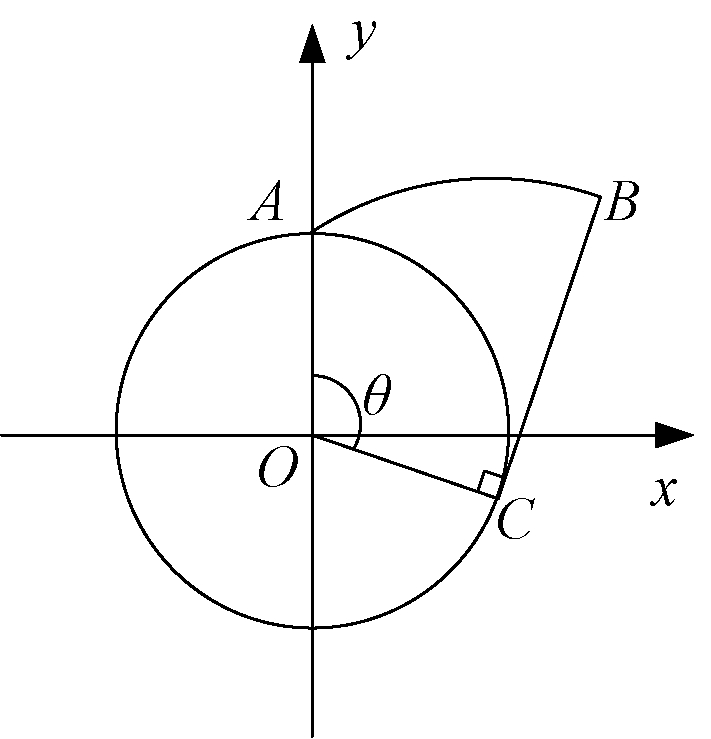
图2 单齿渐开线示意图
Figure 2 The diagram of involute schematic
(11)
式中:Rb为基圆半径;θ为渐开线发生线在基圆上的滚动角。
过盈装配后,x,y坐标变化量为:
(12)
式中:u为齿轮径向位移量。
(13)
则新的齿形坐标可表示为:
(14)
2 有限元仿真分析
2.1 有限元模型的建立
为验证理论解的准确性,以渐开线斜齿轮为研究对象,开展轴-齿轮过盈配合的有限元分析。
图3为斜齿轮与轴最大过盈量装配时所建立的有限元模型,齿轮模数m=2,齿数z=30,压力角α=20°,模型材料为45钢,具体参数E=2.1×105 MPa, μ=0.3,[σ]=300 MPa。

图3 齿轮与轴过盈配合有限元模型
Figure 3 The element model of interference fit
图4为过盈配合区域齿轮配合表面应力分布图,应力从接触区域向四周扩散,接触应力值在66.24~88.639 MPa,中间位置应力79.80 MPa,与理论公式推导出的pmax=77.094 MPa基本一致。
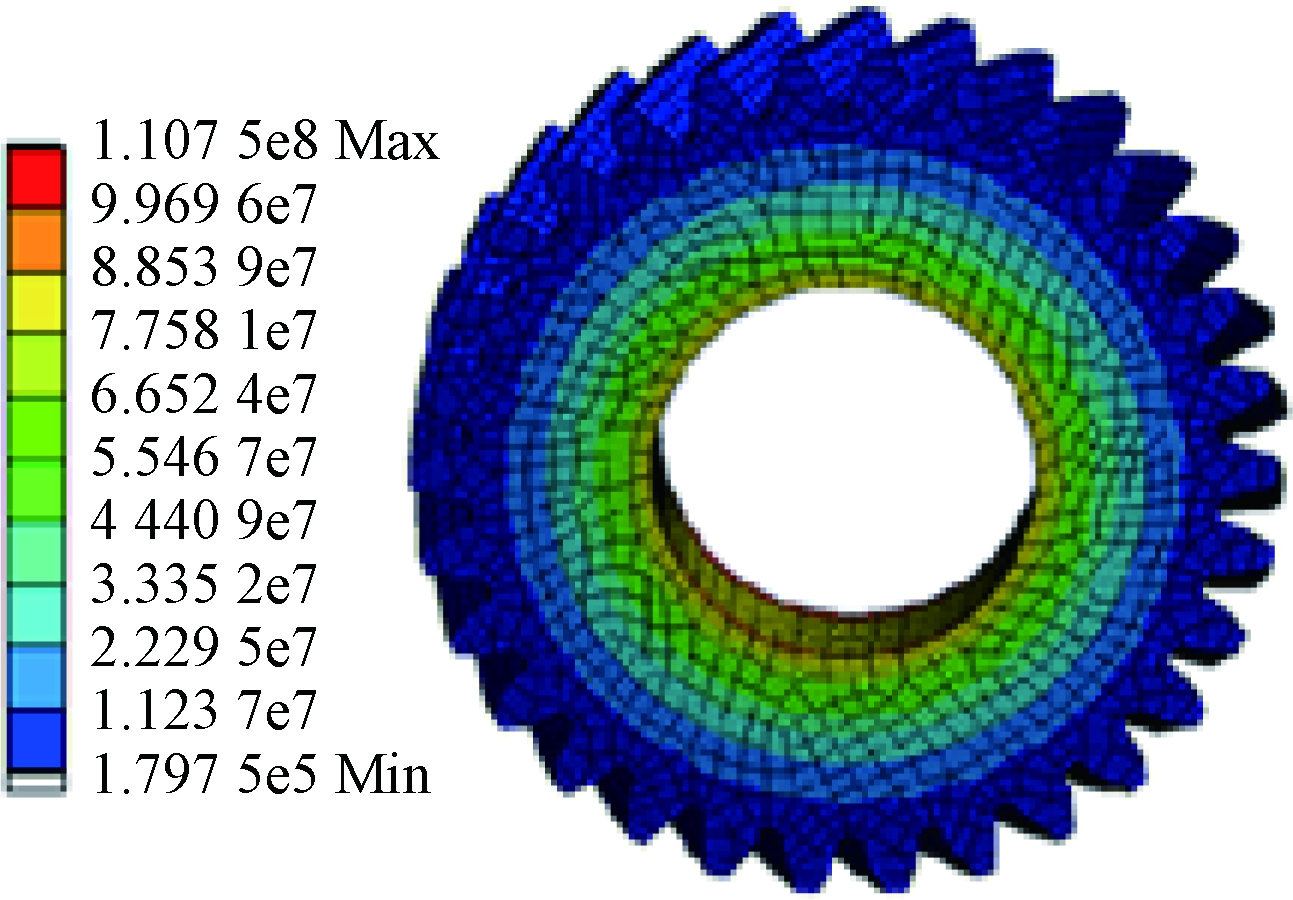
图4 齿轮与轴过盈配合接触应力分布
Figure 4 The distribution of contact stress
2.2 理论计算与仿真结果对比分析
将有限元仿真与理论推导结果进行对比,验证理论公式。选取轴径Ra=15 mm,模数m=2 mm,压力角α=20°,齿数分别为z1=25,z2=30,z3=35,z4=45,z5=50斜齿轮,结果对比如图5、图6所示。
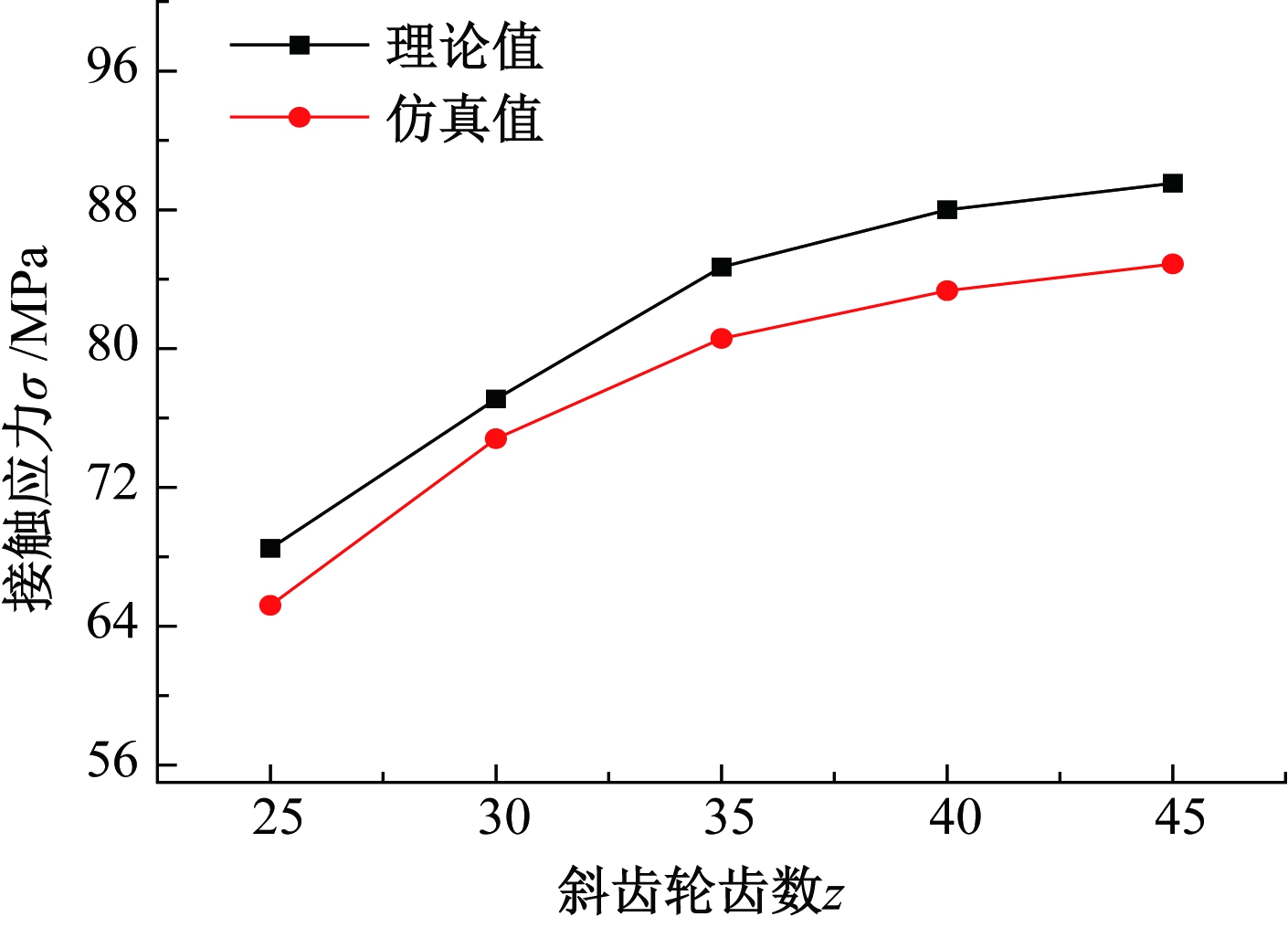
图5 不同齿数接触应力对比图
Figure 5 The contact stress of different number of teeth
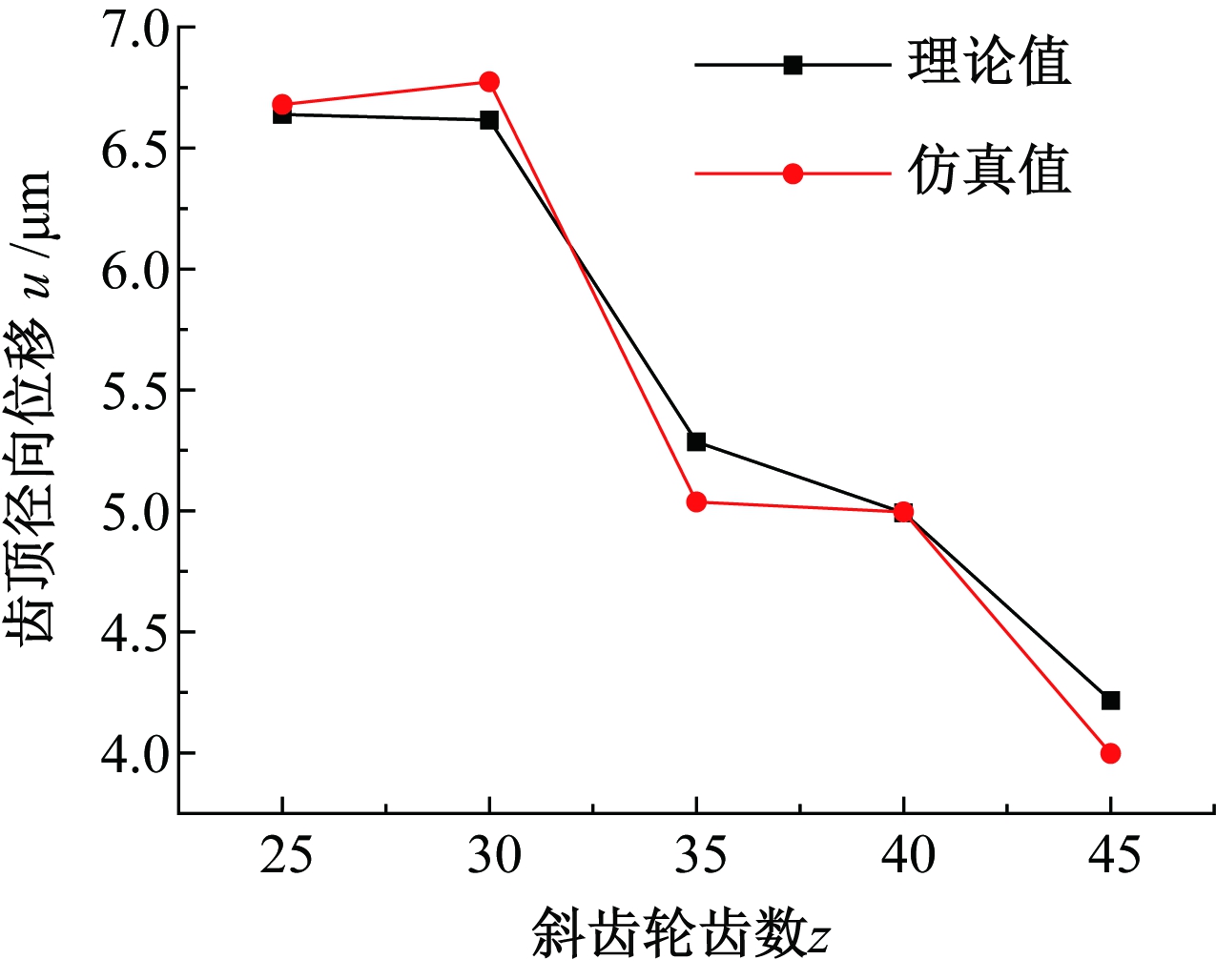
图6 不同齿数齿顶圆的径向位移
Figure 6 The radical displacement under different number of teeth
轴-齿轮过盈装配连接质量取决于装配接合面压力p、摩擦系数β、过盈量Δ等参数。为达到最优装配质量,有必要研究以上参数对接触应力和齿轮变形的影响。
2.3 摩擦系数对接触应力及径向位移的影响
摩擦系数与轴和齿轮表面质量和润滑状态相关,本文摩擦系数β选取范围是0.1~0.2,根据式(9)、(2)、(4)可分别计算出不同β时接触应力、接触面处径向位移及过盈量,其变化趋势如图7~8所示。
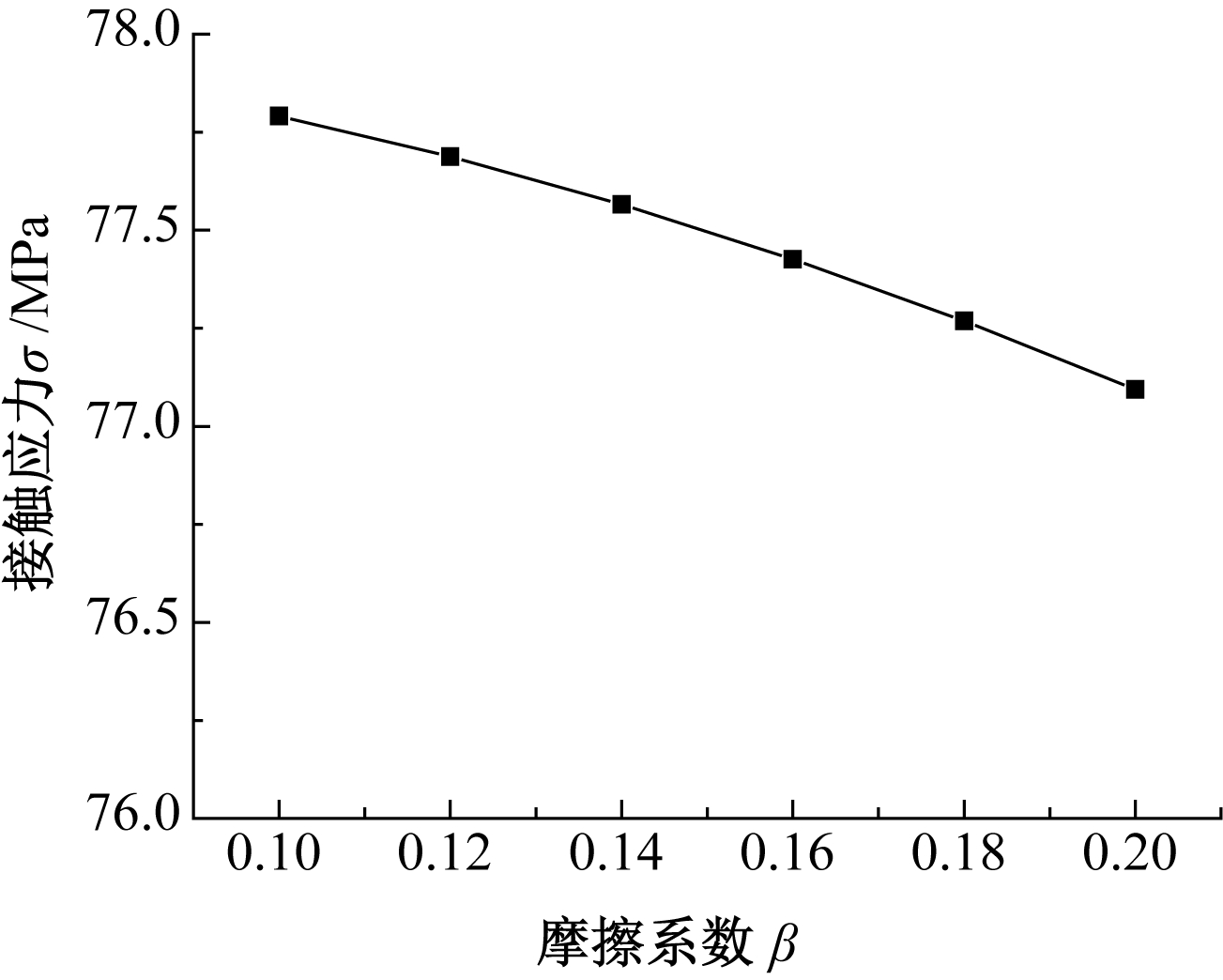
图7 摩擦系数对接触应力的影响
Figure 7 The influence of friction coefficient on contact stress
由图7、图8可得:随着摩擦系数的增加,装配接合面处的接触应力和齿顶处的径向位移逐渐减小。因此,过盈装配时应合理选取β的取值。
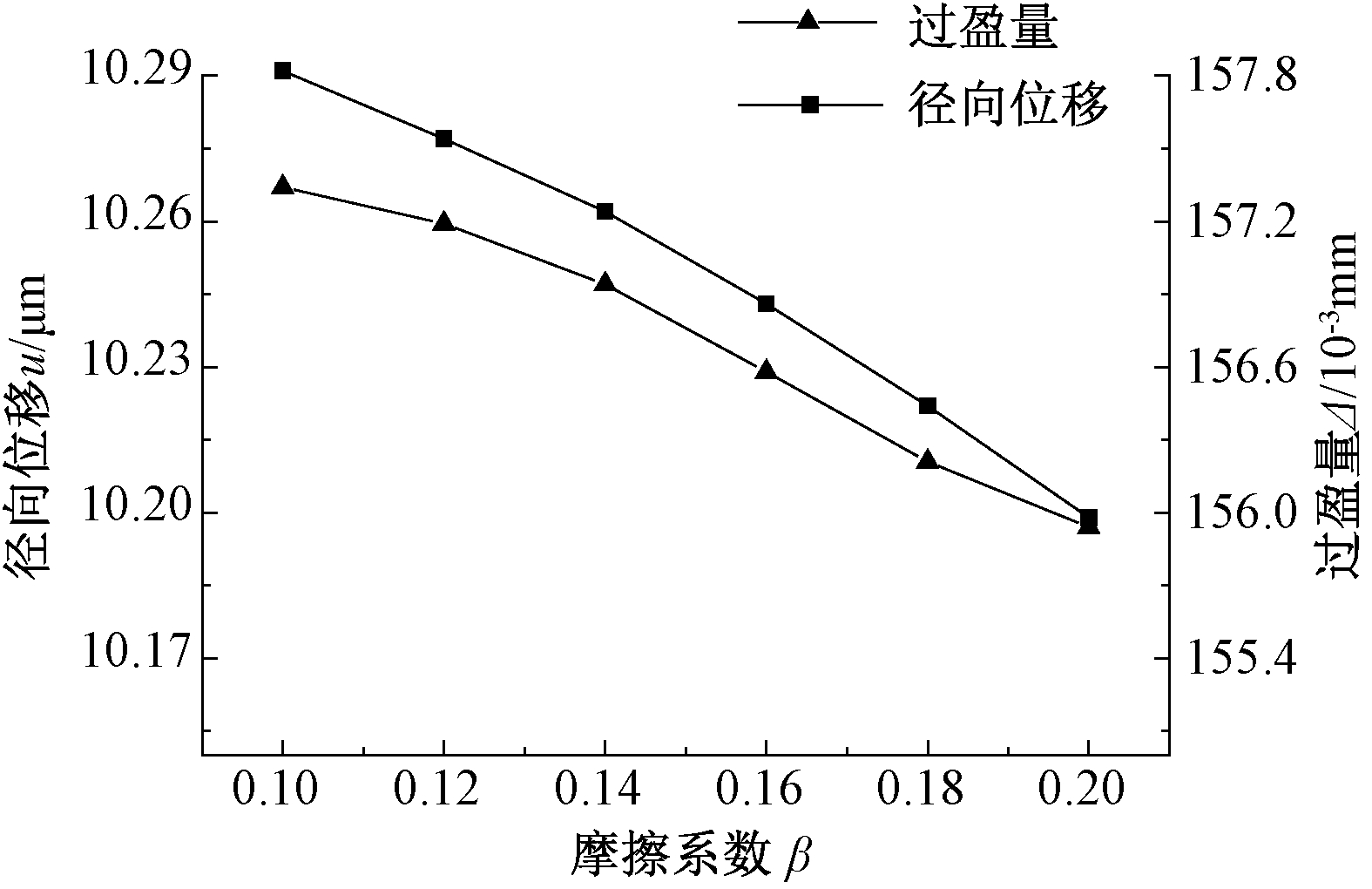
图8 摩擦系数对径向位移与过盈量的影响
Figure 8 The influence of friction coefficient on radical displacement and interference
2.4 过盈量对接触应力及径向位移的影响
过盈量对过盈装配有重要的影响:过盈量过小,会造成齿轮传动过程中出现打滑现象,无法传递力和扭矩;过盈量过大,会造成装配困难,并导致齿轮和轴发生塑性变形。因此,本节讨论过盈量对接触应力和齿形变形的影响。
本节中,斜齿轮齿数z=30,过盈量Δ范围为9~13 μm。根据式(2)、(9)可分别计算出不同过盈量对接触应力和齿顶径向位移,其变化趋势如图9所示。由图9可得:在弹性范围内,随着过盈量的增加,装配接合面处的接触应力、径向位移呈线性增大趋势。
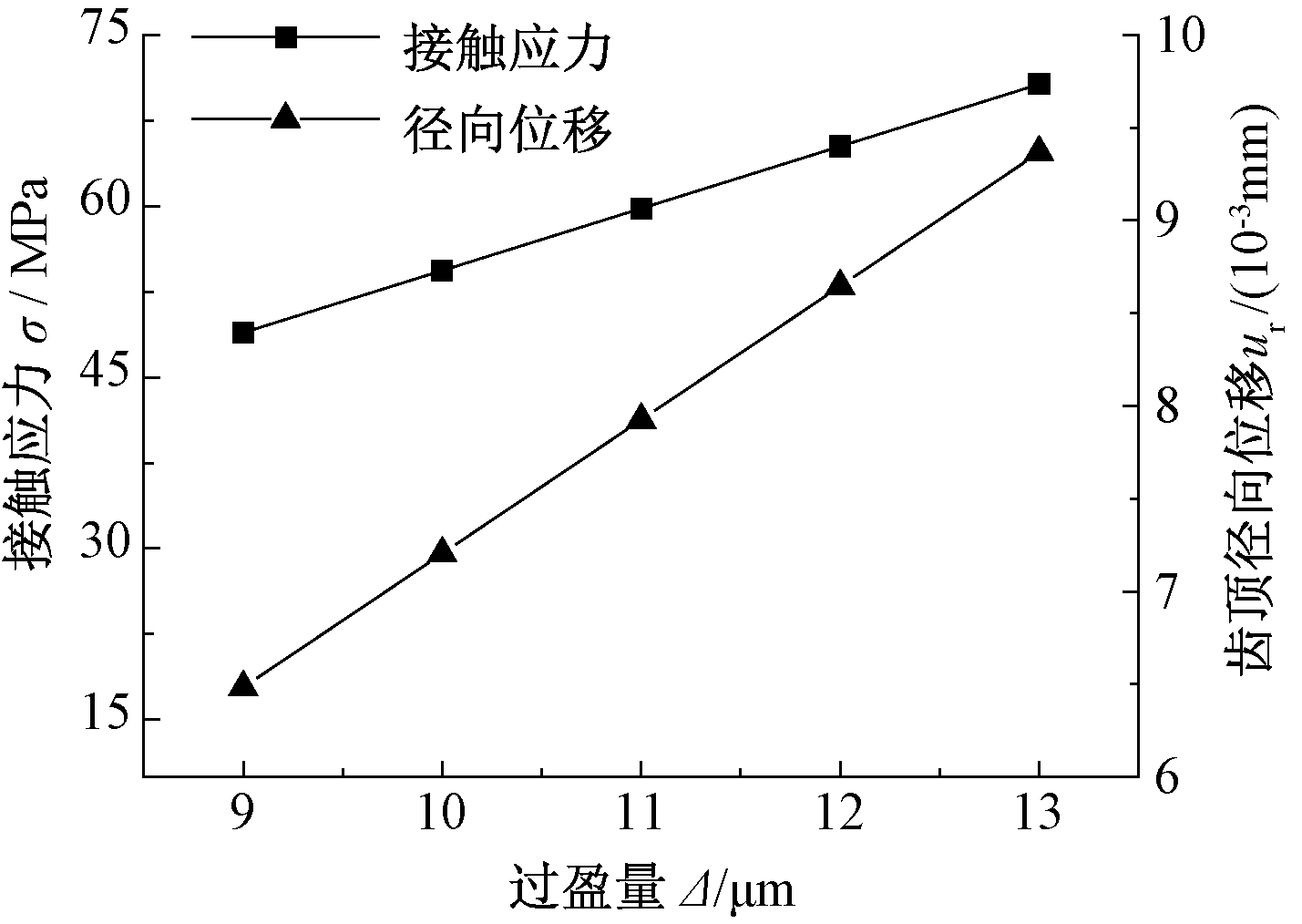
图9 过盈量对接触应力、径向位移的影响
Figure 9 The influence of interference on contact stress and radial displacement
3 装配前后齿形变化
由上述章节可知,过盈配合会导致齿形发生改变,而齿形的变化又会导致齿轮副侧隙发生改变。齿轮侧隙过大会导致齿轮在传动过程中产生冲击,过小则会加剧磨损,严重情况下会造成齿轮咬合卡死,造成齿轮箱损坏。因此,有必要对过盈装配后齿形的变化进行研究。
本节中,轴径为Ra=25 mm,模数m=4 mm,齿数压力角α=20°,齿数z=20,齿轮和轴的材料均选用45号钢。由式(10)和MATLAB编程可得装配前后齿形变化如图10所示。其中,I处放大图如图11所示。
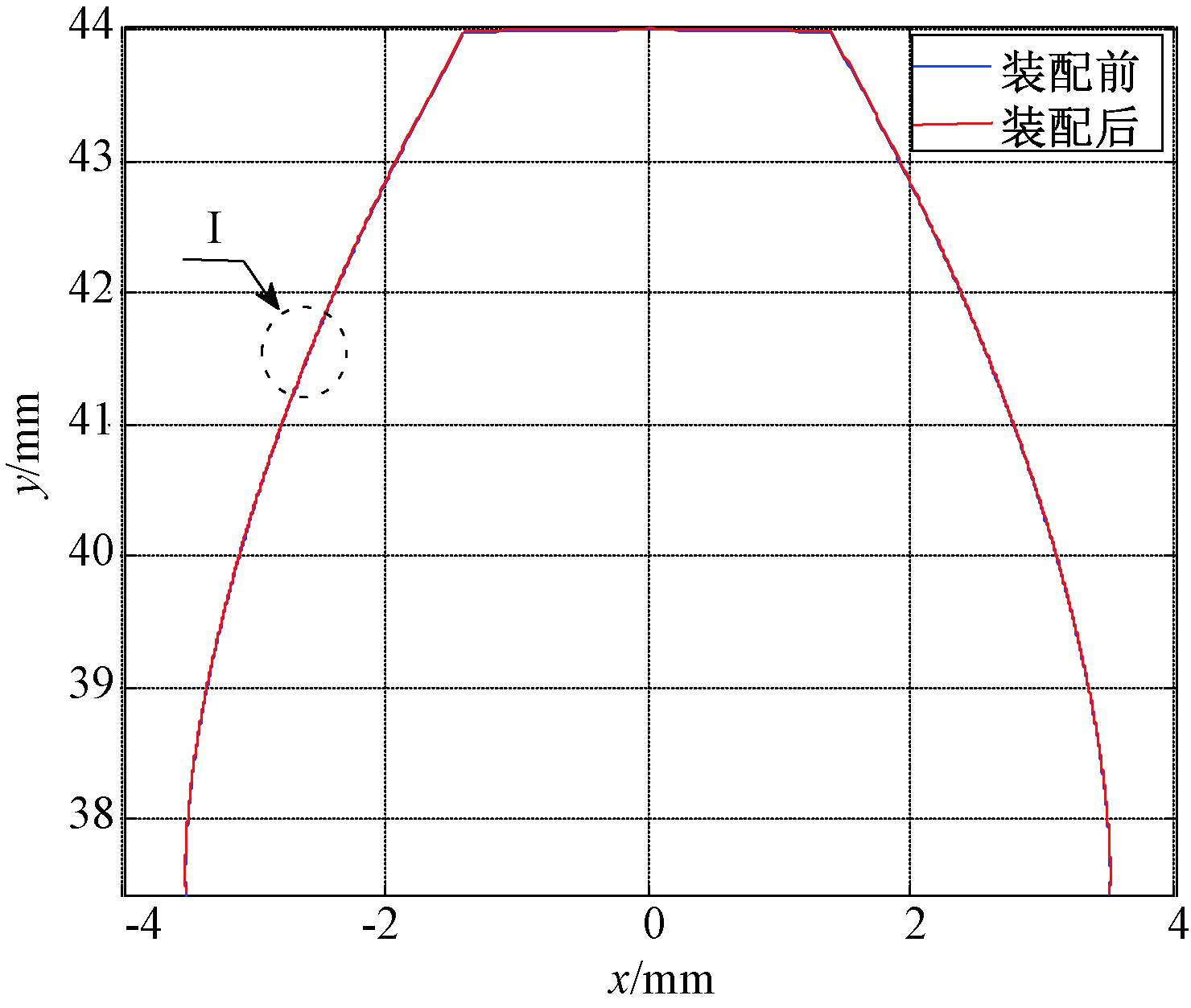
图10 装配前后齿形变化对比图
Figure 10 The contrast of tooth shape before and after assembly
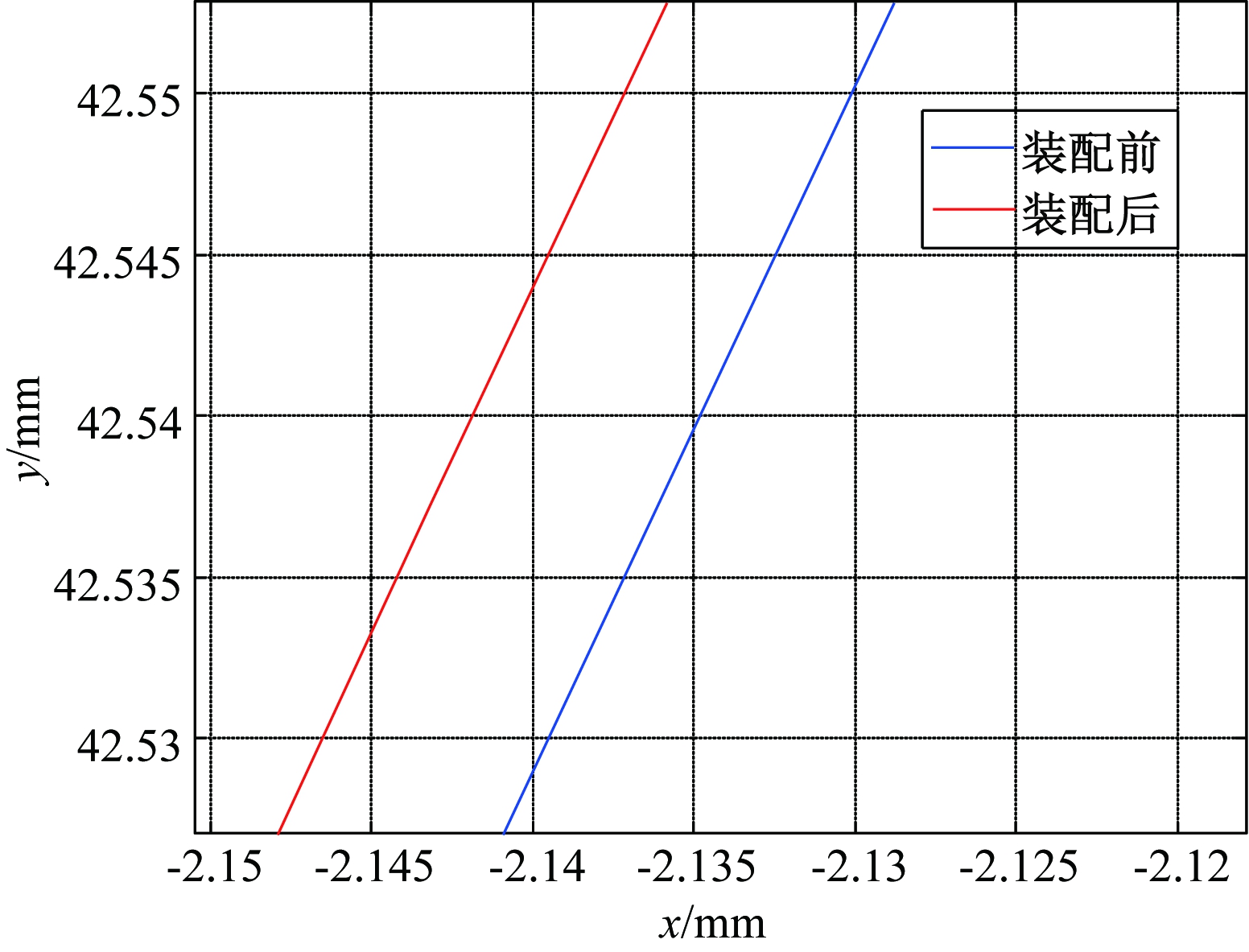
图11 I处放大图
Figure 11 The enlarged figure of I
4 结论
基于弹塑性力学得到轴与齿轮过盈配合时接触应力、径向位移的解析式,并利用有限元软件验证了解析式的正确性。得到变形后齿轮坐标计算公式,为后续齿轮侧隙的分析提供理论计算模型。具体的结论如下:
(1)基于渐开线方程建立齿轮装配后齿形变化量的计算模型,研究过盈装配对齿形的影响,为齿轮侧隙的设计提供理论基础。
(2)计算了不同齿数下装配接合面接触应力和径向位移。随着齿数的增加,接触应力逐渐变大,而径向位移逐渐变小。
(3)研究了摩擦系数对装配接合面接触应力和径向位移的影响。随着摩擦系数的增大,接触应力和径向位移逐渐变小。
(4)讨论了过盈量对装配接合面处接触应力和径向位移的影响规律。最大接触应力和齿形径向位移随着过盈量的增加呈线性增大趋势。
[1] 刘竹丽,赵敏敏,马朋朋,等.基于ANSYS的斜齿轮副接触分析与可靠性分析[J]. 郑州大学学报(工学版),2015,36(2):6-9.
[2] 李亚洲,汤易升,陈炜,等.基于ANSYS Workbench对圆柱面过盈配合接触应力的研究[J]. 天津理工大学学报,2017, 33(3):1-5.
[3] 濮良贵.机械设计[M]. 8版.北京:高等教育出版社,2005:129-136.
[4] JIN X, ZHANG Z J, YE X, et al. Calculating model of interference amount for miniaturized gear and shaft shrinkFit[J]. Journal of Beijing institute of technology, 2006, 15(2):138-143.
[5] ZHANG Y, MCCLAIN B, FANG X D,et al. Design of interference fits via finite element method[J]. International journal of mechanical sciences, 2000, 42(9):1835-1850.
[6] SEN S, AKSAKAL B. Stress analysis of interference fitted shaft-hub system under transient heat transfer conditions[J]. Materials & design, 2004, 25(5):407-417.
[7] 邹渊,孙逢春,王文清, 等. 过盈配合时齿轮内径与预应力关系研究[J]. 机械传动, 2003,27(6):45-46,55.
[8] 王少江,李学明,张安鹏, 等. 大型焊接齿轮与轴过盈配合有限元分析[J]. 煤矿机械, 2015,36(5):140-142.
[9] 关丽坤,任学平,郭书萍,等.过盈联接的有限元分析[J]. 机械设计, 2005, 22(增刊1):275-276.
[10] CHU S J, JEONG T K, JUNG E H,et al. Effect of radial interference on torque capacity of press- and shrink-fit gears[J]. International journal of automotive technology, 2016, 17(5):763-768.
[11] 何亚峰,杨小斌,干为民,等.齿轮与轴压装过程过盈配合研究[J]. 机械传动,2014,38(12):33-36.
[12] 张炳义,戴思锐,冯桂宏,等.磁力齿轮内转子护套过盈量计算及其应力分析[J]. 机电工程, 2017, 34(8):817-822.
[13] 贾国海,龚金科,鄂加强,等.齿轮轴过盈配合对轴肩微动磨损的影响研究[J]. 湖南大学学报(自然科学版),2013,40(5):36-41.
[14] 赵俊,林腾蛟,钟声,等.行星轮-轴承过盈配合部位疲劳寿命及其影响因素分析[J]. 大连理工大学学报, 2016, 56(4):355-361.
[15] LANOUE F, VADEAN A, SANSCHAGRIN B, et al. Finite element analysis and contact modelling considerations of interference fits for fretting fatigue strength calculations[J]. Simulation modelling practice & theory, 2009, 17(10):1587-1620.