0 引言
永磁同步电(permanent magnet synchronous motor，PMSM)以其电流平稳、噪声小、转矩脉动小、转矩/惯量比大、效率高等优势成为高性能调速系统的首选.
传统的PMSM转速和位置检测是通过机械式传感器获取［1］，如光电编码器或旋转变压器.此方法动态响应快、稳态无静差、调速范围宽、控制性强，但当工作环境发生恶劣变化(如高温、低温、空气污浊等)或者存在机械震动时，检测结果将无法保证且成本高.当前的PMSM控制系统正往高效率、高性能、低成本的方向发展.因此，无位置传感器［2］的应用成为 PMSM伺服系统研究的新方向.现有的PMSM无位置传感器控制方法归为两种:①基于电机反电动势的方法［3-4］.比如基于模型参考自适应法、滑模观测器法和扩展卡尔曼滤波法，均利用电机产生的反电动势估计电机转子位置和转速，但此方法只适用于中高速的场合；②基于高频信号注入［5］.即将不同类型的额外高频信号叠加在电机的基频激励上，通过检测电机对高频信号的响应得到电机转子位置和转速信息.此方法利用电机内在的凸极特性检测电机静止时和运动时的速度和位置.这种凸极跟踪算法不依赖于任何电机参数和运行情况，在零速或低速的条件下系统也能够获得稳定的控制性能，但是高频注入法会引起推力波动［6-7］，产生附加的损耗和瞬态干扰，因而这类方法多用于低速段.
在研究扩展卡尔曼滤波法的基础上，通过对扩展卡尔曼滤波算法和高频信号注入法的分析，将两种不同算法进行有机复合，以提高系统的性能.仿真结果表明，复合后的方法增强了系统的动态性能，弥补了两种控制方式各自存在的不足，降低了估计误差，提高了系统的鲁棒性.
1 扩展卡尔曼滤波估计法
扩展卡尔曼滤波(extended kalman filtering，EKF)又称最小方差线性递推滤波，是建立在线性卡尔曼滤波基础上的一种非线性参数估计方法，且参数和方差阵的估计不依赖于它们的初值，通过递推算法实现无偏最优估计［8-9］.
笔者采用表面贴式永磁同步电机，在d-q轴坐标系下建立数学模型，为了对非线性系统进行线性化处理，假设电阻变化率为 dR/dt=0；假设非线性方程一定有解，并且该向量与实际向量之间的关系可以描述成线性的微分方程，同时，该解可真实地反映系统特性.
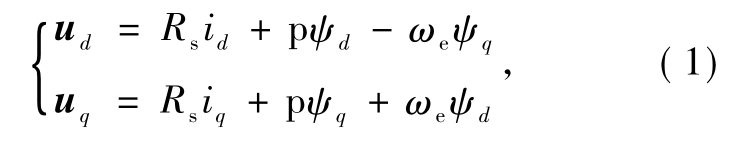
式中:Rs为定子电阻；id、iq分别为定子在 d轴、q轴的电流分量；ud、uq分别为定子在 d轴、q轴的电压分量；p为微分因子.
PMSM定子磁链方程式
PMSM定子电压方程:
式中:ψd和ψq分别为定子在d轴、q轴等效磁链；ψf为转子磁链；Ld和 Lq为定子在 d轴、q轴等效的电枢电感，且Ld=Lq=L.
PMSM电磁转矩方程式:
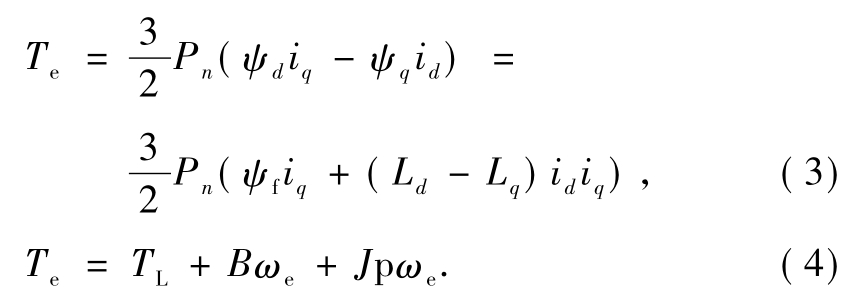
式中:Te为电磁转矩；B为运动阻尼系数；J为转动惯量；TL为负载转矩；Pn为电机极对数；ωe为转子电角速度.
综上，可得PMSM的状态方程式为:
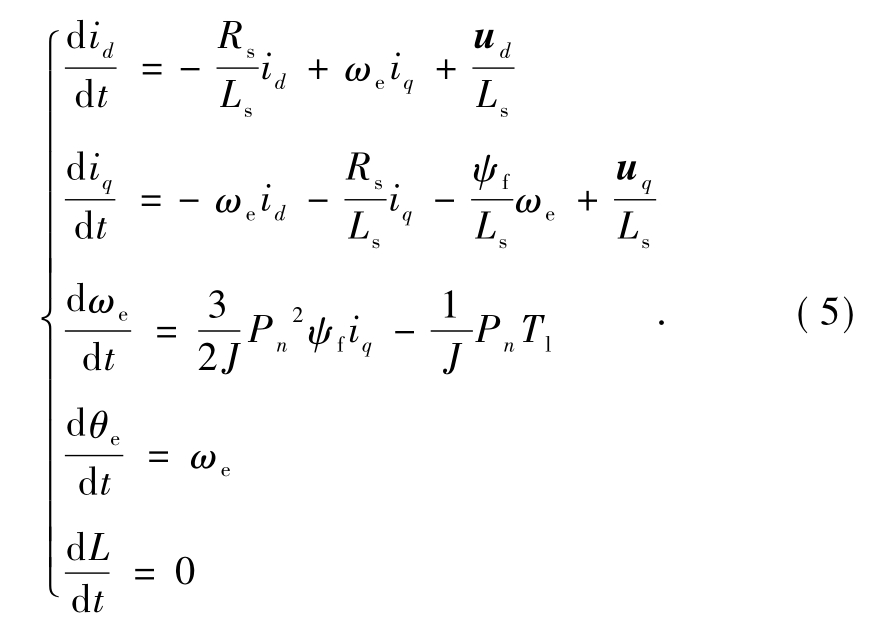
式中:x 为状态变量，且 x=［idiqωeθL］T；y 为状态输出向量，且 y=［idiq］T；u为输入向量，且 u=［uduq］T；A 为系数矩阵，且
则PMSM的状态方程可以表示为:
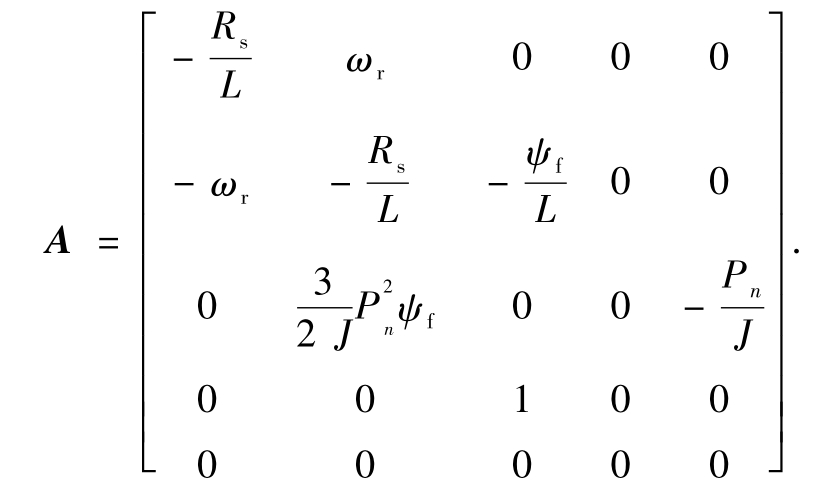
C为系数矩阵，且:
H为系统观测矩阵，且
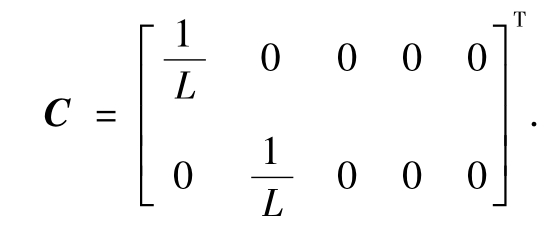
式中:w为系统噪声；Q为系统噪声协方差矩阵；v为测量噪声；R为测量噪声协方差矩阵；w和v均具有零均值高斯白噪声的特性.设 T为采样时间，且T=tk-tk-1，I为单位矩阵；则
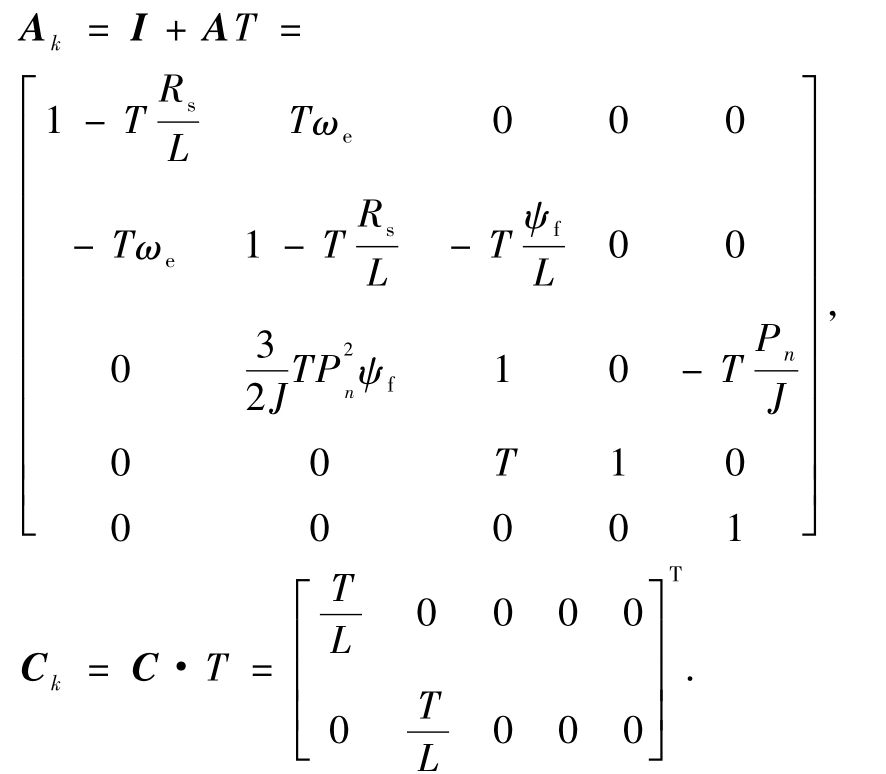
考虑系统噪声和测量噪声的影响，且采样时间T足够短时，构建的PMSM非线性离散时间状态方程为:
根据文献［8］，改进的 EKF法对速度和位置的估计算法步骤如下.
a)状态向量、方差矩阵的初始化.设状态初值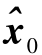 
=［0 0 0 0 L］T；经过反复调试，设
P(0)为五阶非负正定对角矩阵，且设
b)状态估计.
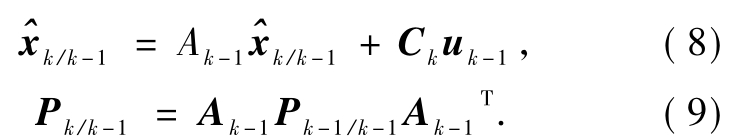
c)计算增益矩阵Kk.
d)状态更新.
2 高频脉振电流注入法
在高频脉振电压注入法［10-11］的基础上，笔者选择高频脉振电流注入法，进行转子位置和转速的检测.PMSM在d-q轴的数学模型如式(1)、(2)所示.由于低速和零速时，交叉耦合项和反电动势项数值较小，且ωe远远小于注入的高频电压频率ωh，可近似为 0.因此，简化后的 d-q轴电压方程为:
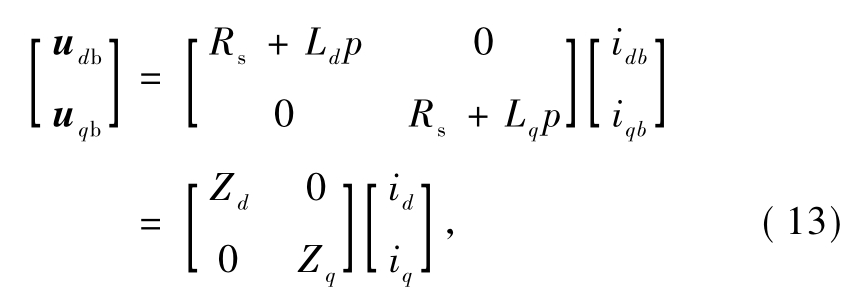
式中:udb、uqb为 d、q 轴注入的高频电压；idb、iqb为 d、q轴注入的高频电流；Zd、Zq为 d、q轴的阻抗.图1为定义的3个坐标系的关系图，其中d-q为实际的同步旋转坐标系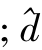
-
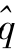是估计的同步旋转坐标系；αβ为实际的两相静止坐标系，并定义
由图1可以得到以下关系
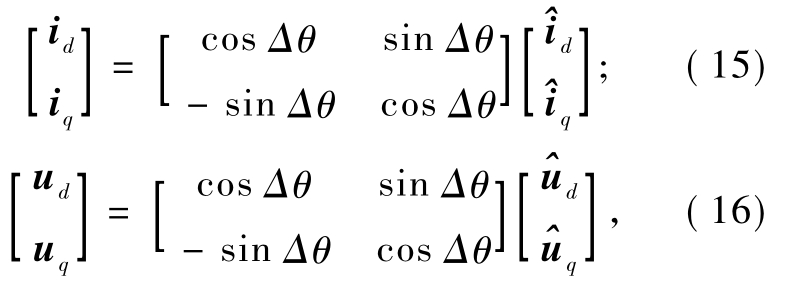
式中:Δθ为估计位置误差；θ为转子实际位置；θ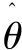
为转子位置估计值
为
坐标系下的电压估计值
为
坐标系下的电流估计值.
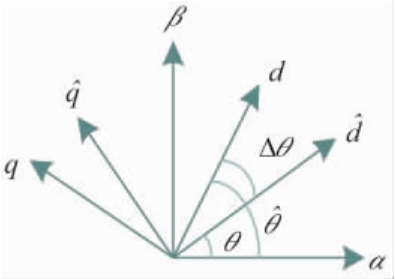
图1 参考坐标系关系图
Fig.1 Reference coordinate system diagram
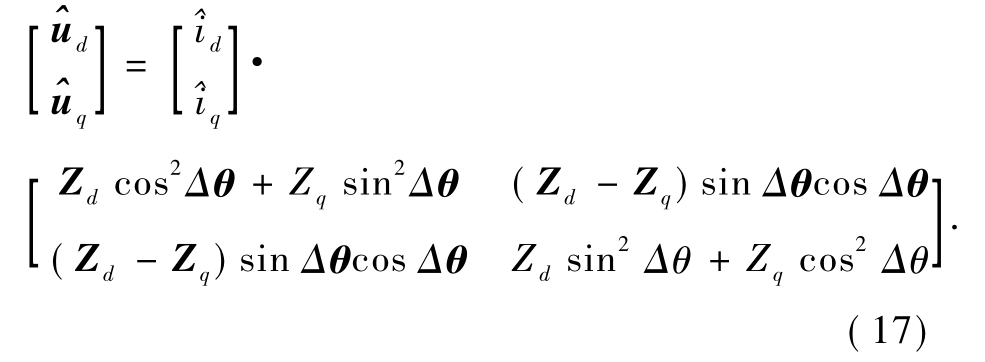
由公式(13)～(16)可以得到如下关系式:
令 Z=(Zd+Zq)/2，ΔZ=(Zd-Zq)/2，则可以得到 Zd=Z+ΔZ，Zq=Z-ΔZ.将其带入式(17)可以得到
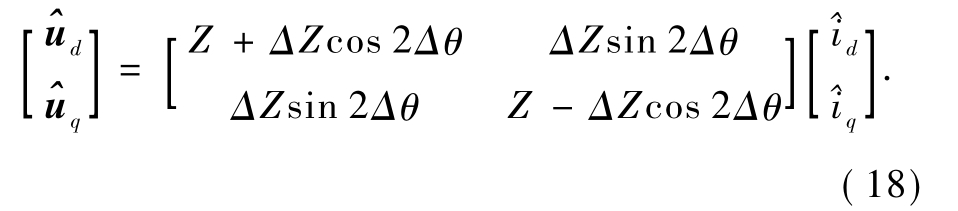
由式(16)可以看出，在 
中均含有与 Δθ有关的量.为了准确获取转子位置，通过高频注入法，在
轴系中注入如下形式电流信号:
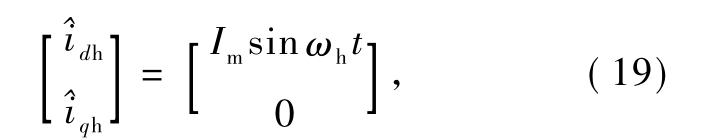
式中:Im为在直轴注入的高频电流信号幅值；ωh为注入信号的角频率.注入高频电流后，在输出侧得到的高频电压响应的表示形式为:
令 L=(Ld+Lq)/2，ΔL=(Ld-Lq)/2，带入式(20)得
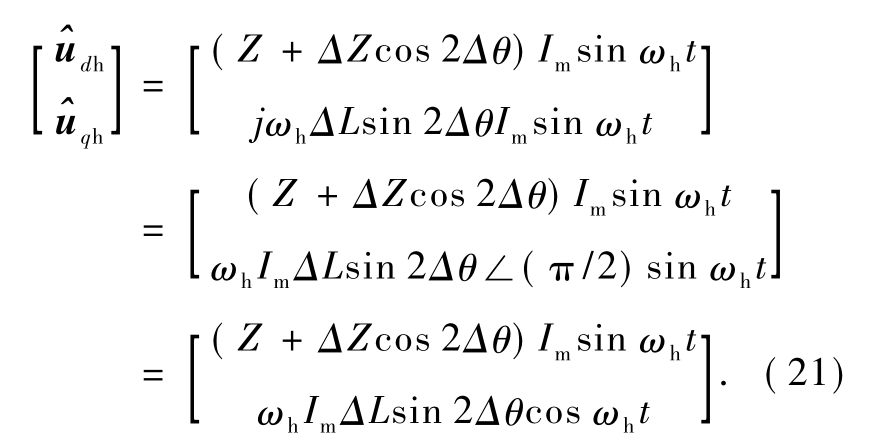
对式(21)进行分析可得:当 Δθ=0时，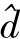
-
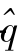坐标系和d-q坐标系一致，因为高频脉振电流仅在
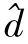轴注入，所以，iqh=
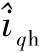=0，这就保证了注入的高频电流不会引起转矩脉动，保证了该方法的良好控制性能.
由式(21)可得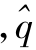
轴上的
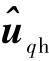为
对式(1)和式(22)进行分析可得，如果可以将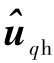 
的幅值调节为零，那么就可以保证Δθ恒等零.所以，可将
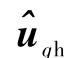首先经过乘法器(cos ωht)，再经过低通滤波器(LPF)得到如下形式信号:
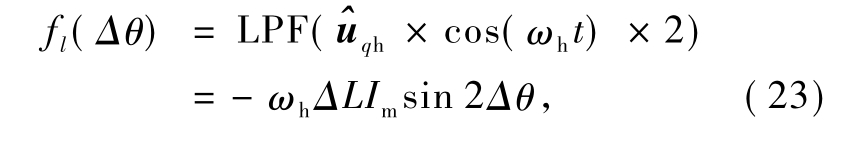
其中，根据等价无穷小定理，当 Δθ很小时，sin 2Δθ≈2Δθ，即式(23)可重写为:
简化后的系统调节结构如图(2)所示，图2中，km为积分系数.
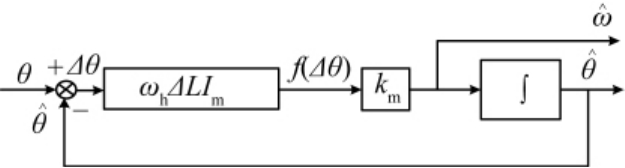
图2 系统调节结构图
Fig.2 System adjustment structure diagram
3 改进EKF与高频注入复合法
笔者将两种方法进行复合，即在低速或零速时采用高频脉振电流注入法，高速时采用改进的EKF法，在低速和高速过渡区采用复合算法.复合算法的关键是全速范围内实现转速的平滑切换［12］.较常用的切换方法是滞环切换法［13］，滞环切换法虽然简单，却存在较大的切换抖动和输出扰动的缺陷，为了改善此弊端，笔者在滞环切换的基础上，采用加权复合方式实现两种算法的复合.
根据两种算法的速度适应范围和运行特性确定过渡区域的速度下限ωr1和上限ωr2.为了使低速、高速域内都能有较好的位置估算精度，ωr1和ωr2的选取需做如下规定:①过渡区域的速度下限ωr1要高于能使EKF精确工作的最低速度；②过渡区域的速度上限要低于高频注入法精确工作的最高速度，并且能够满足电机自启动要求.
利用式(25)和式(26)的线性方程实现两种方法的平滑过渡.如图3所示，加权系数α、β始终满足α+β=1，保证了此切换算法的科学性.具体复合过程如图4所示.
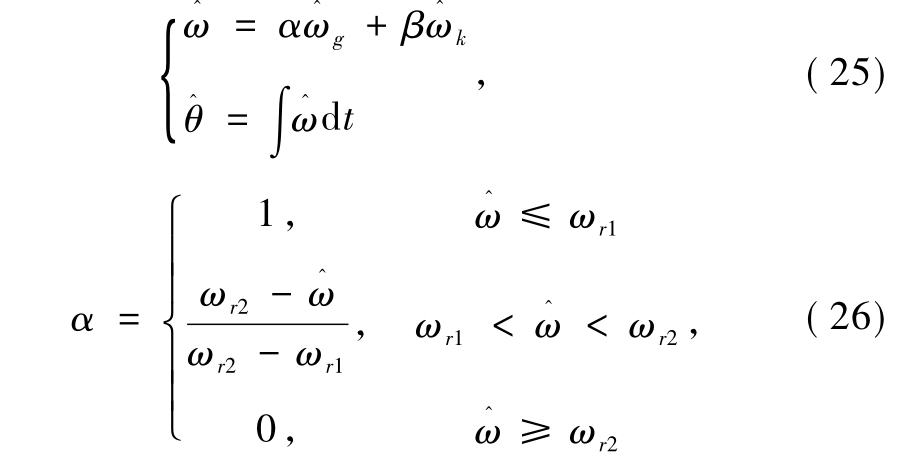
式中:ωg为高频注入法检测转速；ωk为改进EKF检测转速.
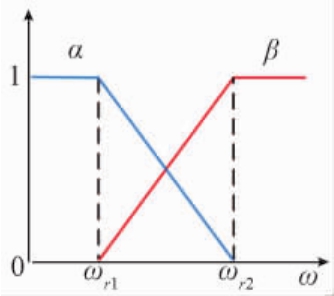
图3 加权系数关系图
Fig.3 Weighted coefficient relation diagram
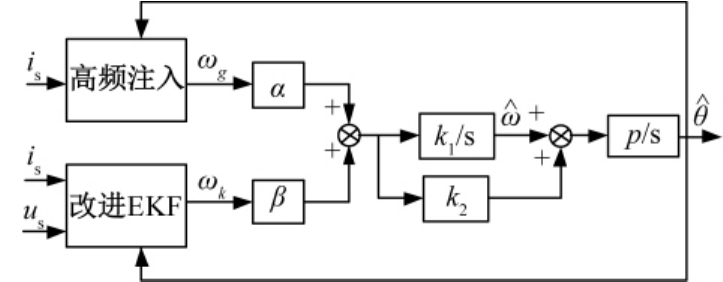
图4 复合算法转子位置估算原理图
Fig.4 The principle diagram of the estimation of the rotor position of the composite algorithm
4 仿真分析
利用Matlab/Simulink搭建仿真模型进行仿真分析.仿真参数参考表面贴式永磁同步电机的实际参数，具体参数设置如下:定子电阻 Rs=2.875 Ω，极对数 Pn=4，定子电感 Ls=8.5 mH，转动惯量 J=0.000 8 kg·m2，黏滞摩擦系数 B=0.000 1 N·m·s，永磁体磁链 ψa=0.175 Wb，PI参数设为:kp=20；ki=50.仿真系统图如图5所示.
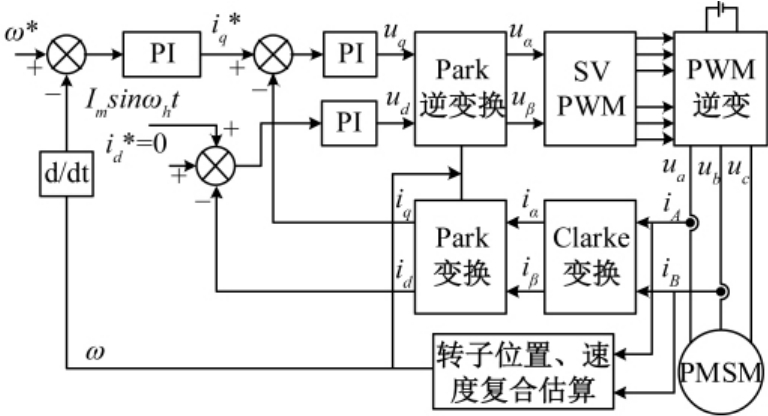
图5 PMSM无传感器复合控制系统
Fig.5 PMSM sensorless composite control system
为了确定复合法的最佳切换区间，在0～1 000 r/min选取不同的额定速度，分别采用两种方法，进行大量的仿真实验.笔者列出额定转速为50、400、500 r/min时，分别采用高频注入法和EKF法时的仿真结果，如图6、7、8所示.
图6中，当电机额定转速为50 r/min时，对比图6(a)和6(c)，明显可以看出，EKF法的观测噪声大，谐波含量高，而高频注入法却能较精确地估计转子位置的实际值，图6(b)和图6(d)更清晰地反映出高频注入法在低速时噪声小，估计精度高，而EKF法在低速时噪声大，估计精度低.
由图7和图8的仿真结果可以看出，当电机额定转速为400 r/min时，采用高频注入法的估计误差低于 EKF法的估计误差.当额定转速为500 r/min时，与额定转速为400 r/min时相比，采用高频注入法的跟踪效果变差，噪声变大，估计误差升高，而采用 EKF法的观测精度变高，噪声变小，误差降低.因此，笔者以 400、500 r/min为低速和中高速的分界点.
图6 额定转速为50 r/min时两种方法的仿真结果
Fig.6 Simulation results of the two control method at rated speed of 50 r/min
图7 额定转速为400 r/min时两种方法的仿真结果
Fig.7 Simulation results of the two control method at rated speed of 400 r/min
图8 额定转速为500 r/min时两种方法的仿真结果
Fig.8 Simulation results of the two control method at rated speed of 500 r/min
为了充分验证复合控制系统的动态性能，在电机额定转速为1 000 r/min，速度切换域为［400 r/min，500 r/min］，且 0.25 s时负载转矩由0 N·m突增到5 N·m的情况下，进行仿真实验.仿真结果如图9所示.
图9 复合控制系统仿真结果
Fig.9 Composite Control System Simulation Results
如图9(a)、(b)所示，改进后的复合控制系统转速跟踪误差小，在进入切换区域后仍然可以稳定运行，并且当负载转矩突变后，能在较短时间内恢复平稳运行状态；图9(c)、(d)表明，改进型无传感器复合控制系统获取的转子位置信息几乎无相位延迟，保证系统在低速到高速段内都有较高的估算精度.
5 结论
首先分析了高频注入法和卡尔曼滤波算法在PMSM无传感器控制系统中的应用特点，根据两种算法在无传感器转子位置估计中的速度适用范围，将两种算法进行了复合统一.利用加权系数法实现了两种算法之间的平滑过渡，并在最后进行了仿真验证.结果表明，所设计的复合式转子位置检测方法结构简单，能够快速精确地检测出转子位置，在负载突变的情况下也能高效、快速跟踪速度的变化，大大提高了系统的动态响应性能，较好地实现了全速范围无位置传感器系统位置与转速的估计.
［1］张猛，肖曦，李永东.基于扩展卡尔曼滤波器的永磁同步电机转速和磁链观测器［J］.中国电机工程学报，2007，27(36):36-40.
［2］高越，罗映红.高频激励下永磁同步电机无传感器控制研究［J］.郑州大学学报(工学版)，2013，34(5):80-84.
［3］陆华才，江明，陈其工.永磁直线同步电机驱动系统速度和位置无传感器检测新方法［J］.电工电能新技术，2011，30(2):5-8.
［4］ZHENG Z Q，ZHANG Y H，ZHANG J S.Application of Kalman Filter in DC Motor Speed Control System［J］.Applied mechanics and materials，2012，1605(150):129-132.
［5］ZHANG Y F，LI S J，ZHOU Y，et al.PMSM Control System Based on a Improved Sliding Mode Observer［J］.Applied mechanics and materials，2013，2324(307).
［6］MORIMOTO S，SHIMMEI A，SANADA M，et al.Position and speed sensorless control system of permanent magnet synchronous motor with parameter identification ［J］.Electrical engineering in Japan，2007，160(2):68-76.
［7］SHENG wen Y E，SHAN mao G U，GUANG c L I，et al.Sensorless Vector Control of Permanent Magnet Synchronous Motor Based on Method of High-frequency Injection Method［J］.Industry ＆ mine automation，2010.
［8］QI X，ZHOU X M，WANG C S，et al.Sensorless control of permanent-magnet synchronous motor based on high-frequency signal injection and Kalman filter［C］∥International Symposium on Systems and Control in Aerospace and Astronautics.IEEE，2009:1-5.
［9］兖涛，刘军，杨明亮，等.基于高频注入法永磁同步电机控制研究［J］.电气自动化，2015，37(3):7-9.
［10］BISHEIMER G，SONNAILLON M O，DE Angelo C H，et al.Full speed range permanent magnet synchronous motor control without mechanical sensors［J］.Electric Power Applications Iet，2010，4(1):35-44.
［11］LI H，XIE H，YI X，et al.Research on low speed control of permanent magnet synchronous motor based on state observer［C］∥ International Conference on Biomedical Engineering and Informatics.IEEE，2011:2018-2022.
［12］ZHANG J，GUO X，HUANG X.Method research of permanent magnet synchronous motor position sensorless control over full speed range［C］∥IEEE International Conference on Industrial Technology.IEEE，2017.
［13］郑国良.永磁同步电动机的全范围无传感器控制研究［D］.郑州:郑州大学电气工程学院，2013.