0 引言
在主动配电网(active distribution network, ADN)优化调度中,不仅要考虑有功、无功的不同优化目标,还需计及分布式电源(distributed generation,DG)、可控负荷(controllable load,CL)、储能系统(energy storage system,ESS)等设备的功率调节以及系统运行的各种约束.对此多目标非线性规划问题的建模和求解有不同的处理方式[1-12].文献[1]建立基于三相潮流的辐射状配电网多时段有功-无功协调动态优化模型,采用混合整数二阶锥规划算法进行求解.文献[2]建立运行成本与越限风险最小的多目标日前优化调度模型,计及各种ADN调度手段,用理想点法处理多目标模型,以和声搜索算法为求解工具,并基于半不变量法随机潮流实现越限风险指标的计算.文献[3]基于模型预测控制实现主动配电网日前调度、日内滚动调度和实时反馈校正.在主动配电网调度优化模型中,可计及较多的影响因素.文献[4]考虑了光伏发电系统的概率特性,文献[5]以可控DG、储能、联络和分段开关为调度手段,文献[6]用鲁棒优化来处理电价的不确定性,文献[7]计及了输电和高压配电网网损的影响,并根据优化模型的特点,采用适宜的求解算法,例如二阶锥规划算法[1,4]、和声搜索算法[2,8-9]、微分进化-细胞膜混合算法[10]、基于微分进化改进的帝国竞争优化算法[11]等.
在以上分析基础上,笔者以配电网运行成本和电压合格率最小为目标,电网和设备运行要求为约束,建立主动配电网日前、日内的有功无功协调优化模型,计及了多种DG、CL、ESS.根据配电网中各类变量的特点,建立相应有效实用的求解模块,通过各模块间的迭代实现总体最优.
1 主动配电网有功无功优化模型
1.1 日前优化调度模型
日内优化调度阶段的时间间隔ΔT为1 h.目标函数为日前配电网运行成本最低.由于主动配电网中分布式电源可能引起的过电压,将电压因素通过权重系数加入目标函数中,构成目标函数:
minF1=![]()
(1)
其中,C1,t=Kgrit,tPgrit,tΔT;
C3,t=Kloss,tPloss,tΔT;
式中:t为时刻;ΔT为时段;NtN为总时段数;R为权重系数;Vi,t为t时刻节点i的电压幅值;Vi,lim为电压允许范围的边界值,电压越上界时取上界值,越下界时取下界值;U为电压越线节点的集合;P为有功功率;K为费用系数;ΔN为变化个数;C1,t为向上级电网净购电成本;C2,t为向DG购电成本;C3,t为网损成本;C4,t为削减DG有功出力的赔偿成本;C5,t为对可中断负荷控制成本;C6,t为ESS调节成本;C7,t为变压器分接头调节成本;C8,t为并联电容器调节成本.
式(1)将两个不同量纲的目标函数合在一起,权重系数本来不易选取,但此处的第二项描述电压越界程度,因此权重系数R应取较大的值,以便最终结果的电压越界量趋近于零,同时不应引起优化过程的收敛稳定性,试算表明,取R=1 000能满足要求.
优化控制变量包括:可控光伏发电(PV)、风电(WT)的有功、无功出力,其他可控分布式电源(例如沼气发电厂BG、垃圾电厂RI)的有功、无功出力,储能设备(ESS)的有功、无功功率、可控负荷(CL)的调节功率、SVC的无功出力、变压器档位、并联电容器投切状态.
优化控制变量构成向量YP,YP可表达为节点电压向量X的显函数.
等式约束为节点功率平衡约束和储能设备时序运行约束:
(2)
式中:Pi0,t、Qi0,t分别为第i点的给定量.
WESS,i,t=WESS,i,t-1-PESS,i,t-1ΔT.
(3)
不等式约束有节点电压约束:
Vi,min≤Vi,t≤Vi,max,
(4)
式中:Vi,min、Vi,max分别为节点i允许的最低和最高运行电压.
支路功率约束:
Si,min≤Si,t≤Si,max,
(5)
式中:Si,min、Si,max分别为支路i允许的最低和最高视在功率.
储能设备的荷电状态、充放电功率上下限和约束:
WESS,i,min≤WESS,i,t≤WESS,i,max;
(6)
PESS,i,min≤PESS,i,t≤PESS,i,max.
(7)
光伏发电、风电、沼气发电厂、垃圾电厂等分布式电源的有功无功出力约束:
PDG,i,min≤PDG,i,t≤PDG,i,max;
(8)
QDG,i,min≤QDG,i,t≤QDG,i,max,
(9)
式中:PDG,i,t、QDG,i,t分别为第i个分布式电源第t时刻的有功、无功功率.
SVC的无功出力约束:
QSVC,i,min≤QSVC,i,t≤QSVC,i,max,
(10)
式中:QSVC,i,t为第i个SVC第t时刻的无功功率.
可控负荷的调节功率约束:
PCL,i,min≤PCL,i,t≤PCL,i,max;
(11)
QCL,i,min≤QCL,i,t≤QCL,i,max,
(12)
式中:PCL,i,t、QCL,i,t分别为第i个可控负荷第t时刻的有功、无功功率.
并联电容器组数约束:
0≤Nc,i,t≤Nc,i,max,
(13)
式中:Nc,i,t为节点i处所安装的电容器组数;Nc,i,max为节点i处安装的最大电容器组数.
可调分接头档位数约束:
0≤Ntap,i,t≤Ntap,i,max,
(14)
式中:Ntap,i,t为第i个变压器的档位值;Ntap,i,max为第i个变压器的档位值的最大值.
优化目标和约束条件中,并联电容器组投切状态、变压器分接头档位为离散变量,其余为连续变量,连续变量可表达为节点电压向量X的显函数.
1.2 日内滚动优化调度模型
日内优化调度阶段的时间间隔ΔT为15 min.电容器组投切状态、变压器分接头档位采用日前优化结果,不再参与优化.目标函数为下一时段(第t时段)内的配电网运行成本加电压越界指标.
minF2=C1,t+C2,t+C3,t+C4,t+C6,t+
(15)
2 算法求解
在优化控制变量中,变压器档位、并联电容器投切状态为离散变量,且电容器分组投切,其余变量为连续变量.
分支定界法和动态规划法是处理该类多时段非线性混合整数问题的相对准确算法,但庞大的计算量往往使得计算时间过长.
2.1 主动配电网优化调度问题分析
在对主动配电网进行优化调度计算时,第i时刻的变压器档位、并联电容器投切状态对i+1时刻的运行成本有直接影响;对i+1之后时刻的运行成本无直接影响,但通过i+1时刻产生间接影响.
储能设备的荷电量要在日前24 h内达到充放电的基本平衡.
这些因素使得各时刻之间不能达到相互独立,但主动配电网具有如下特点,可使分支定界法大幅度简化.
(1)主变之间的解耦关系.对于与大电网相联的主变,主变在低压侧解列运行,10 kV网络开环运行.所以,正常运行时,每台主变单独供电.
(2)主变低压侧母线并联电容器组之间的解耦关系.从高压主变所带10 kV线路区域来看,考虑并联电容器影响时,各区域之间无相互影响.
(3)各主变分接头之间的解耦关系.由于主变之间的解耦关系,在考虑高压主变分接头档位对低压侧影响时,各主变的分接头之间无相互影响.
(4)对于每个高压主变分接头,尽管有较多档位,但在给定运行方式下,由于10 kV侧的运行电压要求,可选用的档位数很有限.
2.2 连续变量优化(模块1)
为描述方便,优化模型统一简写为:
min F(X);
(16)
gi(X)=0;
(17)
hj,min≤hj(X)≤hj,max,
(18)
式中:X为某时刻的直角坐标形式的节点电压构成的列向量.
构成扩展拉格朗日函数:
min ![]()
(19)
式中:αi、βj为拉格朗日乘子;γ为罚因子;D为不满足约束条件的约束编号集合;hj,lim为边界值,越上界时取上界值,越下界时取下界值.
式(19)中的连续变量可表达为节点电压向量X的显函数.优化控制变量构成向量YP,YP也可表达为节点电压向量X的显函数.
最优条件为:
 L=0.
L=0.
(20)
若对式(19)采用牛顿法求解,需用到二阶海森阵,直接利用式(19)的灵敏度表达,可采用更简捷的拟牛顿法求解.
2.3 并联电容器组投切状态选择(模块2)
高压变电站10 kV母线有并联电容器组.为了考虑通用性,本项目通过目标函数对电容器节点k的无功注入Qk的一阶灵敏度来近似估计该点电容器投切引起的目标函数变化量,以此作为衡量指标SQ,k.正的指标值说明宜减少该点现有无功补偿量,而负的指标值则说明宜加大无功补偿量.指标值的大小反映了投切单位补偿量的效果.
对每个时段的所有电容器组采用如下过程处理.
(1)按指标值SQ,k对各点的补偿效果进行排序,并可分为如下两类:(a) 对正值的SQ,k按从大到小排序.考虑可否减少相应母线上的无功补偿量;(b) 对负值的SQ,k按从小到大排序.考虑在这些节点上增加无功补偿量.
(2)按排序结果对每一方案进行准确的潮流计算,计算式(1)的目标函数在该时段i的值F1i,选取最优方案.先逐一处理(a)的电容器组退出方案,再处理(b)的投入方案.
(3)依次进行,确定日前24 h内的并联电容器组投切状态.
(4)在目标函数值F1i的计算中,计入了电容器状态调节费用,即上一时段的影响.
2.4 变压器分接头档位选择(模块3)
主要考虑10 kV线路根部的主变.由于10 kV网络的辐射性运行结构,各主变10 kV侧无耦合关系,对主变分接头档位的选择,可逐台进行.变压器分接头档位主要影响10 kV的运行电压和经济性.
因此,对每个时段的每台变压器分接头档位,采用枚举法计算式(1)的目标函数在该时刻i的值F1i,选取最优档位.依次进行,完成所有时段的计算.
在目标函数值F1i的计算中,计入了档位调节费用,即上一时段的影响.
2.5 离散变量日前状态调整模块(模块4)
配电网的负荷曲线特性决定了日前24 h的主变分接头档位变化趋势.以图1为例,日前24 h内,主变分接头档位的变化曲线有两处峰值段和两处谷值段,有时可能更多.为减小档位调节成本,尝试降低峰值段的档位、抬高谷值段的档位.
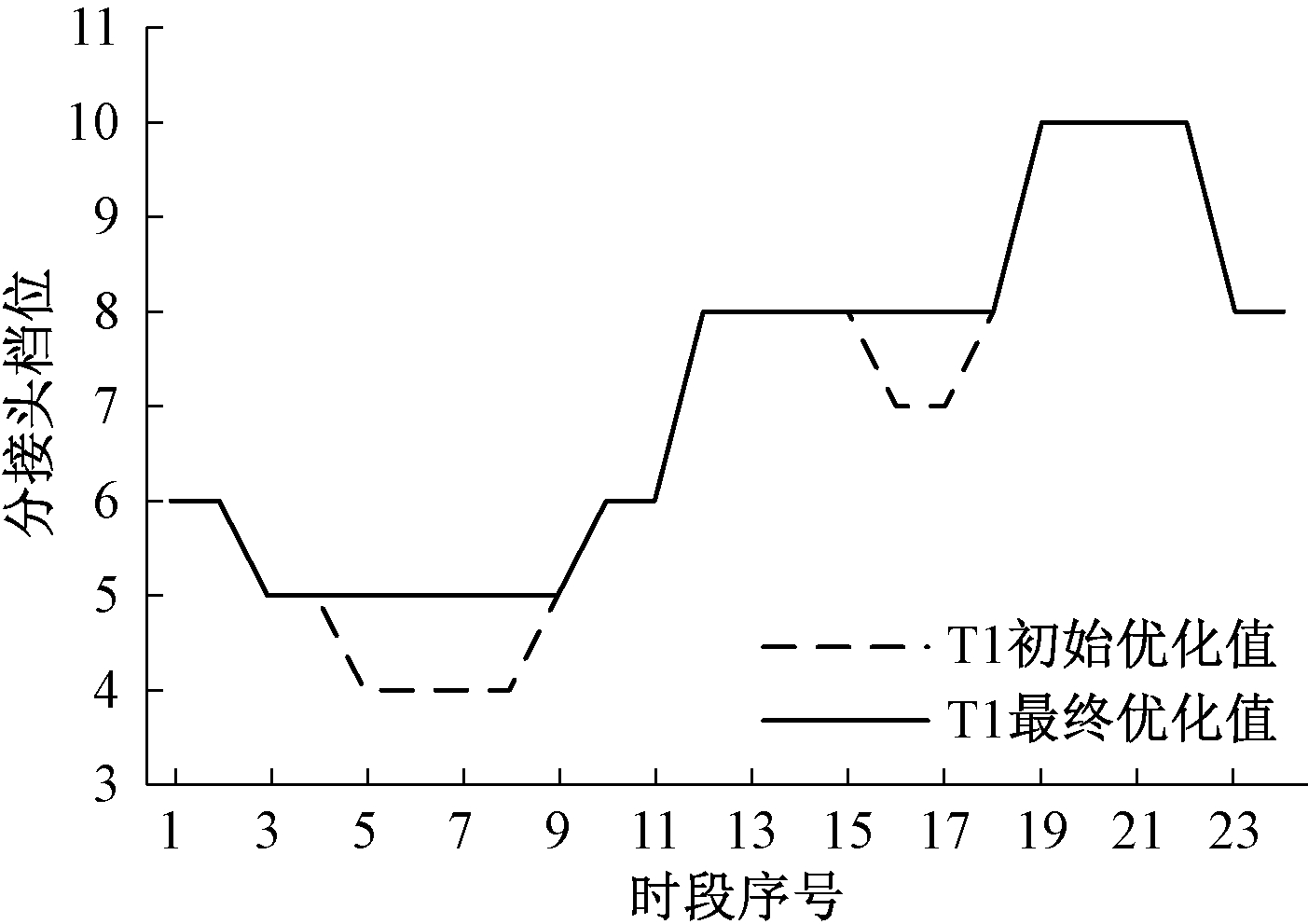
图1 主变T1的分接头档位变化
Fig.1 Variation of tap position of transformer T1
因此,对每台变压器,可采用如下步骤进行.
(1)分析档位变化曲线,确定各峰值段、谷值段的范围和值;
(2)对每一峰值段和谷值段,确定调整方案;
(3)依次处理各调整方案,对每一方案按连续变量优化模块(模块1)计算日前24 h的F1的值,F1降低时采用该方案,否则放弃.
尽管在模块1的连续变量优化过程中,比较的是扩展函数式(19),但此处取计算结束后的F1值.类似地,进行并联电容器组日前投切状态的调整.
2.6 日前调度优化过程
优化过程分为两个阶段:第一阶段为下列步骤的(1)~(4),采用迭代方式确定并联电容器组投切状态、变压器分接头档位的初值;第二阶段为下列步骤的(5)~(7),调整这些离散变量的值.
(1)按模块2选择各时段并联电容器组投切状态;
(2)按模块3选择各时段变压器分接头档位;
(3)按模块1优化各时段的连续变量;
(4)转(1),直到优化控制变量的变化量小于允许值,转(5);
(5)按模块4调整并联电容器组投切状态、变压器分接头档位的日前状态(其中反复调用模块1);
(6)对最终离散变量结果按模块1计算连续变量最终值;
(7)输出结果.
计及2.1节所述的配电网特点,采用模块化迭代处理方式.与传统的非线性混合整数动态规划算法相比,计算的运行方式数大幅度减少,从而减少计算资源的需求.
3 算例分析
3.1 算例系统
按所述算法,使用Fortran 6.5编写程序进行计算.所用算例如图2所示,在IEEE 118节点系统上增加主变和分布式电源、可调负荷.
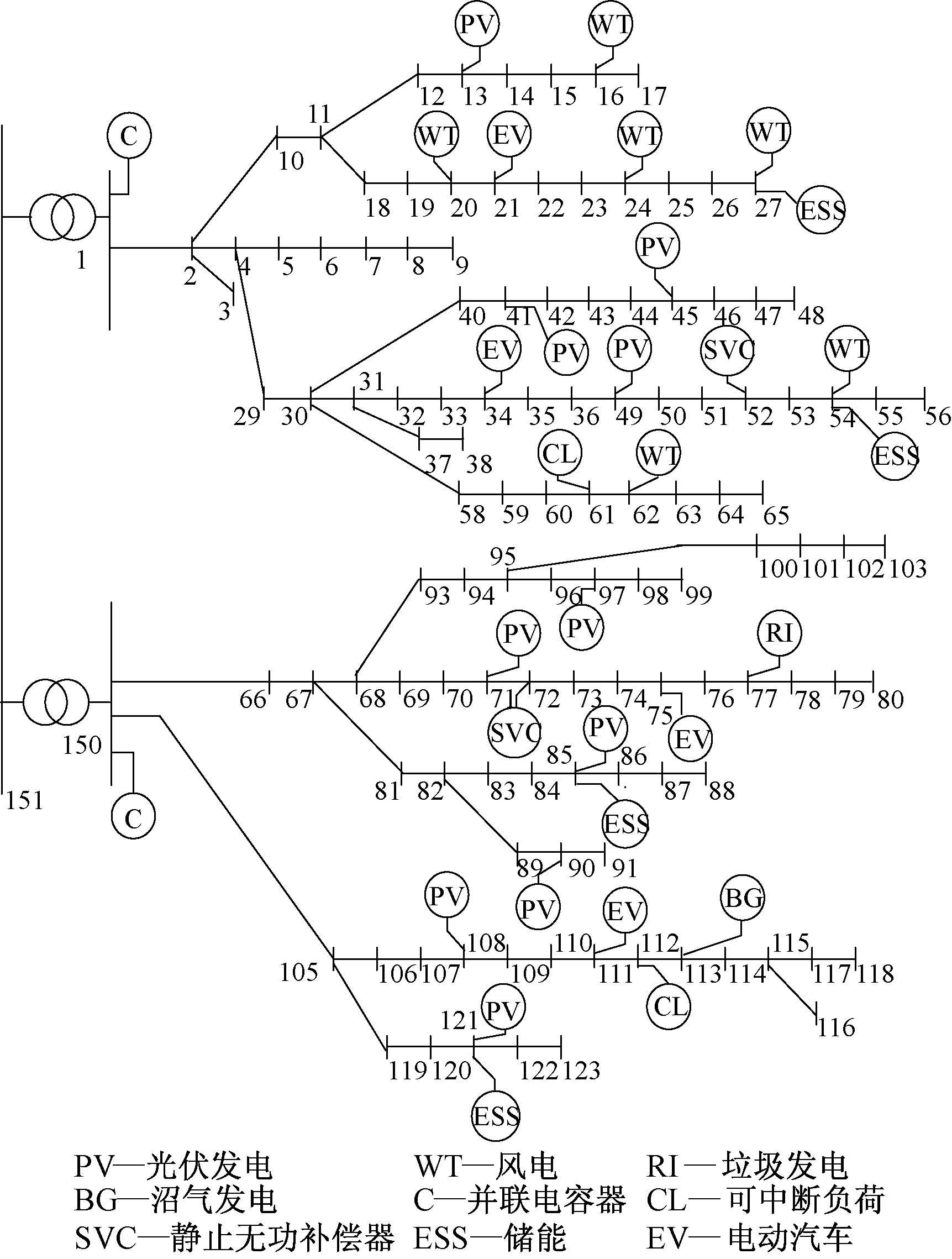
图2 10 kV配电网
Fig.2 10 kV distribution network
图2中,线路(1, 2)所联的馈线1、线路(150, 105)所联的馈线3为生活负荷,线路(150, 66)所联的馈线2为工业负荷,标准化日运行曲线(均值为1)如图3所示.
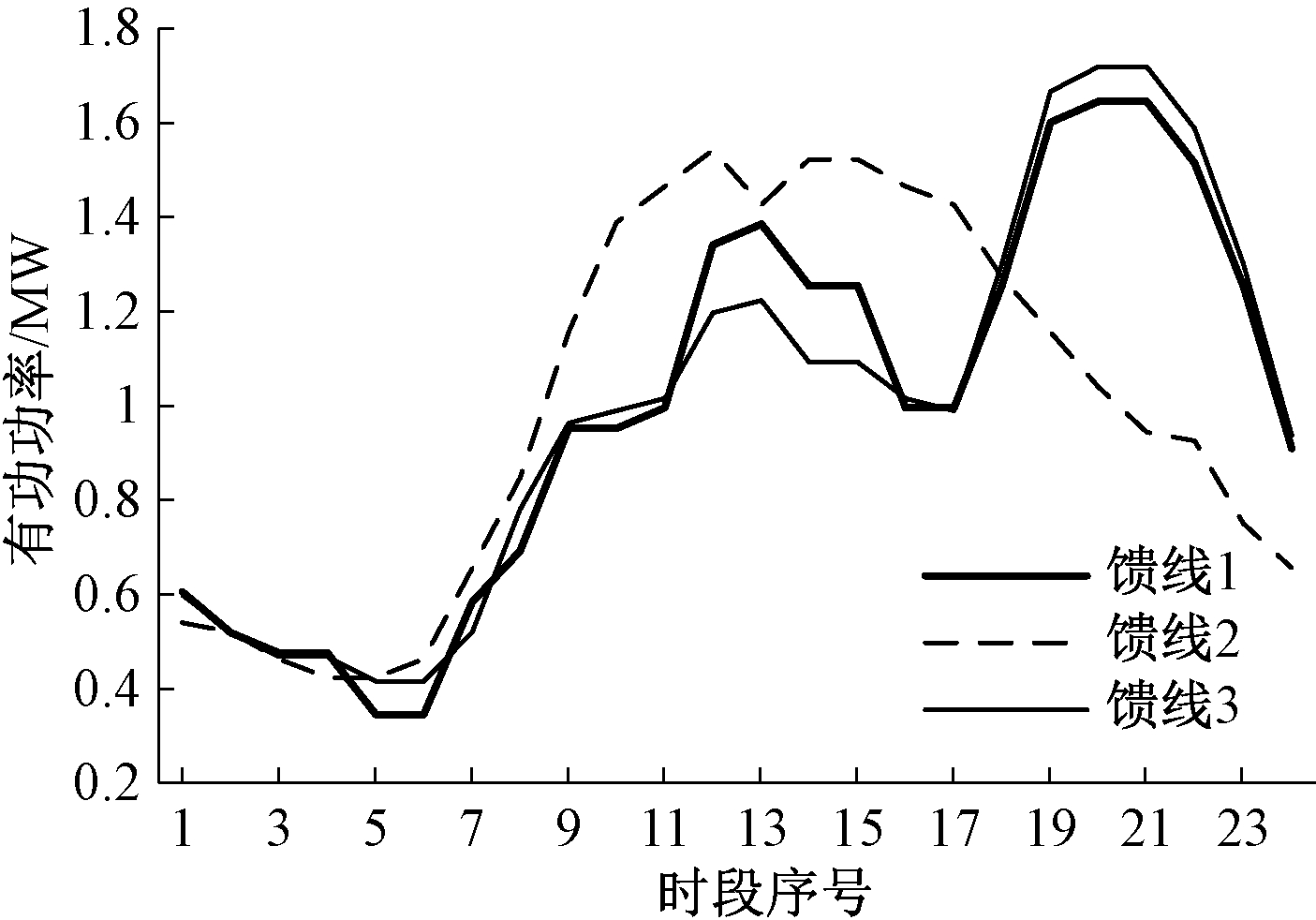
图3 3条馈线负荷标准化日运行曲线
Fig.3 Standardized daily operation curves of three feeder’s loads
110 kV变电站中,两台变压器参数为0.034 5+j0.794 Ω,额定电压和分接头为110±8×0.012 5/11 kV,高压侧分接头最高电压档位编号为1,初始运行档位7.
节点27、54、85、121的光电、风电功率均为1.2 MW,出力可调;其余节点的光电、风电功率均为0.1 MW,不可调.节点52、72的SVC容量均为0.2 Mvar.节点77的垃圾电厂、节点113的燃气电厂额定功率均为2 MW,出力可调.节点121、54、85、27接有储能设备,额定容量均为1 MW·h,最大充放电功率0.4 MW,荷电下限20%,荷电上限90%,荷电初值40%.节点21、33、75、111的电动汽车日平均负荷均为0.6 MW.节点61、112的可调负荷功率分别为0.55+j0.35MVA、0.49+j0.42MVA.部分标准化日运行曲线如图4所示.
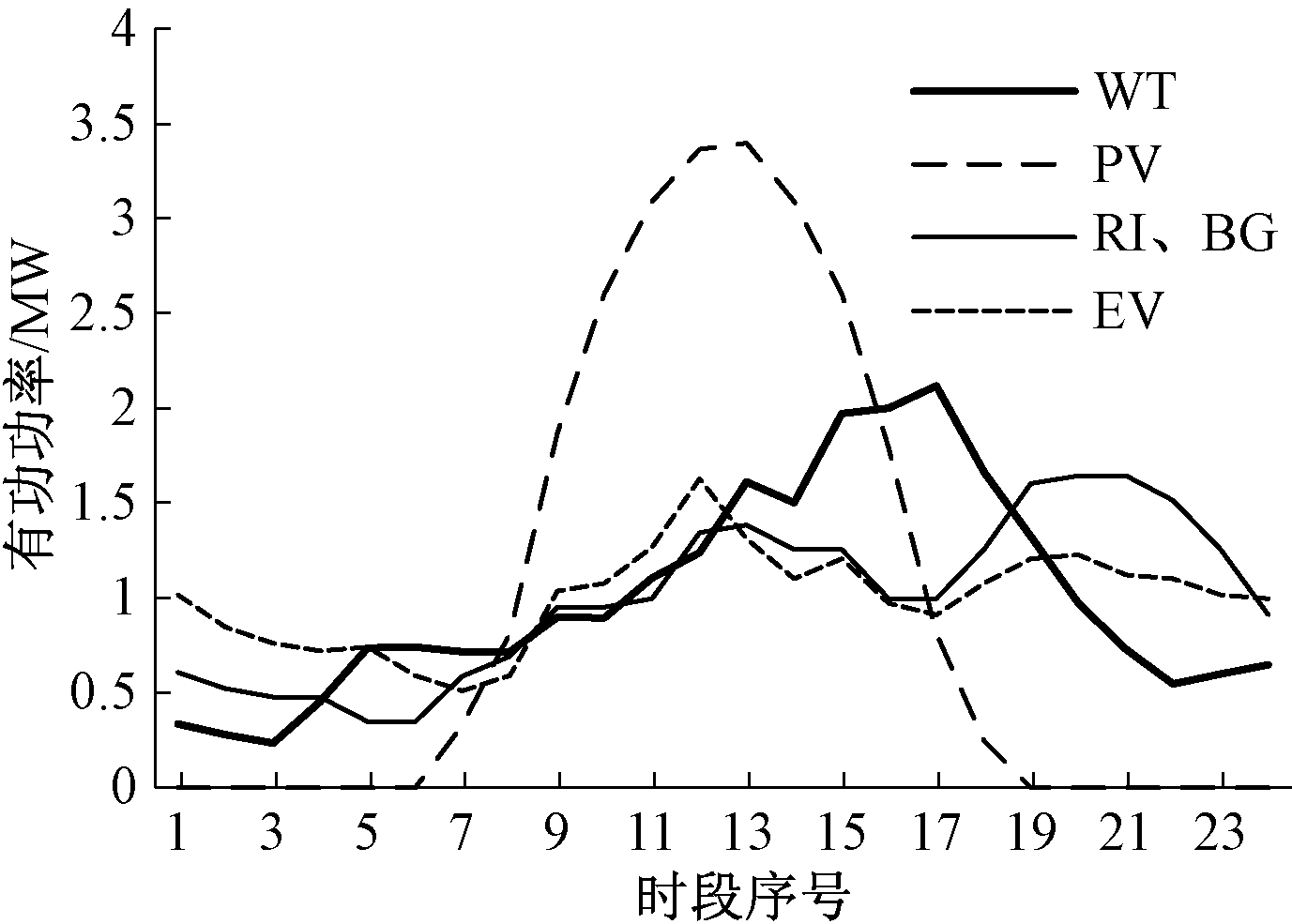
图4 分布式发电和电动汽车标准化日运行曲线
Fig.4 Standardized daily operation curves of distributed generation and electric vehicle
风电上网电价取0.60元/(kW·h),光伏上网电价取1.00元/(kW·h),微型燃气轮机的发电成本为0.66元/(kW·h).主动配电网与上级电网间的电能交易采用峰谷平电价制,1:00~7:00为0.49元,8:00~17:00、23:00~24:00为0.74元,18:00~22:00为0.98元.离散变量调节成本系数[12]取Ktap=20元/档,KC=2元/次.其他成本参数:Kcomp=1.5,Kloss,t=Kgrit,t,KCL,i=0.8元/(kW·h),KESS,i=0.05元/(kW·h).
3.2 日前运行方式优化
日前优化阶段的时间间隔ΔT为1 h.按照第1、2节的算法进行计算.
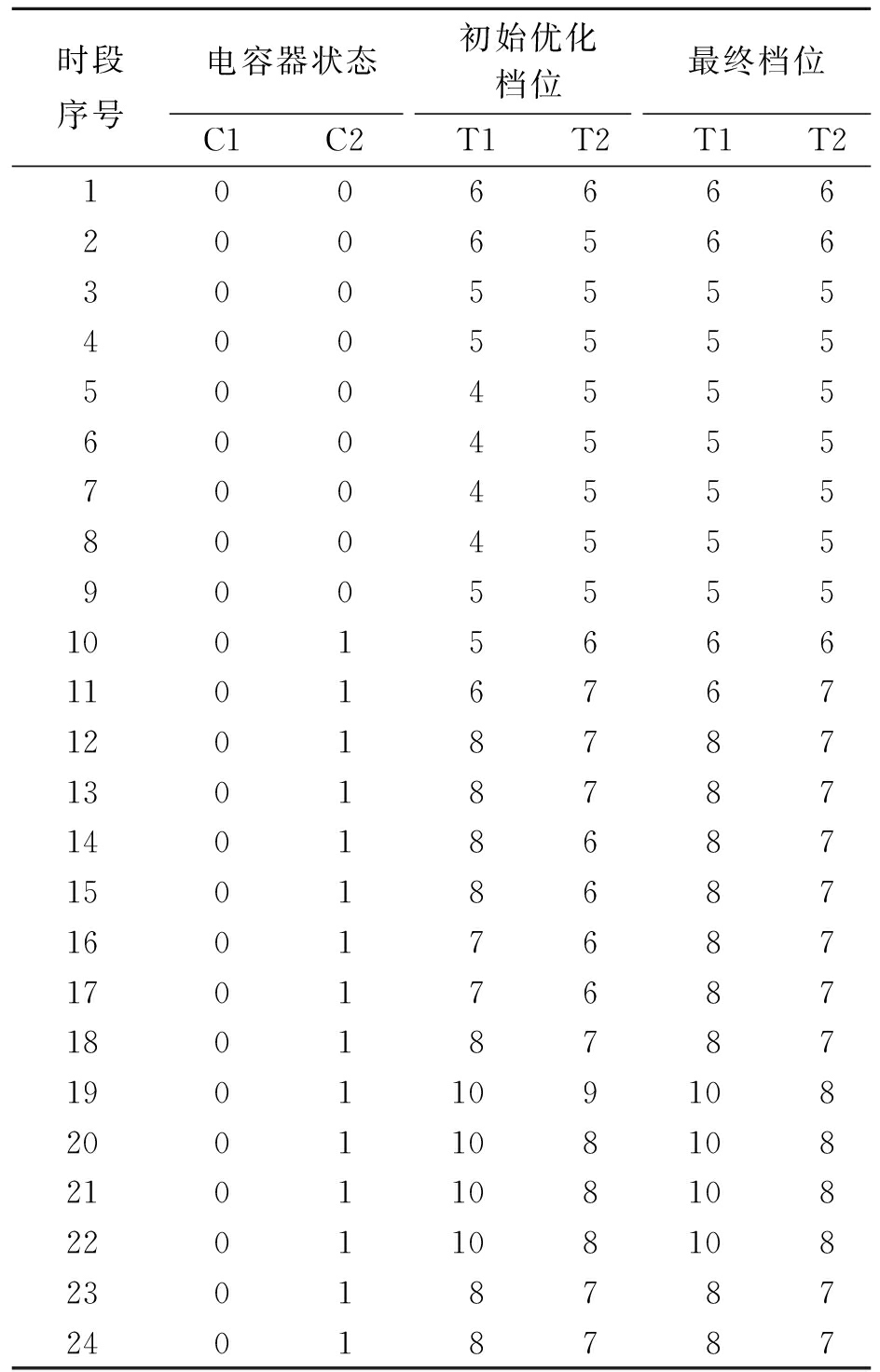
(1)电容器组.经第2.6节过程(1)计算得到的并联电容器组投切状态的结果列于表1的第2、3列,其中1表示投,0表示切.节点1的电容器C1对应于馈线1,全处于切除状态.节点150的电容器C2对应于馈线2、3.由于两类负荷曲线的存在,该电容器在高负荷时段投入,但为满足线路电压的要求而在低负荷时段切除.
表1 电容器、变压器分接头状态
Tab.1 State of capacitors and transformer taps
时段序号电容器状态初始优化档位最终档位C1C2T1T2T1T210066662006566300555540055555004555600455570045558004555900555510015666110167671201878713018787140186871501868716017687170176871801878719011091082001108108210110810822011081082301878724018787
再按第2.6节过程(2)的方法进行调整.尝试调节C2的运行状态,产生两种方案:(a)第9时段开始投入,(b)第11时段开始投入.目标函数F1均变大,维持原结果.
(2)变压器分接头档位.经第2.6节过程(1)确定的两台主变分接头档位结果列于表1的第4、5列.两台主变的分接头变化趋势基本一致.高峰负荷时段取较高档位,抬高10 kV侧电压;其他负荷时段取较低档位,减缓10 kV线路的过电压.
再按第2.6节过程(2)的方法进行调整.结果列于表1的第6、7列.对T1的档位调整如图1所示,调整了两处低谷段的档位.
(3)优化前后指标.表2列出优化前后指标情况.其中第1列为式(1)中的目标函数,优化时采用第2列为式(1)中的经济指标,即配电网的运行成本,供比较.优化前的目标函数大于经济指标,说明有电压越界.电压越界的权重系数为1 000,以表示对电压越界的较重惩罚.优化后二者接近,基本满足电压要求.通过优化,一天减少运行成本0.35万元,其中网损下降0.36 MW·h.
表2 优化前后指标
Tab.2 Indices before and after optimization
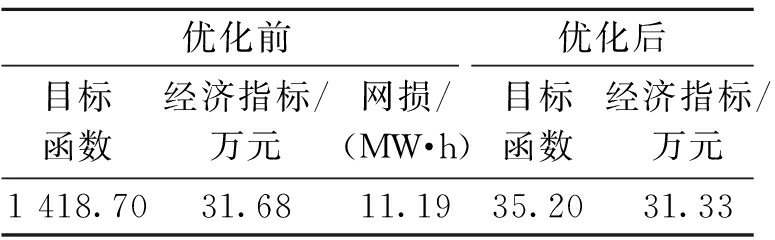
优化前优化后目标函数经济指标/万元网损/(MW·h)目标函数经济指标/万元网损/(MW·h)1 418.7031.6811.1935.2031.3310.83
表3列出优化后其他指标.新能源的平均渗透率为33.06%,最大渗透率达到47.97%.
表3 优化后指标
Tab.3 Indices after optimization
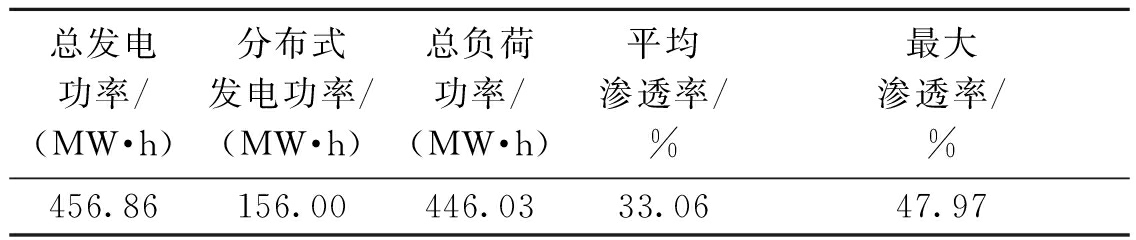
总发电功率/(MW·h)分布式发电功率/(MW·h)总负荷功率/(MW·h)平均渗透率/%最大渗透率/%456.86156.00446.0333.0647.97
(4)各时段指标.表4列出各时段指标优化前后指标情况.优化前,大部分时段的目标函数F1大于经济指标,例如第9~12时段,说明有电压越界现象,优化过程同时处理经济性和电压安全性;在部分时段二者相等,优化的主要工作放在改善经济性,优化后的经济指标下降.优化后,满足电压运行要求.
由于分布式电源运行条件的限制,最小渗透率仅为第3时段的18.54%,最大渗透率为第16时段的47.97%.
(5)运行电压.图5为节点27的24 h电压.节点27为馈线1的末端节点之一,接有风力发电机,低负荷时容易出现过电压,所以同时接有储能设备ESS.节点电压第11时段电压最低,在低负荷时段和风机最大出力时段电压较高,例如第4~6时段、第14~17、19时段.优化后电压满足要求.
(6)储能设备荷电状态.图6给出储能设备荷电状态,图例名的末端数字为所在节点号.初始状态为40%,低负荷时段充电,高负荷时段放电,最终荷电状态接近于40%.
3.3 日内滚动优化
日内优化阶段的时间间隔ΔT为15 min,不再对电容器投切状态和变压器分接头档位进行调整,直接取日前优化结果.因此目标函数中不再考虑电容器状态和变压器档位的调整费用.
表4 各时段指标
Tab.4 Indices of all time intervals
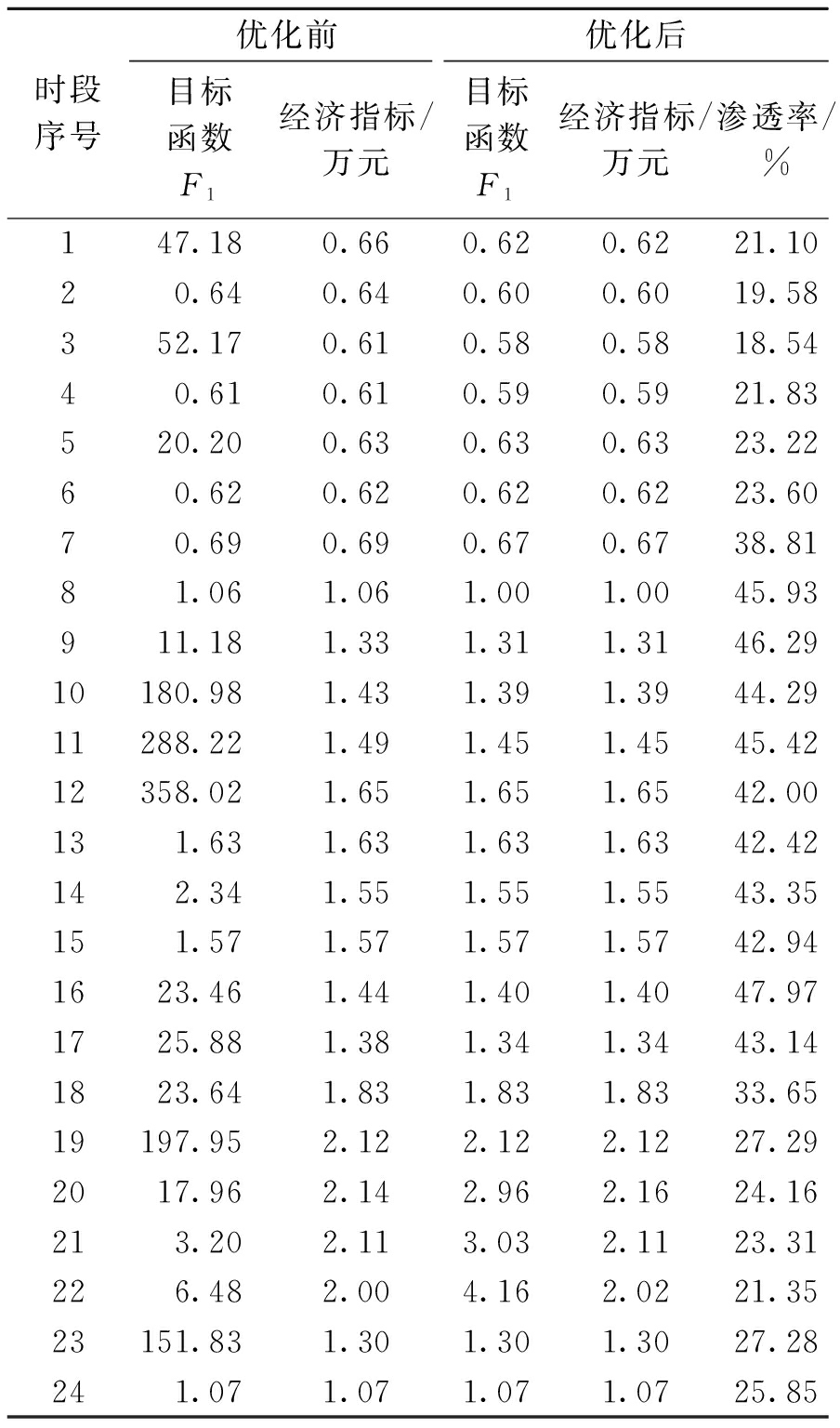
时段序号优化前优化后目标函数F1经济指标/万元目标函数F1经济指标/万元渗透率/%147.180.660.620.6221.1020.640.640.600.6019.58352.170.610.580.5818.5440.610.610.590.5921.83520.200.630.630.6323.2260.620.620.620.6223.6070.690.690.670.6738.8181.061.061.001.0045.93911.181.331.311.3146.2910180.981.431.391.3944.2911288.221.491.451.4545.4212358.021.651.651.6542.00131.631.631.631.6342.42142.341.551.551.5543.35151.571.571.571.5742.941623.461.441.401.4047.971725.881.381.341.3443.141823.641.831.831.8333.6519197.952.122.122.1227.292017.962.142.962.1624.16213.202.113.032.1123.31226.482.004.162.0221.3523151.831.301.301.3027.28241.071.071.071.0725.85
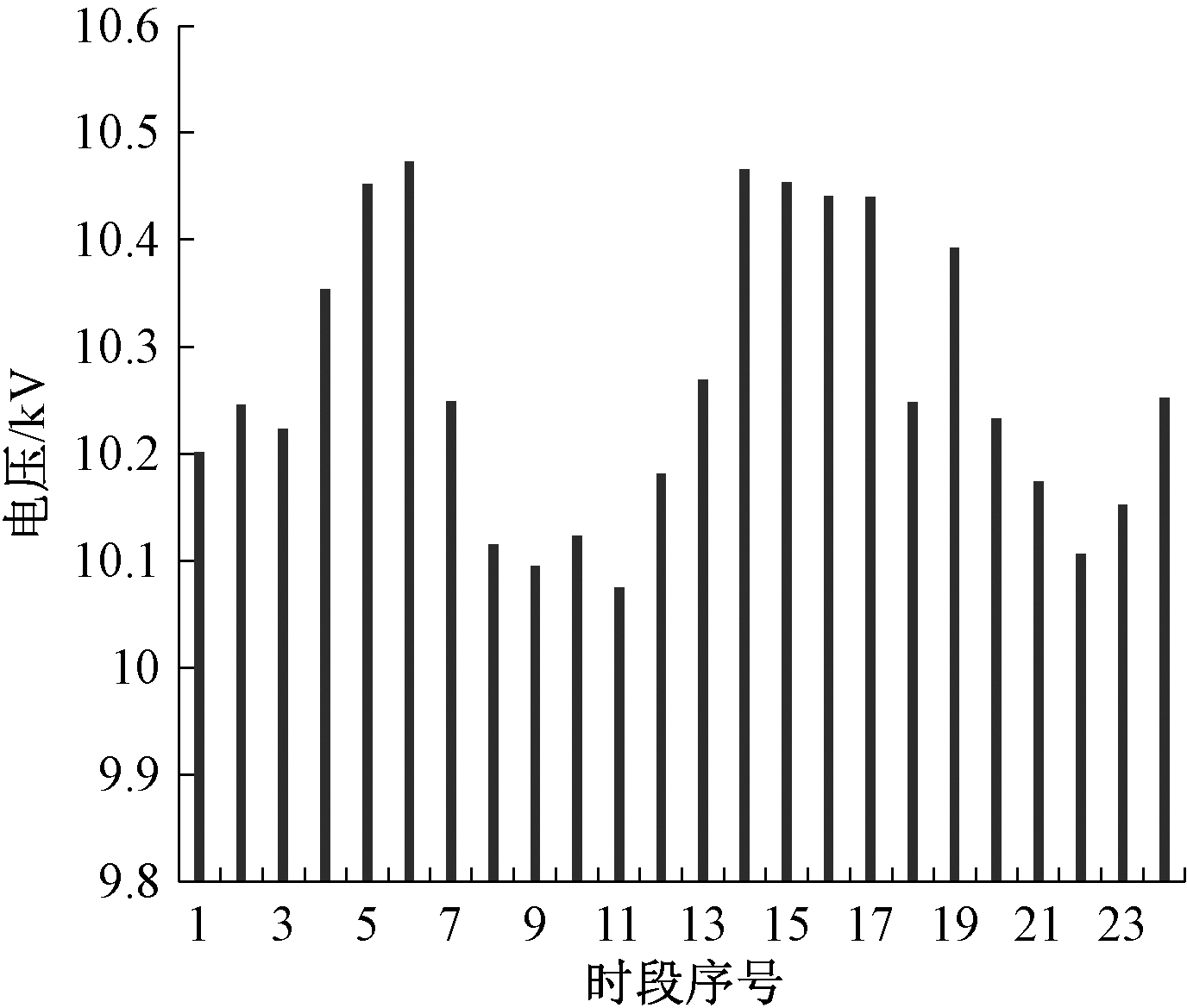
图5 节点27的24 h内电压
Fig.5 Voltages of node 27 in 24 hours
部分时段指标结果列于表5.目标函数F2同时包含经济性、电压安全性指标,优化时采用,经济指标仅为配电网的运行成本.二者之差描述了电压越界的程度.
由于已采用日前优化的电容器投切状态和变压器分接头档位值,在表5中,电压越界状况(第2、3列之差)比表4中的小得多,说明电压越界问题已不太严重,但仍存在.
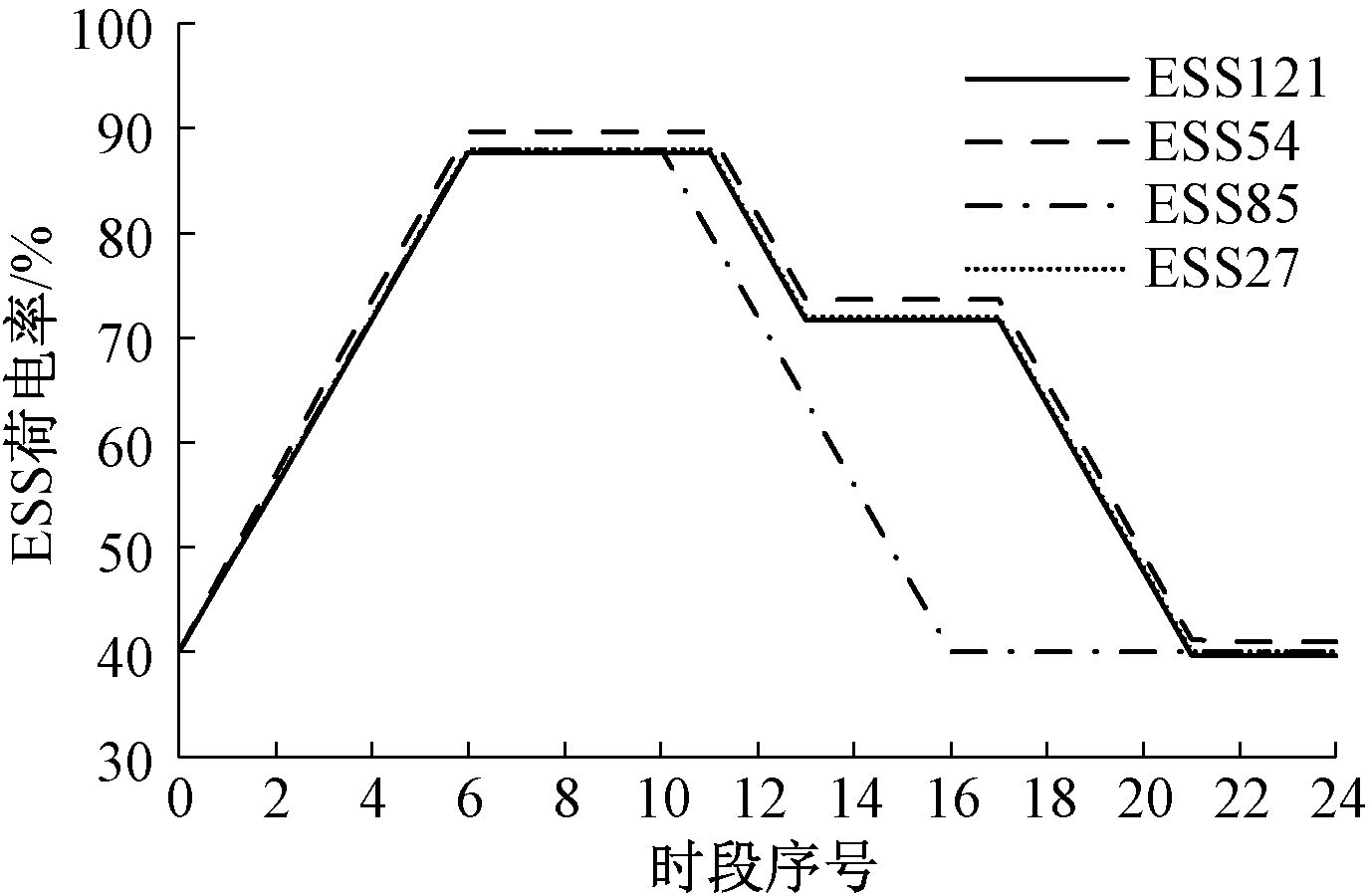
图6 储能设备荷电状态
Fig.6 Charged state of energy storage equipment
表5 部分时段指标
Tab.5 Indices of partial time intervals
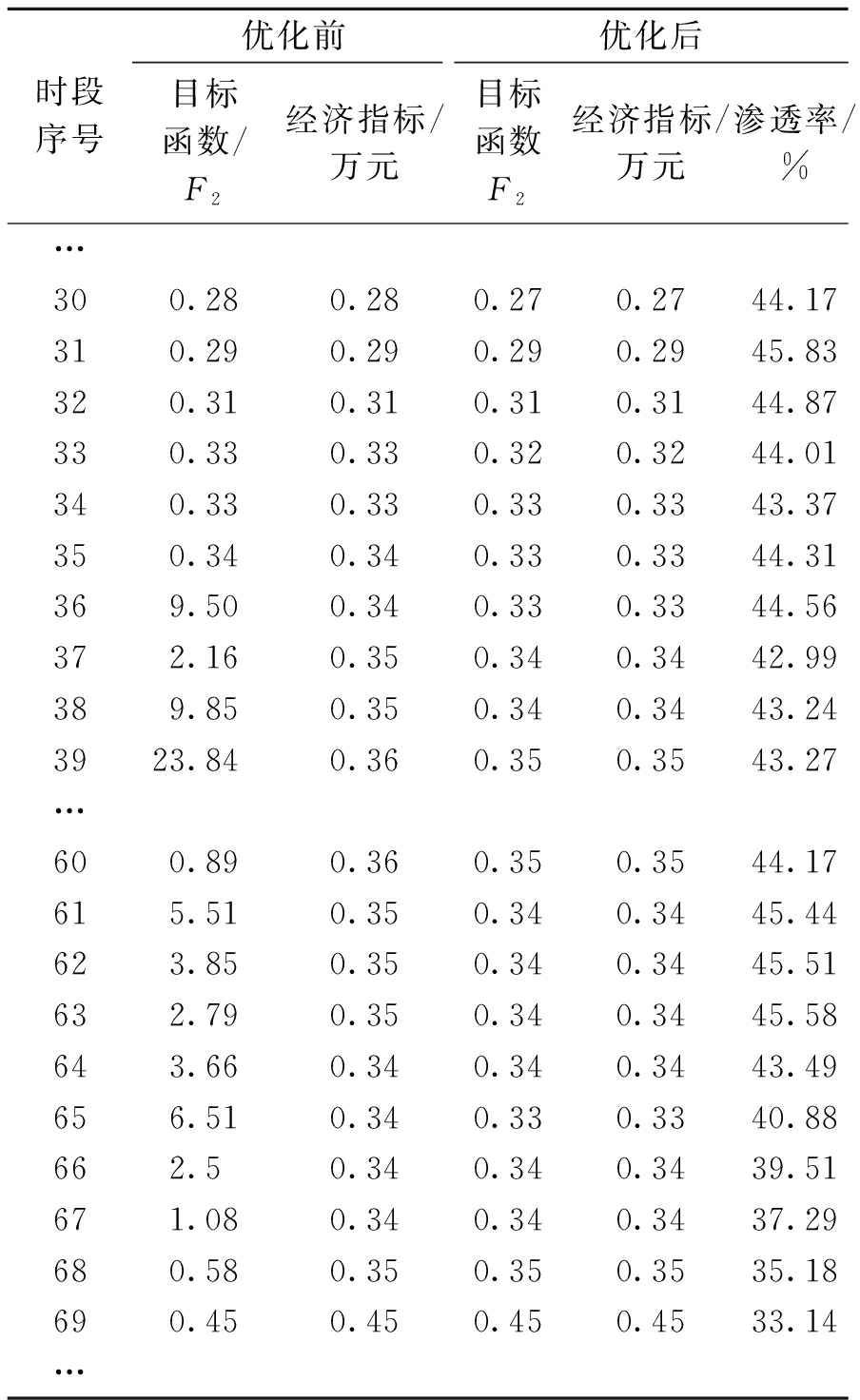
时段序号优化前优化后目标函数/F2经济指标/万元目标函数F2经济指标/万元渗透率/%…300.280.280.270.2744.17310.290.290.290.2945.83320.310.310.310.3144.87330.330.330.320.3244.01340.330.330.330.3343.37350.340.340.330.3344.31369.500.340.330.3344.56372.160.350.340.3442.99389.850.350.340.3443.243923.840.360.350.3543.27…600.890.360.350.3544.17615.510.350.340.3445.44623.850.350.340.3445.51632.790.350.340.3445.58643.660.340.340.3443.49656.510.340.330.3340.88662.50.340.340.3439.51671.080.340.340.3437.29680.580.350.350.3535.18690.450.450.450.4533.14…
优化的目的是使F2下降.当无电压越界时,例如时段30~34,优化过程主要使得经济指标下降,但下降程度各有不同.
当存在电压越界时,例如时段38、39,优化过程需同时考虑经济指标和电压指标.由于电压指标的权重系数值较大,使得电压约束优先满足.甚至在个别极端情况下,存在F2下降,但经济指标略有上升的可能.
优化后的运行方式,均满足各约束条件,运行成本下降.
4 结论
笔者考虑多种分布式电源、SVC、可控负荷、储能设备,以配电网运行成本和电压合格率最小建立主动配电网日前、日内的有功无功协调优化模型.结合配电网和优化模型的特点,笔者建立相应的有效求解模块,可实现对优化模型的大幅度简化,并通过模块间的迭代实现总体最优,具有计算资源需求上的明显优势,是一种实用的处理方式.
[1] 刘一兵, 吴文传, 张伯明, 等. 基于混合整数二阶锥规划的主动配电网有功-无功协调多时段优化运行[J]. 中国电机工程学报, 2014, 34(16): 2575-2583.
[2] 符杨, 廖剑波, 李振坤, 等. 考虑越界风险的主动配电网日前优化调度及运行[J]. 中国电机工程学报, 2017, 37(21): 6328-6336.
[3] 任佳依, 顾伟, 王勇, 等. 基于模型预测控制的主动配电网多时间尺度有功无功协调调度[J]. 中国电机工程学报, 2018, 38(5): 1397-1407.
[4] 张世达, 孙永辉, 卫志农, 等. 考虑可控光伏系统概率模型的主动配电网日前优化调度[J]. 电网技术, 2018, 42(1): 247-253.
[5] 尤毅, 刘东, 钟清, 等. 主动配电网优化调度策略研究[J]. 电力系统自动化, 2014, 38(9):177-183.
[6] SOROUDI A, SIANO P, KEANE A. Optimal DR and ESS scheduling for distribution losses payments minimization under electricity price uncertainty[J]. IEEE transactions on smart grid, 2016, 7(1):261-272.
[7] 窦震海, 牛焕娜, 高燕, 等. 主动型配电网日前调度策略研究[J]. 农业工程学报, 2014, 30(11):126-133.
[8] 廖剑波,李振坤,符杨. “源-网-荷”相协调的主动配电网经济调度[J]. 电力系统及其自动化学报, 2018, 30(1):69-75.
[9] 曾博,杨煦,张建华. 考虑可再生能源跨区域消纳的主动配电网多目标优化调度[J]. 电工技术学报, 2016, 31(22): 148-158.
[10] 黄伟, 熊伟鹏, 闫彬禹, 等. 不同时间尺度下虚拟微网优化调度策略[J]. 电力系统自动化, 2017, 41(19): 12-19.
[11] 曾鸣, 彭丽霖, 王丽华, 等. 主动配电网下分布式能源系统双层双阶段调度优化模型[J]. 电力自动化设备, 2016, 36(6):108-115.
[12] 周晓娟, 王奎英, 张将. 基于辅助函数思想的城市高压电网无功优化[J]. 郑州大学学报(工学版), 2014, 35(4): 79-82.