损失率和综合换热性能评价因子的影响.结合数值模型制作了实验模型并开展了性能测试，将测得的实验数据和模拟结果进行了对比，结果表明,在研究范围内，当管径为6 mm、层间距为3.5 mm、轴向间距为14 mm时，综合换热性能评价因子有最大值，温度差值、压力降模拟结果与实验数据相差1～4 ℃、0.8～1.2 kPa.摘 要： 针对绕管式换热器的结构参数，建立不同管径(6 mm<d0<14 mm)、不同层间距(2 mm<S2<4.5 mm)和不同轴向间距(2 mm<Z<14 mm)的绕管式换热器的两层绕管几何模型.以水为换热介质，应用Fluent中Realizable k-ε湍流模型对绕管式换热器的壳侧流体的流动及换热特性进行了数值模拟，分析了管径、层间距和轴向间距对努赛尔数、场协同数、损失率和综合换热性能评价因子的影响.结合数值模型制作了实验模型并开展了性能测试，将测得的实验数据和模拟结果进行了对比，结果表明,在研究范围内，当管径为6 mm、层间距为3.5 mm、轴向间距为14 mm时，综合换热性能评价因子有最大值，温度差值、压力降模拟结果与实验数据相差1～4 ℃、0.8～1.2 kPa.
绕管式换热器是一种新型高效换热器，它以安全、高效、占地面积小和单位体积换热面积大等特点受到了众多研究者和消费者的青睐[1].阳大清等[2]采用数值模拟的方法对缠绕管式换热器壳侧流动进行分析，发现绕管式换热器壳侧流体流动时，流线呈弯曲状;魏江涛等[3]、贾金才[4]通过数值模拟的方法对绕管式换热器壳侧流体的流动和传热进行了研究，对其内部结构进行了优化，结果表明，随着径向比增大、轴向比减小，传热系数逐渐减小，而缠绕角、缠绕圈数对传热系数影响较小;Lu等[5]应用数值模拟的方法对绕管式换热器的壳侧流体流动状况进行了研究，并根据研究结果整合出努赛尔数Nu、阻力系数f的关联式;Ghorbani等[6]采用实验的方法分析了螺旋管缠绕直径比、螺旋节距在不同雷诺数Re下对壳侧换热系数的影响，拟合出了在不同努赛尔数下，特征长度的求解公式.
笔者对前人的研究结果进行分析发现，绕管式换热器中换热管的管径、轴向间距及层间距是影响换热器壳侧换热性能的主要因素.为了使绕管式换热器得到较好的换热效果，针对上述3个因素建立了不同的几何模型，并进行了数值模拟，用换热器的综合换热性能评价因子和理论对其进行了分析评价，最后将模拟结果与实验数据进行对比.
建立如图1(a)中所示的不同管径(6 mm<d0<14 mm)、不同层间距(2 mm<S2<4.5 mm)和不同轴向间距(2 mm<Z<14 mm)的绕管式换热器的局部结构几何模型，换热管缠绕两层，每层6根同时缠绕，内外层换热管的缠绕方向相反，各个参数对应的绕管式换热器位置如图1(b)所示.
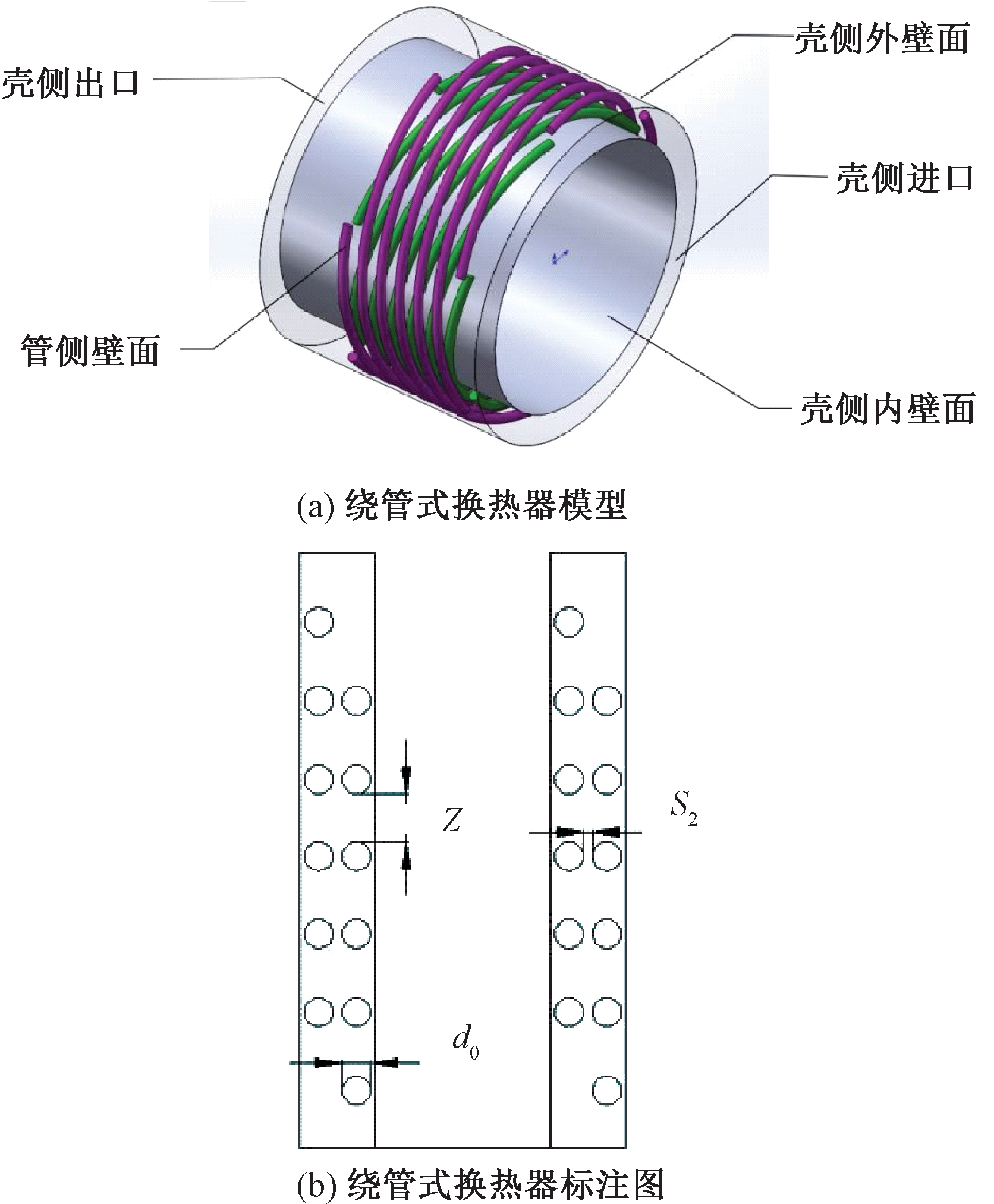
图1 绕管式换热器的局部结构几何模型及具体尺寸
Fig.1 The local structure geometry model and the specific size of spiral tube heat exchanger
根据实际情况对物理模型进行合理假设：①流体为不可压缩流体，物性参数不随温度变化；②流体的流动剪应力大于重力作用，故忽略重力影响；③流体的流动及传热过程均为稳态；④忽略热辐射的影响；⑤流体与壁面之间为无滑移壁面.
壳侧流体流动复杂且包含湍流，采用SIMPLEC算法进行压力-速度耦合，差分格式采用二阶迎风格式，设置收敛精度为10-6，边界条件如下.
进口：壳侧进口(inlet)边界类型为速度进口，速度范围为0.23～1.1 m/s，设置进口温度为293 K.
出口：壳侧出口(outlet)的边界类型为压力出口.
壁面：壳侧内外壁面设定为无滑移的绝热边界，管侧壁面设定为恒壁温，温度为360 K.
Fluent提供的k-ε模型包括：Standard k-ε模型、RNG k-ε模型、Realizable k-ε模型.为了验证这3种湍流模型在模拟中的正确性，分别采用以上3种模型计算努赛尔数Nu，表1所示为不同模型模拟结果与螺旋流道时壳侧努赛尔数Nu关联式中[7-9]计算结果的对比,关联式如式(1)所示.在文献[7]中，壳侧流体的流动轮廓可近似认为是流体流过螺旋形通道外侧，与本数值模拟中湍流的流动状态及大致流型相同，不同点在于在文献[7]中，螺旋管管径及管间距均小于本数值模拟.从表1中可以看出，Realizable k-ε 模型模拟结果和文献中关联式的计算结果最为接近.因此本次模拟采用Realizable k-ε模型.
Nu=0.27Re0.63Pr0.36， Re<200 000.
(1)
表1 3种湍流模型的计算结果
Tab.1 Calculation results of three turbulence models
模型标准k-ε湍流k-ε可实行的k-εNu关联式中计算结果Nu125.29116.20122.83122.77
(1)不同管径条件下的结果分析.图2所示为垂直流动方向(a)和沿着流动方向(b)截面的速度矢量图，从(a)中可以看出,在垂直流动方向截面上形成大量的速度漩涡、二次流；从(b)中可以看出，不同层之间的流体发生剧烈的相互掺混.流体在流动过程中形成的速度漩涡及流体的相互掺混，对换热管壁附近的流体形成巨大的冲刷作用，使边界层变薄，传热热阻减小.
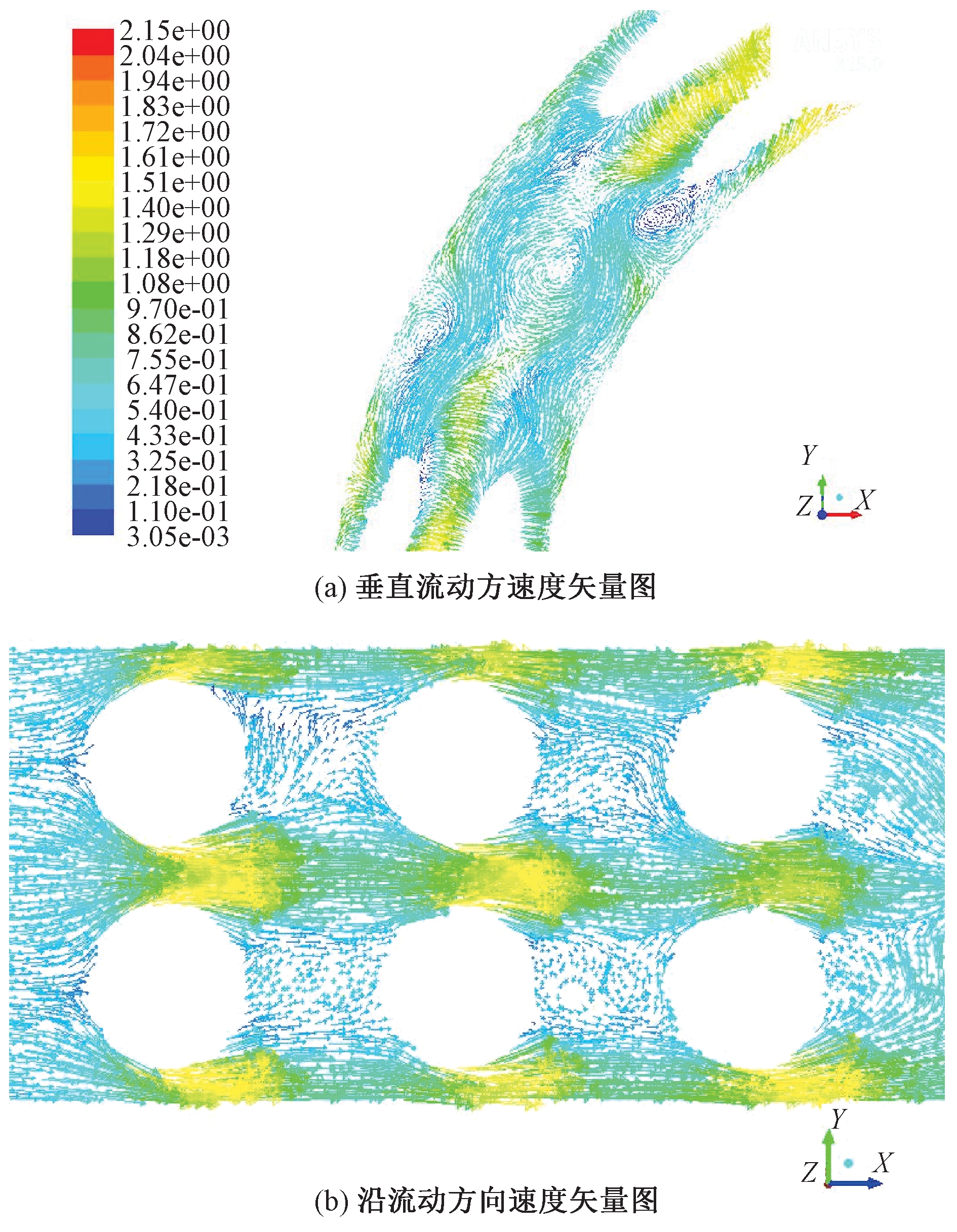
图2 壳侧不同截面的速度矢量图
Fig.2 Velocity vector diagram of different sections of the shell side
图3为绕管式换热器在实验的管径范围内的Nu的变化曲线，图4为场协同数的变化曲线，从图3、4中可得努赛尔数Nu和场协同数随着换热管管径的增大而减小，所以说管径越小，壳侧流体的换热系数越大.场协同数[10-11]表示壳侧流体的速度场和温度梯度场协同程度，其值越大说明整个流场的换热效果越好.随着管径变大，场协同数呈逐渐减小趋势，所以说管径越小换热器的换热效果越好.
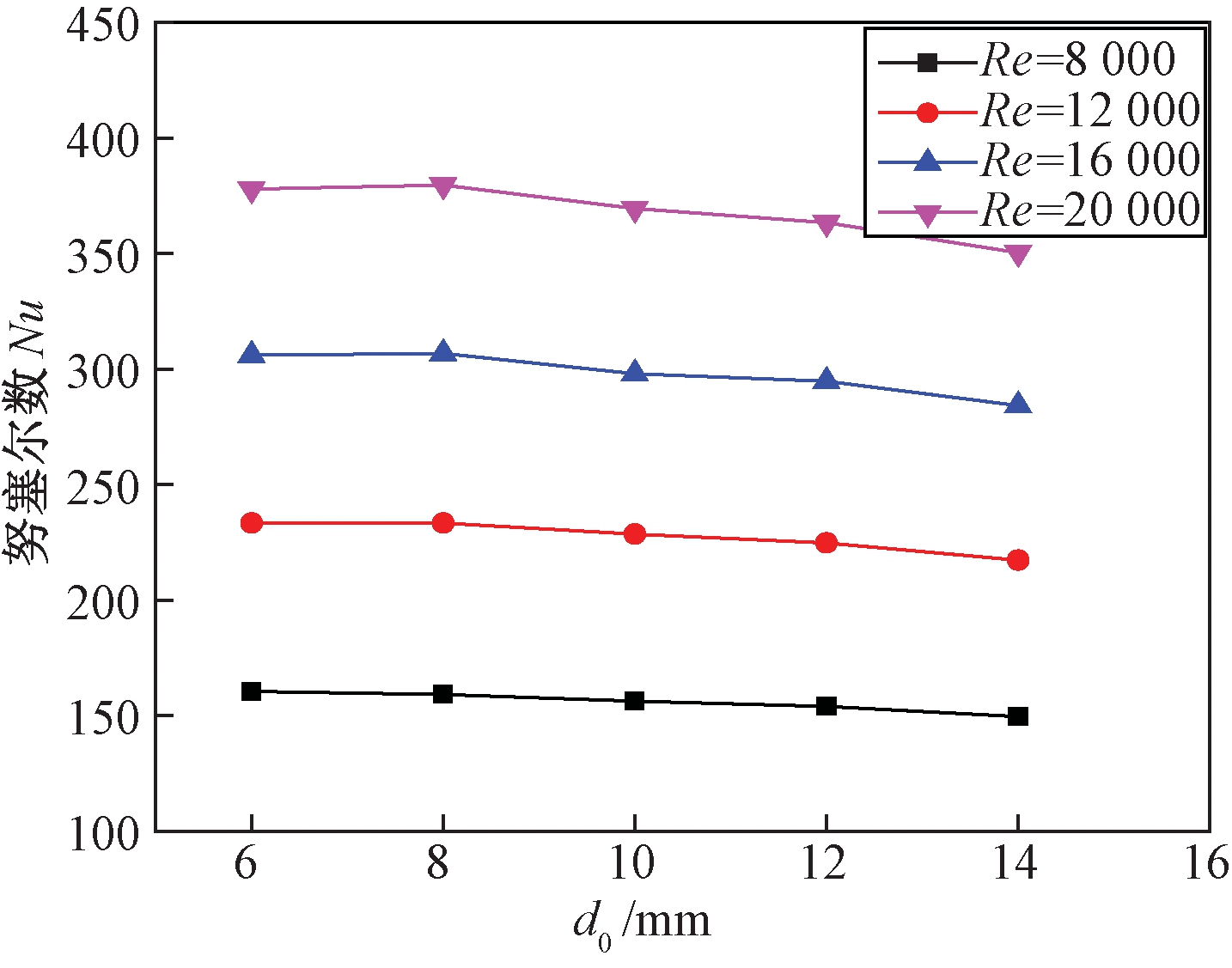
图3 努赛尔数Nu与管径关系
Fig.3 Influence of diameter on Nusselt number
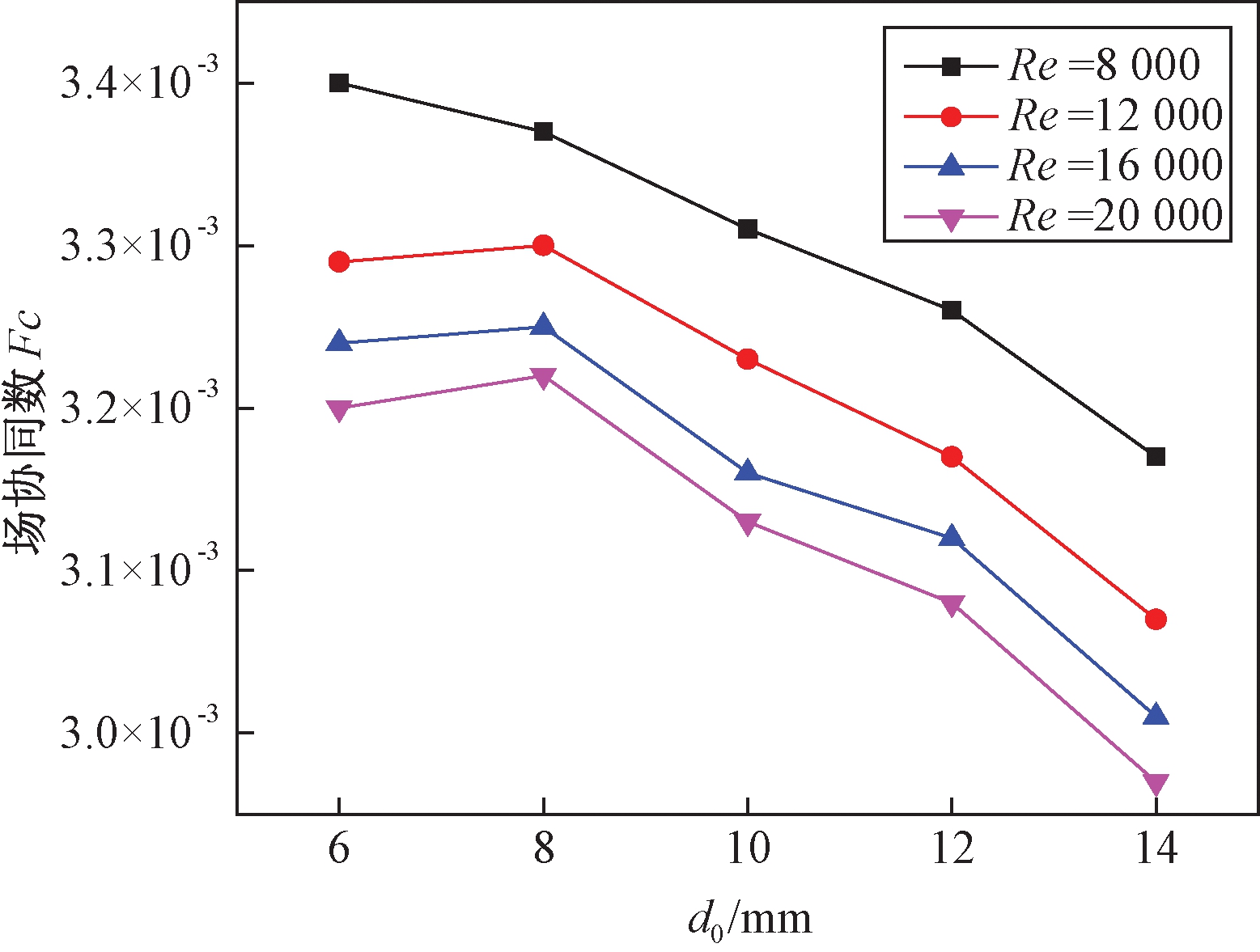
图4 场协同数与管径关系
Fig.4 Influence of diameter on synergetic number
损失率[10]和热阻[12-13]分别表示的是换热过程中损失的占换热过程流入总的比例和单位换热量下的耗散.图5是绕管式换热器在不同管径条件下损失率随管径和Re的变化关系图.从图5可以看出，随着换热管管径的增大，损失率呈增大的趋势，其值越大，说明换热过程中的热量损失越多，热阻越大，对换热过程越不利.该结论同样验证了前文中在研究的管径范围内小管径换热器的换热系数较大的结论.
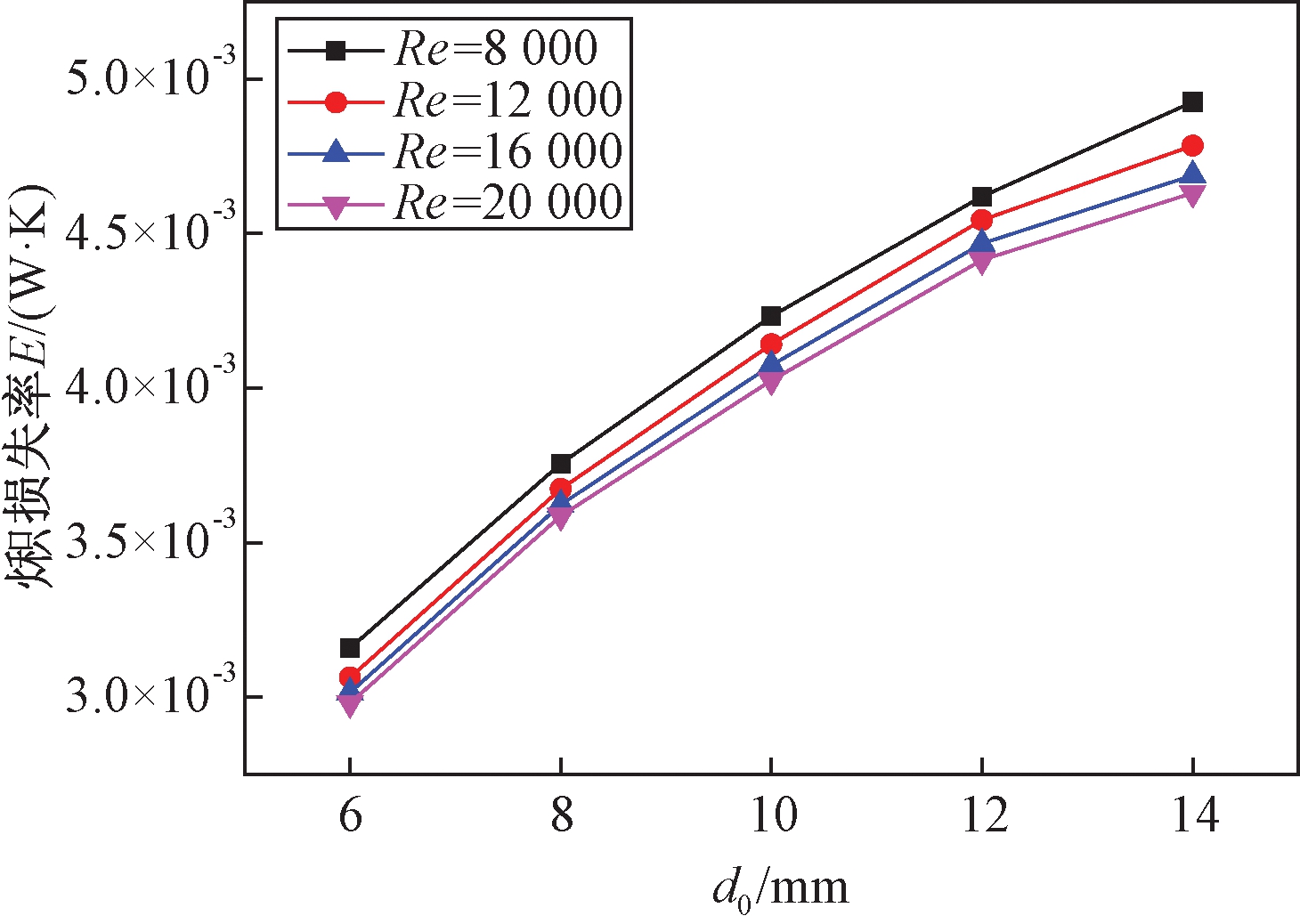
图5 损失率与管径的关系
Fig.5 Influence of diameter on entransy
图6为绕管式换热器的壳侧流体在不同管径下换热器的综合换热性能评价因子P的变化曲线.从图6中可以看出，在相同的Re条件下，P值随着管径的减小而增大，说明换热管径越小，强化换热效果越好，换热器的综合换热性能越好.
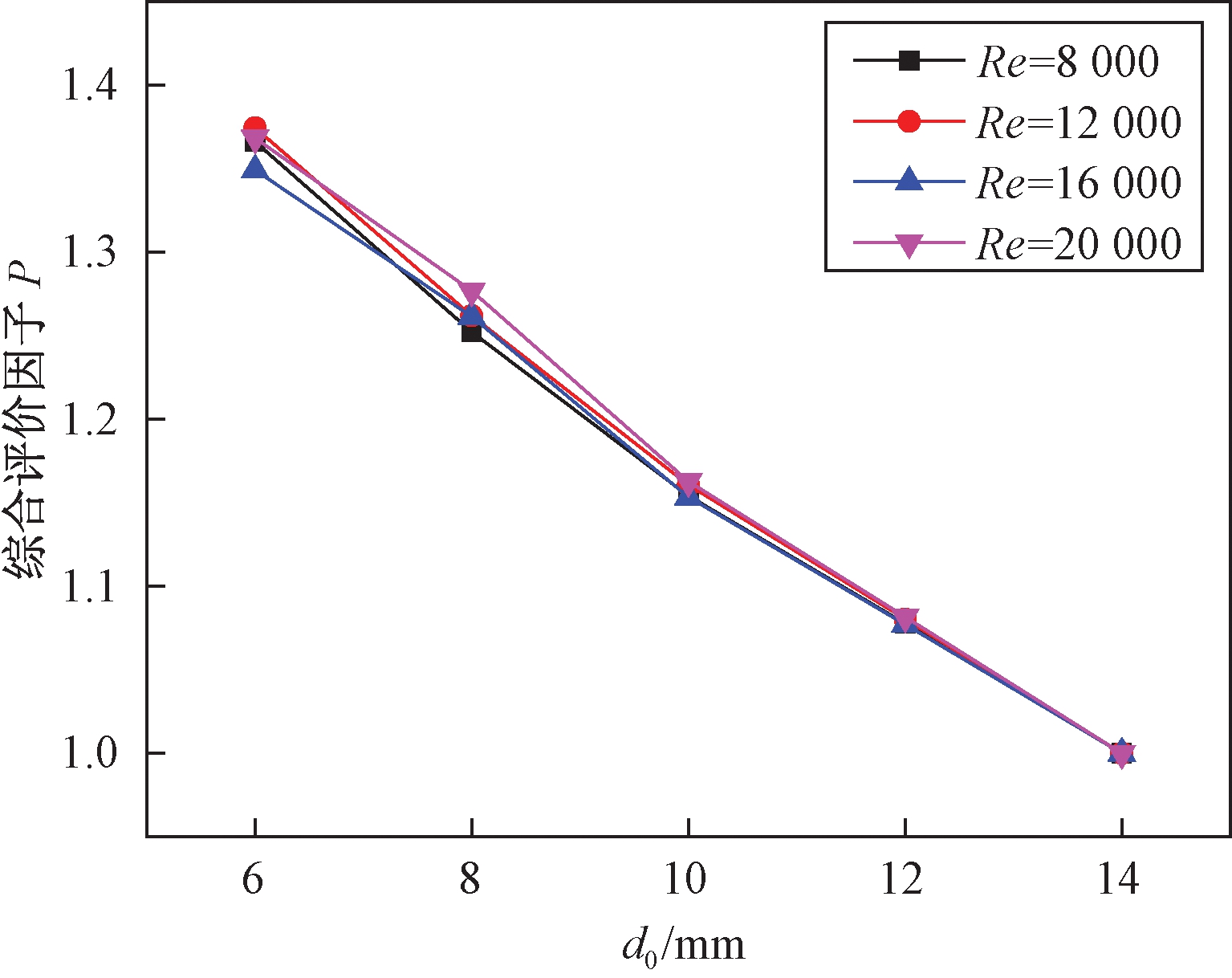
图6 综合评价因子P与管径的关系
Fig.6 Influence of diameter on P
综上可以看出，换热管径在6 mm<d0<14 mm 的范围内，当d0=6 mm时，换热器的综合换热性能最优.
(2)不同层间距条件下的结果分析.图7为不同层间距的绕管式换热器壳侧流体在不同Re条件下努塞尔数Nu的变化曲线.从图7可以看出，在相同Re条件下，不同层间距换热器的Nu变化不大，所以说缠绕管的层间距对Nu影响不大.当层间距相同时，Nu随Re的增大呈变大趋势，因为当Re增大时，流体速度变大，流体在管壁附近的冲刷作用增强，边界层变薄，从而达到强化传热的效果.图8为绕管式换热器在不同层间距条件下场协同数Fc的变化曲线.从图8中可以看出，在一定Re的情况下，随着层间距S2变大，场协同数Fc先变大后减小，当S2为3 mm时，Fc有极大值，此时换热效果最好.
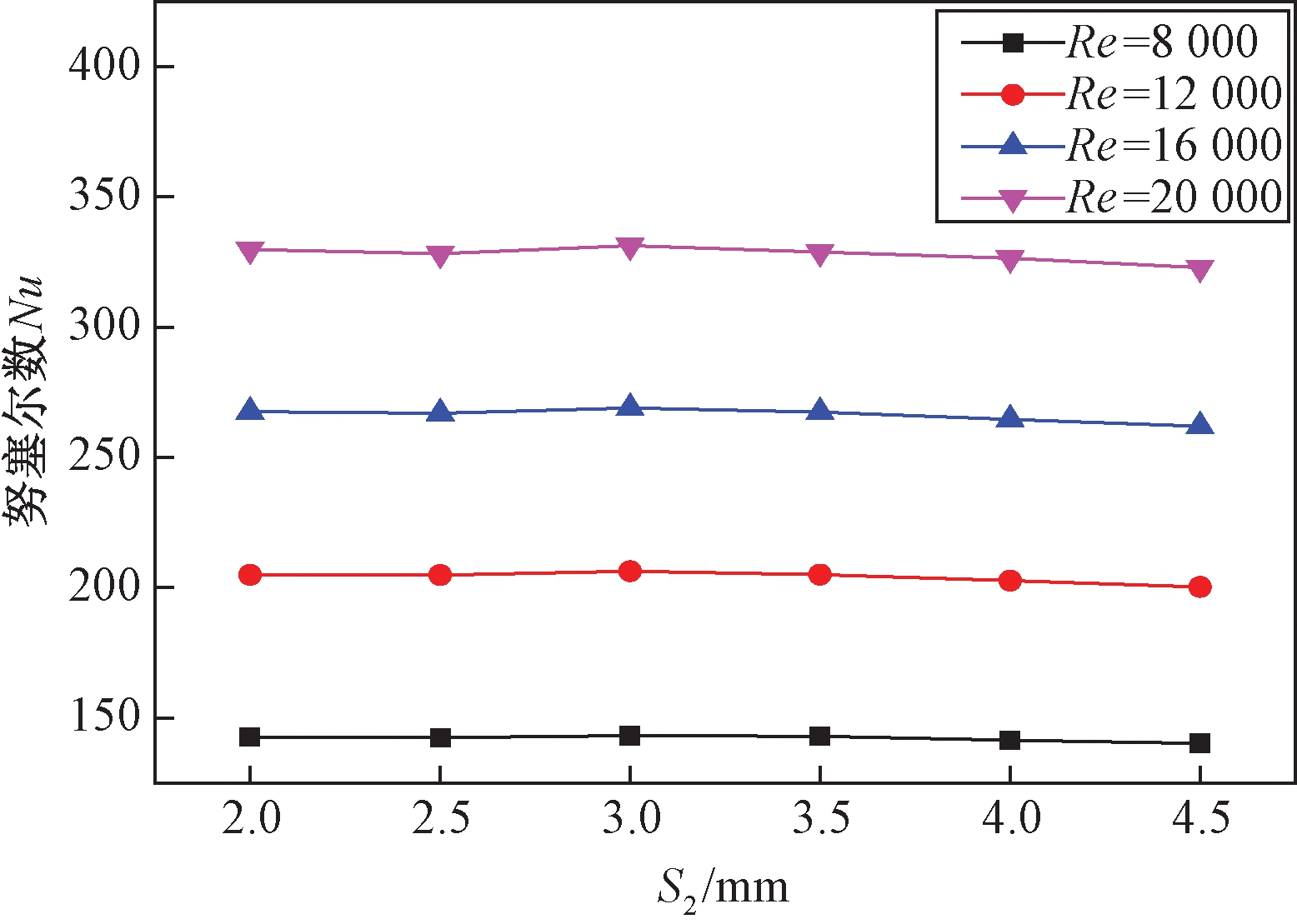
图7 Nu与层间距关系
Fig.7 Influence of thickness bar on Nusselt number
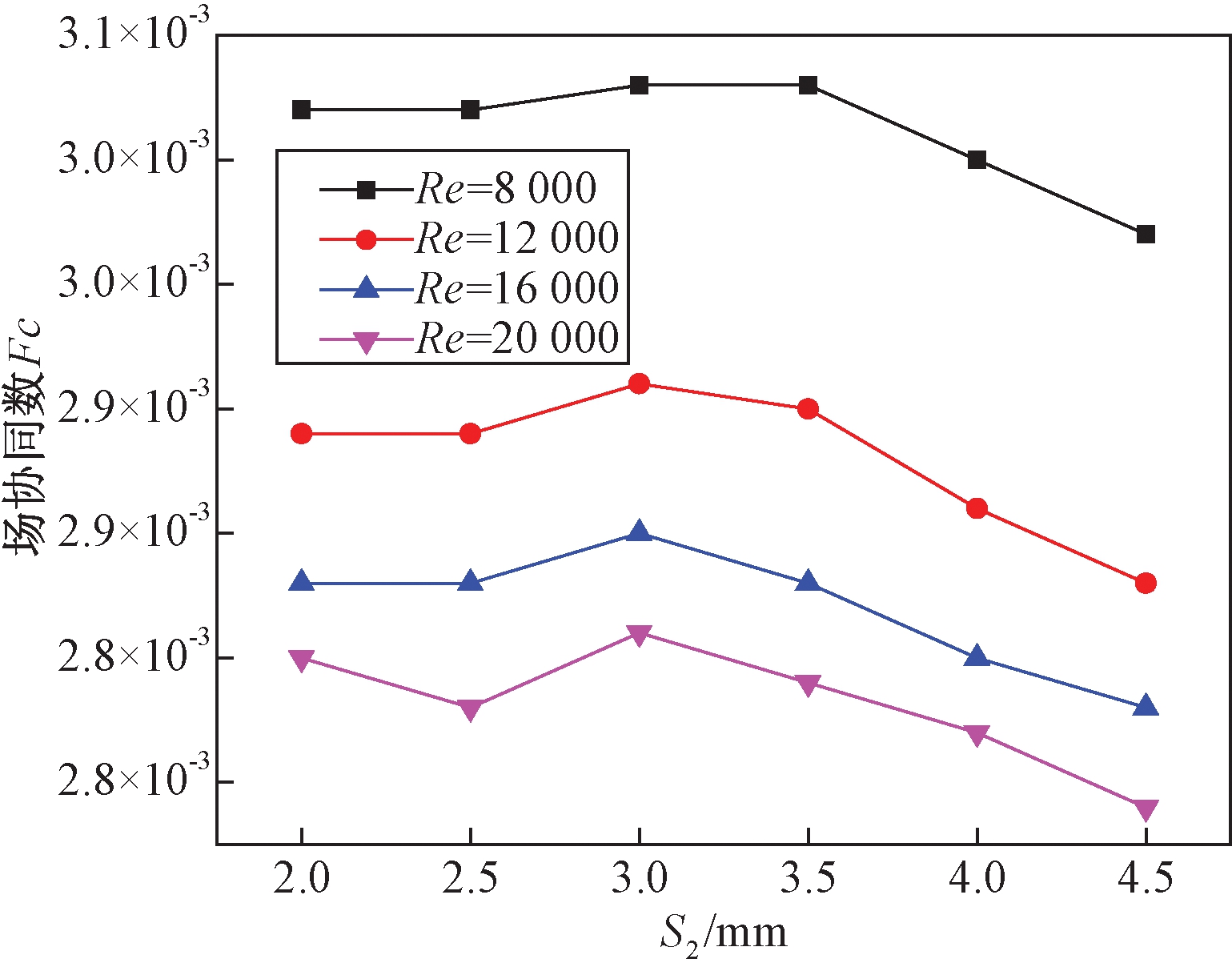
图8 场协同数与层间距关系
Fig.8 Influence of thickness bar on synergetic number
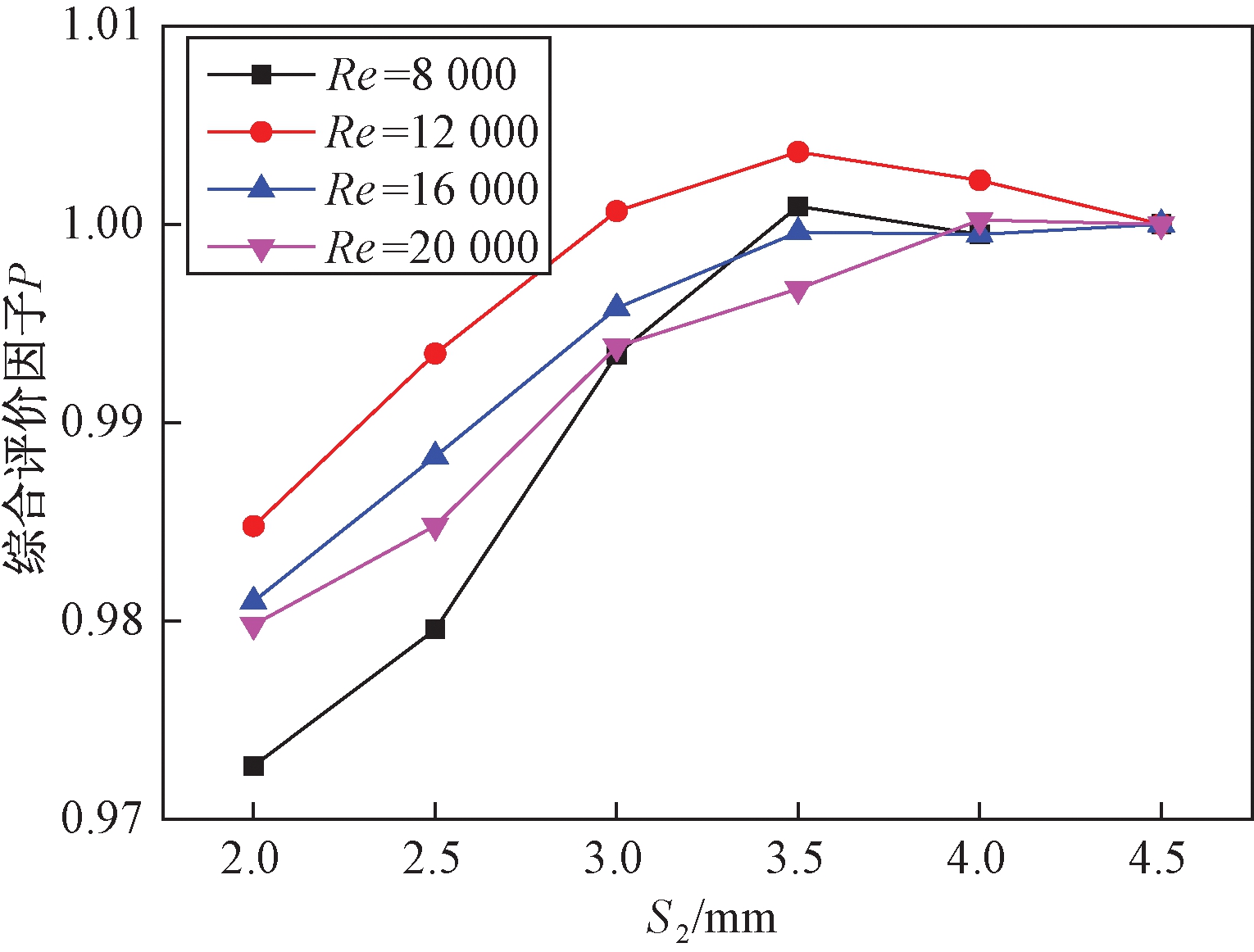
图9 综合评价因子P与层间距的关系
Fig.9 Influence of thickness bar on P
图9为绕管式换热器层间距S2和Re与综合换热性能评价因子P的变化关系图.从图9可以看出，在一定Re的情况下，当层间距S2增大时，P值先达到最大值，而后逐渐减小，最大值在3.5 mm处出现，此时换热性能最优.
(3)不同轴间距条件下的结果分析.图10为绕管式换热器轴向间距Z和Re与Nu的变化关系图.从图10中可知，在一定Re的情况下，Nu随Z值的增大而增大；在相同轴向间距的情况下，随着Re的变大，Nu逐渐变大.Nu越大表示换热器的换热效果越好，所以,绕管式换热器的轴向间距越大对换热越有利.
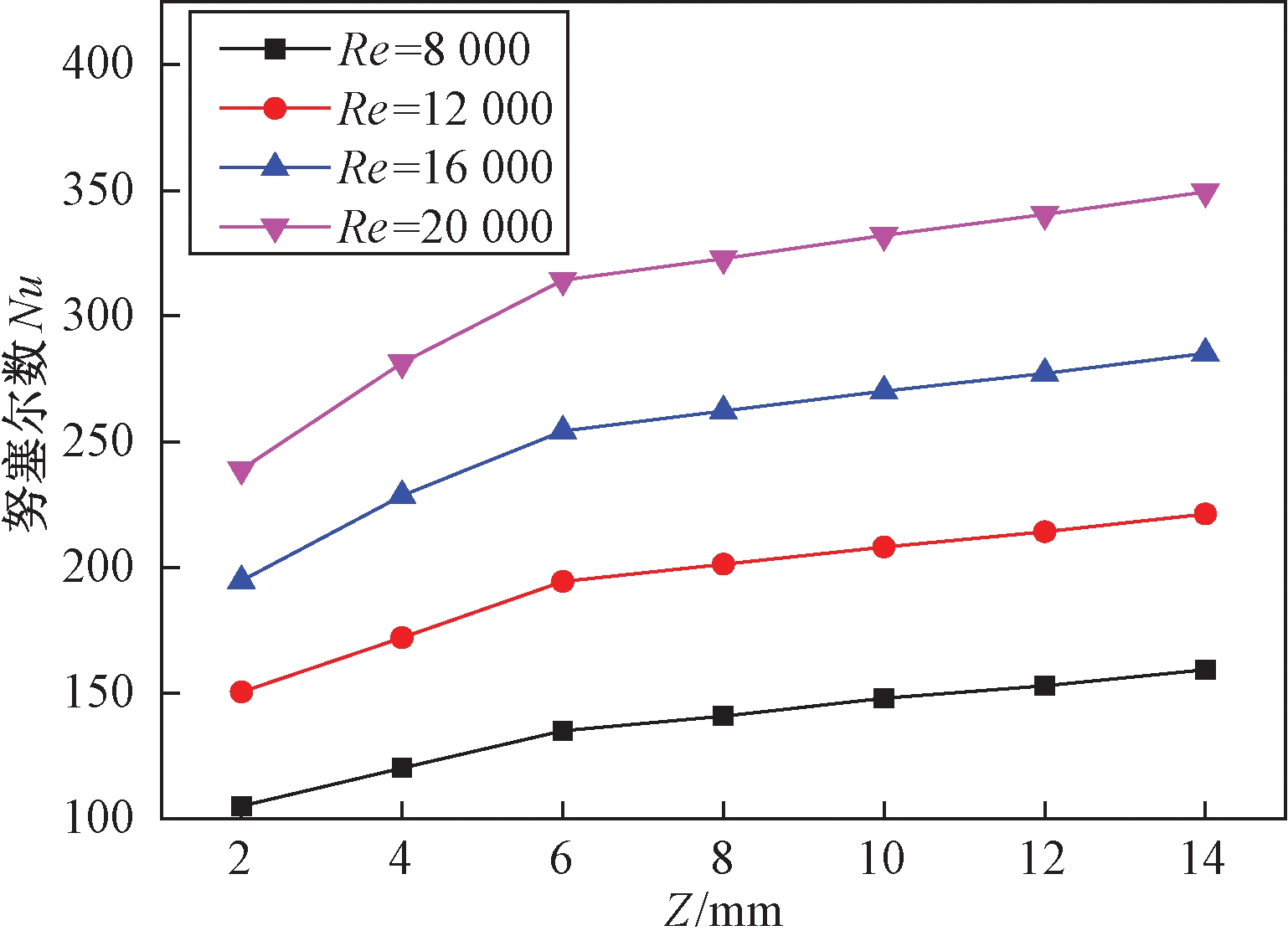
图10 Nu随轴向间距的变化关系图
Fig.10 Influence of tube pitch on Nusselt number
图11为绕管式换热器轴向间距Z和Re与综合换热性能评价因子P的变化关系图.从图11中可知，在相同Z值的情况下，随着Re增大，P值变化不明显，在一定Re的情况下，随着轴向间距Z的变大，P值逐渐增大，当Z=14 mm时达到最大值，此时换热性能最优.
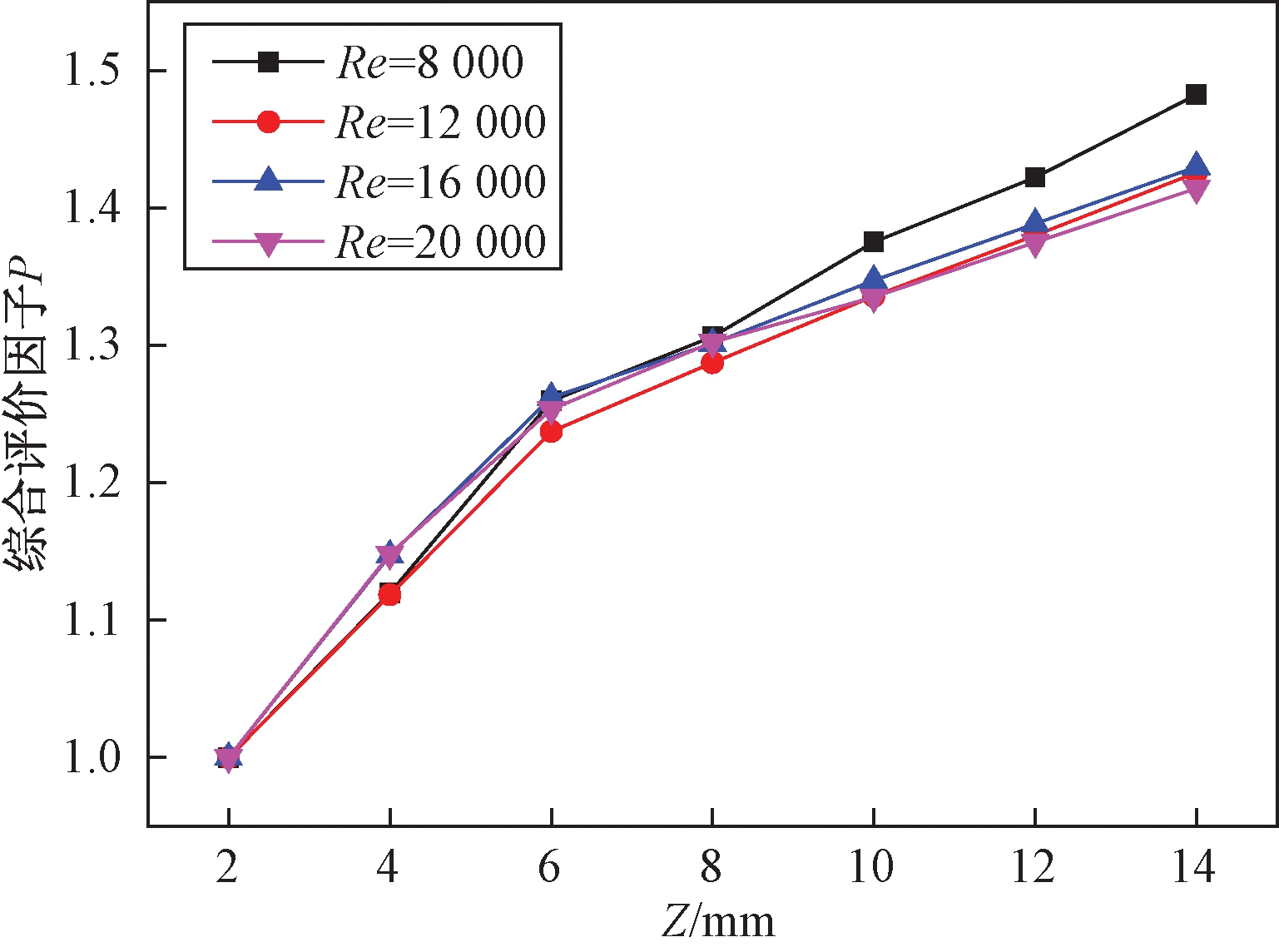
图11 P值随轴向间距的变化曲线图
Fig.11 Influence of tube pitch on P
为了检验前文中数值模拟方法的正确性，笔者搭建了绕管式换热器实验台，并对其换热性能进行实验研究.通过数值模拟结果和实验结果的对比，证明数值模拟方法的准确性.
绕管式换热器性能实验测试平台如图12所示，本测试平台主要由冷水循环系统、蒸汽循环系统、数据采集系统和换热装置系统4个模块组成.热源为蒸汽，冷却介质为温度为20 ℃的自来水，实验过程中改变热侧蒸汽和冷水侧的冷水流量，通过数据采集系统收集管、壳侧进出口温度和压力变化，计算出换热器的传热系数，从而达到测试换热性能的目的.
图12 换热器性能实验测试平台
Fig.12 Experimental test platform for heat exchanger
设定换热器壳侧水流量为1.5～7 m3/h，壳侧水流速为0.23～1.1 m/s，壳侧水温为293 K,此时壳侧冷水Re在2 800～13 000范围内变化，图13为绕管式换热器温度变化量的实验值和模拟值的对比图.从图13可知，当Re相同时，实验值均高于模拟值，相差1～4 ℃，造成误差的原因是：模拟过程中设置壁面边界条件是绝热的，而实验中会有热量向外界传递，二者相对误差在17%～26%之间，在工程应用上数值模拟和实验结果之间的误差在±30%以内认为是可以接受的[14]，且随着Re变大，误差逐渐减小.
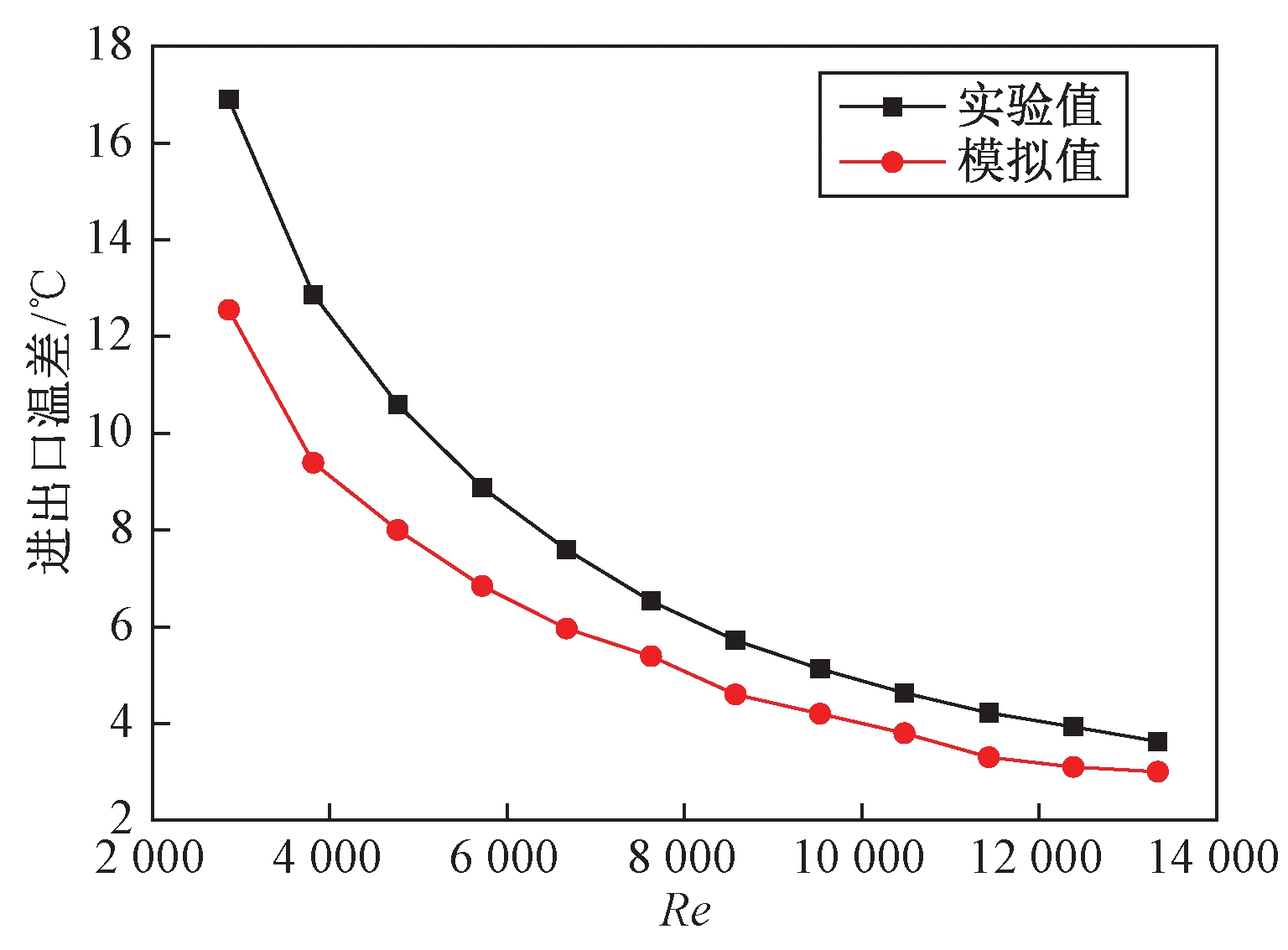
图13 温度变化量随Re变化曲线图
Fig.13 Influence of Reynold number on temperature difference
图14为绕管式换热器压力降的实验值和模拟值的对比图.从图14中可知，当Re相同时，压力降模拟结果与实验数据相差0.8～1.2 kPa.
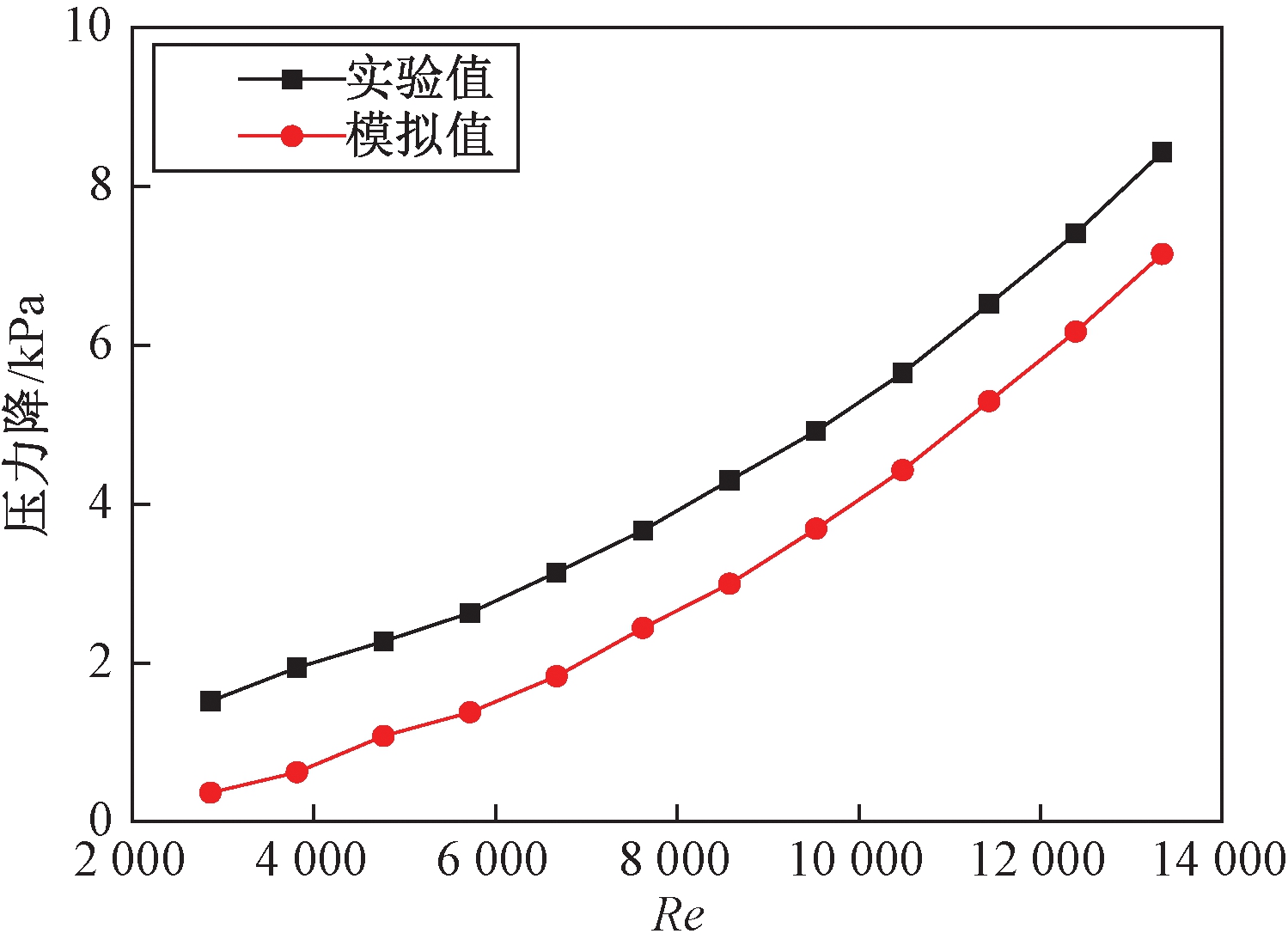
图14 压力降随Re变化曲线图
Fig.14 Influence of Reynold number on pressure drop
通过本节对绕管式换热器的传热性能的模拟结果与实验数据进行对比，发现壳侧流体温度变化、压力降实验和模拟结果的相对误差在工程应用的允许区间内，证明前文中的Realizable k-ε湍流模型对绕管换热器壳侧流体流动及传热过程数值模拟的准确性.
(1)模拟研究表明，在垂直流动方向截面上，壳侧流体会形成大量的速度漩涡、二次流，不同层之间的流体会发生剧烈的相互掺混.
(2)在研究范围内，随着换热管径增大、换热管轴向间距减小，换热器的综合换热评价因子逐渐变小，随着层间距增大，综合换热评价因子呈先增大后减小的趋势.
(3)实验研究表明，在相同Re下,模拟值比实验值整体偏低，温度差值、压力降模拟结果与实验数据相差1～4 ℃、0.8～1.2 kPa.
[1] 吴金星,李亚飞,张灿灿,等.绕管式换热器的结构形式分析及应用前景[J].压力容器,2014,31(2):38-42.
[2] 阳大清,周红桃.绕管式换热器壳侧流场流动与传热的数值模拟研究[J].压力容器,2015,32(11):40-46.
[3] 魏江涛, 曾桃. 缠绕管换热器壳程传热特性的数值研究[J]. 化学工程与装备, 2015(2):21-23.
[4] 贾金才. 几何参数对绕管式换热器传热特性影响的数值研究[J]. 流体机械, 2011,39(8):33-37.
[5] LU X, ZHANG G P, CHEN Y T, et al. Effect of geometrical parameters on flow and heat transfer performances in multi-stream spiral-wound heat exchangers[J]. Applied thermal engineering, 2015,89:1104-1116.
[6] GHORBANI N, TAHERIAN H, GORJI M, et al. Experimental study of mixed convection heat transfer in vertical helically coiled tube heat exchangers[J]. Experimental thermal & fluid science, 2010, 34(7):900-905.
[7] LU X, DU X P, ZENG M, et al. Shell-side thermal-hydraulic performances of multilayer spiral-wound heat exchangers under different wall thermal boundary conditions[J]. Applied thermal engineering, 2014,70(2):1216-1227.
[8] 古新,秦晓柯,王永庆,等.倾斜折流栅式换热器壳程流体流动与传热特性[J].化工进展,2017,36(10):3584-3589.
[9] KHARAT R, BHARDWAJ N, JHA R S. Development of heat transfer coefficient correlation for concentric helical coil heat exchanger[J]. International journal of thermal sciences, 2009,48(12):2300-2308.
[10] HE Y L, TAO W Q. Numerical studies on the inherent interrelationship between field synergy principle and entransy dissipation extreme principle for enhancing convective heat transfer[J]. International journal of heat and mass transfer, 2014,74:196-205.
[11] 过增元. 换热器中的场协同原则及其应用[J]. 机械工程学报, 2003,39(12):1-9.
[12] CHEN Q, LIANG X G, GUO Z Y. Entransy theory for the optimization of heat transfer-A review and update[J]. International journal of heat and mass transfer, 2013,63(15):65-81.
[13] GUO Z Y, ZHU H Y, LIANG X G. Entransy—a physical quantity describing heat transfer ability[J]. International journal of heat and mass transfer, 2007,50(13):2545-2556.
[14] 吴金星,王超,王明强,等.内置扭带管内湍流流动与传热数值模拟[J].郑州大学学报(工学版),2017,38(3):10-14.