0 引言
大规模MIMO(massive multiple input multiple output)技术是未来无线通信系统的关键技术之一[1-2].在实现高频谱效率、功率效率和鲁棒性等方面有巨大的潜力.大规模MIMO系统的信道估计问题引起了研究人员的关注.特别是无线信道的稀疏性已被作为降低导频开销的方法来提高信道估计性能[1].在大规模MIMO系统中，实际信道中包含丰富的多径成分.用户端在局部散射效应的影响下[3-4]，无线信道往往表现出稀疏多径结构，且大部分的路径增益相当低.随着带宽和天线数目的增多，收益下降幅度也急剧攀升[5].由于传统信道估计算法(如LS算法和MMSE算法等)的估计精度较低，无法满足大规模MIMO系统对信道估计精度的要求.为了在不增加导频开销的前提下提高信道估计精度，一些学者提出了稀疏信道估计算法[6-7].Dai等[8]提出一种时频联合的上行稀疏信道估计算法，该算法利用时域的训练序列和频域的正交导频序列作为时频训练信息，分别估计路径延迟和路径增益，在不增加导频开销的情况下提高信道估计精度.然而该算法只适用于时频序列的大规模MIMO系统中，这限制了该算法的应用.文献[9]对于大规模MIMO稀疏上行信道的估计，提出了两种基于贪心追踪的压缩感知方法.Wang等[10-11]考虑在FDD多用户大规模MIMO系统中，通过利用空间相关性，在空间-频率域中以稀疏形式建模信道，结合压缩感知理论(compressed sensing，CS)，提出一种基于改进的正交匹配追踪(OMP)算法来进行有效信道估计.与传统信道估计算法相比，该算法不仅运算复杂度较低，而且收敛速度较快.然而，该算法重构精度较低，仍不能满足系统对信道估计精度的要求，限制了该稀疏信道估计算法的应用.同时由于将信道建模成一维稀疏向量，一次仅能估计出单个用户的信道状态信息，难以实现多用户的联合信道估计.
综上，考虑到三阶张量分解在无线通信中可以充分利用空、时、频多域信息，通过对接收信号多维矩阵建模，在低运算复杂度情况下只需少量导频序列便能联合估计信道矩阵[7，12]，笔者针对多用户大规模MIMO系统的上行链路信道估计问题，提出了一种基于张量分解的联合信道估计方法.该方法将实际物理信道描述为稀疏表示的虚拟信道，再将基站端的接收信号构建信道矩阵、信号矩阵以及编码矩阵为加载矩阵的PARAFAC模型.在满足张量唯一性分解的条件下，利用双线性交替最小二乘(bilinear alternating least squares，BALS)拟合算法进行迭代拟合，来估计多个用户的信道状态信息.笔者所提信道估计方法能够在极少导频数目的情况下联合估计出多个用户的信号矩阵与信道矩阵，从而降低了导频资源的开销，实现了高频谱效率的通信传输.
1 系统模型
1.1 多用户大规模MIMO系统模型
笔者考虑单小区多用户大规模MIMO系统上行链路的信道估计问题，在基站端配置Nb根天线，服务K个单天线用户.其系统模型如图1所示.
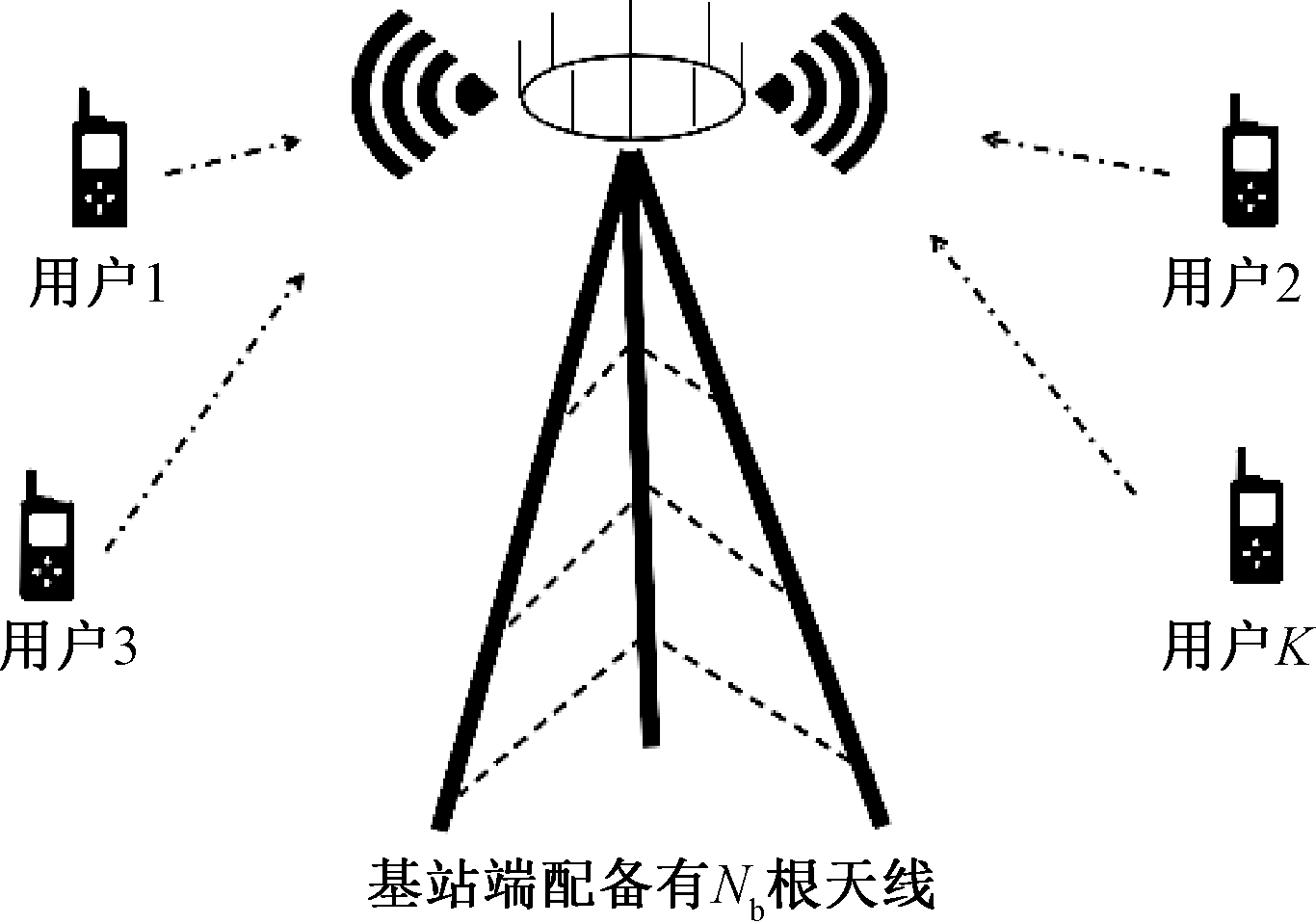
图1 大规模MU-MIMO系统模型
Fig.1 Massive MU-MIMO system model
在上行链路传输中，其信道估计是在基站进行的.将用户端到基站端之间对应的信道矩阵表示为H∈
Nb×K，K个用户传送的符号矩阵为Xt∈K×N.若假定在整个观测时间内为静态信道，可得在第t时隙基站端的接收信号Yt为：
Yt=HXt+Vt，
(1)
式中：Yt∈Nb×N和Vt∈Nb×N依次表示在第t(n=1,2,…,T)个时隙基站端接收到的信号所构成的矩阵与噪声矩阵.
1.2 稀疏信道矩阵模型
用户端到基站端的信道矩阵表示为H∈Nb×K，h(nb,k)表示用户k和第Nb根接收天线之间的频域等效信道衰落.假设噪声服从CN(0，1)独立同分布的复高斯噪声.利用稀疏数学模型将第K个用户与基站端的信道hk表示为[13]：
hk=Φkhnb∈Nb×1,
(2)
式中：hk(k=1,2,…,K)是信道矩阵H的第k列向量；hnb∈L×1为待估计的稀疏矩阵向量.假设信道稀疏度为Nb，即在L条路径中最多只有Nb条路径的路径增益非零且Nb≪L.
式(2)中的Φk∈Nb×L为第K个用户的过完备字典矩阵(在本文中设置L=10Nb)，表示为：
Φk(nb,l)=exp[2jπ(nb-1)(l-1)/l],
(3)
则用户端到基站端的信道矩阵可以和写为：
H=[h1,h1,…hk].
(4)
1.3 发送信号矩阵
用户在第t个时隙内发送的符号序列矩阵为Xt∈K×N，考虑通过Khatri-Rao 空时(KRST)编码来提高信号的抗干扰能力.首先将第t个时隙的信号矩阵Xt∈K×N划分成N个符号块矢量表示的形式，Xt,n∈K×1表示第t(t=1,2,…,T)个时隙的第n(n=1,2,…,N)个符号块矢量.
Xn=[x1,n,x2,n,…,xt,n，…,xT,n]∈K×T.
(5)
将符号块矢量左乘选择星座旋转矩阵Θ∈K×K[14-15]，并将其乘积做对角化处理diag(Θxt,n)∈K×K.
(6)
式中：FK∈K×K是DFT变换矩阵;α=exp(j2π/K).最后diag(Θst,n)右乘可以使编码矩阵增加宽度的范德蒙矩阵CT∈K×M，从而实现对信号矩阵的预编码处理，提高信号的抗衰落能力.
综上，可得基站端的接收信号为：
Yt,n=HnDt[(ΘXn)T]CT+Vt,n, t=1,2，…,T.
(7)
式中：Yt,n∈Nb×K、Vt,n分别指第n个符号矢量、第t个时隙基站端的接收信号矩阵与噪声矩阵；Hn∈Nb×K表示在第n个符号块的复合信道矩阵；Dt(·)表示将第t时隙的发送信号矩阵进行对角化操作.为简化公式书写，令Sn=(ΘXn)T∈T×K.
2 PARAFAC建模及其唯一性分解条件
2.1 PARAFAC模型构建
考虑将基站端在第t个时隙接收到的信号矩阵沿着时间轴t依次堆叠，形成一组三阶张量接收信号Y∈Nb×T×M：
V(nb,t,m),
(8)
式中：Y∈Nb×T×M表示第t(n=1,2,…,T)时隙、第m(m=1,2,…，M)个符号、第nb(nb=1,2,…，Nb)根天线上的接收信号张量，以H、S和C为3个因子加载矩阵；V(nb,t,m)表示三阶噪声矩阵.
2.2 PARAFAC模型唯一性分解条件
根据PARAFAC模型的唯一性分解条件可得[16]：
kH+kS+kC≥2(K+1).
(9)
式中：kH、kC和kS分别为矩阵H、S和C的kruskal秩(k-秩).根据k-秩的定义，若要PARAFAC模型能够唯一性分解，则必须要有：
min(kH+kS+kC)≥2,
(10)
此时，在存在尺度模糊和排列模糊的条件下可得：
(11)
式中：Π∈K×K为排列模糊矩阵；Δi∈K×K(i=1,2,3)为尺度模糊矩阵，而且Δ1Δ2Δ3=IK.其中，矩阵C满k-秩，可得矩阵Π为单位矩阵，由矩阵的性质可知排列模糊矩阵Π与尺度模糊矩阵Δi的乘积为单位阵，可判断Δ2同样为单位矩阵,因此PARAFAC模型的排列模糊已被消除.进而运用自动增益控制(auto gain control，AGC)算法[17]，把发送信号矩阵的首行元素设置为1来消除尺度模糊.
根据k-秩的性质可知：H、S和C这3个因子矩阵满k-秩，则式(9)可写成：
min(Nb,K)+min(T,K)+min(M,K)≥2(K+1).
(12)
由式(12)可知，在PARAFAC模型满足唯一性分解的前提下，可以通过合理的设置基站端天线数目、时隙长度以及编码长度来优化系统参数配置.
3 BALS拟合算法
3.1 BALS拟合算法介绍
PARAFAC模型通常采用三线性交替最小二乘算法(trilinear alternating least square，TALS)来对接收信号进行处理.该算法简单，应用广泛，但其存在较多无效迭代，延长了迭代达到收敛所需要的时间.因此，为了提高TALS的收敛速度，将TALS中的某个加载矩阵设置为已知，那么TALS 算法转化为BALS算法[13].同等条件下，BALS算法所需的迭代次数和单次迭代的计算复杂度都小于TALS算法，且具有更快的收敛速度.
PARAFAC分解模型按照Kiers水平形式展开可得：
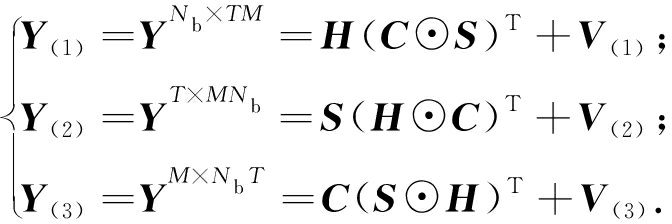
(13)
采用BALS算法对PARAFAC分解模型拟合求解.由于编码矩阵C已知，因此本节的代价函数为：
(14)
式中：‖·‖F是指Frobenius范数，利用交替最小二乘法[12]，可以得到信道矩阵H和信号矩阵S的迭代拟合公式：
(15)
(16)
利用公式(15)和(16)中的矩阵更新来迭代拟合，其过程直至收敛，其性能相对于ALS拟合有明显的改善.同样BALS拟合算法在第一次迭代之前，需要将未知矩阵初始化处理为随机矩阵，从而避免落入到BALS算法中一些特定的慢收敛数据集合.
基于BALS拟合的迭代算法步骤如下：
步骤1给定矩阵C，初始化随机矩阵
设置δ(0)=∞，i=1；
步骤2i←i+1；
步骤3由
根据式(15)更新
由
根据式(16)更新
步骤4计算
如果[δ(i-1)-δ(i)]/δ(i)≤ε，此程序结束，否则跳到步骤2.
3.2 算法复杂度分析
本小节用乘法总次数作为评价算法复杂度的指标.其算法复杂度相对TALS算法的复杂度降低，由式(15)可知，BALS算法在一次迭代运算中[18]，估计信道矩阵H所需的乘法次数为
K3+K2(8TM+1)+K(NbTM+TM)，估计信号矩阵S所需要的乘法次数为
K3+K2(8NbM+1)+K(NbTM+NbM)，可得BALS算法进行一次迭代运算的复杂度为
而TALS算法需要的乘法次数为K3+8K2(NbM+TM+NbT+3)+K(3NbTM+NbM+TMNbT).综合来看，总体的乘法次数降低，从而使得算法复杂度降低，加快了信道估计的收敛速度，提高了信道估计的性能.
4 仿真结果与分析
4.1 仿真算法性能分析
在仿真过程中，假设信道矩阵与噪声矩阵中的元素都满足独立同分布.用户端发送符号的功率大小用ES表示，则用户端的发送信号矩阵
其中,X0是由QPSK调制生成的单位能量矩阵，编码方式考虑使用Khatri-Rao空时编码来抵抗信道衰落，其中编码矩阵C∈CM×K选择截断离散傅里叶变换(DFT)矩阵，其中，m=1,2,…,M，k=1,2,…,K，且M≥K.用归一化均方误差NMSE来衡量算法的信道估计性能：
(17)
式中：
为信道矩阵的估计值.设置参数Nb=32，K=T=M=10，实验采用蒙特卡洛仿真并将仿真次数设为1 000.
从图2仿真结果可以看出，在满足唯一性分解条件的前提下，基于张量分解的BALS信道估计算法性能明显优于基于导频的信道估计方法.
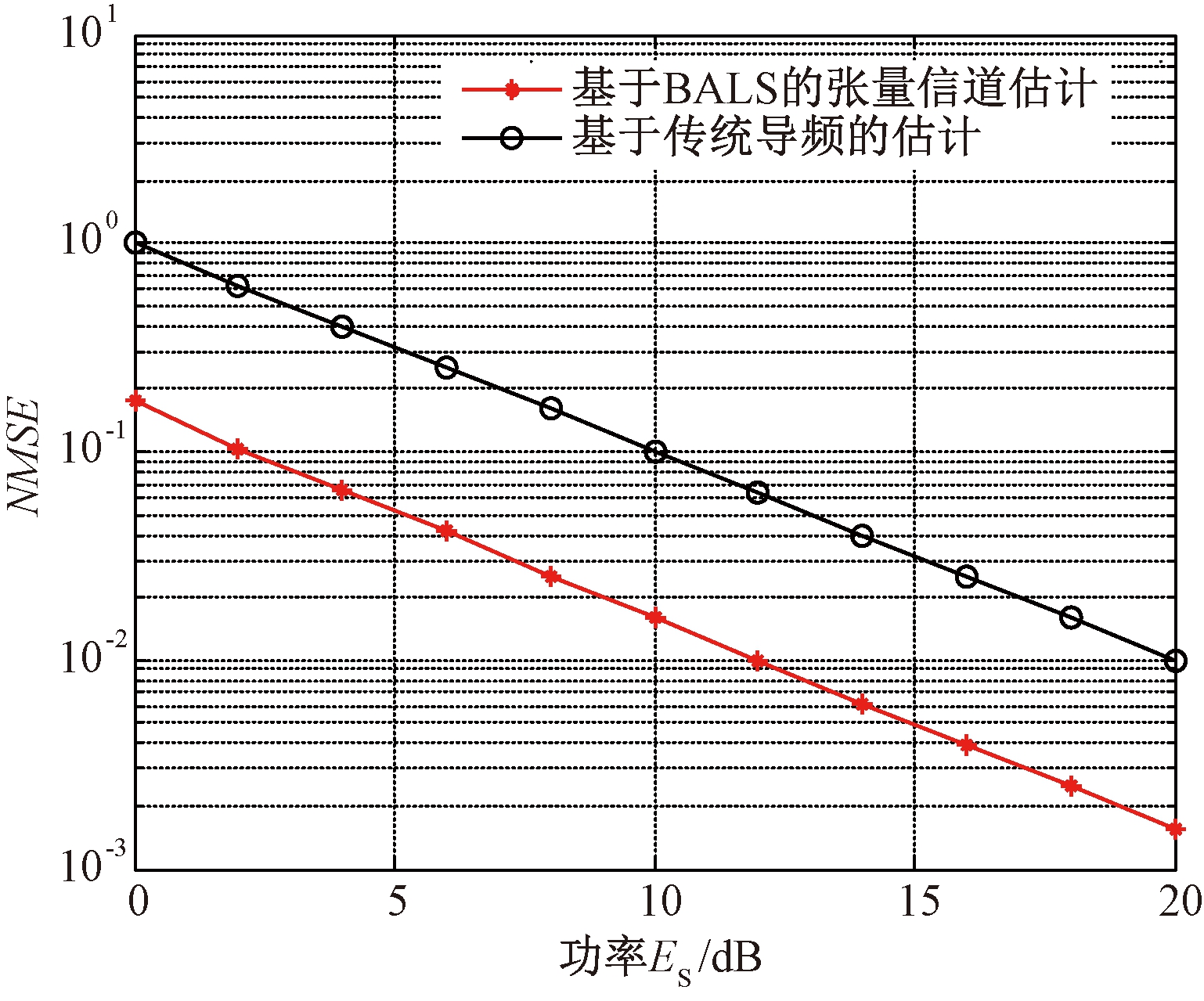
图2 BALS算法与导频估计算法的NMSE对比
Fig.2 Comparison of BALS algorithm and pilot estimation algorithm NMSE
图3仿真分析了两种信道估计方法的系统误比特率(BER)性能.结果显示BALS算法的BER性能随着ES的增加，呈现出减小的趋势.在ES=20 dB时，BALS算法比基于导频的信道估计方法高出了近5 dB.在BER取值为10-2时，本文BALS方法与理想的信道(已知信道状态信息)仅约有3 dB的差距.
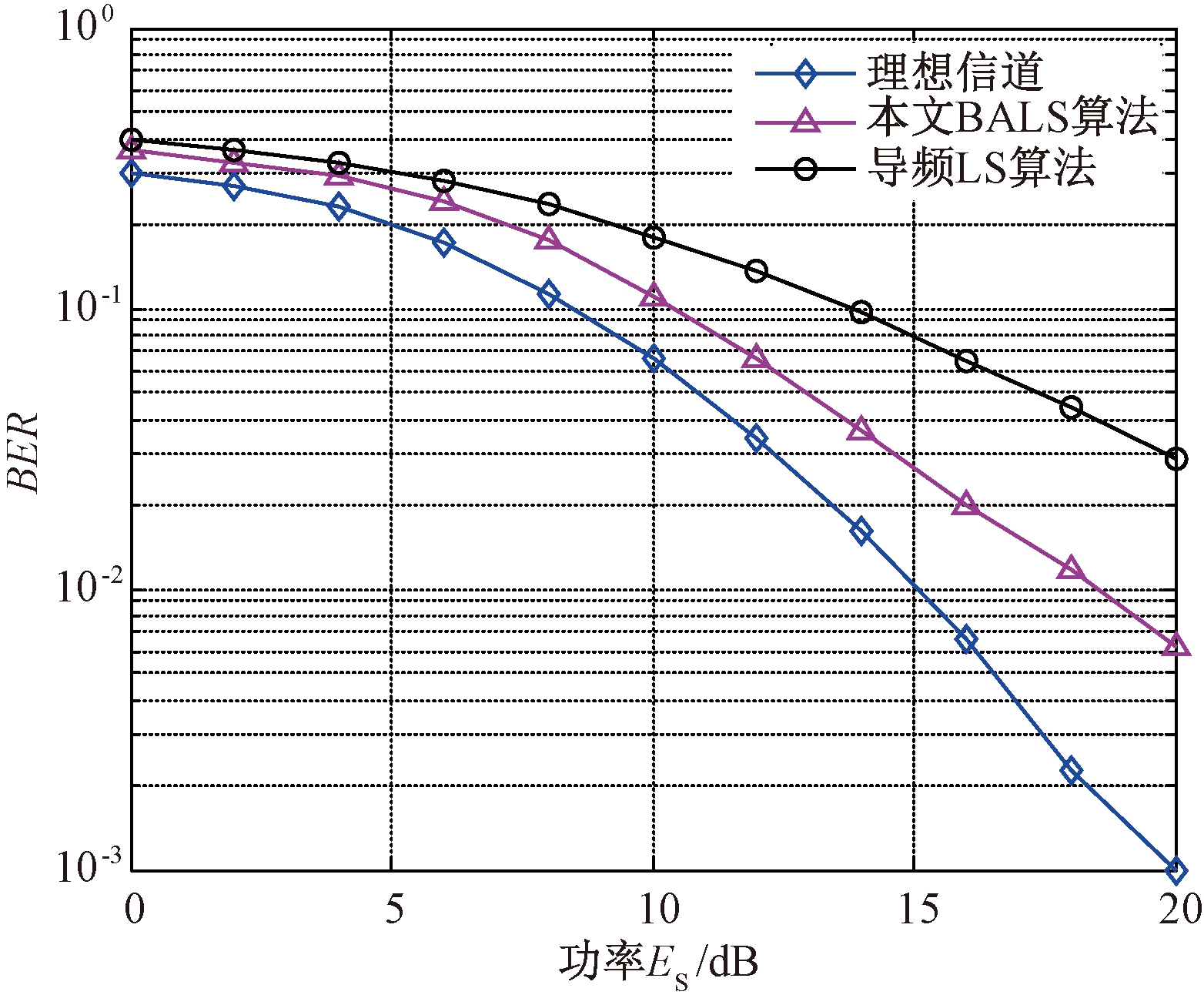
图3 BSLA算法的BER性能比较
Fig.3 BER performance comparison of BSLA algorithm
4.2 算法估计性能分析
本节仿真分析了基站端的天线数目、时间长度及编码长度等各个参数的选取对信道估计性能的影响，以助于系统进行合理的参数设置.
图4给出了基站端天线数目不同时信道估计的NMSE.从图4可以看出，随着基站端天线数目的增多，算法估计性能有所提升，随之而来的是复杂度的增加，且性能的提升有限.因此合理的设置基站端的天线数目对系统整体精度的提高有重大意义.
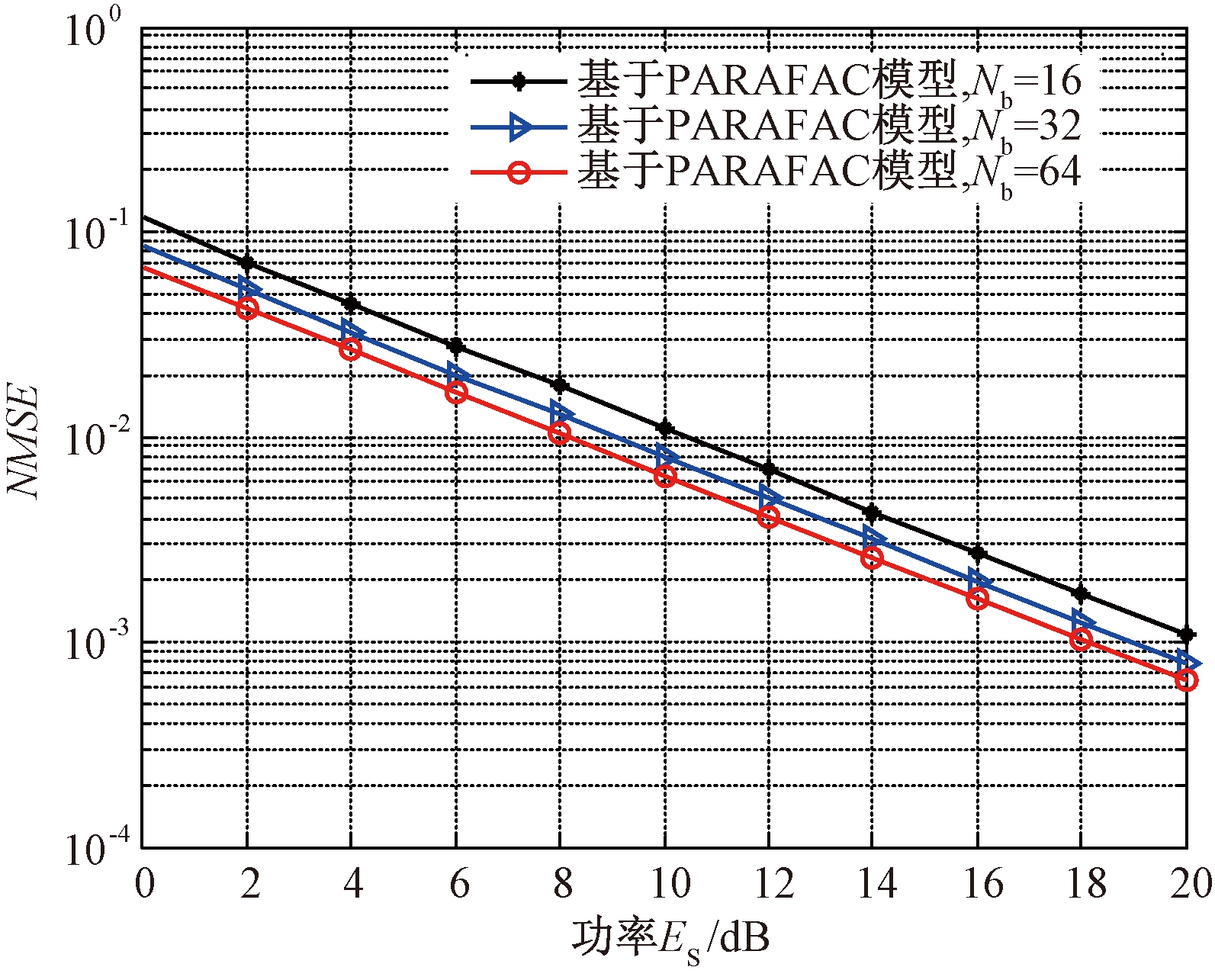
图4 基站端天线数目对估计性能的影响
Fig.4 Effect of number of base station antennas on estimation performance
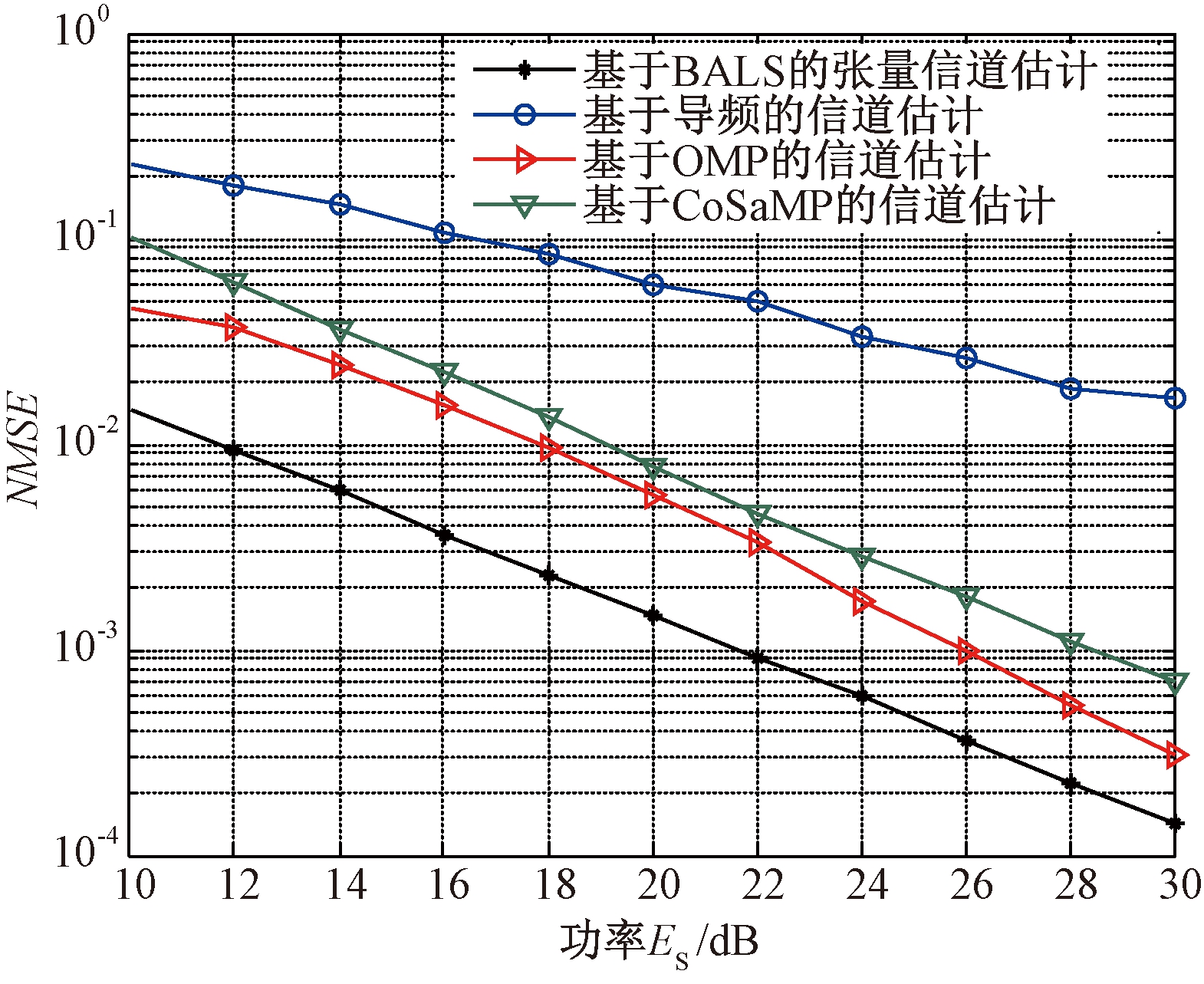
图5 多种算法性能对比
Fig.5 Comparison on performance of multiple algorithms
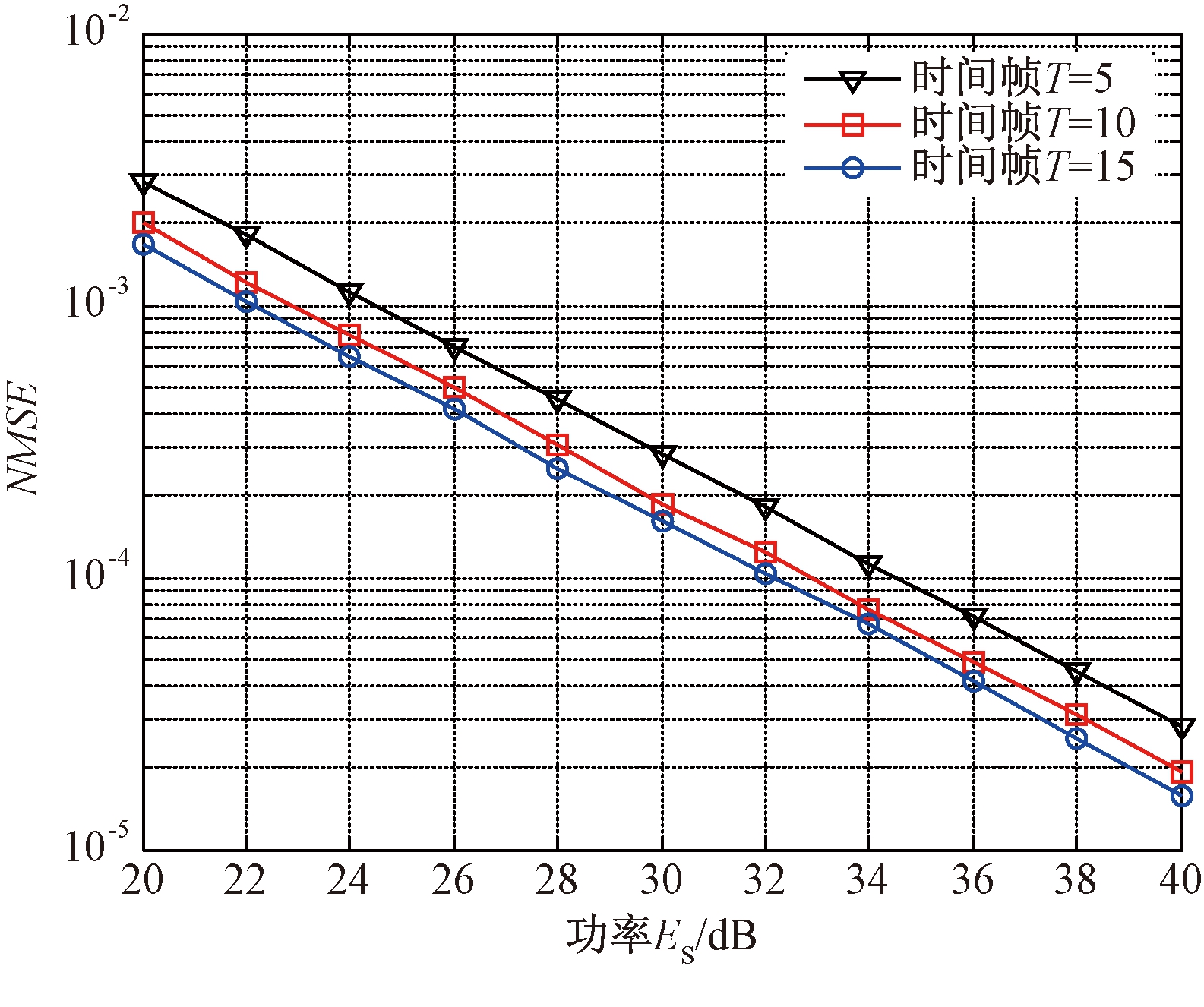
图6 不同时隙长度对信道的NMSE的影响
Fig.6 Effect of different time frame lengths on channel NMSE
图5所示结果验证了所提算法的有效性.由于利用PARAFAC建模，充分利用多维信息，保留了数据结构的整体性，其算法性能明显优于传统的基于导频的信道估计方法；同时较经典的OMP算法与CoSaMP算法有较为明显的提升.充分显示了本文方法的有效性，提高了估计精度，且仅需少量导频，提高了系统的传输效率.
图6仿真结果分析了参数Nb=32、K=M=10时，时隙长度T对算法性能的影响.由图6可以看出,当T增加时，数据观测时间增长，从而获得了更多与系统相关的信息，所提算法具有更高的估计精度,但是系统的复杂度也将大幅度增加.
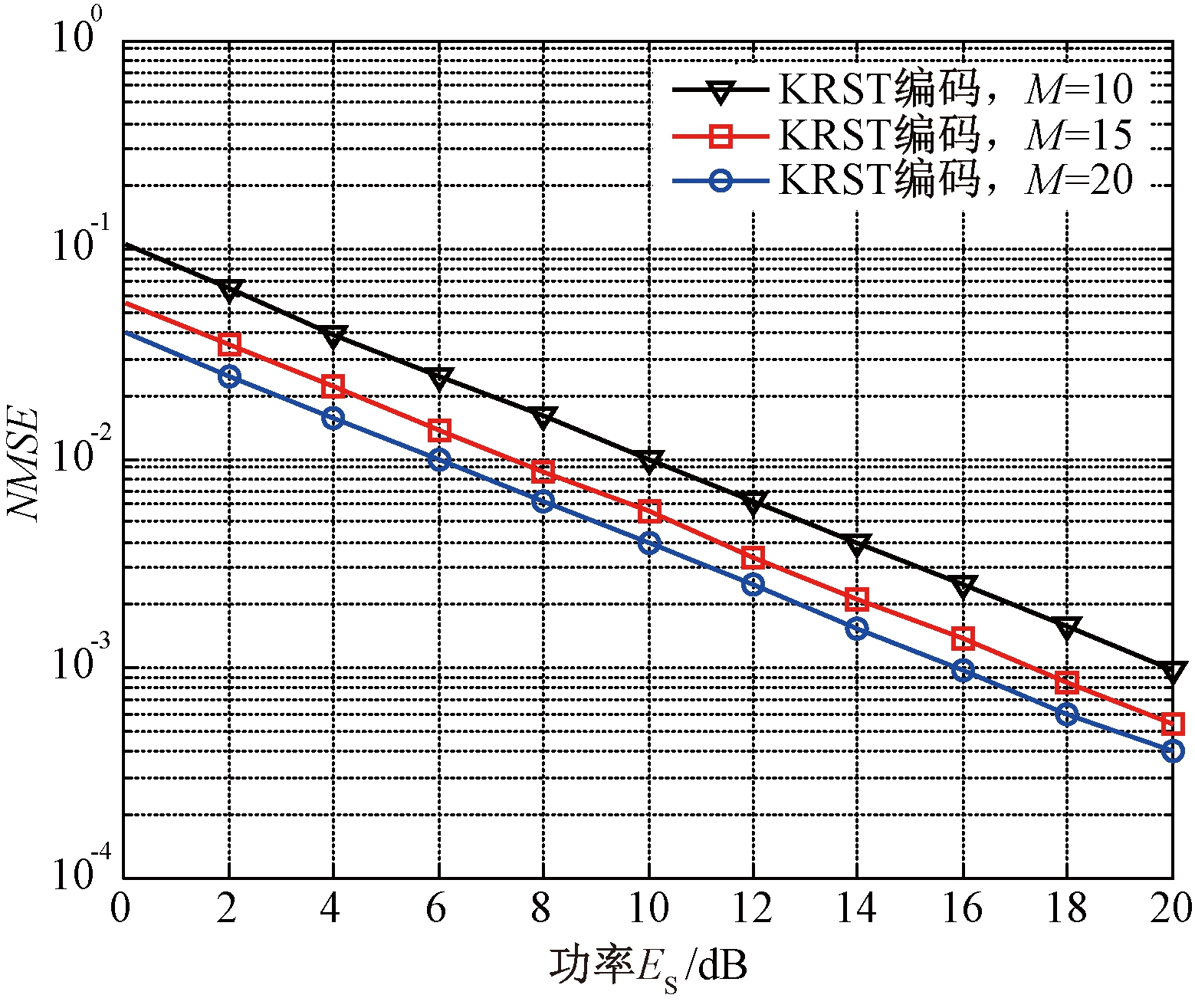
图7 不同时编码长度对信道的NMSE的影响
Fig.7 Effect of different code lengths on channel NMSE
图7给出了Nb=32，K=T=20时，编码矩阵C的编码长度M对算法性能的影响，仿真结果表明,随着M的增加，编码信息的冗余度得到相应的提高，使得信号的抗衰落能力增强，从而使信道估计精度提升.但由于拟合算法的复杂度与M有关，无限制地增大M来换取性能的提升是不明智的，同时需要兼顾PARAFAC模型分解的唯一性条件，在满足存在唯一解的前提下，对参数设置进行折中考虑，以便将此方法更好地发挥作用.
5 结论
笔者针对多用户大规模MIMO上行链路的应用场景，提出了一种基于PARAFAC模型的稀疏信道估计方案.本方案首先利用稀疏表示的相关数学理论，将信道建模为虚拟的稀疏信道，同时对信号矩阵进行编码，以提高其抗衰落能力.核心工作在于将基站端的接收信号进行PARAFAC建模，继而采用BALS算法来拟合估计信道矩阵.仿真结果表明，笔者所提稀疏信道矩阵估计方法，在只需要少量导频的情况下，其估计精度优于其他的估计方法，有效地提高了系统的传输性能.笔者将稀疏理论与张量分解相结合，拓宽了PARAFAC模型在通信信号处理领域的应用范围，为后续研究打下基础.
[1] LARSSON E G, EDFORS O, TUFVESSON F, et al. Massive MIMO for next generation wireless systems[J]. IEEE communications magazine, 2014, 52(2):186-195.
[2] MASOOD M, AFIFY L H, Al-NAFFOURI T Y. Efficient coordinated recovery of sparse channels in massive MIMO[J]. IEEE transactions on signal processing, 2014, 63(1):104-118.
[3] WU S, NI Z, MENG X, et al. Block expectation propagation for downlink channel estimation in massive MIMO Systems[J]. IEEE communications letters, 2016, 20(11):2225-2228.
[4] XIE H X, GAO F F, JIN S. An overview of low-rank channel estimation for massive MIMO systems[J]. IEEE access, 2016, 4:7313-7321.
[5] ENDRA O. Joint optimization of measurement matrix and sparse dictionary in compressive sensing[C]//2012 International Conference on Computer and Communication Engineering. Kuala Lumdur:IEEE,2012: 420-425.
[6] 方昕，刘云驹，曹海燕，等. 大规模MIMO系统中低复杂度的稀疏信道估计[J].电信科学，2016(5)：89-95.
[7] YANG N, XIN S, LI Z. Decision aided uplink compressive channel estimation for massive MIMO systems[J]. Wireless personal communications, 2017,96(1):153-162.
[8] DAI L L, WANG Z C, YANG Z X. Spectrally effcient time-frequency training OFDM for mobile-scale MIMO systems [J]. IEEE journal on selected areas in communications, 2013,31 (2): 251-263.
[9] MANSOOR B, NAWAZ S J, GULFAM S M. Massive-MIMO sparse uplink channel estimation using implicit training and compressed sensing[J]. Applied sciences, 2017, 7(1):63-68.
[10] WANG A, WANG Y, JIANG L. Improved sparse channel estimation for multi-user massive MIMO systems with compressive sensing[C]//International Conference on Wireless Communications & Signal Processing. Nanjing: IEEE, 2015:1-5.
[11] 穆晓敏, 刘越, 李双志,等. 基于张量分解的MIMO多中继系统半盲信道估计方法[J]. 郑州大学学报(工学版), 2016, 37(6):83-86.
[12] RAIMONDI F E D, COMON P. Tensor DoA estimation with directional elements[J]. IEEE signal processing society, 2017, 24(5):648-652.
[13] 王忠勇, 郭秋歌, 王法松,等. 基于分层模型的SC-FDE系统低复杂度稀疏信道估计[J]. 信号处理, 2015, 31(9):1106-1111.
[14] RONG Y, KHANDAKER M R A, XIANG Y. Channel estimation of dual-hop MIMO relay system via parallel factor analysis[J].IEEE transactions on wireless communications, 2012, 11(6):2224-2233.
[15] SIDROPOULOS N D, BUDAMPTI R S. Khatri-Rao space-time codes [J]. IEEE transactions on signal processing, 2002, 50(10): 2396-2407.
[16] KRUSKAL J B. Three-way arrays: rank and uniqueness of trilinear decompositions, with application to arithmetic complexity and statistics[J]. Linear algebra & its applications, 1977, 18(2):95-138.
[17] 张日升. 平行因子技术在DOA估计中的应用研究[D]. 吉林大学通信工程学院, 2007.
[18] RAJIH M, COMON P, HARSHMAN R. Enhanced line search: a novel method to accelerate parafac[J].SIAM journal on matrix analysis and applications,2008,30(3):1128-1147.