0 引言
机械臂的控制是机械臂研究领域中的一个重点方向,该问题是建立在机械臂运动学以及动力学研究基础上的,根据机械臂控制问题所给定输入的参数类型不同,机械臂控制方法又分为位置与轨迹控制、力或力矩控制、力/位置混合控制以及分解运动控制等多种类型[1]。在这些控制方法的基础上,研究者们研究并提出了多种比较先进的控制方法,如自适应控制、变结构控制、预测控制以及智能控制等。
DMC是模型预测控制中的一个类别,该算法一般适用于线性的、有纯时延且开环渐进稳定的非最小相位系统,其对模型要求低并且控制综合效果好[2-3]。该算法作为预测控制的一种常用算法,一般具有模型预测、在线滚动优化和误差反馈校正等基本环节。控制权矩阵是DMC算法控制器中对增量变化剧烈程度进行约束,限制过大的控制量变化的环节,其矩阵参数的取值对控制器收敛效果有很大的影响。在一般的过程控制中,控制对象的不同以及系统阶跃响应点的采样间隔不同,往往会造成控制权矩阵的取值不同。因此,在使用DMC算法进行机械臂控制时,需要采用调参方法并结合自适应控制理论设计算法得到适用于特定被控对象的控制权矩阵。
进化控制系统源于生物的进化机制,一般的进化控制是建立在进化计算(主要是遗传算法)和反馈控制相结合的基础上的。遗传算法作为控制器参数的调节器方法,既可以用于作为机械臂实时控制过程中的在线参数调节器方法,也可以作为离线调整控制参数的方法。遗传算法作为一种智能优化方法,具有较强的通用性,适用于多目标求解问题[4]。在本文中,该算法主要用于解决搜索问题。
目前,对DMC算法的研究主要集中在过程控制领域[5-7]。由于DMC算法具有不需要精准模型的特点,所以其在对复杂的机械臂模型控制中亦能取得较好的效果。虽然遗传算法的研究已经经历了相当长一段时间的发展,但针对不同的算法应用场景还有较灵活的变化[8-9]。一般来说,DMC算法主要适用于线性系统的控制环节,但通过增加扰动向量的方法,也可以使DMC算法适用于一些非线性系统[10]。
对于DMC算法的优化则主要集中在算法稳定性的层面[11-13]。由于DMC算法中有许多作为预测权值而存在的参数以及由这些参数所组成的矩阵或者向量,这些参数对算法的鲁棒性和准确性等控制效果有着直接影响,因此这些参数的最优化取值一直是DMC算法设计的重点之一。
1 动态矩阵预测控制
笔者使用动态矩阵控制作为机械臂的控制方法,控制对象为单关节机械臂。作为机械臂的关节控制器,对单个关节进行控制的DMC算法由预测模型、在线滚动优化和误差反馈校正等环节组成。
1.1 预测模型
动态矩阵预测控制是一种增量式的算法,该算法一般先测定被控对象的单位阶跃响应,并将此响应作为预测模型已知量。如图1所示,以一定的采样周期,在被控对象的单位响应中采样若干点,这些点即组成被控对象单位阶跃响应的模型向量。
.=[a1,a2,…,aN]T,
(1)
式中:.为模型参数向量;N为采样数量。
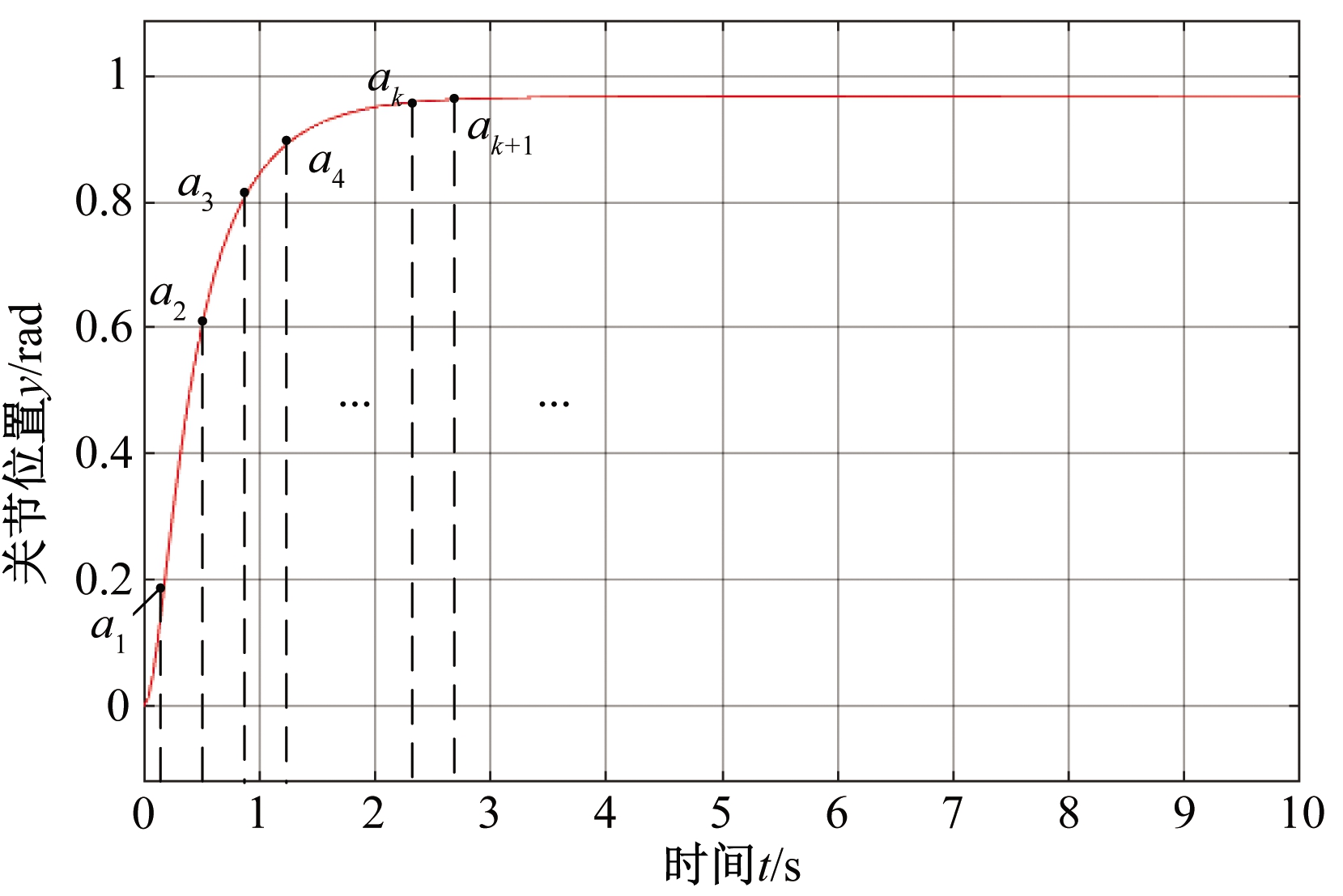
图1 单位阶跃响应及预测模型参数采样
Figue 1 Unit step response and sampling of predictive model parameters
根据线性系统的可叠加性,利用模型参数向量.预测系统未来时刻的输出值。在已知外界有控制作用时,假定当前时刻t=kT, 从t时刻开始连续M个时刻的外界控制增量组成的向量由Δ.M(k)表示,在t时刻对连续N个时刻的未来输出预测向量为:
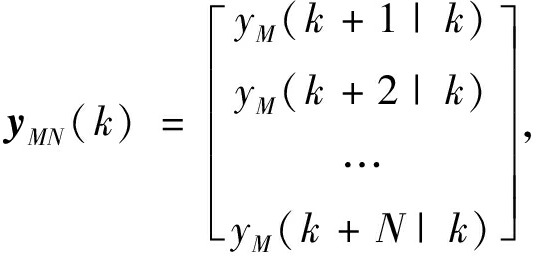
(2)
式中:yM(k+N|k)是在外界有控制作用时,kT时刻对(k+N)T时刻的未来输出预测量。与其对应的无外界控制增量时在t时刻对连续N个时刻的未来输出预测向量为:
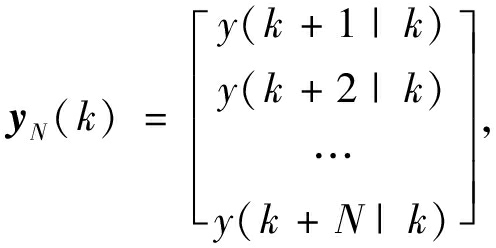
(3)
式中:y(k+N|k)是在外界无控制作用时,kT时刻对(k+N)T时刻的未来输出预测量。上述两个预测向量的关系可以表示为:
.MN(k)=.N(k)+.·Δ.M(k),
(4)
式中:.为动态矩阵,其元素为描述系统动态特性的阶跃响应系数,其定义为:
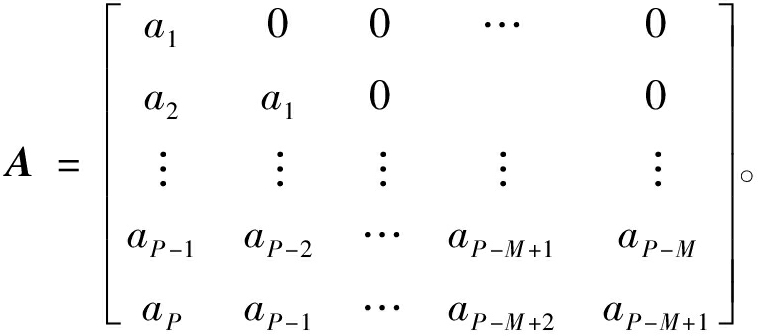
(5)
1.2 滚动优化
优化问题的求解过程是指通过特定方法获得目标函数的最优解。滚动优化环节通过设定优化指标,确定不同采样时刻的未来M个控制增量,进而使未来N个时刻的预测输出接近期望输出。优化指标一般表示为最小二乘问题,并可采用求导或者迭代的方法进行求解。该环节可用公式表示为:
J(k)=![]()
(6)
式中:J(k)为优化的目标函数;.N(k)为未来N个时刻的期望输出值组成的向量;.为输出值误差项向量的二范数的权矩阵,被称为误差权矩阵,一般为q维对角阵;.为外界控制量向量的二范数的权矩阵,被称为控制权矩阵,一般为r维对角阵。
进一步地,优化函数对控制量向量取偏导并令其等于零向量,可以得到最优控制增量序列为:
Δ.M(k)=(.TQA+.)-1.T.(.N(k)-
.N(k))。
(7)
1.3 反馈校正及预测更新
动态矩阵预测控制中的反馈来自于实际输出与预测输出之差,得到模型预测误差为:
.(k+1)=.(k+1)-.(k+1|k),
(8)
式中:.(k+1)是第(k+1)时刻的实际输出。
得到的误差用于对预测输出进行更新,并计算矫正预测值向量,该向量用于更新无控制增量下的预测输出向量,并得到其k+1时刻的取值。其计算公式为:
.cor(k+1)=.MN(k)+.·e(k+1),
(9)
式中:.为误差校正向量,通过调整该矩阵的取值可在更新时增加系统的鲁棒性。
关于矫正预测值向量更新,在无控制增量下的预测输出向量公式为:
.N(k+1)=.·.cor(k+1),
(10)
式中:.为移位矩阵,其定义为:

(11)
1.4 DMC方法实现
笔者采用上述DMC算法作为机械臂的控制器。其中,控制权矩阵对系统的动态响应有着显著的影响,一般需要对其取值进行合理的设定,并基于此设定进行控制方法设计。DMC控制方法框架如图2所示。
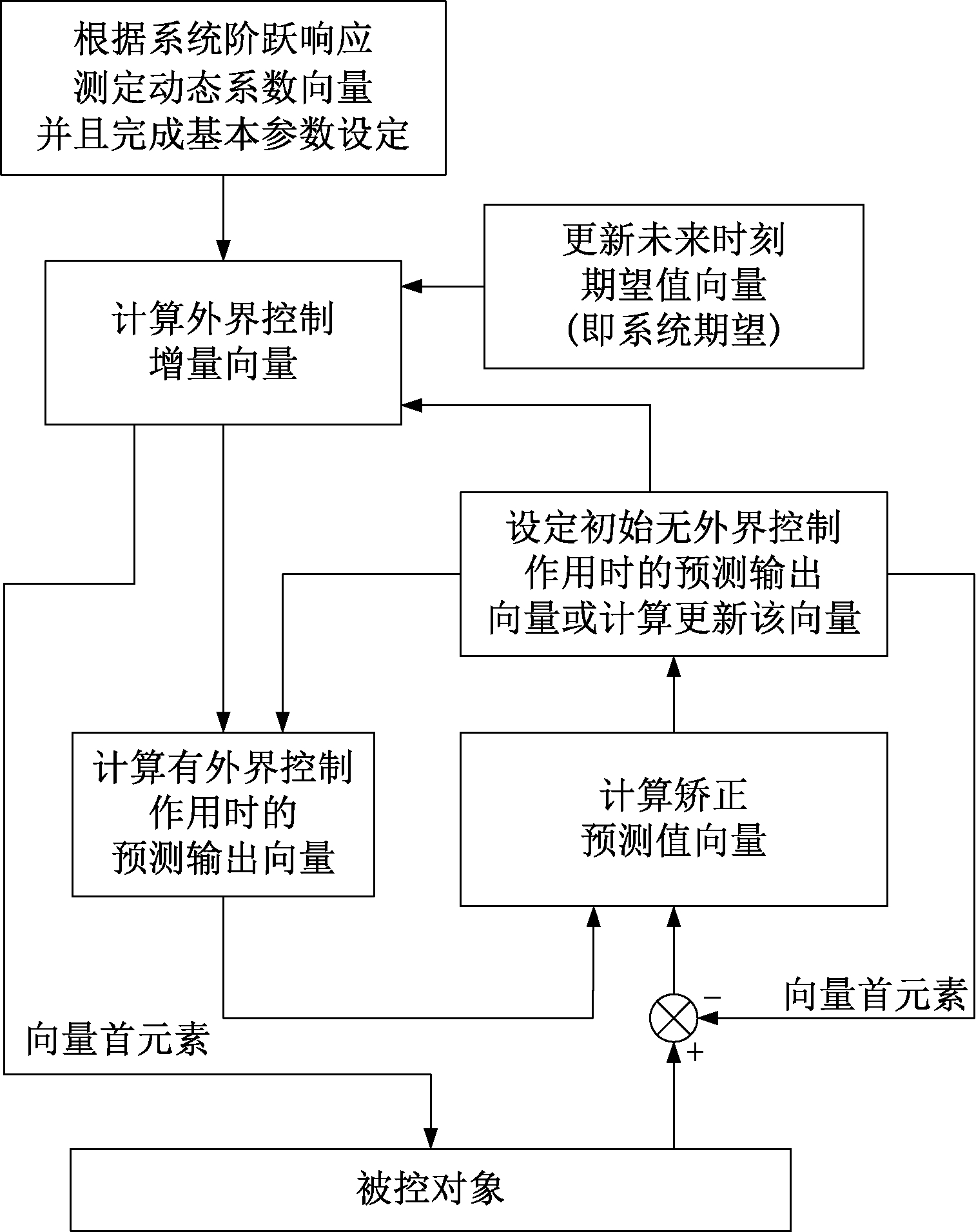
图2 动态矩阵预测控制算法
Figue 2 Dynamic matrix predictive control algorithm
将DMC控制方法的几个环节串联起来并形成闭环回路,通过采样测定动态系数向量之后,计算得到动态矩阵。并且通过经验或者参数调节的算法设定误差权矩阵与控制权矩阵、误差矫正向量的参数值,进而完成DMC控制方法的参数设定。
在参数设定的基础上,通过设定初始的无外界控制作用时的预测输出向量,以及根据初始的系统期望值,计算出最初的外界控制增量向量,并将该向量的首元素作为被控对象的输入控制值。此外,计算得到有外界控制作用时的预测输出向量,其后,通过被控对象的实际输出与初始的无外界控制作用时的预测输出向量首元素的差值,以及计算出的有外界控制作用时的预测输出向量,求解得到矫正预测值向量,再通过该向量对无外界控制作用时的预测输出向量进行更新。
在无外界控制作用时的预测输出向量与系统期望更新之后,重新执行滚动优化、预测模型以及反馈矫正3个环节,直至系统输出趋于稳定。
2 遗传算法
2.1 构建目标优化函数
在本文中,根据控制系统输入量(机械臂关节理想转角)以及输出量(机械臂关节实际转角)之间的关系确定遗传算法的目标优化函数。当系统输出量可以较精确且迅速地跟踪系统输入量时,则会获得较小的目标函数值,从而按照优化函数所包含的优化规则实现优化过程。
在对机械臂进行控制时,为使输出量精确且迅速地跟踪输入,需要建立目标优化函数并使其成为二者差值的函数。规定n为全局跟踪时间内根据一定周期采样输入、输出点的个数,m0与m1为局部(超调量较大部分)跟踪时间内根据一定周期采样输入、输出点的起始与结束时刻值,则目标优化函数可以表示为:
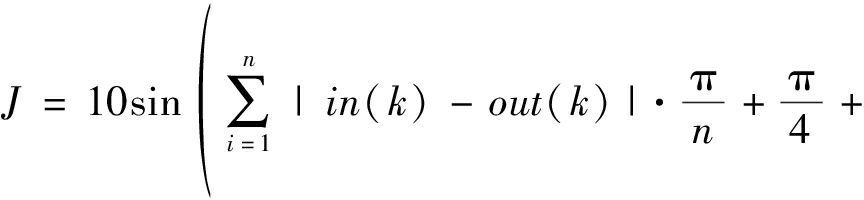
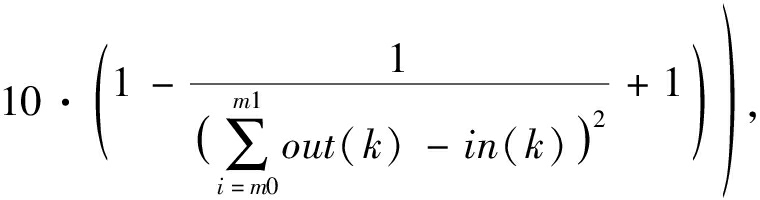
(12)
式中:in(k)为第k个采样输入值;out(k)为第k个采样输出值。
2.2 遗传算法实现
遗传算法寻优的过程采用了概率化的方法,该算法可以不根据确定的规则或者不需要固定的寻优函数参数进行计算,通过设定的概率影响参数取值的改变,该算法可以自动获取参数较优取值并且优化搜索空间,做到自适应地调整搜索方向。其步骤流程如图3所示。
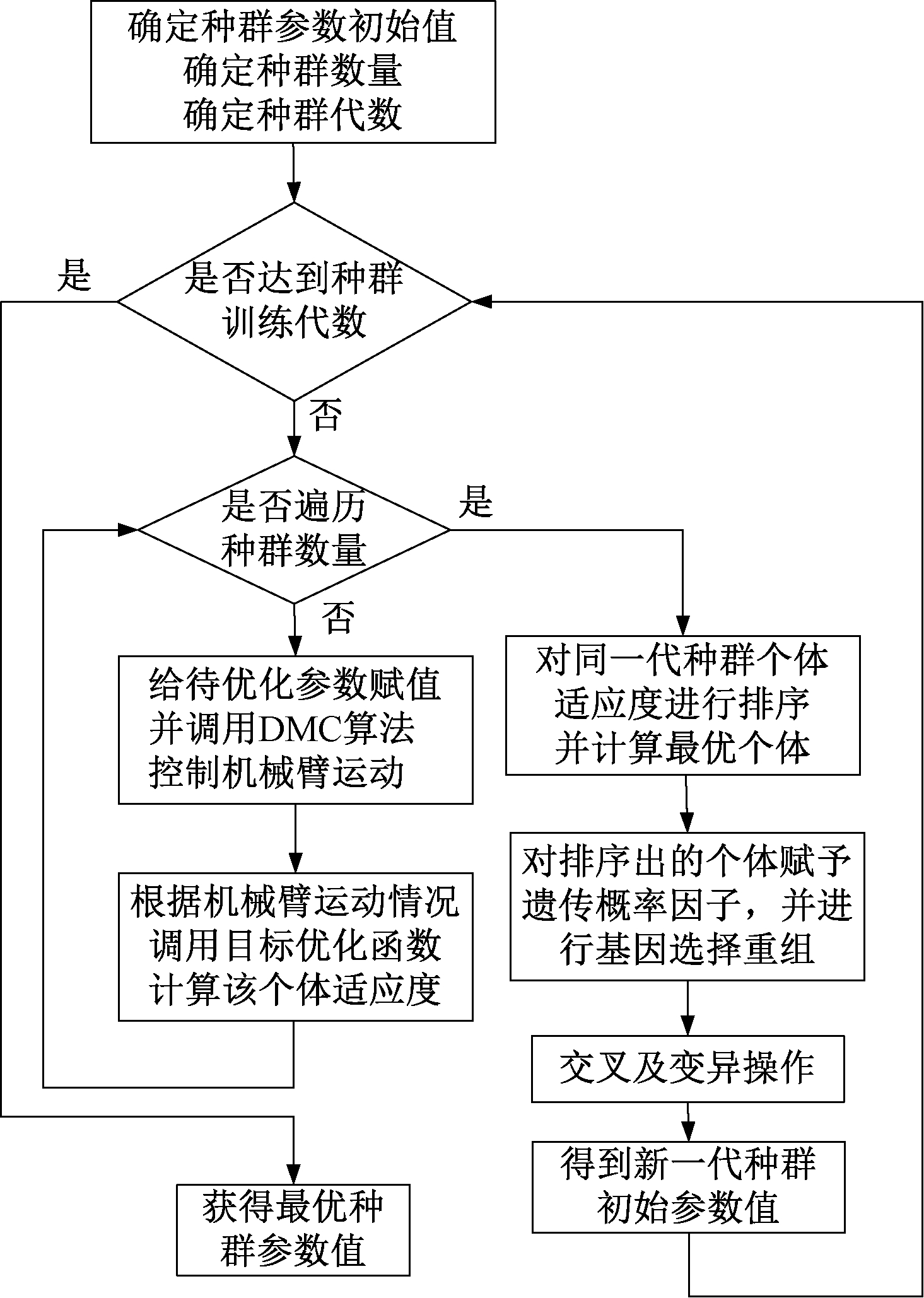
图3 遗传算法流程
Figue 3 Process of genetic algorithms
遗传算法重要环节的具体算法实现如下:
(1)计算适应度与选择、复制。在本文所设计的遗传算法中,本步骤以目标优化函数计算得到的评价值作为输入,经过取倒数、求和、增加最优值适应度、排序等操作,将优化函数所返回的种群评价值序列调整为有序的、评价值较低的种群(即响应输出较优)所占比例较多的新序列,并将其复制给下一代种群。适应度值计算公式为:
f=1/J,
(13)
式中:f为适应度;J为目标优化函数计算值。
(2)二进制编码及变异操作。变异操作模拟生物进化过程中的基因突变方法,以小概率随机地改变染色体字符串某一位的值[14]。笔者在对各个种群个体取值(保留小数点前3位)进行二进制编码的基础上,改变对任意基因所在位点采取固定变异概率值的操作模式。此种方法既可以保证种群个体变异的稳定性,又可以增加种群基因变异可能性,进而优化算法效果。
(3)交叉操作。一般交叉操作针对被选择的个体,以某种交叉方式交换两个字符串相对应的基因,从而产生两个新的个体[15]。此种字符串的交叉方法在十进制数值高位所对应的二进制字符串点位产生交叉时,会有可能造成种群个体较大程度的改变,因此,笔者采用一种改进的方法对交叉操作进行适当的方向引导。在笔者所用遗传算法中,同一种群两个相邻个体会通过加权相加的形式得到两个新的个体,其权值由交叉概率决定。通过交叉操作计算新的相邻种群个体取值公式为:
(14)
式中:.为一对相邻种群个体取值;p为交叉概率。
3 算法验证
3.1 建立被控对象
在MATLAB/SIMULINK中,利用机器人开发工具箱Robotics Toolbox的库函数,并使用其中的slaccel S-函数作为被控对象的传递函数,该函数可以在以关节转矩、关节转角与关节角速度为输入的情况下,计算出关节角加速度,进而求出下一时刻的关节角速度与关节转角。笔者以单关节机械臂作为被控对象,在使用slaccel S-函数时,指定关节角的初始位置q=0,并指定单关节机械臂模型,其D-H表参数[θ,d,a,δ]=[q,0,0,1.570 8],并在slaccel S-函数中定义其为无摩擦模型。为使被控对象的响应更贴近实际状态,将计算获得的角速度通过Coulomb friction函数反馈回关节的力矩输入处,即相当于按照当前状态计算关节转动所受摩擦力并将其作为负反馈作用在输入力矩上。被控对象SIMULINK框图如图4所示。
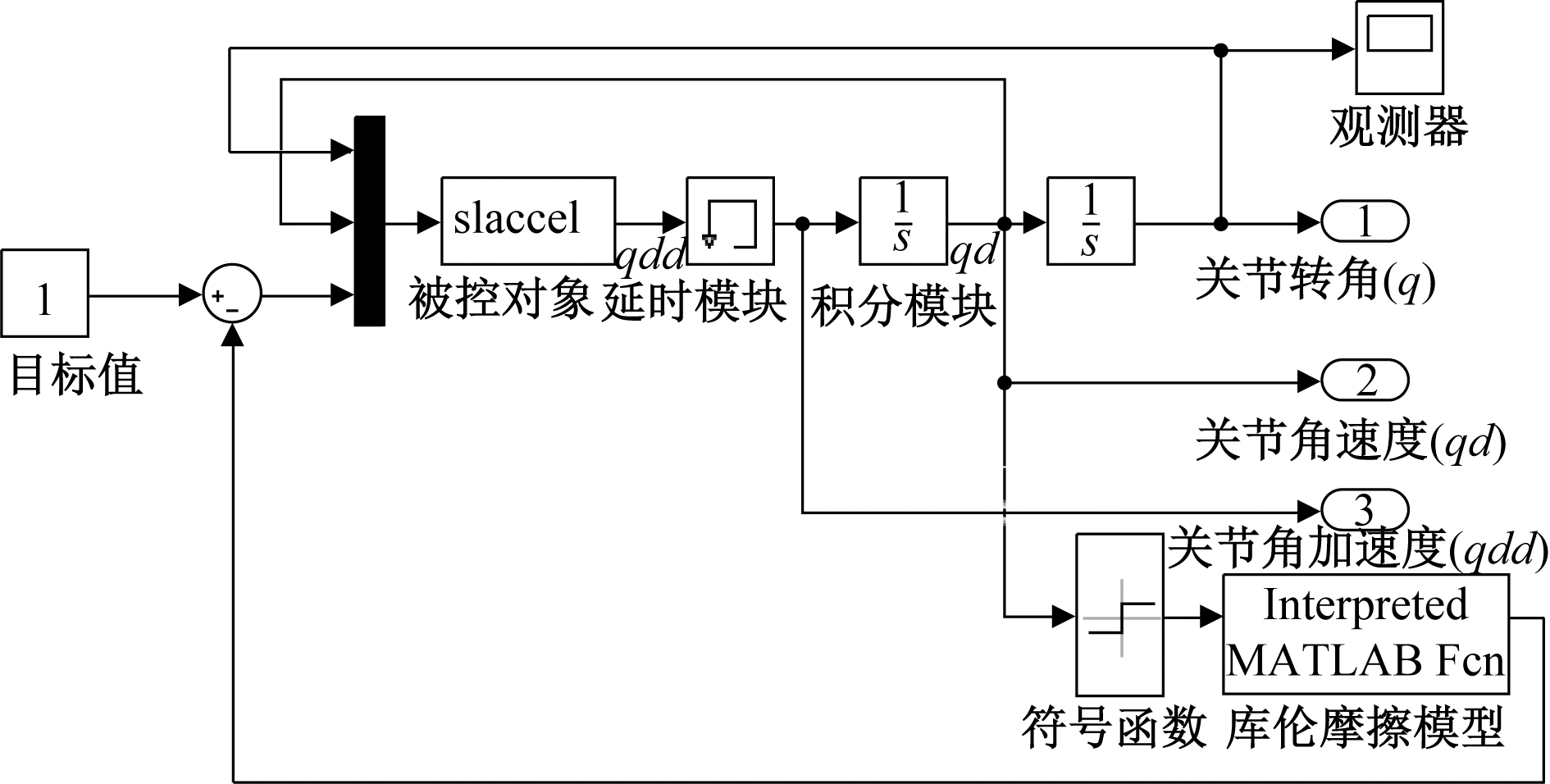
图4 被控对象SIMULINK仿真示意图
Figue 4 SIMULINK simulation sketch of controlled object
3.2 仿真结果
仿真中首先测得被控对象单位阶跃响应并按照固定周期采样得到模型参数向量.。由于所使用单关节机械臂模型的单位阶跃响应不收敛,故在采样被控对象的单位阶跃响应时,添加一个PID控制器作为中间环节,使整个系统的单位阶跃响应处于收敛状态。如此采样得到的模型参数向量.如表1所示。选取采样点个数为30,选取采样间隔时间为仿真时间T=0.08。
使用模型参数向量.作为已知参数,以DMC算法为基础,构造出系统的控制器,进一步地,使用遗传算法训练并得到最优控制权矩阵参数。DMC算法各主要参数取值如表2所示。
表1 模型参数采样值
Table 1 Sampling values of model parameters
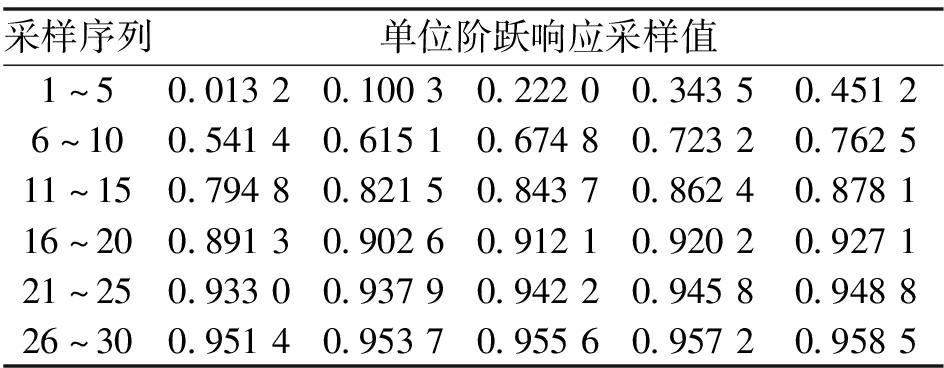
采样序列单位阶跃响应采样值1~50.01320.10030.22200.34350.45126~100.54140.61510.67480.72320.762511~150.79480.82150.84370.86240.878116~200.89130.90260.91210.92020.927121~250.93300.93790.94220.94580.948826~300.95140.95370.95560.95720.9585
表2 DMC算法各主要参数取值
Table 2 Value of major parameters of DMC

QRh30阶单位对角阵遗传算法待优化值组成的对角阵元素均为1的30×1矩阵
在搭建GA算法优化DMC方法的控制系统框架以及确定各主要参数的取值之后,笔者设计了两个对比仿真实验以验证优化DMC方法的效果,实验设置如表3所示。
表3 实验设置
Table 3 Experiment setup

对比实验1对比实验2不同迭代代数遗传算法使用优化后的DMC算法优化DMC方法效果对比与普通PID控制器算法控制被控对象的效果对比
在对比实验1中,根据本项目规模大小,分别选取遗传算法的迭代代数为10、20、40代,选取遗传算法种群数为20,并通过离线调参的方法确定控制权矩阵的最优取值。使用第10、20、40代所得到的最优取值作为控制权矩阵的对角线参数,并且将遗传算法对种群的两个参数的优化区间分别设定为[100,500]以及[0,1]。在同种输入作用下,得到3组不同的控制权矩阵参数值,其取值分别为(379.640,0.188)、(383.371,0.211)、(308.224,0.109),3组值分别对应迭代代数为10、20、40代的仿真情况,并且根据3组矩阵参数取值进行控制算法仿真,得到仿真输出曲线,并对其进行比较,经过比较发现迭代代数为40代的控制权矩阵参数值所对应的仿真结果的响应速度最快,并且稳定误差最小,但相应其超调量最大,而迭代代数为10代的控制权矩阵参数值所对应的仿真结果相反。综合考量可以发现,迭代代数为20代的控制权矩阵参数值所对应的仿真结果在3者之中为最优结果,仿真结果比较如图5所示。
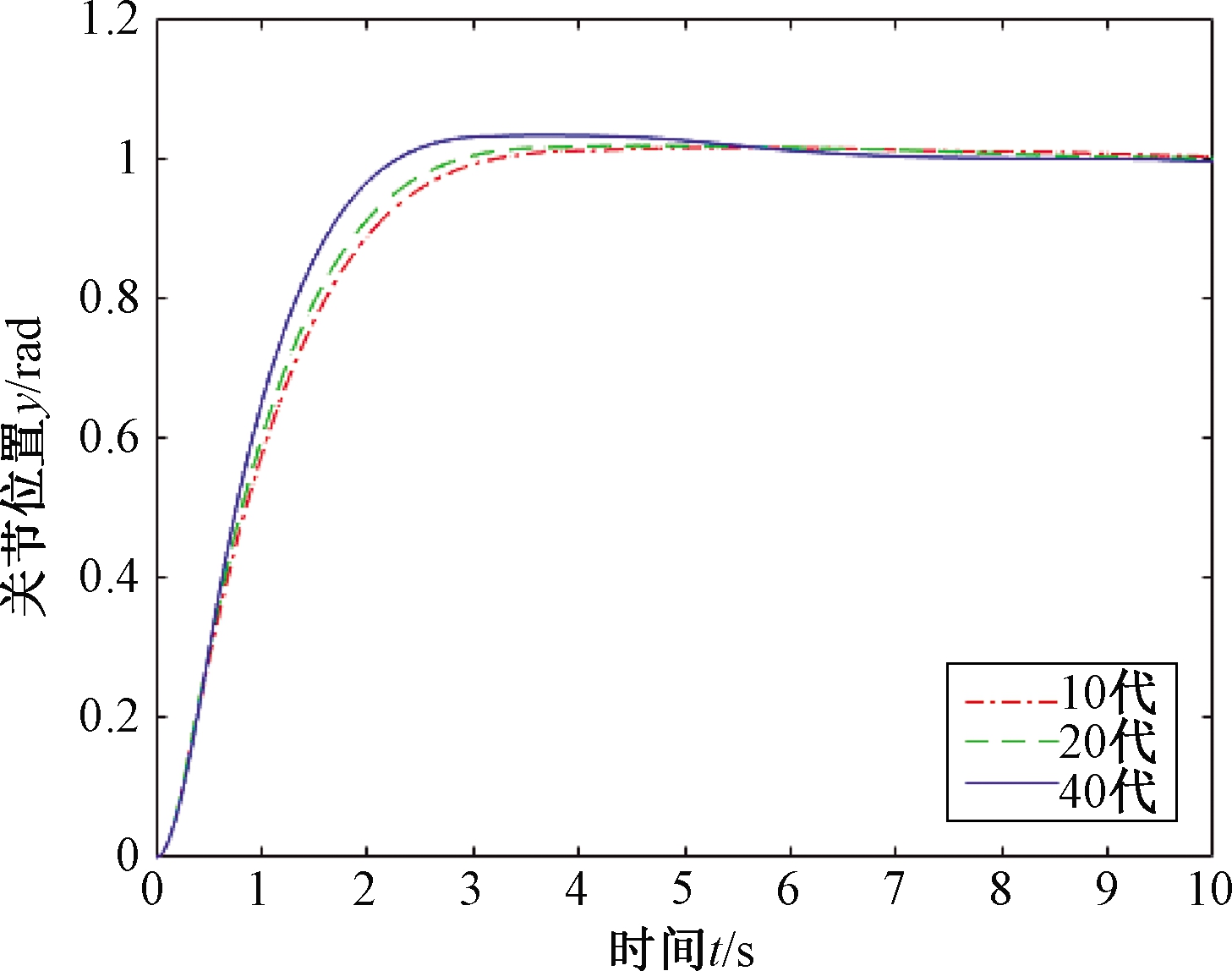
图5 不同迭代代数遗传算法所得结果对比
Figue 5 Comparison of results obtained by different population era of GA
此外,分析3组矩阵参数取值的情况可以发现,第10、20代两组参数取值比较接近,而40代参数取值相对另外两组较远,故存在3组参数取值不都在同一局部取值域的可能。为验证优化效果,以40代矩阵参数取值为参考,选取(308.224,0.900)与(308.224,0.120)、(300, 0.109)、(315, 0.109)4组矩阵参数取值做对比,对比发现40代矩阵参数取值为区域响应速度较快值,而其他4组取值的仿真响应速度较接近,寻优效果明显。但也同时表明,该方法较易陷入局部最优解,对比结果如图6所示。
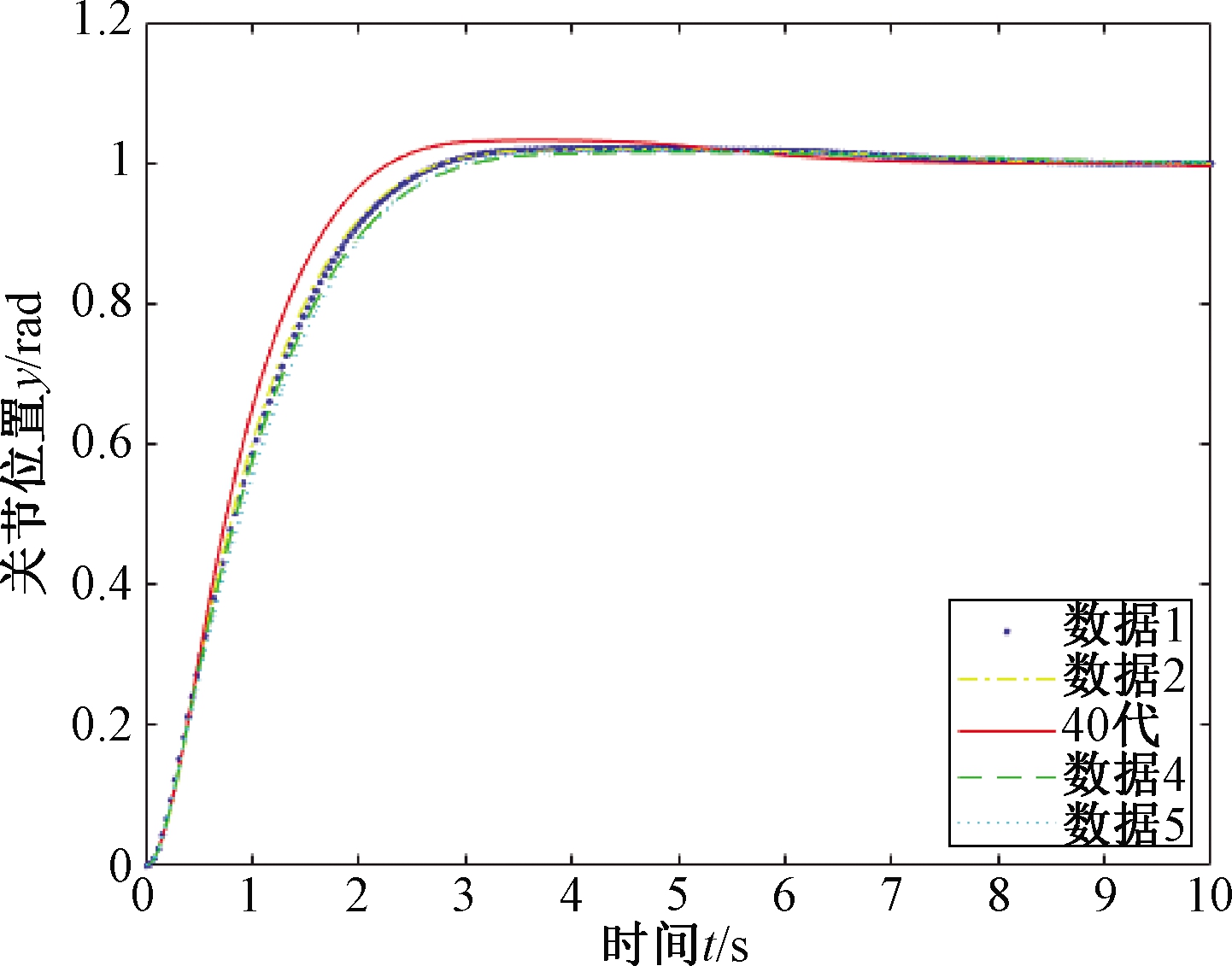
图6 优化效果验证
Figue 6 Validation of optimization effect
在对比实验2中,对比普通PID控制器得到的被控对象输出以及优化DMC算法得到的被控对象输出,可以发现DMC算法相比于所采用的一般PID控制器响应时间慢,且响应时间相对较快的DMC算法仿真结果具有相对明显的超调量。但使用DMC算法所得到的输出响应稳态误差在0.5%以内,远小于PID控制器控制时的稳态误差,对比结果如图7所示。
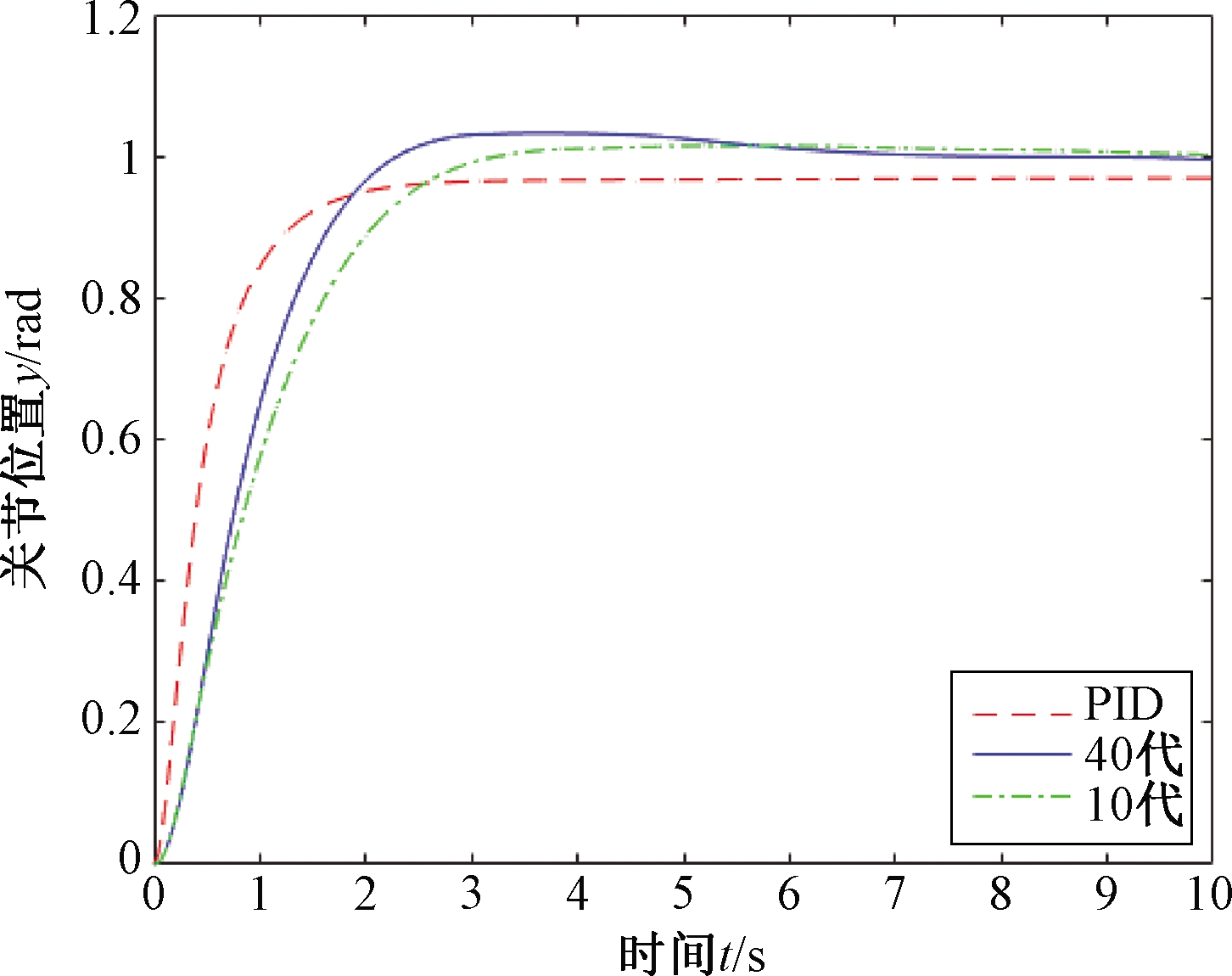
图7 优化DMC算法及普通PID算法效果对比
Figue 7 Comparison of results obtained by augmented DMC algorithm and normal PID algorithm
4 结论
笔者设计了遗传算法优化的DMC控制,并应用Robotics Toolbox实现了控制系统的仿真。仿真结果表明,通过遗传算法的离线调参,仿真系统可以较快(只通过数十代的迭代)地确定局部的DMC算法控制参数的近似最优值。经过离线调参之后的DMC算法控制性能较优,该算法虽然响应速度较慢,但通过遗传算法,在合理的局部取值域中寻找到的控制权矩阵参数值,可以在保证较快响应速度的基础上,产生较小的超调量及稳态误差。该算法不依赖于控制对象的准确模型,在控制参数选择得当时,可以取得较为理想的控制效果。
[1] 蔡自兴,谢斌.机器人学[M].3版.北京:清华大学出版社,2015.
[2] 杨丽华,赵文杰.基于MATLAB的广义预测控制设计方法[J].仪器仪表用户,2012,19(2):82-84.
[3] 袁宇鹏,胡杨,李军,等.基于动态矩阵控制的自主移动机器人模型预测控制方法研究[J].重庆邮电大学学报(自然科学版),2018,30(4):111-117.
[4] 穆瑞杰.基于遗传算法的地铁车站引导标识布点探析[J]郑州大学学报(工学版), 2018, 39(1):77-81.
[5] 惠晶,王存款,朱贺.基于动态矩阵的APF预测控制策略研 究[J].电力电子技术,2010,44(5):28-30.
[6] 张奇智,张彬,张卫东.随机延迟网络控制系统中的分段时戳动态矩阵控制[J].控制与决策,2005,20(8): 873-877.
[7] 戴连奎.SISO动态矩阵控制的鲁棒稳定性条件[J].自动化学报,2001,27(3): 367-370.
[8] 吉根林.遗传算法研究综述[J].计算机应用与软件,2004,21(2):69-73.
[9] 甄文祥,王文田.遗传算法及其应用[J].计算机应用研究,1994,11(5):9-10.
[10] GROSSWINDHAGER S, VOIGT A, KOZEK M.Predictive control of district heating network using fuzzy DMC[J].International journal of modelling identification and control, 2012,19(2): 241-246.
[11] 罗刚,金炜东,李治.动态矩阵控制参数的满意优化[J].信息与控制,1999,28(1):75-79.
[12] 郭伟,姚少杰.基于时域的PID动态矩阵控制算法改进[J].仪器仪表学报,2007,28(12): 2174-2178.
[13] 申涛,诸静.多输入/多输出系统动态矩阵控制鲁棒稳定性[J].控制理论与应用,2005,22(3):445-448.
[14] 白风.基于数据压缩处理算法的数据采集与监控系统的研究[D].阜新:辽宁工程技术大学,2009.
[15] 王文庆,杨楠.基于改进遗传算法的PID参数整定研究[J].计算机与数学工程,2018,46(12):2603-2606,2610.