0 引言
锚杆钻机的性能直接决定了整个工程的进度和质量.钻机的执行机构由推进机构和回转机构两部分构成，二者协调配合，实现对岩石的破碎和钻进.
为实现钻机的高效工作，控制钻机的推进与回转过程是其核心问题.已有研究主要集中在利用推进力的自适应控制来适应岩层变化，从而提高钻机打眼效率[1].然而，钻机在推进旋转破岩的过程中，除了推进力外，回转速度也会受到岩层性状的影响，这也会影响旋转切削和破岩钻孔效果，是提高锚固速度和效率的关键因素之一.目前，钻机旋转速度的控制大都依据工程技术人员经验和意愿来实现，无法根据岩层性状自适应调节，不能实现钻机的高效运行，且关于回转速度自适应控制方法的相关研究较少.
由于锚杆钻机的推进回转机构采用液压油作为动力源，所以钻机控制系统本质上是电液控制系统.目前，电液系统的控制已日趋成熟.Alleyne A等[2]采用PID控制解决了电液伺服系统的位置和力跟踪问题.彭金柱等[3]提出基于DRNN网络的改进鲁棒控制方法，实现轮式机器人控制.针对液压系统固有的非线性和参数不确定，Guo等[4]提出基于高增益观测器的输出反馈控制.该控制器在一定程度上能够保证系统的稳定性，但是控制性能会受到摩擦力和外负载干扰的影响.郭栋等[5]将自抗扰技术应用到钢坯闪光对焊中液压顶锻力控制，提高了系统的鲁棒性以及力伺服响应的速度.然而，锚杆钻机回转系统存在高度非线性、参数时变性与不确定性，这些都使回转系统控制困难.考虑到自抗扰控制器对系统扰动具有较好的抑制作用，笔者采用自抗扰控制器实现锚杆钻机转速的控制.
自抗扰控制器(active-disturbance-rejection co-ntrol，ADRC)具有较多待整定参数，人工试凑法耗时长，且无法兼顾控制系统的各方面要求.李述清等[6]提出利用系统时间尺度的控制器参数整定方法,推导出二阶系统的时间尺度参数整定计算公式.但是，该方法仅针对二阶系统，具有一定局限性，且算法复杂度较高.李海生等[7]和刘丁等[8]分别采用基于惩罚策略的浮点遗传优化算法和自适应遗传算法，实现自抗扰控制器的寻优.
Shi[9]于2011年提出头脑风暴优化(brain storm optimization，BSO)算法，它模拟人类头脑风暴会议过程，能够较好平衡全局搜索和局部搜索能力，目前已在直流无刷电机优化设计、多卫星编队、螺线管优化等诸多优化问题上取得了成功.同时，算法的分类机制和个体更新方法大大提高了粒子的搜索能力.该机制表明，BSO算法在其他优化领域同样具有巨大的应用潜力.基于此，笔者提出基于头脑风暴算法的自抗扰控制器参数整定策略，并将其用于钻机回转速度控制.
1 锚杆钻机回转系统建模
锚杆钻机回转系统的基本组成如图1所示.
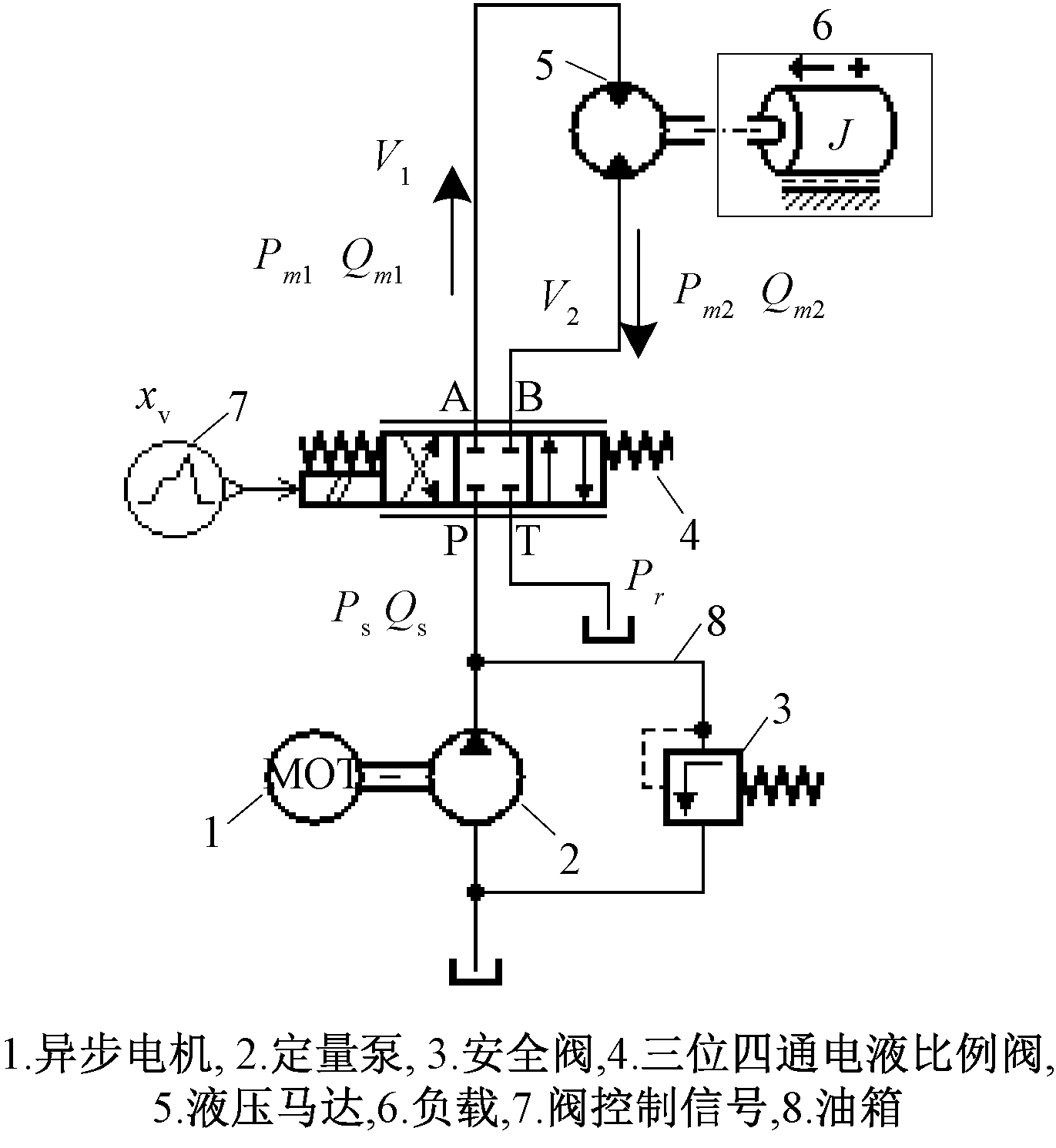
图1 钻机回转系统原理图
Fig.1 The schematic diagram of the rotating system
一台异步电机带动定量泵旋转，使泵出油液经过三位四通电液比例阀，进入锚杆钻机液压马达，控制钻机马达正/反转，从而实现钻杆的钻进和退回.通过改变比例阀开度并调节液压马达输入流量，进而控制钻机转速.
系统核心参数如表1所示.系统压力由泵出口位置安装的16 MPa安全阀提供，钻机转速通过改变比例阀开度进行控制.通过分析液压马达和三位四通电液比例阀两个核心部件的动态、静态传递函数关系，建立锚杆钻机回转系统数学模型.
三位四通电液比例阀根据输入的电流控制信号iv，产生阀芯相应位移xv，通过阀口流量Qv改变负载流量大小QL.记PL=Pm1-Pm2,其阀口流量Qv满足:
xv=kviv；
(1)
(2)
表1 钻机回转系统核心部件相关参数及含义
Tab.1 The anchor-hole drill rotary system core components related parameter and its meaning
关键部件参数含义三位四通电液比例阀Ps/MPa回转系统供油压力PL/MPa负载压力Pm1/MPa马达进油腔压力Pm2/MPa马达回油腔压力Cd流量系数Wv/m阀面积梯度kv电液比例阀放大系数ρ/(kg·m-3)油液密度液压马达θm/rad液压马达转角Qm1/(L·min-1)马达进油腔流量Cmi/(N·s·m-1)马达内泄漏系数V1/m3马达进油腔和进油管道的可控容积βe/(N·m-2)油液有效体积弹性模量Jt/(kg·m2)马达轴等效总惯量Dm/(m3·r)液压马达排量Qm2/(L·min-1)马达回油腔流量Cme/(N·s·m-1)马达外泄漏系数V2/m3马达回油腔和回油管道的可控容积ML/(N·m)负载转矩Bm/(N·s·rad)液压黏性阻尼系数
为便于分析，对上述非线性阀口流量关系进行线性化处理[10]，简化为:
Qv=Kqxv-KcPL.
(3)
液压马达将液压泵提供的液体压力动能转变为其输出轴的机械能(转速或转矩).在回转系统中，根据流量的连续性，建立液压马达的动态微分方程[10]：
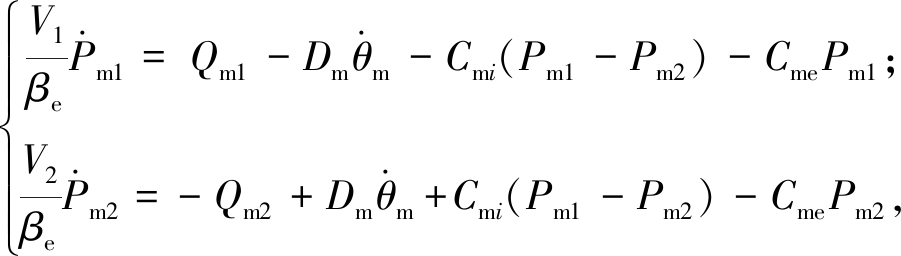
(4)
式中:V1=V01+Dmθm，V2=V02-Dmθm.V01和V02分别为两腔初始容积，满足V01=V02=V0.负载流量满足:
(5)
联立式(4)和式(5),得
QL=
(6)
令Ctm为液压马达总泄漏系数，满足Ctm=(Cmi+Cme)/2；Vt为液压马达两腔及连接管道的总压缩容积，满足Vt=2V0；由于Ps=Pm1+Pm2，所以
则简化式(6)为:
(7)
根据牛顿第二定律，建立上述阀控液压马达系统的负载动力学模型为:
(8)
通常，由于马达的外泄漏量较小，所以在忽略马达外泄漏量条件下，负载流量近似等于阀口流量，即QL=Qv.由此，结合式(3)、式(7)和式(8)，记Kce=Kc+Ctm为总的流量压力系数，得到锚杆钻机回转系统传递函数为:
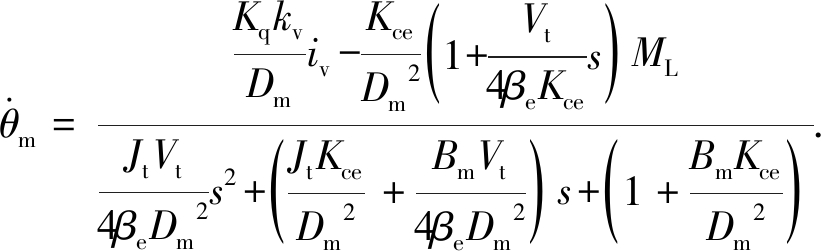
(9)
由式(9)可知，钻机回转系统是一个存在非线性和时变因素，以及多类干扰的典型二阶系统.
2 锚杆钻机转速最优自抗扰控制
自抗扰控制系统的控制器设计不依赖于系统具体模型，只需考虑系统的相对阶数，设计简单.因此，笔者给出一类钻机转速的自抗扰控制策略.然而，由于自抗扰控制器待整定参数较多，人工整定耗时且效果不佳，所以提出一种基于头脑风暴算法的自抗扰控制器参数自整定方法.另外，根据钻进岩层条件来估算最优转速，作为自抗扰控制器的设定值，提供其转速跟踪依据.锚杆钻机转速的最优自抗扰控制系统框图如图2所示.
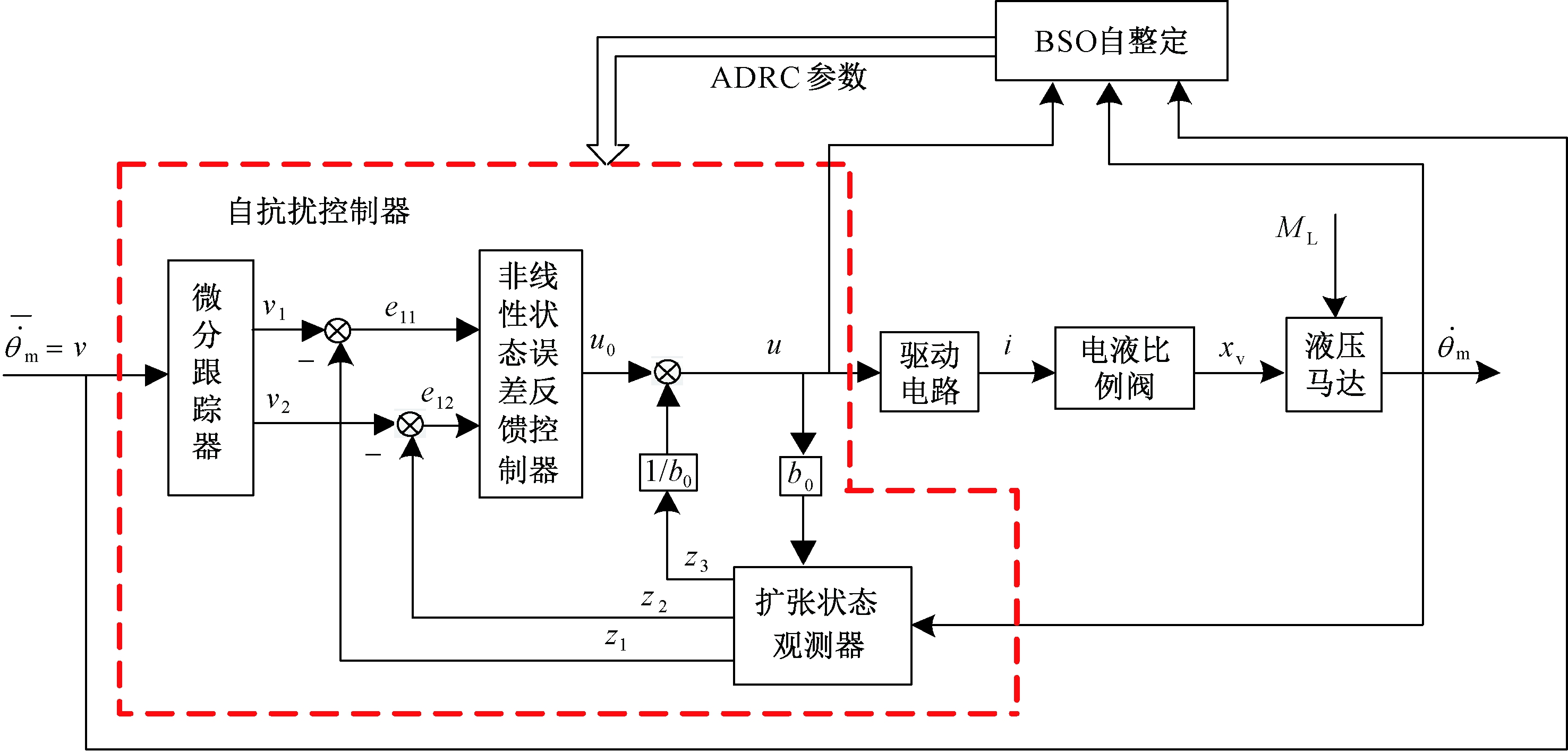
图2 锚杆钻机回转系统控制框图
Fig.2 The control block diagram of the rotating system in anchor-hole drills
2.1 最优转速获取
根据比留柯夫的研究可知，针对某一类岩石，存在一个最优回转转速，且该最优转速与岩石普式硬度系数和钻杆直径的平方根乘积成反比[11].在该转速下，可得到最大的钻进速度.当回转转速超过其最优值时，随着回转转速增大，钻刃切削时的岩石变形得不到充裕时间向前传递，已破碎下来的岩屑来不及排除而造成重复破碎，钻进速度反而降低，造成钻杆严重损坏.
令D为钻头直径，c为切削速度常数，f为岩石硬度系数，则钻机最优回转速度
为：
(10)
2.2 自抗扰控制器结构
自抗扰控制器主要由三个部分组成[12]：微分跟踪器(tracking differentiator，TD)、扩张状态观测器(expansion state observer，ESO)和非线性状态误差反馈控制器(nonlinear state error feedback，NLSEF)，如图2所示.
微分跟踪器用于生成合理的过渡过程，提取相应的微分信号.假设R为被控量给定值，v1和v2分别为R在过渡过程中的期望序列及其一阶微分，h为采样步长，h0为滤波因子，fhan()为最优控制函数[12].由此，建立微分跟踪器模型为：
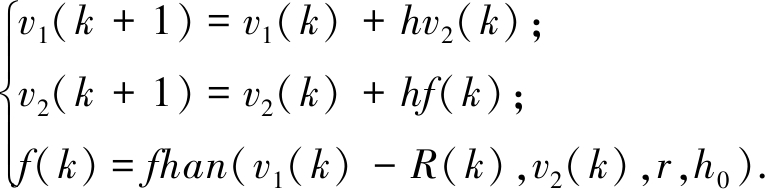
(11)
令z1和z2为状态变量，z3为总干扰量，扩张状态观测器用于实时估计内外扰动总和.
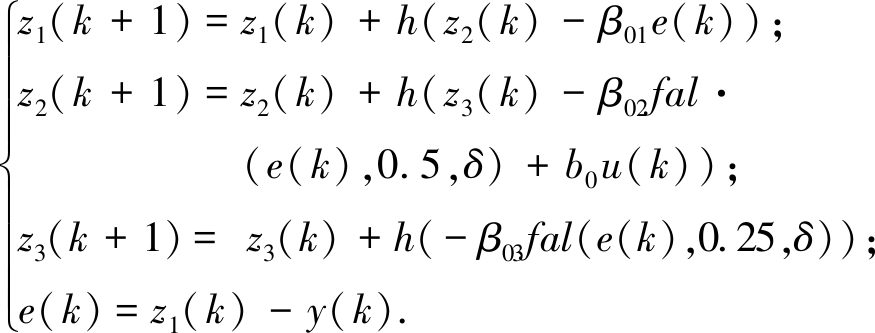
(12)
式中:fal()为非线性函数[12]；观测器增益β01、β02、β03和参数b0为待整定参数.
fal()为非线性函数，
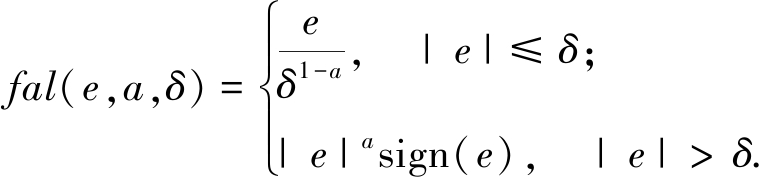
(13)
非线性状态误差反馈控制率用于对TD和ESO的输出量进行非线性组合，并对总干扰进行补偿，记为：
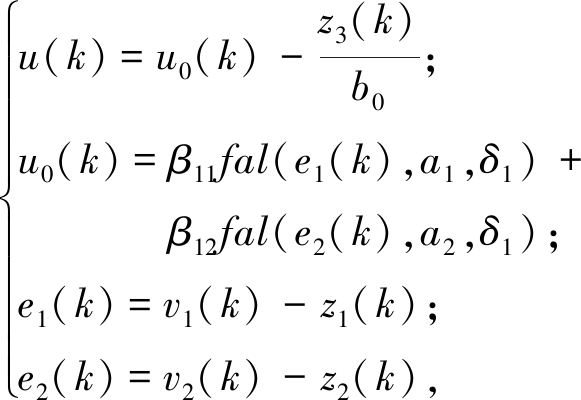
(14)
式中:β11和β12为控制器的比例增益和微分系数；u0为非线性反馈输出；非线性系数a1、a2满足0<a1<1<a2，本文选取a1=0.75，a2=1.25；δ1=0.001.
2.3 自抗扰控制器参数的头脑风暴整定方法
自抗扰控制器中，ESO的β01、β02、β03和b0，以及NLSEF的β11和β12，都会对回转速度的控制性能产生影响.因此，采用头脑风暴优化算法对上述参数进行整定，以获得满意的控制效果.
由于自抗扰控制器中待整定参数均为实数，所以进化个体xi=(β01,β02,β03,β11,β12,b0)采用实数编码[13].采用时间乘绝对误差积分准则这一综合控制性能指标作为目标函数[14].另外，由于转速调节在实际系统中不允许超调，所以在目标函数中增加了系统超调量.记系统的瞬时误差为e(t)，超调量为Mp，时间乘绝对误差和超调量之间的权值为ω1、ω2，得到综合目标函数为：
J=
(ω1t|e(t)|+ω2|Mp|)dt.
(15)
头脑风暴算法的核心在于通过变异算子生成新个体.记xij(t)和
分别为第i个个体的第j维变量变异前后的取值，λ～N(μ,σ)为服从高斯分布的随机数，β～U(0,1)为服从均匀分布的随机数，ξ(t)为变异尺度，c为斜率.t和T分别为进化代数和最大迭代次数，则变异算子为：
(16)
(17)
基于头脑风暴优化算法的自抗扰控制器参数整定方法的具体流程如下.
Step 1初始化. 随机生成n个个体，构成种群.
Step 2评价.将每个个体所对应的自抗扰控制器参数，代入钻机转速控制系统，仿真运行获得其目标值.
Step 3聚类.采用k- means聚类算法，将n个个体聚为m个类，依据每个个体的目标值，对每个类中个体排序，选取具有最佳目标值的最优个体作为聚类中心；产生随机数R1∈[0,1]，判断是否满足R1<P1.如果满足，则随机选择一个聚类中心;否则，随机生成一个个体替代该聚类中心.
Step 4变异.产生随机数R2∈[0,1]，判断是否满足R2<P2.如果满足，则执行Step 4.1；否则，执行Step 4.2.
Step 4.1随机选择一个类，依据随机数R3∈[0,1]，判断是否满足R3<P3.如果满足，则依据该类的中心，通过变异产生新个体；否则，从该类中随机选择一个个体，通过变异产生新个体.
Step 4.2随机选择两个类，依据随机数R4∈[0,1]，判断是否满足R4<P4.如果满足，则依据两类中心，通过变异产生新个体；否则，从两类中各随机选择一个个体，通过变异产生新个体.
Step 4.3如果新生成个体优于原有个体，则采用新个体替代原有个体.
Step 5如果达到最大迭代次数，则终止进化，并输出全局最优解作为控制系统最优参数；否则，跳转到Step 2.
3 实验仿真与结果分析
为验证笔者所设计的锚杆钻机最优自抗扰控制策略的有效性，采用AMESim和Matlab联合仿真平台搭建控制系统，如图3所示.AMESim用于锚杆钻机回转系统的物理模型搭建，Matlab实现基于头脑风暴的转速最优自抗扰控制算法.设定头脑风暴优化算法参数如表2所示.针对表3所示晋城寺河矿巷道顶板岩石状况[15]，实验分析了锚杆钻机在单一围岩钻进时所提控制器性能,验证了岩层性状波动情况下所提控制器的鲁棒性.
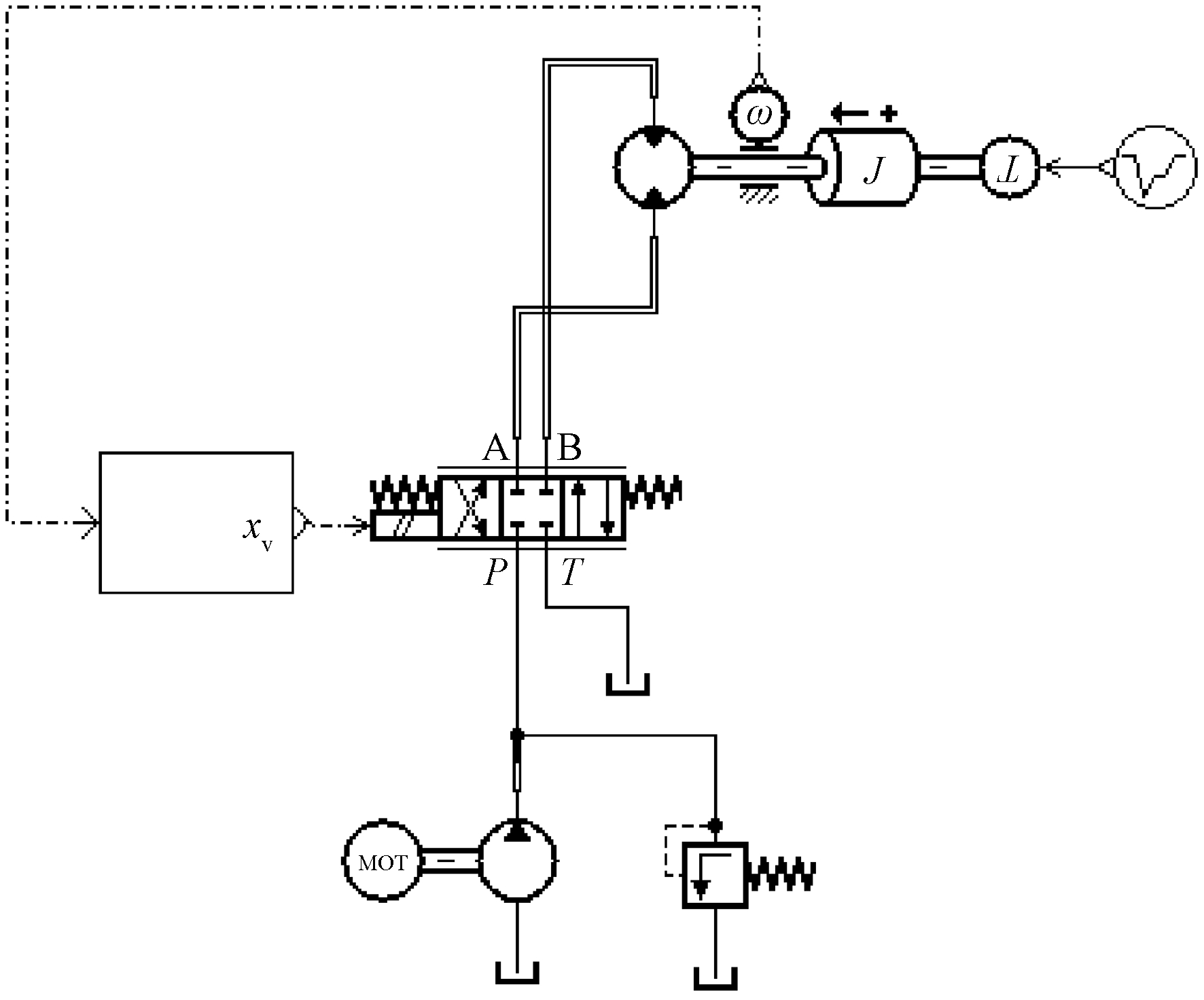
图3 锚杆钻机回转系统的联合仿真平台
Fig.3 The joint simulation platform of the anchor drilling′s rotary system
表2 头脑风暴优化算法参数
Tab.2 Parameters of BSO algorithm
nmP1P2P3P4cT10050.20.80.40.520100
表3 晋城寺河矿巷道顶板围岩性状
Tab.3 The properties of the rock stratum in JinCheng SiHe coal mine
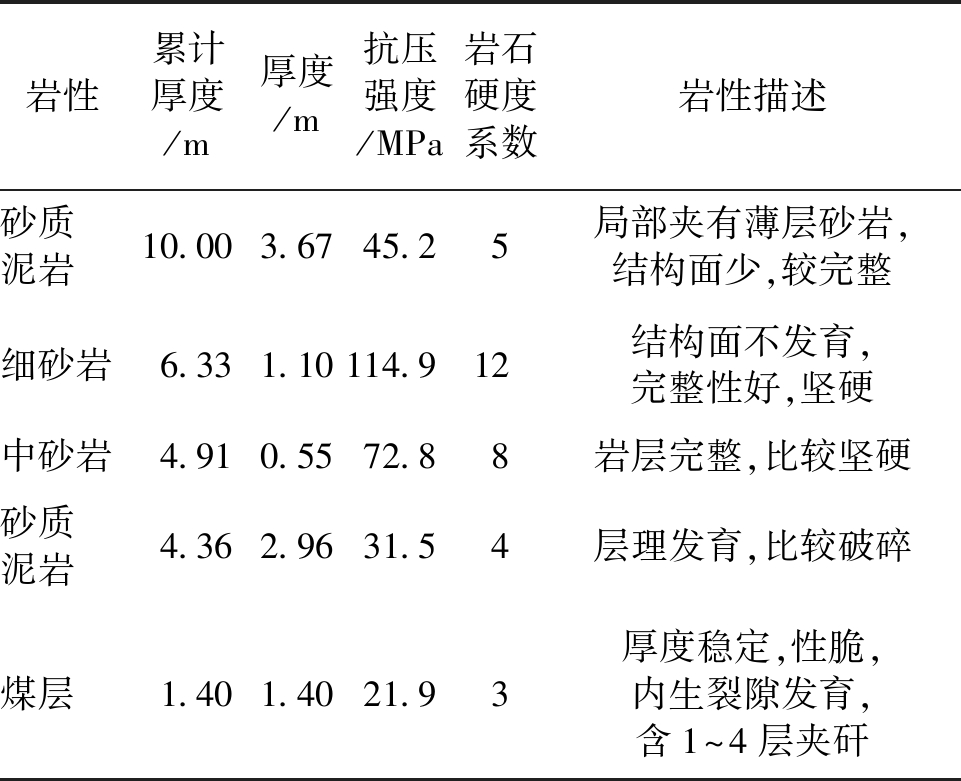
岩性累计厚度/m厚度/m抗压强度/MPa岩石硬度系数岩性描述砂质泥岩10.003.6745.25局部夹有薄层砂岩,结构面少,较完整细砂岩6.331.10114.912结构面不发育,完整性好,坚硬中砂岩4.910.5572.88岩层完整,比较坚硬砂质泥岩4.362.9631.54层理发育,比较破碎煤层1.401.4021.93厚度稳定,性脆,内生裂隙发育,含1～4层夹矸
3.1 单一围岩条件下最优转速跟踪性能
以巷道顶板最常见的砂质泥岩为例，其岩石硬度系数为f=5.由此根据式(10)，得到砂质泥岩的钻机最优旋转速度
采用头脑风暴优化算法，分别对自抗扰控制器和传统PID控制器进行参数寻优.
设定待整定参数的搜索范围：β01∈(0,300),β02∈(0,1 000),β03∈(0,1 000),β11∈(0,700),β12∈(0,50),b0∈(0.01,10),kp∈(0.1,200), ki∈(0.1,0.8),kd∈(0.1,5).
依照图4所示的头脑风暴优化算法参数寻优过程，获得控制器整定参数.①BSO-ADRC：r=9 965.254 8，h0=0.005 2，β01=30.036 1，β02=1 000，β03=0.021 ，β11=485.672 5，β12=0，b0=5.647 1;② BSO-PID：kp=105.264 7，ki=0.103 3， kd=2.996 4.
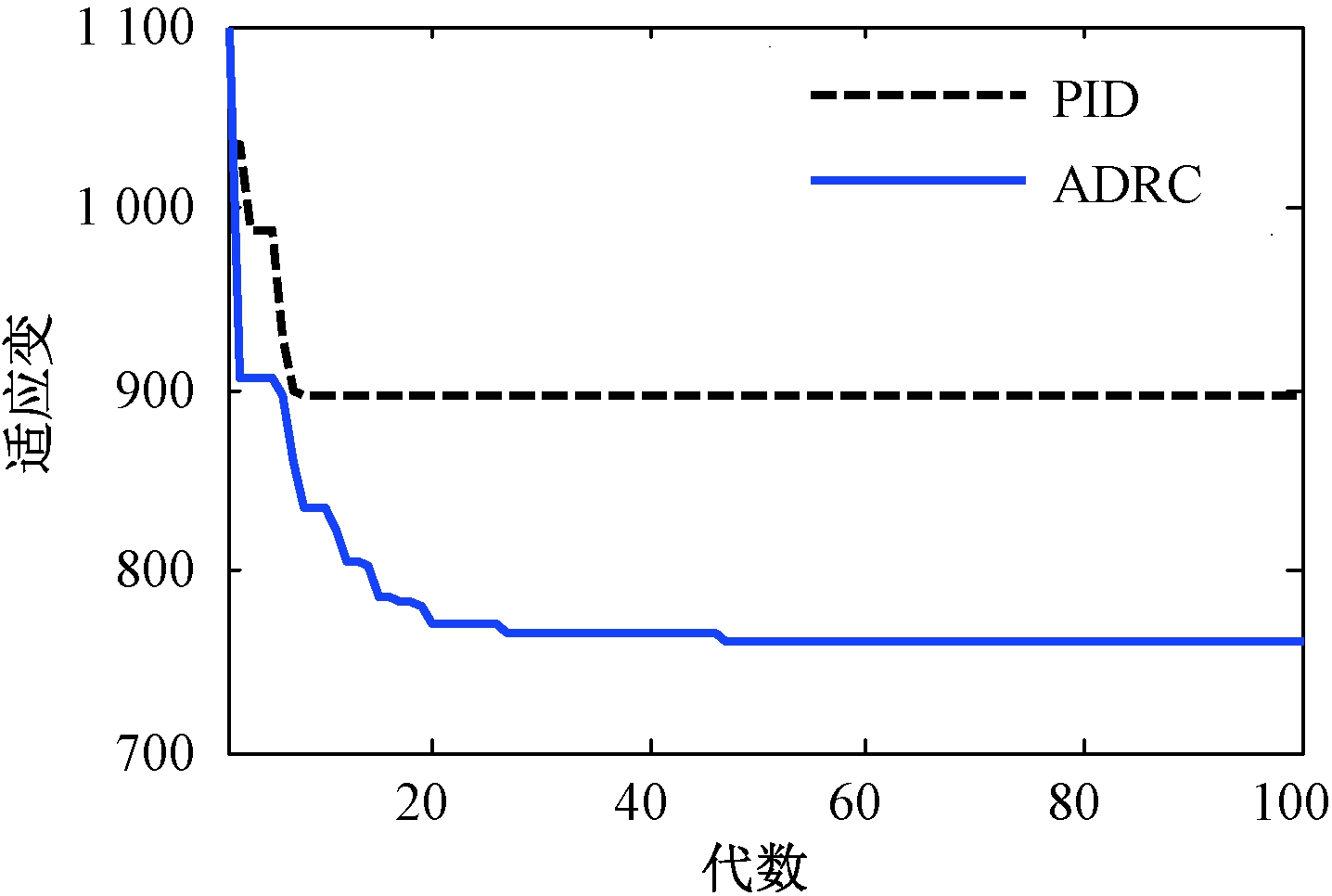
图4 基于BSO的控制器参数寻优过程
Fig.4 The evolution process of BSO-based controller
设定控制器参数为寻优获得的最优参数，得到单一围岩条件下的转速控制性能，如图5所示.
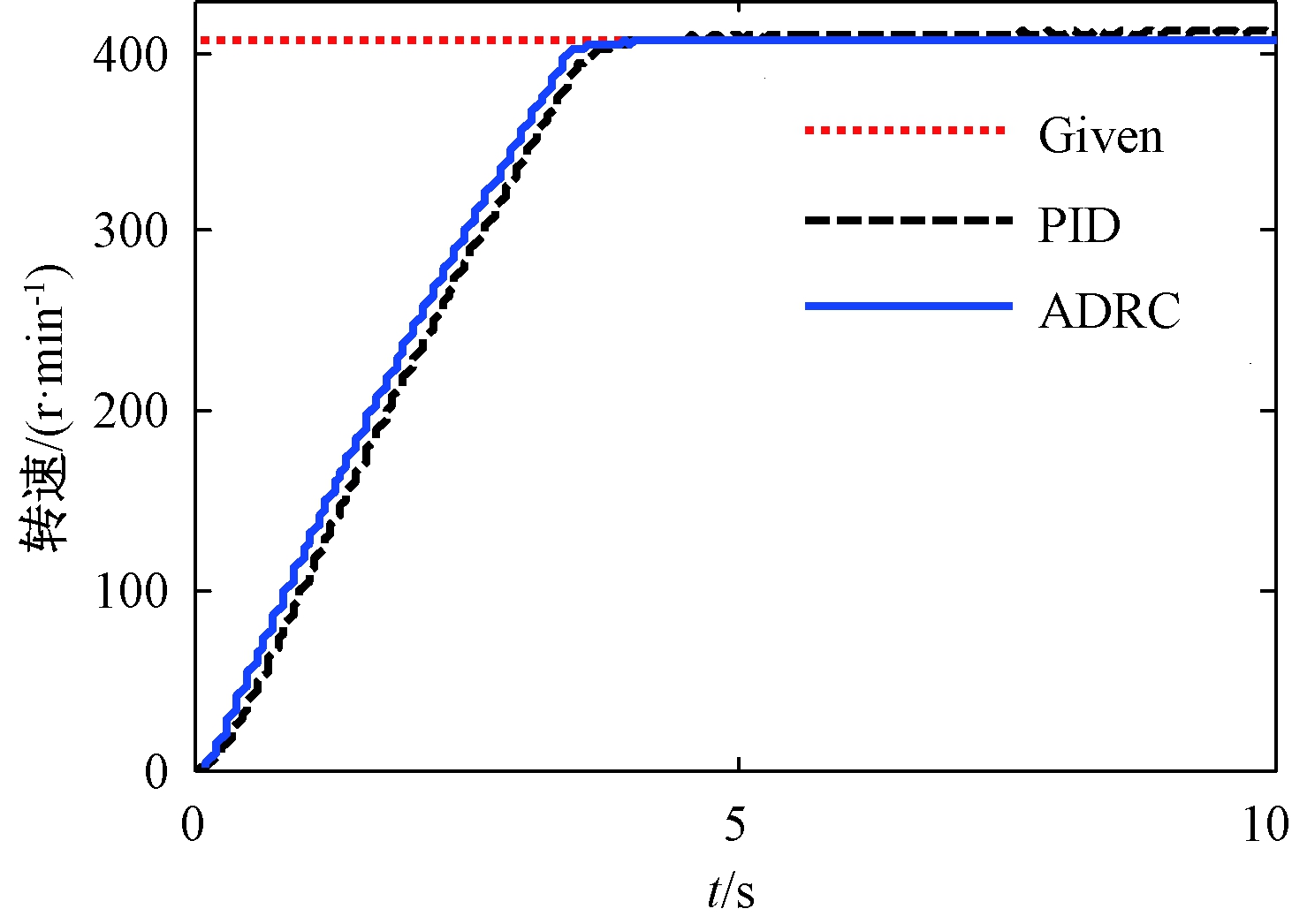
图5 转速控制性能比较
Fig.5 Comparison of controllers performances
由如图4可知，相比于PID控制参数寻优过程，ADRC控制参数寻优过程较慢.这是因为，设定的PID控制参数搜索范围是依据经验整定方法获得的，且待整定参数维度较小.由图5和表4可见，最优自抗扰控制器具有比最优PID控制器更好的控制性能.特别是在无扰动情况下，自抗扰控制器能够很好地满足钻进过程中响应快速且无超调的控制要求.另外，最优PID控制器不仅具有较差的动、稳态性能，其综合控制性能(如图4所示)也劣于最优自抗扰控制器的控制性能.
表4 ADRC与PID控制性能对比
Tab.4 Comparison of ADRC and PID control performance
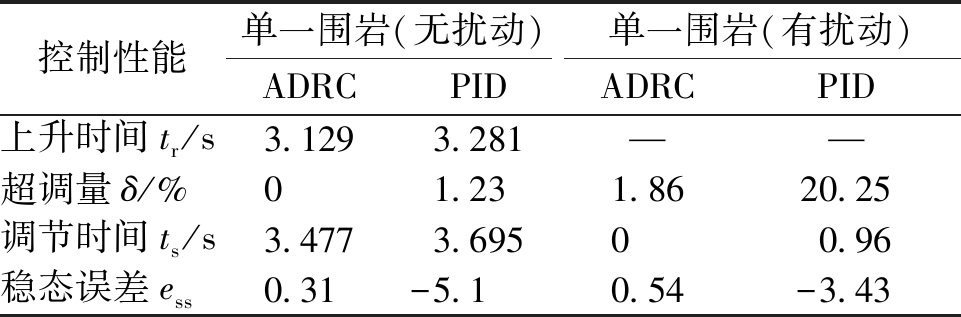
控制性能单一围岩(无扰动)单一围岩(有扰动)ADRCPIDADRCPID上升时间tr/s3.1293.281——超调量δ/%01.231.8620.25调节时间ts/s3.4773.69500.96稳态误差ess0.31-5.10.54-3.43
3.2 转速最优自抗扰控制器鲁棒性能
钻进过程存在诸多干扰因素，为验证所提控制策略的鲁棒性，在单一砂质泥岩的巷道围岩条件下，当t=10 s时，给系统加入15 N·m的干扰，转速跟踪性能如图6所示.
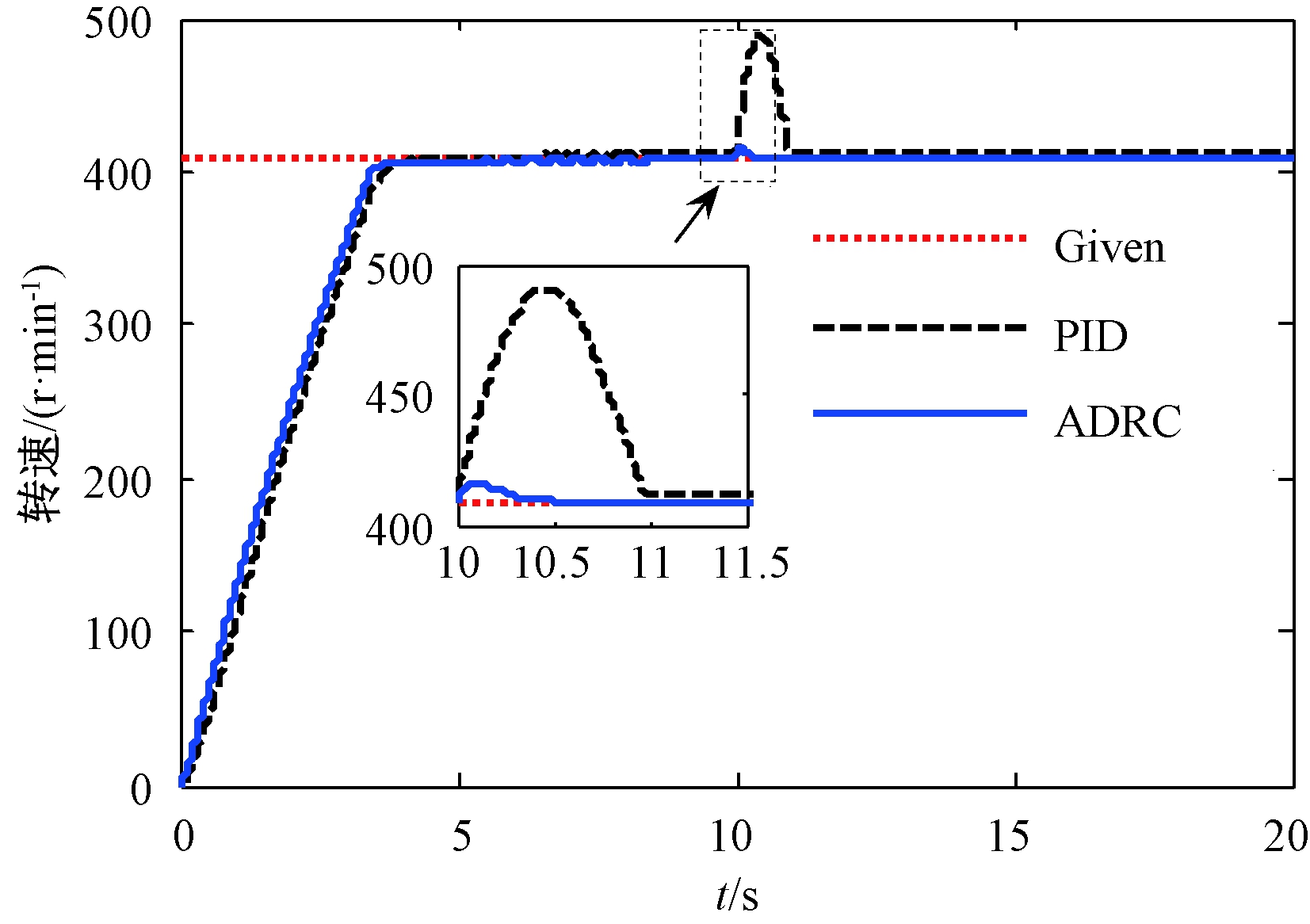
图6 干扰下的转速控制性能
Fig.6 The control performance of rotary speed under disturbance
由图6和表4可见，当突加外部干扰时，PID控制器瞬间产生较大超调，且需要经过1 s左右，才能追踪到原设定转速，鲁棒性较差，不利于钻机运行.相比而言，自抗扰控制器在受到外部扰动时，超调量小于2%稳态值，表明其具有较强鲁棒性；并且，其稳态性能也优于PID控制器，控制更加精确.因此，自抗扰控制具有较好的抗干扰能力，能更好地满足锚杆钻机这种存在多类外部干扰的实际系统的控制需求.
4 结论
锚杆钻机转速的自适应调节是改善钻进效率和钻孔质量的关键因素.因此，笔者提出基于头脑风暴优化算法的钻机转速最优自抗扰控制方法.首先，根据回转系统组成建立其数学模型，经线性化处理后，确定回转系统模型为二阶.其次，根据钻进的顶板围岩性状，估算不同围岩的最佳转速，作为自抗扰控制器的给定信号.由于钻机回转系统具有高度非线性、参数时变特性以及多种内外部扰动，所以采用自抗扰控制器，并采用头脑风暴优化算法，对6个控制参数进行寻优，得到最佳的动、稳态性能.最后，基于Matlab和AMESim的联合仿真平台的验证可知，相比于传统PID控制器，笔者提出的控制方法具有更加优越的动、稳态性能和更强鲁棒性，为实现可靠稳定的巷道掘进支护提供了实现基础.锚杆钻机利用推进系统和回转系统的协调配合完成钻孔工作，因此，推进回转协同控制策略的实施将是后续工作的核心.
[1] 胡志坚, 彭嵩, 耿莉.工程地质钻机回转钻进比例控制系统的模拟分析[J]. 机床与液压, 2009, 37(10): 219-221.
[2] ALLEYNE A, LIU R. On the limitations of force tracking control for hydraulic servosystems[J]. Journal of dynamic systems, measurement & control, 1999, 121(2):184-190.
[3] 彭金柱, 卞英楠, 周树亮. 基于DRNN网络的轮式机器人鲁棒H∞控制[J]. 郑州大学学报(工学版),2018,39(4):64-69.
[4] GUO Q, YU T, JIANG D. High-gain observer-based output feedback control of single-rod electro-hydraulic actuator[J]. IET control theory & applications, 2015, 9(16):2395-2404.
[5] 郭栋，付永领，卢宁，等.自抗扰控制技术在电液力伺服系统中的应用[J]. 北京航空航天大学学报, 2013, 39(1): 115-119.
[6] 李述清, 张胜修, 刘毅男, 等. 根据系统时间尺度整定自抗扰控制器参数[J]. 控制理论与应用, 2012, 29(1)：125-129.
[7] 李海生, 朱学峰. 自抗扰控制器参数整定与优化方法研究[J]. 控制工程, 2004, 11(5)：419-423.
[8] 刘丁, 刘晓丽, 杨延西. 基于AGA的ADRC及其应用研究[J]. 系统仿真学报,2006,18(7)：1909-1911.
[9] SHI Y H. Brain storm optimization algorithm [C]//ICSI′11 Proceedings of the Second International Conference on Advances in Swarm Intelligence. Berlin, Heidelberg: Springer, 2011:303-309.
[10] YANG F G, LI Y B, RUAN J H, et al. ADRC based study on the Anti-braking system of electric vehicles with regenerative braking[C]//2010 8th Word Congress on Intelligent Control and Automation. Jinan: IEEE, 2010:2588-2593.
[11] 贺立军. 新型全液压多功能锚杆钻机关键技术的研究[D]. 武汉：中国地质大学信息与控制工程学院, 2010.
[12] 韩京清. 自抗扰控制技术：估计补偿不确定因素的控制技术[M]. 北京：国防工业出版社, 2008.
[13] GUO Y N,CHENG J,CAO Y Y,et al. A novel multi-population cultural algorithm adopting knowledge migration[J].Soft computing,2011,15(5):897-905.
[14] 曹奔, 袁忠于, 刘洪. 基于粒子群算法的烧结炉系统辨识及神经网络控制[J]. 郑州大学学报(工学版), 2017, 38(5):39-43.
[15] 康红普, 王金华. 煤巷锚杆支护理论与成套技术[M]. 北京：煤炭工业出版社, 2007.
ciency. Especially, the nonlinearities and time-varying parameters, as well as the disturbances resulted from various factors in the anchor-hole drill rotary system should be taken into consideration. A novel optimal active-disturbance-rejection controller was proposed in the paper. The set value of the rotary speed was dynamically estimated in terms of the geological condition of surrounding rocks. Brain storm optimization algorithm was employed to find the optimal parameters of the controller, which could have the best dynamic and steady control performances. Based on the simulation platform composed of AMESim and Matlab, the experimental results for a single surrounding rock with or without the external disturbance showed that the proposed ADRC controller hasd better dynamic and steady performances and stronger robustness than the optimal PID controller.