0 引言
随着GIS向三维领域的发展,三维数字化变电站的研究得到了较快发展,其中基于三维点云的目标识别是需要解决的关键问题.Stein等[1]提出了结构表达法,由表面法向量的分布确定物体局部边缘以及曲面,从而可对任意形态的物体目标进行表达.Zhang等[2]使用调和形状图像的方式对物体进行表达.由于实际的点云会遇到遮挡、缺失和姿态变化等情况,直接进行目标识别无法解决以上的问题.因此,搜寻一种对遮挡、缺失和姿态变化具有较强的鲁棒性,同时又能够有效地通过局部特征进行三维目标整体识别的算法已成为现实需求.
霍夫变换原理是利用点与线的对偶性,原始坐标空间的曲线表达式对应参数空间的一个点,因此图像的特定曲线的检测问题就转化为在参数空间搜寻峰值问题[3].由于霍夫变换是利用全局特征,所以受噪声和边缘数据缺失的影响比较小,鲁棒性高.因此可以通过有效的局部特征描述和霍夫变换进行三维目标识别.
局部特征是三维识别的一个关键,Johnson等[4]将一个平面以特征点法向量为轴旋转,根据周围点落在这个平面上的位置,构造了自旋图特征.该算法对遮挡和复杂场景具有较强的鲁棒性,但是特征维度高,计算量大.Zhong[5]利用球形角度空间中点的分布提出了内蕴形状特征.该特征在现实场景中获得了比自旋图特征更高的识别率,但同一个特征点在多次特征提取试验中可能有不同的特征向量,特征的可重复性受限.窦本君等[6]采用基于Alpha Shapes的滚圆法获取边界曲率并识别目标.但对于边界凹凸变化过于明显的情况,存在一定的局限性.Ye等[7]将室内三维物体的点云投影到平面,将物体平面投影之间的相互关系作为特征,供机器人进行目标识别.Guo等[8]在三个平面上求出点云的投影点,然后获得旋转投影统计特征.三维点的“指纹(Fingerprint)”表达法被Chen等[9]引入,它是通过测地圆在切平面上投影的二维轮廓形成每一点的指纹,测地圆的法向方差信息显示在“指纹”中,找到指纹的对应也就找到点的对应.这两种方法对噪声和遮挡都具有较强的鲁棒性,但特征提取过程的计算量较大、耗时长,不能满足实际场景的识别要求.
以上三维目标识别存在特征维度高、计算量大等问题.据此进行改进,首先利用距离直方图(DSM)进行预识别,然后在预识别的结果中引入局部直方图[10]的特性进行局部特征描述,最后通过霍夫投票进行物体整体性识别.这种识别方法耗时短、特征提取过程中鲁棒性较强、计算效率高,适用于实际场景的三维目标快速识别.
1 算法流程
设备点云识别过程包括:数据预处理、获取DSM、霍夫投票、点云识别.首先,由预处理后的数据得到距离直方图和待测设备的局部描述符;然后,通过待测样本与模型库的距离直方图的相关系数进行初次筛选;最后,进行霍夫投票得到质心票数,输出识别结果.流程如图1所示,线上是对测试数据进行处理识别;线下是后台数据库存储的对比数据和模型.
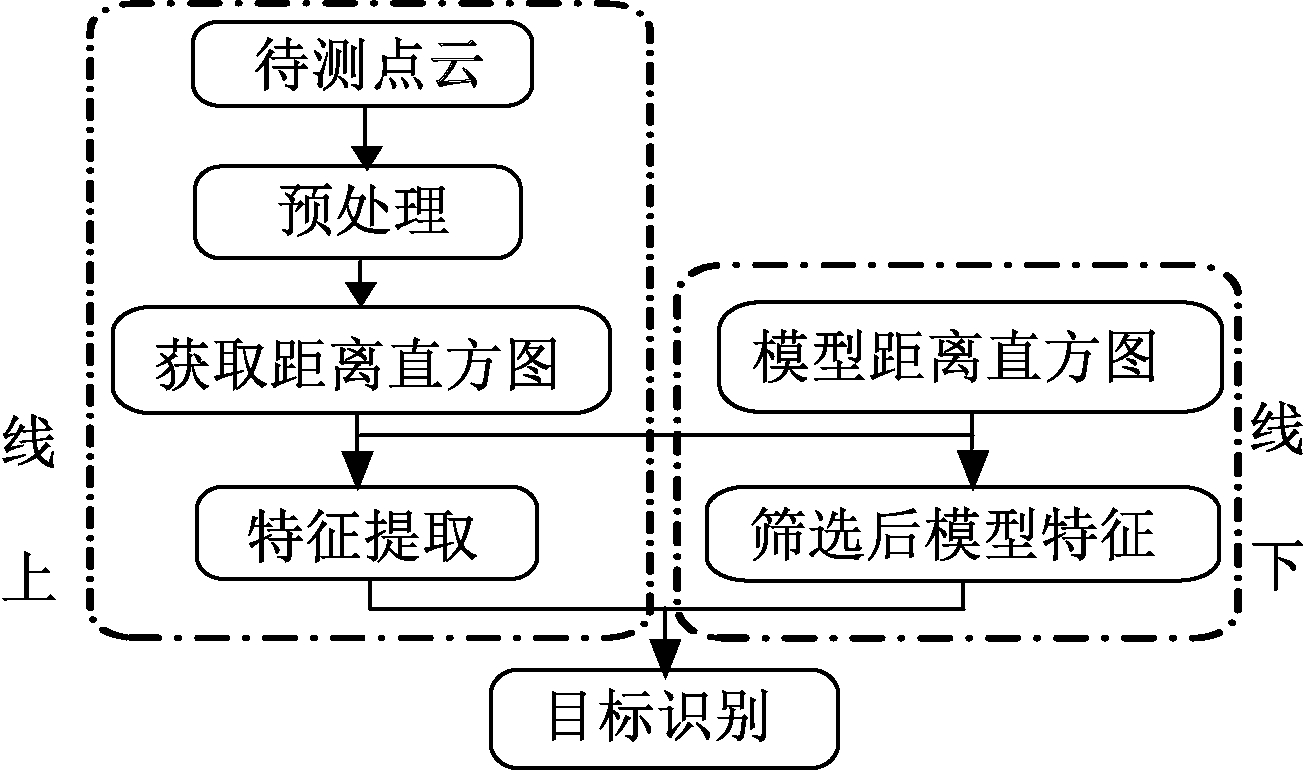
图1 算法流程图
Fig.1 The flow chart of algorithm
该算法的实施步骤为:①对待测点云进行数据预处理;②获取待测点云的距离直方图;③设定阈值,对比目标点云与模型库的距离直方图,将差别超阈值的模型舍去,得到初选结果;④根据局部点云分布得到局部描述符,再进行特征点的匹配;最后将匹配的特征点转换至全局坐标系中,进行投票;⑤若得到的票数超过阈值则直接输出识别结果,否则视为该模型库中无模型与待测点云匹配.
2 点云数据预处理
2.1 数据精简
由于变电站设备的点云数据量大、数据之间不连续、分布散乱,所以直接对数据进行识别会降低效率.笔者用线性八叉树法[11]对变电站设备点云进行精简. 数据精简的步骤如下:①根据最小立方体的边长,确定分割层数;②将点云中的每个点坐标值换成索引值,然后将索引值用二进制表示,构成点的编码值;③按照编码值排序,将编码值一样的点存放于相同的小立方体内;④每个小立方体内,保留距离小立方体的中心点最近的点,删除其他所有的点.
图2是KV500_DS_1A_1设备点云数据精简前后的图像,其中精简前点云数为322 738,精简后为5 421.通过图2可以发现,精简后的点云变得更稀疏,而实体外形特征却未发生任何变化,说明数据精简未改变实体特征,可保证后续识别算法的正确进行.
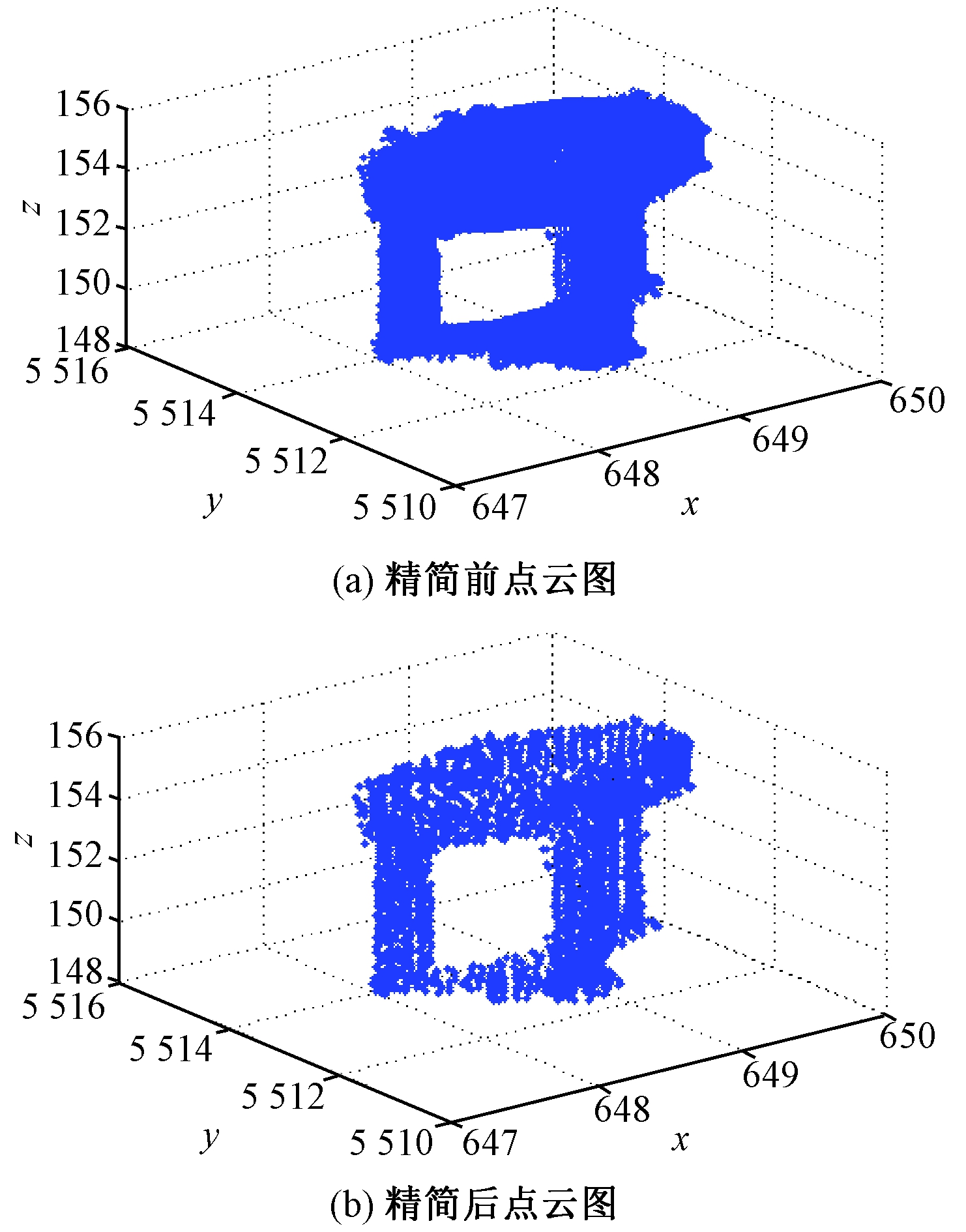
图2 点云精简对比图
Fig.2 Compared diagram of simplifying point cloud
2.2 去噪
2.2.1 去除地面点
由于激光扫描数据含有地面点数据(不是物体表面的点),在识别时应该予以去除.笔者采用高程和梯度相结合的方法将这些点去除.
首先,对设备点云进行水平投影,获得待处理区域的最大和最小坐标.然后,将其在xoy平面按x与y的大小进行网格划分,获得每个网格中的点云数据,求出各区域的高程差;同时获取相邻区域两法向量的余弦值.最后,判断网格中点云的平均高度与设定阈值的关系;同时判断法向量的余弦值.如果小于阈值,则判断为地面点;否则,判断为非地面点.
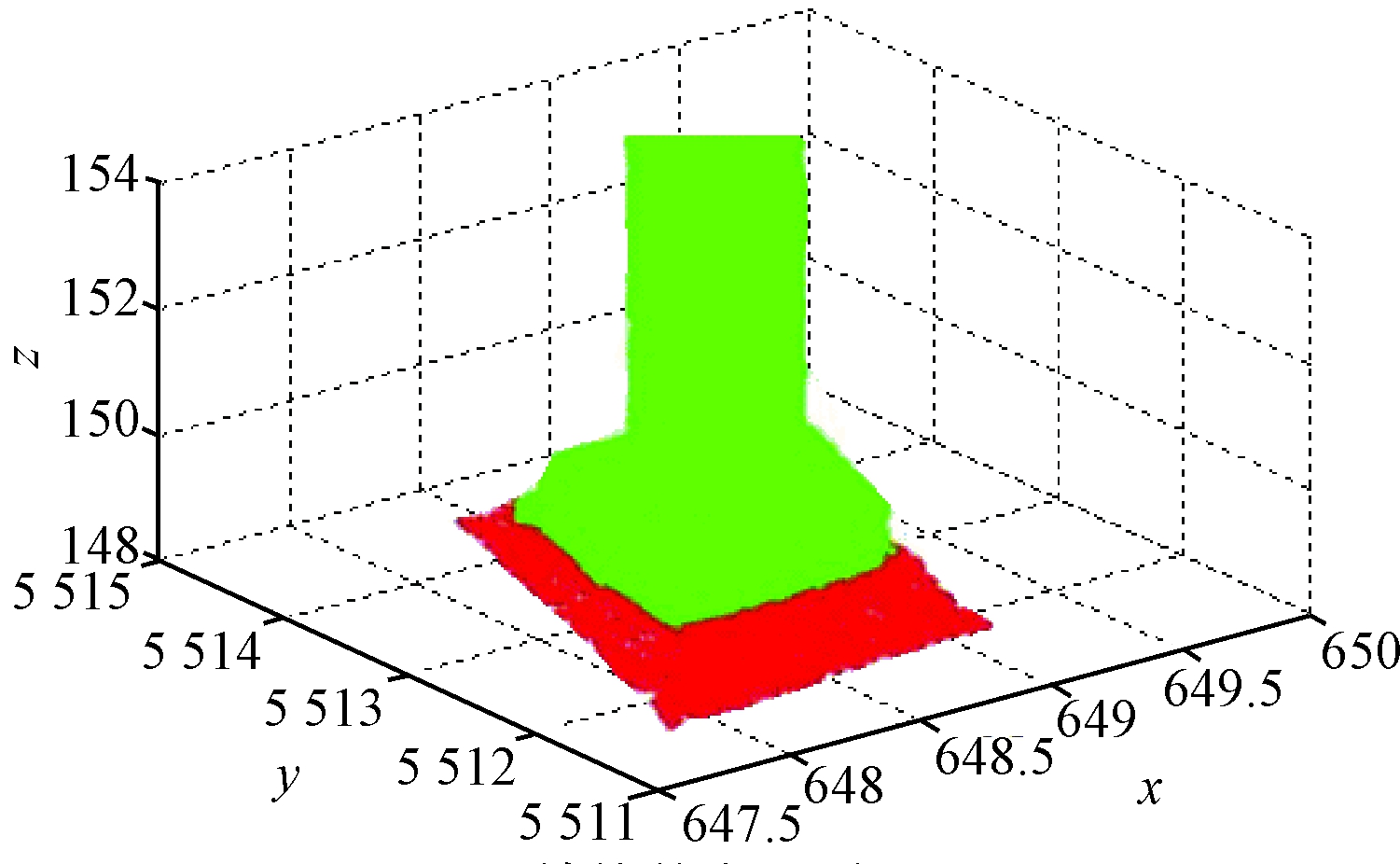
图3 去除点图
Fig.3 Sketch of moving ground points
根据多次不同阈值的试验,从中选取识别率最高的阈值,将既满足高程差小于总高程差的0.5倍且又满足法向量的余弦值大于0.8的区域点云去除,就可以实现去除地面点的要求.图3为去除地面点的效果图,其中深颜色的区域为所去除地面点集合.
2.2.2 离群点去除
笔者选择基于距离的方法,根据数据的精简密度设定阈值,实现对离群点的识别.当某点距离它最近的点大于该阈值时,就将其视为离群点并舍去.在离群点去除的过程中采用八叉树法对无序点云建立空间索引,进行k近邻搜索,可减少大量的计算时间.其中,某元器件点云的离群点去除效果如图4所示.
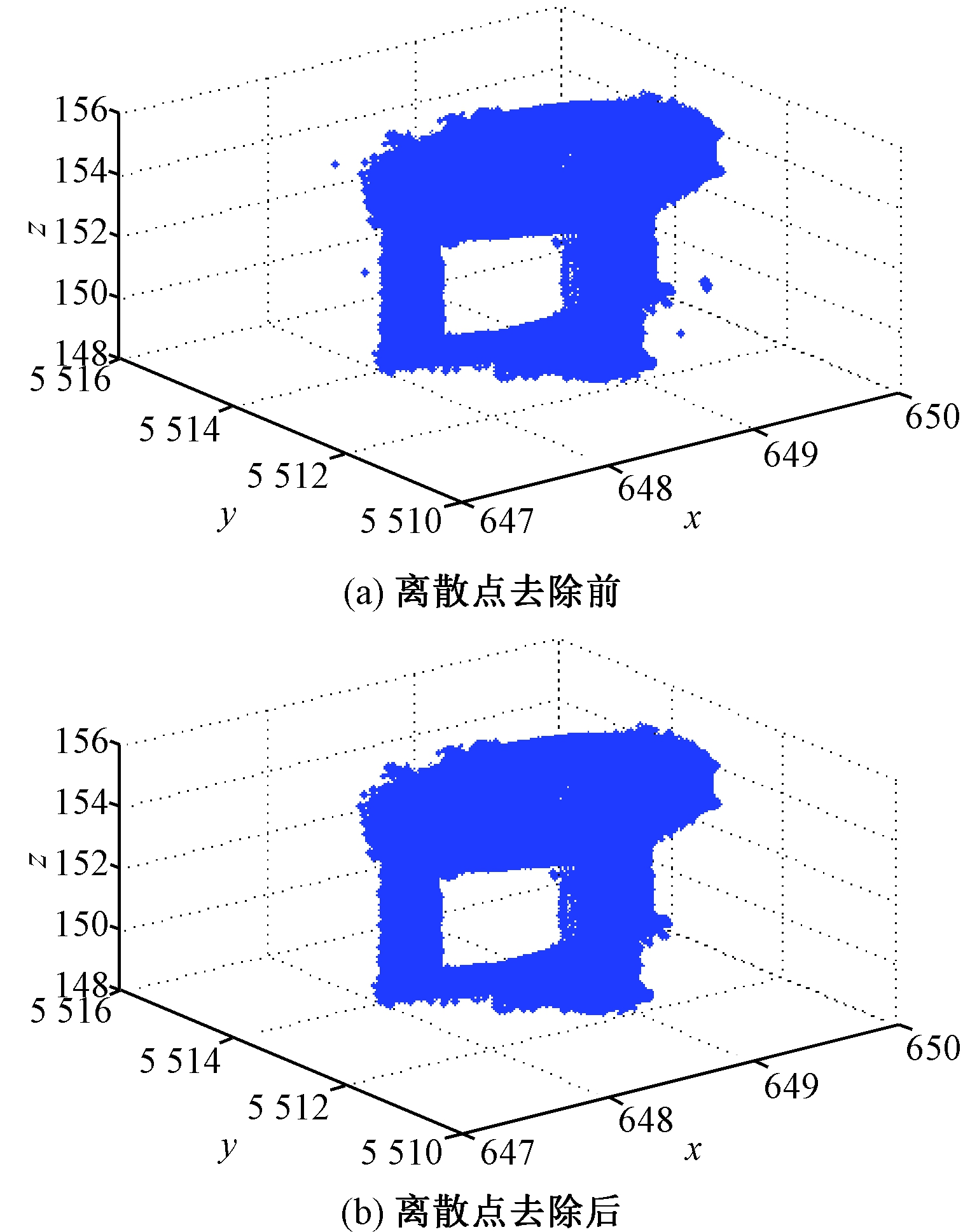
图4 离群点去除图
Fig.4 Sketch of moving noise points
3 距离直方图的初步筛选
3.1 距离直方图
直接对点云进行分割和特征点提取,既耗时长也无法得到满意结果.由点云和深度图像的关系可知,点云是深度图像的间接表达形式,距离直方图的深度值经过换算可得到点云坐标,因此利用点云生成深度图像.当多个点的x和y的值一样时,只选取高度坐标值大的点,其中避雷器与阻波器的深度图像如图5所示.
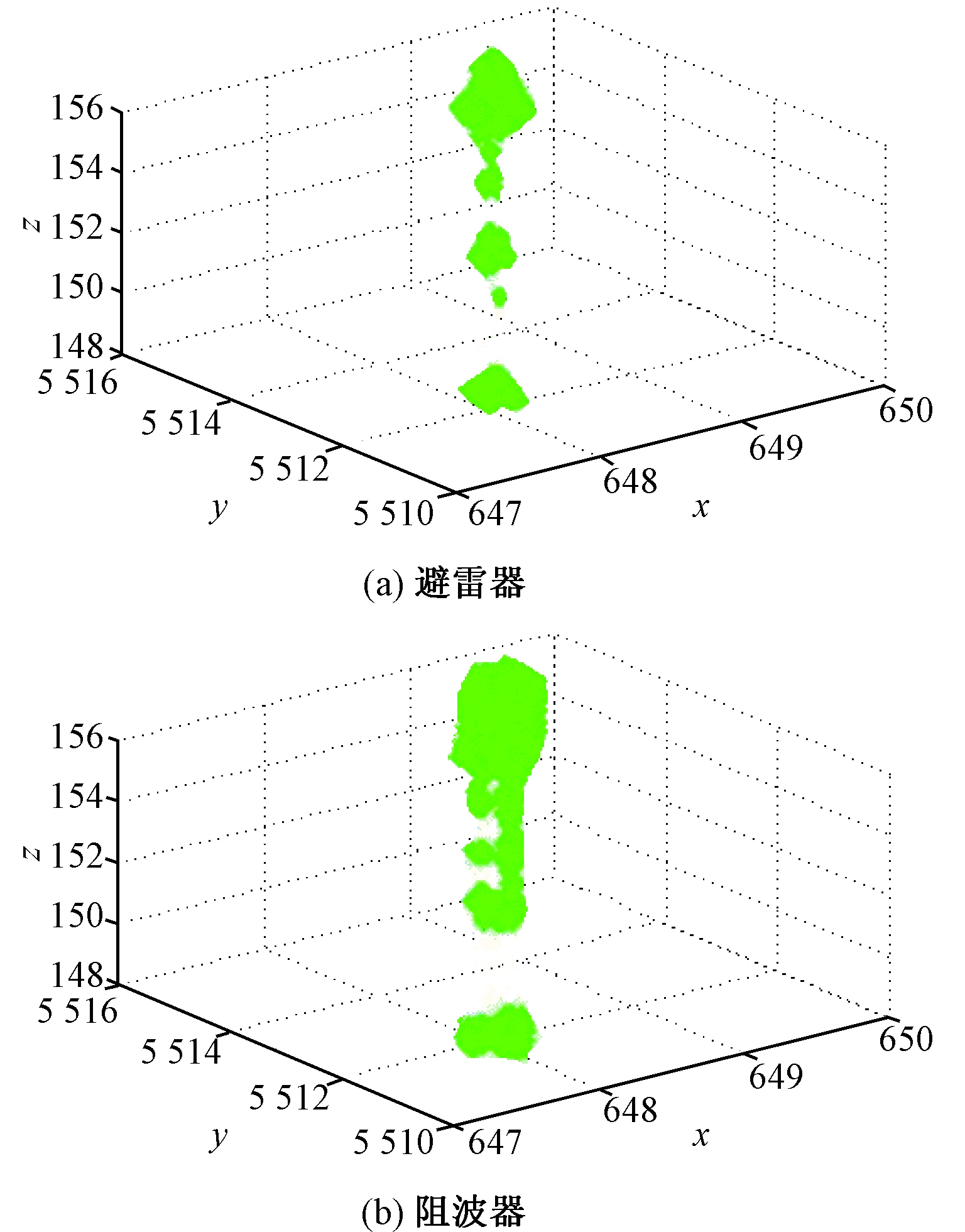
图5 设备的深度图像
Fig.5 The figure of depth image
深度图像的深度特征在解决三维识别问题中有辅助作用,所以可以通过深度分布得到距离直方图,阻波器的距离直方图如图6所示.其中,纵坐标表示具有该深度的点占所有深度点的比例.
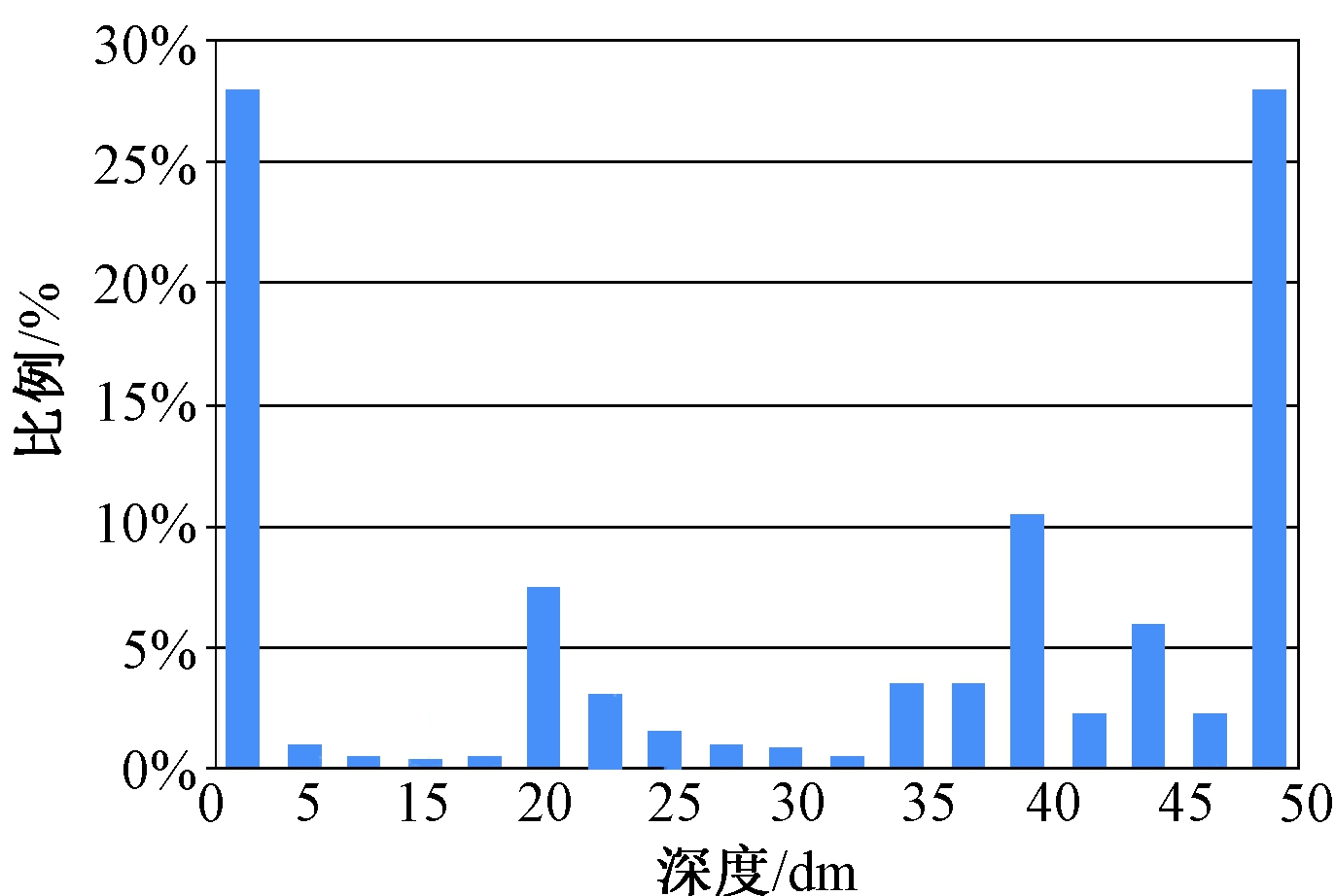
图6 距离直方图
Fig.6 The distance histogram
3.2 直方图相似度测量
在进行目标识别的过程中,往往需要比较待测数据和目标数据的相似度大小,其中比较相似度的方法[12]也较多,例如闵可夫斯基距离、豪斯多夫距离和相关测度等[13].笔者选择一种既区分简单、又效果较好的相关测度方法,它的基本原理是将直方图转化为表达物体特征的矢量,它们之间的相似性测度就是距离测度[14].由于在同等条件下,余弦相似度倾向给出更优解,即最准确的度量差异,因此相似度采用余弦相似度,corr的值越大相似度越高,计算公式如下:
(1)
式中:cov(x,y)为协方差; var为方差;x为待测数据的直方图对应的特征矢量;y为目标数据的直方图对应的特征矢量.
4 基于霍夫变换的霍夫投票
4.1 特征点的局部坐标建立
特征点即前面点云进行稀疏得到的所有点.点云特征提取是提取局部点云的分布方位直方图,局部坐标构建是特征提取的基础.对于特征点F和所有以特征点F为球心、半径为r的球内的点的协方差为:
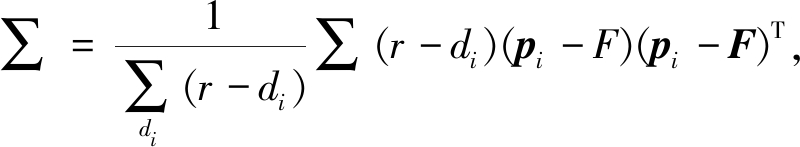
(2)
式中:![]() 为pi到F之间的距离.
为pi到F之间的距离.
通过式(2)得到三个特征值,并由大到小排列,对应的单位特征向量为S1、S2、S3,它们的方向为点云的高密度方向.协方差得到的特征向量相互垂直,其中,特征向量S2可用另外两个特征向量的内积表示,则局部参考系的x、y、z轴分别由S1、S2、S3表示,坐标原点为特征点F.
4.2 描述符的构建
描述符的构建对于识别至关重要,它的鲁棒性和描述能力将会影响到识别的精准性.以特征点F为球心、半径为r,获得沿半径4等分、仰角2等分和方位角8等分的空间子块.根据点云的分布个数得到特征点的特征向量Q=|Q1,Q2,…,Q64|,其中,Qi为第i空间子块中点的总个数.然后,对特征向量进行归一化,这样描述符具有更强的鲁棒性.
4.3 识别
标准模型中的每一点在局部参考系空间中都有一个64维的投票向量.将场景中的点与模型库中的点进行比较,若能找到特征之间的欧氏距离小于某一阈值的点,即对应点,如式(3)所示,则模型中的点和场景中的点具有一样的局部投票向量.
(3)
式中:QM为模型的特征点对应的特征向量;QS为场景设备的特征点对应的特征向量;τ为比较的阈值.
在模板中,所有的特征点在同一个三维空间中,具有相同的全局坐标系,质心点CM和特征点![]() 之间的关系可以由矢量
之间的关系可以由矢量![]() 表示(如图7中的实线向量所示,目标中的矢量用
表示(如图7中的实线向量所示,目标中的矢量用![]() 表示),如式(4)所示:
表示),如式(4)所示:
(4)
另外,全局向量![]() 可以由坐标的转换矩阵,转化成在局部坐标系下的表示方式,如式(5)所示:
可以由坐标的转换矩阵,转化成在局部坐标系下的表示方式,如式(5)所示:
(5)
式中:旋转矩阵![]() 的每一行是由点
的每一行是由点![]() 及周围点构成的局部坐标系的特征向量组成,如式(6)所示:
及周围点构成的局部坐标系的特征向量组成,如式(6)所示:
(6)
通过求模板与目标特征点描述符的欧氏距离获得特征对应点,即![]() ↔
↔![]() 所以,目标的特征点位置就是对应模板特征点的位置.由于在局部坐标系表示的特征点至质心的矢量具有旋转和平移不变性,并且在局部坐标系建立时已经单位化,则目标的特征点至质心的矢量
所以,目标的特征点位置就是对应模板特征点的位置.由于在局部坐标系表示的特征点至质心的矢量具有旋转和平移不变性,并且在局部坐标系建立时已经单位化,则目标的特征点至质心的矢量![]() 与模板中的矢量
与模板中的矢量![]() 可认为相等.因此,将
可认为相等.因此,将![]() 转化至全局坐标系下的
转化至全局坐标系下的![]() 如式(7):
如式(7):
(7)
式(7) 为局部和全局之间的向量转换.其中,![]() 为全局坐标系下的矢量;
为全局坐标系下的矢量;![]() 为局部坐标系下的矢量.
为局部坐标系下的矢量.
对于旋转矩阵![]() 每一列都是由点
每一列都是由点![]() 及周围点构成的局部坐标系的特征向量组成,如式(8):
及周围点构成的局部坐标系的特征向量组成,如式(8):
(8)
将场景中的所有对应的特征点转换至全局坐标系中,在转换过程中特征点与物体质心点之间的向量保持不变[14].每个特征点根据式(7)通过自己与质心的矢量都能找到目标的质心,这样通过局部特征转化为对目标质心的投票.如果有足够的投票,则可确定该物体所在的位置以及类别.这样,就可以由特征点局部向量转换至全局的一个微小的三维空间霍夫投票,如图7所示.根据阈值可判定模型库是否有该模型,并输出识别结果.
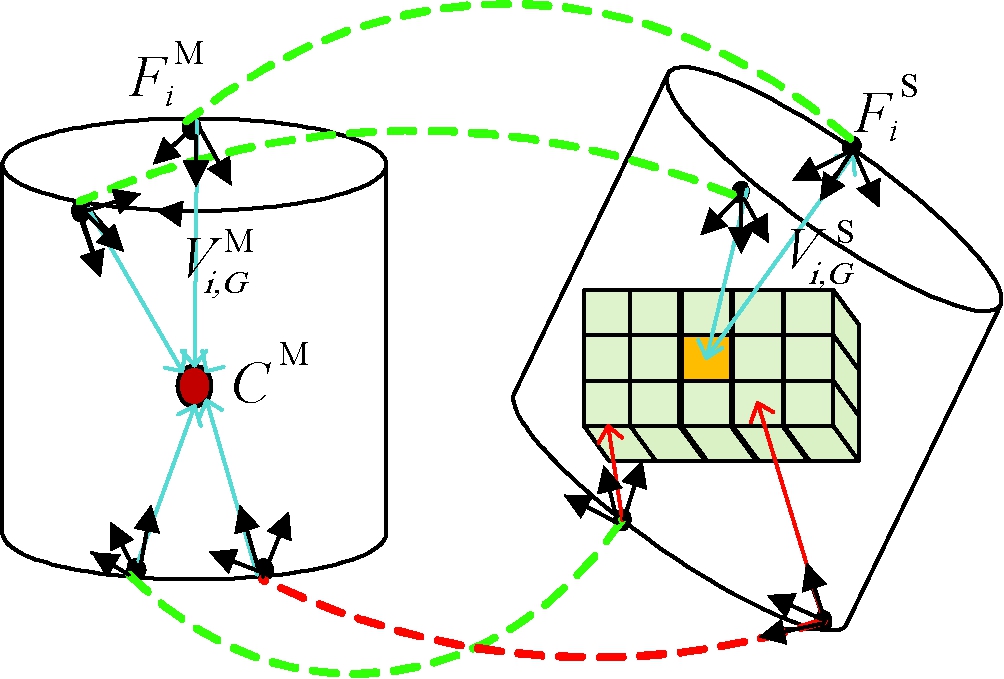
图7 霍夫投票示意图
Fig.7 The picture of Hough voting
5 实验结果与分析
5.1 实验数据及参数设置
利用激光扫描仪获取郑州某变电站设备点云数据,共200组数据,33种类型设备,每种类型平均6组数据.每种类型选取一组作为模板,其余为测试样本.用MATLAB实现上述算法和目标识别.
通过不断地调整实验得到相关参数:数据精简时压缩量为84,获取局部曲面特征时选取的邻域个数为27,搜寻半径为0.1,距离直方图的相似度阈值为0.7,对应点搜寻的阈值为0.1,霍夫投票的阈值为0.2.
5.2 目标识别
理想状态下的目标识别是指获取的数据和模型数据是在无视点差异情况下获取的,姿态一致,无数据的缺失,但实际过程中无法获取无差异的数据.表1列举了4种设备之间的距离直方图的相似度,通过相似度可反映出不同类别设备的距离直方图的差异.由于同类设备之间一样,所以将相似度都定为1,识别率为1.虽然这是理想情况下的一种假设,但是通过表1可以看出,使用距离直方图相似度的方法能够很好地将不同类型的设备进行初步选择.
表1 4种设备的距离直方图的相似度
Tab.1 Similarity of DSM of four kinds of device
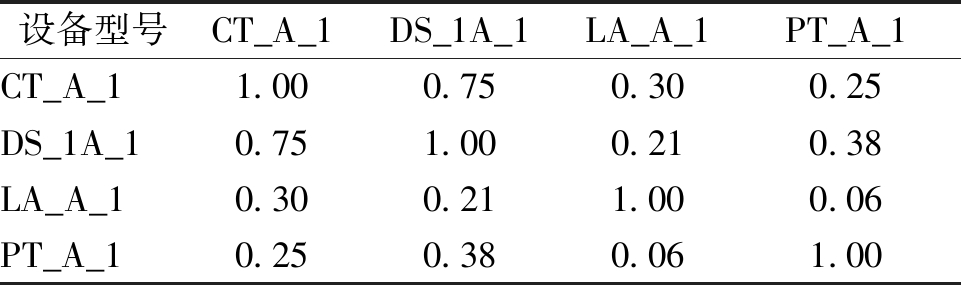
设备型号CT_A_1DS_1A_1LA_A_1PT_A_1CT_A_11.000.750.300.25DS_1A_10.751.000.210.38LA_A_10.300.211.000.06PT_A_10.250.380.061.00
在实验中对于实际场景中出现遮挡情况的模拟方法为:将模型中的某些连续的点的位置坐标值置0.例如,对于设备KV500_DS_1A_1,将模型中的4 299个顶点中的407个顶点三维坐标值变为0,则遮挡占比为9.5%,如图8所示,其中深色的是位置坐标值为0的点.
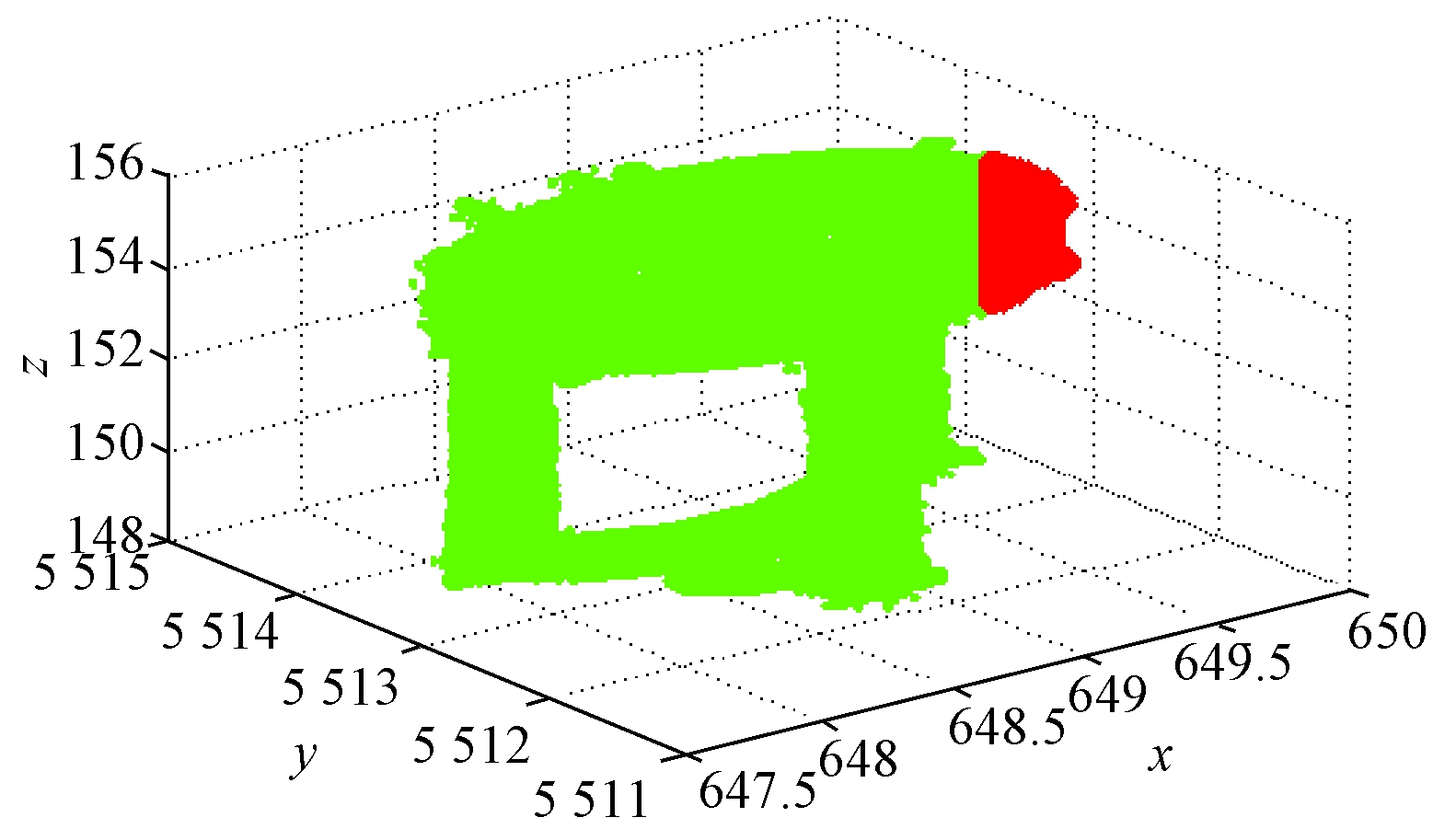
图8 设备被遮挡的情形
Fig.8 Device is shielded
表2中的相关系数阈值为利用DSM深度图像进行预识别时的阈值,票数阈值为霍夫投票的阈值.所以,在三维目标识别的过程中,首先,通过求取距离直方图的相关系数进行初步识别,即将待测的距离直方图与模型库中的距离直方图相对比,求取大于相关系数阈值的设备类型;然后,在初选结果的设备类型中进行霍夫投票.若票数最大值大于投票的阈值则直接输出结果,否则识别失败.
表2 同一遮挡占比(6%)下设备的识别率
Tab.2 Recognition rates of the same shielding percentage(6%)

相关系数阈值票数阈值识别率/%1.04083.60.93585.50.93086.70.83089.10.73084.8
表2为遮挡占比为固定时(6%)识别率与阈值之间的关系.选取不同的阈值进行实验,由于篇幅限制,只列出几个关键的阈值和对应的识别率.因此,选取识别率最高的相关系数阈值为0.8和票数阈值为30作为该遮挡占比下的最终阈值.据此,对不同遮挡占比下的识别率进行了测试,结果如表3所示.
表3 不同遮挡占比下设备的识别率
Tab.3 Recognition rates of different shielding percentages
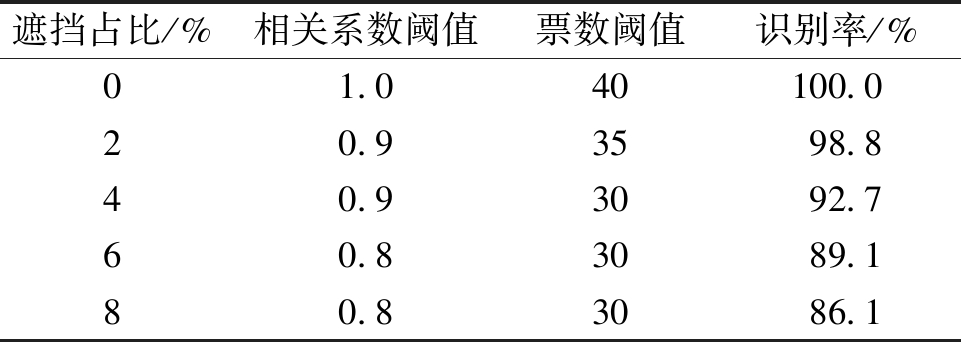
遮挡占比/%相关系数阈值票数阈值识别率/%01.040100.020.93598.840.93092.760.83089.180.83086.1
表3中,当遮挡占比为8%时,相关系数的阈值为0.8,投票的阈值为30时,识别率为86.1%;当遮挡占比为2%时,识别率增加到98.8%.结果表明,在实际运用过程中,当遮挡占比下降的时候,通过适当提高相关系数阈值和票数阈值,可以提高识别率.
5.3 实验对比
为了验证本文方法的有效性,将本文方法与同样进行变电站设备识别的边界点曲率法[6]进行比较.文献[6]使用半径为α的圆来实现对设备在三个投影面上边界点的提取,然后利用点到弦的距离积累求出设备点云在三个投影面上的边界点曲率.选取5.1节中33种类型变电站设备数据作为测试数据,其中包括47个设备,进行两种方法的识别效果比较.本次的实验过程在同一台计算机上进行测试,测试数据共172个,边界曲率法正确识别170个,本文方法正确识别155个.本文算法部分结果如表4所示.
表4 两种方法识别效果比较
Tab.4 Comparison of recognizing effect of two methods
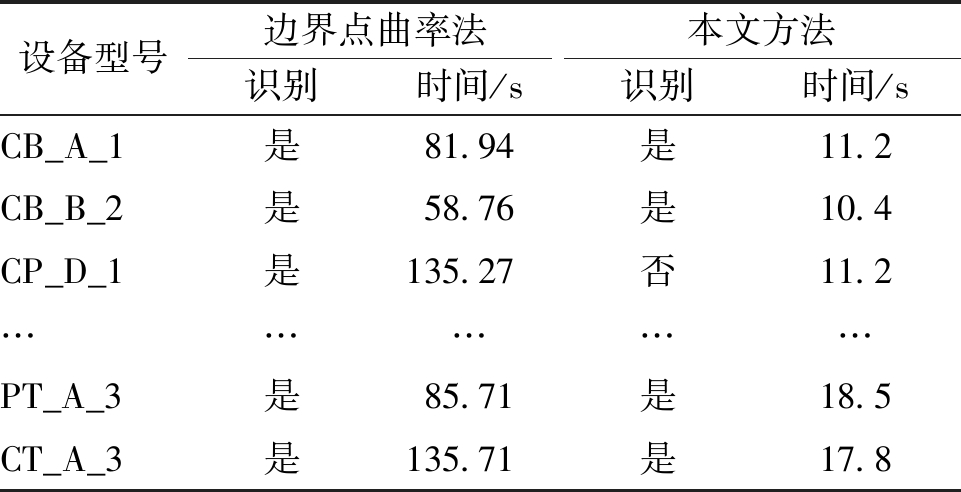
设备型号边界点曲率法本文方法识别时间/s识别时间/sCB_A_1是81.94是11.2CB_B_2是58.76是10.4CP_D_1是135.27否11.2……………PT_A_3是85.71是18.5CT_A_3是135.71是17.8
由表4可得,边界点曲率法识别率为98.8%,平均识别时间85.91 s;本文方法的识别率为90.1%,平均识别时间为15.6 s.从识别率上看,边界点曲率法优于本文方法,但平均识别时间却长于本文方法.究其原因,本文方法首先用八叉树法对数据进行精简,可大大缩短识别时间,另外使用距离直方图法与模型库数据进行初步筛选,也可减少数据的处理量.而文献[6]对点云3个方向的曲率都进行计算,由于曲率计算非常耗时,文献[6]整体计算时间势必增加,因此霍夫投票的方法用时要少于边界点曲率法.
综上可见,尽管边界点曲率法识别率较高,但用时太长.而本文方法尽管识别率略有降低,但是识别时间减少了一个数量级.在实际工程中,如果按照边界点曲率法进行识别,计算机在十几个小时内都很难完成.而本文方法可保证在数小时内完成整个变电站识别.因工程项目要求一般识别率应达到80%以上,而采用本文方法识别率可达90%,因此,完全可以满足该类实际问题的要求.
6 结论
(1)采取霍夫识别方法对三维设备进行识别.首先通过八叉树法对点云数据进行精简,并通过基于距离直方图的方法去噪得到高质量的点云数据,然后由DSM深度图像得到距离直方图.
(2)通过与模型库距离直方图对比求相关系数,相似度满足某一阈值的模型样本作为比较样本.
(3)最后通过霍夫投票算法获得识别结果.以Foucus 3D激光扫描仪获取的某变电站设备点云数据对以上方法进行检验,结果表明该方法能将不同设备进行有效分类,可达到预期效果.
[1] STEIN F, MEDIONI G. Structural indexing: efficient 3-D object recognition[J]. IEEE transactions on pattern analysis & machine intelligence, 1992,14(2):125-145.
[2] ZHANG D M, HEBERT M. Harmonic maps and their applications in surface matching[C]//IEEE Computer Society Conference on Computer Vision and Pattern Recognition. Fort Collins: IEEE,1999:524-530.
[3] 张新雨, 刘丁, 杨文,等. 基于人工鱼群霍夫变换的单晶硅直径检测[J]. 仪器仪表学报, 2014, 35(4):940-947.
[4] JOHNSON A E, HEBERT M. Using spin images for efficient object recognition in cluttered 3D scenes[J]. IEEE transactions on pattern analysis & machine intelligence, 1999, 21(5):433-449.
[5] ZHONG Y. Intrinsic shape signatures: A shape descriptor for 3D object recognition[C]//IEEE 12th International Conference on Computer Vision Workshops. Kyoto: IEEE, 2010:689-696.
[6] 窦本君, 纪勇, 郑尚高,等. 基于降维数据边界点曲率的变电站设备识别[J]. 郑州大学学报(工学版), 2017, 38(2):61-65.
[7] YE C, QIAN X F. 3D object recognition of a robotic navigation aid for the visually impaired[J]. IEEE transactions on neural systems and rehabilitation engineering, 2018, 26(2):441-450.
[8] GUO Y Y, SOHEL F, BENNAMOUN M, et al. Rotational projection statistics for 3D local surface description and object recognition[J]. International journal of computer vision, 2013, 105(1): 63-86.
[9] CHEN H, BHANU B. 3D free-form object recognition in range images using local surface patches[J]. Pattern recognition letters,2007,28(10):1252-1262.
[10] SALTI S, TOMBARI F, STEFANO L D. SHOT: Unique signatures of histograms for surface and texture description [J]. Computer vision & image understanding, 2014, 125(8):251-264.
[11] 贾世宇, 张维忠, 于晓康,等. 基于八叉树的柔性体切割仿真中并行化的碰撞算法[J]. 计算机辅助设计与图形学学报, 2017, 29(12):2180-2188.
[12] RAMANI K, LOU K, JAYANTI S, et al. Three-dimensional shape searching: state-of-the-art review and future trends[J]. Computer-aided design, 2005, 37(5):509-530.
[13] 方民权, 张卫民, 周海芳. 集成众核上快速独立成分分析降维并行算法[J]. 计算机研究与发展, 2016, 53(5):1136-1146.
[14] ALDOMA A, TOMBARI F, STEFANO L D, et al. A global hypotheses verification method for 3d object recognition[C]// European Conference on Computer Vision. Berlin: Springer, 2012:511-524.