0 引言
正交频分复用(orthogonal frequency division multiplexing,OFDM)技术具有良好的抗多径干扰能力和极高的频谱利用率,可以灵活地和其他接入方式结合衍生出新的系统,目前已广泛地应用在无线通信系统和L-band数字航空通信系统(l-band digital aeronautical communication system,L-DACS)中[1-3]。在实际航空通信中,飞机的高速运动以及飞机间较大的通信距离会产生高多普勒频移和大传播时延，这对OFDM技术在航空通信中的应用提出巨大挑战。多普勒频移破坏子载波间的正交性，造成子载波间的功率泄漏，从而产生子载波间干扰(inter-carrier interference,ICI);大时延会产生符号间干扰，因而时变信道背景下的信道估计和均衡技术成为航空通信系统中的一个关键技术问题[4-5]。
近年来，基于导频的信道估计算法在无线通信系统背景下得到广泛的研究。导频位置及导频疏密对于信道估计性能具有很大影响[6]，时变信道下梳状导频可以更好地适应时变信道[7-8]。 航空场景下的高多普勒频移将导致信道的快速时变性。笔者充分考虑航空通信信道的快速时变性，在插入梳状导频前提下寻找满足信道估计的导频数量。传统估计算法中，最小二乘(least-square,LS)估计算法具有计算量小、实现简单的特点，但估计性能不理想。Edfors等[9]提出的线性最小均方误差(linear minimum mean square error,LMMSE)估计算法，虽然利用奇异值分解降低了复杂度，但需要已知信道的二阶统计特性，当信道二阶统计特性难以准确获得时，信道估计性能显著恶化。文献[10-11]介绍了基于迭代反馈的算法，迭代反馈算法是将经过信道估计之后的检测信号作为导频信息再次进行估计的算法。
传统的估计算法适合慢时变或时不变信道，不能实时跟踪航空通信系统的快时变信道。通过增加导频数量提升信号估计将严重降低频率效率；且导频数量的增加也将增加处理时延，难以跟踪快速时变信道。笔者利用少量导频信号基于LS算法进行初始信道估计，并充分利用信道译码器的及时纠错能力来提高信号检测的准确性，之后将检测信号作为虚拟的导频信号反馈至信道估计器，增加有效的导频数量，从而显著提升信道估计的精确度。通过仿真表明，在LS算法的基础上加入反馈迭代可以显著提高信道估计的精确性，较其他传统信道算法在航空通信中可以达到更好的估计效果。
1 系统与信道模型
1.1 系统模型
以空对地(air-to-ground,ATG)航空通信为背景，研究航空通信系统信道估计算法。航空通信系统的信道可以建模为两径模型[12]，如图1所示，输入信息比特流经过星座映射、串并变换为N路并行比特流，插入导频之后经过逆傅里叶变换(inverse discrete fourier transform,IDFT)得到等效基带OFDM信号：
(1)
式中：N为总的子载波个数；k为子载波序号；n为第n个抽样时刻。
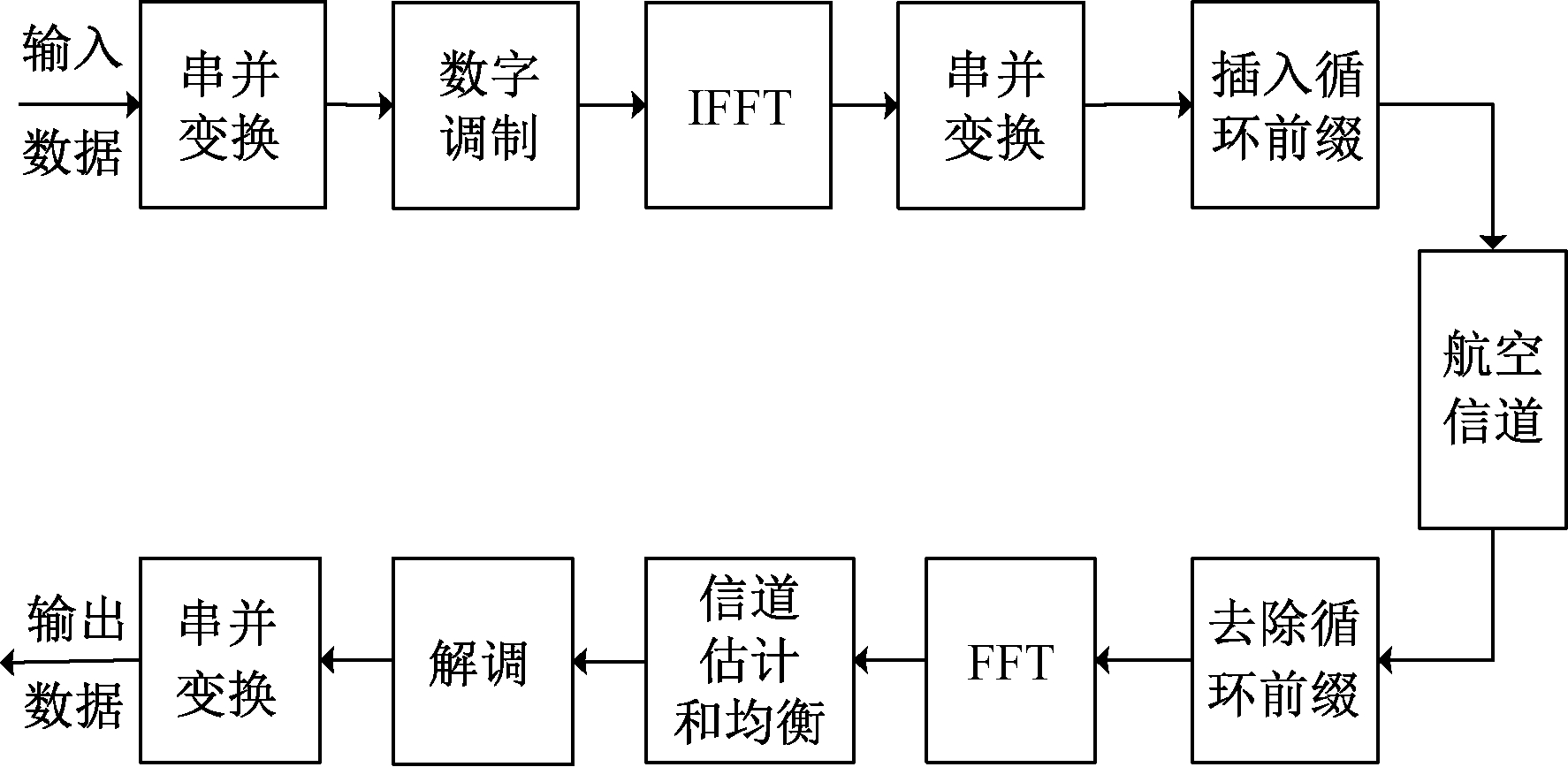
图1 基于OFDM的数字航空通信系统
Figure 1 Digital aeronautical communication system based on OFDM
为消除多径造成的ICI，引入循环前缀(cyclic prefix,CP)充当保护间隔，串并变换后进行信道传送。
1.2 信道模型
根据Haas[12]研究，航空通信在不同飞行状态下具有不同信道特征，其中巡航阶段信道具有莱斯特性，即同时存在直射路径(line-of-sight,LOS)和散射路径。图2给出飞机处于巡航状态下信道示意图，飞机与地面基站之间存在直射路径和散射路径，此时航空信道可以建立为两径模型，信道的莱斯因子K取典型值15 dB，信道服从莱斯分布。
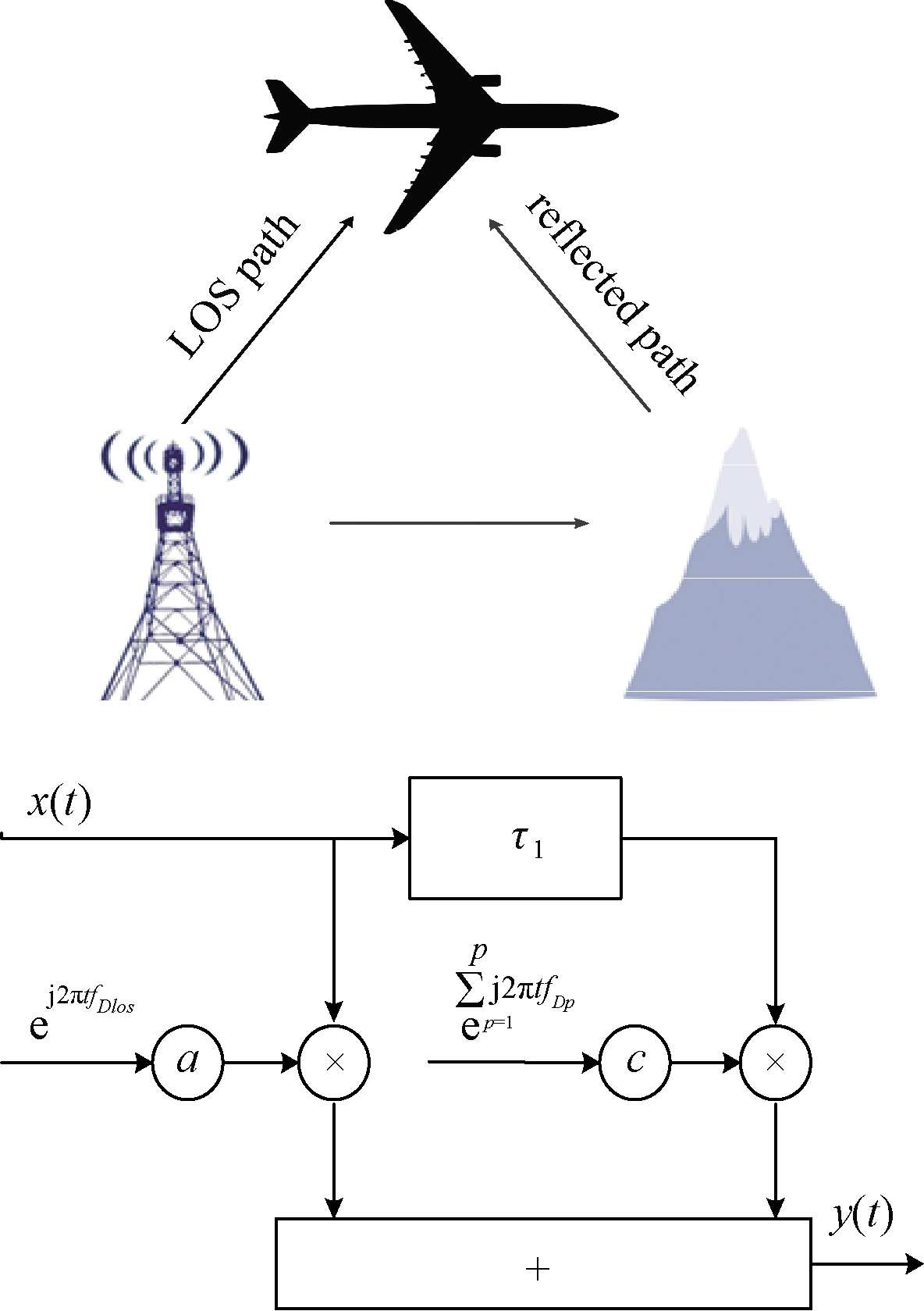
图2 航空信道两径模型
Figure 2 Two-ray Model of Aeronautical Channel
根据广义平稳非相关散射信道模型[13]，建立两径模型信道表达式：
h(t,τ)=a·ej2πtfDlosσ(τ-τ0)+
(2)
式中：p表示散射多径信道总个数，文中多径总数p=20；θp为第p条径的初始相位；根据定义莱斯因子K=a2/c2,其中
为直射路径的多普勒频移；fDp为第P条散射径的多普勒频移；τ0和τ1分别为直射路径时延值和散射路径时延值。
信号x(n)通过具有加性高斯白噪声(a-dditive white gaussian noise,AWGN)的信道之后，接收信号可表达为：
y(n)=x(n)⊗h(n)+w(n),
(3)
式中：⊗表示卷积；w(n)为均值为0、协方差为σ2的高斯白噪声；h(n)为时域信道冲激响应。
经过傅里叶变换(discrete fourier transform,DFT)之后，接收信号的频域形式可以表达为：
Y[k]=X[k]H[k]+W[k],0≤k≤N，
(4)
式中：k为子载波序号；H[k]为第k个子载波的信道频域响应；X[k]表示发送信号；W[k]表示噪声频域响应。
2 信道估计准则
根据式(4)，去除子载波序号k，我们可以进一步得
Y=XGh+W，
(5)
式中：X=diag{X(1),X(2),…,X(NP-1)}为频域导频信号；Y=[Y(1),Y(2),…,Y(NP-1)]为频域接收信号；h=[h0,h1,h2,…,hL]为时域信道冲激响应；矩阵G是NP×L的傅里叶矩阵，其中L是信道的有效长度。
G=e-j2πlin/N,0≤n≤Np-1,0≤l≤L-1，
(6)
式中：{in,0≤n≤NP-1}为导频符号插入位置。
2.1 最小二乘(LS)估计
最小二乘估计算法包括时域最小二乘和频域最小二乘。时域信道估计算法如下，在不考虑噪声的情况下由式(5)我们可以推出：
(7)
式中：GH表示矩阵的共轭转置；令V=GHG,为L×L矩阵,则V-1为V求逆运算。
信道频域响应可以展开为：
(8)
式中:F=e-j2πkn/N,0≤n≤N,0≤k≤L-1。
频域信道估计算法如下。为得到
需要最小化代价函数：
(9)
令上述代价函数关于的偏导数等于0，可得
(10)
由式(10)可推出
由此得到频域信道估计的解为：
(11)
导频符号位置处的频域响应获得后，可以通过线性插值得到全部的估计信道频域响应。
2.2 线性最小均方误差估计
线性最小均方误差估计算法是基于线性操作的低复杂度最小均方误差估计算法。该算法主要思路是利用信道的自相关矩阵，由式(4)可以得到一个OFDM符号内基于LS估计准则的频域信道冲激响应：
(12)
进而，利用信道相关性和噪声协方差的统计特性，可以进一步得到LMMSE估计信道响应：
(13)
式中：
为信道冲激响应的自相关矩阵；
为加性高斯噪声方差。
当信号发生变化时，矩阵RHH就会随之改变，为了进一步降低算法的复杂度，可以用期望值E{(XXΗ)-1}代替(XXΗ)-1。
2.3 反馈迭代估计算法
反馈迭代信道估计算法将基于估计的信道进行信号检测，并将检测信号反馈至信道估计器作为导频符号再次进行信道估计，直至收敛。相比传统信道估计算法，判决反馈信道估计可以充分利用数据信息，在节约导频的基础上获得更好的估计效果。此外基于航空信道的快时变性，笔者提出的基于编码的反馈估计方法充分利用信道解码器的纠错能力，可以有效地避免传统反馈方法中由于判决错误带来的误差积累[6]。具体而言，通过导频进行初始信道估计之后，可以采用反馈迭代算法来更新信道信息，将所得的符号判决作为已知的训练序列进行迭代信道参数估计,从而能有效地改善信道估计的性能并消除载波间干扰。笔者采用的反馈迭代估计算法原理结构如图3所示。
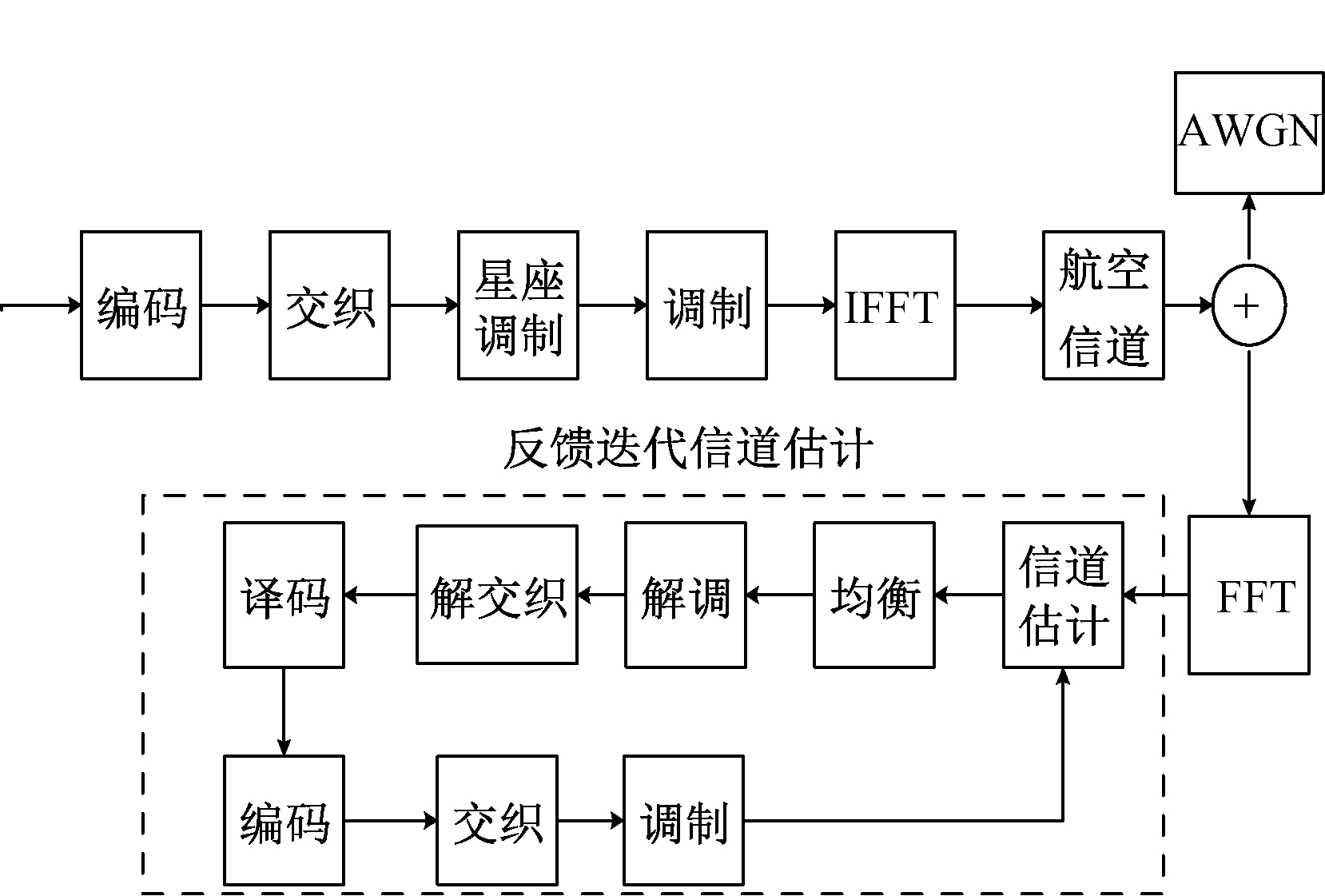
图3 反馈信道估计
Figure 3 Feedback channel estimation
算法具体步骤为：
Step1 处理发送信号，即将发送信号进行编码、交织、映射、调制及反傅里叶变换;
Step2 将处理过的发送信号送入飞机巡航状态下的两径莱斯信道;
Step3 将时域接收信号进行傅里叶变换为频域信号，并以此得出初始的信道估计
Step4 根据Xk=Yk/Hk做信号均衡；
函数f是将均衡之后所得信号进行Step1的逆操作，即解调、解交织及译码；
Step6 对解调信号再次进行编码、交织与调制。同时调制后的信号作为导频符号再次反馈到信道估计器，再次重复Step2的信道估计；
Step7 如此迭代到该算法收敛为止。
3 信道估计性能分析及导频设计
根据导频图案的不同，导频结构分为块状、梳状、格状3种，文献[13-14]给出时变信道下的最佳导频插入位置和疏密度，结合信道特点仿真采取等间隔插入梳状导频方案。插入间隔需满足：
(14)
(15)
式中：St、Sf分别表示时域和频域两个维度的导频间隔；Bd为最大多普勒频移；τmax为最大多径时延。
导频插入位置和疏密程度在信道估计中的影响直接体现在估计所得均方误差MSE的大小[15]，最小均方误差和归一化均方误差分别为：
(16)
(17)
4 仿真结果
为了验证提出的反馈迭代信道估计算法的估计性能，笔者在建立航空通信系统模型的基础上，通过实际的L-DACS1系统[1]进行仿真测试。表1给出了采用L-DACS1的具体系统参数。
表1 L-DACS1系统参数
Table 1 System parameter of L-DACS1
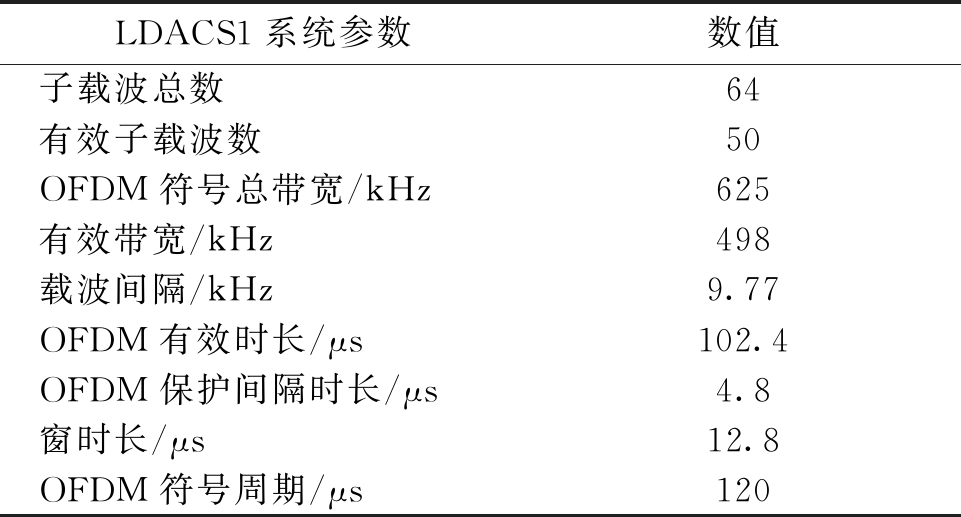
LDACS1系统参数数值子载波总数64有效子载波数50OFDM符号总带宽/kHz625有效带宽/kHz498载波间隔/kHz9.77OFDM有效时长/μs102.4OFDM保护间隔时长/μs4.8窗时长/μs12.8OFDM符号周期/μs120
图4～7比较了插入导频数量分别为16和32 时的信道估计均方误差和信号检测误码率性能。笔者采用航空信道巡航阶段的一些经典测试数据[1]：飞机速度设定为300 m/s，载波频率为1 GHz，归一化多普勒为0.12，散射径时延取33 μs。莱斯因子为15 dB,结果显示导频为16时，采用最小二乘时域信道估计，由于巡航阶段散射径时延较大，此时导频数量不符合式(15)中导频间隔条件，导致式(17)所得信道估计误差较大，具体如图5所示。相比之下，LMSSE和LS频域信道估计算法性能相仿,较时域估计有所提升。导频数量增加至32时3种方法均可以达到相近效果。相比之下，在相同的情况下LS时域信道估计可以和LMMSE达到近似的估计效果，但LS信道估计算法比LMMSE信道估计算法具有更低计算复杂度，因此笔者在反馈信道估计中采用LS信道估计算法和反馈迭代相结合来进一步优化估计性能。
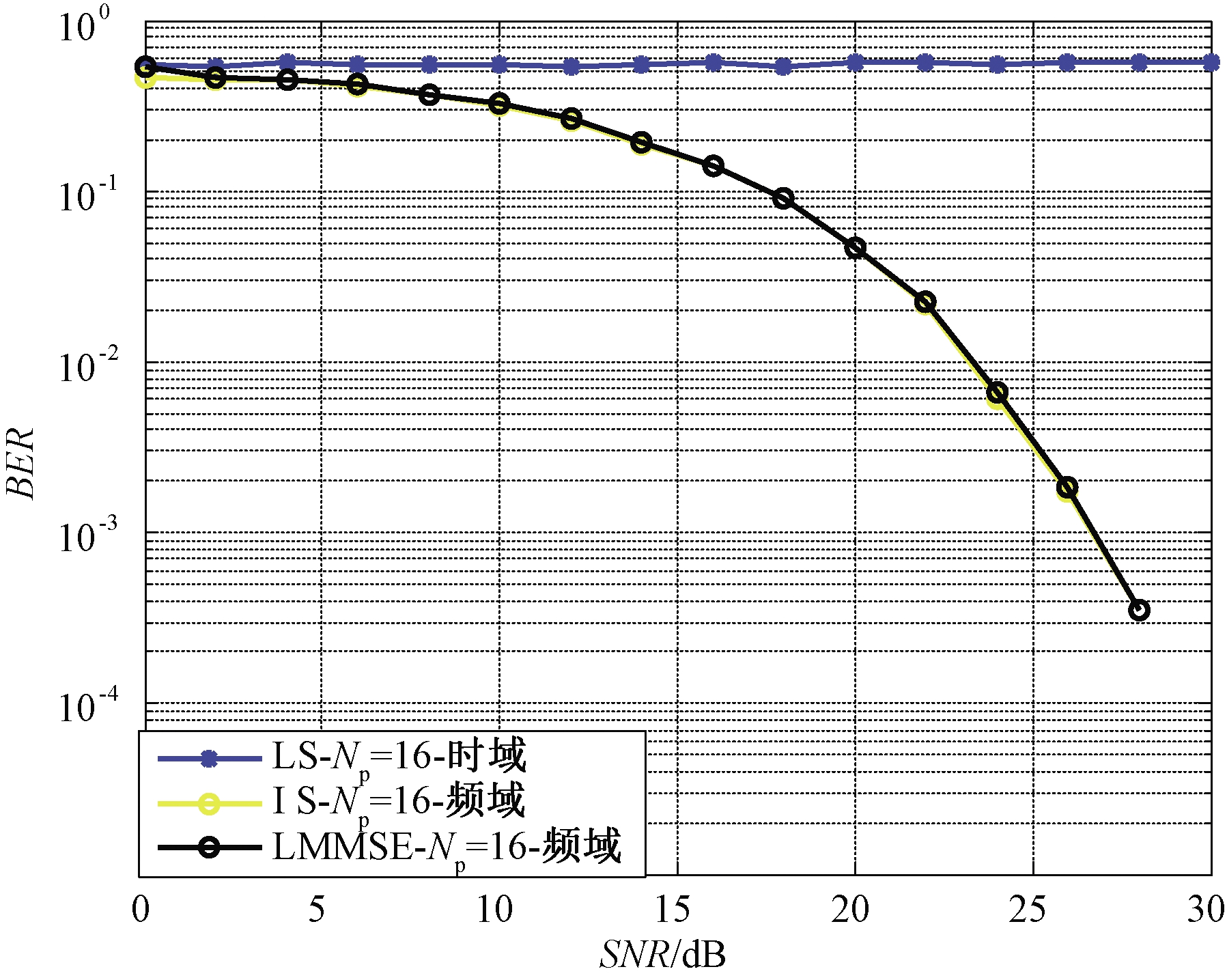
图4 误码率性能比较(导频为16)
Figure 4 Bit error rate performance comparison (number of pilot is 16)
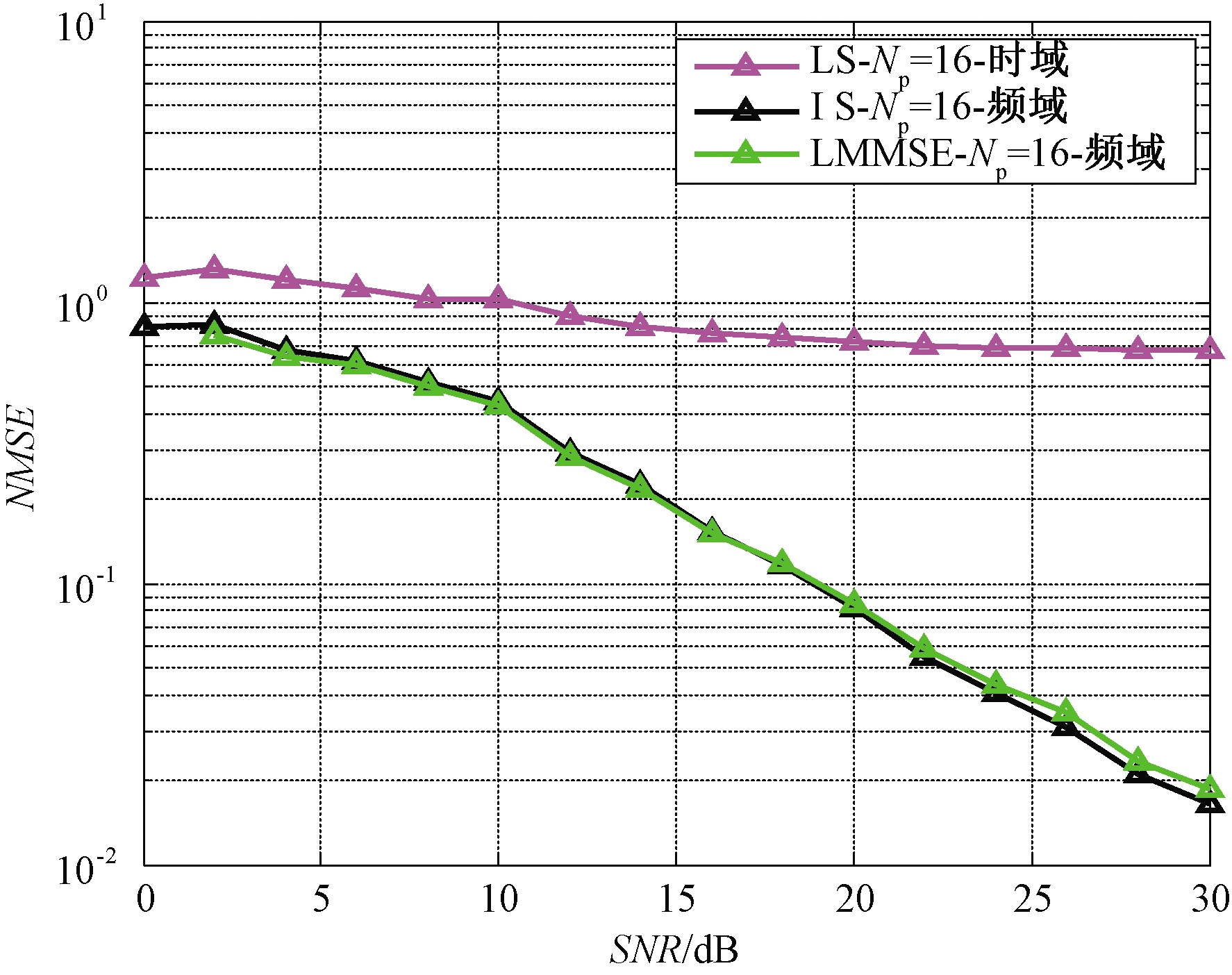
图5 信道特性的归一化均方误差(导频为16)
Figure 5 NMSE of the channel characteristics ( number of pilot is 16)
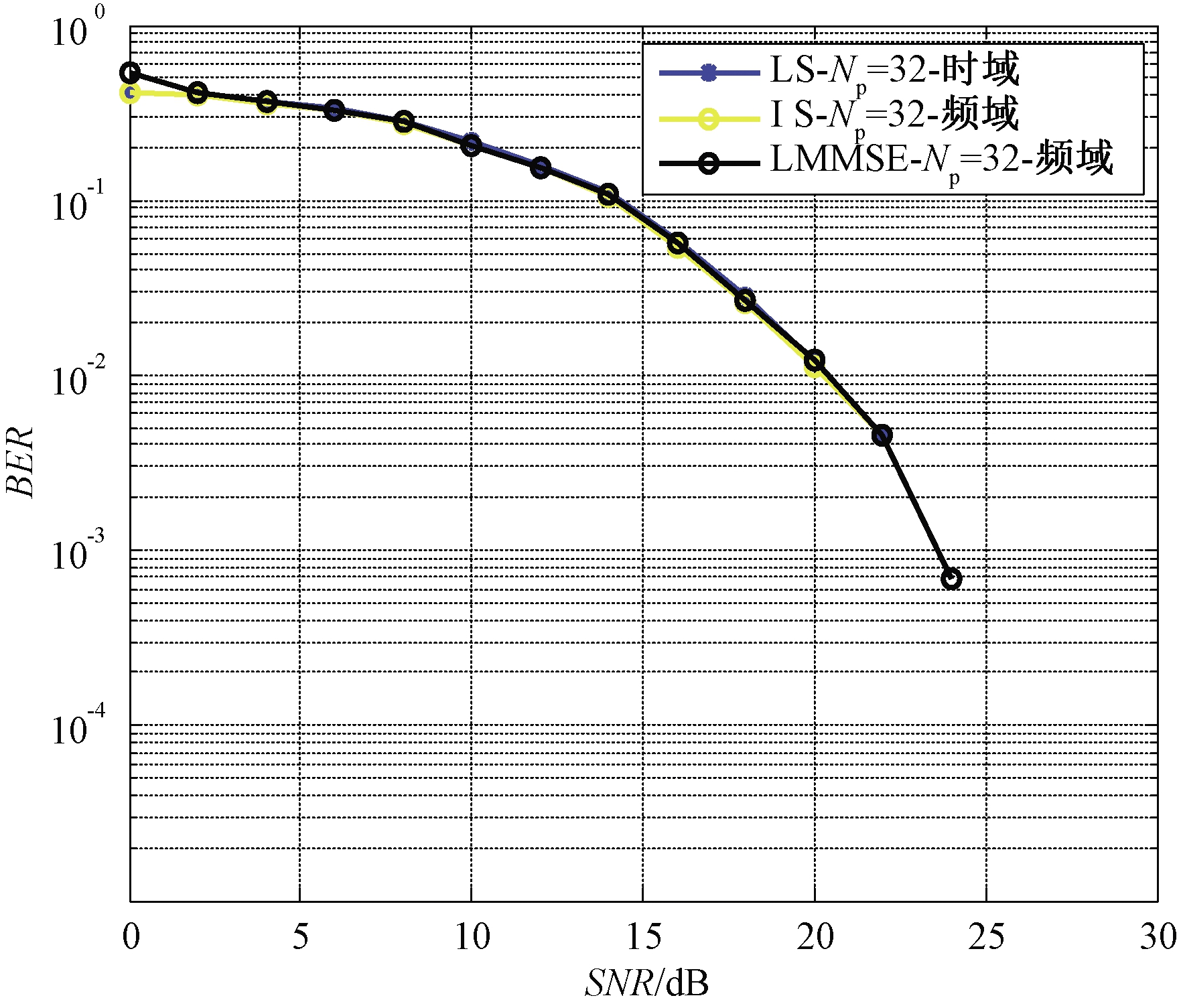
图6 误码率性能比较(导频为32)
Figure 6 Bit error rate performance comparison (number of pilot is 32)
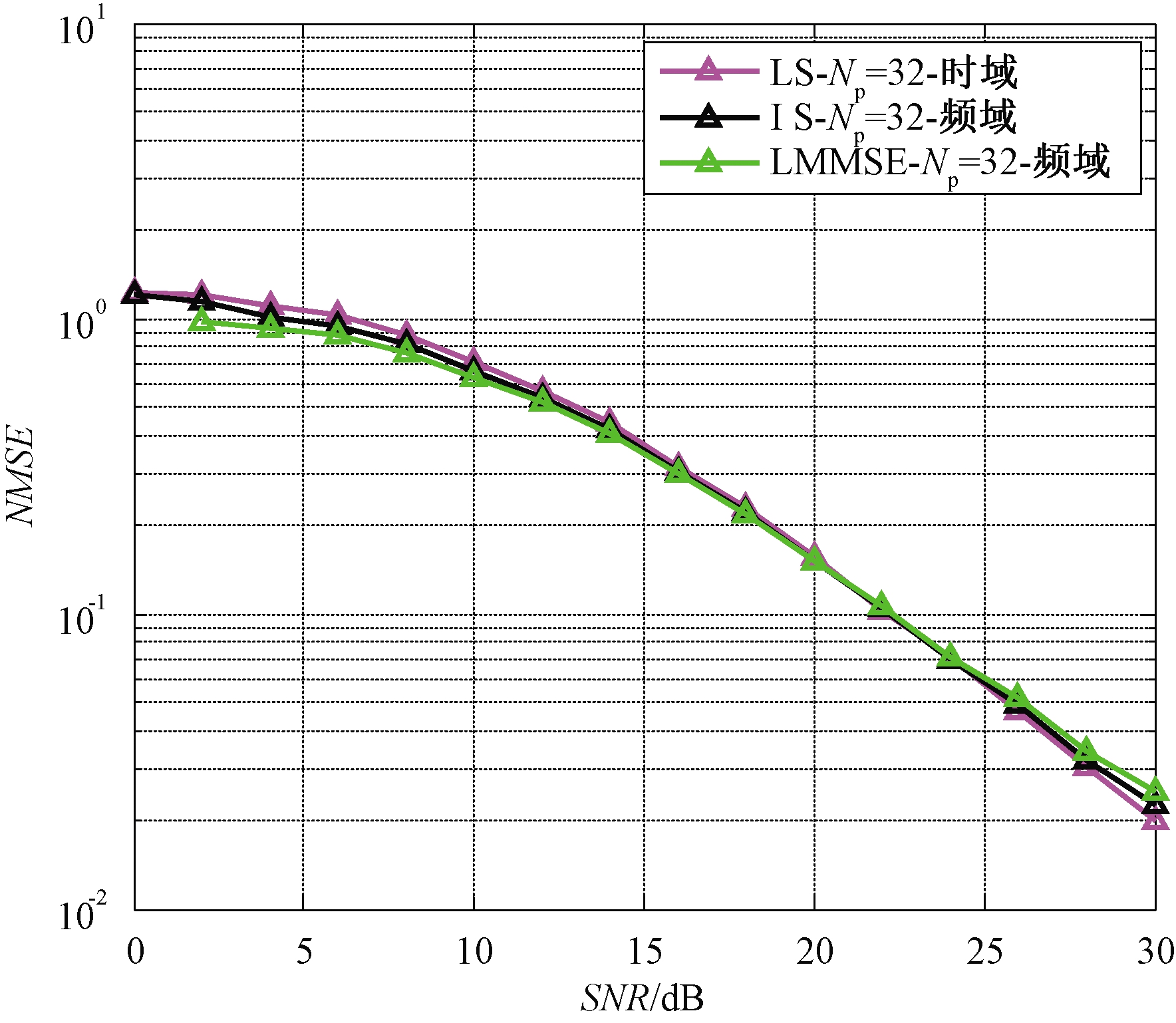
图7 信道特性的归一化均方误差(导频为32)
Figure 7 NMSE of the channel characteristics (number of pilot is 32)
图8和图9给出了基于反馈迭代信道估计算法的性能仿真，其中编码采用编码速率r=1/2的(2，1，3)卷积码。结果表明，在经过两次迭代之后系统基本收敛。具体而言，当信噪比SNR小于25 dB时，笔者提出的反馈迭代信道估计的归一化均方误差相比于无反馈的传统方法，可获得大约2 dB的增益,误码率也较无反馈时有所降低。
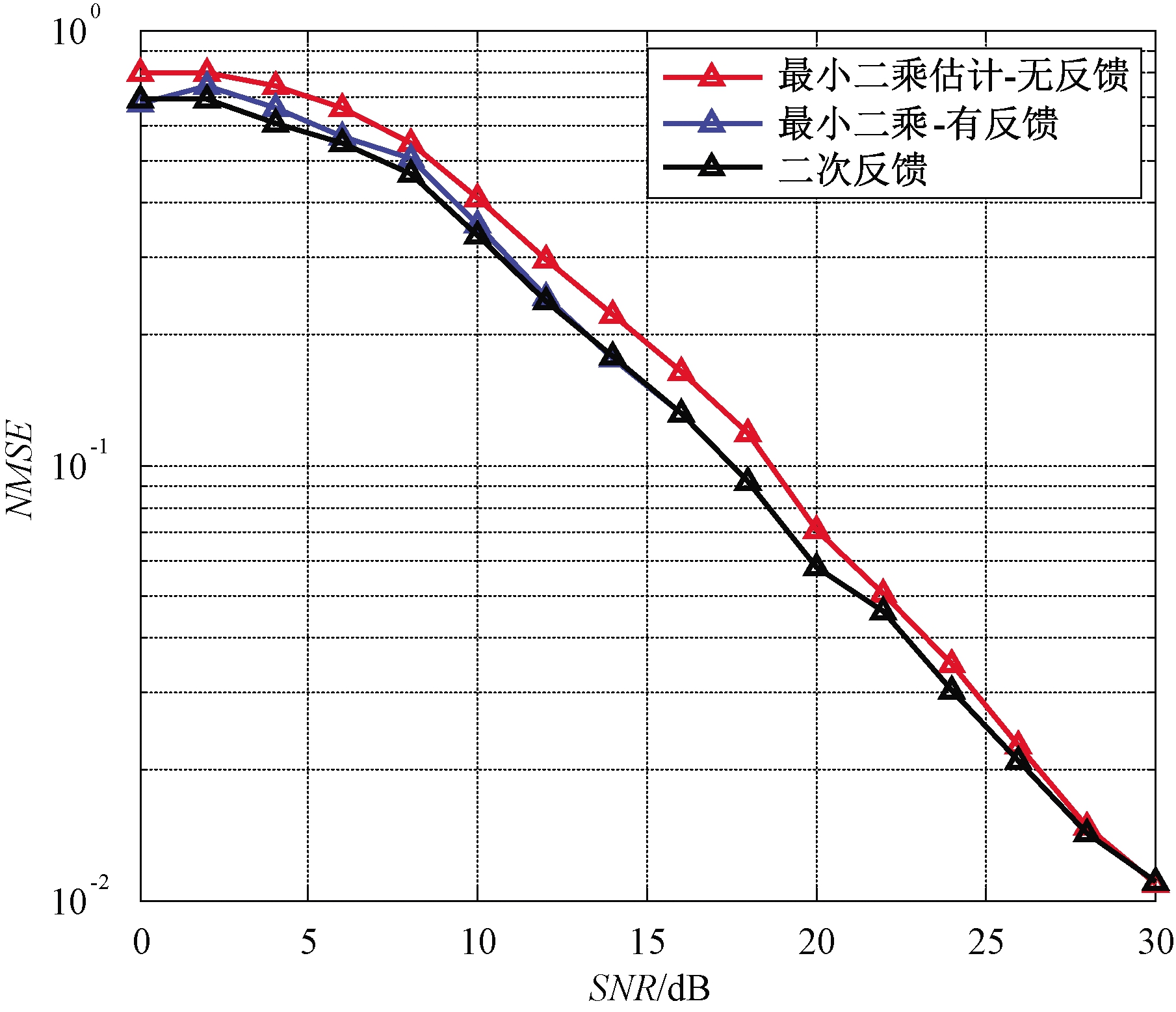
图8 基于反馈迭代的信道特性的归一化均方误差
Figure 8 NMSE of the channel characteristics based on feedback iterative
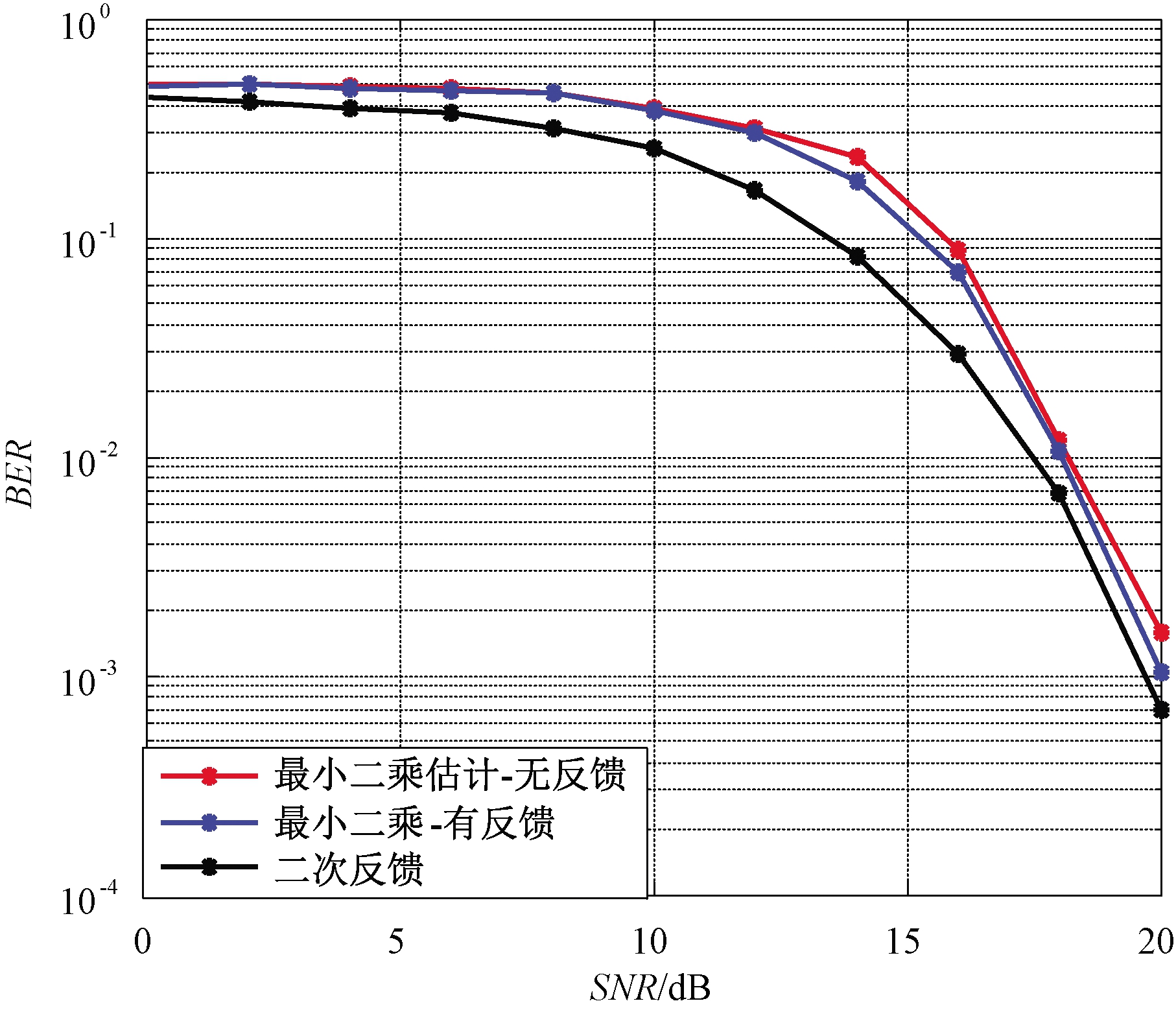
图9 基于反馈迭代的误码率性能比较
Figure 9 Bit error rate performance comparison based on feedback iterative
5 结论
针对飞机通信中的高多普勒频移和大多径时延扩展特点，笔者提出一种反馈迭代的信道估计算法。该算法利用少量原始导频粗略估计信道信息进行信号检测，并将检测信号再次反馈至信道估计器，进行信道估计。同时，利用信道解码器的纠错功能，防止误码扩散现象。将所提出的信道方案在实际L-DACS1航空系统针对巡航场景进行了仿真验证。结果表明，提出的反馈迭代信道估计算法可以显著地提高信道估计的性能，改善L-DACS1航空通信系统的检测性能。
[1] BILZHAUSE A, BELGACEM B, MOSTAFA M, et al. Datalink security in the L-band digital aeronautical communications system (LDACS) for air traffic management[J]. IEEE aerospace & electronic systems magazine, 2017, 32(11):22-33.
[2] ZHANG J K, CHEN S, MAUNDER R G, et al. Adaptive coding and modulation for large-scale antenna array based aeronautical communications in the presence of co-channel interference[J]. IEEE transactions on wireless communications, 2018, 17(2):1343-1357.
[3] ZHANG J K, CHEN S, MAUNDER R G, et al. Regularized zero-forcing precoding aided adaptive coding and modulation for large-scale antenna array based air-to-air communications[J]. IEEE journal on selected areas in communications,2018,36(9):2087-2103.
[4] 陈恩庆,肖素珍.基于因子图的MIMO-OFDM时变信道估计[J].郑州大学学报(工学版),2016,37(1):87-91.
[5] DU Z, SONG X G, CHENG J L, et al. Maximum likelihood based channel estimation for macrocellular OFDM uplinks in dispersive time-varying channels[J]. IEEE transactions on wireless communications, 2011, 10(1):176-187.
[6] 张建康,穆晓敏,陈恩庆,等. OFDM系统基于导频的信道估计算法分析[J]. 通信技术, 2009, 42(8):91-94.
[7] 赵俊义. MIMO-OFDM无线通信系统信道估计算法研究[D]. 哈尔滨：哈尔滨工业大学, 2009.
[8] 穆晓敏,刘越,李双志,等.基于张量分解的MIMO多中继系统半盲信道估计方法[J].郑州大学学报(工学版)，2016,37(6):83-86.
[9] EDFORS O, SANDELL M, VAN DE BEEK J J, et al. OFDM channel estimation by singular value decomposition[J]. IEEE transactions on commu-nications, 1998, 46(7):931-939.
[10] 王刚,李鸿林.一种基于叠加导频的OFDM系统迭代信道估计算法[J].哈尔滨商业大学学报(自然科学版), 2012, 28(6):686-688.
[11] ZHANG J, MU X, CHEN E, et al. Decision-directed channel estimation based on iterative linear minimum mean square error for orthogonal frequency division multiplexing systems[J]. IET communications, 2009, 3(7):1136-1143.
[12] HAAS E. Aeronautical channel modeling [J]. IEEE transactions on vehicular technology, 2002, 51(2):254-264.
[13] HOEHER P. A statistical discrete-time model for the wssus multipath channel [J]. IEEE transactions on vehicular technology, 1992, 41(4):461-468.
[14] MORELLI M, MENGALI U. A comparison of pilot-aided channel estimation methods for OFDM systems[J]. IEEE transactions on signal processing, 2001, 49(12):3065-3073.
[15] LI Y. Simplified channel estimation for OFDM systems with multiple transmit antennas[J].IEEE transactions on wireless communications, 2002, 1(1):67-75.