0 引言
排水固结法是软土地基加固处理的一种有效方法,特别适合处理淤泥质土、吹填土等饱和软黏土地基.在排水固结法中,通常需要设置竖向排水体(如袋装砂井、塑料排水板)加快地基的固结,通常称为砂井地基.Barron[1]最早于1948年基于Terzaghi固结理论,分别在等应变和自由应变假定下对理想砂井地基的固结度给出了解析解.此后,众多学者展开了对砂井地基固结问题的深入研究[2-9],分别给出了不同条件下砂井地基的固结解答,这些解答考虑了井阻效应、涂抹区渗透系数变化、初始孔压非均匀分布、土体变形非线性等影响.
实际工程中,当处理的饱和软黏土层较厚,打穿整个软黏土层不经济或者施工较为困难时,可采用未打穿砂井.要全面掌握未打穿砂井地基的固结规律,需要同时考虑砂井区的固结和下卧层地基的固结特性.针对未打穿砂井问题,Hart等[10]针对软土层底面不排水的未打穿理想井,率先提出了未打穿砂井地基总平均固结度近似计算式.陈根媛[11]据砂井底面孔隙水压力的连续性,提出“双层地基法”.Tang等[12]将砂井范围内土层及下卧层的固结分别视为轴对称和一维问题,给出了未打穿砂井固结问题的解析解.王立忠等[13]对未打穿砂井地基固结分析的半排水法和双层地基法进行了改进.郝玉龙等[14]将未打穿砂井地基等效为多层地基的一维固结问题进行求解.谢康和等[15]给出了单面和双面排水条件下考虑土层三维渗流的解析解.闫富有[16]则将砂井下卧层视为虚拟砂井,将其转化为多段打穿砂井进行了数值求解.郭彪等[17]采用虚拟砂井法且考虑涂抹作用得到了未打穿砂井地基的固结解析解.Geng等[18]对堆载联合真空预压未打穿砂井地基处理方法的有效性进行了讨论.孙立强等[19]针对未打穿砂井地基大变形固结特性进行了研究,并结合工程实例进行了对比分析.
以上研究均采用Darcy渗流假定,而Hansbo等对多个砂井地基实际观测的资料分析表明,Barron固结理论与实际情况存在较大差异,主要是由于软黏土渗流偏离Darcy定律.因此,笔者基于Hansbo渗流模型,推导了未打穿砂井地基在非Darcy渗流条件下的轴对称固结方程,并采用FlexPDE软件进行了求解.在此基础上,研究了砂井打入深度、Hansbo渗流模型参数和涂抹区范围及渗透系数对未打穿砂井地基平均固结度的影响规律.
1 基本假定及分析模型
1.1 问题的基本描述
设某均质饱和黏土层厚度为H,已在自重作用下完全固结.饱和黏土层顶面透水,底面不透水.地基中设置砂井进行排水固结,砂井井径和影响半径分别为rw和re,考虑砂井施工扰动的影响,扰动区(涂抹区)半径为rs.砂井为未打穿砂井,砂井深度为H1.未打穿砂井地基的计算模型如图1所示.
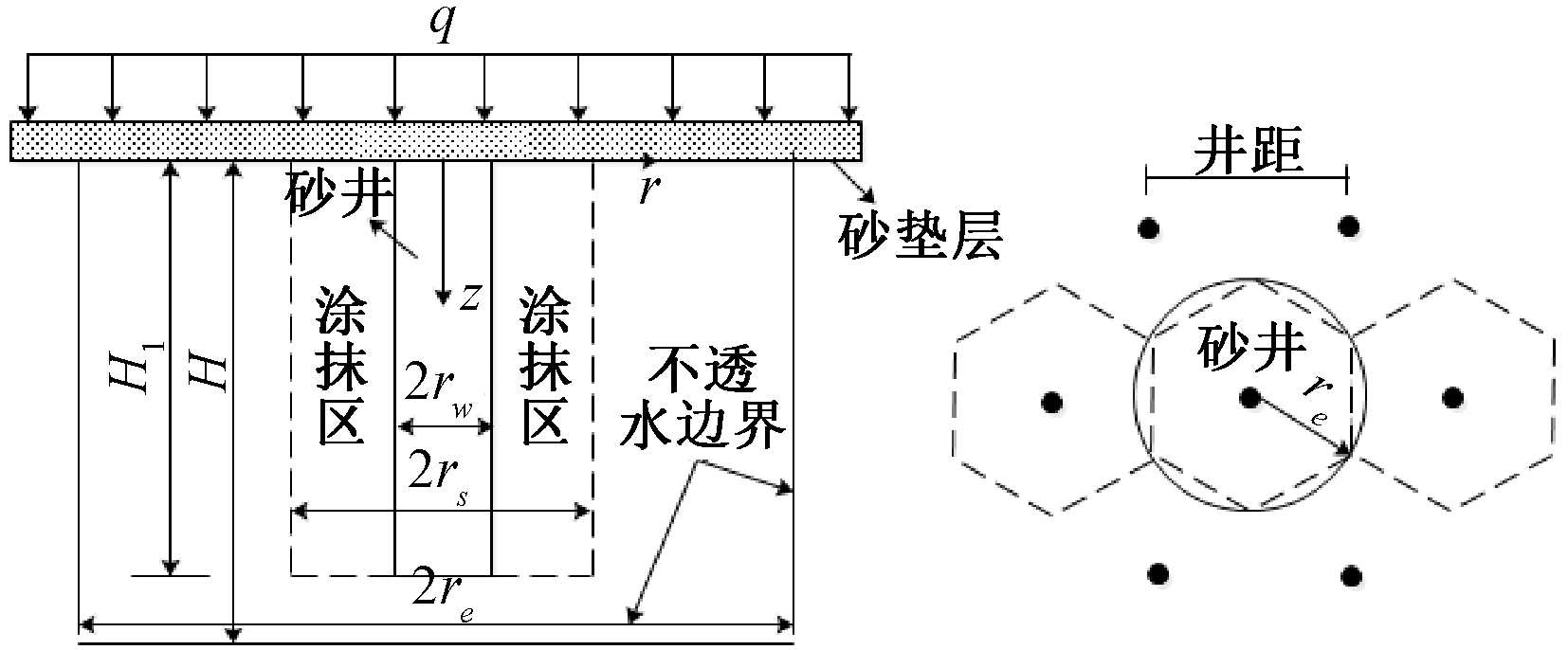
图1 未打穿砂井地基的计算模型
Fig.1 Model of ground by partially penetrated sand drain
1.2 基本假定
砂井地基的固结问题是一个复杂的三维问题,为简化分析,笔者遵从Barron固结的方法,即将砂井固结问题视为轴对称固结问题进行求解,并作出如下假定:
(1)饱和黏土层顶面瞬时施加均布荷载q,初始时刻,荷载全部由超孔隙水压u承担;
(2)固结过程中,地面均布荷载不会因差异沉降而改变其分布形式,即竖向应变可以自由发展;
(3)土体仅发生竖向变形,忽略土体水平方向的变形;
(4)土体渗流为轴对称渗流,即同时考虑竖向和水平径向渗流,渗流遵从Hansbo渗流模型且Hansbo渗流模型参数在固结过程中保持不变;
(5)考虑涂抹区影响时,涂抹区内的渗透系数不随距井边距离而变化.
1.3 分析模型的建立
图2为Hansbo渗流模型,可用式(1)表示:
(1)
式中:v为孔隙水渗流速度;m为由实验确定的常数;i为水力梯度;i1为直线渗流的起始水力梯度;i0和![]() 分别为直线渗流计算起始水力梯度和开始段指数渗流中的渗透系数,有式(2)所示的关系.
分别为直线渗流计算起始水力梯度和开始段指数渗流中的渗透系数,有式(2)所示的关系.
(2)
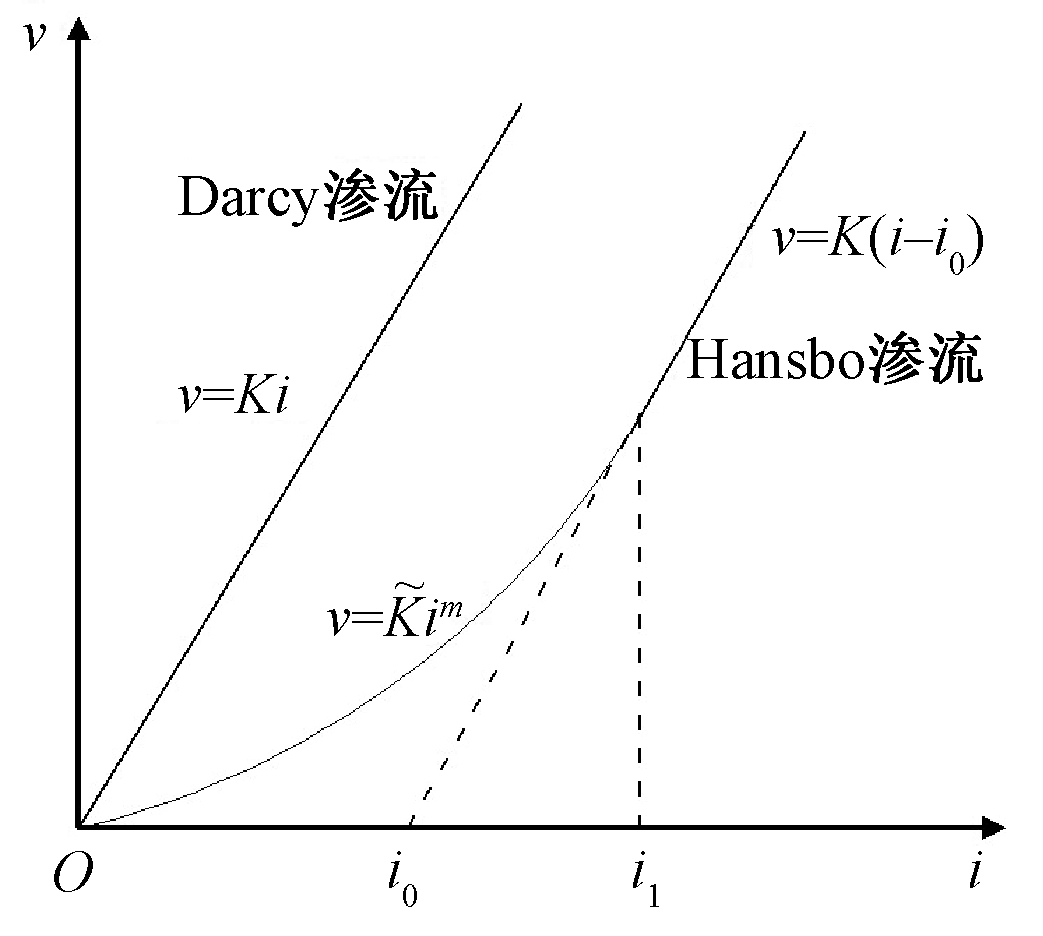
图2 Hansbo渗流模型
Fig.2 Hansbo′s flow model
考虑砂井地基的轴对称渗流时,需要对式(1)进行适当修改.砂井地基中,孔隙水渗流速度![]() 的竖向和径向分量分别表示为vz和vr;相应水力梯度
的竖向和径向分量分别表示为vz和vr;相应水力梯度![]() 的竖向分量和径向分量可表示式(3).
的竖向分量和径向分量可表示式(3).
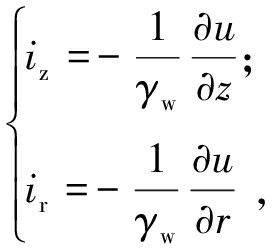
(3)
式中:γw为水的重度;u为超静孔隙水压力.
轴对称渗流时,Hansbo渗流模型可表示为(4).
(4)
式中:![]()
因此,孔隙水的竖向和径向渗流速度可表示为公式(5).
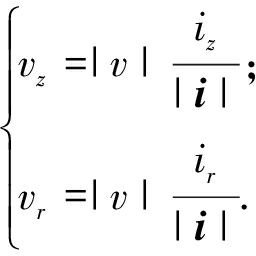
(5)
根据Barron的研究,轴对称条件下的渗流连续性方程可表示为公式(6):
(6)
式中:εv为体应变,有
(7)
式中:E′和ν′分别为饱和软黏土排水条件下的弹性模量和泊松比.
将式(3)~(5)和式(7)代入式(6),整理后,最终可得轴对称条件下的固结方程(8):
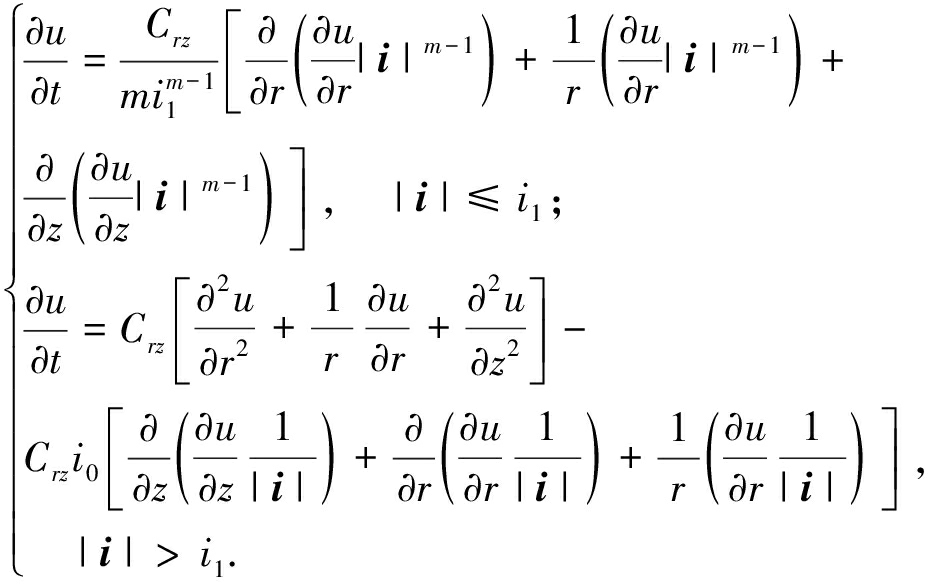
(8)
式中:![]() 其他参数同前.
其他参数同前.
未打穿砂井地基可分为三个区域:涂抹区、砂井固结区和砂井下卧土层区,如图1所示.每个区的固结控制方程形式相同,即式(8)表示的固结方程,但每个区固结方程中的土性参数不同,为简单起见,这里不再一一列出.此外,不同区域之间满足渗流连续性条件.
为求解式(8)所示的轴对称固结方程,需要给出初始条件和边界条件.根据未打穿砂井地基的问题描述及基本假定,本模型的初始条件和边界条件分别为式(9)和(10).
(9)
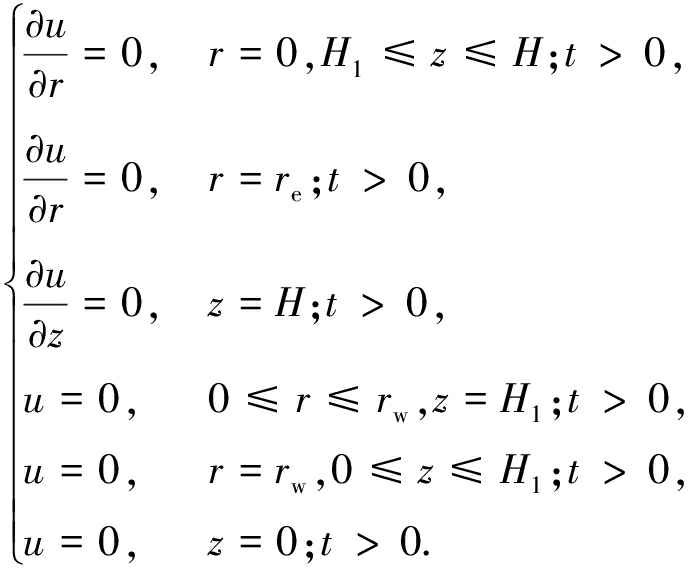
(10)
2 固结方程的FlexPDE求解及算法验证
2.1 固结方程的FlexPDE求解
与已有研究不同,笔者采用FlexPDE软件进行未打穿砂井地基固结方程的求解.FlexPDE软件是一款基于有限元法的偏微分方程求解软件.该软件可以求解一维到三维的发展问题、稳态问题以及特征值问题,可获得偏微分方程的数值解.FlexPDE软件采用非常“自然”的脚本语言来描述所分析问题的偏微分控制方程、求解域及其边界条件,使研究人员和工程技术人员的精力主要集中于所研究问题控制方程的推导和建立,从而节省大量的计算程序编制时间,降低了复杂问题的研究门槛.
采用FlexPDE软件求解未打穿砂井地基的固结问题时,涂抹区、砂井固结区和砂井下卧区三个区域间的渗流连续性条件为有限元内部边界条件,可由有限元方法自动满足,无需进行额外处理.
2.2 算法验证
当m=1时,式(1)描述的Hansbo渗流退化为Darcy渗流.从图3可以看出,时间因子T=0.5时,m=1的Hansbo渗流计算的固结度约是Darcy渗流计算值的86%.这也就解释了Darcy渗流并不能很好地解释小水力梯度下的饱和黏性土渗流规律的原因.因此,采用Hansbo渗流模型计算砂井地基固结问题是必要的.此外,文献[20]采用有限差分法研究了基于Hansbo渗流的理想砂井地基固结问题.为验证本文算法在Hansbo渗流条件下的可靠性,对文献[20]的算例进行了计算.计算参数如表1所示,计算结果如图3所示.由图3可知,本文计算结果与文献[20]计算结果吻合较好,说明本文算法合理可靠.
表1 Hansbo渗流条件下理想砂井地基的计算参数
Tab.1 Parameters for consolidation of ground with sand drains based on Hansbo′ flow

井径比n渗流参数α起始水力梯度i1渗流参数m时间因子T50.2101.0,1.8Crzt4r2e
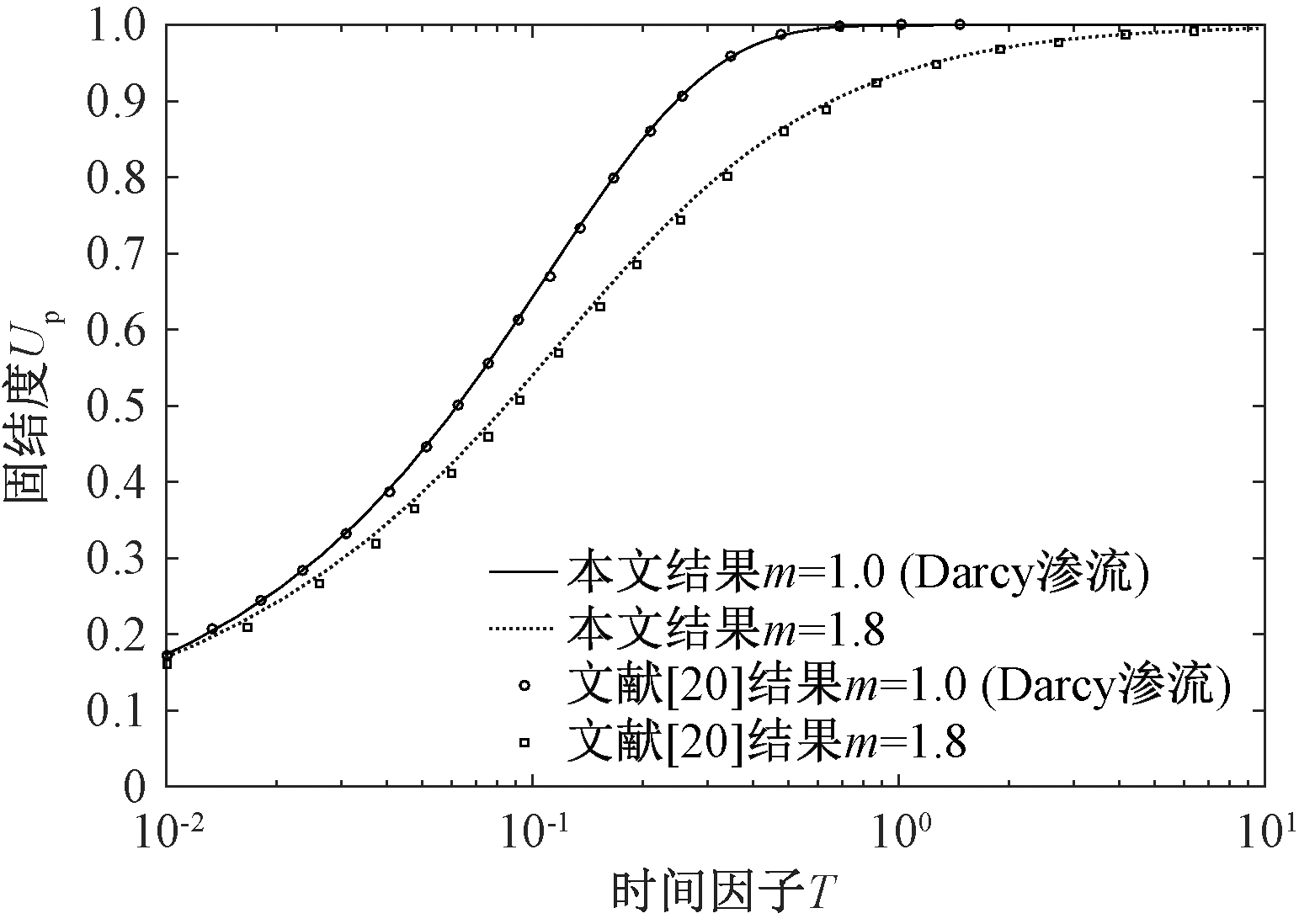
图3 本文计算结果与文献[20]对比
Fig.3 Compare of the results to those of literature[20]
3 未打穿砂井地基的固结特性分析
笔者主要研究Hansbo渗流条件下未打穿砂井地基的固结问题,探讨Hansbo渗流参数m和I1、砂井打入深度以及涂抹区对未打穿砂井地基固结的影响.砂井地基的井径比n取20,α取0.1,其他参数取值范围见表2所示.
表2 计算参数取值范围
Tab.2 Parameter range
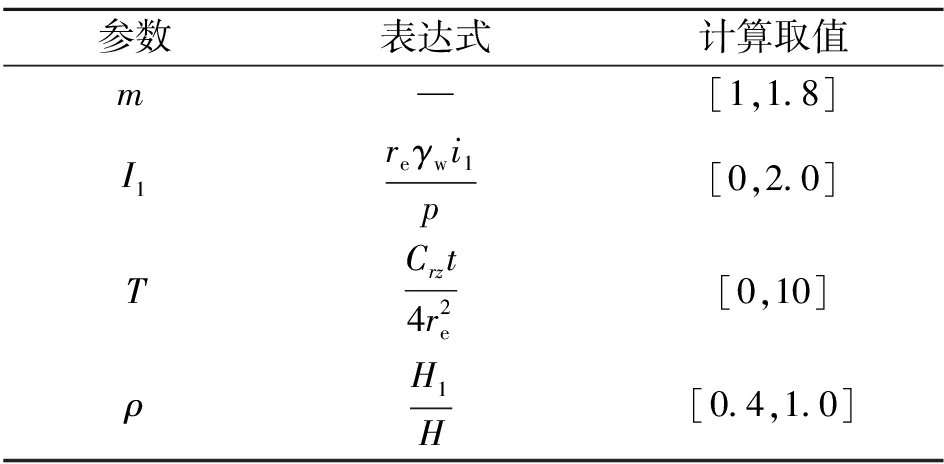
参数表达式计算取值m—[1,1.8]I1reγwi1p[0,2.0]TCrzt4r2e[0,10]ρH1H[0.4,1.0]
3.1 砂井打入深度的影响
为分析砂井打入深度对未打穿砂井地基固结的影响,砂井打入深度比ρ取0.4~1.0(ρ=1.0时为理想砂井地基);Hansbo渗流模型参数取m=1.5和I1=1,计算结果如图4所示.
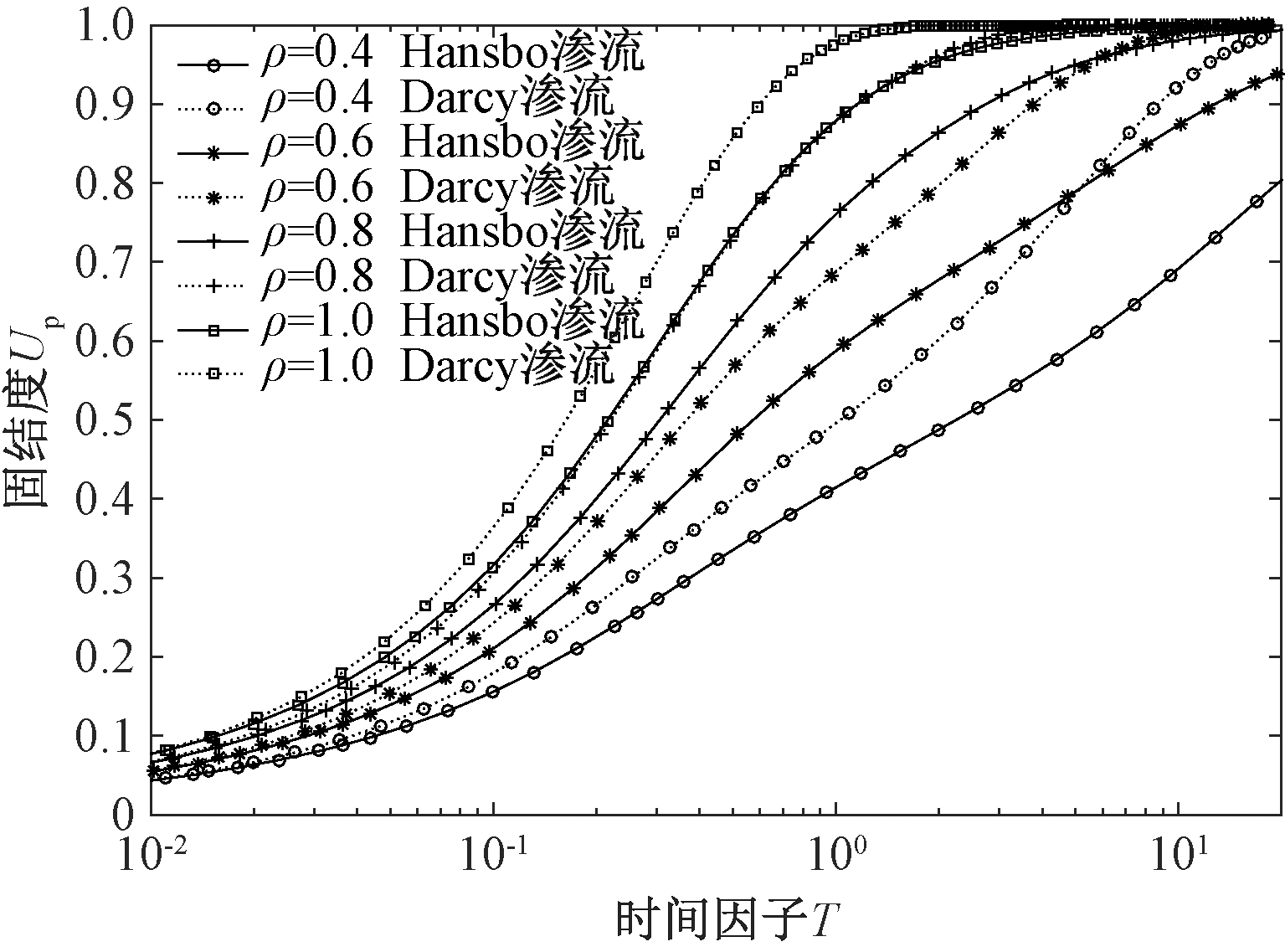
图4 砂井打入深度对未打穿砂井地基平均固结度的影响
Fig.4 Influence of depth of sand drain on average consolidation degree of partially penetrated sand-drained foundation
由图4可知,无论是Darcy渗流还是Hansbo渗流,砂井打入深度比ρ越大,地基的平均排水路径就越短,因而地基的固结速率就越快.例如,考虑Hansbo渗流的情况,砂井地基平均固结度达到90%时,理想砂井地基所需时间T≈1; ρ=0.8的砂井地基所需时间T≈1.8; ρ=0.6的砂井地基所需时间T≈10.因此,砂井打入深度对地基的平均固结度影响非常大,实际工程中应尽量保证砂井的打入深度.
3.2 Hansbo渗流模型参数的影响
为分析Hansbo渗流模型参数对未打穿砂井地基固结的影响,取参数m=1.0~1.8、I1=0~2.0;砂井打入深度比ρ=0.6,不考虑涂抹区影响.计算结果如图5和图6所示.
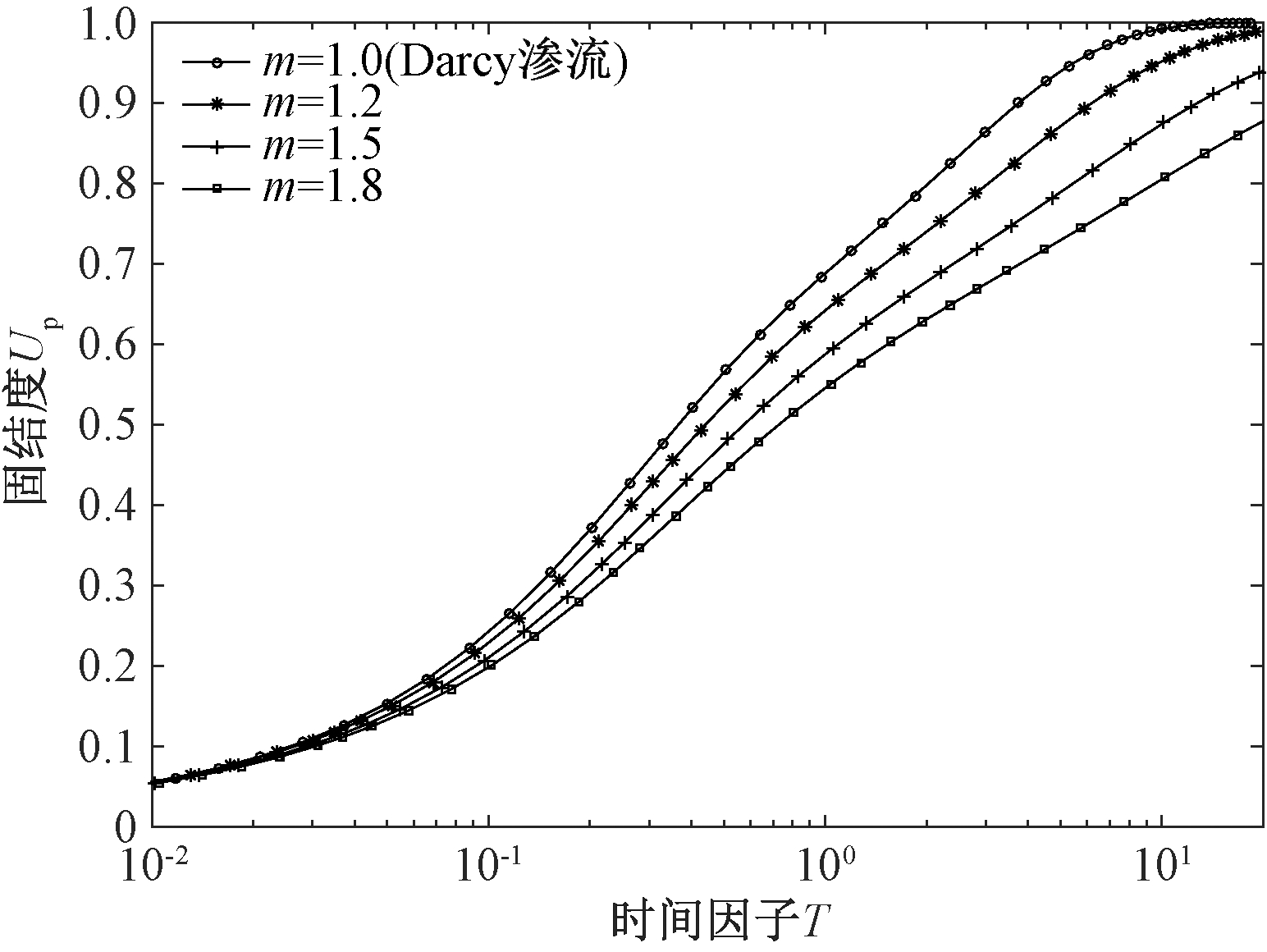
图5 m值对未打穿砂井地基平均固结度的影响
Fig.5 Influence of m on average consolidation degree of partially penetrated sand-drained foundation
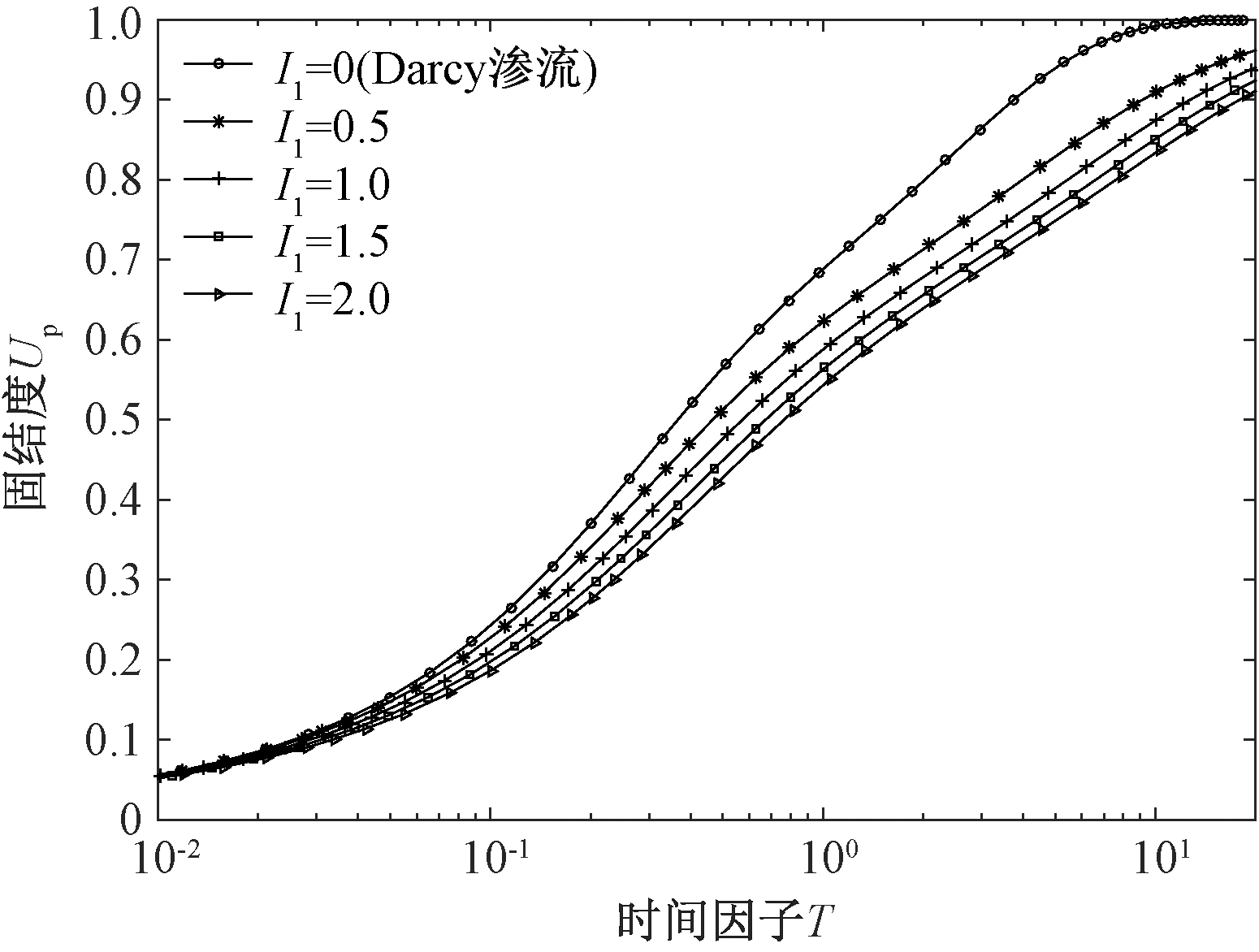
图6 I1值对未打穿砂井地基平均固结度的影响
Fig.6 Influence of I1 on average consolidation degree of partially penetrated sand-drained foundation
由图可知,Hansbo渗流参数m和I1越大,同一时刻砂井地基的平均固结度越小,即砂地基的固结速率越低.Darcy渗流状态下未打穿砂井地基的固结速率较Hansbo渗流的快,这表明不考虑软黏土的Hansbo渗流特性会过高估计未打穿砂井地基的平均固结度.
3.3 涂抹区的影响
由于砂井施工时会对砂井周边土体产生扰动,在砂井周边形成涂抹区(扰动区),由于涂抹区土体渗透系数的降低,从而对砂井地基的固结产生影响.为分析涂抹区对未打穿砂井地基固结的影响,假定涂抹区孔隙水的渗流也符合Hansbo渗流模式,不考虑Hansbo渗流参数m和i1的改变,仅考虑渗透系数K的改变.
假定涂抹区半径为rs、渗透系数为Ks,定义s=rs/rw,δ=Ks/K.计算时,工况1中s=0~10(s=0时为不考虑涂抹区的工况),δ=0.2,ρ=0.6,计算结果如图7所示;工况2中δ=0.1~1(δ=1时为不考虑涂抹区的工况),ρ=0.6,s=5,计算结果图8所示.
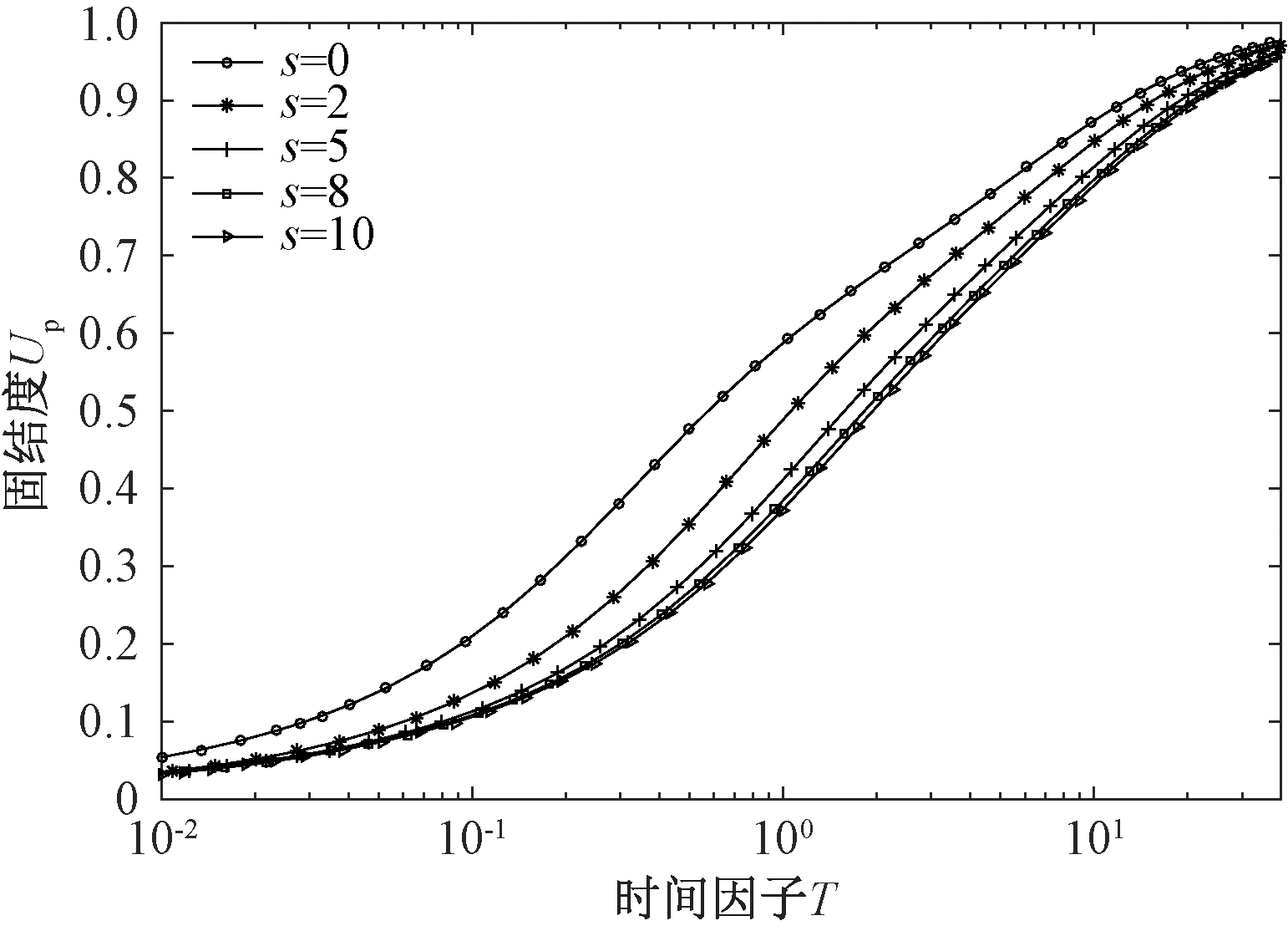
图7 s对未打穿砂井地基平均固结度的影响
Fig.7 Influence of s on average consolidation degree of partially penetrated sand-drained foundation
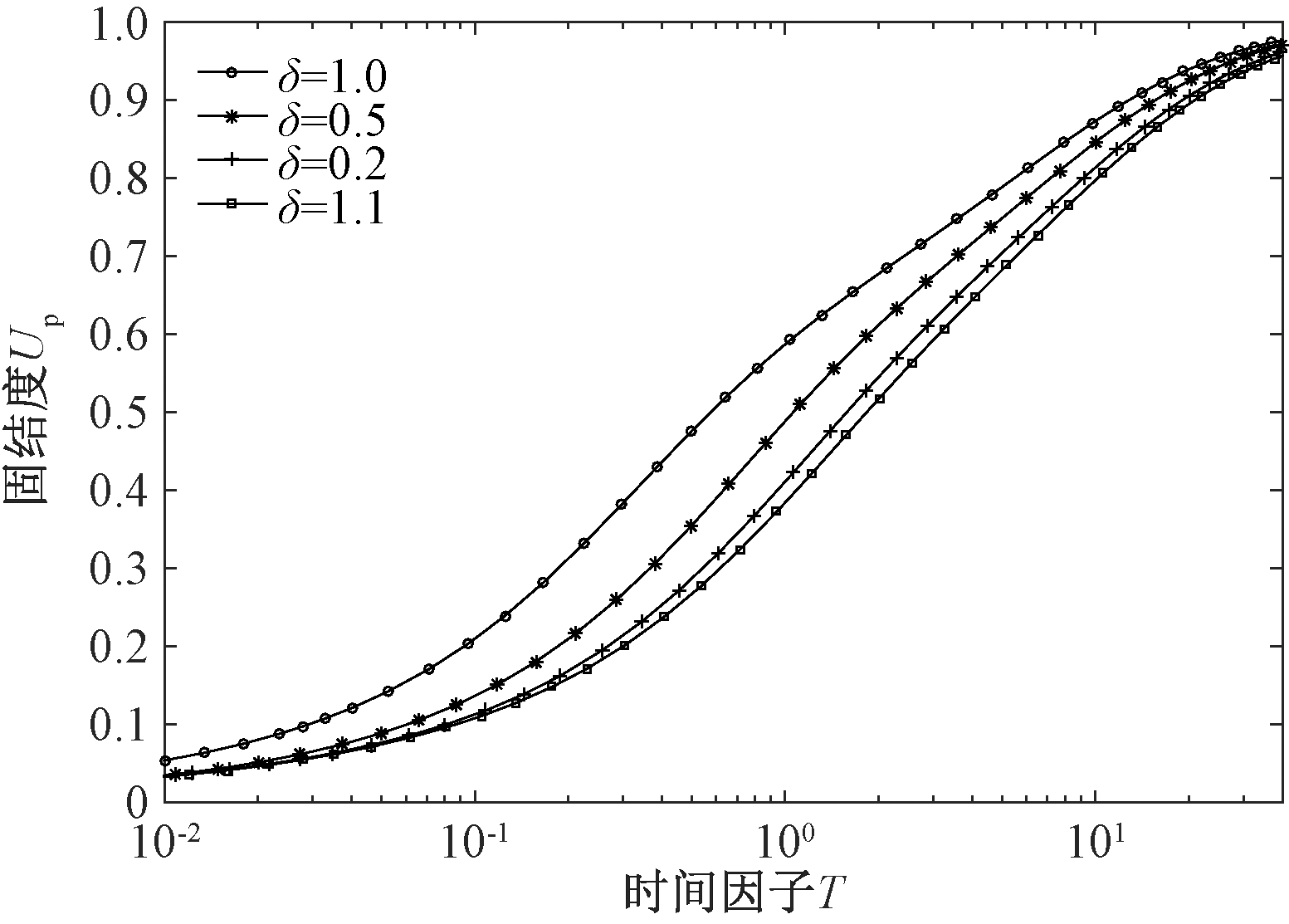
图8 δ未打穿砂井地基平均固结度的影响
Fig.8 Influence of δ on average consolidation degree of partially penetrated sand-drained foundation
由图7可知,随着涂抹区范围的增大,同一时刻未打穿砂井地基的平均固结度逐渐降低,表明涂抹区的存在降低了砂井地基的固结速率;当涂抹区范围较大时,例如,s≥8时,砂井地基的平均固结度基本不随涂抹区范围的增大而变化.此外,在固结中期,涂抹区的范围对未打穿砂井地基平均固结度的影响最大;而在固结后期,涂抹区的影响逐渐降低,同一时刻各工况下的平均固结度差异不大.
由图8可知,随着涂抹区土体渗透系数的减小,同一时刻未打穿砂井地基的平均固结度也随之降低,且砂井地基固结速率逐渐降低;在固结中期,涂抹区土体渗透系数的变化对未打穿砂井地基平均固结度影响较大;而在固结后期,涂抹区渗透系数的变化对未打穿砂井地基平均固结度的影响逐渐降低.
4 结论
基于Hansbo渗流模型,推导了未打穿砂井地基在非Darcy渗流条件下的轴对称固结方程,采用FlexPDE软件对固结方程进行求解计算,并通过算例验证了本文方法的可靠性.在此基础上,研究了砂井打入深度、Hansbo渗流模型参数和涂抹区对未打穿砂井地基平均固结度的影响规律.主要结论如下:
(1)砂井打入深度对未打穿砂井地基的影响非常大,砂井打入深度比ρ=0.6时平均固结度达到90%所需时间大约是理想砂井地基的10倍.
(2)随着Hansbo渗流模型参数m和I1的逐渐增大,未打穿砂井地基的平均固结度逐渐减小.不考虑Hansbo渗流影响会高估砂井地基的固结程度.
(3)随着涂抹区范围的增大和渗透系数的降低,未打穿砂井地基的平均固结度也随之降低;涂抹区半径超过井径8倍后,未打穿砂井地基平均固结度基本不随涂抹区范围的改变而发生变化.
(4)在固结中期,涂抹区范围和渗透系数对未打穿砂井地基的平均固结度影响较大;而在固结后期,各种工况下未打穿砂井地基的平均固结度差别不大.
[1] BARRON R A.Consolidation of fine-grained soils by drain wells[J].Transactions of the american society of civil engineerings, 1948, 113:718-742.
[2] HANSBO S, JAMIOLKOWSKI M, KOK L.Consolidation by vertical drains[J].Géotechnique, 1981, 31(1):45-66.
[3] YOSHIKUNI H, NAKANADO H.Consolidation of fine-grained soils by drain well with finite permeability[J].Soils and foundations, 1974, 14(2): 35-46.
[4] LEKHA K R, KRISHNASWAMY N R, BASAK P.Consolidation of clay by sand drain under time-dependent loading[J].Journal of geotechnical and geoenvironmental engineering, 1998, 124(1): 91-94.
[5] 谢康和, 曾国熙.等应变条件下的砂井地基固结解析理论 [J].岩土工程学报, 1989, 11(2): 3-17.
[6] HANSBO S.Consolidation equation valid for both Darcian and non-Darcian flow[J].Géotechnique, 2001, 51(1): 51-54.
[7] 刘忠玉, 刘忠广, 马崇武.考虑起始水力梯度时饱和粘土的一维固结[J].郑州大学学报(工学版), 2006, 27(3): 21-24.
[8] 闫富有.砂井地基径向非线性固结解析[J].郑州大学学报(工学版),2007,28(2):35-38.
[9] 蔡新, 谢康和, 徐妍,等.初始孔压非均布条件下涂抹区渗透系数变化的砂井地基固结解[J].岩土工程学报,2010, 32(1): 104-108.
[10] HART E G, KONDNER R L, BOYER W C.Analysis for partially penetrating sand drains[J].Journal of the soil mechanics and foundation division,1958, 84(4): 1-15.
[11] 陈根媛.多层地基的一维固结计算方法与砂井地基计算的改进建议[J].水利水运科学研究,1984(2):18-30.
[12] TANG X W, ONITSUKA K.Consolidation of ground with partially penetrated vertical drains[J].Geote-chnical engineering journal,1998, 29(2):209-231.
[13] 王立忠,李玲玲.未打穿砂井地基下卧层固结度分析[J].中国公路学报, 2000, 13(3): 4-8.
[14] 郝玉龙, 陈云敏, 王军.深厚软土未打穿砂井超载预压地基孔隙水压力消散规律分析[J].中国公路学报,2002,15(2): 36-39.
[15] 谢康和, 周开茂.未打穿竖向排水井地基固结理论[J].岩土工程学报, 2006, 28(6): 679-684.
[16] 闫富有.成层未打穿砂井地基固结 Lagrange插值解法[J].岩石力学与工程学报, 2007, 26(9): 1932-1939.
[17] 郭彪, 龚晓南, 卢萌盟,等.考虑涂抹作用的未打穿砂井地基固结理论分析[J].岩石力学与工程学报, 2009, 28 (12): 2561-2568.
[18] GENG X Y, INDRARATNA B, RUJIKIATKAMJORN C.Effectiveness of partially penetrating vertical drains under a combined surcharge and vacuum preloading[J].Canadian geotechnical journal, 2011, 48(6):970-983.
[19] 孙立强, 贾天强, 闫澍旺,等.基于大变形的未打穿砂井固结理论研究[J].岩石力学与工程学报, 2017, 36(2):504-512.
[20] 刘忠玉, 焦阳.基于Hansbo渗流的理想砂井地基固结分析[J].岩土工程学报, 2015, 37(5): 792-801.