0 引言
随着机械设备越来越向重载、高速的方向发展，对其动力学性能的要求也越来越高.润滑不但可以有效减小摩擦，降低磨损，提高设备工作效率，而且对设备的振动、噪声等动力学性能的改善具有重要的作用.所以，近年来，研究机械动力学时考虑润滑的作用开始引起研究者的注意和重视.
早期对摩擦副的动力学特性进行研究时，多忽略润滑油膜.Datta等[1]在研究滚动轴承的动特性时，假设摩擦副为Hertz接触，求得了等效刚度，但忽略了润滑油的阻尼作用.Harsha等[2]在预测转子系统的动特性时，使用Hertz理论获得滚动件与座圈间的刚度，也没考虑润滑油的影响.随着研究的深入，Hagiu[3]将系统动特性与润滑理论耦合，建立了比较符合实际工况的动力学模型，后来在文献[4-10]中都用到了这种耦合方法，但是，其中Wijnant[6]、Venner[7]和张鑫磊[8]的研究中选取了常数作为无量纲自然频率.张玉言[9]和柳剑[10]则认为这种方法存在问题，他们根据实际工作载荷、速度计算出无量纲自然频率，并对其进行了研究.对比这些学者的研究还发现：Wijnant和柳剑[6]认为弹流状态下摩擦副的阻尼随载荷增加呈现出下降的趋势；张鑫磊[8]的计算结果则正好与之相反；而张玉言则认为在不同的参数范围内刚度阻尼的变化趋势都不同.笔者认为这些结论的不同与无量纲自然频率的选取有关，故笔者针对无量纲自然频率对摩擦副刚度、阻尼的影响规律进行研究.
1 线接触摩擦副动力学-弹流润滑耦合系统方程
1.1 弹流基本方程
(1)Reynolds方程：
(1)
式中：u为卷吸速度；p为油膜压力；h为膜厚；η为油黏度；ρ为油密度；t为时间.
(2)油膜厚度方程：
(2)
式中：h00为刚体中心位移；E′为等效弹性模量；R为等效曲率半径.
(3)黏压方程：
η=η0exp{(lnη0+9.67)×
[(1+5.1×10-9p)z-1]}，
(3)
式中：η0为润滑油的环境黏度；z为Roelands方程黏压系数.
(4)密压方程：
(4)
式中：ρ0为润滑油环境密度.
(5)载荷平衡方程：
p(x,t)dx=w，
(5)
式中：w为线载荷.
1.2 动力学方程
将弹流油膜简化为弹簧阻尼，则摩擦副的动力学模型如图1所示.其动力学方程为：
(6)
式中：q(t)为外载荷；ffilm为油膜力；m为摩擦副等效质量；δ为弹性趋近量.
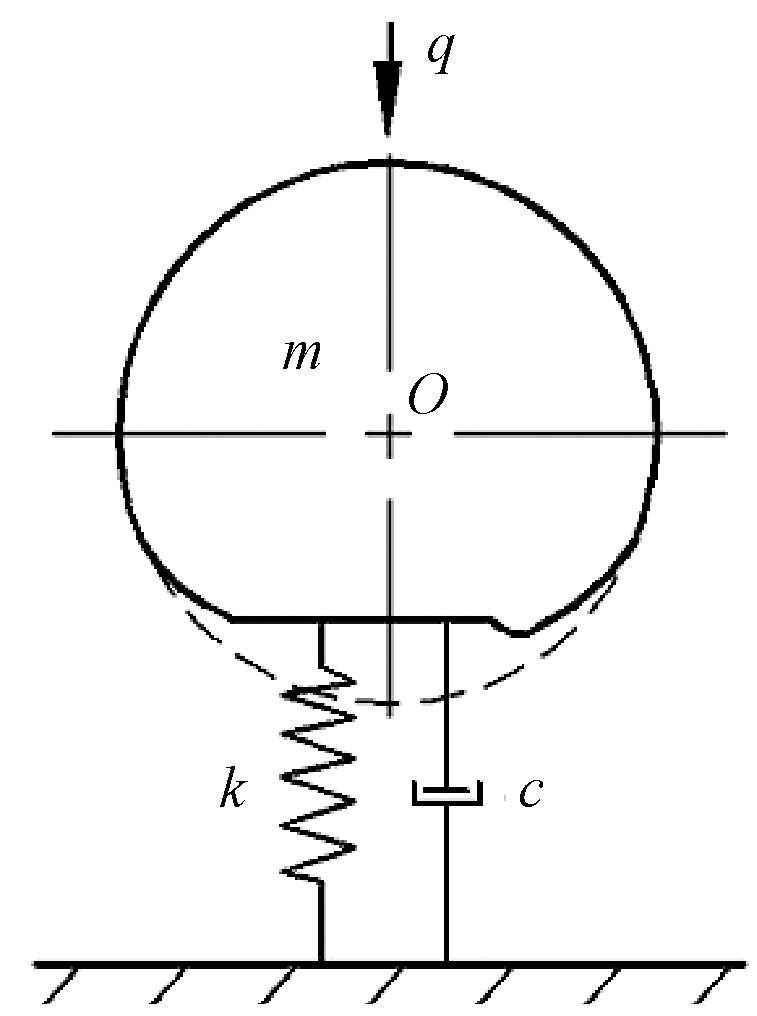
图1 弹流状态下线接触摩擦副动力学模型
Fig.1 Dynamic model of line contact friction pairs in EHL condition
1.3 耦合方程
对比动力学方程和弹流基本方程，得耦合方程：
ffilm=lp(x,t)dx;
(7)
δ(t)=-h00(t)+c00,
(8)
式中：l为磨擦副有效接触长度；c00为待定常数.
1.4 方程的无量纲化
弹流基本方程(1)～(5)的无量纲化参见文献[11].动力学方程(6)的无量纲化参见文献[10].
2 摩擦副的刚度、阻尼计算模型
2.1 油膜力的线性化
在图1中，设外载荷为静载荷q0时，摩擦副的弹性趋近量为δ0，此时油膜力与外载荷平衡，即ffilm(δ0)=q0.当系统受到外加干扰时，弹性趋近量δ将发生变化，此时将油膜力ffilm(δ)按泰勒级数展开，并略去式中的二阶及高阶小量，可得
(9)
式中：k和c分别为摩擦副有量纲刚度和有量纲阻尼.
在自由振动条件下，摩擦副的动力学方程为：
(10)
将式(9)代入式(10),得
(11)
将式(11)按照文献[10]进行无量纲化，并令Δ*=Δ-Δ0，得
(12)
式中：Ωc为无量纲自然频率；R为等效曲率半径；Δ为无量纲弹性趋近量；b为Hertz接触区半宽；T为无量纲时间；K为无量纲刚度；C为无量纲阻尼.
2.2 摩擦副刚度阻尼计算模型
式(12)可以看做质量为
刚度为K、阻尼为C的单自由度振动系统，其振动响应曲线如图2.
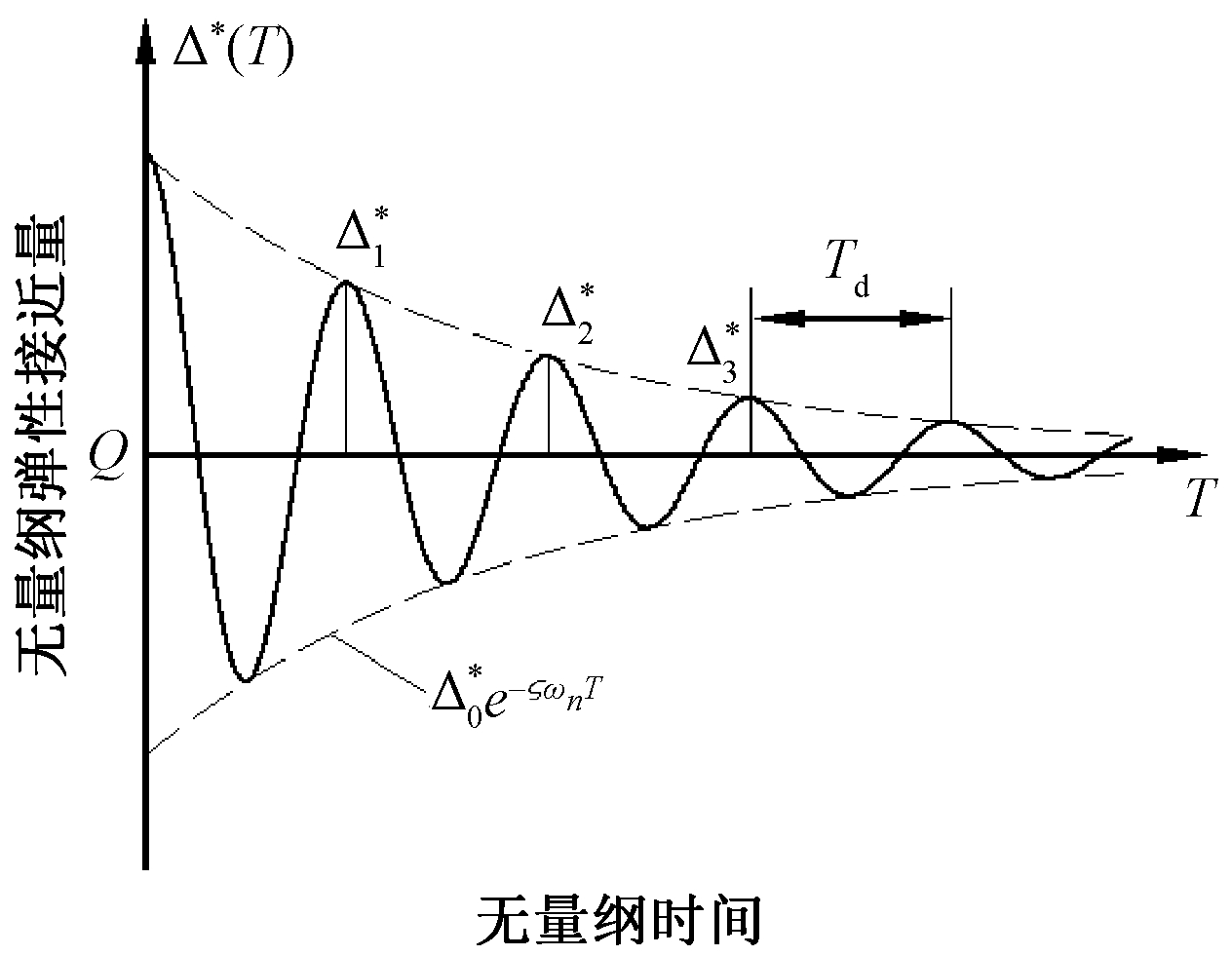
图2 单自由度系统自由振动曲线
Fig.2 Free vibration characteristic curve of SDOF
根据振动响应曲线，可以得到摩擦副的刚度和阻尼.具体计算过程参见文献[8].
3 数值求解
对Reynolds方程进行离散，在空间坐标轴上选择三点中心差分离散格式，时间坐标轴上采用隐式欧拉差分离散格式.对动力学方程采用Newmark法[6]进行离散.数值求解的流程如图3所示.
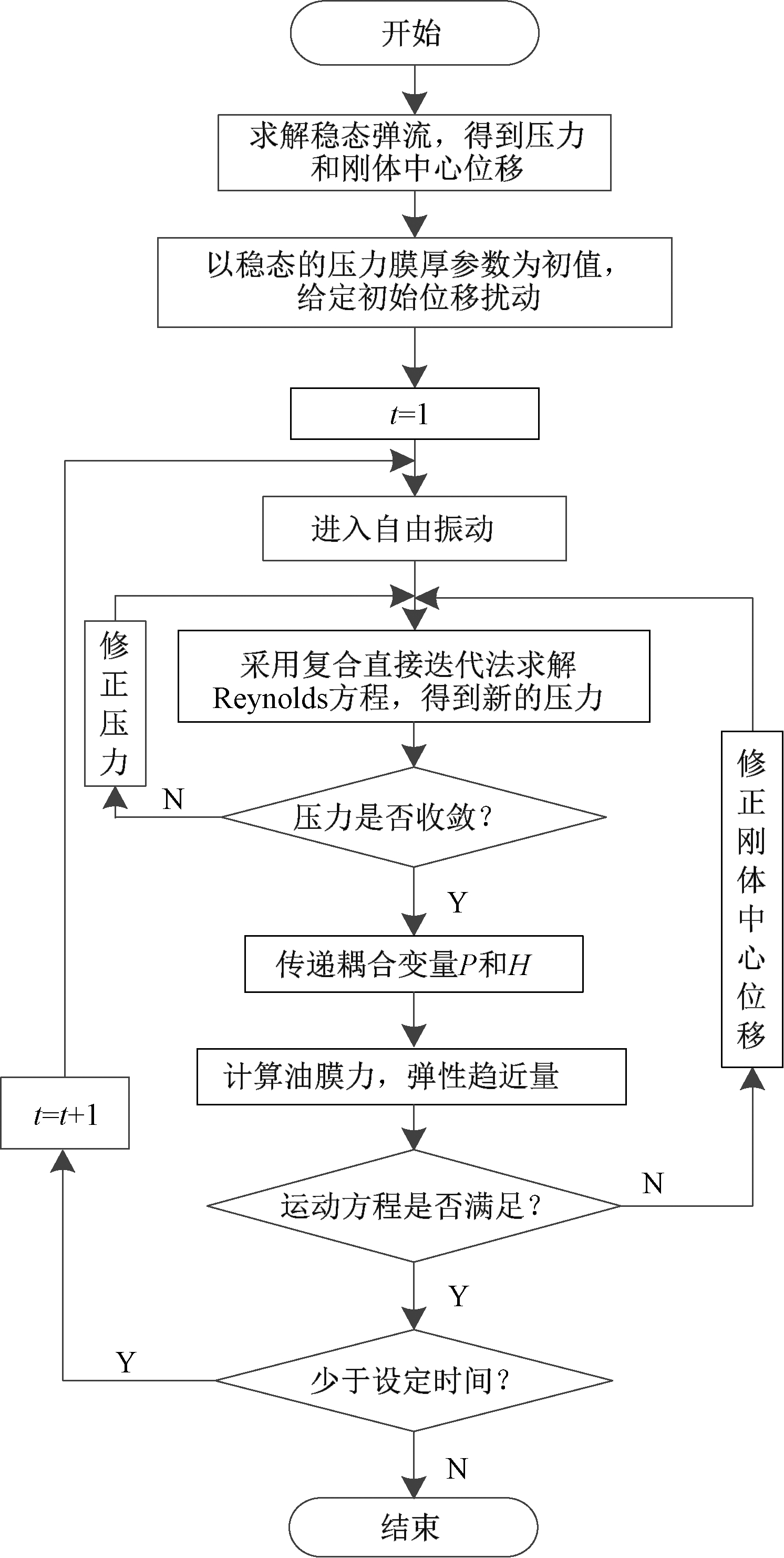
图3 摩擦副动力学特性求解流程
Fig.3 Solving process of dynamic characteristics of friction pairs
按照图3的求解流程，给出了自由振动下摩擦副的振动响应过程，如图4所示.图5为张鑫磊[8]在其研究过程中给出的油膜自由振动曲线.对比两图可知：本文方法计算得到的点数较密，根据这些数据得到的振动曲线计算摩擦副的刚度、阻尼，可以在很大程度上提高计算结果的准确性.
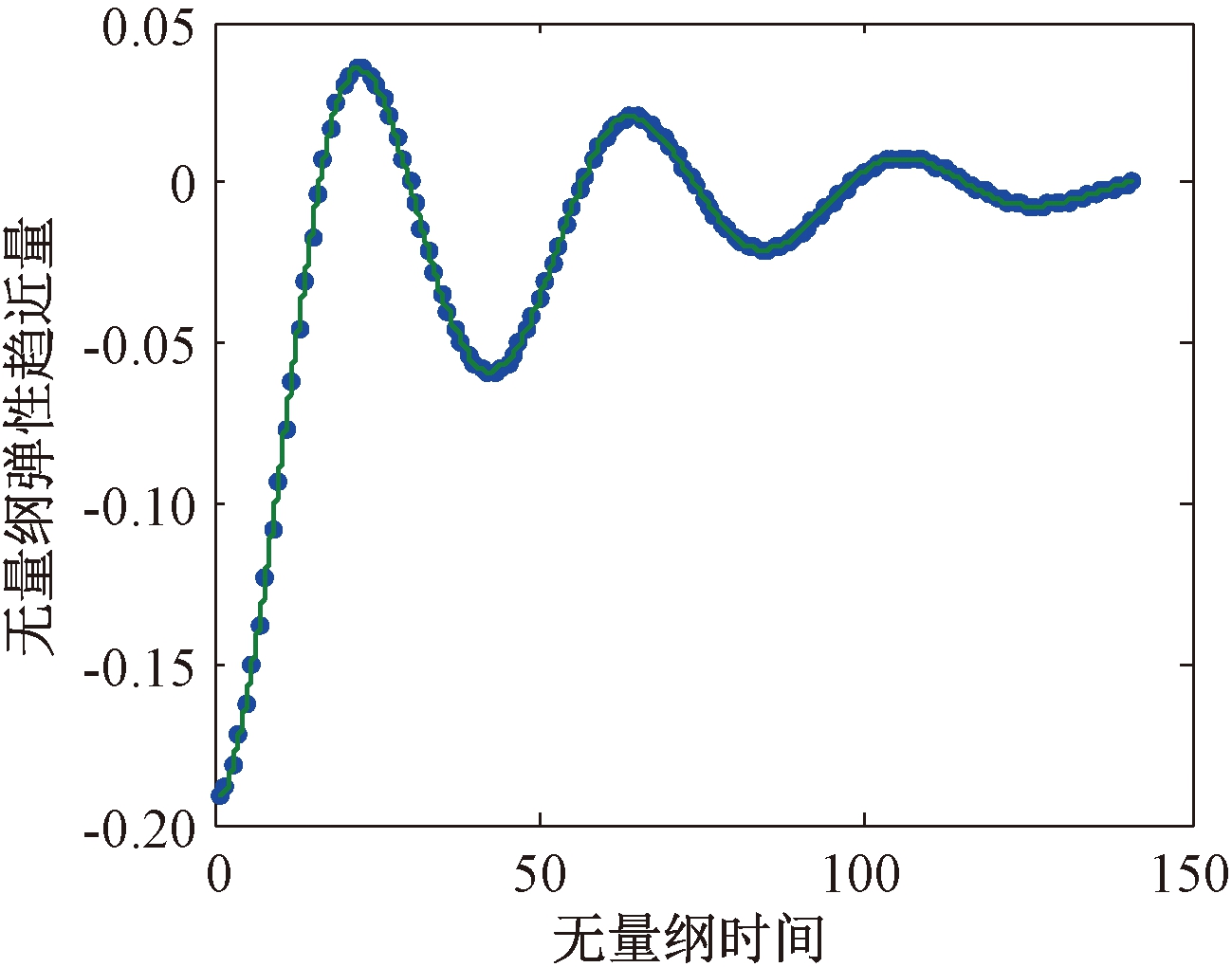
图4 自由振动条件下摩擦副的动特性响应曲线
Fig.4 Response curve of the dynamic characteristics of friction pairs under free vibration condition
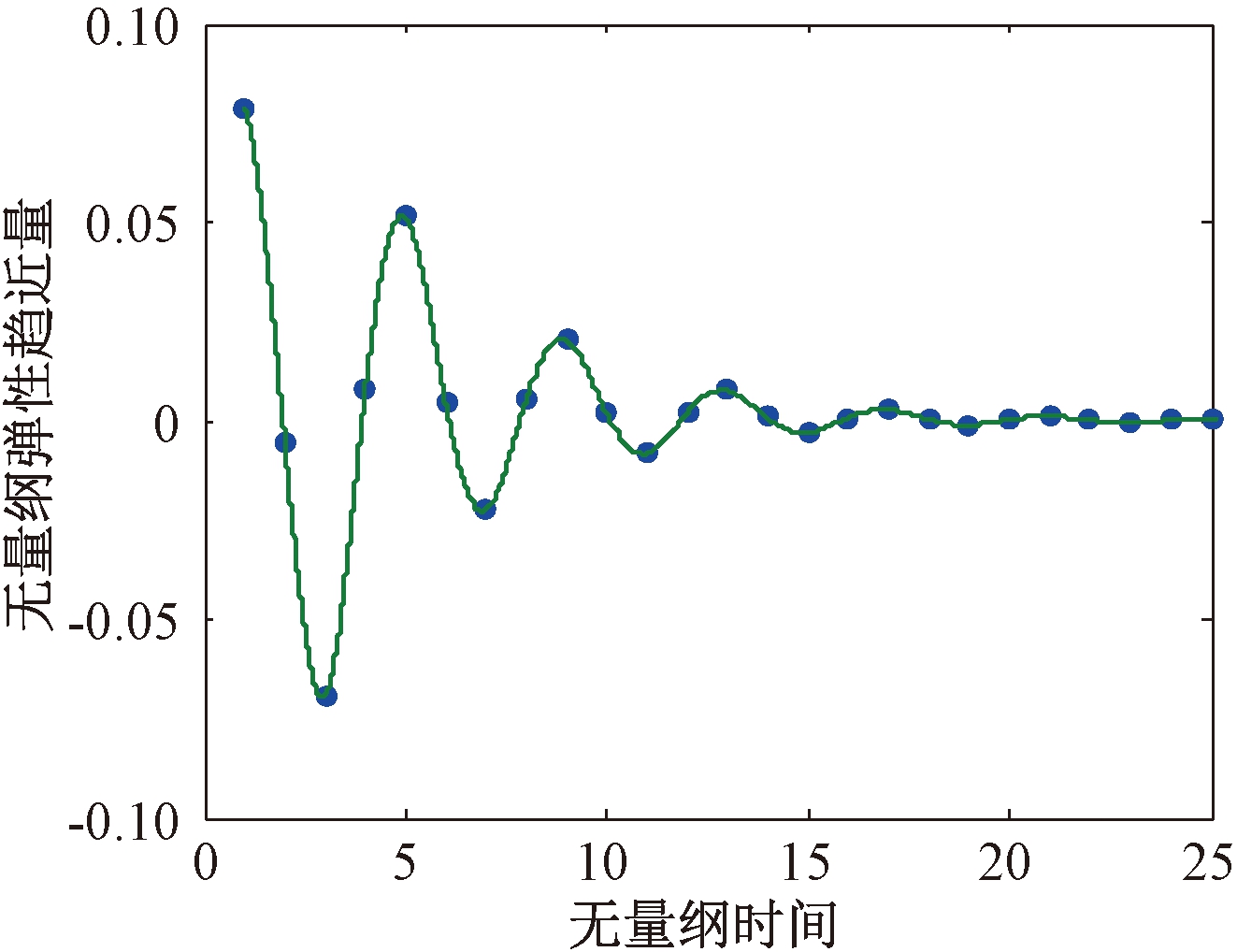
图5 位移扰动下弹流油膜的自由振动曲线
Fig.5 Free vibration curve of elastomeric oil film under displacement disturbance
4 自然频率对摩擦副刚度、阻尼的影响
由无量纲自然频率Ωc的定义可知，当载荷、速度不变时，改变摩擦副等效质量m就等于是改变Ωc的大小.所以，研究m对摩擦副刚度阻尼的影响就等效于研究Ωc对摩擦副刚度阻尼的影响.
取载荷q=1 000 N，速度u=0.1 m/s，时间步长Δt=1.0×10-4 s，位移扰动量h0=1.2h00，质量分别取m、2m、4m、6m、8m、10m，其中m=0.009 2 kg，根据图6中计算得到的摩擦副的振动响应曲线，得到各算例下摩擦副的刚度、阻尼，如表1所示.
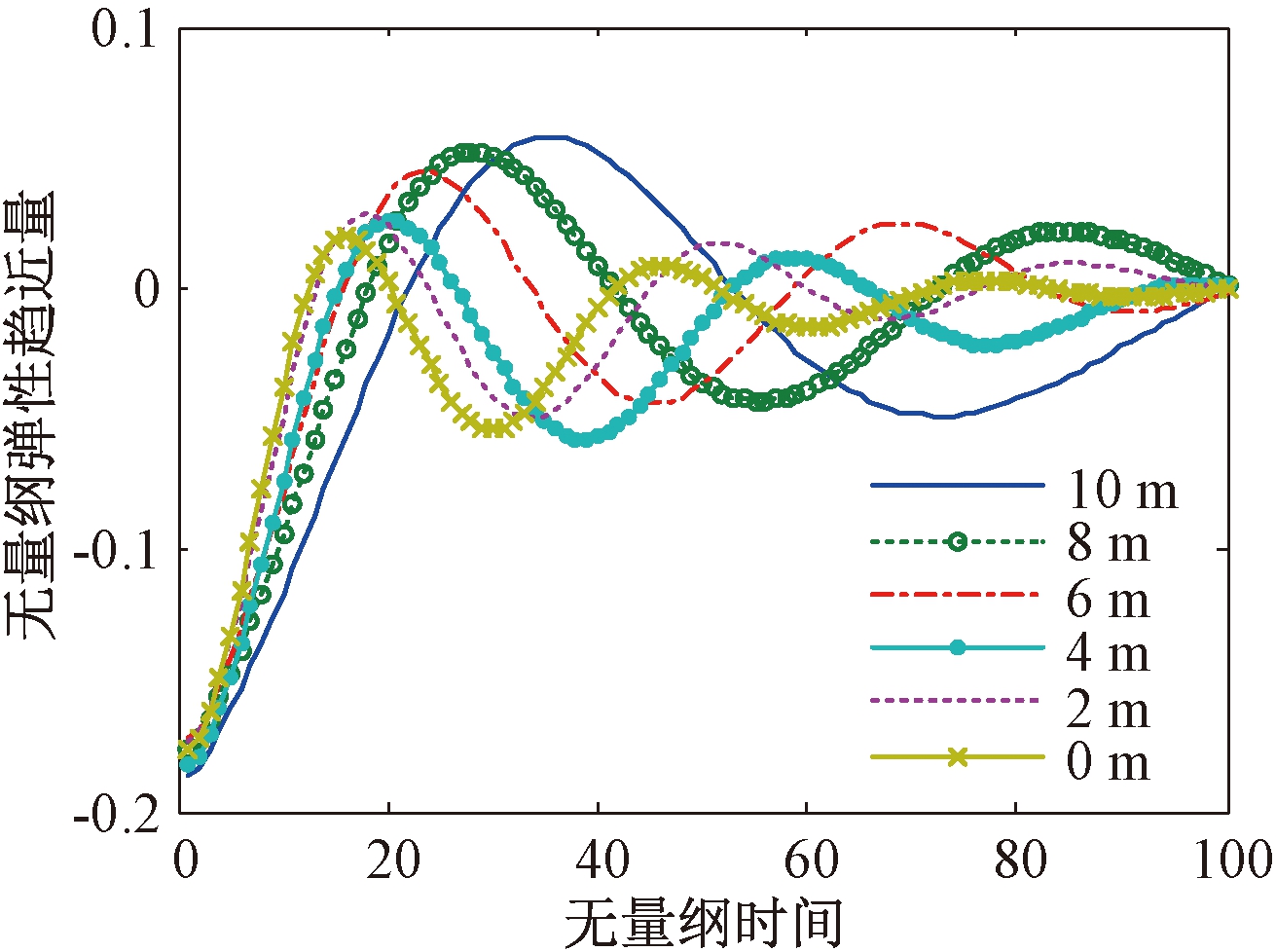
图6 等效质量对摩擦副振动响应的影响
Fig.6 Effect of equivalent mass on vibration response of friction pairs
由图6可见，随着等效质量m的增大，摩擦副的振动幅值和周期也随之增大.但从表1可见，摩擦副等效质量的变化并不影响摩擦副的刚度阻尼.故在研究摩擦副的刚度阻尼特性时，将等效质量或者无量纲自然频率取为定值，不影响所得结论的普适性.需注意的是，根据计算经验，等效质量或者无量纲自然频率的取值，影响时间步长的选取，二者需要匹配，才能保证计算的收敛性和高收敛精度.
表1 等效质量对摩擦副刚度阻尼的影响
Tab.1 Effect of equivalent mass on stiffness and damping of friction pairs
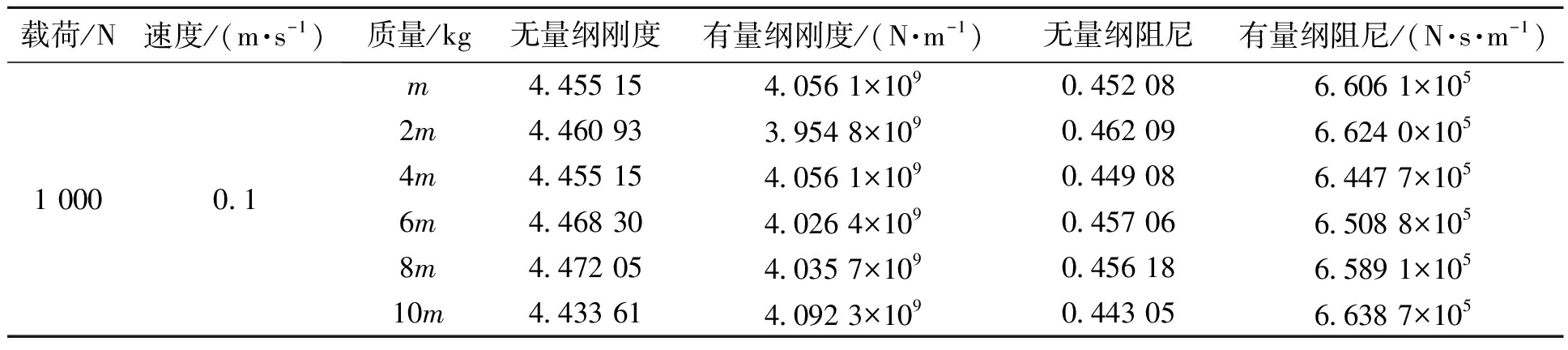
载荷/N速度/(m·s-1)质量/kg无量纲刚度有量纲刚度/(N·m-1)无量纲阻尼有量纲阻尼/(N·s·m-1)1 0000.1m4.455 154.056 1×1090.452 086.606 1×1052m4.460 933.954 8×1090.462 096.624 0×1054m4.455 154.056 1×1090.449 086.447 7×1056m4.468 304.026 4×1090.457 066.508 8×1058m4.472 054.035 7×1090.456 186.589 1×10510m4.433 614.092 3×1090.443 056.638 7×105
5 激励方式和激振频率对摩擦副刚度和阻尼的影响
5.1 简谐激励下摩擦副动力学-弹流润滑耦合方程
对图1所示的摩擦副动力学模型，设平衡状态时，摩擦副所受外载荷为定值q0，施加简谐力Δq=q0cwsin ωet，则等效质量m所受总的外载荷q(t)=q0+q0cwsin ωet.等效质量m在简谐激励作用下做周期性振动，其振动方程为：
(13)
式中：cw<1，为动载系数；ωe为激励频率.
因为惯性力是保守力，所以当m受到稳定的强迫振动时，在一个振动周期内，惯性力所做的功为零.记一个振动周期内外载荷q(t)所做的功为ΔE，则
ΔE=
q0(1+cwsin ωet)dx=(ffilm+
ffilmdx.
(14)
所以，ffilm=q0(1+cwsin ωet)，其无量纲形式如下：
Ffilm=1+cwsin ΩeT,
(15)
式中：
为无量纲简谐激励下的频率.
5.2 简谐激励下摩擦副系统的刚度和阻尼
对于油膜力Ffilm可表示如下：
(16)
式中：Δ*为摩擦副无量纲刚体位移.
当m作强迫振动时，
(17)
式中：
为摩擦副无量纲振动幅值.
将式(17)代入式(16)中，得
(18)
Ffilm(t)随着Δ*的变化形成了一条闭合的曲线，即阻尼环，如图7所示.阻尼环的面积代表系统振动一个周期所消耗的能量E，即
(19)
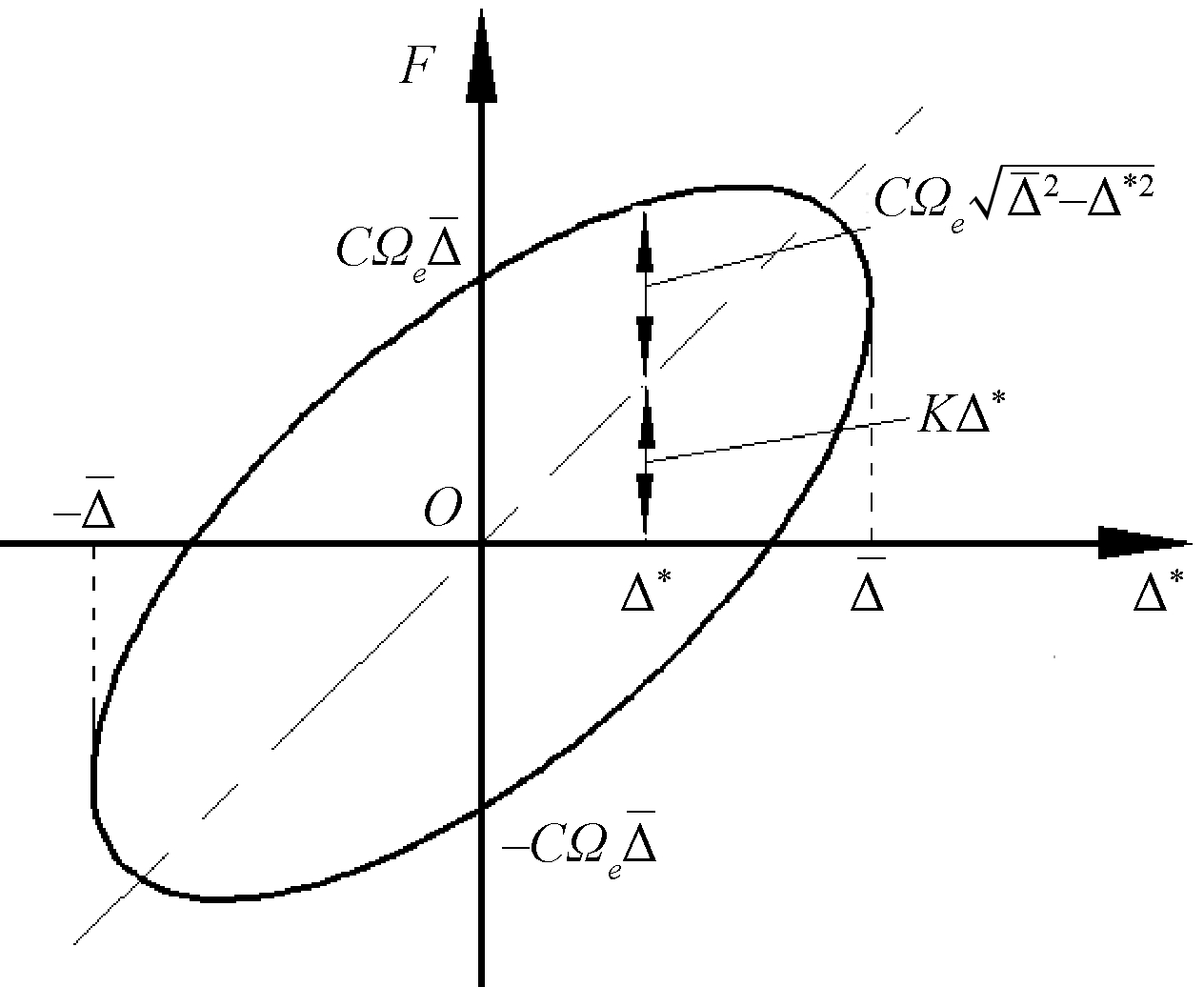
图7 阻尼环
Fig.7 Damping loop
由阻尼环面积及长轴斜率，可求得摩擦副刚度和阻尼如下：
具体可参见文献[12].
5.3 算例及分析
5.3.1 激励方式的影响
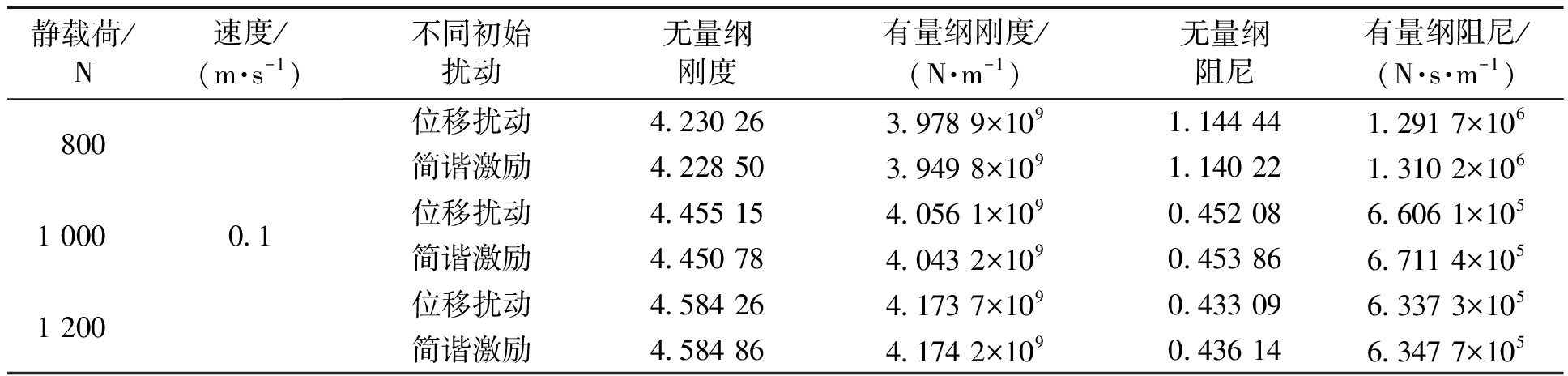
选取速度为0.1 m/s，静载荷q0分别为800、1 000、1 200 N，时间步长Δt=1.0×10-4 s.在位移扰动下，扰动量为h0=1.2h00；在简谐激励下，外加简谐激励为
分别计算每种工况下摩擦副的刚度、阻尼，结果如表2所示.
5.3.2 激振频率的影响
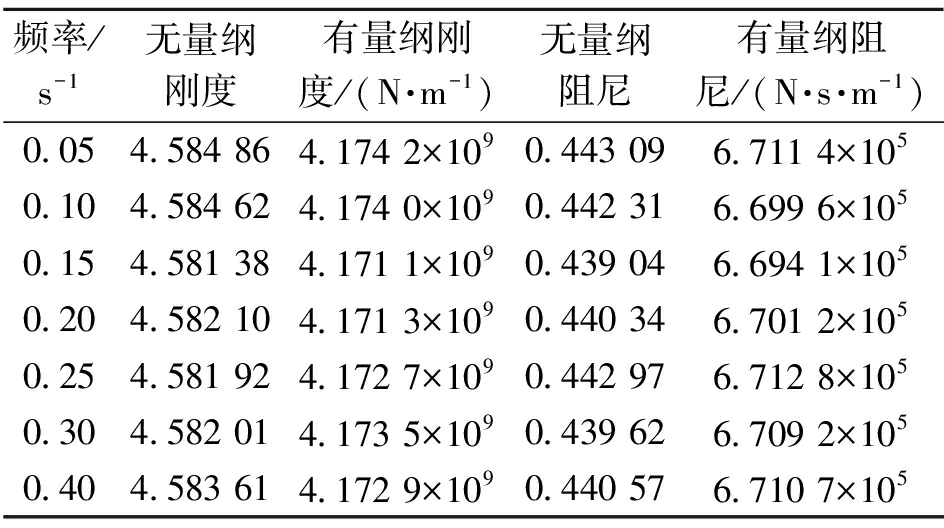
表3为不同简谐激振频率作用下求得的摩擦副的刚度和阻尼值.具体计算参数为静载荷q0=1 200 N，速度u=0.1 m/s，简谐激励Δq=200sin(2πf·t).
表2 激励方式对摩擦副刚度和阻尼的影响
Tab.2 Influence of incentive method on stiffness and damping of friction pairs
静载荷/N速度/(m·s-1)不同初始扰动无量纲刚度有量纲刚度/(N·m-1)无量纲阻尼有量纲阻尼/(N·s·m-1)8001 0001 2000.1位移扰动4.230 263.978 9×1091.144 441.291 7×106简谐激励4.228 503.949 8×1091.140 221.310 2×106位移扰动4.455 154.056 1×1090.452 086.606 1×105简谐激励4.450 784.043 2×1090.453 866.711 4×105位移扰动4.584 264.173 7×1090.433 096.337 3×105简谐激励4.584 864.174 2×1090.436 146.347 7×105
表3 激振频率对摩擦副刚度和阻尼的影响
Tab.3 Effect of vibration frequency on stiffness and damping of friction pairs
频率/s-1无量纲刚度有量纲刚度/(N·m-1)无量纲阻尼有量纲阻尼/(N·s·m-1)0.054.584 864.174 2×1090.443 096.711 4×1050.104.584 624.174 0×1090.442 316.699 6×1050.154.581 384.171 1×1090.439 046.694 1×1050.204.582 104.171 3×1090.440 346.701 2×1050.254.581 924.172 7×1090.442 976.712 8×1050.304.582 014.173 5×1090.439 626.709 2×1050.404.583 614.172 9×1090.440 576.710 7×105
5.3.3 对比分析
由表2和表3可知，摩擦副的刚度和阻尼与激励形式无关，与激振频率无关.此结论与张鑫磊[8]的研究结论相同，但是张鑫磊[8]在对各自的研究中只选取一组参数进行对比，而本节选取了多组参数，所得结论更具有说服性；另外，由于选取了可以使程序很好收敛的无量纲自然频率进行研究，提高了计算结果的精度，同时也提高了所得结论的准确性.
6 结论
(1)在弹流润滑状态下，磨擦副的刚度和阻尼与磨擦副等效质量无关，与激励方式、激励频率无关;
(2)磨擦副等效质量取值虽不影响摩擦副的刚度、阻尼，但和时间步长要相匹配，否则影响收敛精度；
(3)在研究激励方式和激振频率对摩擦副刚度和阻尼的影响时，选取了可以使程序很好地收敛的无量纲自然频率值，很大程度上提高了计算结果的精度和所得结论的准确性.
[1] DATTA J, FARHANG K.A nonlinear model for structural vibrations in rolling element bearings,part 1: derivation of governing equations[J].Journal of Tribology, 1997, 119(1):126-131.
[2] HARSHA S P, KUMAR S, PRAKASH R.Non-linear dynamic behaviors of rolling element bearings due to surface waviness[J].Journal of sound and vibration, 2004, 272(3/5):557-580.
[3] HAGIU G D, GAFITANU M D.Dynamic characteris-tics of high speed angular contact ball bearings[J].Wear, 1997, 211(1):22-29.
[4] SARANGI M, MAJUMDAR B C, SEKHAR A S.Stiffness and damping characteristics of lubricated ball bearing considering the surface roughness effect, part 1: theoretical formulation[J].Proceedings of the institution of mechanical engineers, Part J: journal of engineering tribology, 2004, 218(6):529-538.
[5] SARANGI M, MAJUMDAR B C,SEKHAR A S.Stiffness and damping characteristics of lubricated ball bearing considering the surface roughness effect，part 2:numerical results and application[J].Proceedings of the institution of mechanical engineers, Part J: journal of engineering tribology, 2004, 218(6):539-548.
[6] WIJNANT Y H.Contact dynamics in the field of elastohy-drodynamic lubrication[D].Enschede, Netherlands: University Twente, 1998.
[7] VENNER C H, POPOVICI G, WIJNANT Y H.Contact dynamics of EHL contacts with time varying operating conditions[J].Tribology and interface engineering series, 2003, 43(3):189-200.
[8] 张鑫磊.线接触弹流润滑油膜动特性及压力极值研究[D].郑州：郑州大学, 2016.
[9] 张玉言,王晓力,闫晓亮.非稳态弹流润滑状态下滚动体-滚道摩擦副的动力特性研究[J].摩檫学学报, 2012, 32(6):626-633.
[10] 柳剑.弹流润滑状态下的滚动轴承摩擦副动力学特性研究[D].武汉：华中科技大学, 2014.
[11] 温诗铸,杨沛然.弹性流体动力润滑[M].北京：清华大学出版社, 1992:63-129.
[12] 徐梦霞.线接触弹流润滑状态下摩擦副的动力学特性研究[D].郑州：郑州大学, 2018.