0 引言
脑血管疾病是因颅内血液循环障碍而造成脑组织损害的一组疾病,以急性发病居多,多表现为半身不遂、言语障碍等.每年有大量的病人忍受着脑血管问题所带来的常见疾病,例如颈动脉狭窄和动脉瘤等疾病.脑血管疾病如不能被早期诊断,将会有引发脑中风的危险.组织结构的切分对辅助诊断、治疗和手术规划具有重要的意义.因此,脑血管的精确检测与分割,尤其是低密度细小血管的提取,有助于脑血管疾病的辅助诊断与治疗.
血管造影可以进行体内血管的无创检查.基于MR的血管造影是颅内血管评价中最常用的非侵入性成像技术.磁共振血管成像(MRA)图像提供了血管与背景之间相对出色的对比度和较高的空间分辨率,这为血管结构的提取创造了较为丰富的前提条件[1].
从复杂数据集准确的可视化和量化的病情状况来看,分割是一个基本的步骤.国内外学者从未间断对脑血管提取算法的探索.到目前为止,已有许多2D或3D的血管分割方法.但绝大多数2D算法无法直接用于3D数据的分割.3D血管分割技术大致可分为两类[2]:基于活动轮廓模型的方法和基于概率统计的方法.基于活动轮廓模型的方法的基本思想是在图像力的作用下驱动曲线到达物体的边界.活动轮廓模型通常分为参数活动轮廓模型[3]和几何活动轮廓模型[4].几何活动轮廓模型可进一步分为基于边界[5-6]的模型、基于区域的模型[7-8]和混合模型[9-12].分割曲线的演化通常由最小化某种变分能量泛函来实现.常用的数值计算此类活动轮廓演化的方法是Osher等[13]提出的水平集方法.但此类方法需针对不同的图像设置不同的参数才能获取较好的分割效果,也即此类算法的性能依赖于所设计的能量函数.
除了活动轮廓模型,利用统计信息进行图像分割的方法一直是一个活跃的研究领域.统计模型将图像数据中的体素分成血管区域和非血管区域[14].从MRA数据中提取血管的自适应统计方法由Wong等[15]提出.Hassouna 等[16]也提出从时间飞跃法(TOF)中采用随机模型方法进行分割.Roy等[17]提出了利用基于期望最大化的瑞利混合模型的瑞利分类器进行分割.实验结果表明,基于统计信息的概率模型在信噪比较低的图像中提高了分割方法的鲁棒性,但其准确性依赖于底层概率模型的设计.
血管形态结构的复杂性使得单一的算法很难获得满意的分割效果,目前较为有效的方法是混合分割方法,这也是血管分割的一个研究趋势.Gao等[18]提出了一种基于统计模型的快速活动轮廓模型对脑血管进行分割,同时为提取MRA数据集的三维脑血管提高了曲线演化的效率.Tian等[19]结合统计信息及血管形状模型的向量场设计了适合血管的活动轮廓模型进行血管分割.混合模型算法实验结果是令人满意的,但对于细小血管的提取依然有提升的空间.
笔者在传统的统计方法基础上,即采用有限混合模型对体数据密度进行建模,采用期望最大进行参数估计的方法,以后验概率的方式提取血管的主体部分,而对于血管的边缘区域和细小的血管则首先计算其梯度值,采用基于改进的K均值聚类方法对剩余体数据中的血管进行进一步提取.
1 本研究算法
笔者所提出的算法主要由两个部分构成.第一步由瑞利高斯混合模型提取血管的主体部分;第二步由改进的K均值聚类算法进一步提取血管边界及细小血管部分.算法过程图如图1所示.
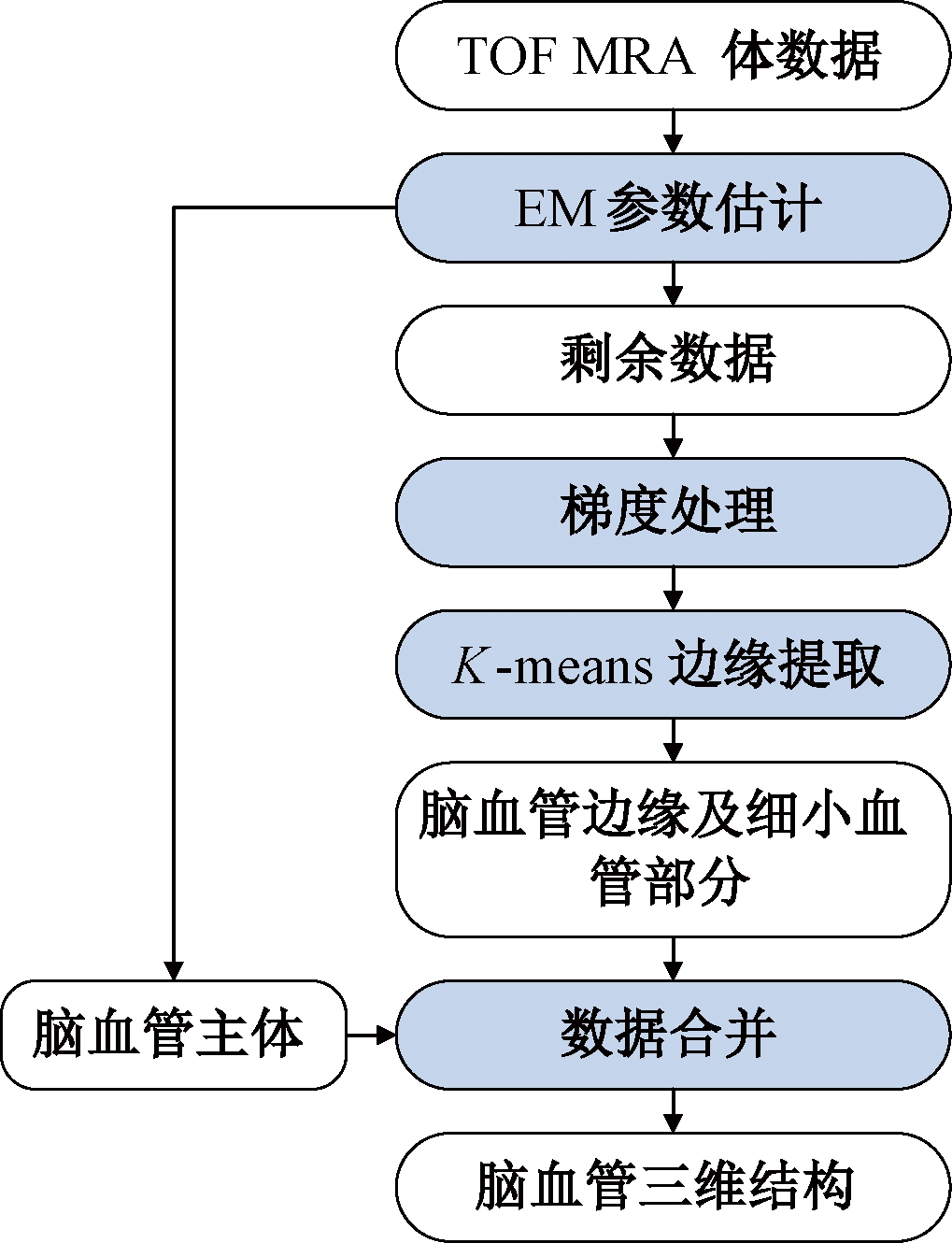
图1 算法过程图
Fig.1 Process of the algorithm
1.1 基于有限混合模型的脑血管主体提取
传统的基于统计的方法对时间飞跃法磁共振血管成像(TOF MRA)数据进行血管分割时,首先根据TOF MRA数据密度分布特征将体素划分为3个区域.低密度区域对应于脑脊液、骨骼和背景;中密度区域对应于脑组织,包括灰质和白质;高密度区域主要包括脑血管.采用高斯分布、瑞利分布或是统一分布(一般用于Phase-Contrast MRA数据)分别对3种密度区域进行建模,然后采用期望最大算法对模型进行参数估计,最后将每一体素点的密度值带入混合模型中,确定该点是否属于血管部分的概率,从而实现对血管的分割.
笔者对血管主体部分的分割亦是采用传统方式进行.在这里,我们首先用瑞利高斯混合模型对体素进行建模,如式(1)所示.
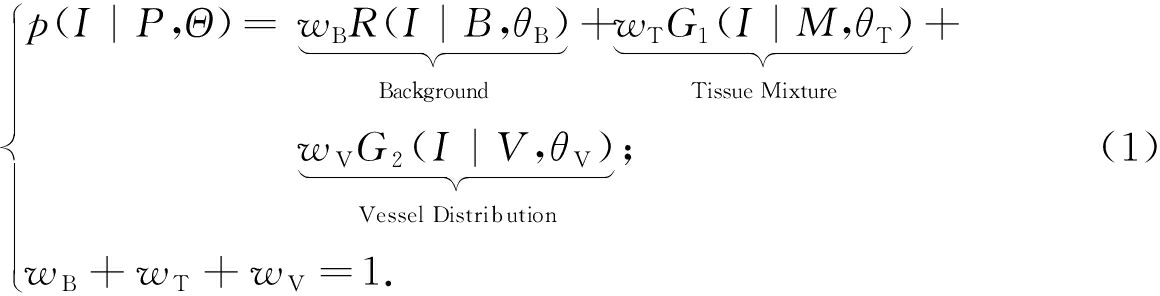
式中:wB、wT、wV分别为3类分布的权重,其中下标B代表低密度区域,包括脑脊液、骨骼和背景(background);T代表中密度区域,包括脑组织(tissue mixture);V代表高密度区域,主要包括脑血管(vessel distribution).
R为瑞利分布:
(2)
Gk (k=1, 2)为高斯分布:
(3)
有限混合模型中包含一个瑞利、两个高斯分布,分别对应了低、中、高3个密度分布区域.高密度区域包含了目标血管部分.由此可以将从体数据中分割血管的问题转换为从有限混合模型判断哪些体素属于高密度区域所对应高斯分布的问题.由于整体分布由几个函数分布混合而成,无法直接得知每个体素所属的分布,故而采用期望最大算法(EM)对分布函数的参数进行估计.
1.2 基于自适应聚类中心的脑血管边缘提取
完成血管主体部分的初步分割,我们发现剩余数据中含有部分未分割出的血管边界和细小血管.由于剩余数据中包含血管的数据量较小,若再利用密度值进行分割,存在较大困难.尽管剩余部分血管的数据量相对于体数据来说较小,但是目标体素多出现于血管的边界,因此将该部分数据进行梯度处理,以提高剩余部分血管边界的对比度,从而进行下一步分割.
首先将数据按垂直方向分层,分别在每一层计算数据梯度,以获取梯度值数据.因处于边缘处血管的梯度值较大,为了提取出梯度数据中较亮的血管部分,笔者采用改进的自适应聚类的K均值方法,且是对梯度数据而非密度数据进行聚类,从而找出目标血管.
观察到血管边缘被包含于梯度值较高的部分,因此笔者考虑找到一个梯度值的分水岭,比该分水岭大的部分包含尽可能多的血管,同时比该分水岭小的部分包含尽可能少的血管.笔者通过梯度值表示体素,并通过该梯度值的欧氏距离度量体素之间距离.由于随着聚类中心数目的上升,分水岭存在于K均值聚类中心值最大的类别中(尽管聚类中心数目过大会使得分水岭从中心值最大的类别中脱离,但是在较少的类别时,分水岭仍存在于中心值最大的类别中).因此,笔者通过自动调节聚类数目使得聚类中心值最大的类别包含尽可能多的血管部分,同时包含尽可能少的非血管部分.
随着聚类中心数目逐渐上升,聚类中心值最大的类别包含的非血管部分越来越少,同时在整体上,聚类中心的最大值逐渐增大.观察到在上述过程中,当聚类中心的最大值出现明显上升时,拥有最大值的聚类中心表示的类别包含了较多的血管边缘以及较少的非血管部分.因此,笔者通过调节聚类中心数目不断增大并观察聚类中心最大值的变化,从而识别聚类中心最大值的明显上升.此时,该聚类中心的最大值可以作为上述分水岭对血管边缘进行分割.
1.3 K均值聚类中心数目的确定
观察数据后发现,剩余数据中血管部分的数值高于其他部分的数值,并且血管部分与非血管部分的数值大小差异相对于非血管部分的内部差异更为明显.上述差异给予提示可通过调节K均值聚类中心的数目,找到合适的聚类中心数使得最大的聚类中心作为分水岭取得较好的分割效果.
如图2所示,笔者的方法是逐步增加聚类中心点数目,通过观察聚类中心最大值变化的差异来判定合适的聚类中心点数,相应聚类中心的最大值即作为分割的分水岭.K均值在N簇(cluster)中心点下进行聚类时,血管部分往往包含于聚类中心较大的簇中.比如,当N=2时,由K均值计算,将整体数据聚为两类,即cluster1和cluster2,其聚类中心点分别是center1和center2.其中center1<center2,即cluster1包含了梯度数据中拥有较小值的部分,cluster2包含了梯度数据中拥有较大值的部分.
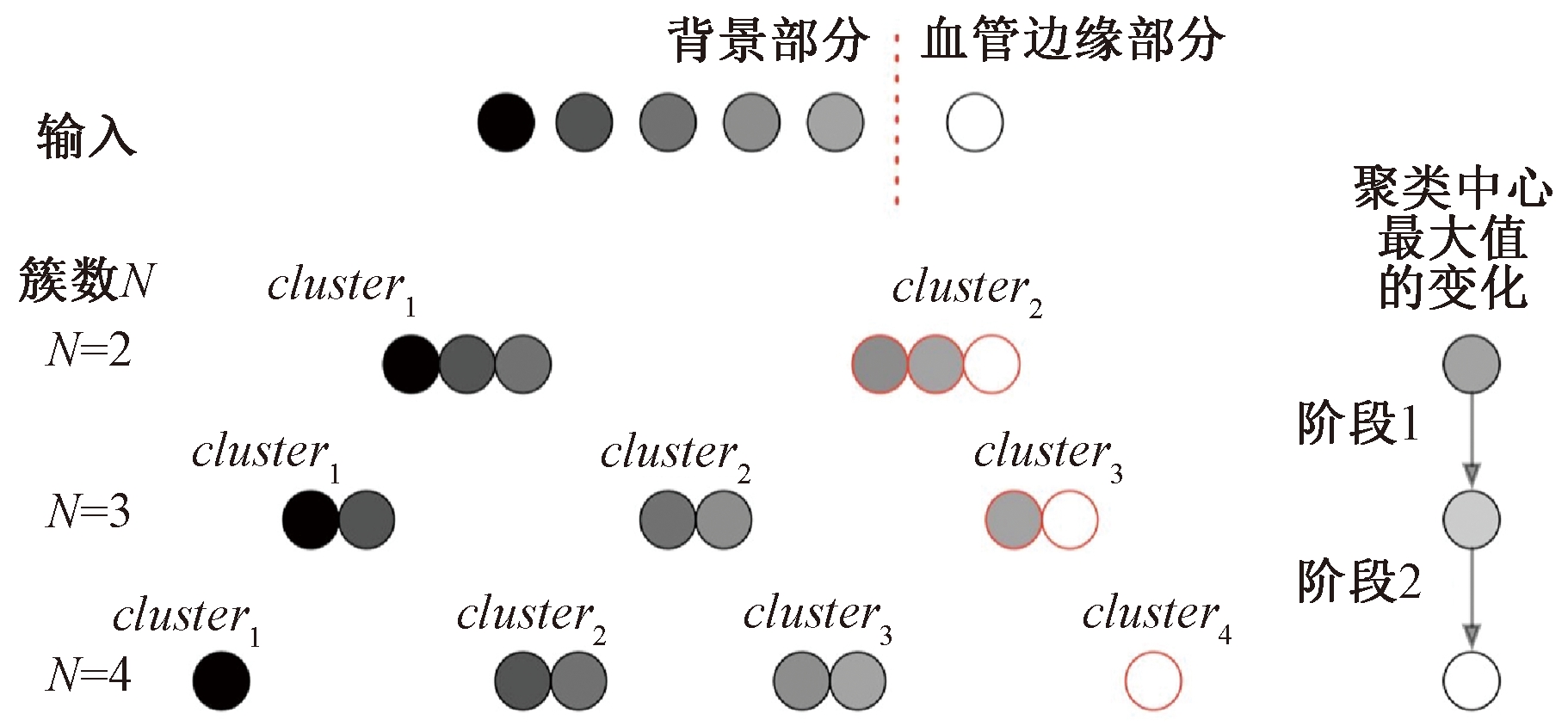
图2 基于K均值血管边缘提取示意图
Fig.2 Boundary extraction of vessel with K-Means
由于血管数据在整体梯度数据中是较亮的部分,因此cluster2中包含血管数据.但是由于仅仅将整体数据聚成两类,在cluster2中仍包含了大量的非血管部分的数据.因此可以将cluster2中的数据表示为nonvessel+vessel两个部分,其中nonvessel是非血管数据,vessel是血管数据.随着聚类数目N的增大,在最大聚类中心所对应的clusterN中nonvessel的比例逐渐减少,vessel的比例逐渐上升.从数据特征上看,非血管部分的数据值与血管部分数据值存在较为明显边界,表现在数值上差异较大.因此,当聚类数目N上升至Ntarget,相应聚类中心点在数值上出现明显的突增,最大中心对应的簇中包含的可以将Ntarget对应的聚类中心的最大值作为血管边缘与非血管部分梯度值的分水岭.
因此,寻找目标值的整体算法步骤如下:nonvessel比例相对较小,而vessel比例相对较大,可以将Ntarget对应的聚类中心的最大值作为血管边缘与非血管部分梯度值的分水岭.因此寻找目标值的整体算法步骤如下.
输入:密度梯度数据.
输出:血管边缘与非血管部分梯度值分水岭.
Step1:对梯度数据依次聚为2类,3类,…,20类,记录每次聚类中心点的最大值的有序序列.
Step2:对Step1中序列的每个数据依次进行两两求差,并记录差值中的最大值.
Step3:Step2中的差值d=centerj-centeri,其中centeri和centerj属于步骤Step1中聚类中心点最大值的集合且j=i+1.当d为最大值时,centerj标值.
2 实验结果与分析
实验所用数据是从海军总医院获取的TOF MRA数据,大小为512 mm×512 mm×136 mm,空间分辨率为0.69 mm×0.69 mm×1.4 mm, TR=18 ms,TE=2.4 ms.测试平台为普通PC机,Windows 7,64位操作系统.
这里,选择瑞利-高斯模型对体数据密度分布进行建模分析.瑞利-高斯模型的估计参数如表1所示.图3为提取结果.从图3(a)可以看出,瑞利-高斯混合模型的误差为0.179 4.统计方法获取的血管主体部分结果如图3(b)所示.图3(c)是在血管主体部分基础上,进一步采用改进自适应聚类中心的K均值方法进行血管边缘提取后的效果图.从图3可以看出,传统的统计方法所提取的血管主体部分相对较完整,但在血管边缘和细小血管部分有不连续的分支存在.而改进的方法在提取血管边缘和细小血管分支的完整性及连续性方面则有较为明显的提高.
表1 瑞利-高斯混合模型拟合参数
Tab.1 Fitting parameters of Rayleigh-Gauss mixed model

参数ωμσ血管部分0.049 266422.945 335214.559 955中间部分0.871 902195.101 54647.124 292背景部分0.078 832—35.926 031
在图3中也给出了部分改善区域的标记(蓝色).从标记的部分处,即在细小血管处,可以看出,基于改进K均值梯度聚类的血管边缘提取方法相比于基于参数估计的统计方法,对细小血管部分的提取效果在视觉上有明显改善.
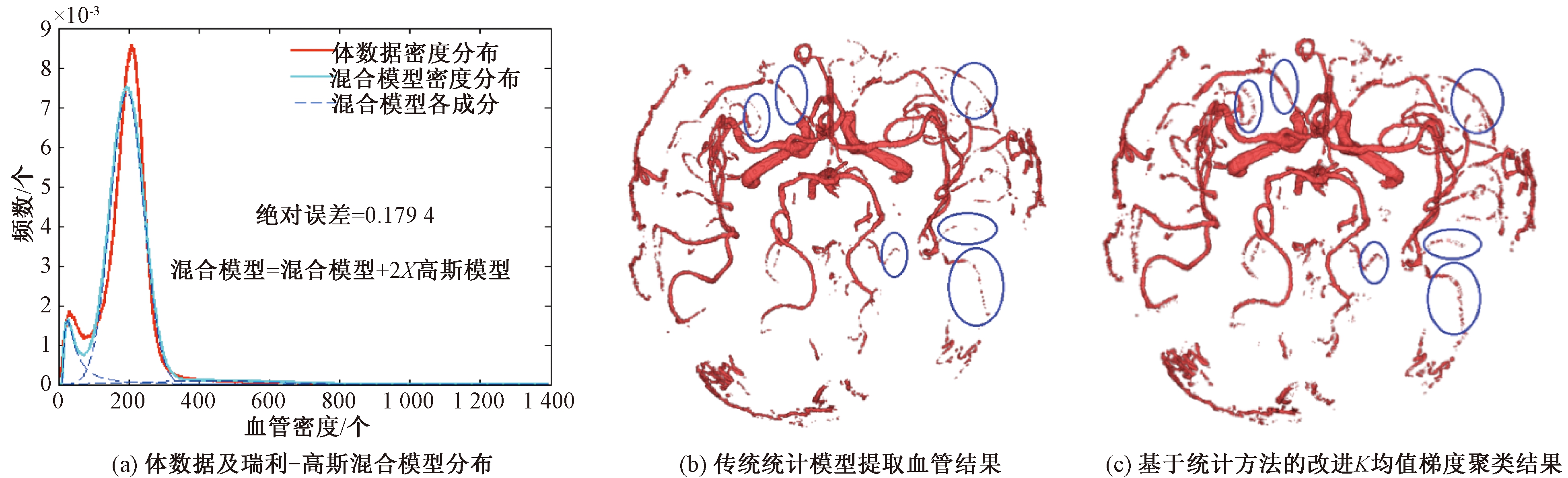
图3 瑞利-高斯混合分布血管提取结果
Fig.3 Results of Rayleigh-Gauss mixed model
图4是两种方法(瑞利-高斯模型方法与改进的方法)的血管提取结果密度统计分布图.其中蓝色部分是第一步,即由基于参数估计的传统统计方法获取血管主体部分的分布情况.红色部分是第二步,即在第一步的基础上采用改进K均值的血管边缘提取出的结果分布情况.从图4可以看出,传统统计的方法最终的结果是找一个相对合适的全局目标值,使得血管能够尽可能地提取出来.但这个目标值大多是基于数据的密度值的,因而最终的分割结果在密度分布图上可以看到明显的切分点.
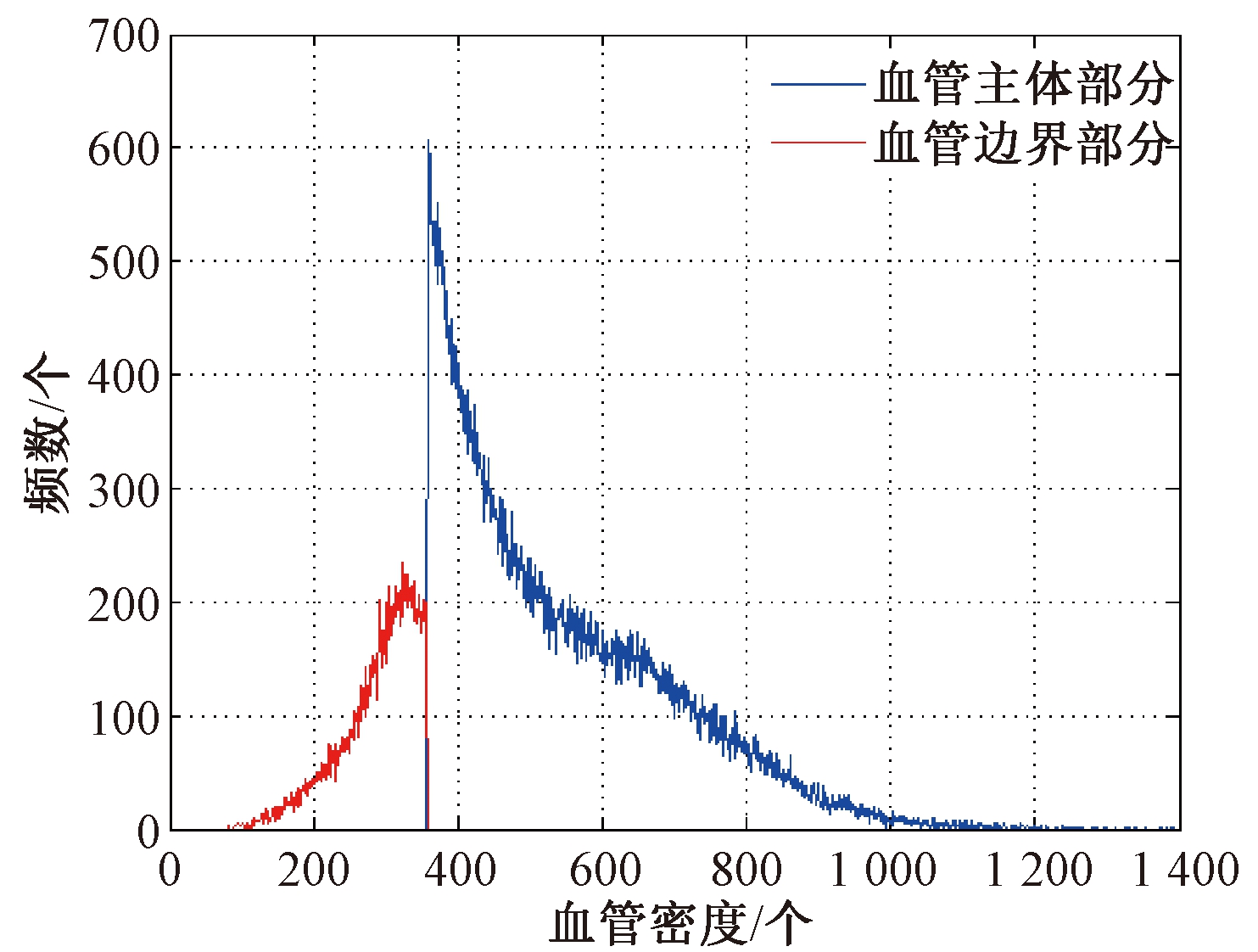
图4 两步血管提取密度统计分布图
Fig.4 Intensity distribution of two stages of vessel extraction
但因血管的密度范围分布较广,单纯靠一个基于密度的目标值很难获得完整的血管结构.因此采用了基于梯度的方式来弥补由密度值分割所带来的缺陷.因血管在边缘处才会有较为明显的梯度值,且经过第一步提取后,血管主体部分已获取,剩余部分是密度值较小且与周围组织较为接近的边缘及细小血管部分,只需对此部分重点分析提取即可.因此并非在整个体数据中计算梯度,而是在经过第一步分割之后,对剩余部分的数据进行梯度计算.从图4中可以看出,经过K均值梯度聚类后的结果,是对蓝色部分的截面处进行明显的补充,而且此部分(红色曲线)也更符合血管的密度值分布(范围广),也使得最终结果的密度分布更加完整.
为了更好地评估算法分割效果的准确率,采用公认的相似性系数DSC来评价分割算法.
(4)
式中:M和G分别为算法结果与真实结果;N为血管体素个数,当M和G中的元素都相同时为1时,若 M和G没有任何相同元素则为0.同时,放射科专家提供了13套手动切割的结果作为真实结果,数据如表2所示.
表2 时间飞跃法磁共振血管成像数据参数
Tab.2 TOF MRA parameter
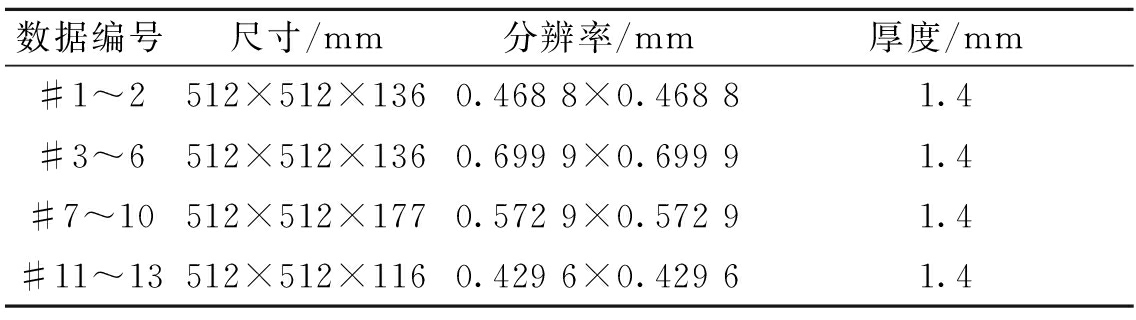
数据编号尺寸/mm分辨率/mm厚度/mm#1~2512×512×1360.468 8×0.468 81.4#3~6512×512×1360.699 9×0.699 91.4#7~10512×512×1770.572 9×0.572 91.4#11~13512×512×1160.429 6×0.429 61.4
此外,笔者所提出的算法还与传统的有限混合模型方法[16]以及当前流行的基于水平集框架的活动轮廓模型[19]方法的分割效果进行了对比.图5给出了其中一套数据的3种方法的分割结果.从图5可以看出,对于大的血管,3种方法都能得到较为满意的结果.但对于细小血管,传统的有限混合模型出现血管分支间断现象,这是由于细小血管部分的密度值相对较低,在整个体数据中,采用唯一的判别准则很难将此部分提取出来.而活动轮廓模型,将各种因素融合设计新的能量泛函,利用水平集求解能量函数,能提取出部分细小血管的分支,如图5(b)圆角矩形框所示.而笔者所提出的改进的方法,在细小血管的提取方面相对于统计模型也有不同程度的提高,而且在血管的边缘处,能看到更为明显的效果,此外改进的方法在获取细小血管的连续性方面效果更好.
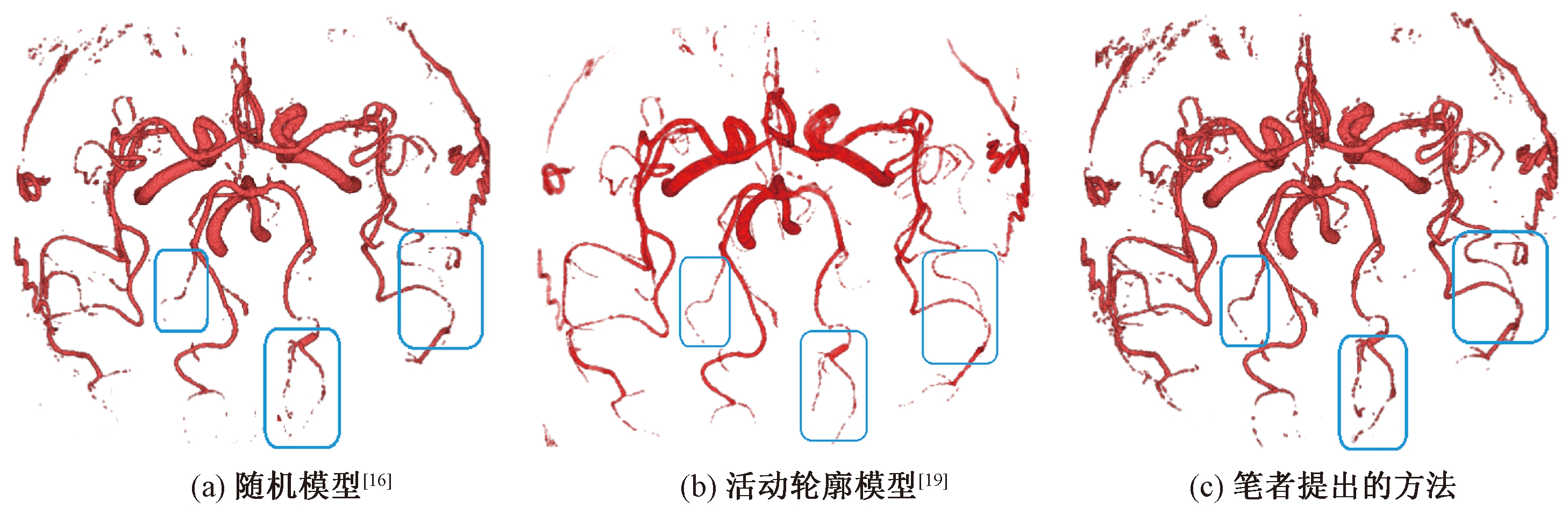
图5 3种方法的分割效果
Fig.5 Extraction results comparison among three method
图6给出了13套数据的3种方法的DSC的对比结果.笔者所提方法的DSC平均在80% 以上,有的数据甚至达到了94%,比传统统计模型的结果平均高出10.7%,比活动轮廓模型的结果高出8.5%.传统有限混合模型仅基于数据的密度值而并没有考虑像一阶导数等其他因素,且依赖于混合模型的选择.活动轮廓模型将密度与梯度等参数融合至统一的能量函数,其分割结果要比有限混合模型的效果好,尤其是在细小血管分支的连续性方面有较为明显的提高.但活动轮廓模型对整个体数据同时应用密度和梯度值.而笔者的算法是在前一步密度处理结果的基础上运用梯度进行血管边缘的提取,因此在细小血管分支的连续性及血管的边缘方面优于活动轮廓模型.
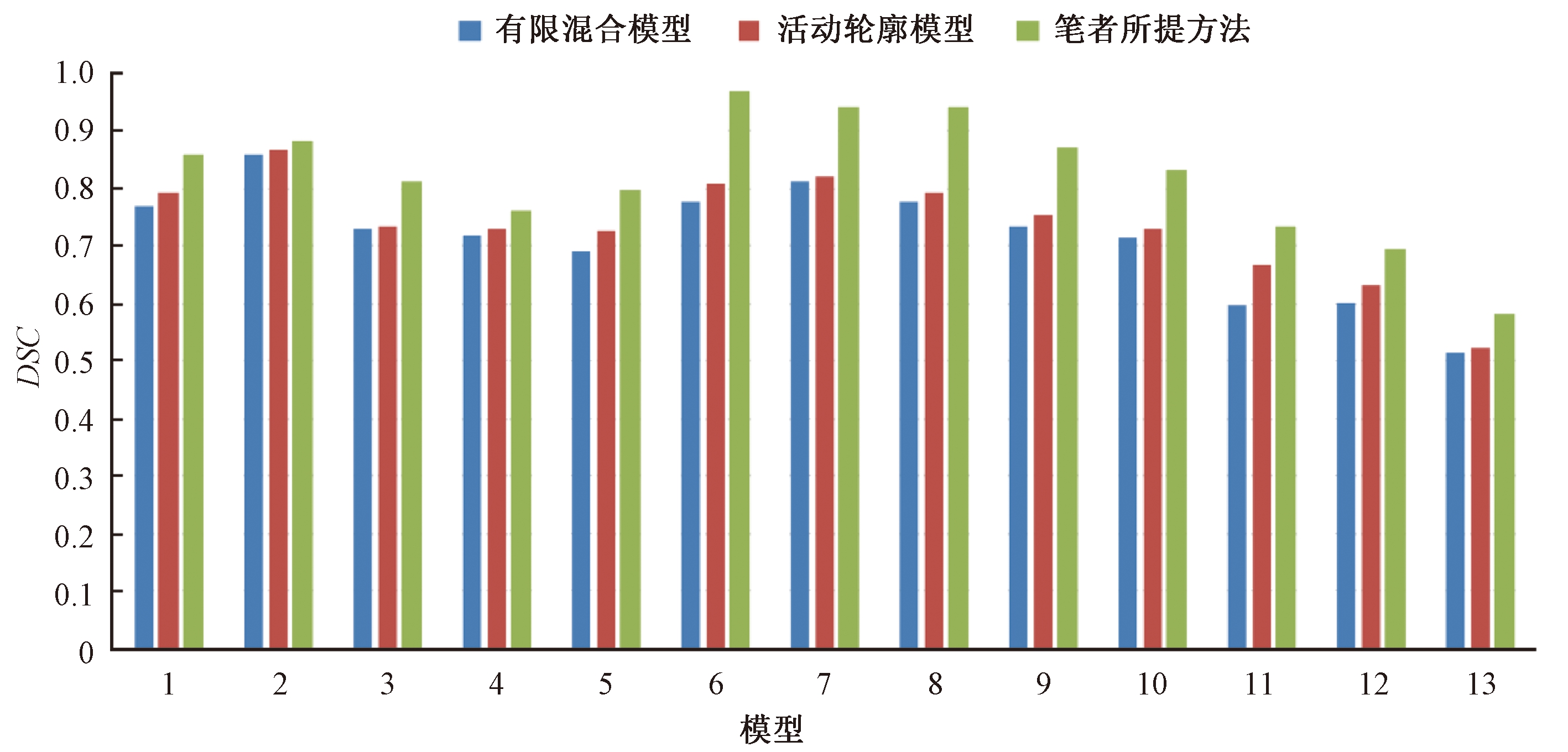
图6 3种方法相似性系数DSC的比较
Fig.6 DSC comparison among three methods
3 结论
笔者在有限混合模型的血管分割基础上,提出了一种基于自适应聚类中心的K均值梯度聚类方法.该方法首先使用瑞利-高斯混合模型的方法对时间飞跃法磁共振血管成像数据建模,并采用期望最大参数估计的方法获取混合模型的参数,进而利用后验概率提取出血管的主体部分;随后对剩余体素数据进行梯度化处理,并采用改进的K均值聚类方法在剩余梯度数据中提取出血管的边缘以及细小血管部分,将两部分结果合并进行可视化处理便可得到血管的三维结构.实验结果表明,笔者进一步采用基于改进自适应聚类中心的梯度聚类方法,不管从视觉上还是精确度上,分割结果在血管的细节部分都有较为明显的改善.在下一步的研究工作中,笔者将融合更多血管几何形态特征,进一步提高血管分割的精度.
[1] FORKERT N D, SARING D, FIEHLER J, et al. Automatic brain segmentation in time-of-flight MRA images[J]. Methods of information in medicine, 2009, 48(5):399-407.
[2] ZHAO S, ZHOU M, TIAN Y, et al. Extraction of vessel networks based on multiview projection and phase field model[J]. Neurocomputing, 2015, 162:234-244.
[3] KASS M, WITKIN A, TERZOPOULOS D. Snakes: Active contour models[J]. International journal of computer vision, 1988, 1(4):321-331.
[4] CASELLES V, COLL T. A geometric model for active contours in image processing[J]. Numerische mathematik, 1993, 66(1):1-31.
[5] VASILEVSKIY A, SIDDIQI K. Flux maximizing geometric flows[J].IEEE transactions on pattern analysis and machine intelligence, 2003,24(12):1565-1568.
[6] LI C M, XU C Y, FOX M D. Level set evolution without re-initialization: a new variational formulation[C]//Proceedings of the 2005 IEEE computer society conference on computer vision and pattern recognition. Washington D C: IEEE, 2005:430-436.
[7] CHAN T F, VESE L A. Active contour without edges[J]. IEEE transactions on image processing, 2001, 10(2):266-277.
[8] SHANG Y, YANG X, ZHU L, et al. Region competition based active contour for medical object extraction[J]. Computerized medical imaging & graphics, 2008, 32(2):109-117.
[9] SUM K W, CHEUNG P Y S. Vessel extraction under non-uniform illumination: a level set approach[J]. IEEE transactions on biomedical engineering, 2008, 55(1):358.
[10] LANKTON S, TANNENBAUM A. Localizing region-based active contours[J]. IEEE transactions on image processing, 2008, 17(11):2029-2039.
[11] TIAN Y, DUAN F, et al. Active contour model combining region and edge information[J]. Machine vision & applications, 2013, 24(1):47-61.
[12] ZHAO S F, ZHOU M Q, JIA T R, et al. Multi-branched cerebrovascular segmentation based on phase-field and likelihood model[J]. Computers & graphics, 2014, 38:239-247.
[13] OSHER S, SETHIAN J A. Fronts propagating with curvature-dependent speed: algorithms based on Hamilton-Jacobi formulations[J]. Journal of computational physics, 1988, 79(1):12-49.
[14] EL-BAZ A, FARAG A, GIMELFARB G. Cerebrovascular segmentation by accurate probabilistic modeling of TOF-MRA images[C]//Proceding of the 14th Scandinavian Conferrence on Image Analysis. Berlin, Heidelberg: Springer, 2014:239-247.
[15] WONG W C K, CHUNG A C S. Bayesian image segmentation using local iso-intensity structural orientation[J]. IEEE transactions on image processing, 2005, 14(10):1512-1523.
[16] HASSOUNA M S, FARAG A A, HUSHEK S, et al. Cerebrovascular segmentation from TOF using stochastic models[J]. Medical image analysis, 2006, 10(1):2-18.
[17] ROY S, CARASS A, BAZIN P L, et al. Consistent segmentation using a rician classifier[J]. Medical image analysis, 2012, 16(2):524-535.
[18] GAO X, UCHIYAMA Y, ZHOU X R, et al. A fast and fully automatic method for cerebrovascular segmentation on time-of-flight (TOF) MRA image[J]. Journal of digital imaging, 2011, 24(4):609-625.
[19] TIAN Y, DUAN F, LU K, et al. A flexible 3D cerebrovascular extraction from TOF-MRA images[J]. Neurocomputing, 2013, 121(18):392-400.